高二数学经典例题 (50)
(完整版)高二数学归纳法经典例题

例1.用数学归纳法证明:()()1212121751531311+=+-++⨯+⨯+⨯n n n n . 请读者分析下面的证法:证明:①n =1时,左边31311=⨯=,右边31121=+=,左边=右边,等式成立. ②假设n =k 时,等式成立,即:()()1212121751531311+=+-++⨯+⨯+⨯k k k k . 那么当n =k +1时,有:()()()()3212112121751531311++++-++⨯+⨯+⨯k k k k ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+-++⎪⎭⎫ ⎝⎛+--++⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-=3211211211217151513131121k k k k 322221321121++⋅=⎪⎭⎫ ⎝⎛+-=k k k ()1121321+++=++=k k k k 这就是说,当n =k +1时,等式亦成立.由①、②可知,对一切自然数n 等式成立.评述:上面用数学归纳法进行证明的方法是错误的,这是一种假证,假就假在没有利用归纳假设n =k 这一步,当n =k +1时,而是用拆项法推出来的,这样归纳假设起到作用,不符合数学归纳法的要求.正确方法是:当n =k +1时.()()()()3212112121751531311++++-++⨯+⨯+⨯k k k k ()()3212112++++=k k k k ()()()()()()321211232121322++++=++++=k k k k k k k k()1121321+++=++=k k k k 这就说明,当n =k +1时,等式亦成立,例2.是否存在一个等差数列{a n },使得对任何自然数n ,等式:a 1+2a 2+3a 3+…+na n =n (n +1)(n +2)都成立,并证明你的结论.分析:采用由特殊到一般的思维方法,先令n =1,2,3时找出来{a n },然后再证明一般性. 解:将n =1,2,3分别代入等式得方程组.⎪⎩⎪⎨⎧=++=+=60322426321211a a a a a a , 解得a 1=6,a 2=9,a 3=12,则d =3.故存在一个等差数列a n =3n +3,当n =1,2,3时,已知等式成立.下面用数学归纳法证明存在一个等差数列a n =3n +3,对大于3的自然数,等式a 1+2a 2+3a 3+…+na n =n (n +1)(n +2)都成立.因为起始值已证,可证第二步骤.假设n =k 时,等式成立,即a 1+2a 2+3a 3+…+ka k =k (k +1)(k +2)那么当n =k +1时,a 1+2a 2+3a 3+…+ka k +(k +1)a k +1= k (k +1)(k +2)+ (k +1)[3(k +1)+3]=(k +1)(k 2+2k +3k +6)=(k +1)(k +2)(k +3)=(k +1)[(k +1)+1][(k +1)+2]这就是说,当n =k +1时,也存在一个等差数列a n =3n +3使a 1+2a 2+3a 3+…+na n =n (n +1)(n +2)成立. 综合上述,可知存在一个等差数列a n =3n +3,对任何自然数n ,等式a 1+2a 2+3a 3+…+na n =n (n +1)(n +2)都成立.例3.证明不等式n n 2131211<++++ (n ∈N).证明:①当n =1时,左边=1,右边=2.左边<右边,不等式成立.②假设n =k 时,不等式成立,即k k 2131211<++++ .那么当n =k +1时,11131211++++++k k1112112+++=++<k k k k k ()()12112111+=++=++++<k k k k k k这就是说,当n =k +1时,不等式成立.由①、②可知,原不等式对任意自然数n 都成立.说明:这里要注意,当n =k +1时,要证的目标是1211131211+<++++++k k k ,当代入归纳假设后,就是要证明: 12112+<++k k k .认识了这个目标,于是就可朝这个目标证下去,并进行有关的变形,达到这个目标.例4.已知数列{a n }满足a 1=0,a 2=1,当n ∈N 时,a n +2=a n +1+a n .求证:数列{a n }的第4m +1项(m ∈N )能被3整除.分析:本题由a n +1=a n +1+a n 求出通项公式是比较困难的,因此可考虑用数学归纳法.①当m =1时,a 4m +1=a 5=a 4+a 3=(a 3+a 2)+(a 2+a 1)=a 2+a 1+a 2+a 2+a 1=3,能被3整除.②当m =k 时,a 4k +1能被3整除,那么当n =k +1时,a 4(k +1)+1=a 4k +5=a 4k +4+a 4k +3=a 4k +3+a 4k +2+a 4k +2+a 4k +1=a 4k +2+a 4k +1+a 4k +2+a 4k +2+a 4k +1=3a 4k +2+2a 4k +1由假设a 4k +1能被3整除,又3a 4k +2能被3整除,故3a 4k +2+2a 4k +1能被3整除.因此,当m =k +1时,a 4(k +1)+1也能被3整除.由①、②可知,对一切自然数m ∈N ,数列{a n }中的第4m +1项都能被3整除.例5.n个半圆的圆心在同一条直线l上,这n个半圆每两个都相交,且都在直线l的同侧,问这些半圆被所有的交点最多分成多少段圆弧?分析:设这些半圆最多互相分成f (n)段圆弧,采用由特殊到一般的方法,进行猜想和论证.当n=2时,由图(1).两个半圆交于一点,则分成4段圆弧,故f (2)=4=22.当n=3时,由图(2).三个半径交于三点,则分成9段圆弧,故f (3)=9=32.由n=4时,由图(3).三个半圆交于6点,则分成16段圆弧,故f (4)=16=42.由此猜想满足条件的n个半圆互相分成圆弧段有f (n)=n2.用数学归纳法证明如下:①当n=2时,上面已证.②设n=k时,f (k)=k2,那么当n=k+1时,第k+1个半圆与原k个半圆均相交,为获得最多圆弧,任意三个半圆不能交于一点,所以第k+1个半圆把原k个半圆中的每一个半圆中的一段弧分成两段弧,这样就多出k条圆弧;另外原k个半圆把第k+1个半圆分成k+1段,这样又多出了k+1段圆弧.∴ f (k+1)=k2+k+(k+1)=k2+2k+1=(k+1)2∴满足条件的k+1个半圆被所有的交点最多分成(k+1)2段圆弧.由①、②可知,满足条件的n个半圆被所有的交点最多分成n2段圆弧.说明:这里要注意;增加一个半圆时,圆弧段增加了多少条?可以从f (2)=4,f (3)=f (2)+2+3,f (4)=f (3)+3+4中发现规律:f (k+1)=f (k)+k+(k+1).。
高二数学数列的经典例题

高二数学数列的经典例题
例题一:等差数列的通项公式
已知等差数列{an} 的首项a1 = 1,公差 d = 2,求第n 项的通项公式。
解:根据等差数列的通项公式,我们有:
an = a1 + (n - 1)d
将已知条件代入公式,得:
an = 1 + (n - 1) * 2
化简得:
an = 2n - 1
例题二:等比数列的求和公式
已知等比数列{bn} 的首项b1 = 2,公比q = 3,求前n 项和Sn。
解:根据等比数列的求和公式,我们有:
Sn = b1 * (1 - q^n) / (1 - q)
将已知条件代入公式,得:
Sn = 2 * (1 - 3^n) / (1 - 3)
化简得:
Sn = (3^n - 1)
例题三:数列的综合应用
已知数列{cn} 满足c1 = 1,且对任意的n ∈ N*,都有cn+1 = 2cn + 1,求数列{cn + 1} 的前n 项和Tn。
解:首先,我们将给定的递推关系式进行变形:
cn+1 + 1 = 2(cn + 1)
这说明数列{cn + 1} 是一个等比数列,其首项为c1 + 1 = 2,公比为2。
然后,我们利用等比数列的求和公式来求{cn + 1} 的前n 项和Tn:
Tn = (c1 + 1) * (1 - 2^n) / (1 - 2)
代入已知条件,得:
Tn = 2 * (2^n - 1)
化简得:
Tn = 2^(n+1) - 2。
高二数学第一学期 能力训练(50)

1.设集合,}2,1{=A ,}4,3,2{=B ,则 )(B A U 等于( )A .}2{B .}5{C .}4,3,2,1{D .}5,4,3,1{2.若222x y x y ≤⎧⎪≤⎨⎪+≥⎩,则目标函数 z = x + 2 y 的取值范围是 ( )A .[2 ,6]B . [2,5]C . [3,6]D . [3,5]3.甲,乙,丙三名运动员在某次测试中各射击20次,三人测试成绩的频率分布条形图分别如图1,图2和图3,若甲s ,乙s ,丙s 分别表示他们测试成绩的标准差,则( )A .丙乙甲s s s <<B .乙丙甲s s s <<C .丙甲乙s s s <<D .乙甲丙s s s <<4.某工厂生产A 、B 、C 三种不同型号的产品,产品数量之比依次为2:3:5.现用分层抽样的方法抽出一个容量为n 的样本,样本中A 种型号的产品共有16件,那么此n =( )A .80B .90C . 100D .1205.以(5,6)和(3,-4)为直径端点的圆的方程是( )A .072422=+-++y x y xB .064822=-+++y x y x C .092822=---+y x y x D . 052422=-+-+y x y x 6.在一次数学测验中,统计7名学生的成绩分布茎叶图如右图所示,若这7名学生的平均成绩为77分,则x 的值为( )A.5B.6C.7D.87.已知向量(3,4),(sin ,cos ),a b αα==且a ∥b ,则αtan = ( )A .34-B . 34C .34D .34- 8.若函数f (x )=sin ωx +cos ωx (ω>0)的最小正周期为π,则它的图象的一个对称中心为( )A .(0,0) B.)(0,8πC .)—(0,8πD .)—(0,4π9.数列}{n a 的前n 项和为S n ,若32()n n S a n N =+∈*,则这个数列一定是( )A .等比数列B .等差数列C .从第二项起是等比数列D .从第二项起是等差数列10.方程3)2(42+-=-x k x 有两个不等实根,则k 的取值范围是( )A .)125,0(B .]43,31[C .),125(+∞D .]43,125(答案:。
高二数学经典例题

一. 设方程x 2+kx +2=0的两实根为p 、q ,若(p q)2+(q p)2≤7成立,求实数k 的取值范围。
二. 已知.))((,1,0,xy bx ay by ax b a b a ≥++=+>求证:且三. 求经过点)1,2(-A ,和直线1=+y x 相切,且圆心在直线x y 2-=上的圆的标准方程.四. 设422+-=x y z ,式中变量y x , 满足条件⎪⎩⎪⎨⎧≥-≤≤≤≤122010x y y x ,求z 的最小值和最大值.五. 若M 为直线032:=+-y x l 上的一点,A (4,2)为一定点,又点P 在直线AM 上运动,且,3=PMAP 求动点P 的轨迹方程.六. 如图, 直线y=21x 与抛物线y=81x 2-4交于A 、B 两点, 线段AB 的垂直平分线与直线y=-5交于Q 点.(1)求点Q 的坐标;(2)当P 为抛物线上位于线段AB 下方(含A 、B )的动点时, 求ΔOPQ 面积的最大值.(本小题14分)七.P 为椭圆192522=+yx上一点,1F 、2F 为左右焦点,若︒=∠6021PF F(1)求△21PF F 的面积;(2)求P 点的坐标.(本小题12分) 配方法1. 在正项等比数列{a n }中,a 1♦a 5+2a 3♦a 5+a 3∙a 7=25,则 a 3+a 5=_______。
3. 已知sin 4α+cos 4α=1,则sin α+cos α的值为______。
A. 1 B. -1 C. 1或-1 D. 0 4. 函数y =log 12(-2x 2+5x +3)的单调递增区间是_____。
A. (-∞, 54]B. [54,+∞)C. (-12,54]D. [54,3)例1. 设非零复数a 、b 满足a 2+ab +b 2=0,求(a a b+)1998+(b a b+)1998 。
换元法1.y =sinx ·cosx +sinx+cosx 的最大值是_________。
高二常考的三角函数的试题整理

高二常考的三角函数的试题整理经典数学题【例一】1.(2009·江苏常州一模)已知角α是第三象限角,则角-α的终边在第________象限. 2.(2010·连云港模拟)与610°角终边相同的角表示为______________.1sin 2θ3.(2010·浙江潮州月考)已知2<1,则θ所在象限为第________象限.π3π4.(2010·南通模拟)已知角θ的终边经过点P(-4cos α,3cos α)(<α<,则sin θ+cos θ=________.22ππ-且sin θ+cos θ=a,其中a∈(0,1),则关于tan θ的值,以下四个答案中,可能正5.(2010·福州调研)已知θ∈22111确的是________(填序号).①-3 ②3或③- ④-3或-3336.(2009·江西九江模拟)若角α的终边与直线y=3x重合且sin α<0,又P(m,n)是角α终边上一点,且|OP|10,则m-n=________.|sin α||cos α|7.(2010·山东济南月考)已知角α的终边落在直线y=-3x (x<0)上,则=________.sin αcos α8.(2010·南京模拟)某时钟的秒针端点A到中心点O的距离为5 cm,秒针均匀地绕点O旋转,当时间t=0时,点A与钟面上标12的点B重合.将A、B两点间的距离d(cm)表示成t(s)的函数,则d=________,其中t∈[0,60].π49.(2010·泰州模拟)若0”,“<”或“=”填空).2π210.(2010·镇江模拟)已知角θ的终边上一点P(3,m),且sin θm,求cos θ与tan θ的值.411.(2010·江苏南京模拟)在单位圆中画出适合下列条件的角α的终边的范围,并由此写出角α的集合:31(1)sin α;(2)cos α.2212.(2010·佳木斯模拟)角α终边上的点P与A(a,2a)关于x轴对称(a≠0),角β终边上的点Q与A关于直线y=x对称,求sin α·cos α+sinβ·cosβ+tan α·tan β的值.同角三角函数的基本关系及诱导公式1.(2010·南通模拟)cos(-174-sin(-174π)的值为___________________________.2.(2010·江苏镇江一模)设tan(5π+α)=m,则sin(α-3π)+cos(π-α)sin(-α)-cos(π+α)的值为__________.3.(2009·辽宁沈阳四校联考)已知sin α+cos αsin α-cos α=2,则sin αcos α=________.4.(2008·浙江理,8)若cos α+2sin α=-,则tan α=__________.5.(2008·四川理,5)设0≤α<2π,若sin α3cos α,则α的取值范围是____________.6.(2010·吉林长春调研)若sin α+cos α=tan α0<α<π2,则α的取值范围是__________. 7.(2009·苏州二模)sin21°+sin22°+sin23°+…+sin289°=________.8.(2010·浙江嘉兴月考)已知f(x)= 1-xπ1+xα∈(2,π),则f(cos α)+f(-cos α)=________.9.(2009·北京)若sin θ=-45tan θ>0,则cos θ=____________________________________.10.(2010·泰州模拟)化简:(1)1-cos4α-sin4α1-cosα-sinα2sin(π4x)+6cos(π; 4-x).11.(2010·盐城模拟)已知sin22α+sin 2αcos α-cos 2α=1,α∈(0,π2),求sin α、tan α的值.12.(2009·福建宁德模拟)已知0<α<π52sin αcos α-cos α+12cos α-sin α=-5,试求1-tan α和差倍角的三角函数1.(2010·山东青岛模拟)cos 43°cos 77°+sin 43°·cos 167°的值为________. 2.(2010·南京模拟)已知α、β均为锐角,且cos(α+β)=sin(α-β),则tan α=________.3.(2009·湖北四校联考)在△ABC中,3sin A+4cos B=6,4sin B+3cos A=1,则∠C的大小为________.4.(2009·湖南长沙调研)在锐角△ABC中,设x=sin A·sin B,y=cos A·cos B,则x,y的大小关系是________.5.(2009·广东韶关模拟)已知tan α=2,则sin 2α-cos 2α1+cosα________.6.(2010·无锡模拟)1+tan x1-tan x2 010,则1cos 2x+tan 2x的值为________.7.(2010·苏州调研)若锐角α、β满足(1+3tan α)·(13tan β)=4,则α+β=________. 8.(2009·江苏南通二模)已知sin αcos β=12,则cos αsin β的取值范围是____________.9.(2010·苏、锡、常、镇四市调研)若tan(α+β)=2π1π5,tan(β-4)=4,则tan(α+4=________.10.(2008·广东)已知函数f(x)=Asin(x+φ) (A>0,0<φ<π) (x∈R)的最大值是1,其图象经过点Mπ13,2. (1)求f(x)的解析式;(2)已知α、β∈0,π2,且f(α)=3125,f(β)=13,求f(α-β)的值.11.(2010·宿迁模拟)已知向量a=(cos α,sin α),b=(cos β,sin β),|a-b|=41313(1)求cos(α-β)的值;(2)若0<α<π2,-π42β<0,且sin β=-5,求sin α的值.三角函数的图象与性质1.(2009·大连一模)y=sin(2x+π6)的最小正周期是_____________________________.2.(2010·扬州模拟)y=2-cos__________,此时x=________.3π3.(2010·盐城模拟)函数y=tan(x)的定义域是________________.4.(2009·牡丹江调研)已知函数y=2cos x(0≤x≤1 000π)的图象和直线y=2围成一个封闭的平面图形,则这个封闭图形的面积是________5.(2010·江苏盐城月考)已知函数y=tan ωx在(-,内是减函数,则ω的取值范围是________________.7.(2009·浙江宁波检测)定义在R上的函数f(x)既是偶函数又是周期函数,若f(x)的最小正周8.(2010·连云港模拟)sin 2,cos 1,tan 2的大小顺序是________________.9.(2008·全国Ⅱ理)若动直线x=a与函数f(x)=sin x和g(x)=cos x的图象分别交于M、N两点,则|MN|的最大值为_______.11.(2008·陕西)已知函数f(x)=2sincos+3cos.12.(2010·山东济宁第一次月考)设a=sin2b. ,cos x+sin x,b=(4sin x,cos x-sin x),f(x)=a·4(1)求函数f(x)的解析式(3)设集合A=x6x≤3,B={x||f(x)-m|<2},若A⊆B,求实数m的取值范围.三角函数的`最值及应用1.(2010·连云港模拟)函数y3sin(2x)-cos 2x的最小值为________.2.(2010·泰州模拟)若函数y=2cos ωx在区间[0,上递减,且有最小值1,则ω的值可以是________.3.(2010·湖北黄石调研)设函数f(x)=2sin(+.若对任意x∈R,都有f(x1)≤f(x)≤f(x2)成立,则|x1-x2|的最小值为____.4.(09·湖南株州模拟)函数y=sin 2x按向量a平移后,所得函数的解析式是y=cos 2x+1,则模最小的一个向量a=__.5.(2009·广东惠州二模)函数y=Asin(ωx+φ)(ω>0,|φ|<在同一单调区间内的x=x29291小值-________________________.2a+b,ab≤0,6.(2010·广西南宁检测)定义运算a*b=a则函数f(x)=(sin x)*(cos x)的最小值为________., ab>0,b7.(2010·苏州调研)一半径为10的水轮,水轮的圆心距水面7,已知水轮每分钟旋转4圈,水轮上点P到水面距离y与时间x(s)满足函数关系y=Asin(ω+φ)+7(A>0,ω>0),则A=________,ω=________. 8.(2009·徐州二模)函数y=(sin x-a)2+1,当sin x=a时有最小值,当sin x=1时有最大值,则a的取值范围是_______. 9.(2009·江苏)函数y=Asin(ωx+φ)(A、ω、φ为常数,A>0,ω>0)在闭区间[-π,0]上的图象如图所示,则ω=10.(2010·镇江模拟)已知函数f(x)=cos(2ωx+2φ) (A>0,ω>0,0<φ<),且y=f(x)的最大值为2,其图象上相邻两对称轴间的距离为2,并过点(1,2).(1)求φ;(2)计算f(1)+f(2)+…+f(2 008).11.( 10·辽宁瓦房店月考)如图所示,某地一天从6时到14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b. (1)求这段时间的最大温差; (2)写出这段曲线的函数解析式.12.(2010·吉林延吉模拟)如图,在一个奥运场馆建设现场,现准备把一个半径为3 m的球形工件吊起平放到6 m高的平台上,工地上有一个吊臂长DF=12 m的吊车,吊车底座FG高1.5 m.当物件与吊臂接触后,钢索CD的长可通过顶点D处的滑轮自动调节并保持物件始终与吊臂接触.求物件能被吊车吊起的最大高度,并判断能否将该球形工件吊到平台上?解三角形1.(2010·江苏靖江调研)在△ABC中,若(a+b+c)(b+c-a)=3bc,则A=________.2.(2010·宿迁模拟)在△ABC中,已知acos A=bcos B,则△ABC的形状为____________. 3.(2010·江苏淮阴模拟)如果把直角三角形的三边都增加同样的长度,则这个新的三角形的形状为____________. 4.(2010·浙江绍兴模拟)△ABC中,a,b,c分别为∠A,∠B,∠C的对边,如果a,b,c成等差数列,∠B=30°,△ABC的面积为,那么b=__________.25b,A=2B,则cos B=________. 26.(2010·南通模拟)一船以每小时15 km的速度向东航行,船在A处看到一个灯塔M在北偏东60°方向,行驶4 h后,船到达B处,看到这个灯塔在北偏东15°方向,这时船与灯塔的距离为________km.7.(2009·福建泉州二模)如图所示,我炮兵阵地位于地面A处,两观察所分别位于地面C处和D处,已知CD=6 000 m,∠ACD=45°,∠ADC=75°,目标出现于地面B处时测得∠BCD=30°,∠BDC=15°,则炮兵阵地到目标的距离是________________(结果保留根号).8.(2009·江西宜泰模拟)线段AB外有一点C,∠ABC=60°,AB=200 km,汽车以80 km/h的速度由A向B行驶,同时摩托车以50 km/h的速度由B向C行驶,则运动开始____ h后,两车的距离最小. 9.(2009·广东改编)已知△ABC中,∠A、∠B、∠C的对边分别是a、b、c,若a=c=6+2,且∠A=75°,则b=________.10.(2009·安徽)在△ABC中,C-A=sin B=23(1)求sin A的值;(2)设AC=6,求△ABC的面积.11.(2009·山东泰安第二次月考)在海岸A处,发现北偏东45°方向,距A处3-1)海里的B处有一艘走私船,在A处北偏西75°方向,距A处2海里的C处的缉私船奉命以103海里/小时的速度追截走私船,此时走私船正以10海里/小时的速度从B处向北偏东30°的方向逃窜,问缉私船沿什么方向能最快追上走私船,并求出所需要的时间.5.(2008·四川,7)△ABC的三内角A、B、C的对边边长分别为a、b、c.若a=三角函数的综合应用1.(2009·济宁期末)已知a=(cos 2α,sin α),b=(1,2sin α-1),α∈π),若a·b=,则25πtan(α+的值为________.2.(2008·江苏)若AB=2,AC2BC,则S△ABC的最大值是________.3.(2009·肇庆期末)定义运算a*b=a2-ab-b2,则sin=________.4.(2009·广州第二次联考)已知a,b,x,y∈R,a2+b2=4,ax+by=6,则x2+y2的最小值为________.5.(2010·宿州模拟)若函数f(x)=sin(x+α)-2cos(x-α)是偶函数,则cos2α=________.6.(2010·泰州调研)函数f(x)=(sin2x+(cos2x+)的最小值是________. 2 009sinx2 009cosx7.(2009·福建文)已知锐角△ABC的面积为33,BC=4,CA=3,则角C的大小为________.8.(2010·苏南四市模拟)俗话说“一石激起千层浪”,小时候在水上打“水漂”的游戏一定不会忘记吧.现在一个圆形2π波浪实验水池的中心已有两个振动源,在t秒内,它们引发的水面波动可分别由函数y1=sin t和y2=sin(t+来描3述,当这两个振动源同时开始工作时,要使原本平静的水面保持平静,则需再增加一个振动源(假设不计其他因素,则水面波动由几个函数的和表达),请你写出这个新增振动源的函数解析式______________. 9.(2010·南通模拟)2002年在北京召开的国际数学家大会,会标是以我国古代数学家赵爽的弦图为基础设计的.弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形(如图).如果小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为θ,那么cos 2θ的值等于____________.经典数学题【例二】知识考点:本节知识的考查一般以填空题和选择题的形式出现,主要考查锐角三角函数的意义,即运用sina、cosa、tana、cota准确表示出直角三角形中两边的比(a为锐角),考查锐角三角函数的增减性,特殊角的三角函数值以及互为余角、同角三角函数间的关系。
高二数学选择题(50题含答案)

1、若a<1,那么那么 ( )(A )a1>1, (B)|a|<1, (C)a 2<1, (D)a 3<1 2、若a,b 为实数,且a+b=2,则3a +3b的最小值为(的最小值为() (A )18, (B )6, (C )23, (D )243 3、与不等式xx --23≥0同解的不等式是同解的不等式是 ( ) (A )(x-3)(2-x)≥0, (B)0<x-2≤1, (C)32--x x ≥0, (D)(x-3)(2-x)>0 4、直线3x+2y+6=0的斜率为k ,在y 轴上的截距为b ,则,则 ( )(A)k=-23,b=3 (B)k=,b=3 (B)k=--32,b=-2 (C)k=(C)k=--23,b=-3 (D) k=,b=-3 (D) k=--32,b=-3 5、如果直线ax+2y+2=0与直线3x-y-2=0平行,那么a 等于等于 ( ) (A )-)-33, (B )-)-66, (C )-23, (D )32 6、已知L 1:x :x––3y+7=0, L 2:x+2y+4=0, :x+2y+4=0, 下列说法正确的是下列说法正确的是下列说法正确的是 (( )) (A )L 1到L 2的角为p 43, ((B )L 1到L 2的角为4p(C )L 2到L 1的角为43p , ((D )L 1到L 2的夹角为p 43 7、和直线3x 3x––4y+5=0关于x 轴对称的直线方程是轴对称的直线方程是 (( ))(A )3x+4y 3x+4y––5=0, (B)3x+4y+5=0, (C)-3x+4y (C)-3x+4y––5=0, (D)-3x+4y+5=08、直线y=x+23被曲线y=21x2截得线段的中点到原点的距离是( )(A )29 (B )29 (C )429 (D )229 9、直线y=x –1上的点到圆x 2+y 2+4x –2y+4=0上的点的最近距离是上的点的最近距离是 ( ) (A )22 (B )2-1-1 (C )22-1-1 (D )1 10、椭圆252x +92y =1上一点p 到一个焦点的距离为5,则p 到另一个焦点的距离为(到另一个焦点的距离为( )(A )5 (B )6 (C )4 (D )10 11、双曲线:、双曲线:的准线方程是191622=-x y ( )(A)y=±716 (B)x= (B)x=±±516 (C)X= (C)X=±±716(D)Y= (D)Y=±±516 1212、抛物线:、抛物线:、抛物线:y=4ax y=4ax 2的焦点坐标为的焦点坐标为 ( ) (A )(a41,0) ((B )(0, a161) (C)(0, -a161) (D) (a161,0)13、下列命题中为真命题的是(下列命题中为真命题的是( )A .若11x y=,则x y =. B .若21x =,则1x =.C .若x y =,则x y =. D .若x y <,则22x y <. 14、已知00<<<<d c b a ,,那么下列判断中正确的是(,那么下列判断中正确的是( )A .ac b d -<- B .a c b d >C . a d bc< D .a d b c > 15、设变量x ,y 满足约束条件:3123x y x y x y +³ìï-³-íï-£î.则目标函数z=2x+3y 的最小值为的最小值为(A )6 (B )7 (C )8 (D )23 16、 在ΔABC 中, 角A 、B 、C 的对边分别为a 、b 、c , 已知A =3p, 3=a , 1=b ,则=c ( ) A .1 B .2 C .3-1 D .317、已知方程22111x y k k-=+-表示双曲线,则k 的取值范围是(的取值范围是( ) A .11k -<< B .0k > C .0k ³ D .11k k ><-或18、一元二次方程2210(0),ax x a ++=¹有一个正根和一个负根的充分不必要条件是(有一个正根和一个负根的充分不必要条件是( ) A .0a < B .0a > C .1a <- D .1a >19、若双曲线122=-y x 的右支上一点P (a ,b ,b)到直线)到直线x y =的距离为a 则,2+b 的值(的值( ))A .21-B .21 C .-.-2 2 D .220、如图F 1,F 2分别是椭圆22221(0,0)x y a b a b +=>>的两个焦点,A 和B 是以O 为圆心,以1OF 为半径的圆与该左半椭圆的两个交点,且2F AB D 是等边三角形,则椭圆的离心率为:是等边三角形,则椭圆的离心率为:A .32 B .12 C .22D .31-2121、数列、数列{a n }的通项公式是a n =2n -12n ,其前n 项和S n =32164,则项数n = A .13 B .10 C .9 D .6 22、在ABC D 中,若cos a B c =,则ABC D 的形状一定是(的形状一定是( )A .锐角三角形.锐角三角形B B B.钝角三角形.钝角三角形.钝角三角形C C C.直角三角形.直角三角形.直角三角形D D D.等腰三角形.等腰三角形.等腰三角形2323、已知数列、已知数列{a n }的通项公式为a n =log 2n +1n +2(n ∈N *),设其前n 项和为S n ,则使S n <-5成立的自然数n A .有最大值63 B .有最小值63 C .有最大值32 D .有最小值32 24、设过点()y x P ,的直线分别与x 轴的正半轴和y 轴的正半轴交于A 、B 两点,点Q 与点P 关于y 轴对称,O 为坐标原点,若PA BP 2=,且1=×AB OQ ,则P 点的轨迹方程是(点的轨迹方程是( )A. ()0,0132322>>=+y x y x B. ()0,0132322>>=-y x y xC. ()0,0123322>>=-y x y x D. ()0,0123322>>=+y x y x25.在回归直线方程表示回归系数中b bx a y,ˆ+= ( )A .当0x =时,y 的平均值的平均值B .当x 变动一个单位时,y 的实际变动量的实际变动量C .当y 变动一个单位时,x 的平均变动量D .当x 变动一个单位时,y 的平均变动量的平均变动量26.下面几种推理是类比推理的是下面几种推理是类比推理的是 ( ) A .两条直线平行,同旁内角互补,如果A Ð和B Ð是两条平行直线的同旁内角,则是两条平行直线的同旁内角,则 180=Ð+ÐB AB .由平面向量的运算性质,推测空间向量的运算性质.由平面向量的运算性质,推测空间向量的运算性质C .某校高二级有20个班,1班有51位团员,2班有53位团员,3班有52位团员,由此可以推测各班都超过50位团员位团员 D .一切偶数都能被2整除,1002是偶数,所以1002能被2整除整除27.若,1a >则1a 1a -+的最小值是的最小值是( )A .2 B .aC .3 D .1a a2- 28.在对分类变量X, Y 进行独立性检验时,算得k 2=7有以下四种判断有以下四种判断(1) 有99﹪的把握认为X 与Y 有关;(2)有99﹪的把握认为X 与Y 无关;(3)在假设H 0:X 与Y 无关的前提下有99﹪的把握认为X 与Y 有关;(4)在假设H 1: : X X 与Y 有关的前提下有99﹪的把握认为X 与Y 无关.以上4个判断正确的是正确的是( ) A . (1)、(2) B . (1)、(3) C . (2)、(4) D . (3)、(4) A B C D I H G F E 4 3 1 2 3 1 2 3 2 3 2 4 1 1 3 5 29.不等式0)1)(1(>-+x x 的解集是的解集是( )A .{}10<£x xB .{}1,0-¹<x x xC .{}11<<-x xD .{}1,1-¹<x x x 30.已知c b a <<,且0=++c b a ,则ac b 42-的值的值( )A .大于零.大于零B .小于零.小于零C .不大于零.不大于零D .不小于零.不小于零31.把一块边长是a 的正方形铁片的各角切去大小相同的小正方形,再把它的边沿着虚线折转成一个无盖方底的盒子,盒子的容积最大时,切去的正方形边长是方底的盒子,盒子的容积最大时,切去的正方形边长是 ( ) A .3aB .4aC .5aD .6a32.的最小值求且已知y x x a R b a y x +=+Î+1,y b ,,,, ( )A .b a +B .ba 11+C .b a +D . 2)(b a +33.如图,第n 个图形是由正n+2边形“扩展”而来,(n=1、2、3、…) 则在第n 个图形中共有(个图形中共有( )个顶点. ( )A .(n+1)(n+2) B . (n+2)(n+3) C .2nD .n 34.在回归分析中,代表了数据点和它在回归直线上相应位置的差异的是在回归分析中,代表了数据点和它在回归直线上相应位置的差异的是( ) A .总偏差平方和 B .残差平方和 C .回归平方和 D .相关指数R2 35.设()f n 为正整数n (十进制)的各数位上的数字的平方之和,比如()22212312314f =++=.记1()()f n f n =,1()(())k k f n f f n +=,1,2,3...k =, 则2006(2006)f =( )A .20 B .4 C .42 D .145 36.某大学的信息中心A 与大学各部门、各院系B ,C ,D ,E ,F ,G ,H ,I 之间拟建立信息联网工程,实际测算之间拟建立信息联网工程,实际测算 的费用如图所示(单位:万元).请观察图形,可以不请观察图形,可以不建部分网线,而使得中心与各部门、院系彼此都能连通建部分网线,而使得中心与各部门、院系彼此都能连通 (直接或中转),则最少的建网费用(万元)是(,则最少的建网费用(万元)是( )A .12 B .13 C .14 D .16 37.化简°-160sin 1的结果是的结果是 ( ) A .°80cos B .°-160cosC .°-°80sin 80cosD .°-°80cos 80sin38.下列命题:①00a = ;②()()a b c a b c =;③若,a b 共线同向,则a b a b = ;④0,0a b ¹¹ ,则0a b ¹ ;⑤a b a b = ;⑥若,a b 均为单位向量,则22a b = ,正确的个数是(,正确的个数是( )A .③⑥.③⑥B .③⑤.③⑤C .②③④.②③④D .①②⑤⑥.①②⑤⑥ 39.已知在ABC D 中,cos cos c Cb B=,则此三角形为( ) A .直角三角形.直角三角形B .等腰直角三角形.等腰直角三角形C .等腰三角形.等腰三角形D .等腰或直角三角形.等腰或直角三角形40.已知向量()()()2,0,2,2,2cos ,2sin OB OC CA a a ===,则OA 与OB 夹角的范围是( ) A .0,4p éùêúëû B .5,412p p éùêúëû C .5,1212p p éùêúëûD .5,122p p éùêúëû 41.函数()lg(1)f x x =+的定义域是(的定义域是( )A .(,1)-¥-B .(--1]¥,C .(1)-+¥,D .[1,)-+¥ 42. 点A (1,2,3)关于xOy 平面对称的点B 坐标是(坐标是( )A .(-1,2,3)B .(1,-2,3)C .(1,2,-3)D .(-1,-2,3)43. 设()833-+=x x f x ,用二分法求方程()2,10833Î=-+x x x在内近似解的过程中得()()(),025.1,05.1,01<><f f f 则方程的根落在区间(则方程的根落在区间( )A .(1,1.25)B .(1.25,1.5)C .(1.5,2)D .不能确定.不能确定 44.利用斜二测画法得到的.利用斜二测画法得到的 ①三角形的直观图是三角形①三角形的直观图是三角形②平行四边形的直观图是平行四边形②平行四边形的直观图是平行四边形 ③正方形的直观图是正方形③正方形的直观图是正方形 ④菱形的直观图是菱形④菱形的直观图是菱形 以上结论,正确的是(以上结论,正确的是( )A .①②.①② B. ① C .③④.③④ D. ①②③④①②③④45.设函数()f x 和()g x 分别是R 上的偶函数和奇函数,则下列结论恒成立的是(上的偶函数和奇函数,则下列结论恒成立的是( )A .()f x +|()|g x 偶函数偶函数B .()f x -|()|g x 是奇函数是奇函数C .|()f x | +()g x 是偶函数是偶函数D . |()f x |- ()g x 是奇函数是奇函数 46.棱长为2的正方体的外接球的表面积为(的正方体的外接球的表面积为( )A .4πB .12πC .24πD .48π 47.在下列命题中, 错误的是(错误的是( )A .如果两个平面有三个不共线的公共点,那么这两个平面重合.如果两个平面有三个不共线的公共点,那么这两个平面重合B .如果两条直线都与第三条直线平行,那么这两条直线平行.如果两条直线都与第三条直线平行,那么这两条直线平行C .如果两条直线都与第三条直线垂直,那么这两条直线垂直.如果两条直线都与第三条直线垂直,那么这两条直线垂直D .如果两个平行平面同时与第三个平面相交,那么它们的交线平行.如果两个平行平面同时与第三个平面相交,那么它们的交线平行48. 直线l 经过抛物线2-31y x x =+与y 轴的交点,且与直线20x y +=平行,则直线l 的方程是(的方程是( )A .2-20x y +=B .2-20x y -=C .+220x y +=D .+220x y -= 49.在30°的二面角l a b --中,P ∈a ,PQ ⊥b , 垂足为Q ,PQ =2,则点Q 到平面a 的 距离QH 为(为( ) A .3 B .32C .1 D .332 50. 如图所示的是某池塘中的浮萍蔓延的面积y (2m )与时间t (月)的关系: ty a =,有以下叙述:有以下叙述:① 这个指数函数的底数是2;② 第5个月时,浮萍的面积就会超过230m ; ③ 浮萍从24m 蔓延到212m 恰好经过1.5个月;个月; ④ 浮萍每个月增加的面积都相等;其中正确的是浮萍每个月增加的面积都相等;其中正确的是 ( ) A .①②.①② B . ①②③①②③ C . ②③④②③④ D . ①②③④①②③④DBBCB ABDCA DBABB BACBD DCBAD BCBDA DDDBD BDACC CCBAA BCDAA 2 1 t /月2 1 y /m 8 0 4 3 。
高二数学例题大全

1、在平面直角坐标系中,点A的坐标为(3, -2),若将点A向上平移4个单位,再向左平移2个单位,得到点B,则点B的坐标为:A. (1, 2) (答案)B. (5, -6)C. (1, -6)D. (5, 2)2、已知集合A = {1, 2, 3},B = {2, 3, 4},则A与B的交集为:A. {1, 4}B. {2, 3} (答案)C. {1, 2, 3, 4}D. 空集3、若直线l经过点(2, -1)且斜率为-2,则直线l的方程为:A. y = -2x + 3B. y = -2x - 5 (答案)C. y = 2x - 5D. y = 2x + 34、已知等差数列{an}的前n项和为Sn,若a1 = 1,S3 = 9,则a3 =:A. 4B. 5 (答案)C. 6D. 75、在三角形ABC中,若角A = 60°,b = 4,c = 2√3,则三角形ABC的面积为:A. 6√3B. 6C. 3√3D. 12 (答案)6、已知圆C的方程为(x - 1)2 + (y - 2)2 = 4,则圆心C的坐标和半径r分别为:A. (1, 2),4B. (1, 2),2 (答案)C. (-1, -2),4D. (-1, -2),27、设随机变量X服从二项分布B(3, 0.5),则P(X = 2)等于:A. 1/8B. 3/8 (答案)C. 5/8D. 7/88、在复平面内,复数z = 1 + i对应的点位于:A. 第一象限(答案)B. 第二象限C. 第三象限D. 第四象限9、若直线x + y + k = 0与圆x2 + y2 = 4相交于M,N两点,且|MN| = 2√2,则k的值为:A. ±√2B. ±2 (答案)C. ±√3D. ±310、已知向量a = (1, 2),b = (2, -1),则向量a与b的夹角为:A. 30°B. 45°C. 60°(答案)D. 90°。
高二文科数学《立体几何》经典练习题(含解析)-
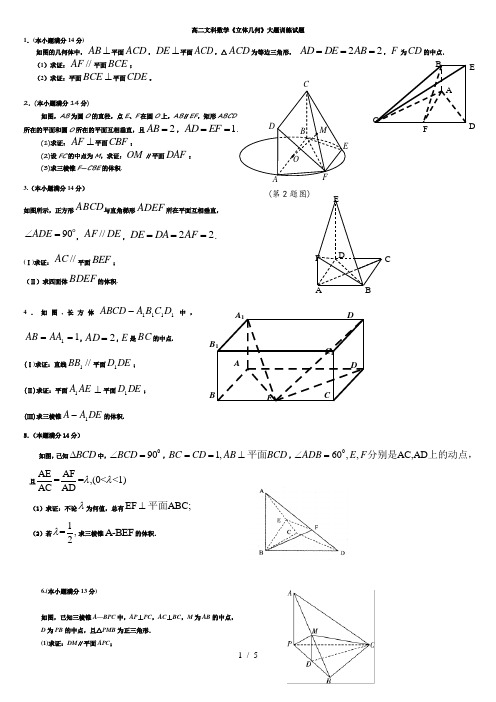
FAEOB DM(第2题图)A 1B 1C 1DA BCDE高二文科数学《立体几何》大题训练试题1.(本小题满分14分)如图的几何体中,AB ⊥平面ACD ,DE ⊥平面ACD ,△ACD 为等边三角形, 22AD DE AB ===,F 为CD 的中点.(1)求证://AF 平面BCE ; (2)求证:平面BCE ⊥平面CDE 。
2.(本小题满分14分)如图,AB 为圆O 的直径,点E 、F 在圆O 上,AB ∥EF ,矩形ABCD 所在的平面和圆O 所在的平面互相垂直,且2AB =,1AD EF ==.(1)求证:AF ⊥平面CBF ;(2)设FC 的中点为M ,求证:OM ∥平面DAF ;(3)求三棱锥F -CBE 的体积.3.(本小题满分14分)如图所示,正方形ABCD 与直角梯形ADEF 所在平面互相垂直,90ADE ∠=o ,DE AF //,22===AF DA DE .(Ⅰ)求证://AC 平面BEF ;(Ⅱ)求四面体BDEF 的体积.4.如图,长方体1111D C B A ABCD -中,11==AA AB ,2=AD ,E 是BC 的中点.(Ⅰ)求证:直线//1BB 平面DE D 1;(Ⅱ)求证:平面AE A 1⊥平面DE D 1;(Ⅲ)求三棱锥DE A A 1-的体积.5.(本题满分14分)如图,己知BCD ∆中,090BCD ∠=,1,BC CD AB BCD ==⊥平面,060,,AC,AD ADB E F ∠=分别是上的动点,且AE AF==,(0<<1)AC ADλλ (1)求证:不论λ为何值,总有EF ABC;⊥平面(2)若1=,2λ求三棱锥A-BEF 的体积.6.(本小题满分13分)如图,已知三棱锥A —BPC 中,AP ⊥PC ,AC ⊥BC ,M 为AB 的中点, D 为PB 的中点,且△PMB 为正三角形. (1)求证:DM ∥平面APC ;AB C DFEB AEDCFABCD图2BCD 图1(2)求证: BC ⊥平面APC ;(3)若BC =4,AB =20,求三棱锥D —BCM 的体积.7、(本小题满分14分)如图1,在直角梯形ABCD 中,90ADC ∠=︒,//CD AB ,2,1AB AD CD ===.将ADC ∆沿AC 折起,使平面ADC ⊥平面ABC ,得到几何体D ABC -,如图2所示.(1) 求证:BC ⊥平面ACD ;(2) 求几何体D ABC -的体积.8、(本小题满分14分)已知四棱锥P ABCD - (图5) 的三视图如图6所示,PBC ∆为正三角形,PA 垂直底面ABCD ,俯视图是直角梯形.(1)求正视图的面积;(2)求四棱锥P ABCD -的体积;(3)求证:AC ⊥平面PAB ;参考答案1.(本小题满分14分) (1)证明:取CE 的中点G ,连结FG BG 、.∵F 为CD 的中点,∴//GF DE 且12GF DE =.∵AB ⊥平面ACD ,DE ⊥平面ACD , ∴//AB DE ,∴//GF AB .又12AB DE =,∴GF AB =. …………3分∴四边形GFAB 为平行四边形,则//AF BG .……………5分∵AF ⊄平面BCE ,BG ⊂平面BCE , ∴//AF 平面BCE .…………7分(2)证明:∵ACD ∆为等边三角形,F 为CD 的中点,∴AF CD ⊥…………9分∵DE ⊥平面ACD ,AF ACD ⊂平面,∴DE AF ⊥.……………10分又CD DE D ⋂=,∴AF ⊥平面CDE .……………………………12分 ∵//BG AF ,∴BG ⊥平面CDE .…………………………………13分 ∵BG ⊂平面BCE , ∴平面BCE ⊥平面CDE .………………14分2.解:(1)Θ平面ABCD ⊥平面ABEF ,CB AB ⊥,平面ABCD I 平面ABEF AB =,CB ∴⊥平面ABEF , ∵AF ⊂平面ABEF ,∴AF CB ⊥,……… 2分又AB 为圆O 的直径,∴AF BF ⊥, ∴AF ⊥平面CBF . ……… 4分B AEDC FG(2)设DF 的中点为N ,则MN//12CD ,又AO //12CD , 则MN//AO ,四边形MNAO 为平行四边形,∴//OM AN ,又AN ⊂平面DAF ,OM ⊄平面DAF ,∴//OM 平面DAF . …… 8分(3)∵BC ⊥面BEF ,∴13F CBE C BEF BEF V V S BC --∆==⨯⨯,B 到EF 的距离等于O 到EF 的距离,过点O 作OGEF ⊥于G ,连结OE 、OF , ∴OEF ∆为正三角形,∴OG 为正OEF ∆的高,∴OG==……… 11分∴13F CBEC BEF BEFV V S BC --∆==⨯⨯ ……12分1111113232EF OG BC =⨯⨯⨯⨯=⨯⨯=。
