六年级数学平面图形总复习题
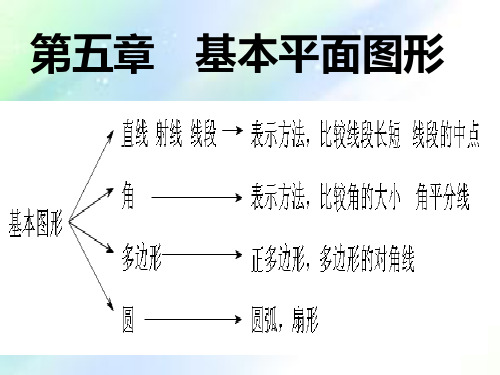
鲁教版数学六年级下册第五章《基本平面图形》复习
A DC
B
2. 如图,AB=6cm,点C是线段AB的中点,点D 是线段CB的中点,那么AD有多长呢?
解:∵点C是线段AB的中点 A
∴AC=CB= 1 AB 3cm
CD
1
2
CB 1.5cm
2
AD AC CD 4.5cm
CDB
►考点二 角 例2 8点30分时,钟表的时针与分针的夹角为__________°
数学·新课标(BS)
线段中点的符号语言表示:
反之, A
C
B
如图,∵点C在线段AB上且AC=BC ∴点C是线段AB的中点.
如图,∵点C是线段AB的中点,
12 ∴AC=BC= AB
练习:1、如图,已知点C是线段AB的中点,点D是 线段AC的中点,完成下列填空:
(1)AB= _2_ BC ,BC= _2_ AD (2)BD= _3_ AD
圆 圆心 圆心角
B
A
O
钟表指针的运动
考点攻略
►考点一 直线、射线、线段 例1 如图4-1,C、D是线段AB上两点,若CB=4 cm,DB=7 cm,且D是AC的中点,则AC的长等于( )
数学·新课标(BS)
第四章 |过关测试
A.3 cm
B.6 cm
C.11 cm D.14 cm
[解析] B 先利用线段的和差求出DC的长,再根据线段的中点 定义求AC的长.
[答案] A
数学·新课标(BS)
4.在一次航海中,在一艘货轮的北偏东54°的方向上有一艘渔 船,那么货轮在渔船的________方向上.
[答案] 南偏西54°
数学·新课标(BS)
3计算: (1)90°-45°32″; (2)6°32′25″×7.
数学六年级下册《平面图形的特征和面积》整理复习

《图形的认识》(10)1、直线、射线和线段:端点个数是否可以延伸长度直线射线线段2、同一平面内两条直线有哪几种位置关系?并画图表示。
3、角:()<锐角<()直角=()()<钝角<()平角=()周角=() 1周角=()平角 =()直角4、三角形:三角形内角和等于()°;任意两边之和()。
等腰三角形的()相等,()相等。
5、四边形:(1)平行四边形内角和是()度。
对边()且相等,对角()。
(2)长方形有()条对称轴;正方形有()条对称轴;等腰三角形有()条对称轴;等边三角形有()条对称轴;等腰梯形有()条对称轴。
6、圆:(1)圆是轴对称图形,有()条对称轴。
(2)在同圆或等圆中,直径=(),半径=()。
(3)()确定圆的位置,圆的大小由()确定。
1、填空:(1)三角形具有()性、四边形具有()性、圆具有()性。
(2)一个三角形三个内角度数之比是1:1:2,这是个()三角形。
(3)一用2根分别长4㎝、6㎝长的小棒,再配一根围成一个三角形,这根小棒最长()㎝,最短( )㎝。
(取整厘米)(4)把一个等边三角形沿一条高分开,分成的直角三角形的两个锐角的度数分别是()度和()度。
(5)如果等腰三角形的顶角比它的一个底角大150,这个等腰三角形的一个底角是()0 ,顶角是()0。
(6)在一个等腰三角形的周长是20cm,其中有两条边之比是1:2,腰长() cm,底边长()cm。
2、判断:(1)线段和射线都是直线的一部分。
()(2)两条直线不相交就一定平行。
()(3)利用一幅三角尺可以画出是15的倍数的角。
()(4)把一个长方形框拉成平行四边形后,周长和面积都没有变。
()(5)长方形、正方形、平行四边形都是轴对称图形。
( ) (6)锐角三角形有三条高,直角三角形和钝角三角形只有一条高。
()(7)钝角大于900。
()(8)平角是一条直线,周角是一条射线。
()(9)角的两条边越长,这个角越大。
()3、解决问题。
六年级下册数学试题-总复习专项训练8·平面图形苏教版(无答案) (1)

专项训练8·平面图形一、填空题。
(每小題2分,共24分)1.下图中一共有( )条直线,( )条射线,( )条线段。
2.如图,∠1=75°,那么∠3=( ),如果∠2:∠4=3:2,那么∠2=( );∠4=( )。
第1题图第2题图3.一个平行四边形的面积是12 2cm,与它等底等高的三角形的面积是( )4.一个三角形的三个内角的度数比是1:6:5,则最大的一个内角是( )度,按角分,它是一个( )角三角形。
5.一个直角三角形的三条边分别为6厘米、8厘米、10厘米,它的周长是( )厘米,面积是( )平方厘米。
6.在一个周长为25.12厘米的圆内,画一个最大的正方形,正方形的面积是( )平方厘米。
7.将一个长方形的长和宽都增加6cm,这个长方形的面积就增加1142cm,原来长方形的周长是( )cm。
8.如图,7个完全相同的小长方形刚好拼成1个大长方形,小长方形的长与宽的比是( ),大长方形的长与宽的比是( )。
第8题图第9题图9.右图中长方形的周长是24cm,一个圆的周长是( )cm。
10.一个梯形上底与下底的比是4:9,把下底减少15 cm,就变成一个正方形,这个正方形的面积与原来梯形的面积比是( )。
11.如图,阴影部分的面积是( )平方厘米。
12.如图,平行四边形ABCD的底边BC长5 cm,直角三角形BCE的直角边EC长4cm,已知两块阴影部分的面积和比△EFG的面积大52cm,则CF=( )cm。
第11题图第12题图二、判断题。
(对的画”√”,错的画“×”)(6分)1.角的大小与它的边的长短没有关系。
( )2.在同一平面内,不相交的两条直线一定平行。
( )3.用12.56厘米的铁丝分别鵬成长方形、正方形、圆,面积最大的是正方形。
( )4.一个等腰三角形的一个底角是45°,这个三角形一定是等腰直角三角形。
( )5.一个长方形的长和宽都增加5厘米,它的面积增加25平方厘米。
小升初专项复习:平面图形(试题)-六年级下册数学通用版

通用版小升初专项复习:平面图形一、填空题1.已知一个等腰三角形的一边是3cm ,一边是7cm ,这个三角形的周长是 cm 。
2.若a 和b 都是非0自然数,并且满足 a 3+b 7=1621,那么以a+b= 。
3.下图是由5个完全相同小长方形合成的大长方形,大长方形的周长是44厘米,这个大长方形的面积是 平方厘米。
4.要画一个周长是18.84厘米的圆,圆规两脚间的距离应为 厘米,这个圆的面积是 平方厘米。
5.如图,把圆分成若干等份,剪拼成了一个近似的长方形,周长比原来增加了6厘米,这个圆的面积是 平方厘米。
6.圆的 除以 的商是一个固定的数,我们把它叫作 ,用字母 表示,它是一个 小数,通常取 进行计算。
7.井盖做成圆的主要是为了 。
8.45 吨的 12 是 吨,合 千克。
9.在一个长是8厘米,宽是6厘米的长方形里剪一个最大的圆,这个圆的半径是 厘米,周长是 厘米,面积是 平方厘米。
10.一个圆锥的底面周长是18.84cm ,高是5cm ,从顶点沿高把它切成相等的两半,这两半的表面积之和比原来圆锥的表面积增加了 cm 2。
11.已知∠1、∠2是直角三角形中的两个锐角.(1)∠1=38°∠2= °(2)∠2=46°∠1= °12.一块梯形广告牌的下底是8米,上底是5米,高是下底的一半,它的面积是 平方米。
13.一个长方形花坛的面积是56平方米,扩建时长不变,宽由7米增加到12米,扩建后花坛的面积是平方米。
14.如果把一个圆的半径扩大到原来的3倍,那么直径扩大到原来的倍,周长扩大到原来的倍,面积扩大到原来的倍。
15.一个棋盒里有黑子和白子若干枚,若取出一枚黑子,则余下的黑子数与白子数之比为9:7;若放回黑子,再取出一枚白子,则余下的黑子数与白子数之比为7:5。
那么棋盒里原有的黑子比白子多枚。
二、单选题16.周长是80米的正方形,面积是()。
A.20平方米B.80平方米C.400平方米D.6400平方米17.如图,大圆内有一个最大的正方形,正方形内有一个最大的圆,那么大圆面积和小圆面积的比是()。
小学六年级数学小升初珍藏版复习资料第14讲 平面图形的认识与测量(原卷)

2022-2023学年小升初数学精讲精练专题汇编讲义第14讲平面图形的认识与测量知识点一:线和角的认识1.线段、直线、射线的特点(1)线段有两个端点,可以度量长度;射线只有一个端点,它可以向一端无限延伸,不可以度量长度;直线没有端点,它可以向两端无限延伸,不能度量长度。
(2)两点之间线段最短。
2.垂直与平行(1)同一平面内,两条直线的位置关系是平行和相交。
如果两条直线相交成直角,就说这两条直线互相垂直,其中一条直线叫作另一条直线的垂线,它们的交点叫作垂足。
过直线外一点只能画一条已知直线的垂线。
(2)平行线之间的距离处处相等;点到直线的所有连线中,垂线段最短。
3.角(1) 由一点出发的两条射线组成的图形叫角;角的大小与两边的画出的长短无关,与两边张开的大小有关。
(2)角的分类锐角直角钝角平角周角大于0。
小于90。
90。
大于90。
小于180。
180°360°知识点二:三角形的认识与测量1.三角形的认识知识精讲(1)三角形的特殊性质:三角形具有稳定性。
(2)三角形三边关系:在一个三角形中,任意两边之和大于第三边,任意两边之差小于第三边。
(3)三角形的分类:三角形按角分,分为锐角三角形、直角三角形和钝角三角形;按边分,分为特殊三角形和一般三角形。
等腰三角形和等边三角形是特殊三角形,等边三角形是特殊的等腰三角形。
(4)三角形的内角和是( 180° )2.三角形的面积两个完全一样的三角形可以拼成一个平行四边形,这个平行四边形的底就是三角形的底,所拼成平行四边形的高就是三角形的高。
每个三角形的面积是所拼成平行四边形面积的一半。
因为平行高四边形的面积=底×高,所以三角形的面积= 1底×高,用字母2ah 。
表示为: S=12知识点三:四边形的认识与测量1.四边形的认识(1)四边形的特殊性质:不稳定,易变形。
(2)平行四边形两组对边分别平行且相等,梯形只有一组对边平行。
2022年精品解析鲁教版(五四制)六年级数学下册第五章基本平面图形专题训练练习题(含详解)

六年级数学下册第五章基本平面图形专题训练考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、在下列生活、生产现象中,可以用基本事实“两点确定一条直线”来解释的是()①用两颗钉子就可以把木条固定在墙上;②把笔尖看成一个点,当这个点运动时便得到一条线;③把弯曲的公路改直,就能缩短路程;④植树时,只要栽下两棵树,就可以把同一行树栽在同一条直线上.A.①②B.①④C.②③D.③④2、如图,小红同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是()A.两点之间,线段最短B.两点确定一条直线C.过一点,有无数条直线D.连接两点之间的线段叫做两点间的距离3、下列说法正确的是()A .正数与负数互为相反数B .如果x 2=y 2,那么x =yC .过两点有且只有一条直线D .射线比直线小一半4、下列说法错误的是( )A .两点之间,线段最短B .经过两点有一条直线,并且只有一条直线C .延长线段AB 和延长线段BA 的含义是相同的D .射线AB 和射线BA 不是同一条射线5、如图,某同学从A 处出发,去位于B 处的同学家交流学习,其最近的路线是( )A .A C DB →→→B .AC F B →→→ C .A C E F B →→→→D .A C M B →→→6、上午8:30时,时针和分针所夹锐角的度数是( )A .75°B .80°C .70°D .67.5°7、如图,BOC ∠在AOD ∠的内部,且20BOC ∠=︒,若AOD ∠的度数是一个正整数,则图中所有角...的度数之和可能是( )A .340°B .350°C .360°D .370°8、如图,线段21cm AD =,点B 在线段AD 上,C 为BD 的中点,且13AB CD =,则BC 的长度( )A .6cmB .7cmC .8cmD .9cm 9、如图,点D 是线段AB 的中点,点E 是AC 的中点,若6cm AB =,14cm AC =,则线段DE 的长度是( )A .3cmB .4cmC .5cmD .6cm10、如图,C 为线段AB 上一点,点D 为BC 的中点,且30cm AB =,4AC CD =.则AC 的长为( )cm .A .18B .18.5C .20D .20.5第Ⅱ卷(非选择题 70分)二、填空题(5小题,每小题4分,共计20分)1、将一副直角三角板按如图放置,使两直角重合,则∠1的度数为______.2、一个角为2440︒',则它的余角度数为 _____.3、如图,线段13cm AB =,点C 是线段AB 上一点,点M 、N 分别是AC 、BC 的中点,则MN 的长为__________cm .4、把一个直径是10厘米的圆分成若干等份,然后把它剪开,照如图的样子拼起来,拼成的图形的周长比原来圆的周长增加_______厘米.5、如图,已知O 为直线AB 上一点,OC 平分∠AOD ,∠BOD =3∠DOE ,∠COE =α,则∠BOE =_____.(用含α的式子表示)三、解答题(5小题,每小题10分,共计50分)1、如图,OD 平分BOC ∠,OE 平分AOC ∠.若35BOD ∠=︒,50AOC ∠=︒.(1)求出AOB ∠的度数;(2)求出DOE ∠的度数,并判断DOE ∠与AOB ∠的数量关系是互补还是互余.2、点M ,N 是数轴上的两点(点M 在点N 的左侧),当数轴上的点P 满足PM =2PN 时,称点P 为线段MN 的“和谐点”.已知,点O ,A ,B 在数轴上表示的数分别为0,a ,b ,回答下面的问题:(1)当a =﹣1,b =5时,求线段AB 的“和谐点”所表示的数;(2)当b =a +6且a <0时,如果O ,A ,B 三个点中恰有一个点为其余两个点组成的线段的“和谐点”,直接写出此时a 的值.3、如图,在直线上顺次取A 、B 、C 三点,使得AB =40cm ,BC =280cm .点P 、点Q 分别由A 点、B 点同时出发向点C 运动,运用时间为t (单位:s ),点P 的速度为3cm/s ,点Q 的速度为1cm/s(1)请求出线段AC 的长;(2)若点D 是线段AC 的中点,请求出线段BD 的长;(3)请求出点P 出发多少秒后追上点Q ?(4)请计算出点P 出发多少秒后,与点Q 的距离是20cm ?4、如图,已知点A ,B ,C ,请按要求画出图形.(1)画直线AB 和射线CB ;(2)连结AC ,并在直线AB 上用尺规作线段AE ,使2AE AC =;(要求保留作图痕迹)5、如图,已知线段a ,b .(尺规作图,保留作图痕迹,不写作法)求作:线段2AB a b =-.-参考答案-一、单选题1、B【解析】【分析】直接利用直线的性质以及线段的性质分析求解即可.【详解】①用两颗钉子就可以把木条固定在墙上,可以用基本事实“两点确定一条直线”来解释;②把笔尖看成一个点,当这个点运动时便得到一条线,可以用基本事实“无数个点组成线”来解释;③把弯曲的公路改直,就能缩短路程,可以用基本事实“两点之间线段最短”来解释;④植树时,只要栽下两棵树,就可以把同一行树栽在同一条直线上,可以用基本事实“两点确定一条直线”来解释;综上可得:①④可以用“两点确定一条直线”来解释,故选:B.【点睛】此题主要考查了直线的性质以及线段的性质,正确把握相关性质是解题关键.2、A【解析】【分析】根据两点之间线段最短的性质解答.【详解】解:∵用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,∴线段AB的长小于点A绕点C到B的长度,∴能正确解释这一现象的数学知识是两点之间,线段最短,故选:A .【点睛】此题考查了实际生活中两点之间线段最短的应用,正确理解图形的特点与线段的性质结合是解题的关键.3、C【解析】【分析】A 中互为相反数的两个数为一正一负;B 中两个数的平方相等,这两个数可以相等也可以互为相反数;C 中过两点有且只有一条直线;D 中射线与直线无法比较长度.【详解】解:A 中正数负数分别为12-,,()1210+-=-≠,错误,不符合要求; B 中22x y =,可得x y =或x y =-,错误,不符合要求;C 中过两点有且只有一条直线 ,正确,符合要求;D 中射线与直线都可以无限延伸,无法比较长度,错误,不符合要求;故选C .【点睛】本题考查了相反数,直线与射线.解题的关键在于熟练掌握相反数,直线与射线等的定义.4、C【解析】【分析】根据两点之间线段最短的性质、两点确定一条直线、延长线的定义以及射线的定义依次分析判断.【详解】解:A. 两点之间,线段最短,故该项不符合题意;B. 经过两点有一条直线,并且只有一条直线,故该项不符合题意;C. 延长线段AB和延长线段BA的含义是不同的,故该项符合题意;D. 射线AB和射线BA不是同一条射线,故该项不符合题意;故选:C.【点睛】此题考查了两点之间线段最短的性质、两点确定一条直线、延长线的定义以及射线的定义,综合掌握各知识点是解题的关键.5、B【解析】【分析】根据两点之间线段最短,对四个选项中的路线作比较即可.【详解】解:四个选项均为从A→C然后去B由两点之间线段最短可知,由C到B的连线是最短的由于F在CB线上,故可知A→C→F→B是最近的路线故选B.【点睛】本题考查了两点之间线段最短的应用.解题的关键在于正确理解两点之间线段最短.6、A【解析】【分析】根据钟面平均分成12份,可得每份的度数;根据时针与分针相距的份数乘以每份的度数,可得答案.【详解】解:钟面平均分成12份,钟面每份是30°,上午8:30时时针与分针相距2.5份,此时时钟的时针与分针所夹的角(小于平角)的度数是30°×2.5=75°.故选:A .【点睛】本题考查了钟面角,时针与分针相距的份数乘以每份的度数是解题关键.7、B【解析】【分析】根据角的运算和题意可知,所有角的度数之和是∠AOB +∠BO C +∠COD +∠AOC +∠BOD +∠AOD ,然后根据20BOC ∠=︒,AOD ∠的度数是一个正整数,可以解答本题.【详解】解:由题意可得,图中所有角的度数之和是∠AOB +∠BOC +∠COD +∠AOC +∠BOD +∠AOD=3∠AOD+∠BOC∵20BOC ∠=︒,AOD ∠的度数是一个正整数,∴A、当3∠AOD+∠BOC =340°时,则AOD ∠=3203︒ ,不符合题意; B 、当3∠AOD+∠BOC =3×110°+20°=350°时,则AOD ∠=110°,符合题意;C 、当3∠AOD+∠BOC =360°时,则AOD ∠=3403︒,不符合题意; D 、当3∠AOD+∠BOC =370°时,则AOD ∠=3503︒,不符合题意. 故选:B .【点睛】本题考查角度的运算,解题的关键是明确题意,找出所求问题需要的条件.8、D【解析】【分析】设AB x =cm ,则3BC CD x ==cm ,根据题意列出方程求解即可.【详解】解:设AB x =,则3CD x =,∵C 为BD 的中点,∴3BC CD x ==,∴3321x x x ++=,解得3x =,339BC =⨯=cm ,故选:D .【点睛】本题考查了线段的和差和线段的中点,解一元一次方程,解题关键是明确相关定义,设未知数列出方程求解.9、B【解析】【分析】根据中点的定义求出AE和AD,相减即可得到DE.【详解】解:∵D是线段AB的中点,AB=6cm,∴AD=BD=3cm,∵E是线段AC的中点,AC=14cm,∴AE=CE=7cm,∴DE=AE-AD=7-3=4cm,故选B.【点睛】本题考查了中点的定义及两点之间的距离的求法,准确识图是解题的关键.10、C【解析】【分析】根据线段中点的性质,可用CD表示BC,根据线段的和差,可得关于CD的方程,根据解方程,可得CD的长,AC的长.【详解】解:由点D为BC的中点,得BC=2CD=2BD,由线段的和差,得AB=AC+BC,即4CD+2CD=30,解得CD=5,AC=4CD=4×5=20cm,故选:C;【点睛】本题考查了两点间的距离,利用了线段中点的性质,线段的和差.二、填空题1、165°【解析】【分析】由三角板得∠C=30°,得到∠BAC的度数,利用邻补角关系得到∠1的度数.【详解】解:如图,∵∠C=30°,∴∠BAC=45°-30°=15°,∴∠1=180°-∠BAC=165°,故答案为:165°.【点睛】此题考查了三角板有关的计算,正确掌握三角板各角的度数及邻补角的定义是解题的关键.【解析】【分析】根据余角的定义计算即可.【详解】解:90°-2440︒',=6520︒',故答案为:6520︒'.【点睛】本题考查了余角的定义,如果两个角的和等于90°那么这两个角互为余角,其中一个角叫做另一个角的余角.3、6.5【解析】【分析】根据中点的性质得出MN =12AB 即可.【详解】∵点M 、N 分别是AC 、BC 的中点∴MC =12AC ;CN =12BC ,∴MN =MC +CN =12AC +12BC =12AB =1132⨯故答案为6.5.【点睛】本题考查了线段中点的定义和性质,解题的关键是熟练应用中点的性质进行计算.4、10【解析】【分析】由圆的面积推导过程可知:将圆拼成近似的长方形后,长方形的长就等于圆的周长的一半,宽就等于圆的半径,从而可知,这个长方形的周长比原来圆的周长多出了两个半径的长度,据此即可求解.【详解】解:因为将圆拼成近似的长方形后,长方形的长就等于圆的周长的一半,宽就等于圆的半径,所以这个长方形的周长比原来圆的周长多出了两个半径的长度,即多出了一个直径的长度,也就是10厘米.故答案为:10.【点睛】本题考查认识平面图形,理解图形周长的意义和拼图前后之间的关系是解决问题的关键.5、360°-4α【解析】【分析】设∠DOE=x,根据OC平分∠AOD,∠COE=α,可得∠COD=α-x,由∠BOD=3∠DOE,可得∠BOD=3x,由平角∠AOB=180°列出关于x的一次方程式,求解即可.【详解】解:设∠DOE=x,∵OC 平分∠AOD ,∠BOD =3∠DOE ,∠COE =α,∴∠AOC =∠COD =α-x ,∠BOD =3x ,由∠BOD +∠AOD =180°,∴3x +2(α-x )=180°解得x =180°-2α,∴∠BOE =∠BOD -∠DOE =3x -x =2x=2(180°-2α)=360°-4α,故答案为:360°-4α.【点睛】本题考查了角平分线的定义,平角的定义,一元一次方程的应用,掌握角平分线的定义是解题的关键.三、解答题1、 (1)120︒(2)60︒,互补【解析】【分析】(1)先根据角平分线的定义求出∠BOC 的度数,然后可求AOB ∠的度数;(2)先根据角平分线的定义求出∠COD、∠COE 的度数,然后可求DOE ∠的度数,进而可判断DOE ∠与AOB ∠的数量关系.(1)解:∵OD 平分BOC ∠,35BOD ∠=︒,∴270BOC BOD ∠=∠=︒,又∵50AOC ∠=︒,∴7050120AOB BOC AOC ∠=∠+∠=︒+︒=︒;(2)解:∵OD 平分BOC ∠,OE 平分AOC ∠,50AOC ∠=︒,∴35COD BOD ∠=∠=︒,1252COE AOC ∠=∠=︒,∴352560DOE COD COE ∠=∠+∠=︒+︒=︒,∴60120180DOE AOB ∠+∠=︒+︒=︒,∴DOE ∠与AOB ∠的数量关系是互补.【点睛】本题主要考查角平分线的定义和补角的定义,关键是根据补角的定义解答.如果两个角的和等于90°,那么这两个角互为余角,其中一个角叫做另一个角的余角;如果两个角的和等于180°,那么这两个角互为补角,其中一个角叫做另一个角的补角.2、 (1)3或11;(2)a 的值为-12,-9,-4,-3.【解析】【分析】(1):设线段AB 的“和谐点”表示的数为x ,根据a =﹣1,b =5,分三种情况,①当1x <-时, 列出方程12(5)x x --=-.②当15x -≤<时,列出方程12(5)x x +=-.③当5x ≥时,列出方程12(5)x x +=-解方程即可. (2):点O 为AB 的“和谐点”OA =2OB ,列方程()020a b -=-或()020a b -=-,根据b =a +6且a <0,可得()0206a a -=--或()0260a a -=+-解方程,当A 为OB 的“和谐点”当b <0时,AB =2AO ,即6=-a ,不合题意,当b >0时,AO =2AB ,a =12>0,不合题意,当点B 为AO 的“和谐点”BA =2BO ,点B 在点O 的左边,6=2(-a -6),点B 在点O 的右边,6=2(a +6),解方程即可.(1)解:设线段AB 的“和谐点”表示的数为x ,①当1x <-时,列出方程12(5)x x --=-.解得11x =.(舍去)②当15x -≤<时,列出方程12(5)x x +=-.解得3x =.③当5x ≥时,列出方程12(5)x x +=-解得11x =.综上所述,线段AB 的“和谐点”表示的数为3或11.(2)解:点O 为AB 的“和谐点”OA =2OB ,()020a b -=-或()020a b -=-,∵b =a +6且a <0,()0206a a -=--,解得12a =-,()0260a a -=+-,解得4a =-,当A 为OB 的“和谐点”,当b <0时,a <-6,AB =2AO ,即6=-a ,解得a =-6,不合题意,当b >0时,AO =2AB ,即a =2×(b -a ),∵b=a+6,解得a=12>0,不合题意,当点B为AO的“和谐点”BA=2BO,点B在点O的左边,6=2(-a-6),解得:a=-9,点B在点O的右边,6=2(a+6),解得:a=-3,综合a的值为-12,-9,-4,-3.【点睛】本题考查新定义线段的和谐点,数轴上两点距离,一元一次方程,线段的倍分关系,掌握新定义线段的和谐点,数轴上两点距离求法,解一元一次方程,线段的倍分关系是解题关键.3、 (1)320cm(2)120cm(3)20秒(4)10或30秒【解析】【分析】(1)根据AB+BC=AC,已知AB=40cm,BC=280cm,代入数据,即可解得线段AC的长;(2)根据线段的中点定理可得11602AD AC cm==,而BD=AD﹣AB,即可求出线段BD的长;(3)这属于追击问题,设点P出发t秒后追上点Q,即当追上时有AP AB BQ=+,可方程3t=t+40,即可得本题之解;(4)设点P出发t秒,点Q的距离是20cm;分两种情况,①是当P在Q的左侧时,3t=40+t+20;②是当P在Q的右侧时,3t=40+t+20,分别解这两个方程,即可得出本题答案.(1)解:∵AB+BC=AC,∴AC=320cm;(2)解:∵D是线段AC的中点,∴11602AD AC cm==,∴BD=AD﹣AB=120cm;(3)解:设点P出发t秒后追上点Q,依题意有:3t=t+40,解得t=20.答:点P出发20秒后追上点Q.(4)解:当P在Q的左侧时,此时3t+20=40+t,解得:t=10;当P在Q的右侧时,此时3t=40+t+20,解得:t=30.答:点P出发10或30秒后,与点Q的距离是20cm.【点睛】本题主要考查了线段的有关计算,一元一次方程的应用等知识.4、 (1)见解析(2)见解析【解析】【分析】(1)根据直线和射线的定义画图即可;(2)先连结AC,然后以点A圆心,以AC为半径,在直线AB上顺次截取2次即可;(1)如图所示;(2)如图所示,或【点睛】本题主要考查了作图知识及把几何语言转化为几何图形的能力,比较简单,直线向两方无限延伸,射线向一方无限延伸,而线段不延伸.也考查了作一条线段等于已知线段的尺规作图.5、见解析【解析】【分析】作射线AM,在射线AM,上顺次截取AC=a,CD=a,再反向截取DB=b,进而可得线段AB.【详解】.解:如图,线段AB即为所求作的线段2a b【点睛】本题考查尺规作图—线段的和差,是基础考点,掌握相关知识是解题关键.。
2024年西师大版六年级下册数学小升初分班考必刷专题:平面图形

2024年西师大版六年级下册数学小升初分班考必刷专题:平面图形一、单选题1.圆形花坛的半径是2米,绕花坛走一周,长度是()。
A.25.12米B.12.56米C.12.56平方米D.25.12平方米2.已知一个三角形两边的长度分别是9厘米、12厘米,那么,这个三角形的周长可能是()厘米。
A.24B.30C.42D.453.如图,在边长相等的两个正方形内剪圆片,比较剩下的材料,()A.甲、乙剩下一样多B.甲剩下多C.乙剩下多D.无法确定4.一个等腰三角形的两条边分别是2厘米和5厘米,则这个等腰三角形的周长是()A.7厘米B.9厘米C.12厘米D.9厘米或12厘米5.用三根同样长的铁丝分别围成平行四边形、正方形、长方形三个不同的图形,三个图形的面积相比,()A.平行四边形面积最大B.正方形面积最大C.长方形面积最大D.三个图形的面积相等6.如图,大圆直径2cm,小圆贴着大圆的内侧从P点开始按箭头所指方向滚动,小圆至少需要滚动()周才能回到P点。
A.2B.3C.4D.5二、填空题7.已知一个三角形的两个内角分别为30°和40°,这是一个角三角形。
8.一个等腰三角形中两个内角的比是1:4,这个等腰三角形的顶角可能是度。
9.一个等腰三角形的两条边分别是7cm和3cm。
它的周长是cm。
10.一个三角形面积是18cm2,与它等底等高的平行四边形面积是cm2。
11.如图:若圆的半径是1dm,则涂色部分面积是。
12.下图(1)中,长方形的周长是24厘米,空白部分是半圆。
阴影部分的面积是平方厘米,周长是厘米。
13.如图,把一个圆沿半径分成若干等份后,拼成一个近似的长方形,近似长方形的周长比圆的周长增加了20厘米,这个圆的半径是厘米。
14.大小两个圆的半径比是4:3,它们的直径比是,面积比是。
15.图中有条对称轴;如果圆的直径是dcm,那么长方形的面积是cm2。
16.靠墙用篱笆围一个半径是5米的半圆形鸡舍(靠墙一面不围),需要篱笆米。
鲁教版五四制六年级下册数学 第五章 基本平面图形 综合复习题(含答案解析)

参考答案与试题解析一.选择题1.下列说法正确的是()A.画一条长3cm的射线B.射线、线段、直线中直线最长C.射线是直线的一部分D.延长直线AB到C解:A.画一条长3cm的射线,说法错误,射线可以向一个方向无限延伸;B.射线、线段、直线中直线最长说法错误,射线可以向一个方向无限延伸,直线可以向两个方向无限延伸;C.射线是直线的一部分,正确;D.延长直线AB到C说法错误,直线可以向两个方向无限延伸.故选:C.2.在下列生活、生产现象中,可以用基本事实“两点确定一条直线”来解释的是()①用两颗钉子就可以把木条固定在墙上;②把笔尖看成一个点,当这个点运动时便得到一条线;③把弯曲的公路改直,就能缩短路程;④植树时,只要栽下两棵树,就可以把同一行树栽在同一条直线上.A.①③B.②④C.①④D.②③解:①用两颗钉子就可以把木条固定在墙上,可以用基本事实“两点确定一条直线”来解释;②把笔尖看成一个点,当这个点运动时便得到一条线,可以用基本事实“无数个点组成线”来解释;③把弯曲的公路改直,就能缩短路程,可以用基本事实“两点之间线段最短”来解释;④植树时,只要栽下两棵树,就可以把同一行树栽在同一条直线上,可以用基本事实“两点确定一条直线”来解释.故选:C.3.直线AB,线段CD,射线EF的位置如图所示,下图中不可能相交的是()A.B.C.D.解:A选项中,直线AB与线段CD无交点,符合题意;B选项中,直线AB与射线EF有交点,不合题意;C选项中,线段CD与射线EF有交点,不合题意;D选项中,直线AB与射线EF有交点,不合题意;故选:A.4.如图,下列说法中正确的是()A.直线AC在线段BC上B.射线DE与直线AC没有公共点C.直线AC与线段BD相交于点AD.点D在直线AC上解:A.直线AC上的点C在线段BC上,故本选项错误;B.射线DE与直线AC有公共点,故本选项错误;C.直线AC与线段BD相交于点A,故本选项正确;D.点D在直线AC外,故本选项错误;故选:C.5.下列叙述中正确的是()①线段AB可表示为线段BA②射线AB可表示为射线BA③直线AB可表示为直线BA④射线AB和射线BA是同一条射线A.①②③④B.②③C.①③D.①②③解:①线段AB可表示为线段BA,正确;②射线AB不可表示为射线BA,错误;③直线AB可表示为直线BA,正确;④射线AB和射线BA不是同一条射线,错误;故选:C.6.如图所示,某同学的家在A处,书店在B处,星期日他到书店去买书,想尽快赶到书店,请你帮助他选择一条最近的路线()A.A→C→D→B B.A→C→F→B C.A→C→E→F→B D.A→C→M→B解:根据两点之间的线段最短,可得C、B两点之间的最短距离是线段CB的长度,所以想尽快赶到书店,一条最近的路线是:A→C→F→B.故选:B.7.如图,延长线段AB到点C,使BC=2AB,D是AC的中点,若AB=5,则BD的长为()A.2B.2.5C.3D.3.5解:∵AB=5,BC=2AB,∴BC=10,∴AC=AB+BC=15,∵D为AC的中点,∴AD=AC=7.5,∴BD=AD﹣AB=7.5﹣5=2.5,故选:B.8.点C在线段AB上,下列条件中不能确定点C是线段AB中点的是()A.AC=BC B.AC+BC=AB C.AB=2AC D.BC=AB 解:A、AC=BC,则点C是线段AB中点;B、AC+BC=AB,则C可以是线段AB上任意一点;C、AB=2AC,则点C是线段AB中点;D、BC=AB,则点C是线段AB中点.故选:B.9.如图,用圆规比较两条线段AB和A′B′的长短,其中正确的是()A.A′B′>AB B.A′B′=ABC.A′B′<AB D.没有刻度尺,无法确定解:由图可知,A′B′<AB;故选:C.10.线段AB=9,点C在线段AB上,且有AC=AB,M是AB的中点,则MC等于()A.3B.C.D.解:∵AB=9,∴AC=AB=3,∵M是AB的中点,∴AM=AB=∴MC=AM﹣AC=﹣3=故选:B.11.如图,∠1=20°,∠AOC=90°,点B,O,D在同一条直线上,则∠2的度数为()A.95°B.100°C.110°D.120°解:∵∠1=20°,∠AOC=90°,∴∠BOC=∠AOC﹣∠1=90°﹣20°=70°,∴∠2=180°﹣∠BOC=180°﹣70°=110°,故选:C.12.如图所示,OB是∠AOC平分线,∠COD=∠BOD,∠COD=17°,则∠AOD的度数是()A.70°B.83°C.68°D.85°解:∵∠COD=∠BOD,∠COD=17°,∴∠BOC=2∠COD=2×17°=34°,∵OB是∠AOC平分线,∴∠AOC=2∠BOC=2×34°=68°,∴∠AOD=∠AOC+∠COD=68°+17°=85°,故选:D.13.下列角度不能用一副三角板画出来的是()A.75°B.65°C.45°D.15°解:A、用45°+30°角画出,故能画出;B、没有两个角的和或差是65°,故不能画出;C、直接用三角板就可画出,故能画出;D、用60°﹣45°就可以画出,故能画出.故选:B.14.如图:如果∠1=∠3,那么()A.∠1=∠2B.∠2=∠3C.∠AOC=∠BOD D.∠1=∠BOD 解:根据题意,∠1=∠3,有∠1+∠2=∠3+∠2,即∠AOC=∠BOD;故选:C.15.如图,小明顺着大半圆从A地到B地,小红顺着两个小半圆从A地到B地,设小明、小红走过的路程分别为a、b,则a与b的大小关系是()A.a=b B.a<b C.a>b D.不能确定解:设小明走的半圆的半径是R.则小明所走的路程是:πR.设小红所走的两个半圆的半径分别是:r1与r2,则r1+r2=R.小红所走的路程是:πr1+πr2=π(r1+r2)=πR.因而a=b.故选:A.二.填空题16.如图,OB平分∠AOC,∠AOD=78°,∠BOC=20°,则∠COD的度数为38°.解:∵OB平分∠AOC,∠BOC=20°,∴∠COD=40°,∵∠AOD=78°,∴∠COD=38°.故答案为38.三.解答题17.如图,平面内有A、B、C、D四点.按下列语句画图.(1)画直线AB,射线BD,线段BC;(2)连接AC,交射线BD于点E.解:(1)如图所示,直线AB,射线BD,线段BC即为所求;(2)连接AC,点E即为所求.18.如图,OE平分∠AOC,OF平分∠BOC,且∠BOC=60°,若∠AOC+∠EOF=156°,求∠EOF的度数.解:∵OF平分∠BOC,∠BOC=60°,∴∠COF=30°,∴∠EOF=∠COE﹣∠COF=∠COE﹣30°,∵OE平分∠AOC,∴∠AOC=2∠COE,又∵∠AOC+∠EOF=156°,∴2∠COE+∠COE﹣30°=156°,解得∠COE=62°,∴∠EOF=62°﹣30°=32°.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、对号入座。
1、三角形的一个内角正好等于其余两个内角的和,这是一个()三角形。
2、一个等腰三角形,它的顶角是72º,它的底角是()度。
3、一个等腰三角形的两条边分别是5厘米和8厘米,那么它的周长最多是()厘米,最少是()厘米。
(第三条边为整厘米数)
4、用圆规画一个周长是12 .56厘米的圆,圆规两脚间的距离应该是()厘米。
5、用360厘米长的铁丝围成一个三角形,三条边长度的比是1:2:3,它的三条边的长度分别是().()和()厘米。
6、270平方厘米=()平方分米 1.4公顷=()平方米
7、一个梯形上底与下底的和是15厘米,高是8.8厘米,面积是()。
8、一个挂钟的时针长5厘米,一昼夜这根时针的尖端走了()厘米,针尖扫的面积是()平方厘米。
9、用4个边长是2厘米的小正方形拼成一个大长方形,长方形的周长可能是()厘米,也可能是()厘米。
10、在长22厘米,宽2分米的长方形里画一个最大的圆,圆的周长是()面积是()。
11、把一平行四边形的框架拉成一长方形,面积( ),周长( )。
12、一个圆的半径扩大3倍,周长扩大( ),面积扩大( )。
13、下图是三个半径相等的圆组成的图形,它有()条对称轴。
14、用百分数表示以下阴影部分是整个图形面积的百分之几。
15、”和“”的周长之比是(),面积之比是()。
16、在一块边长是20厘米的正方形木板上锯下一个最大的圆,这个圆的面积是()平方厘米,剩下的边料是()平方厘米。
17、一张正方形纸的边长为,从这张纸上剪下一个边长为(>)的小正方形,用字母表示剩余部分的面积是()。
18、如下图,平行四边形与梯形的面积的最简整数比是()。
二、明辨是非。
1、半径是2米的圆,周长和面积相等。
()
2、两端都在圆上的线段中,直径最长。
()
3、大圆的圆周率大于小圆的圆周率。
()
4、如果长方形、正方形、圆它们周长相等,那么圆的面积最大。
()
5、因为三角形不易变形,所以房子的梁架做成三角形形状。
()
6、三角形中最大的角不小于60度。
()
7、将一张正方形纸连续对折三次,展开后其中一份是这张纸的。
()
8、只要有一个角是直角的平行四边形,就是长方形或正方形。
()
9、把一个长方形拉成一个平行四边形后,面积变小了。
()
10、半圆的周长就是圆的周长的一半。
()
11、一个正方形的边长与一个圆的直径相等,那么这个正方形的周长一定大于圆的周长。
()
12、左图是一个轴对称图形。
()
13、圆的周长是它的直径的3.14倍。
()
14、压路机滚筒在地上滚动一周所压的路面正好是压路机滚筒的表面积。
三、慎重选择。
1、用一根木条给一个长方形加固,若只考虑加固效果的话,采用()最好。
2、下图能画()条对称轴。
A、2条
B、4条
C、8条
3、下面图形中,哪些图形的阴影部分占整个图形的。
()
4、下图中,甲和乙两部分面积的关系是()。
A、甲>乙
B、甲<乙
C、甲=乙www.
5、用一条长16厘米的铁丝围成一个长方形,如果长和宽都是质数,它的面积是()平方厘米。
A、6
B、10
C、15
D、21
6、两个完全相同的长方形(如下图),将图①和图②阴影部分的面积相比,()。
图①图
A、图①大
B、图②大
C、图①与图②相等
7、正方形与圆的面积相等,那么正方形的周长()圆的周长。
A、等于
B、小于
C、大于
8、平行四边形有()高,梯形有()条高,三角形有()条高。
A.无数条B.一条C.三条
9、等腰梯形周长是48厘米,面积是96平方厘米,高是8厘米,则腰长()。
A.24厘米B.12厘米C.18厘米D.36厘米
10、圆的半径由6厘米增加到9厘米,圆的面积增加了()平方厘米。
A.9 B.45 C.45π
11、下面图形周长较长的是()
A. 甲比乙大
B. 甲比乙小
C. 甲和乙一样大
D. 无法比较
四、走进生活
1.小明说:我用11厘米.1厘米.1厘米的三根小棒围成了一个等腰三角形。
他的话对吗?为什么?
2.小芳说:我用两块一样的三角板拼成了一个大的三角形,这个三角形的内角和是360º。
她的话对吗?为什么?
3、张大爷用篱笆围一块梯形菜地,一面靠墙(如下图)。
篱笆全长48米,如果每平方米收白菜10千克,这块地一共可以收白菜多少千
克?
4、学校有一块长方形空地,长50米,宽40米,要在这块空地内留出的面积进行绿化。
在绿化面积内用的面积种植花卉,在剩余的面积内规划一个最大的三角形种植草坪。
请你设计一下,并画出草图。
(比例尺1:1000)
5、刘老师从家到学校的路程是6000米,早上7:30他骑自行车从家去学校上班,这辆自行车轮子的外直径是70厘米,平均每分钟转100圈,如果学校8:00上课,刘老师会不会迟到?
五、挑战自我
1、如下图,两个完全一样的直角三角形重叠一部分,图中阴影部分面积是()平方厘米。
2、如下图(单位:米),阴影部分的面积分别是和,与的比为1:4,求、。
3、如图是一个园林的规划图,其中正方形的3/4是草地;园的6/7是竹林;竹林比草地多占地450平方米。
问:水池占地多少平方米?
4、我们已经知道三角形三个内角度数的和是180°,
(1)你能运用这个知识求出四边形、五边形、六边形等多边形的内角和吗?
(2)你发现的规律是什么?()
(3)请用字母式子表示n边形内角和。
5.在生产、生活中,我们经常把一些同样大小的圆柱捆扎起来,下面我们来探索捆扎时怎样求绳子的长度。
假设每个圆柱管的直径都是10厘米,当圆柱管的放置方式是“单层平放”时,捆扎后的横截面如下图所示:
请你根据图形,完成下表:
★【智慧开新花】
1、一只猫追赶一只老鼠,老鼠沿A B C方向跑,猫沿A D C 方向跑,结果在E点将老鼠抓住了。
老鼠与猫的速度比是17:20,C点与E点相距3米,四边形ABCD为平行四边形。
猫和老鼠所用的时间相等。
(1)猫比老鼠多跑了几米才追到老鼠?
(2)猫和老鼠所跑的四边形的周长是多少米?
2、下图由19个棱长是2厘米的小正方体重叠而成。
求这个立体图形的表面积。
3、一个等边三角形与一个正六边形的周长相等,如果三角形的面积是36平方厘米,那么六边形的面积是多少平方厘米?。
