稳态误差计算
合集下载
系统的稳态误差为
r (t ) t
e ss
1
r (t ) t
e ss
1
2
Kp
0型 I型 II型
Kv
0
Ka
0 0
ess
1
1
2
1 K
K
p
KvKp1来自 1Ka
K
0 0
Kv
K
0
Ka
三、系统稳定误差的计算
综述，系统的稳态误差与输入信号形式有 关，对于一个结构确定的系统，如果给定 输入形式不同，其稳态误差就不同；同时 稳态误差与系统结构也密切相关，如果给 定信号一定，不同结构的系统稳态误差也 不同。 按静态误差系数法计算稳态误差的方法， 是基于拉氏变换的终值定理，只能使用阶 跃、斜坡及加速度或他们的组合，如果输 入是其他任意时间函数，以上结论则不能 成立。
ess
特征方程为D( s) 1 Gk ( s) an s n an 1s n 1 ... a2 s 2 a1s a0 0
n n 1 2 a s a s ... a s 等式两边同除以 n n 1 2 a1s a0 1 Gk ( s) 0 1 0 则 n n 1 2 an s an 1s ... a2 s 得 a1s a0 Gk ( s) 该系统为Ⅱ型系统 an s n an 1s n 1 ... a2 s 2 开环增益为 a0 a1s a0 K 2 a2 n2 n 3 s (an s an 1s ... a2 )
ess
1、先求取系统的开环传递函数 Gk ( s)
Gk (s)
C(s)
设开环传递函数为 Gk ( s) M ( s) 即，开环传递函数 N ( s) 与闭环传递函数 M (s) 有相同的零点 Gk ( s ) M (s) N (s) GB ( s ) a s a0 1 Gk ( s ) 1 M ( s ) N ( s ) M ( s ) 得 Gk ( s ) 1 ? N (s)
3-5稳态误差的分析与计算
0型 系统
m
K (TjS 1) G(s) j1
n
(TiS 1)
i 1
抛物线输入 Ⅱ型系统
系统开环传递函数中 不含积分环节
KPlim G(s)K
s0
ess
1 1 K
阶跃输入时，误差系数=K
输出始终不会等于输入，存在稳态误差
Klim SG (s)0 斜坡输入时，误差系数=0
e s 0 ss 稳态误差无穷大（输出不能跟随输入）
三种典型输入下对应于“0”“I”“Ⅱ”型三 种系统
有九种情况，误差的计算公式列表如下：
给定输入
给定稳态误差的终值 0型系统 I型系统 Ⅱ型系统
1(t)
1/(1+K)
0
0
t
∞1/K0源自t2/2∞∞1/K
注意: (1) 尽管将阶跃输入、速度输入及加速度输入下 系统的误差分别称之为位置误差、速度误差和加 速度误差，但对速度误差、加速度误差而言并不 是指输出与输入的速度、加速度不同，而是指输 出与输入之间存在一确定的稳态位置偏差。
i1 n1
(is1) (k2s2 2kks1)
k1 n2
(Tjs1) (Tl2s2 2lls1)
j1
l1
稳态误差系数仅与系统参数K、(积分环节个数—系统 型号)有关，对应＝0、1、2 称 0、I、Ⅱ型系统
0、I、Ⅱ型三种系统 分别三种典型输入 稳态误差有九种情况
阶跃输入 斜坡输入
0型系统 I型系统
3. 稳态误差与系统传递系数有关
4. 稳态误差与扰动有关
本章结束
给定输入下的稳态误差与稳态误差系数
阶跃输入下:
e ssr
1
1 K
P
KPlimG(s) s0
线性系统的稳态误差计算
函数为
G( s) K S ( S 2 bS C )
p 1 p 2 b C 4 2 p 2 C 2 p K 0.5C K 2 b 3
因为 ess 按定义
1 2 Kr
s 0
Kv
K 0.5, K 0.5C C
令r (t ) Rt 2 / 2，R 常量，R(s) R / s3。
sR(s) sR / s3 R R R ess lim lim lim 2 2 lim 2 s 0 1 G( s) H ( s ) s 0 1 G( s ) H ( s ) s 0 s s G ( s ) H (s ) s 0 s G (s ) H (s ) Ka
系统稳态误差计算通式则可表示为
ess
1 lim s R ( s )
s 0
sR( s) ess lim sE ( s) lim s 0 s 0 1 G ( s ) H ( s )
K lim s
s 0
系统型别 e ss 与 K 开环增益有关 R ( s ) 输入信号
def
E ( s) 1 R(s) 1 H ( s)G( s)
E ( s ) e ( s ) R( s ) R( s ) 1 H ( s)G( s)
e(t ) L1[e (s)R(s)] ets (t ) ess (t )
瞬态分量
稳态分量
E ( s ) e ( s ) R( s )
要求对于阶跃作用下不存 在稳态误差，则必须选用 Ⅰ型及Ⅰ型以上的系统
4.斜坡输入作用下的稳态误差和静态速度误差系数
r (t ) Rt，R 常量，R(s) R / s 2。
G( s) K S ( S 2 bS C )
p 1 p 2 b C 4 2 p 2 C 2 p K 0.5C K 2 b 3
因为 ess 按定义
1 2 Kr
s 0
Kv
K 0.5, K 0.5C C
令r (t ) Rt 2 / 2，R 常量，R(s) R / s3。
sR(s) sR / s3 R R R ess lim lim lim 2 2 lim 2 s 0 1 G( s) H ( s ) s 0 1 G( s ) H ( s ) s 0 s s G ( s ) H (s ) s 0 s G (s ) H (s ) Ka
系统稳态误差计算通式则可表示为
ess
1 lim s R ( s )
s 0
sR( s) ess lim sE ( s) lim s 0 s 0 1 G ( s ) H ( s )
K lim s
s 0
系统型别 e ss 与 K 开环增益有关 R ( s ) 输入信号
def
E ( s) 1 R(s) 1 H ( s)G( s)
E ( s ) e ( s ) R( s ) R( s ) 1 H ( s)G( s)
e(t ) L1[e (s)R(s)] ets (t ) ess (t )
瞬态分量
稳态分量
E ( s ) e ( s ) R( s )
要求对于阶跃作用下不存 在稳态误差，则必须选用 Ⅰ型及Ⅰ型以上的系统
4.斜坡输入作用下的稳态误差和静态速度误差系数
r (t ) Rt，R 常量，R(s) R / s 2。
3-6线性系统的稳态误差计算
i=1 n 1 i k =1 n2 k j =1 j l =1 l
m 1
m2
2
+ 2ζ kτk s +1) + 2ζlTs +1) l
∏(T s +1)∏(Ts
=
2
K ⋅ G0 (s) sν
sR(s) 1 essr = lim = = s→0 1+ G (s) 1+ limGk (s) k
s→0
1 1 = K 1+ Kp 1+ lim ν ⋅ G0 (s) s→0 s
三、扰动作用下的稳态误差(3) 扰动作用下的稳态误差(3) [例]系统结构图如图所示。当 r(t) = n(t) = 1(t) 系统结构图如图所示。 时，求系统的稳态误差 ess；若要求稳态误差 为零，如何改变系统结构。 为零，如何改变系统结构。 解：该系统对给定输入而言属于Ⅰ型系统。 该系统对给定输入而言属于Ⅰ型系统。 所以当给定输入为单位阶跃函数时的稳态误差 essr = 0
3、单位抛物线输入时的稳态误差
R(s) =
1 s3
sR(s) 1 essr = lim = = 2 s→0 1+ G (s) lims ⋅ Gk (s) k
s→0
1 1 = K Ka lim ν −2 ⋅ G0 (s) s→0 s
∞ 1 = K 0
Ka
根据
ν =0,1 ν =2 ν ≥3
m2
=
K ⋅ G0 (s) ν s
K－开环增益
系统型别（即积分环节的个数） ν − 系统型别（即积分环节的个数）
当ν =0，无积分环节，称为0型系统 无积分环节，称为0
当 = ，有一个积分环节，称为Ⅰ型系统 ν 1 有一个积分环节，称为Ⅰ
m 1
m2
2
+ 2ζ kτk s +1) + 2ζlTs +1) l
∏(T s +1)∏(Ts
=
2
K ⋅ G0 (s) sν
sR(s) 1 essr = lim = = s→0 1+ G (s) 1+ limGk (s) k
s→0
1 1 = K 1+ Kp 1+ lim ν ⋅ G0 (s) s→0 s
三、扰动作用下的稳态误差(3) 扰动作用下的稳态误差(3) [例]系统结构图如图所示。当 r(t) = n(t) = 1(t) 系统结构图如图所示。 时，求系统的稳态误差 ess；若要求稳态误差 为零，如何改变系统结构。 为零，如何改变系统结构。 解：该系统对给定输入而言属于Ⅰ型系统。 该系统对给定输入而言属于Ⅰ型系统。 所以当给定输入为单位阶跃函数时的稳态误差 essr = 0
3、单位抛物线输入时的稳态误差
R(s) =
1 s3
sR(s) 1 essr = lim = = 2 s→0 1+ G (s) lims ⋅ Gk (s) k
s→0
1 1 = K Ka lim ν −2 ⋅ G0 (s) s→0 s
∞ 1 = K 0
Ka
根据
ν =0,1 ν =2 ν ≥3
m2
=
K ⋅ G0 (s) ν s
K－开环增益
系统型别（即积分环节的个数） ν − 系统型别（即积分环节的个数）
当ν =0，无积分环节，称为0型系统 无积分环节，称为0
当 = ，有一个积分环节，称为Ⅰ型系统 ν 1 有一个积分环节，称为Ⅰ
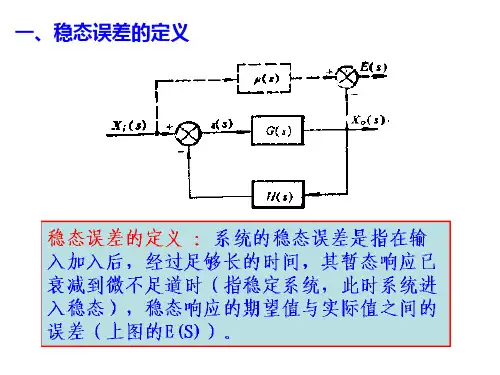
稳态误差
2! e(0) r ( t ) 1 Fe(0)( t ) e ss ( t ) Fe(0)r ( t ) F r 2! C 0 r ( t ) C1r ( t ) C 2( t ) r
拉普拉斯反变换，得
注意: (1) 尽管将阶跃输入、速度输入及加速度输入下 系统的误差分别称之为位置误差、速度误差和加 速度误差，但对速度误差、加速度误差而言并不 是指输出与输入的速度、加速度不同，而是指输 出与输入之间存在一确定的稳态位置偏差。 (2) 如果输入量非单位量时，其稳态偏差（误差） 按比例增加。 (3) 系统在多个信号共同作用下总的稳态偏差误 差等于多个信号单独作用下的稳态偏差（误差） 之和。
给定稳态误差与扰动稳态误差 一
终值定理： ess tlim e(t ) lim SE(s) s0 与输入有关！ 给定稳态误差终值的计算
1 essr lim SEr (s) lim SR (s)Fr(s) lim S R (s) s 0 s 0 s 0 1 G(s)
消除或减少稳态误差的方法 • 产生稳态误差的原因
给定输入 1(t) 系统型号越高，无差度 t 越高。可以串联积分环 t2/2
输入信号是实际 的需要，不能变
给定稳态误差的终值 0型系统 I型系统 Ⅱ型系统 1/(1+K) 0 0 ∞ 1/K 0 ∞ ∞ 1/K
节提高系统型号。 1. 稳态误差与输入信号有关 传递系数越大，稳态误差越小。 2. 稳态误差与系统型号有关 3. 稳态误差与系统传递系数有关 4. 稳态误差与扰动有关
ess =
esr
+ esn
s 1 / H s
E s X or s X o s s X i s X o s X i s H s X o s / H s
拉普拉斯反变换，得
注意: (1) 尽管将阶跃输入、速度输入及加速度输入下 系统的误差分别称之为位置误差、速度误差和加 速度误差，但对速度误差、加速度误差而言并不 是指输出与输入的速度、加速度不同，而是指输 出与输入之间存在一确定的稳态位置偏差。 (2) 如果输入量非单位量时，其稳态偏差（误差） 按比例增加。 (3) 系统在多个信号共同作用下总的稳态偏差误 差等于多个信号单独作用下的稳态偏差（误差） 之和。
给定稳态误差与扰动稳态误差 一
终值定理： ess tlim e(t ) lim SE(s) s0 与输入有关！ 给定稳态误差终值的计算
1 essr lim SEr (s) lim SR (s)Fr(s) lim S R (s) s 0 s 0 s 0 1 G(s)
消除或减少稳态误差的方法 • 产生稳态误差的原因
给定输入 1(t) 系统型号越高，无差度 t 越高。可以串联积分环 t2/2
输入信号是实际 的需要，不能变
给定稳态误差的终值 0型系统 I型系统 Ⅱ型系统 1/(1+K) 0 0 ∞ 1/K 0 ∞ ∞ 1/K
节提高系统型号。 1. 稳态误差与输入信号有关 传递系数越大，稳态误差越小。 2. 稳态误差与系统型号有关 3. 稳态误差与系统传递系数有关 4. 稳态误差与扰动有关
ess =
esr
+ esn
s 1 / H s
E s X or s X o s s X i s X o s X i s H s X o s / H s
《自动控制原理》第三章 35 稳态误差计算
两种定义的联系： E ' ( s ) E ( s ) H (s)
H ( s ) 1时， E ( s ) E ' ( s )
能源与动力学院 第三章 线性系统的时域分析法
3
1. 误差与稳态误差的定义…
e(t ) L1[ E (s)] L1[e (s) R (s)] L1[ R (s) ] 1 G(s)H (s)
3-6 线性系统的稳态误差计算 （Steady-state error）
稳定性 系统性能 动态性能
稳态性能 稳态误差
稳态性能
原理性误差 结构性误差 (附加稳态误差）
系统结构 输入类型、形式 摩擦，间隙 死区等非线性
能源与动力学院
第三章 线性系统的时域分析法
1
3-6 线性系统稳态误差计算
本节内容：
N(s)
C(s)
G2 (s)
H (s)
输出端误差定义
E'n
(s)
Cn(s)
G2(s)
1G1(s)G2(s)H(s)
N(s)
输入端误差定义
En(s)
Cn(s)H(s)
G2(s)H(S) 1G1(s)G2(s)H(s)
ets (t ) ess (t ) 稳态误差
ess ( )
Lim
s0
sE (s)
Lim
s0
1
sR (s) G(s)H
(s)
ess():终值误差 条件s： E(s)在右半平面及析 虚（ 轴原 上点 解除外）
能源与动力学院 第三章 线性系统的时域分析法
4
1. 误差与稳态误差的定义…
例1
R(s) E(S)
误差与稳态误差的定义 系统的类型 输入作用下稳态误差计算 扰动作用下稳态误差 减小或消除稳态误差的措施
稳态误差
p
在单位阶跃作用下， 0 的系统为有差系统，此时开环增益K 越大稳态误差越小； 1 的系统为无差系统。
13
3.6 稳态误差分析
单位斜坡函数输入时的稳态误差
当输入为R ( s )
e ssr lim
s 0
1 s
2
时（单位斜坡函数）
s 1 s
2
1 Gk (s)
1 lim s G k ( s )
s 0
s K
可见给定作用下的稳态误差与外作用有关；与时间常数形式的 开环增益有关；与积分环节的个数有关。
11
3.6 稳态误差分析
开环系统的型
系统的无差度阶数（开环传递函数的型） 通常称开环传递函数中积分的个数为系统的无差度阶数，并将系 统按无差度阶数进行分类。 当 0 ，无积分环节，称为0型系统 当 1 ，有一个积分环节，称为Ⅰ型系统 当 2 ，有二个积分环节，称为Ⅱ型系统 ……………… 当 2 时，使系统稳定是相当困难的。因此除航天控制系统外， Ⅲ型及Ⅲ型以上的系统几乎不用。
s 0
当 2时 ， K v lim
Kv
K s
s 0
G0 (s) ,
14
K 的大小反映了系统在斜坡输入下的稳态精度。 v 越大，e ss 越 小。所以说 K v 反映了系统跟踪斜坡输入的能力。 根据 K v 计算的稳态误差是系统在跟踪速度阶跃输入时位置上的 误差。
3.6 稳态误差分析
2
3.6 稳态误差分析
显然，只有当系统稳定时，研究稳态误差才有意义；对于不 稳定的系统而言，根本不存在研究稳态误差的可能性。 有时，把在阶跃函数作用下没有原理性稳态误差的系统， 称为无差系统；而把具有原理性稳态误差的系统，称为有差系 统。
在单位阶跃作用下， 0 的系统为有差系统，此时开环增益K 越大稳态误差越小； 1 的系统为无差系统。
13
3.6 稳态误差分析
单位斜坡函数输入时的稳态误差
当输入为R ( s )
e ssr lim
s 0
1 s
2
时（单位斜坡函数）
s 1 s
2
1 Gk (s)
1 lim s G k ( s )
s 0
s K
可见给定作用下的稳态误差与外作用有关；与时间常数形式的 开环增益有关；与积分环节的个数有关。
11
3.6 稳态误差分析
开环系统的型
系统的无差度阶数（开环传递函数的型） 通常称开环传递函数中积分的个数为系统的无差度阶数，并将系 统按无差度阶数进行分类。 当 0 ，无积分环节，称为0型系统 当 1 ，有一个积分环节，称为Ⅰ型系统 当 2 ，有二个积分环节，称为Ⅱ型系统 ……………… 当 2 时，使系统稳定是相当困难的。因此除航天控制系统外， Ⅲ型及Ⅲ型以上的系统几乎不用。
s 0
当 2时 ， K v lim
Kv
K s
s 0
G0 (s) ,
14
K 的大小反映了系统在斜坡输入下的稳态精度。 v 越大，e ss 越 小。所以说 K v 反映了系统跟踪斜坡输入的能力。 根据 K v 计算的稳态误差是系统在跟踪速度阶跃输入时位置上的 误差。
3.6 稳态误差分析
2
3.6 稳态误差分析
显然，只有当系统稳定时，研究稳态误差才有意义；对于不 稳定的系统而言，根本不存在研究稳态误差的可能性。 有时，把在阶跃函数作用下没有原理性稳态误差的系统， 称为无差系统；而把具有原理性稳态误差的系统，称为有差系 统。
稳态误差计算(普通解法)
⎡ K ⎤ 1 ⎤ ⎡1 G( z) = Z ⎢ = KZ ⎢ − ⎥ ⎣ s s + 1⎥ ⎦ ⎣ s ( s + 1) ⎦
z ⎛ z =K⎜ − −T ⎝ z −1 z − e
系统特征方程为
图 6-21 离散系统结构图
K (1 − e−T ) z ⎞ = ⎟ −T ⎠ ( z − 1)( z − e )
D( z ) = ( z − 1)( z − e −T ) + K (1 − e −T ) z = z 2 + [(1 − e −T ) K − 1 − e −T ]z + e −T = 0
利用朱利稳定判据
⎧ D(1) = K (1 − e −T ) > 0 ⎪ ⎨ −T −T ⎪ ⎩ D(−1) = 2(1 + e ) − K (1 − e ) > 0
e(∞) = lim
z →1
( z − 1)( z − 0.368) =0 z 2 − 0.736 z + 0.368
2
当 r (t ) = t ，相应 r (nT ) = nT 时， R ( z ) = T z ( z − 1) ，于是由式(6-59)求得
e(∞) = lim
z →1
T ( z − 0.368) = T =1 z − 0.736 z + 0.368
G( z) =
e − T z + 1 − 2e − T 0.368 z + 0.264 = 2 −T ( z − 1)( z − e ) T =1 z − 1.368 z + 0.368
2
0.368 z + 0.264 →∞ z − 1.368 z + 0.368 0.368 z + 0.264 =1 K v = lim( z − 1) 2 z →1 z − 1.368 z + 0.368 K p = lim
3.5 控制系统的稳态误差分析与计算终
2.系统的类型
K 1s 1 2 s 1 Gk s Gs H s v s T1s 1T2 s 1
K为开环增益 τ1、τ2……和T1、T2……为时间常数
n m
1、系统对单位阶跃输入的稳态偏差 K 1s 11 2 s 1 s lim G G sE H s n m s s lim X s k v s ss i s 0 s s0 T1 s G 1 T s 1 1 s2 H s
s s Gk s
K 1s 1 对0型系统 K a lim s 0 s 0 T1s 1 1s 1 2 K 对I型系统 K a lim s 0 s 0 sT1s 1 1s 1 2 K
2
稳态加速度偏差系数 令：K
a
ss s 0 s 0 i s 0 k
2
K 1s 1 对0型系统 K v lim s 0 ss s 0 T1s 1 K 1s 1 1 对I型系统 K v lim s K ss s 0 sT1s 1 K K 1s 1 对II型系统 K v lim s 0 ss 2 s 0 s T1s 1
lim s Gs H s lim s Gk s
2 2 s 0 s 0
ss
ss
1 ss K
对II型系统 K a lim s s 0
s T1s 1
2
K
1t
t
1 ss Kv
Kv 0
K p lim Gk s K v lim sGk s K a lim s 2Gk s s 0 s 0 s 0
2 i
s H s s 1 Gs H s 1 G s T s 1T s1
《自动控制原理》第三章-3-5-稳态误差计算
伺服电动机
R(s)
E(s)
1
C(s)
-
s(s 1)
K 1, 1
r(t) 1(t),k p , ess 0
r(t) t, kv 1, ess 1
r(t)
1 2
t2, ka
0, ess
位置随动系统
能源与动力学院 第三章 线性系统的时域分析法
14
4.扰动作用下稳态误差
R(s)
-
E(s)
R(s) E(s) 20
s4
N (s)
+
2
C(s)
s(s 2)
能源与动力学院 第三章 线性系统的时域分析法
28
3-20
R
-
K1
U
K2 S(T1S 1)
C
G(s)
K1K 2
B
s(T1s 1)(T2s 1)
1 T2S 1
(s)
C(s) R(s)
T1T2 s 3
K1K2 (T2s 1) (T1 T2 )s2 s
1
能源与动力学院 第三章 线性系统的时域分析法
7
3.输入作用下稳态误差计算
（1）阶跃作用下的稳态误差
r(t) R 1(t), R(s) R s
ess
Lim sR(s) s0 1 G(s)H (s)
Lim s1R(s)
s0
K Lim s
s0
1
R LimG(s)H (s)
Lim s R
s0
K Lim s
27
参考答案: Kp= ,kv=5,ka=0,essr=0.4，essn=-0.2
四、控制系统如图, r(t) 1 2t, n(t) 1(t), 试计算
§3-5稳态误差的分析与计算
R(s) H1(s) G1(s) N(s) G2(s) C(S)
G 2 (s) E n (s) Cn (s) N(s) 1 G1 (s)G 2 (s)H(s)
s 0
s 0
给定输入下的稳态误差与稳态误差系数
1 e ssr 阶跃输入下: 1 KP 斜坡输入下: essr 1 Kv 1 e ssr 抛物线输入下: Ka
K (TjS 1) G (s) S (TiS 1)
i 1 j1 n
K G( s) v s
i 1
n
系统开环传递函数中 不含积分环节
KP lim G (s) K
s 0
e ss 1 1 K
阶跃输入时，误差系数=K
输出始终不会等于输入，存在稳态误差
K lim SG (s) 0 斜坡输入时，误差系数=0 s 0
ess
2
稳态误差无穷大（输出不能跟随输入）
Ka lim S G (s) 0抛物线输入时，误差系数=0 s 0 ess 输出不能跟随输入，
KP lim G(s)
K lim SG(s)
s 0
s 0
Ka lim S G(s)
s 0
m2
2
m
( s 1) (
i i 1 n1 k 1 n2 j j 1 l 1
m1
2 2 k
s 2 k k s 1) s 2 l l s 1)
(T s 1) (T
2 2
l
稳态误差系数仅与系统参数K、(积分环节个数—系统 型号)有关，对应＝0、1、2 称 0、I、Ⅱ型系统
0、I、Ⅱ型三种系统 分别三种典型输入 稳态误差有九种情况
G 2 (s) E n (s) Cn (s) N(s) 1 G1 (s)G 2 (s)H(s)
s 0
s 0
给定输入下的稳态误差与稳态误差系数
1 e ssr 阶跃输入下: 1 KP 斜坡输入下: essr 1 Kv 1 e ssr 抛物线输入下: Ka
K (TjS 1) G (s) S (TiS 1)
i 1 j1 n
K G( s) v s
i 1
n
系统开环传递函数中 不含积分环节
KP lim G (s) K
s 0
e ss 1 1 K
阶跃输入时，误差系数=K
输出始终不会等于输入，存在稳态误差
K lim SG (s) 0 斜坡输入时，误差系数=0 s 0
ess
2
稳态误差无穷大（输出不能跟随输入）
Ka lim S G (s) 0抛物线输入时，误差系数=0 s 0 ess 输出不能跟随输入，
KP lim G(s)
K lim SG(s)
s 0
s 0
Ka lim S G(s)
s 0
m2
2
m
( s 1) (
i i 1 n1 k 1 n2 j j 1 l 1
m1
2 2 k
s 2 k k s 1) s 2 l l s 1)
(T s 1) (T
2 2
l
稳态误差系数仅与系统参数K、(积分环节个数—系统 型号)有关，对应＝0、1、2 称 0、I、Ⅱ型系统
0、I、Ⅱ型三种系统 分别三种典型输入 稳态误差有九种情况
自动控制理论_12稳态误差分析及计算
试求系统的稳态误差。
解：① 判断稳定性。系统的闭环特征方程为
s2 (Tm s 1) K1Km ( s 1) 0 Tm s3 s2 K1Km s K1Km 0
稳定条件：（1）Tm，K1，Km， 均应大于零； （2） Tm
② 根据系统结构与稳态误差之间的关系，可以直接 求 ess 从结构图看出，该系统为单位反馈且属Ⅱ型系统。因此
K 5
K 1
K 0
2
ess lim sE ( s )
s 0
1 K1
G1 ( s)
用一待定的G1 ( s)来代替图中的 K1 ,然后找出消除系 统在干扰n(t)作用下的误差时， G1 ( s ) 需具备的条件。
选择G1 (s)首先要保证sEN (s)的所有极点在s平面的左半平面。 这时essn K2 lim s[ N (s)],当n(t )为单位阶跃干扰时，有 s 0 s G1 (s) K 2
在零初始条件下，对上式进行拉氏反变换，得 到误差信号e(t)的稳态分量
1 ess (t ) e (0)r (t ) e (0) r (t ) e (0) r (t ) 2!
ess (t ) Ci r (t )
(i ) i 0
式中
C0 e (0)
当输入r(t)=1(t)时，ess1 0； 当输入r (t ) t时，ess 2 0； a0 1 2 1 当输入r(t)= t 时，ess 3 2 K K1 K m 所以系统的稳态误差ess ess1 ess 2 ess 3 1 K1 K m
4、任意输入信号
利用动态误差系数，可以求解输入信号为任意 时间函数时的系统稳态误差。
解.由题意写出系统的误差传递函数
解：① 判断稳定性。系统的闭环特征方程为
s2 (Tm s 1) K1Km ( s 1) 0 Tm s3 s2 K1Km s K1Km 0
稳定条件：（1）Tm，K1，Km， 均应大于零； （2） Tm
② 根据系统结构与稳态误差之间的关系，可以直接 求 ess 从结构图看出，该系统为单位反馈且属Ⅱ型系统。因此
K 5
K 1
K 0
2
ess lim sE ( s )
s 0
1 K1
G1 ( s)
用一待定的G1 ( s)来代替图中的 K1 ,然后找出消除系 统在干扰n(t)作用下的误差时， G1 ( s ) 需具备的条件。
选择G1 (s)首先要保证sEN (s)的所有极点在s平面的左半平面。 这时essn K2 lim s[ N (s)],当n(t )为单位阶跃干扰时，有 s 0 s G1 (s) K 2
在零初始条件下，对上式进行拉氏反变换，得 到误差信号e(t)的稳态分量
1 ess (t ) e (0)r (t ) e (0) r (t ) e (0) r (t ) 2!
ess (t ) Ci r (t )
(i ) i 0
式中
C0 e (0)
当输入r(t)=1(t)时，ess1 0； 当输入r (t ) t时，ess 2 0； a0 1 2 1 当输入r(t)= t 时，ess 3 2 K K1 K m 所以系统的稳态误差ess ess1 ess 2 ess 3 1 K1 K m
4、任意输入信号
利用动态误差系数，可以求解输入信号为任意 时间函数时的系统稳态误差。
解.由题意写出系统的误差传递函数
电气及其自动化专业之静态误差系数与稳态误差计算
电气及其自动化专业之静态误差系数与稳态误差计算首先，我们需要明确什么是静态误差系数与稳态误差。
静态误差系数是指系统对于稳定输入信号的响应的误差与输入信号的比值。
而稳态误差则是指系统在稳定状态下输出信号与输入信号之间的差异。
对于一个控制系统，如果输入信号为单位阶跃函数（即从0瞬时跃变为1），则系统的静态误差系数为系统的稳态误差。
静态误差系数可以用于评估系统的稳定性和精度，因此在控制系统设计和分析中，静态误差系数的计算是非常重要的任务。
静态误差系数可以分为三个主要类型：零误差系数、恒定误差系数和恒定值误差系数。
零误差系数是指系统对于单位阶跃输入信号的响应是无误差的，即在稳态下，系统的输出完全等于输入信号。
恒定误差系数是指系统的静态误差是一个常数，不受输入信号的幅值大小的影响。
恒定值误差系数是指系统的静态误差与输入信号的幅值大小成线性关系。
计算电气及其自动化专业中的静态误差系数和稳态误差可以通过以下步骤进行：1.建立系统的传递函数模型。
传递函数模型描述了输入与输出之间的关系，是进行稳态误差计算的基础。
2.将传递函数模型转换为控制系统的闭环传递函数模型。
闭环传递函数模型考虑了系统的反馈回路，可以更准确地描述系统的动态响应和稳态误差。
3.根据闭环传递函数模型，计算系统的静态误差系数。
静态误差系数可以通过将输入信号设置为单位阶跃函数，然后计算系统的稳态误差得到。
4.根据系统的静态误差系数，判断系统的稳定性和精确度。
根据系统的静态误差系数，可以判断系统的性能是否满足要求，如果不满足要求，则需要进行控制器的设计和调整。
在实际应用中，静态误差系数和稳态误差计算在控制系统的设计和优化中起着重要的作用。
通过准确计算静态误差系数和稳态误差，可以评估系统的性能和稳定性，并进行控制器的设计和调整，以达到所需的控制精度和稳定性。
总结起来，电气及其自动化专业中的静态误差系数与稳态误差计算是控制系统中一个重要的内容。
通过计算静态误差系数和稳态误差，可以评估系统的性能和稳定性，并进行控制器的设计和调整。
3-4 线性系统的稳态误差计算
ess 3 lim s
s 0
s(Ts 1) A 3 s(Ts 1) K s
Tips: 系统的稳态误差与系统自身的结构参数、 外作用的类型（控制量，扰动量及其作用点）以 及外作用的形式（阶跃、斜坡或加速度）有关
21:08
2.系统类型
控制系统的稳态误差与开环传递函数的结构和输入信 号的形式密切相关 对于一个给定的稳定系统，当输入信号形式一定时， 系统是否存在稳态误差取决于开环传递函数描述的系 统结构 系统开环传递函数在s平面坐标原点的极点数（开环 传函中串联积分环节的数目）与不同输入信号形式下 系统的稳态误差具有规律性的关系
21:08
依据开环传函中串联积分环节的数目：
B( s) G( s) H (s) R( s)
K ( i s 1) s (T j s 1)
j 1 i 1 n
m
0,0型系统
2, 2型系统
1,1型系统
注意： 尾1形式
3, 使系统稳定相当困难，一般很少采用。
1 K 1 s(Ts 1) s(Ts 1) s(Ts 1) K
e ( s)
E ( s) R( s )
若 r (t ) n(t ) t
s0
e ssr lim s e ( s ) R( s ) lim s
s 0
21:08
s(Ts 1) 1 1 2 s(Ts 1) K s K
若 r (t ) A 1(t )
则
ess1 lim s
s 0
s(Ts 1) A 0 s(Ts 1) K s
s(Ts 1) A A 2 s(Ts 1) K s K
稳态误差计算
课程回顾
稳定性的概念 稳定的充要条件
limk(t) 0
t
系统闭环特征方程的所有根都具有负的实部 或所有闭环特征根均严格位于左半s平面
稳定判据
D(s) an sn an1sn1 a1s a0 0
（1）判定稳定的必要条件 ai 0
（2）劳斯判据 （3）劳斯判据特殊情况的处理
判定系统的稳定性 （4）劳斯判据的应用 确定使系统稳定的参数取值范围
静态速度误差系数
K
Kv
lim
s0
s G1(s)H(s)
lim
s0
sv1
A A
1
A
K essa
lim s
s0
e (s)
R(s)
lim s
s0
s3
1 G1(s)H (s)
lim
s0
s
2
G1
(
s
)
H
(
s
)
a
静态加速度误差系数
Ka
lim
s0
s
2
G1
(s)H
(
s)
lim
s0
K sv2
第11页/共21页
D(s) s1s2 K1K2 K3Ts K1K2 K3 0
K1 T
K
2K 0
3
0
essr
lim
s0
s
e
(s)
A s3
lim
s0
A s2
s1 s2
s1 s2 K1K 2 K 3Ts
K1K2K3
A K1K2K3
en(s)
E(s) N (s)
1
K 2 K 3 (Ts 1) K1K 2 K 3 (Ts 1)
稳定性的概念 稳定的充要条件
limk(t) 0
t
系统闭环特征方程的所有根都具有负的实部 或所有闭环特征根均严格位于左半s平面
稳定判据
D(s) an sn an1sn1 a1s a0 0
（1）判定稳定的必要条件 ai 0
（2）劳斯判据 （3）劳斯判据特殊情况的处理
判定系统的稳定性 （4）劳斯判据的应用 确定使系统稳定的参数取值范围
静态速度误差系数
K
Kv
lim
s0
s G1(s)H(s)
lim
s0
sv1
A A
1
A
K essa
lim s
s0
e (s)
R(s)
lim s
s0
s3
1 G1(s)H (s)
lim
s0
s
2
G1
(
s
)
H
(
s
)
a
静态加速度误差系数
Ka
lim
s0
s
2
G1
(s)H
(
s)
lim
s0
K sv2
第11页/共21页
D(s) s1s2 K1K2 K3Ts K1K2 K3 0
K1 T
K
2K 0
3
0
essr
lim
s0
s
e
(s)
A s3
lim
s0
A s2
s1 s2
s1 s2 K1K 2 K 3Ts
K1K2K3
A K1K2K3
en(s)
E(s) N (s)
1
K 2 K 3 (Ts 1) K1K 2 K 3 (Ts 1)
自动控制理论_哈尔滨工业大学_3 第3章控制系统的时域分析_(3.7.1) 3.7稳态误差计算及减小的方法
0
e ( )d
lim
s0
0
e
(
)e
s
d
lim
s0
e
(s)
C1
0 e ( )d
lim d s0 ds
0 e
(
)e
s
d
lim
s0
d ds
e
(s)
……
Cn
lim
s0
dn ds n
e
(s)
误差系数也可以由
e
(
s)
1
1 G(s)
C(s)
s(T2s+1)
按输入的全补偿
令N(s)=0, Er(s)=
s (T1s+1)(T2s+1) - k2 (T1s+1)Gr(s) R(s) s (T1s+1)(T2s+1) + k1k2
令分子=0，得Gr(s)= s (T2s+1)/ k2
按输入的稳态补偿
essr=
lism→0sEr(s)=
例：设单位反馈系统的开环传递函数为 G(s) 100 s(0.1s 1)
若输入信号为 r(t) sin(5t) 试求该系统的稳态误差。
解1：输入为正弦，无法采用静态误差系数，所以采用动态误差系数法。
e (s)
1
1 G(s)
s(0.1s 1) 0.1s2 s 100
c0 0, c1 10-2, c2 910-4, c3 -1.910-5,
Er
(s)
1
稳态误差的计算_图文(精)
System: untitled1 Final Value: 0.909 System: untitled4 Final Value: 0.5
G G1G2
1 s 11.67s 1
35
Байду номын сангаас
0
>> step(feedback(tf(1*[0.0,1],conv([1,1],[1.67,1])),1),0:.01:35) 5 10 15 20 25 30
3-6 线性系统的稳态误差分析 项目 内容
教 学 目 的 理解稳态及稳态误差的概念，掌握其计算方法和
计算结果，进而熟悉减小或消除稳态误差的措施。
教 学 重 点 稳态误差系数定义和典型输入信号作用下的稳态
误差，即表3－5 ；减小或消除稳态误差的措施。
教学难点
广义（动态）误差的概念和广义（动态）误差系 数的计算方法，各种补偿措施。
二、给定输入作用下系统的误差分析
这时，不考虑扰动的影响。 可以写出随动系统的误差 ： 1 1 E ( s) R( s ) R( s ) 1 G1G2 H 1 Gk
R( s )
E (s)
H
G2
G1
sR( s) ess lim e(t ) lim sE ( s) lim t s 0 s 0 1 G ( s ) k
Time (sec)
从图形中体会误差和稳态误差
单位斜坡函数输入时的稳态误差 1 当输入为R ( s ) 2 时（单位斜坡函数） s sR(s) 1 1 1 ess lim s 0 1 G ( s) lim s Gk (s) lim K G (s) Kv k s 0 0 s 0 s 1 K v lim s Gk ( s ) 称为速度误差系数； 式中：
西工大、西交大自动控制原理 第六节 线性系统的稳态误差计算11-12
G2 s Cs
e
s
BERsss
1
1
GH1 ssG2
s
H
s
ef
s
Es F s
1
G2 sH s G1sG2 sH
s
1. 误差与稳态误差
稳态误差的计算
第六节 线性系统的稳态误差计算
Es Er s E f s e sRs ef sF s
1
G1
s
1
G2
s
H
s
Rs
1
G2 sH s G1sG2 sH
；e() R / K
▪ 对Ⅲ型以上系统v 3 ，K a ；e() 0
第六节 线性系统的稳态误差计算
2.用静态误差系数法求稳态误差
系 静态误差 阶跃输入 斜坡输入
统 系数 型 别
R 1t Rt
位置误差 速度误差
K
p
Kv
Ka
ess
R
(1 K p )
ess
R Kv
0K 00 R
1 K
Ⅰ K0 0
2.用静态误差系数法求稳态误差
静态加速度误差系数 K a
定义： Ka
lim
s0
s
2GK
s
lim
s0
s
2Gk
0
s
lim
s0
K sv2
e R R
lim
s0
K s 2
Ka
“加速度误差”
▪ ▪ ▪
对0型系统 对Ⅰ型系统 对Ⅱ型系统
v0
v 1 v2
，，K, KKaaa
0
0 K
；e() ；e()
第六节 线性系统的稳态误差计算
3-6稳态误差计算
i
E ( s ) e ( s) R( s )
5
0.046 cos 5t 0.105 sin 5t
0.115 sin( 5t 23.7) 。
7 扰动作用下的稳态误差 在理论上，扰动作用下的稳态误差的分析方 法与输入作用下的分析方法相同，即在理论上将 扰动信号看作是另一个输入信号。 E (s) en ( s) ； 要点：扰动误差传递函数
G (s )
C (s )
图3-31 等效单位反馈系统
E ( s)
t
1
1
H ( s) 1 G( s) H ( s)
s 0
R( s ) e ( s ) R( s )
lim e(t ) lim sE ( s ) lim s e ( s ) R( s ) (应用条件)
s 0
1 s 1.2s 0.2s
(2 0.4s) 1 s 1.2s 0.2s
2 3
；
；
信号各阶导数
r (t ) t ，r (t ) 1；r (i ) (t ) 0 ， i 1； (i ) n(t ) 1(t ) ； n (t ) 0 ， i 0 。
1 G(s) T s 1
(1)
R(s)=1/s 3； E ( s)
1 2 t / T
1 s (s 1 / T )
2
T s
2
T
2
T
2
s
s 1/ T
；
e(t ) L [ E (s)] T e
(2) R(t)= ω/ (s 2 +ω2)； E ( s)
T (t T ) ； ess (t ) T (t T ) ； T s
E ( s ) e ( s) R( s )
5
0.046 cos 5t 0.105 sin 5t
0.115 sin( 5t 23.7) 。
7 扰动作用下的稳态误差 在理论上，扰动作用下的稳态误差的分析方 法与输入作用下的分析方法相同，即在理论上将 扰动信号看作是另一个输入信号。 E (s) en ( s) ； 要点：扰动误差传递函数
G (s )
C (s )
图3-31 等效单位反馈系统
E ( s)
t
1
1
H ( s) 1 G( s) H ( s)
s 0
R( s ) e ( s ) R( s )
lim e(t ) lim sE ( s ) lim s e ( s ) R( s ) (应用条件)
s 0
1 s 1.2s 0.2s
(2 0.4s) 1 s 1.2s 0.2s
2 3
；
；
信号各阶导数
r (t ) t ，r (t ) 1；r (i ) (t ) 0 ， i 1； (i ) n(t ) 1(t ) ； n (t ) 0 ， i 0 。
1 G(s) T s 1
(1)
R(s)=1/s 3； E ( s)
1 2 t / T
1 s (s 1 / T )
2
T s
2
T
2
T
2
s
s 1/ T
；
e(t ) L [ E (s)] T e
(2) R(t)= ω/ (s 2 +ω2)； E ( s)
T (t T ) ； ess (t ) T (t T ) ； T s
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
s0
A Ka
静态加速度误差系数 K a lim s 2 G1 ( s ) H ( s ) lim
s 0 s 0
K sv2
§3.6.3
静态误差系数法（3）
§3.6.3
静态误差系数法（4）
2
例 3 系统结构图如图所示，已知输
Routh
s3 s2 s1
s0
2
1+0.6K
3
3(1+0.6K)-2K 3 K
K
0 3-0.2K>0 K>0 K<15
10 < K <15
课程小结
§3.6.1 误差与稳态误差
误差定义: (1)按输入端定义误差；(2)按输出端定义误差 稳态误差： (1)静态误差； (2)动态误差
( s ) K * ( s z1 )(s z2 )( s zm ) Cn C1 C2 ( s 1 )(s 2 )( s n ) s 1 s 2 s n
e2t
k(t ) C1e1t C2
Cne nt
闭环零点影响系数Ci ，会改变动态性能，但不影响稳定性。
解． G( s )
K 1 (Ts 1) K K1 a s 2 ( s a) v 2 K1 ( s ) 2 s ( s a ) K 1 (Ts 1)
D( s) s 3 as2 K1Ts K1 0
r1 (t ) 2t
1 r2 ( t ) 4t 8 t 2 2
s 0
e ssn lim s en ( s ) N ( s ) lims
s0
A K 2 K 3 s1 (Ts 1) A K1 s 2 s1 s2 K1 K 2 K 3Ts K1 K 2 K 3
举 例
例1 系统结构图如图所示，当r(t)=t 时，要求ess<0.1，求K的范围。 解 . G( s )
通常把在阶跃输入作用下没有原理性稳态误 差的系统称为“无差系统”； 而把有原理性稳态误差的系统称为“有差系统” 。
§3.6
线性系统的稳态误差(2)
§3.6.1 误差与稳态误差
按输入端定义的误差
E ( s ) R( s ) H ( s )C ( s )
按输出端定义的误差
E ( s ) R( s ) C ( s) H ( s)
按前馈补偿的复合控制方案可以有效提高系统的稳态精度
§3.6.4
在主反馈口到干扰作用点之间的前向通道中 提高增益、设置积分环节，可以同时减小或消 除控制输入和干扰作用下产生的稳态误差。 干扰作用引起的稳态误差分析
r ( t ) At 2 2 例 5 系统如图所示，已知输入 ， n( t ) At 求系统的稳态误差。 K K1 K 2 K 3 解． G( s) K1 K 2 K 3 (Ts 1) s1 s2 v 2
D( s) Ts2 s K 0
e ssr lim s e ( s ) R( s ) lim s
s 0 s 0
Kn Tn s 1 K n s(Ts 1) E ( s) en ( s ) K N ( s) (Tn s 1)s(Ts 1) K 1 s(Ts 1) K n s(Ts 1) 1 Kn essn lim s en ( s ) N ( s ) lim s 2 s 0 s 0 (Tn s 1)s(Ts 1) K s K
e ( s) E ( s) R( s )
D( s) s1 s2 K1 K 2 K 3Ts K1 K 2 K 3 0
essr lims e ( s )
s 0
1 s1 s2 K K K (Ts 1) s1 s2 K 1 K 2 K 3 (Ts 1) 1 1 2 3 s1 s2
闭环极点决定模态，因此决定系统的稳定性，也影响动态性能。
(3) 闭环系统的稳定性与其开环是否稳定无直接关系。
自动控制原理
§3
（第 12 讲） 线性系统的时域分析与校正
概述
一阶系统的时间响应及动态性能 二阶系统的时间响应及动态性能
§3.1
§3.2 §3.3
§3.4
§3.5 §3.6
高阶系统的阶跃响应及动态性能
K (0.6s 1) s( s 1)(2s 1) 1 r (t ) t e ss 0.1 K
K v 1
K 10
D( s) s( s 1)(2s 1) K (0.6s 1) 2s 3 3s 2 (1 0.6K )s K 0
稳态误差 动态误差：误差中的稳态分量 e ( t ) s
e ss lim e( t ) e( ) 静态误差： t
§3.6.2 计算稳态误差的一般方法
（1）判定系统的稳定性 （2）求误差传递函数
e ( s)
E ( s) , R( s )
en ( s )
s e ( s ) R( s ) en ( s ) N ( s ) （3）用终值定理求稳态误差 e ss lim s0
K K v 1
D( s) Ts2 s K 0
KGc ( s ) E ( s) s(Ts 1) s(Ts 1) KGc ( s ) e ( s) K R( s ) s(Ts 1) K 1 s s(Ts 1) Gc ( s ) K K K A sT 1 Gc ( s ) A1 Gc ( s ) A s s 0 e ss lims e ( s ) 2 lim s 0 s 0 s s(Ts 1) K K 1
（1）判定稳定的必要条件 ai 0 （2）劳斯判据 （3）劳斯判据特殊情况的处理 （4）劳斯判据的应用 判定系统的稳定性 确定使系统稳定的参数取值范围
课程回顾 (2)
关于系统的稳定性：
(1) 稳定性是系统自身的属性，与输入的类型，形式无关。 (2) 系统稳定与否，只取决于闭环极点，与闭环零点无关。
r (t ) A 2 t 2
e ss 2 lim s
s 0
e ss 3 lim s
s 0
系统自身的结构参数
影响 ess 的因素：
外作用的类型（控制量，扰动量及作用点）
外作用的形式（阶跃、斜坡或加速度等）
§3.6.3
静态误差系数法（1）
ess 的计算规律
K ( 1 s 1) ( m s 1) K G0 ( s ) v v s (T1 s 1) (Tnv s 1) s
E ( s) 1 R( s ) 1 G1 ( s ) H ( s )
§3.6.3
s0
静态误差系数法（2）
e ss lim s e ( s ) R( s ) lim s R( s )
s0
1 lim s R( s ) 1 G1 ( s ) H ( s ) s 0
lim G0 ( s ) 1
s0
静态误差系数法 —— r(t) 作用时
G( s ) G1 ( s ) H ( s )
G0 ( s )
e ( s)
( 1 s 1) ( m s 1) (T1 s 1) (Tn v s 1)
1 K 1 v G0 ( s ) s 1 ess lim s e ( s ) R( s ) lim s R( s ) s0 s0 K 1 v G0 ( s ) s
静态位置误差系数 K p lim G1 ( s ) H ( s ) lim
s 0 s 0
K sv
s0
A 1 K p
r (t ) A t
e ssv lim s e ( s ) R( s ) lim s
s0 s0
A 1 A s 2 1 G1 ( s ) H ( s ) lim s G1 ( s ) H ( s )
E ( s) N ( s)
§3.6.2
解． e ( s )
计算稳态误差的一般方法 (1)
E ( s) R( s ) 1 1 K s(Ts 1) s(Ts 1) s(Ts 1) K
s(Ts 1) 1 1 2 s(Ts 1) K s K
例１ 系统结构图如图所示，已知 r(t) = n(t) = t，求系统的稳态误差。
A 1 A e lim s ( s ) R ( s ) lim s e r ( t ) A 1(t ) ssp s 0 s 0 s 1 G1 ( s ) H ( s ) 1 lim G1 ( s ) H ( s )
s0
1 K 1 v G0 ( s ) s
自动控制原理
自动控制原理
本次课程作业
(12)
3 — 22, 23, 25 3 — 26（选做）
课程回顾
§3.5.1 §3.5.2
k (t ) 0 稳定性的概念 lim t 稳定的充要条件
系统闭环特征方程的所有根都具有负的实部
或所有闭环特征根均严格位于左半s平面
§3.5.3
稳定判据
D( s) an s n an1 s n1 a1 s a0 0
线性系统的稳定性分析 线性系统的稳态误差
§3.7
线性系统时域校正
自动控制原理
（第 12 讲）
§3.6 线性系统的稳态误差
§3.6
线性系统的稳态误差(1)
概
述
稳态误差是系统的稳态性能指标， 是对系统控制精度的度量。 对稳定的系统研究稳态误差才有意义， 所以计算稳态误差以系统稳定为前提。
本讲只讨论系统的原理性误差， 不考虑由于非线性因素引起的误差。
A Ka
静态加速度误差系数 K a lim s 2 G1 ( s ) H ( s ) lim
s 0 s 0
K sv2
§3.6.3
静态误差系数法（3）
§3.6.3
静态误差系数法（4）
2
例 3 系统结构图如图所示，已知输
Routh
s3 s2 s1
s0
2
1+0.6K
3
3(1+0.6K)-2K 3 K
K
0 3-0.2K>0 K>0 K<15
10 < K <15
课程小结
§3.6.1 误差与稳态误差
误差定义: (1)按输入端定义误差；(2)按输出端定义误差 稳态误差： (1)静态误差； (2)动态误差
( s ) K * ( s z1 )(s z2 )( s zm ) Cn C1 C2 ( s 1 )(s 2 )( s n ) s 1 s 2 s n
e2t
k(t ) C1e1t C2
Cne nt
闭环零点影响系数Ci ，会改变动态性能，但不影响稳定性。
解． G( s )
K 1 (Ts 1) K K1 a s 2 ( s a) v 2 K1 ( s ) 2 s ( s a ) K 1 (Ts 1)
D( s) s 3 as2 K1Ts K1 0
r1 (t ) 2t
1 r2 ( t ) 4t 8 t 2 2
s 0
e ssn lim s en ( s ) N ( s ) lims
s0
A K 2 K 3 s1 (Ts 1) A K1 s 2 s1 s2 K1 K 2 K 3Ts K1 K 2 K 3
举 例
例1 系统结构图如图所示，当r(t)=t 时，要求ess<0.1，求K的范围。 解 . G( s )
通常把在阶跃输入作用下没有原理性稳态误 差的系统称为“无差系统”； 而把有原理性稳态误差的系统称为“有差系统” 。
§3.6
线性系统的稳态误差(2)
§3.6.1 误差与稳态误差
按输入端定义的误差
E ( s ) R( s ) H ( s )C ( s )
按输出端定义的误差
E ( s ) R( s ) C ( s) H ( s)
按前馈补偿的复合控制方案可以有效提高系统的稳态精度
§3.6.4
在主反馈口到干扰作用点之间的前向通道中 提高增益、设置积分环节，可以同时减小或消 除控制输入和干扰作用下产生的稳态误差。 干扰作用引起的稳态误差分析
r ( t ) At 2 2 例 5 系统如图所示，已知输入 ， n( t ) At 求系统的稳态误差。 K K1 K 2 K 3 解． G( s) K1 K 2 K 3 (Ts 1) s1 s2 v 2
D( s) Ts2 s K 0
e ssr lim s e ( s ) R( s ) lim s
s 0 s 0
Kn Tn s 1 K n s(Ts 1) E ( s) en ( s ) K N ( s) (Tn s 1)s(Ts 1) K 1 s(Ts 1) K n s(Ts 1) 1 Kn essn lim s en ( s ) N ( s ) lim s 2 s 0 s 0 (Tn s 1)s(Ts 1) K s K
e ( s) E ( s) R( s )
D( s) s1 s2 K1 K 2 K 3Ts K1 K 2 K 3 0
essr lims e ( s )
s 0
1 s1 s2 K K K (Ts 1) s1 s2 K 1 K 2 K 3 (Ts 1) 1 1 2 3 s1 s2
闭环极点决定模态，因此决定系统的稳定性，也影响动态性能。
(3) 闭环系统的稳定性与其开环是否稳定无直接关系。
自动控制原理
§3
（第 12 讲） 线性系统的时域分析与校正
概述
一阶系统的时间响应及动态性能 二阶系统的时间响应及动态性能
§3.1
§3.2 §3.3
§3.4
§3.5 §3.6
高阶系统的阶跃响应及动态性能
K (0.6s 1) s( s 1)(2s 1) 1 r (t ) t e ss 0.1 K
K v 1
K 10
D( s) s( s 1)(2s 1) K (0.6s 1) 2s 3 3s 2 (1 0.6K )s K 0
稳态误差 动态误差：误差中的稳态分量 e ( t ) s
e ss lim e( t ) e( ) 静态误差： t
§3.6.2 计算稳态误差的一般方法
（1）判定系统的稳定性 （2）求误差传递函数
e ( s)
E ( s) , R( s )
en ( s )
s e ( s ) R( s ) en ( s ) N ( s ) （3）用终值定理求稳态误差 e ss lim s0
K K v 1
D( s) Ts2 s K 0
KGc ( s ) E ( s) s(Ts 1) s(Ts 1) KGc ( s ) e ( s) K R( s ) s(Ts 1) K 1 s s(Ts 1) Gc ( s ) K K K A sT 1 Gc ( s ) A1 Gc ( s ) A s s 0 e ss lims e ( s ) 2 lim s 0 s 0 s s(Ts 1) K K 1
（1）判定稳定的必要条件 ai 0 （2）劳斯判据 （3）劳斯判据特殊情况的处理 （4）劳斯判据的应用 判定系统的稳定性 确定使系统稳定的参数取值范围
课程回顾 (2)
关于系统的稳定性：
(1) 稳定性是系统自身的属性，与输入的类型，形式无关。 (2) 系统稳定与否，只取决于闭环极点，与闭环零点无关。
r (t ) A 2 t 2
e ss 2 lim s
s 0
e ss 3 lim s
s 0
系统自身的结构参数
影响 ess 的因素：
外作用的类型（控制量，扰动量及作用点）
外作用的形式（阶跃、斜坡或加速度等）
§3.6.3
静态误差系数法（1）
ess 的计算规律
K ( 1 s 1) ( m s 1) K G0 ( s ) v v s (T1 s 1) (Tnv s 1) s
E ( s) 1 R( s ) 1 G1 ( s ) H ( s )
§3.6.3
s0
静态误差系数法（2）
e ss lim s e ( s ) R( s ) lim s R( s )
s0
1 lim s R( s ) 1 G1 ( s ) H ( s ) s 0
lim G0 ( s ) 1
s0
静态误差系数法 —— r(t) 作用时
G( s ) G1 ( s ) H ( s )
G0 ( s )
e ( s)
( 1 s 1) ( m s 1) (T1 s 1) (Tn v s 1)
1 K 1 v G0 ( s ) s 1 ess lim s e ( s ) R( s ) lim s R( s ) s0 s0 K 1 v G0 ( s ) s
静态位置误差系数 K p lim G1 ( s ) H ( s ) lim
s 0 s 0
K sv
s0
A 1 K p
r (t ) A t
e ssv lim s e ( s ) R( s ) lim s
s0 s0
A 1 A s 2 1 G1 ( s ) H ( s ) lim s G1 ( s ) H ( s )
E ( s) N ( s)
§3.6.2
解． e ( s )
计算稳态误差的一般方法 (1)
E ( s) R( s ) 1 1 K s(Ts 1) s(Ts 1) s(Ts 1) K
s(Ts 1) 1 1 2 s(Ts 1) K s K
例１ 系统结构图如图所示，已知 r(t) = n(t) = t，求系统的稳态误差。
A 1 A e lim s ( s ) R ( s ) lim s e r ( t ) A 1(t ) ssp s 0 s 0 s 1 G1 ( s ) H ( s ) 1 lim G1 ( s ) H ( s )
s0
1 K 1 v G0 ( s ) s
自动控制原理
自动控制原理
本次课程作业
(12)
3 — 22, 23, 25 3 — 26（选做）
课程回顾
§3.5.1 §3.5.2
k (t ) 0 稳定性的概念 lim t 稳定的充要条件
系统闭环特征方程的所有根都具有负的实部
或所有闭环特征根均严格位于左半s平面
§3.5.3
稳定判据
D( s) an s n an1 s n1 a1 s a0 0
线性系统的稳定性分析 线性系统的稳态误差
§3.7
线性系统时域校正
自动控制原理
（第 12 讲）
§3.6 线性系统的稳态误差
§3.6
线性系统的稳态误差(1)
概
述
稳态误差是系统的稳态性能指标， 是对系统控制精度的度量。 对稳定的系统研究稳态误差才有意义， 所以计算稳态误差以系统稳定为前提。
本讲只讨论系统的原理性误差， 不考虑由于非线性因素引起的误差。