捷联惯性导航系统的解算方法
捷联惯导初始对准以及姿态解算
第三部分：基于“存储数据与迭代计算对准”罗经法对准
3.2 罗经法对准过程中的调整策略（以北向通道为例）
g
y
f
p N
1
VN
1
s
R
-
K1
K2 R
K3 s
Control algorithm
cE -
x
1
s
x
-
ie cos L
z
实线所示的北向通道：本质上是一个休拉回路，失准角作无阻尼振荡。
采取的策略：1）引入内反馈环节（虚线）实现衰减振荡；2）引入前馈环节（点画 线）缩短振荡周期；3）引入积分环节（双点画线）消除罗经项的影响。
3.5 SINS罗经法对准如何实现迭代计算？
fˆNn -
b ib
fb cU
Cˆbn
Cˆbn
b ib
Cnbine
Cnbc
cN
fˆ n Cˆbn f b
1
VN
s
1
cE
R
K1
K2 R
K3 s
Control algorithm
上述过程中，可以实现迭代计算。
Page 15
第三部分：基于“存储数据与迭代计算对准”罗经法对准
导航坐标系 n （b）SINS
GINS中的测量数据直接反映失准角的大小； SINS中的测量数据不直接反映失准角；只有投影数据能够反映失准角的大小；相同 的测量数据经过不同的姿态矩阵进行投影，可以获取不同的投影数据。 注：上述均不考虑仪表误差。
对于SINS而言，分析一种理想的情况：仪表无误差，载体无机动，此时在整个对准 过程中，仪表测量数据均相等。整个对准过程，其实只用了一组仪表参数。
3.6 SINS罗经法对准中存储数据如何使用？
捷联惯性导航系统的解算方法
捷联惯性导航系统的解算方法捷联惯性导航系统（Inertial Navigation System，简称INS）是一种利用陀螺仪和加速度计等惯性测量单元测量物体的加速度和角速度，然后通过对这些测量值的积分计算出物体的速度和位置的导航系统。
INS广泛应用于航空航天、无人驾驶车辆和船舶等领域，具有高精度和自主性等特点。
INS的解算方法一般分为初始对准、运动状态估计和航位推算三个主要过程。
初始对准是指在启动导航系统时，通过利用外部辅助传感器（如GPS）或静态校准等方法将惯性传感器的输出与真实姿态和位置进行初次校准。
在初始对准过程中，需要获取传感器的初始偏差和初始姿态，一般采用标定或矩阵运算等方法进行。
运动状态估计是指根据惯性传感器的测量值，使用滤波算法对物体的加速度和角速度进行实时估计。
常用的滤波算法包括卡尔曼滤波、扩展卡尔曼滤波和粒子滤波等。
其中，卡尔曼滤波是一种最优估计算法，通过对观测值和状态进行线性组合，得到对真实状态的最佳估计。
扩展卡尔曼滤波则是基于卡尔曼滤波的非线性扩展，可以应用于非线性INS系统。
粒子滤波是一种利用蒙特卡洛采样技术进行状态估计的方法，适用于非高斯分布的状态估计问题。
航位推算是指根据运动状态估计的结果，对物体的速度和位置进行推算。
INS最基本的航位推算方法是利用加速度值对速度进行积分，然后再对速度进行积分得到位置。
但是，在实际应用中，由于传感器本身存在噪声和漂移等误差，导致航位推算过程会出现积分漂移现象。
为了解决这个问题，通常采用辅助传感器（如GPS）和地图等数据对INS的输出进行校正和修正。
当前，还有一些先进的INS解算方法被提出，如基于深度学习的INS 解算方法。
这些方法利用神经网络等深度学习模型，结合原始传感器数据进行端到端的学习和预测，以实现更高精度的位置和姿态估计。
综上所述，捷联惯性导航系统的解算方法主要包括初始对准、运动状态估计和航位推算三个过程。
其中，运动状态估计过程利用滤波算法对传感器的测量值进行处理，得到物体的加速度和角速度的估计。
捷联惯性导航原理
2.捷联惯导力学编排方程
姿态角定义： ψ航向角----载体纵轴在水平面的投影与地理子午线之间 的夹角，用ψ表示，规定以地理北向为起点，偏东方向 为正，定义域0~360°。 θ俯仰角----载体纵轴与纵向水平轴之间的夹角，用θ表 示，规定以纵向水轴为起点，向上为正，向下为负，定 义域-90 ° ~+90 ° 。 γ横滚角----载体纵向对称面与纵向铅垂面之间的夹角， 用γ表示，规定从铅垂面算起，右倾为正，左倾为负， 定义域-180 ° ~+180° 。（载体纵向对称面和 纵轴空 间 铅垂面）
捷联惯性导航原理
2010.11.30 北航通信导航与自动测试实验室
如果载体真实地理位置以纬度、经度、高度 表示，则与此对应的载体在地球坐标系中的 真实位置(x，y，z)可通过下式求得:
地球各点重力加速度近似计算公式: g=g0(1-0.00265cos&)/1+(2h/R) g0:地球标准重力加速度9.80665(m/平方秒) &:测量点的地球纬度 h:测量点的海拔高度 R: 地球的平均半径(R=6370km) s:时间 ？？？？？？？？？？？？？？？？？？？？
f 为地球椭球模型的椭圆度，f= 1/298.257223563
R1 RN h R2 RM h
注意从瞬时速度过来那条线，用来计算w（enn）
3、捷联惯导系统的算法
3.1 姿态更新算法 四元数法：
Q(q0 , q1 , q2 , q3 ) q0 q1i q2 j q3k
1. 惯性导航中的常用坐标系
yt
yb
z e zi
北
xb
zb
zt
xt
O
东
Oe
捷联惯导系统算法.ppt
cos
b Ebz
注意事项：当 θ= 90 度时，方程出现奇点
姿态计算 矩阵方程精确解1
二、方向余弦矩阵微分方程及其解 C C
其中
C bE
CbE
b Eb
0
b Eb
z
z
0
y
x
y x
0
由于陀螺仪直接测得的是载体 相对惯性空间的角速度，所以：
CbE
b ib
E iE
C
E b
或四元数微分方程：
q(t)
(
b ib
b iE
)q(t)
注意事项： 1、上述两个方程中的角速度表达式不一样 2、方程第二项较小，计算时速度可以低一些
增量算法 矩阵方程精确解
一、角增量算法
角增量：陀螺仪数字脉冲输出，每个脉冲代表一个角增量
一个采样周期内，陀螺输出脉冲数对应的角增量为：
C
0
0
c os
0 0 0 sin
sin
sin
c os
cos cos
求解欧拉角速率得
1 0
0
cos
0 sin
惯性器件的误差补偿
姿态计算 欧拉角微分方程1
姿态矩阵的计算 假设数学坐标系模拟地理坐标系 飞行器姿态的描述：
航向角ψ、俯仰角θ、滚动角γ 一、欧拉微分方程
从地理坐标系到载体坐标系 的旋转顺序：
Ψ →θ →γ
捷联惯性导航系统的解算方法课件
02
CATALOGUE
捷联惯性导航系统组成及工作 原理
主要组成部分介绍
惯性测量单元
包括加速度计和陀螺仪，用于测量载体在三个正交轴上的加速度 和角速度。
导航计算机
用于处理惯性测量单元的测量数据，解算出载体的姿态、速度和 位置信息。
控制与显示单元
用于实现人机交互，包括设置导航参数、显示导航信息等。
工作原理简述
学生自我评价报告
知识掌握情况
学生对捷联惯性导航系统的基本原理、解算 方法和实现技术有了深入的理解和掌握。
实践能力提升
通过实验和仿真，学生的动手实践能力得到了提升 ，能够独立完成相关的实验和仿真验证。
团队协作能力
在课程项目中，学生之间的团队协作能力得 到了锻炼和提升，能够相互协作完成项目任 务。
对未来发展趋势的预测和建议
捷联惯性导航系统的解算 方法课件
CATALOGUE
目 录
• 捷联惯性导航系统概述 • 捷联惯性导航系统组成及工作原理 • 捷联惯性导航系统解算方法 • 误差分析及补偿策略 • 实验验证与结果展示 • 总结与展望
01
CATALOGUE
捷联惯性导航系统概述
定义与基本原理
定义
捷联惯性导航系统是一种基于惯性测量元件（加速度计和陀螺仪）来测量载体（如飞机、导弹等）的加速度和角 速度，并通过积分运算得到载体位置、速度和姿态信息的自主导航系统。
01
高精度、高可靠性
02
多传感器融合技术
随着科技的发展和应用需求的提高， 捷联惯性导航系统需要进一步提高精 度和可靠性，以满足更高层次的应用 需求。
为了克服单一传感器的局限性，可以 采用多传感器融合技术，将捷联惯性 导航系统与其他传感器进行融合，提 高导航系统的性能和鲁棒性。
车载捷联惯导系统基本原理
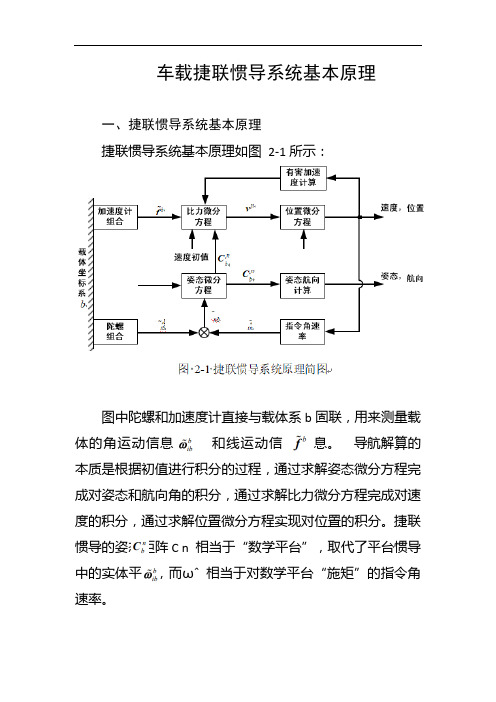
车载捷联惯导系统基本原理一、捷联惯导系统基本原理捷联惯导系统基本原理如图2-1所示：图中陀螺和加速度计直接与载体系b固联，用来测量载体的角运动信息和线运动信息。
导航解算的本质是根据初值进行积分的过程，通过求解姿态微分方程完成对姿态和航向角的积分，通过求解比力微分方程完成对速度的积分，通过求解位置微分方程实现对位置的积分。
捷联惯导的姿态矩阵C n 相当于“数学平台”，取代了平台惯导中的实体平台，而ωˆ相当于对数学平台“施矩”的指令角速率。
二、捷联惯导微分方程（一）姿态微分方程在捷联惯导系统中，导航坐标系n 和载体坐标系b 之间的角位置关系通常用姿态矩阵、四元数和欧拉角表示，相应也存在姿态矩阵微分方程、四元数微分方程和欧拉角微分方程三种形式。
姿态矩阵微分方程的表达式为：在欧拉角微分方程式(2.2-7)中，当俯仰角θ趋于90º时，cosθ趋于0，tanθ趋于无穷，方程存在奇异性，所以这种方法不能在全姿态范围内正常工作；姿态矩阵微分方程式(2.2-1)可全姿态工作，但姿态矩阵更新相当于求解包含9个未知量的线性微分方程组，计算量大；四元数微分方程式(2.2-6)同样可以全姿态工作，且更新算法只需求解4个未知量的线性微分方程组，计算量小，算法简单，是较实用的工程算法。
（二）速度微分方程速度微分方程即比力方程，是惯性导航解算的基本关系式：三、捷联惯性导航算法捷联惯导解算的目的是根据惯性器件输出求解载体姿态、速度和位置等导航信息，实际上就是求解三个微分方程的过程，相应存在姿态更新算法、速度更新算法和位置更新算法。
（一）姿态更新算法求解微分方程式(2.2-6)可得四元数姿态更新算法为：在车辆行驶过程中，一般不存在高频大机动环境，并且车载导航系统往往不工作在纯惯性导航方式，而是利用里程仪或零速条件进行组合导航，所以算法误差的影响有限，常用的5ms采样周期和二子样优化算法即可满足要求。
四、捷联惯导误差模型传感器误差、初值误差和算法误差是SINS的主要误差源，其中器件误差和初值误差又是影响导航结果的主要因素。
基于四元数法的捷联式惯性导航系统的姿态解算
0
sin C
cos C
b X EbZ
( 1) 根据欧拉角微分方程, 由角速度可 以求解 3 个姿态角。欧拉角微分方程式只有 3 个, 但每个 方程 Û x = f ( co s x , sin x ) X 都含有三角函数的运 算, 计算速度慢 , 且方程会出现/ 奇点0 , 方程式退 化, 故不能全姿态工作。 2. 2 方向余弦矩阵微分方程式 当一个坐标系相对另一个坐标系做一次或多 次旋转后可得到另外一个新的坐标系 , 前者往往 被称为参考坐标系或固定坐标系, 后者被称为动 坐标系, 他们之间的相互关系可用方向余弦表来 表示。方向余弦矩阵微分方程式可写为载体坐标 系相对导航坐标系旋转角速度的斜对称矩阵表达 式, 方向余弦表是对这两种坐标系相对转动的一 种数学描述。
E b C ÛE b = Cb 8 Eb , b Eb
2
姿态矩阵的计算方法
由于载体的姿态方位角速率较大 , 所以针对
姿态矩阵的实时计算提出了更高的要求。通常假 定捷联系统/ 数学平台0 模拟地理坐标系 , 即导航 坐标系; 而确定载体的姿态矩阵即为研究载体坐 标系 ( b) 和导航坐标系 ( E ) 的空间转动关系 , 一般
第 16 卷
第 10 期
光学 精密工程
O pt ics and Precision Eng ineer ing
2008 年 10 月 文章编号 1004 -924X( 2008) 10 - 1963 - 08
V ol. 16 N o. 10 Oct. 2008
பைடு நூலகம்
捷联惯导的解算程序
%====本程序为捷联惯导的解算程序(由惯性器件的输出解算出飞行器的位置、速度、姿态信息)======clear all;close all;clc;deg_rad=pi/180; %由度转化成弧度rad_deg=180/pi; %由弧度转化成度%-------------------------------从源文件中读入数据----------------------------------fid_read=fopen('IMUout.txt','r'); %path1_Den.dat 是由轨迹发生器产生的数据[AllDataNumofAllData]=fscanf(fid_read,'%g %g %g %g %g %g %g %g %g %g %g %g %g %g %g %g',[17 inf]);AllData=AllData';NumofEachData=round(NumofAllData/17);Time=AllData(:,1);longitude=AllData(:,2); %经度单位：弧度latitude=AllData(:,3); %纬度单位：弧度High=AllData(:,4); %高度单位：米Ve=-AllData(:,6); % 东向、北向、天向速度单位：米/妙Vn=AllData(:,5);Vu=AllData(:,7);fb_x=AllData(:,9); %比力（fx，fy，fz）fb_y=AllData(:,8); %指向右机翼方向为x正方向，指向机头方向为y正向，z轴与x轴和y轴构成右手坐标系单位：米/秒2fb_z=-AllData(:,10); %右前上pitch=AllData(:,11); %俯仰角（向上为正）单位:弧度head=-AllData(:,13); %偏航角（偏西为正）roll=AllData(:,12); %滚转角（向右为正）omigax=AllData(:,15); %陀螺输出（单位：弧度/秒，坐标轴的定义与比力的相同）omigay=AllData(:,14);omigaz=-AllData(:,16);%-------------------------------程序初始化--------------------------------------latitude0=latitude(1);longitude0=longitude(1); %初始位置High0=High(1);Ve0=Ve(1);Vn0=Vn(1); %初始速度Vu0=Vu(1);pitch0=pitch(1);head0=head(1); %初始姿态roll0=roll(1);TimeEach=0.005; %周期和仿真总时间TimeAll=(NumofEachData-1)*TimeEach;Omega_ie=0.7292115147E-4;%0.00007272205216643040; %地球自转角速度单位：弧度每妙g0=9.78;%------------------------------导航解算开始--------------------------------------%假设没有初始对准误差pitch_err0=pitch0+0*deg_rad;head_err0=head0+0*deg_rad;roll_err0=roll0+0*deg_rad;%初始捷联矩阵的计算《捷联惯导系统》P63 旋转顺序 head - pitch - roll %导航坐标系n为东北天方向载体坐标系b为右前上偏航角北偏西为正Tbn(1,1)=cos(roll_err0)*cos(head_err0)-sin(roll_err0)*sin(pitch_err0) *sin(head_err0);Tbn(1,2)=cos(roll_err0)*sin(head_err0)+sin(roll_err0)*sin(pitch_err0) *cos(head_err0);Tbn(1,3)=-sin(roll_err0)*cos(pitch_err0);Tbn(2,1)=-cos(pitch_err0)*sin(head_err0);Tbn(2,2)=cos(pitch_err0)*cos(head_err0);Tbn(2,3)=sin(pitch_err0);Tbn(3,1)=sin(roll_err0)*cos(head_err0)+cos(roll_err0)*sin(pitch_err0) *sin(head_err0);Tbn(3,2)=sin(roll_err0)*sin(head_err0)-cos(roll_err0)*sin(pitch_err0) *cos(head_err0);Tbn(3,3)=cos(roll_err0)*cos(pitch_err0);Tnb=Tbn';%位置矩阵的初始化《捷联惯导系统》P46 其中游动方位角 a＝0 假使初始经纬度确知Cne(1,1) = - sin(longitude0);Cne(1,2) = cos(longitude0);Cne(1,3) = 0;Cne(2,1) = - sin(latitude0) * cos(longitude0);Cne(2,2) = - sin(latitude0) * sin(longitude0);Cne(2,3) = cos(latitude0);Cne(3,1) = cos(latitude0) * cos(longitude0);Cne(3,2) = cos(latitude0) * sin(longitude0);Cne(3,3) = sin(latitude0);Cen=Cne';%初始四元数的确定《捷联惯导系统》 P151-152 方法本身保证了q1^2+q2^2+q3^2+q4^2=1q(2,1) = sqrt(abs(1.0 + Tnb(1,1) - Tnb(2,2) - Tnb(3,3))) / 2.0; q(3,1) = sqrt(abs(1.0 - Tnb(1,1) + Tnb(2,2) - Tnb(3,3))) / 2.0; q(4,1) = sqrt(abs(1.0 - Tnb(1,1) - Tnb(2,2) + Tnb(3,3))) / 2.0;q(1,1) = sqrt(abs(1.0 - q(2,1) ^2 - q(3,1) ^2 - q(4,1) ^2));% 判断q(1,1)的符号flag_q11=cos(head_err0/2.0)*cos(pitch_err0/2.0)*cos(roll_err0/2.0)-sin(head_err0/2.0)*sin(pitch_err0/2.0)*sin(roll_err0/2.0);if (flag_q11 >0) %此时q(1,1)取正if (Tnb(3,2) < Tnb(2,3))q(2,1) = - q(2,1);endif (Tnb(1,3) < Tnb(3,1))q(3,1) = - q(3,1);endif (Tnb(2,1) < Tnb(1,2))q(4,1) = - q(4,1);endelse %此时q(1,1)取负或0q(1,1) = - q(1,1);if (Tnb(3,2) > Tnb(2,3))q(2,1) = - q(2,1);endif (Tnb(1,3) > Tnb(3,1))q(3,1) = - q(3,1);endif (Tnb(2,1) > Tnb(1,2))q(4,1) = - q(4,1);endend%-------------------------迭代推算用到的参数的初始化------------------------Wiee_e = 0;Wiee_n = 0;Wiee_u = Omega_ie;Wiee = [Wiee_e Wiee_n Wiee_u]'; %地球速率在地球系中的投影东－北－天Lat_err(1)=latitude0;Lon_err(1)=longitude0;High_err(1)=High0;Ve_err(1)=Ve0;Vn_err(1)=Vn0;Vu_err(1)=Vu0;pitch_err(1)=pitch_err0;head_err(1)=head_err0;roll_err(1)=roll_err0;Re=6378137.0;%6378245.0; %地球长轴《惯性导航系统》 P28e=0.0033528106647474807198455286185206; %地球扁率精确值ee=0.00669437999014131699614;%----------------------------迭代推算开始-----------------------------------for i=1:NumofEachData%----------------------------惯性仪表数据的获得------------------------Wibb(1,1)=omigax(i); %指向右机翼方向为x正方向，指向机头方向为y正向，z轴与x轴和y轴构成右手坐标系Wibb(2,1)=omigay(i); %单位：弧度/妙Wibb(3,1)=omigaz(i); %右前上fb(1,1)=fb_x(i); %指向右机翼方向为x正方向，指向机头方向为y正向，z轴与x轴和y轴构成右手坐标系fb(2,1)=fb_y(i); %单位：米/秒2fb(3,1)=fb_z(i); %右前上%--------计算在姿态矩阵和位置矩阵更新时用到的参数------------------ RM=Re*(1.0-2.0*e+3.0*e*Cne(3,3)^2)+High_err(i); %《捷联惯导系统》P233 P235RN=Re*(1.0+e*Cne(3,3)^2)+High_err(i);% RN=Re*(1-ee)/(sqrt(1-ee*sin(Lat_err(i))))^3+High_err(i);% RM=Re/sqrt(1-ee*sin(Lat_err(i)))+High_err(i);%实验当地重力加速度计算《捷联惯导系统》P150 《惯性导航系统》 P35g=g0*((1.0+0.0052884*Cne(3,3)^2)-0.0000059*(1-(1-2*Cne(3,3)^2)^2))*(1 .0-2.0*High_err(i)/Re);tmp_slat=sin(Lat_err(i))*sin(Lat_err(i));Wien = Cne * Wiee; %地球速率在导航系中的投影Wenn(1,1) = -Vn_err(i)/RM;Wenn(2,1) = Ve_err(i)/RN; % <<惯性导航系统>> P45 考虑了地球转动的影响.Wenn(3,1) = Ve_err(i)*tan(Lat_err(i))/RN; %计算Wenn(不太精确)，更新速度和位置矩阵时用Winn=Wien+Wenn;Winb=Tbn*Winn;Wnbb=Wibb-Winb; %姿态速率在姿态更新时用到fn=Tnb*fb; % x-y-z 东－北－天% 速度的更新《捷联惯导系统》 P30 33 东－北－天difVe_err=fn(1,1)+(2*Wien(3,1)+Wenn(3,1))*Vn_err(i)-(2*Wien(2,1)+Wenn (2,1))*Vu_err(i);difVn_err=fn(2,1)-(2*Wien(3,1)+Wenn(3,1))*Ve_err(i)+(2*Wien(1,1)+Wenn (1,1))*Vu_err(i);difVu_err=fn(3,1)+(2*Wien(2,1)+Wenn(2,1))*Ve_err(i)-(2*Wien(1,1)+Wenn (1,1))*Vn_err(i)-g;Ve_err(i+1)=Ve_err(i)+difVe_err*TimeEach;Vn_err(i+1)=Vn_err(i)+difVn_err*TimeEach;Vu_err(i+1)=Vu_err(i)+difVu_err*TimeEach;High_err(i+1)=High_err(i)+Vu_err(i)*TimeEach;% 位置矩阵的实时更新《惯性导航系统》 P190Cne(1,1)=Cne(1,1)+TimeEach*(Wenn(3,1)*Cne(2,1)-Wenn(2,1)*Cne(3,1)); Cne(1,2)=Cne(1,2)+TimeEach*(Wenn(3,1)*Cne(2,2)-Wenn(2,1)*Cne(3,2)); Cne(1,3)=Cne(1,3)+TimeEach*(Wenn(3,1)*Cne(2,3)-Wenn(2,1)*Cne(3,3)); Cne(2,1)=Cne(2,1)+TimeEach*(-Wenn(3,1)*Cne(1,1)+Wenn(1,1)*Cne(3,1)); Cne(2,2)=Cne(2,2)+TimeEach*(-Wenn(3,1)*Cne(1,2)+Wenn(1,1)*Cne(3,2)); Cne(2,3)=Cne(2,3)+TimeEach*(-Wenn(3,1)*Cne(1,3)+Wenn(1,1)*Cne(3,3)); Cne(3,1)=Cne(3,1)+TimeEach*(Wenn(2,1)*Cne(1,1)-Wenn(1,1)*Cne(2,1)); Cne(3,2)=Cne(3,2)+TimeEach*(Wenn(2,1)*Cne(1,2)-Wenn(1,1)*Cne(2,2)); Cne(3,3)=Cne(3,3)+TimeEach*(Wenn(2,1)*Cne(1,3)-Wenn(1,1)*Cne(2,3));% Mat_Wenn(1,1)=0;% Mat_Wenn(1,2)=Wenn(3,1);% Mat_Wenn(1,3)=-Wenn(2,1); %Wenn的反对阵矩阵取负% Mat_Wenn(2,1)=-Wenn(3,1); %这里位置矩阵的及时修正为:dCne/dt=Mat_Wenn*Cne% Mat_Wenn(2,2)=0;% Mat_Wenn(2,3)=Wenn(1,1);% Mat_Wenn(3,1)=Wenn(2,1);% Mat_Wenn(3,2)=-Wenn(1,1);% Mat_Wenn(3,3)=0;%% Mat_Wenn=Mat_Wenn*Cne*TimeEach;% Cne=Cne+Mat_Wenn;Cen=Cne';% 计算经纬度Lat_err(i+1)=asin(Cne(3,3));Lon_err(i+1)=atan(Cne(3,2)/Cne(3,1)); %这是经度的主值if (Cne(3,1) < 0)if (Lon_err(i+1) > 0)Lon_err(i+1) = Lon_err(i+1) - pi;elseLon_err(i+1) = Lon_err(i+1) + pi;endend% 四元数的及时修正《惯性导航系统》 P194% Mat_Wnbb=[ 0, -Wnbb(1,1), -Wnbb(2,1), -Wnbb(3,1); % Wnbb(1,1), 0, Wnbb(3,1), -Wnbb(2,1); % Wnbb(2,1), -Wnbb(3,1), 0, Wnbb(1,1); % Wnbb(3,1), Wnbb(2,1), -Wnbb(1,1), 0];% q=q+Mat_Wnbb*q*TimeEach/2.0;q(1,1)=q(1,1)+TimeEach*(-Wnbb(1,1)*q(2,1)-Wnbb(2,1)*q(3,1)-Wnbb(3,1)* q(4,1))/2.0;q(2,1)=q(2,1)+TimeEach*(Wnbb(1,1)*q(1,1)+Wnbb(3,1)*q(3,1)-Wnbb(2,1)*q (4,1))/2.0;q(3,1)=q(3,1)+TimeEach*(Wnbb(2,1)*q(1,1)-Wnbb(3,1)*q(2,1)+Wnbb(1,1)*q (4,1))/2.0;q(4,1)=q(4,1)+TimeEach*(Wnbb(3,1)*q(1,1)+Wnbb(2,1)*q(2,1)-Wnbb(1,1)*q (3,1))/2.0;% 四元数归一化处理q_norm=sqrt(sum(q.*q));q=q/q_norm;% 计算姿态矩阵 TnbTnb(1,1) = q(1,1) ^2 + q(2,1) ^2 - q(3,1)^2 - q(4,1)^2;Tnb(1,2) = 2.0 * (q(2,1) * q(3,1) - q(1,1) * q(4,1));Tnb(1,3) = 2.0 * (q(2,1) * q(4,1) + q(1,1) * q(3,1));Tnb(2,1) = 2.0 * (q(2,1) * q(3,1) + q(1,1) * q(4,1));Tnb(2,2) = q(1,1)^2 - q(2,1)^2 + q(3,1)^2 - q(4,1)^2;Tnb(2,3) = 2.0 * (q(3,1) * q(4,1) - q(1,1) * q(2,1));Tnb(3,1) = 2.0 * (q(2,1) * q(4,1) - q(1,1) * q(3,1));Tnb(3,2) = 2.0 * (q(3,1) * q(4,1) + q(1,1) * q(2,1));Tnb(3,3) = q(1,1)^2 - q(2,1)^2 - q(3,1)^2 + q(4,1)^2;Tbn=Tnb';flag_pitch=asin(Tnb(3,2));flag_roll=atan(-Tnb(3,1)/Tnb(3,3));flag_head=atan(-Tnb(1,2)/Tnb(2,2));if(Tnb(3,3)<0)if(flag_roll<0)flag_roll=flag_roll+pi;endif(flag_roll>0)flag_roll=flag_roll-pi;endend% 偏航角范围 -180度——180度北偏西为正if(Tnb(2,2)<0)if(flag_head<0)flag_head=flag_head+pi;endif(flag_head>0)flag_head=flag_head-pi;endend% 姿态角更新pitch_err(i+1)=flag_pitch;head_err(i+1)=flag_head;roll_err(i+1)=flag_roll;% 解算完毕由对准结果、陀螺、加表的输出解算出载体的位置、速度、姿态%----------------------计算解算误差------------------ddLat(i)=(Lat_err(i)-latitude(i))*rad_deg; %纬度误差单位：度ddLog(i)=(Lon_err(i)-longitude(i))*rad_deg; %经度误差单位：度ddHigh(i)=High_err(i)-High(i); %高度误差单位：米ddVe(i)=Ve_err(i)-Ve(i);ddVn(i)=Vn_err(i)-Vn(i); % 速度误差单位：米/妙2ddVu(i)=Vu_err(i)-Vu(i);ddpitch(i)=(pitch_err(i)-pitch(i))*rad_deg*3600; %姿态误差单位：度ddhead(i)=(head_err(i)-head(i))*rad_deg*3600;ddroll(i)=(roll_err(i)-roll(i))*rad_deg*3600;endfclose(fid_read);%---------------------------绘图开始--------------------------------- figure(1)plot(Time,ddLog)ylabel('经度误差(度)'),xlabel('时间(秒)');figure(2)plot(Time,ddLat)ylabel('纬度误差(度)'),xlabel('时间(秒)');figure(3)plot(Time,ddHigh);ylabel('高度误差(米)'),xlabel('时间(秒)');figure(4)plot(Time,ddhead)ylabel('偏航角误差(角妙)'),xlabel('时间(秒)'); figure(5)plot(Time,ddpitch)ylabel('俯仰角误差(角妙)'),xlabel('时间(秒'); figure(6)plot(Time,ddroll);ylabel('滚转角误差(角妙)'),xlabel('时间(秒)'); figure(7)plot(Time,ddVe);ylabel('东向速度误差(米/秒)'),xlabel('时间(秒)'); figure(8)plot(Time,ddVn)ylabel('北向速度误差(米/秒)'),xlabel('时间(秒)'); figure(9)plot(Time,ddVu)ylabel('天向速度误差(米/秒)'),xlabel('时间(秒)');%------------------------------绘图结束-------------------------------。
捷联惯导结算原理
0 cos sin ， Rz sin 0 cos
sin cos 0
0 0 1
cos cos sin sin sin cos cos sin sin cos sin cos T11 T12 T13 Ry Rx Rz cos sin cos cos sin T21 T22 T23 sin cos cos sin sin sin sin cos sin cos cos cos T T T 31 32 33 b 由姿态矩阵 C n 反解飞行器姿态欧拉角：
（5） 速度的计算
t t t t t 0 2iez etz ety 2iey Vxt Vx 0 t t b t t t t 0 2iex etx Vyt 0 Vy Cb f 2iez etz t Vz g Vzt 2 t t 2 t t 0 iey ety iex etx
o o sin 1 T23 , 90 , 90
tg 1
T13 180o , 180o , T33
tg 1
T21 o o , 180 , 180 T 22
图 6 东向北向速度变化曲线
阶段总结：1.学习了平台式和捷联式惯导的惯导解算方法并进行了仿真计算。 2.平台式惯导物理平台时刻跟踪当地水平东北天地理系， 加速计的比 力信息直接投影在导航系中，可直接进行导航速度和位置解算。载体的姿态可直 接从平台框架直接得出；而捷联式惯导用数学平台取代实体的物理平台，通过求
用四元数法的捷联惯性导航姿态解算程序
;no dirg ;)')s/m( /yticoleV'(lebaly ;)')sm01( / emiT'(lebalx ;)'noitaluclaC yticoleV'(eltit ;)'Z :etanidrooC noitagivaN','Y :etanidrooC noitagivaN','X :etanidrooC noitagivaN'(dnegel )yticolev,mt(tolp erugif ;no dirg ;)')eerged( /legnA'(lebaly ;)')sm01( / emiT'(lebalx ;)'noitaluclaC erutseG'(eltit ;)'legnA waY','legnA lloR','legnA hctiP'(dnegel ;)'.-b',):,3(ELGNA,mt,'.g',):,2(ELGNA,mt,'-r',):,1(ELGNA,mt(tolp ;ip/081*ELGNA=ELGNA erugif dne
值比度速加/压电的向轴个三计度速加% ?=za_orez% ?=ya_orez% ?=xa_orez% 压电点零的向轴个三计度速加%
*********************************************************% % 值度速加的应相为换转据数将% 3*4201/cca_atad=cca_atad ;]z_cca;y_cca;x_cca[=cca_atad 压电拟模为换转字数度速加% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% ;)'txt.zetarelecca'(daol=z_cca ;)'txt.yetarelecca'(daol= y_cca ;)'txt.xetarelecca'(daol= x_cca ;4201/3=etar_cca% **************据数的计度速加入读****************% ;)'txt.zoryg'(daol=z_oryg ;)'txt.yoryg'(daol=y_oryg ;)'txt.xoryg'(daol=x_oryg 据数的仪螺陀入读**********% 据数入读****************************% ;']g-,0,0[=G 2^s/m8.9 位单%;24108.9=g 量矢度速加的生产力重% ;lla raelc ;lla esolc
2.2 捷联惯航系统算法
2.1 四元数基础知识
i, j, k 服从如下运算公式
i i j j k k 1 i j j i k j k k j i k i i k j qP 1i P 2 jP 3k
PP 泛指矢量部分
λ 称作标量部分， P 1i P 2 jP 3 k 称作矢量部分 四元数的另一种表示法 q ,
1
2.3 姿态计算 姿态角方法
T33 T23 0 0
真 /2 / 2 主 主 主 1800 主 1800
象限
(0 0 ,900 ) (0 0 ,900 ) (900 ,1800 ) (1800 ,2700 )
T11 T12 真 0 /2 0 3 / 2 主 主 3600
q
2 2 1 2 2 2 3
q qq* P P P
则称为规范化四元数
q 1
2.1 四元数基础知识
5．逆四元数
q
1
1 q
q* q
当 q 1时
q
1
q*
6．四元数的除法
若 qh
若 hq
M M
则 则
q Mh
1
1
qh M
（含义不确切 ）
M 不能表示为 q h
18
2.3 姿态计算 姿态角方法
根据四元数乘法可知，两个相同的单位四元数相乘， 其结果为-1，即
sin n n sin 2 2 2 2
从而可以求出
2
n q
cos n sin 2 2 2 2
用四元数法的捷联惯性导航姿态解算程序
用四元数法的捷联惯性导航姿态解算程序close all;clear all;%重力产生的加速度矢量g=9.80142;%单位9.8m/s^2G=[0,0,-g]';%****************************读入数据%**********读入陀螺仪的数据gyro_x=load('gyrox.txt');gyro_y=load('gyroy.txt');gyro_z=load('gyroz.txt');%****************读入加速度计的数据**************%acc_rate=3/1024;acc_x =load('acceleratex.txt');acc_y =load('acceleratey.txt');acc_z=load('acceleratez.txt'); %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %加速度数字转换为模拟电压data_acc=[acc_x;acc_y;acc_z];data_acc=data_acc/1024*3%将数据转换为相应的加速度值%%*********************************************************%加速度计三个轴向的零点电压%zero_ax=?%zero_ay=?%zero_az=?%加速度计三个轴向的电压/加速度比值%rate_ax=? %单位是m/s^2/V%rate_ay=?%rate_az=?%acc_x=acc_x*acc_rate;%acc_y=acc_y*acc_rate;%acc_z=acc_z*acc_rate;aver_acc_x=mean(acc_x)aver_acc_y=mean(acc_y)aver_acc_z=mean(acc_z)%采样时间dtime=0.01;tm=0:dtime:0.01* (size(gyro_x,2)-1);%个数numn_point=size(gyro_x,2);%图1figureplot(tm,data_acc(1,:),'-',tm,data_acc(2,:),'.',tm,data_acc(3,:),'-.'); title('加速度计的采样曲线');legend('x_ACC','Y_ACC','Z_ACC');xlabel('Time / (10ms)');ylabel('Accelerate/ (m/s'')');grid on;%plot(tm,acc_x,'-',tm,acc_y,'.',tm,acc_z,'-.');%title('加速度的计的采样曲线'):%对采样曲线进行低通滤波a=[1,2,4,2,1];%gyro_x=filter(a/sum(a),1,gyro_x);%gyro_y=filter(a/sum(a),1,gyro_y);%gyro_z=filter(a/sum(a),1,gyro_z);%比例变换gyro_x=gyro_x/1024*3/0.6;gyro_y=gyro_y/1024*3/0.6;gyro_z=gyro_z/1024*3/0.6;%零点电压--陀螺仪，取前80个数的平均电压zero_gx=sum(gyro_x(1:80))/80zero_gy=sum(gyro_y(1:80))/80zero_gz=sum(gyro_z(1:80))/80%减去零点gyro_x=(gyro_x-zero_gx)/0.0125/180*pi; gyro_y=(gyro_y-zero_gy)/0.0125/180*pi; gyro_z=(gyro_z-zero_gz)/0.0125/180*pi;%gyro_x=(gyro_x-2.5)/0.0125/180*pi;%gyro_y=(gyro_y-2.5)/0.0125/180*pi;%gyro_z=(gyro_z-2.5)/0.0125/180*pi;%测试数据accelerate=zeros(3,n_point);accelerate(1,1:100)=10;accelerate(1,101:200)=-10;accelerate(1,201:300)=0;%陀螺仪数据gyro_x=zeros(1,n_point);gyro_y=zeros(1,n_point);gyro_z=zeros(1,n_point);gyro_z(1:100)=pi/3;gyro_z(101:200)=-pi/3;%重力轴始终有加速度accelerate(3,:)=accelerate(3,:)+9.8;figureplot(tm,accelerate(1,:),'-',tm,accelerate(2,:),'.',tm,accelerate(3,:),'-.');title('加速度计的采样曲线');legend('x_ACC','Y_ACC','Z_ACC');xlabel('Time / (10ms)');ylabel('Accelerate/ (m/s'')');grid on;%画出陀螺仪的采样曲线figureplot(tm,gyro_x,'r-',tm,gyro_y,'g.',tm,gyro_z,'b-.');title('陀螺仪的采样曲线');legend('x_Gyro','Y_Gyro','Z_Gyro');xlabel('Time / (10ms)');ylabel('Angel_rate/ (degree/s)');grid on;%size(gyro_x)%size(gyro_y)%size(gyro_z)data_gyro=[gyro_x;gyro_y;gyro_z];%转移矩阵--即方向余弦矩阵T=eye(3); %T是3*3的单位矩阵,初始转移矩阵%四元数矩阵，存储每步更新之后的四元数，方便以后绘图Q=zeros(4,n_point);%四元数的初始值确定，假定一开始导航坐标系与载体坐标系是重合的，因此方向余弦矩阵，是单位矩阵，利用它们之间的关系确定四元数的初始值。
捷联惯性导航系统的解算方法
CC
RP
0 0
H.
C
R
P0. 0
R0.
0
2010-03-19
整理课件
Yb'' Yb Yb' H
N
17
b nbx b nby
cos
0
R
b nbz
sin R
P. cos R 0
R.
0
1
H. sin R 0
0 sin R cos P P.
1
sin P R.
kb jn
ib j
kn k
b n kb kn
2010-03-19
21
整理课件
固定矢量的坐标变换
矢量的坐标变换
固定矢量的坐标变换是一个在空间大小和方向都不 变的矢量在两个不同方位的坐标系轴向分量之间的变 换关系，也即同一个矢量在两个不同的坐标系轴向投 影之间的变换关系。
旋转矢量的坐标变换
是指一个矢量大小不变，但在方向上转动了一个位 置，这个矢量转动前和转动后在同一个坐标系轴向 分量之间的变换关系。
2010-03-19
22
整理课件
固定矢量的坐标变换
一个矢量r，写成载体坐标系轴向分量形式：
r X bib Yb jb Z b kb r bT b
rb
X Y
b
b
ib j
b
Zb
kbb
b:载体坐标系 n:地理坐标系
同一个矢量r，如果写成地理坐标系轴向分量形式：
r X nin Yn jn Z n k n r nT n 由于r是同一个矢量，故
惯性导航系统原理
1
整理课件
3 捷联式惯导系统
捷联惯性导航总结
z
0 x
y
姿态矩阵计算方法
3 四元数微分方程及其解
1 qk 1 exp( )qk Mq k qk rk 2
rk ac as x i as y j as z k
(0.5 )2 (0.5 )4 ac cos( ) 1 2 2! 4!
tk b nb
t
v f dt
b tk
t
速度微分方程求解
2 速度积分算法
v f dt [2ω ωen ] v dt g1 dt
n n 0 0 n ie n n n 0
t
t
t
v
n k 1
v u gt
n k n
b
v
n l 1
[ I 2Ωie tl Ωen tl ]v
v f dt
b
t
1 tk 1 αk 1 α ωdt 2 tk
α ωdt
tk
tk
t
捷联导航算法
捷联惯导误差分析
主要误差源
1 初始对准误差
2 惯性器件误差
3 计算误差
误差传播方程：误差源与系统性能的相互关系的 方程，主要用来阐述各种类型误差随时间的传播 过程。
捷联惯导误差分析
sin( / 2) (0.5 ) (0.5 ) as 0.5(1 ) 3! 5!
2 4
姿态矩阵计算方法
4 圆锥误差
σ αk 1 αk 1
α ωdt
tk t
1 tk 1 αk 1 α ωdt 2 tk
姿态矩阵计算方法
5 姿态角计算
b nbz
捷联式惯性导航系统原理
1、方向余弦表cos cos sin sin sin sin cos cos sin sin cos sin sin cos cos cos sin cos sin sin sin cos sin sin cos sin cos cos cos C ψϕψθϕψϕψθϕθϕψθψθθψϕψθϕψϕψθϕθϕ-+-⎡⎤⎢⎥=-⎢⎥⎢⎥+-⎣⎦（1.0.1）X E Y C N Z ζ⎡⎤⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦（1.0.2） 在列写惯导方程需要采用方向余弦表，因为错误！未找到引用源。
α较小，经常采用两个假设，即：cos 1sin 1αα≈≈ （1.0.3）式中 α-两坐标系间每次相对转动的角度。
由于在工程实践中可以使其保持很小，所以进一步可以忽略如下形式二阶小量，即：sin sin 0αβ≈ （1.0.4）式中β-两坐标系间每次相对转动的角度。
可以将C 近似写为：111C ψϕψθϕθ-⎡⎤⎢⎥=-⎢⎥⎢⎥-⎣⎦（1.0.5） 2、用四元素表示坐标变换对于四元素123q p i p j p k λ=+++，可以表示为如下形式cossincos sincos sincos 2222q i j k θθθθαβγ=+++ （2.0.1）式（2.0.1）的四元数称为特殊四元数，它的范数1q =。
1'R q Rq -= （2.0.2）式中''''R xi yj zk R x i y j z k=++=++ （2.0.3）将q 和1q -的表达式及式（2.0.3）带入（2.0.2），然后用矩阵表示为：()()()()()()()()()22221231231322222123213231222213223131222''22'22p p p p p p p p p x x y p p pp p p p p p yz z p p p p p p p p p λλλλλλλλλ⎡⎤+--+-⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=-+--+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥+-+--⎣⎦（2.0.4）由四元素到方向余弦表的建立123cos cos22sin cos22sin sin22cos sin22p p p θψϕλθψϕθψϕθψϕ-=-=-=+= （2.0.5） 将式（2.0.5）带入式（2.0.4），有cos cos sin cos sin cos sin sin cos cos sin sin sin cos cos cos sin sin sin cos cos cos cos sin sin sin sin cos cos C ϕψϕθψϕψϕθψϕθϕψϕθψϕψϕθψϕθθψθψθ-+⎡⎤⎢⎥=---+⎢⎥⎢⎥-⎣⎦（2.0.6）3、四元数转动公式的进一步说明采用方向余弦矩阵描述飞行器姿态运动时，需要积分姿态矩阵微分方程式，即C C =Ω （3.0.1）式中 C -动坐标系相对参考坐标系的方向余弦阵Ω-动坐标系相对参考坐标系角速度ω的反对称矩阵表达式 其中C 为公式（1.0.5）提供000z y zx y xωωωωωω⎡⎤-⎢⎥Ω=-⎢⎥⎢⎥-⎣⎦（3.0.2）采用（3.0.1）计算需要列写9个一阶微分方程式，计算量大。
捷联惯性导航原理
1 0 0 cos 0 sin cos sin 0
Cnb 0 cos
sin
0
1
0
sin
cos
0
0 sin cos sin 0 cos 0 0 1
cos cos
sin cos
sin
2.捷联惯导力学编排方程
姿态矩阵：从导航坐标系(n系)到载体坐标系(b系)的变 换矩阵；
sin sin sin cos cos
Cnb
sin cos
cos sin sin sin cos
cos sin sin sin cos cos cos
陀螺输出为角速度）-----应将(h/6) （1/2）等括起来
q(t h) q(t) h / 6(k1 2k2 2k3 k4 )
k1
1/
2[q(t
)
*
b tb
(t
)]
k3
k2
1/
1/ 2{[q(t)
2{[q(t)
k22k21h]h*] *tbbtbb(t(thh//22))}}
初始对准
对于平台式惯导系统而言，初始对准的 任务是控制平台使其跟踪导航坐标系
2(q1q3 q0q2 )
2(q1q2 q0q3 ) q02 q12 q22 q32
2(q2q3 q0q1)
2(q1q3 q0q2 ) 2(q2q3 q0q1)
q02 q12 q22 q32
3.31 、姿态捷更新联算法惯导系统的算法
V ak ak1
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2010-03-19
10
（6）制导和控制信息的提取
制导和控制信息的提取，载体的姿态既可用 来 显示也是控制系统最基本的控制信息。 此外，载体的角速度和线速度信息也都是控 制 载体所需要的信息。
这些信息可以从姿态矩阵的元素和陀螺加速 度 计的输出中提取出来。
2010-03-19
11
捷联式惯导系统算法流程图
2010-03-19 20
方向余弦法
写成矩阵形式为：
ib ib in j j i b b k b n in kb ib bj b k b ib in j i b Cn b n kb in
2010-03-19
ib jn j j
b
kb n jn
ib k n in j k j b n n kb k n k n in n j
b b Cn n
k n
ib kn j k b n kb k n
2010-03-19
（3）惯性仪表的误差补偿
对捷联式惯导系统来说，由于惯性仪表直接安装 在载体上，因此，载体的线运动和角运动都引起 较大的误差。 为了保证系统的精度，必须对惯性仪表的误差进 行 补偿，最好的补偿方法是计算机补偿。
在计算机中通过专用的软件来实现误差补偿。
2010-03-19
8
（4）姿态矩阵的计算
''
2010-03-19
Zb
Zb U Z ' b
''
P
. H . R
Yb'' Yb Yb
'
H O
. P
N
E
Xb
' Xb
R
Xb
15
用欧拉角表示的姿态矩阵
' X b cos H sin H 0 E N ' 0 cos H Y sin H b ' 0 0 1 U Zb － v___ CH '' 0 1 X b Y '' b 0 cos P 0 sin vP - cos P Z Z '' ___ b b － CP ' 0 X b ' sin P Yb '
2010-03-19
6
（2）系统初始化 为何要初始化？
给定载体（舰船、飞行器、车辆等）的初始位置 （经度和纬度）和初始速度等初始信息。 导航平台的初始对准 平台式 用物理的方法来实现 捷联式 姿态矩阵的初始值 惯性仪表的校准 陀螺仪 标度系数 漂移 进行测定 偏置 加速度计
7
Calibration
2010-03-19
22
固定矢量的坐标变换
一个矢量r，写成载体坐标系轴向分量形式 ib X ： Y b j bT r r X b ib Yb jb Z b k b r b b
b
b b Z b
k b
b:载体坐标系 n:地理坐标系
Zb
'' Zb U PZ b
'
. H R .
Yb'' Yb
H
Yb'
O E
'' Xb ' Xb
N
R
Xb
P .
X b cos R 0 sin 0 1 Yb 0 v - cos R Z Z b sin R 0 ___ b －
CR
'' R X b Yb'' ''
. H sin R 0 cos R
b nbz
2010-03-19
返回3.2
19
3.2.2 方向余弦法
方向余弦表示的姿态矩阵
方向余弦法——用矢量的方向余弦来表示姿态矩阵的方法。
用in, jn, kn——表示沿地理坐标系轴向的单位矢量。 ib, jb, kb——沿载体坐标系轴向的单位矢量。ib在地理坐 标系内的方位完全可以由ib的三个方向余弦来确定，其 表达式为
2010-03-19
4
接联式惯导的算法的基本内容
（1）系统的启动和自检测 （2）系统初始化 （3）惯性仪表的误差补偿 （4）姿态矩阵的计算 （5）导航计算 （6）制导和控制信息的提取
2010-03-19
5
（1）系统的启动和自检测
系统启动后，各个部分的工作是否正常，要 通过自检测程序加以检测，其中包括电源、惯 性 仪表、计算机以及计算机软件。 通过自检测，发现有不正常，则发出告警信息(或 故障码)。系统的自检测是保证系统进入导航状态 后能正常工作、提高系统可靠性的措施。
. P R . . H
. H cos P cos R b . P cos R 0 sin R cos P 1 nbx b R . 0 1 sin P nby . b sin R cos P cos R H 0 nbz b sin R cos P 0 nbx 1 cos P cos R b sin P sin R nby cos P cos R sin P cos P b cos R sin R nbz 0
启动
自检测 初始化
姿态阵计算
NO
迭代次数
YES
导航计算
控 制 信息提 取
返回9
2010-03-19 12
3.2 姿态矩阵的计算
捷联式惯导中，载体地理位置就是地理坐标系相 对 地球坐标系的方位。而载体的姿态和航向则是载 体 坐标系相对于地理坐标系的方位关系。确定两 个坐 标系的方位关系问题，是力学中的刚体定点 转到理 论。在刚体定点转动理论中，描述动坐标系 相对参 考坐标系方位关系的方法有多种。 三参数法 欧拉角法 ，是欧拉在1776年提出的。 四元数法。威廉.哈密顿(William Hamilton)在 四参数法 1843年发明的，首先在数学中引入四元数， 以 后用在刚体定位问题。凯里.克莱茵（ CayleyKlein）参数法，是在1897年提出的。 九参数法 基于方向余弦的概念，也称 方向余弦法。 13 2010-03-19 等效转动矢量法
同一个矢量r，如果写成地理坐标系轴向分量形式：
Cn
b
18
欧拉角法应用中的问题
求解方程可以直接得到航向和姿态信息，欧 拉角法得到的 姿态阵永远是正交阵，用这个矩 阵将比力fb→fn信息的坐标 变换时，变换后的信 息中不存在非正交误差。因此，用欧拉 角法得 到的姿态矩阵无需进行正交化处理。 欧拉角微分方程中包含三角函数的运算， 给实时计算 垂 带来困难，当P=90 时，方程式 出现“奇点”，使计算溢出 直 。 发 射 困 b . P sin R cos P nbx cos P cos R 0 1 难 R sin P sin R b cos P cos R sin P nby ！ . cos P
3.2 姿态矩阵的计算
3.2.1 欧拉角法 3.2.2 方向余弦法 3.2.3 四元数法 3.2.4 等效转动矢量法
2010-03-19
14
3.2.1 欧拉角法
一个动坐标系相对参考坐标系的方位，完全可以由动坐 标系依次绕3个不同的轴转动的3个转角来确定。 如把OXbYbZb作为动坐标系， ENU作为参考坐标系，则航向 角H，纵摇角（俯仰角）P和横 摇角（横滚角、倾斜角）R。就 是一组欧拉角。 欧拉角没有严格的定义，根 据需要，可以选用不同的欧拉 角组。第一次转动，可以绕三 个轴中的任一个转动，故有3种 可能，第二次有2种可能，第三 次也有2种可能。总共有12种可 能。
惯性导航系统原理
3 捷联式惯导系统 程向红 2010.03.19
3 捷联式惯导系统
3.1 捷联式惯导算法概述 3.2 姿态矩阵的计算 3.3 姿态矩阵计算机执行算法
2010-03-19
2
3.1 捷联式惯导算法概述
加速度计组
b SF n Cb n SF b in
初始条件
VE
导航计算机
b ib b f ib
捷联式惯导算法
P, R, H
, L,VE ,VN
根据捷联式惯导的应用和功能要求不同，计算的内容和要 求，有很大的差别。常有
SINS——Strapdown Inertial Navigation Systems SVRU—— Strapdown Vertical Reference Uint SAHRS——Strapdown Attitude and Heading Reference Systems IMU——Inertial measurement Unit
陀螺仪组
ib
b
姿态矩 阵计 算
H P R
VN
t
b ib b f ib
捷联式惯导算法
P, R, H
, L,VE ,VN
捷联式惯导航系统是一个信息处理系统，就是将载体上安装的惯性 仪表所测量的载体运动信息，经过计算处理成所需要的导航信息。
2010-03-19 3
捷联式惯性导航系统=信息处理系统
ib (ib in )in (ib j n ) j n (ib k n )k n cos(ib in )
j b ( j b i n )i n ( j b j n ) j n ( j b k n ) k n