第五章动力吸振器
第五章动力吸振器

F (t ) FA sin t
4
回顾:单自由度强迫振动的解。
Cx Kx F (t ) m x
方程的通解由两部分组成, x(t ) x1 (t ) x2 (t )
x1 (t ) Xe
n t
F (t ) FA sin t
sin( 1 nt )
41
减振器
减振器的作用
• 减振器与弹性元件承担着缓冲击和减振的任务, 阻尼力过大,将使悬架弹性变坏,甚至使减振 器连接件损坏。因面要调节弹性元件和减振器 这一矛盾。 • (1) 在压缩行程(车桥和车架相互靠近),减振 器阻尼力较小,以便充分发挥弹性元件的弹性 作用,缓和冲击。这时,弹性元件起主要作 用。 • (2) 在悬架伸张行程中(车桥和车架相互远离), 减振器阻尼力应大,迅速减振。 • (3) 当车桥(或车轮)与车桥间的相对速度过大 时,要求减振器能自动加大液流量,使阻尼力 始终保持在一定限度之内,以避免承受过大的 42 冲击载荷。
33
Thank you for your listening!
34
【作业9】如图示梁中点放一电动机。系统的固 有频率 0 为31.3,转速为300r/min,产生的动荷 载幅值P=1kN 问:1)应加动力吸振器吗?2)设计吸振器。 (许可振幅为1cm)
Psinθt
35
【作业】:如图示梁中点放一点动机。重2500N,电动机使梁中点
2 K m 式中,0 为主振动系统的固有频 率; 为吸振器与 M M 主振系的质量比 ; b 为吸振器与主振系的固 有频率之比。 17 0
一个特殊情况就是动力吸振器的频率 等于主振系固有频率的情况。此时,
ω0 b
系统固有频率与质量比的关系曲线
动力吸振器研究发展历史

动力吸振器的研究历史主要分为黎明期、发展期、扩展期和应用期4个阶段。
一、黎明期(1909年到20世纪30年代)仅由质量和弹簧构成的无阻尼动力吸振器很久以前就已出现,这种动力吸振器从1909年开始就出现在论文和专利中,其力学模型如图1所示。
图1 无阻尼动力吸振器这里,M 、K 是主振动系统的质量和弹簧刚度,m 、k 是动力吸振器的质量和弹簧刚度。
x1、x2分别为主振动系统和动力吸振器的位移。
假设作用在主振动系统上的定常激励力为t P ωsin 0,则其响应为:t P k m k M k K m k x ωωωωsin ))(-(022221--+-= 1928年,Ormondroyd 与 Den Hartog 发表的论文指出,对于激励力频率变动的情况,有阻尼动力吸振器有效,并且存在最优阻尼使得振幅为最小。
由此引起了对于有阻尼动力吸振器,也就是通常所说的动力吸振器的最优设计的研究热潮。
四年后的1932年, Erich Hahnkamm 在德国杂志 ngenleur - Archiv 上发表了题为“变频激励力作用下的机械振动的阻尼”的论文。
该论文首次揭示了动力吸振器的阻尼为零和为无限大时响应曲线的两个交点是不随阻尼变化的特定点,并且利用这两个定点的特点推导出了最优同调的条件。
二、发展期(20世纪40年代到50年代)1940年出版的由 Den Hartog 著的“ Mechanical Vibration (第2版)”中,非常完美地推导出了最优同调条件的简便设计关系式,进一步完善了定点理论,Den Hartog 给出的最优同调条件为unn+=Ω11ω 在此条件下,PQ 定点的高度为 uu +=2|x x max st 1 其中M m u /=为质量比,n n Ω和ω分别为动力吸振器和主振动系统的固有角频率。
1946年,在最优同调关系的基础上, Brock 推导出了最优阻尼的条件式。
这个结果是在两个定点等高,并且为曲线上最大点的条件下经过非常复杂的推导得来的。
第十二讲—动力吸振器
切向无外力,故切向加速度为0
( ) Rθ cosϕ + Rθ 2 sinϕ + r θ +ϕ = 0
cosϕ ≈ 1,sinϕ ≈ ϕ,θ ≈ ω
ϕ
+
R r
ω 2ϕ
=
R+ r
r
θ0ω 2
sin ωt
单摆运动方程
16
机械与运载工程学院
单摆运动方程 单摆固有频率
ϕ
+
R r
ω 2ϕ
=
R+ r
r
θ0ω 2
sin ωt
x2
无阻尼动力吸振器系统
m2
m1、 k1:主系统的质量和弹簧刚度
k2 x1
m1 上作用有简谐激振力
F1 sin ωt
m1
阻尼动力吸振器:
k1
质量 m2 弹簧 k2
4
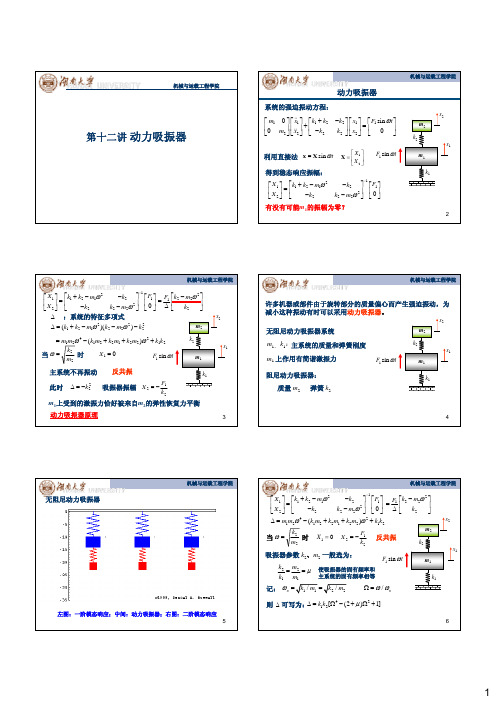
无阻尼动力吸振器
机械与运载工程学院
左图:一阶模态响应;中间:动力吸振器;右图:二阶模态响应 5
机械与运载工程学院
⎡ ⎢⎣
X1 X2
⎤ ⎥⎦
⎡X1 ⎤
⎢ ⎣
X
2
⎥ ⎦
=
F1 Δ
⎡⎢k2 ⎣
− m2ω k2
2
⎤ ⎥ ⎦
X 0 = F1 / k1
X1 =
1− Ω2
X 0 Ω4 − (2 + μ)Ω2 +1
X2 =
1
X0 Ω4 − (2 + μ)Ω2 +1
7
机械与运载工程学院
4 X1 / X0
2
X2 / X0
μ = 0.3 X1 =
1− Ω2
反共振
动力吸振器

动力吸振器————————————————————————————————作者:————————————————————————————————日期:分类号:U27;U4610710- 2009122042硕士学位论文变质量动力吸振器及其控制策略研究房祥波导师姓名职称高强教授申请学位级别工学硕士学科专业名称车辆工程论文提交日期年月日论文答辩日期年月日学位授予单位长安大学ﻬStudyof Tuned VibrationAbsorberBasedonVariableMassand It’s Control StrategyA Dissertation Submitted for theDegree of MasterCandidate: FangXiangboSupervisor:Prof.GaoQiangChang’an University, Xi’an, Chinaﻬ论文独创性声明本人声明:本人所呈交的学位论文是在导师的指导下,独立进行研究工作所取得的成果。
除论文中已经注明引用的内容外,对论文的研究做出重要贡献的个人和集体,均已在文中以明确方式标明。
本论文中不包含任何未加明确注明的其他个人或集体已经公开发表的成果。
本声明的法律责任由本人承担。
论文作者签名:年月日论文知识产权权属声明本人在导师指导下所完成的论文及相关的职务作品,知识产权归属学校。
学校享有以任何方式发表、复制、公开阅览、借阅以及申请专利等权利。
本人离校后发表或使用学位论文或与该论文直接相关的学术论文或成果时,署名单位仍然为长安大学。
(保密的论文在解密后应遵守此规定)论文作者签名: 年月日导师签名: 年月日摘要自适应动力吸振器是振动控制领域的研究热点,其通过调整自身参数改变固有频率,以跟踪外界激励频率,从而在较大的带宽上减小主系统振动,克服了传统动力吸振器有效带宽过窄的缺点。
与当前常用的通过改变刚度调整自身固有频率的方法不同,本论文提出了一种新的基于变质量调谐的吸振器—变质量动力吸振器,通过在传统吸振器中引入一个液体箱作为变质量单元,改变其中液体体积,就可以改变吸振器质量及固有频率,从而获得较大的有效带宽。
船体振动智慧树知到答案章节测试2023年华中科技大学

绪论单元测试1.要产生振动,需要()。
A:时变作用B:空气C:弹性D:质量答案:ACD2.属于振动的是()。
A:敲鼓B:钟摆C:心脏搏动D:说话时的声带答案:ABCD3.已知船体结构的动态特性,计算在输入作用下的输出。
属于()。
A:系统识别B:响应分析C:环境预测D:系统设计答案:B4.在已知外界激励下设计合理的船体系统参数,使系统的动态响应或输出满足要求。
属于()。
A:系统识别B:响应分析C:系统设计D:环境预测答案:C5.已知系统的输入和输出,求出船体系统的参数。
属于()。
A:系统识别B:系统设计C:环境预测D:响应分析答案:A6.在已知系统的响应和系统参数的条件下,预测系统的输入。
属于()。
A:系统识别B:系统设计C:环境预测D:响应分析答案:C第一章测试1.在下图所示的结构中小球质量为m,梁的质量忽略不计,梁的长度为L,截面惯性矩为I,材料的弹性模量为E。
若要使小球的自振频率ω增大,可以()。
A:增大IB:减小EC:增大mD:增大L答案:A2.如图a所示,梁的质量忽略不计,小球的自振频率;若在小球处添加刚度为k的弹簧,如图b所示,则系统的自振频率ω1为:()。
A:B:C:D:答案:D3.单自由度系统自由振动的幅值仅取决于系统的()。
A:固有频率B:质量C:初速度和初位移D:刚度答案:C4.已知某单自由度系统质量为m,刚度为k,阻尼系数为c,阻尼因子为ξ。
若令系统刚度为4k,则下列说法正确的是()。
A:新的阻尼因子为1/2 ξB:新的阻尼因子为1/4 ξC:新的阻尼系数为1/2 cD:新的阻尼系数为1/4 c答案:A5.单自由度系统只有当阻尼比时,才会产生振动现象。
()A:ξ<1B:ξ≤1C:ξ>1D:ξ=1答案:A6.已知结构的自振周期T=0.3s,阻尼比ξ=0.04,质量m在y0=3mm,v0=0的初始条件下开始振动,则至少经过个周期后,振幅可以衰减到0.1mm以下。
()A:14B:13C:12D:11答案:A7.速度导纳的单位是()。
动力吸振器在轿车低频轰鸣声控制中的应用

动力吸振器在轿车低频轰鸣声控制中的应用动力吸振器在轿车低频轰鸣声控制中的应用随着社会的发展,汽车已经成为人们出行的首选工具。
虽然现在汽车的品质越来越高,但在行驶过程中仍然会遇到一些问题。
其中之一就是低频轰鸣声。
这种声音给驾驶员和乘客带来了很大的不适和安全隐患,因此需要寻找相关的解决方法。
动力吸振器是一种有效的解决方案,下面就简单介绍一下它在轿车低频轰鸣声控制中的应用。
一、低频轰鸣声的产生原因低频轰鸣声是指在汽车行驶过程中发出的低频噪声。
这种噪声大多数是由发动机、传动系统、底盘结构等发出的。
主要原因是这些部件在运动时会产生很大的振动能量,导致周围的空气和车身震动,从而产生低频噪声。
二、动力吸振器动力吸振器是一种用于减少机械振动和噪声的器件。
它由质量块、弹簧和阻尼装置组成。
质量块的质量和弹性特性决定了吸振器的工作频率,当振动频率等于吸振器的工作频率时,质量块会随振动周期性地作相对运动,从而吸收振动能量。
阻尼装置的作用是在质量块震动时提供能量损耗,从而消除振动能量,减少噪声。
三、动力吸振器在低频轰鸣声控制中的应用动力吸振器在汽车的低频轰鸣声控制中发挥了重要的作用。
一般来说,吸振器主要应用于引擎和底盘结构的振动消除。
其中,引擎振动主要是由于发动机在高转速时运转不平稳,产生的振动能量传到车身上,导致低频轰鸣声。
而底盘结构的振动大多数源于车辆通过凹凸不平的路面时,该结构会受到很大程度的振动,从而导致低频轰鸣声。
动力吸振器可以被安装在车辆的壳体和底盘结构上,以减少振动和噪声。
安装在发动机上的吸振器可以消除引擎的振动,而安装在底盘结构上的吸振器可以消除路面的振动。
这样,汽车的低频轰鸣声就会大大减小。
四、结论总之,动力吸振器是一种对于低频轰鸣声有效控制的器件。
它的应用可以减少汽车发动机和底盘结构的振动,提高汽车的驾乘舒适性和安全性。
作为汽车制造工业里的重要组成部分,在未来的发展中,动力吸振器将会越来越受到重视。
五、动力吸振器的发展趋势目前,随着汽车行业的快速发展,动力吸振器的技术也在不断创新和进化。
动力吸振器自_图文(精)

第 22卷第 324期 2007年 8月实验力学J OU RNAL OF EXPERIM EN TAL M ECHANICSVol. 22No. 324 Aug. 2007文章编号 :100124888(2007 03&0420429206磁流变弹性体自调谐式吸振器及其优化控制 3王莲花 , 龚兴龙 , 邓华夏 , 倪正超 , 孔庆合(中国科学技术大学力学和机械工程系 , 中国科学院材料力学行为与设计重点实验室 , 安徽合肥 230027摘要 :本文研制了一种基于磁流变弹性体的自调谐式吸振器 ,能材料作为吸振器的弹性元件和阻尼元件 ,吸振器的固有频率 , 实现吸振器的移频。
, 。
实验结果表明 ,减振效果最佳点 ,减振效果 , 减振效果最高可达关键词 :; ;:A0引言动力吸振器自 1911年问世以来 [1], 在实践中得到了广泛的应用。
它通过在需要减振的结构 (称为主系统上附加子结构 , 改变系统的振动能量的分布和传递特性 , 使振动能量转移到附加的子结构上 , 从而达到控制主系统振动的目的。
传统的动力吸振器多属被动控制 , 它对于主系统的窄带响应有着良好的吸振效果 , 但由于其吸振带宽不可调节 , 对于宽频激励引起的主系统的振动 , 吸振效果不是很理想。
近年来 , 对于主动吸振器的大量研究表明 , 主动吸振器可以根据主系统的振动状态 , 自动调节自身的结构参数或振动状态 , 实现宽频吸振 , 提高了吸振器减振效果 , 大大拓宽了吸振器的应用范围。
根据吸振器自动调节机理的不同 , 主动吸振器可分为全主动式吸振器和半主动式吸振器。
全主动式吸振器是根据主系统的振动状态反馈调节吸振器的振动状态 , 使其对主系统的动态作用力与主系统的振动加速度反相 , 从而实现主系统实时宽频振动控制。
Tewanim 等人首先将主动振动控制技术与动力吸振器结合起来 , 提出了主动动力吸振器 [2]。
很多研究都表明全主动式吸振器对宽频振动确实可起到很好的控制作用 [3~6], 但它也不可避免地存在耗能大、系统易出现不稳定等问题。
动力吸振器课程设计

动力吸振器课程设计一、课程目标知识目标:1. 学生能够理解动力吸振器的基本原理,掌握其工作方式和功能。
2. 学生能够描述动力吸振器在工程中的应用,并解释其对于机械设备稳定性和减震效果的重要性。
3. 学生能够掌握动力吸振器的结构组成及其参数对吸振效果的影响。
技能目标:1. 学生能够运用物理知识分析动力吸振器的动力学问题,具备设计和优化吸振器参数的能力。
2. 学生能够运用数学工具对动力吸振器的振动方程进行求解,预测其吸振效果。
3. 学生能够通过实验操作,验证动力吸振器的吸振性能,并能够分析实验数据,提出改进措施。
情感态度价值观目标:1. 学生能够培养对物理学科的兴趣,激发对工程技术的热爱。
2. 学生能够认识到科学技术在生活中的应用,增强实践与创新意识。
3. 学生能够养成合作、探究的学习习惯,培养面对工程问题积极解决的信心和责任感。
课程性质:本课程属于物理学科,结合实际工程应用,强调理论联系实际,注重培养学生的动手能力和实际问题解决能力。
学生特点:学生处于高中阶段,具有一定的物理基础和数学素养,对实际工程问题充满好奇心,但需要引导和激发。
教学要求:教师应注重理论与实践相结合,关注学生个体差异,提供多样化的教学手段,确保学生能够达到课程目标。
在教学过程中,分解目标为具体学习成果,以便进行有效的教学设计和评估。
二、教学内容1. 理论基础:- 动力吸振器的基本原理与分类- 振动系统的数学模型及振动方程- 动力吸振器参数对吸振性能的影响教学内容关联教材第十二章“机械振动与波”的相关内容。
2. 实践应用:- 动力吸振器在工程中的应用案例分析- 动力吸振器的设计原则与优化方法- 动力吸振器性能测试方法及数据分析教学内容关联教材第十五章“工程技术案例分析”的相关内容。
3. 实验操作:- 搭建动力吸振器实验装置,进行吸振性能测试- 分析实验数据,验证理论模型的正确性- 针对实验结果,提出优化措施,改进吸振性能教学内容关联教材第十六章“实验设计与操作”的相关内容。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
10
由主系统和动力吸振器构成的无阻尼二自由度系 统强迫振动方程的解为:
解得:x1 Asin ωt, x2 Bsin ωt
F(t) FA sin t
式中,A为主振动系统强迫振动振幅,而B为动力吸振器附加
质量块的强迫振动振幅。式中 有频率。
b
k / m为动力吸振器的固
11
F(t) FA sint x1 Asin ωt, x2 B sin ωt
当 ω b
结论3:
A0 B X st FA / K FA
k/K k/K k
如果激振力的频率 恰好等于吸振器的固有频 率,b 则主振系质量块的振幅将变为零。
12
பைடு நூலகம்
F(t) FA sint x1 Asin ωt, x2 B sin ωt
15
二自由度系统一般有两个固有频率,这个二自由度系统的固有频率可 以通过令下式的分母为零得到。
FA sin t
M
2 1,2
1 [(K 2M
k
k ) m
( K k )2 2 k ( K k ) ( k )2 ] M m MM m M
02 [1 2 2 (1 2 )2 24 22 (1 2 )]
K M 2
4
对于无阻尼系统,可以得到质量块 M的强迫振动振幅为:
A0
FA
(K M 2 )2 (C)2
F (t) FA sin t
FA
(K M 2 )2
FA
K M 2
1
FA
/K
2
K/M
X st
1 ( / 0 )2
5
对于无阻尼系统,可以得到质量块
M的强迫振动振幅为:
静位移
A0
X st
22
阻尼动力吸振器的优点:
阻尼无穷 大
与无阻尼动力吸振器不同的是,阻尼动力 吸振器不受频带的限制,因此被称为宽带吸 振器。
23
5.3 动力吸振原理
其原理是在振动物体上附加质量弹簧系统, 附加系统对主系统的作用力正好平衡了主系统 上的激励力FAsinωt。当激励力以单频为主,或 频率很低,不宜采用一般隔振器时,动力吸振器 特别有用。
第五章 动力吸振
5.1 无阻尼动力吸振器 5.2 阻尼动力吸振器 5.3 动力吸振器原理 5.4 动力吸振器设计步骤
2
5.1 无阻尼动力吸振器
5.1.1 无阻尼动力吸振器
如图所示的单自由度系统,质量为M,刚 度为K,在一个频率为ω、幅值为FA的简谐外 力激励下,系统将作强迫振动。
F(t) FA sin t
3
回顾:单自由度强迫振动的解。
mx Cx Kx F (t)
方程的通解由两部分组 成, x(t) x1(t) x2 (t)
F(t) FA sin t
x1(t) Xent sin( 1 2nt ) x2 (t) X sin( t )
X
FA
(K M 2 )2 (C)2
arctan( C )
当 ω b
A0 B X st FA / K FA
k/K k/K k
此时吸振器弹簧作用于主系统上的力为:
Fk k x2 k Bsint FA sin t 13
总结:
F(t) FA sin t
k x2 FA sin t
可见吸振器作用于主系统上的力 FA sin t 完全 平衡了主系统受到的力 FA sin t 。只要吸振器的固有
阴影线部分为吸振器的设计范围,在此范围内, 吸振效果是满意的。
归一化频率 / b
主振系的振幅与激励频率关系
归一化频率 / b
吸振器的振幅与激励频率关系
18
无阻尼动力吸振器的缺点:
只有在动力吸振器固有频率附近很 窄的激振频率范围内,动力吸振器才 有效,而在紧邻这一频带的相邻频段, 产生了两个共振峰。因此,如果动力 吸振器使用不当,不但不能吸振,反 而易于产生共振,这是无阻尼动力吸 振器的缺点。
频率与b 激振力的频率 相同,任何一个吸振器均能起
到减振作用,因此,吸振器的参数选取范围较宽。
14
5.1.2 无阻尼动力吸振器使用条件 并非所有的振动系统都需要附加动
力吸振器,动力吸振器的使用是有条件 的,可简单归纳如下:
1. 激振频率 接近或等于系统固有频
率,0 且激振频率基本恒定;
2.主振系阻尼较小; 3.主振系有减小振动的要求。
21
吸振器阻尼对主系统振幅具有影响。
阻尼无穷 大
当吸振器无阻尼时,主振系的共振峰为无穷大;当吸
振器阻尼无穷大时,主振系的共振峰同样也为无穷大;
只有当吸振器具有一定阻尼时,共振峰才不至于为无穷
大。因此,必然存在一个合适的阻尼值,使得主振系的
共振峰为最小,这个合适的阻尼值就是阻尼动力吸振器
设计的一项重要任务。
8
当系统阻尼很小时,动力吸振将是一个有效的办法。
如图所示,在主系统上附加一个动力吸振器,动力吸振器的质 量为m,刚度为k。
主系统
F (t) FA sin t
动力吸振器
9
F(t) FA sin t
Kx1
M
kx2 kx1 kx2 kx1
F(t) FA sin t
m
建立微分方程
Mx1 (K k)x1 kx2 FA sin t
19
5.2 阻尼动力吸振器
如果在动力吸振器中设计一定的阻尼,可以 有效拓宽其吸振频带。
如图所示,在主振系上附加一阻尼动力吸振
器,吸振器的阻尼系数为 c 。
20
则主振系的质量块和吸振器的质量块分别 对应的振幅为:
上式中,A为主振动系统强迫振动振幅, 而B为动力吸振器附加质量块的强迫振动 振幅。式中各主要参数为:
1 ( / 0 )2
F(t) FA sin t 激励频率
固有频率
结论1:
当激励频率 接近或等于系统固有频率 0
时,其振幅就变得很大。
6
无阻尼是一种理想状态,实际振动系统总是具有一定阻尼, 因此振幅不可能为无穷大。在考虑系统的黏性阻尼C之后, 其强迫振动的振幅则为:
5
7
5
结论2:
由图可见:由于阻尼的存在,使得强 迫振动的振幅降低了,阻尼比c/c0越大, 振幅的降低越明显,特别是在ω/ω0=1的 附近,阻尼的减振作用尤其明显。因此, 当系统存在相当数量的黏性阻尼时,一般 可以不考虑附加措施减振或吸振。
2
式中,0
K 为主振动系统的固有频率; m 为吸振器与
M
M
主振系的质量比; b 为吸振器与主振系的固有频率之比。
0
16
一个特殊情况就是动力吸振器的频率 等于主振系固有频率的情况。此时,
ω0 b
17
系统固有频率与质量比的关系曲线
下图给出了主振系和吸振器的振幅随频率变化的
规律( ω0)。 b
