动力吸振器自_图文(精)
吸振器

D1 P k 22 2 m2 k12 P2 1 D2 P2 k11 2
k 21 k11 m1
2
m k
1
21P 1
D
k 21
0
如果荷载频率θ与任一个自振频率 ω1、 ω2重合,则D0=0, 当D1、D2 不全为零时,则出现共振现象
5
例:质量集中在楼层上m1、m2 ,层间侧移刚度为k1、k2 解:荷载幅值:P1=P,P2=0,求刚度系数: k11=k1+k2 , k21=-k2 , k22=k2 , k12=-k2
两个主振型相互正交,因与质量有关,称为第一正交关系。 3
由功的互等定理:
2 2 (m112Y11 )Y12 (m212Y21 )Y22 (m12 Y12 )Y11 (m22 Y22 )Y21
m1Y11Y12 m2Y21Y22 0(15.51)
上式分别乘以ω12、ω22,则得:
如图示对称结构在对称荷载作用下。
k11 k22 , k12 k21
与ω2相应的振型是
Psinθt m l/3 l/3
Psinθt m l/3
Y12 k12 2 2 =-1 k 22 2 m k11 2 m k12 k 21 2 2 m Y22 k11
当θ=ω2 ,D0=0 ,也有: 对称体系在对称荷载作用下时, 只有当荷载频率与对称主振型的自 2 D1 P k 22 2 m2 k12 P2 振频率相等时才发生共振;当荷载 P k 22 2 m k12 P 0 1 频率与反对称主振型的自振频率相 2 D2 P2 k11 2 m1 k 21P 等时不会发生共振。同理可知:对 P k11 2 m k 21P 0 1 称体系在反对称荷载作用下时,只 有当荷载频率与反对称主振型的自 D1 D2 不会趋于无穷大,不发生共振, Y1 , Y2 振频率相等时才发生共振。 D0 D0 共振区只有一个。
Dynamic Vibration Absorbers

Dynamic VibrationAbsorbersIntelligent optimization of comfortCERTCERTContiTech Vibration AbsorbersFuture-oriented products foractive and passive vibration reductionBackrest absorberSteering wheel absorberTorsional vibration absorbercardan shaftHydraulic absorberchassis subframe/rear-axle supportHollow shaft absorberdrive shaftBrake absorberActive absorbere.g. on the engine mountA passive, one-dimensional, linear vibration absorber is considered to be a system consisting of spring, mass and damper. It is basically defined by its natural frequency f 0, its vibrating mass m and damping factor ζ. Here, the natural frequency f 0represents the point of ideal absorption (compensation), where the mass vibrates exactly in antiphase to the excitation. The damping ζindicates the range and extent of the absorber effect. Often, the Q factor, which is derived directly from the natural frequency and damping, is specified instead of the damping. The vibrating mass serves to amplify the characteristic over the entire frequency range, thus determining the force which is applied for absorption.Absorber: Variation of dampingAbsorber: Variation of massM a g n i t u d eFrequencyM a g n i t u d eFrequencyIf the absorber is coupled to a structure that has resonance, a vibration minimum arises at the natural frequency f 0(absorber effect) as well as two resonance frequencies below and above f 0. Particular attention must be paid to the position and nature of the new resonance frequencies, so no additional interferences are generated.In the design process, an optimum between absorption in the resonance and a flattened frequency curve can be found by varying the damping. To carry out this task in the best possible way, we have developed high-performance simulation software.Absorber effect on structureMass m A ↑Structure without absorber with absorber, f 0,A = f 0,S with absorber, f 0,A = f 0,S ,m A ↑c Sc Ax 1x 2k SS t r u c t u r e mSA b s o r b e r mAk Ak = spring stiffness c = damping coefficient m = massx = displacementM a g n i t u d eFrequencyThe basics of vibration absorptionζ= 0.025ζ= 0.1ζ= 0.2ζ= 0.5Vehicle measurement: airborne and structure-borne noiseWithout absorberTest the bestTesting of materials and componentsThe ContiTech division is a development partner and original equipment supplier to numerous industries for high-quality functional parts, components and systems. As a part of Continental AG, it has 8 specialized business units for rubber and plastics technology that make use of their pooled know-how.That is what ContiTech stands for.Dynamic/mechanical analysis of elastomersAutomated measurement of an absorberTorsional test benchM o d u l e G ´, G ´´Temperature [˚C]-70070140ContiTech Vibration Control has state-of-the-art testing facilities for the development of vulcanized components and specific absorber designs. The characterization of vulcanized components is carried out with dynamic/mechanical analyses, permitting the quantification of frequency, temperature and amplitude factors.For the dynamic characterization and service life assessment of the absorber, electro-dynamic shakers as well as hydropulse facilities are used. On the shaker test bench, individual tests can be run between 5 Hz and 5000 Hz.A periodic force in the effective direction is specified for the absorber, while the excitation acceleration or displacement across the frequency is maintained at a constant level . This system is ideal for the development,acceptance testing and the quality assurance of small assemblies and components in the automotive industry.The component is excited with a frequency sweep that records the transmission function between vibrating mass and base point. The absorber’s measured natural frequency is at the maximum amplitude of the frequencyresponse. With the help of a program tool, further parameters for the characterization of the absorber can be calculated; the measurement data are issued and archived in a standard format.Long-term testing is carried out on shaker and hydro-pulse facilities, in which the absorber is excited with constant frequency. After a defined time interval has passed, the absorber undergoes a frequency sweep.This process is repeated cyclically. The change in the parameters is recorded as a function of time.G´G´´tan deltat a n d e l t aControl unitControl "On"Control "Off"20004500R P M[m i n -1]100200100200300。
动力吸振器研究发展历史

动力吸振器的研究历史主要分为黎明期、发展期、扩展期和应用期4个阶段。
一、黎明期(1909年到20世纪30年代)仅由质量和弹簧构成的无阻尼动力吸振器很久以前就已出现,这种动力吸振器从1909年开始就出现在论文和专利中,其力学模型如图1所示。
图1 无阻尼动力吸振器这里,M 、K 是主振动系统的质量和弹簧刚度,m 、k 是动力吸振器的质量和弹簧刚度。
x1、x2分别为主振动系统和动力吸振器的位移。
假设作用在主振动系统上的定常激励力为t P ωsin 0,则其响应为:t P k m k M k K m k x ωωωωsin ))(-(022221--+-= 1928年,Ormondroyd 与 Den Hartog 发表的论文指出,对于激励力频率变动的情况,有阻尼动力吸振器有效,并且存在最优阻尼使得振幅为最小。
由此引起了对于有阻尼动力吸振器,也就是通常所说的动力吸振器的最优设计的研究热潮。
四年后的1932年, Erich Hahnkamm 在德国杂志 ngenleur - Archiv 上发表了题为“变频激励力作用下的机械振动的阻尼”的论文。
该论文首次揭示了动力吸振器的阻尼为零和为无限大时响应曲线的两个交点是不随阻尼变化的特定点,并且利用这两个定点的特点推导出了最优同调的条件。
二、发展期(20世纪40年代到50年代)1940年出版的由 Den Hartog 著的“ Mechanical Vibration (第2版)”中,非常完美地推导出了最优同调条件的简便设计关系式,进一步完善了定点理论,Den Hartog 给出的最优同调条件为unn+=Ω11ω 在此条件下,PQ 定点的高度为 uu +=2|x x max st 1 其中M m u /=为质量比,n n Ω和ω分别为动力吸振器和主振动系统的固有角频率。
1946年,在最优同调关系的基础上, Brock 推导出了最优阻尼的条件式。
这个结果是在两个定点等高,并且为曲线上最大点的条件下经过非常复杂的推导得来的。
动力吸振结构的原理与应用

动力吸振结构的原理与应用1. 引言动力吸振结构是一种广泛应用于工程领域的减震装置,其原理是通过改变结构的固有频率以降低外界震动对结构的影响。
本文将介绍动力吸振结构的原理及其在工程实践中的应用。
2. 动力吸振结构的原理动力吸振结构的原理基于共振现象,即当外界震动频率等于结构的固有频率时,会产生共振效应,使结构发生剧烈振动。
为了降低共振效应对结构的影响,动力吸振结构通过改变结构的固有频率,使其远离外界震动频率,从而减小结构振动幅度。
常见的动力吸振结构包括质量阻尼器、液体阻尼器和有源阻尼器等。
2.1 质量阻尼器质量阻尼器是一种常见的动力吸振结构,它通过增加结构的质量来改变其固有频率。
质量阻尼器通常由一个或多个重物组成,这些重物与结构相连,并能够自由移动。
当结构受到外界震动时,阻尼器内的重物也会受到相同的震动力,从而减小结构振动幅度。
2.2 液体阻尼器液体阻尼器是一种基于液体阻尼原理的动力吸振结构。
在液体阻尼器中,通过将液体引入特定的装置中,使得结构在振动时与液体发生摩擦作用,转化为热能消耗,从而减小结构的振动能量。
液体阻尼器的优点是结构简单、维护成本低,并且可以根据具体应用需求进行设计。
2.3 有源阻尼器有源阻尼器是一种利用控制器对结构进行主动控制的动力吸振结构。
有源阻尼器通过传感器实时监测结构的振动状态,并根据预设的控制策略调整阻尼力,从而降低结构的振动响应。
有源阻尼器具有较高的灵活性和自适应性,可以适应不同工作条件下的变化要求。
3. 动力吸振结构的应用动力吸振结构在各个工程领域都有广泛的应用,下面列举几个常见的应用场景。
3.1 桥梁减震桥梁是人们出行的重要交通设施,但常常受到地震、风力等外界因素的影响,容易发生共振现象。
通过在桥梁结构中引入动力吸振装置,可以调节结构的固有频率,减少地震和风力对桥梁的影响,提高桥梁的抗震性能。
3.2 高层建筑减振高层建筑常因风力或地震而发生较大的振动,影响居住舒适性和结构安全性。
几种典型的主动控制动力吸振器

图 2为质量可调式动力吸 振器的一种形式 。控制信号指 令作动器使附加质量 处于 12位 置时 , 、 其固有频率分别 为
、 / , / = ∞、
形 成了频率可调 式动力吸振器 。
1 】
的惯性元件 或弹性元件 的特性 , 或直接驱 动吸 振器的振 动体 按 一定规律运动 , 受控对象 的振动转 移到吸振 器 i, 到 使 =达 减振 的 目的, 称为主动吸振 。主动吸振器 是主动 吸振系统 中
11 惯 性 可调 式 动 力 吸振 器 .
1. . 1转动惯量 可调的动力吸振器 1 图 1为转动惯量可调的倒立摆的示意图, 其固有频率为
【 关键词】 动力吸振器 ; 动主动控制; 振 类型
【 中图分类号] B 3 【 T 5 5 文献标识码】 A 【 文章编号】 0 8 5 9 - 2 0 )5 0 8 一) 10 — 6 6 (0 6 0 - 0 0 ( 3
必不可少的一个环节 。
1 主 动 吸振 器 的 类 型
主动吸振器 有频率可调式和非频率可调式两类。频 率可
调式动 力吸振器 的固有频 率能 自动跟 随外界激 励频 率 的变
2
化, 始终 处于调 谐状态 , 从而 使受控对 象处 于振动达到 最小
投稿 日期 :0 6 0 — 7 2 0 — 3 0
为零 。磁拉力随偏离量 的增大而增人 , 力的方 向 与偏 离方 向 相 反, 即形成 电磁弹簧 。该弹簧刚度 可通 过改变励磁 电流加
以调整 , 从而 改变吸振器的固有振动频率 。 1 . 调间隙的半主动 吸振器 . 3可 2 图 5所示为一种 可调 间隙的 半主动 吸振器 的力学 模型 图。其 中 x是主系统的位移 , y是吸 振器质量相对 于主系统 的位移, 为吸振器 的质 量, 为弹簧 刚度 , d为弹性元件 的间隙,
第十二讲—动力吸振器
切向无外力,故切向加速度为0
( ) Rθ cosϕ + Rθ 2 sinϕ + r θ +ϕ = 0
cosϕ ≈ 1,sinϕ ≈ ϕ,θ ≈ ω
ϕ
+
R r
ω 2ϕ
=
R+ r
r
θ0ω 2
sin ωt
单摆运动方程
16
机械与运载工程学院
单摆运动方程 单摆固有频率
ϕ
+
R r
ω 2ϕ
=
R+ r
r
θ0ω 2
sin ωt
x2
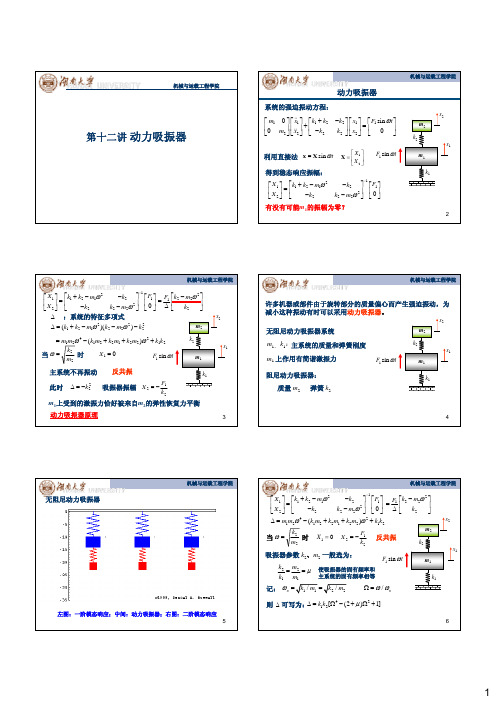
无阻尼动力吸振器系统
m2
m1、 k1:主系统的质量和弹簧刚度
k2 x1
m1 上作用有简谐激振力
F1 sin ωt
m1
阻尼动力吸振器:
k1
质量 m2 弹簧 k2
4
无阻尼动力吸振器
机械与运载工程学院
左图:一阶模态响应;中间:动力吸振器;右图:二阶模态响应 5
机械与运载工程学院
⎡ ⎢⎣
X1 X2
⎤ ⎥⎦
⎡X1 ⎤
⎢ ⎣
X
2
⎥ ⎦
=
F1 Δ
⎡⎢k2 ⎣
− m2ω k2
2
⎤ ⎥ ⎦
X 0 = F1 / k1
X1 =
1− Ω2
X 0 Ω4 − (2 + μ)Ω2 +1
X2 =
1
X0 Ω4 − (2 + μ)Ω2 +1
7
机械与运载工程学院
4 X1 / X0
2
X2 / X0
μ = 0.3 X1 =
1− Ω2
反共振
机械动力学第1、2章

2
2
1 2 2 1 d n 根据 Td 2 k mn cc 2mn
ln(16) 2.7726
k 200 3.43382 2358.2652( N / m) cc 2 200 3.4338 1373.54( N s / m) c cc 0.4037 1373.54 554.4981( N s / m)
第一章 单自由度系统
• • • • •
常用的推导动力学方程的方法 牛顿第二定律 达朗贝尔原理 虚位移原理 能量守恒原理
无阻尼自由振动
1.无阻尼自由振动解
如果一个质点偏离其平衡位置的距离 为 xm, 则其将进行自由振动,有牛顿 定律,质点力的平衡方程为
ma F W k st x kx
高塔消振 高塔消振 台北 101 大厦内部装有阻尼耗能减振器 台北 101 大厦内部装有阻尼耗能减振器
有阻尼自由振动的应用
网球 (( 羽毛球 )) 拍消 网球 羽毛球 拍消 网球拍或羽毛球拍在击球后产生自由振动,若不在 网球拍或羽毛球拍在击球后产生自由振动,若不在 下次击球之前停止振动,将影响再次击球的方向和 下次击球之前停止振动,将影响再次击球的方向和 角度,为此在铁合金管外面绕上石墨纤维,并在其 角度,为此在铁合金管外面绕上石墨纤维,并在其 外面用塑料捆扎住,石墨纤维外表面的库仑阻尼, 外面用塑料捆扎住,石墨纤维外表面的库仑阻尼, 使球拍在击球后,以最快的时间稳定下来 使球拍在击球后,以最快的时间稳定下来
p103
【解】由于x1.5=x1/4, 因而x2=x1/16
n t2
x1 Ae nt1 sin( 1 2 n t1 ) x2 Ae
动力吸振器在飞轮振动控制中的应用_虞自飞_图文(精)

第 33巻第 5期噪声与振动控制文章编号:1006-1355(201305-0173-06动力吸振器在飞轮振动控制中的应用虞自飞 1, 2,王涛 1,沈海军 1, 2,杜冬 1, 2,周徐斌 1, 2(1. 上海卫星工程研究所,上海 200240;2. 上海卫星工程研究所空间机热一体化技术实验室,上海 200240摘要 :为了研究动力吸振器对飞轮振动的抑制效果, 采用多变量多变异位自适应遗传算法得到阻尼系统的吸振器最优参数, 运用回归分析得到最优参数的数学表达式。
通过仿真和实验验证最优吸振器设计的合理性和检验吸振器的减振性能。
分析表明, 最优吸振器能够降低飞轮的振动响应, 采用遗传算法能够高效的计算最优参数, 仿真和实验验证吸振器对飞轮振动的抑制效果非常明显。
关键词 :振动与波; 振动控制; 动力吸振器; 自适应遗传算法; 回归分析; 减振性能中图分类号:TB535.1文献标识码:A DOI 编码:10.3969/j.issn.1006-1335.2013.05.038 Application of Dynamic Vibration Absorber inFlywheel Vibration ControlYU Zi-fei 1, 2, WANG Tao 1, SHEN Hai-jun 1, 2,DU Dong 1, 2, ZHOU Xu-bin 1, 2(1. Shanghai Institute of Satellite Engineering, Shanghai 200240, China;2. Laboratory of Space Mechanical and Thermal Integrative Technology,Shanghai Institute of Satellite Engineering, Shanghai 200240, ChinaAbstract :Dynamic vibration absorber (DVA for reduction of flywheel vibration was developed. The optimum tuning frequency and damping ratio of the absorber in the damping system were derived by multi-variable multi-mutation adaptive genetic algorithm (MMAGA.Then mathematical formulae of the optimal parameters were obtained by regression analysis. The rationality of design and damping performance of the DV A were verified by experimental testing and numerical simulation. It is concluded that the optimum absorber can reduce the vibration response of the flywheel. MMAGA was suitable for calculating optimum parameters of the absorber efficiently. Simulation and test validates that the DV A can effectively depress the vibration of the flywheel.Key words :vibration and wave ; vibration control ; dynamic vibration absorber ; adaptive genetic algorithm ; regression analysis ; damping performance我国卫星敏感载荷精度越来越高, 对平台微振动环境要求越来越苛刻。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第 22卷第 324期 2007年 8月实验力学J OU RNAL OF EXPERIM EN TAL M ECHANICSVol. 22No. 324 Aug. 2007文章编号 :100124888(2007 03&0420429206磁流变弹性体自调谐式吸振器及其优化控制 3王莲花 , 龚兴龙 , 邓华夏 , 倪正超 , 孔庆合(中国科学技术大学力学和机械工程系 , 中国科学院材料力学行为与设计重点实验室 , 安徽合肥 230027摘要 :本文研制了一种基于磁流变弹性体的自调谐式吸振器 ,能材料作为吸振器的弹性元件和阻尼元件 ,吸振器的固有频率 , 实现吸振器的移频。
, 。
实验结果表明 ,减振效果最佳点 ,减振效果 , 减振效果最高可达关键词 :; ;:A0引言动力吸振器自 1911年问世以来 [1], 在实践中得到了广泛的应用。
它通过在需要减振的结构 (称为主系统上附加子结构 , 改变系统的振动能量的分布和传递特性 , 使振动能量转移到附加的子结构上 , 从而达到控制主系统振动的目的。
传统的动力吸振器多属被动控制 , 它对于主系统的窄带响应有着良好的吸振效果 , 但由于其吸振带宽不可调节 , 对于宽频激励引起的主系统的振动 , 吸振效果不是很理想。
近年来 , 对于主动吸振器的大量研究表明 , 主动吸振器可以根据主系统的振动状态 , 自动调节自身的结构参数或振动状态 , 实现宽频吸振 , 提高了吸振器减振效果 , 大大拓宽了吸振器的应用范围。
根据吸振器自动调节机理的不同 , 主动吸振器可分为全主动式吸振器和半主动式吸振器。
全主动式吸振器是根据主系统的振动状态反馈调节吸振器的振动状态 , 使其对主系统的动态作用力与主系统的振动加速度反相 , 从而实现主系统实时宽频振动控制。
Tewanim 等人首先将主动振动控制技术与动力吸振器结合起来 , 提出了主动动力吸振器 [2]。
很多研究都表明全主动式吸振器对宽频振动确实可起到很好的控制作用 [3~6], 但它也不可避免地存在耗能大、系统易出现不稳定等问题。
半主动式吸振器则融合了被动吸振器和全主动式吸振器的优点 , 它通过调整动力吸振器的结构参数 , 使之跟踪主系统的外界干扰频率 , 最大限度地抑制主系统的振动 , 其结构相对简单 , 耗能低 , 且能实现宽频吸振。
目前半主动式吸振器多为刚度连续可调结构 , 如机械式 [7]、电液式 [8]、电磁式 [9]等 , 而将新材料如压电 [10]、记忆合金 [11]和磁流变弹性体 [12]等用于半主动式吸振器的设计也成为当今研究的热点。
本文在前期工作的基础上 , 以磁流变弹性体作为智能变刚度单元 , 改进设计了一种自调谐式吸振器 (A TVA , 将遗传算法改进移植到吸振器上 , 对其减振性能进行优化控制。
1磁流变弹性体自调谐式吸振器1. 1吸振器的工作原理图 1是磁流变弹性体自调谐式吸振器的结构示意图 , 图 2是其实物图。
图中 1表示基座 ,2表示导3收稿日期 :2007204212基金项目 :中国科学院“ 百人计划” 项目 ; 国家自然科学基金 (10672154 ; 高等学校博士学科点专项科研基金 (20050358010 通讯作者 :龚兴龙 (1966- , 男 , 教授 , 博士生导师。
主要从事电磁流变材料和振动控制的研究。
E 2mail :gongxl@. cn杆组 ,3表示支撑弹簧 ,4表示线性轴承 ,5表示铜制安装基 ,6表示上轴线圈 ,7表示盖板 ,8表示上轴铁芯 ,9表示导磁侧板 ,10表示侧轴线圈 ,11表示侧轴铁芯 ,12表示剪切片 ,13表示磁流变弹性体。
上轴线圈、上轴铁芯、导磁侧板、侧轴线圈和侧轴铁芯等组件与磁流变弹性体构成闭合磁回路 , 这些组件安装在铜制安装基上 , 构成了吸振器的动子。
吸振器的基座上安装有四根导杆 , 以保证吸振器工作在剪切模式下。
导杆外套有支撑弹簧 , 这些支撑弹簧主要用来支撑动质量 , 从而消除了原来作用在磁流变弹性体中的静变形量。
分析可知 ,f =2π(1 式中 f 是吸振器的固有频率 ; G 为磁流变弹性体剪切模量 ; A 为磁流变弹性体发生剪切的面积 ; h 为磁流变弹性体厚度 ; m 为振子的质量。
根据磁偶极子模型 [13], 磁流变弹性体中的铁磁性颗粒在磁场作用下被磁化 , 磁化后颗粒之间的磁场作用力导致剪切模量的增加。
由 (1 式可知 ,加磁场改变时 , 磁流变弹性体的剪切模量将发生改变 , , 最终引起吸振器的固有频率的改变。
这样 ,, 使之跟踪主系统的外界干扰频率。
图 1吸振器结构示意图Fig. 1Schematic diagram of the developed A TVA图 2吸振器实物图Fig. 2 Photograph of the developed A TVA图 3吸振器移频特性测试系统Fig. 3 The evaluation system for frequency 2shift property1. 2吸振器的动力特性为了测试吸振器移频特性 , 建立了如图 3所示的测试系统 , 根据振动理论中模态分析法的峰值检测法 , 我们用加速度传感器测量基础激励与吸振器的响应信号 ,再通过频谱分析仪可得到响应信号与基础激励传递函数的相关信息 , 如传递函数的幅值和相位 , 进而得到吸振器的固有频率。
改变与吸振器相连的程控电源的电流可得到不同电流下吸振器的固有频率 , 进而得到其移频曲线。
测试系统中所用各仪器的型号为 :江苏联能电子科技有限公司生产的 J ZK 210型激励器 , 基础激励为白噪声随机信号 ; 江苏联能电子科技有限公司生产的 YE5858A 型电荷放大器 ; 美国 PCB 公司的 M353B18型加速度传感器 ; 美国迪飞公司的 Signal Calc ACE 型动态信号分析仪。
图 4是所测得的吸振器移频特性图 , 其横坐标是激励频率 , 纵坐标是传递函数。
从图中可看出 , 随着电流的增大 , 传递函数曲线向右移动。
这是因为, 电流的逐渐增大导致加在磁流变弹性体上的磁场逐 034实验力学 (2007年第 22卷渐增强 , 磁场的增强提高了磁流变弹性体的剪切模量进而提高了吸振器的固有频率。
提取图 4中电流与吸振器的固有频率关系得到图 5所示曲线。
图中横坐标为吸振器工作电流大小 , 纵坐标为吸振器固有频率 , 从图中可看出 , 当吸振器的工作电流从 0A 增大至 1A 时 , 吸振器的固有频率从 24Hz 移频至 50Hz , 吸振器移频范围达到了 26Hz , 当所加电流超过 1A 时 , 由于磁流变弹性体达到磁饱和状态 , 吸振器的固有频率保持在 50Hz 。
图 4吸振器移频特性Fig. 4 The transfer f unction5between resonance f requency and applied current2 , 当吸振器固有频率与外界激励频率相等时 , 吸振器减振效果最佳。
磁流变弹性体自调谐式吸振器控制系统的目标是吸振器能自动跟踪外界激励的变化使吸振器固有频率与激励频率相等 , 但在实际使用中 , 吸振器固有频率与电流的准确定量关系难以确定 , 目前也是通过实验方法提取出大概的趋势图。
故在本控制系统中 , 并不直接判断吸振器固有频率与激励频率是否相等 , 而是通过吸振器安装点的减振效果判断吸振器是否工作在最佳状态 , 即当吸振器安装点的减振效果最好时 , 吸振器工作在最佳状态。
因此如何准确且快速寻找到吸振器最佳工作状态是很关键的问题。
图 6磁流变弹性体自调谐式吸振器控制系统图 Fig. 6 The control system of A TVA 遗传算法是以达尔文的生物进化论和孟德尔遗传变异理论为基础 , 模拟生物界进化过程 ,它是一种自适应、启发式、全局优化的搜索算法。
它依赖于概率 , 又不同于随机算法 , 把启发性指导与随机算法有机结合 , 使其更具有鲁棒性 ; 它的另一个特点是始终保持一组可能的结果 , 从而保证在全局范围内搜索 , 得到全局最优解。
另外 , 遗传算法在进化搜索时基本不利用外部信息 , 仅以适应度函数为依据 , 利用种群中每个个体的适应度值进行搜索。
这种算法适合处理传统方法难以解决的复杂问题和非线性问题。
如高峰等人成功地用遗传算法解决了动力吸振器优化设计的非线性多维离散问题 [14]。
本文改进了遗传算法 , 将其移植到吸振器的控制系统中 , 对吸振器的输入参数进行优化 , 使吸振器能准确且快速寻找到其最佳工作状态。
2. 1硬件设计控制系统如图 6所示 , 主要由上位机、数据采集卡和程控电源组成。
由于吸振器采用磁流变弹性体作为智能刚度元件 , 其响应时间是毫秒量级的 , 为了提高整个系统的控制时间 , 对程控电源性能提出了很高的要求 , 考虑电源的响应时间和精度我们选用了朝阳市电源有限公司生产的 4N IC 2C K 2HL 的一体化程控电源 , 它采用 RS232接口进行通讯。
结合上位机和控制系统对采集信号的要求 , 我们选用北京中泰研创公司 U SB7325B 型号的数据采集模块 , 本模块采用双端输入 , 程控触发 , 批量采集 , 从 FIFO 读取采集数据。
2. 2软件设计软件设计的主要思路是先对激励信号采样并进行傅立叶变换 , 提取激励频率 , 然后用改进的遗传算法进行全局搜索 , 寻找此时吸振器的最佳工作状态时所对应的输入参数。
遗传算法流程图如图 7所示 , 其中图 7(a 是遗传算法原始流程图 , 图 7(b 是控制系统中对应的遗传算法流程图。
图 7遗传算法流程图Fig. 7 The flow chart of genetic algorithms遗传算法的改进之处在于在初始化种群时 , 将实验测得的激励频率所对应的电流值或附近电流值作为其中一条染色体 , 其他染色体随机产生。
与随机产生的大部分染色体相比 , 这条染色体的健壮性优于其他染色体。
这样遗传算法能更快地找到最优解。
遗传算法适应度函数选用吸振器安装点信号均方根的倒数。
当吸振器达到最佳工作状态时 , 吸振器减振效果最好 , 此时信号均方根应最小 , 则信号均方根的倒数即个体适应度最大 , 而遗传算法所寻找的最优解即为个体适应度最大的个体。
2. 3控制减振效果根据图 6所示的系统测试吸振器的减振特性 , 决定控制系统中遗传算法的输入参数如表 1所示 :表 1控制系统中遗传算法输入参数Tab. 1 Input parameters of genetic algorithms in control system种群大小染色体长度最大进化代数交叉概率变异概率 10740. 550. 05吸振器的减振效果为加上吸振器时被减振系统中吸振器安装点的激励响应与在相同激励下不加吸振器时被减振系统中同一点的激励响应的幅值之比。
