牙膏的销售量(matlab程序)
数学建模基础练习一及参考答案

数学建模基础练习一及参考答案数学建模基础练习一及参考答案练习1matlab练习一、矩阵及数组操作:1.利用基本矩阵产生3×3和15×8的单位矩阵、全1矩阵、全0矩阵、均匀分布随机矩阵([-1,1]之间)、正态分布矩阵(均值为1,方差为4),然后将正态分布矩阵中大于1的元素变为1,将小于1的元素变为0。
2.利用fix及rand函数生成[0,10]上的均匀分布的10×10的整数随机矩阵a,然后统计a中大于等于5的元素个数。
3.在给定的矩阵中删除含有整行内容全为0的行,删除整列内容全为0的列。
4.随机生成10阶的矩阵,要求元素值介于0~1000之间,并统计元素中奇数的个数、素数的个数。
二、绘图:5.在同一图形窗口画出下列两条曲线图像,要求改变线型和标记:y1=2x+5;y2=x^2-3x+1,并且用legend标注。
6.画出下列函数的曲面及等高线:z=sinxcosyexp(-sqrt(x^2+y^2)).7.在同一个图形中绘制一行三列的子图,分别画出向量x=[158101253]的三维饼图、柱状图、条形图。
三、程序设计:8.编写程序计算(x在[-8,8],间隔0.5)先新建的,在那上输好,保存,在命令窗口代数;9.用两种方法求数列:前15项的和。
10.编写程序产生20个两位随机整数,输出其中小于平均数的偶数。
11.试找出100以内的所有素数。
12.当时,四、数据处理与拟合初步:13.随机产生由10个两位随机数的行向量A,将A中元素按降序排列为B,再将B重排为A。
14.通过测量得到一组数据:t12345678910y4.8424.3623.7543.3683.1693.0383.0343.0163.0123.005分别采用y=c1+c2e^(-t)和y=d1+d2te^(-t)进行拟合,并画出散点及两条拟合曲线对比拟合效果。
15.计算下列定积分:16.(1)微分方程组当t=0时,x1(0)=1,x2(0)=-0.5,求微分方程t在[0,25]上的解,并画出相空间轨道图像。
牙膏销售量问题的微分方程模型
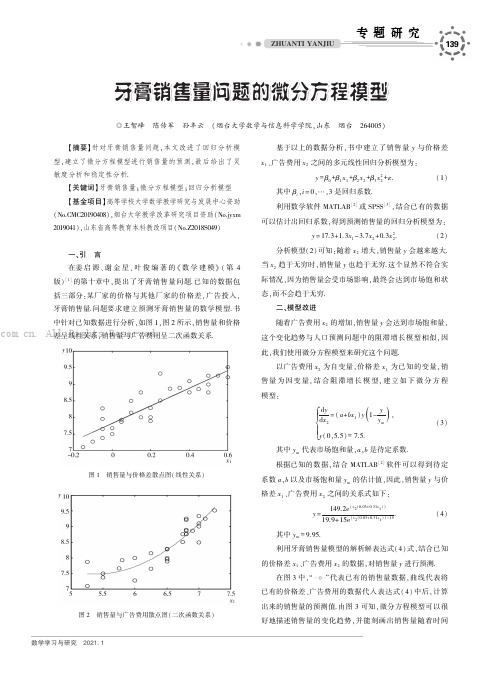
㊀㊀㊀139㊀数学学习与研究㊀2021 1牙膏销售量问题的微分方程模型牙膏销售量问题的微分方程模型Һ王智峰㊀陈传军㊀孙丰云㊀(烟台大学数学与信息科学学院,山东㊀烟台㊀264005)㊀㊀ʌ摘要ɔ针对牙膏销售量问题,本文改进了回归分析模型,建立了微分方程模型进行销售量的预测,最后给出了灵敏度分析和稳定性分析.ʌ关键词ɔ牙膏销售量;微分方程模型;回归分析模型ʌ基金项目ɔ高等学校大学数学教学研究与发展中心资助(No.CMC20190408),烟台大学教学改革研究项目资助(No.jyxm2019041),山东省高等教育本科教改项目(No.Z2018S049)一㊁引㊀言在姜启源㊁谢金星㊁叶俊编著的‘数学建模“(第4版)[1]的第十章中,提出了牙膏销售量问题.已知的数据包括三部分:某厂家的价格与其他厂家的价格差,广告投入,牙膏销售量.问题要求建立预测牙膏销售量的数学模型.书中针对已知数据进行分析,如图1,图2所示,销售量和价格差呈线性关系,销售量与广告费用呈二次函数关系.图1㊀销售量与价格差散点图(线性关系)图2㊀销售量与广告费用散点图(二次函数关系)基于以上的数据分析,书中建立了销售量y与价格差x1㊁广告费用x2之间的多元线性回归分析模型为:y=β0+β1x1+β2x2+β3x22+ε.(1)其中βi,i=0, ,3是回归系数.利用数学软件MATLAB[2]或SPSS[3],结合已有的数据可以估计出回归系数,得到预测销售量的回归分析模型为:y=17.3+1.3x1-3.7x2+0.3x22.(2)分析模型(2)可知:随着x2增大,销售量y会越来越大.当x2趋于无穷时,销售量y也趋于无穷.这个显然不符合实际情况,因为销售量会受市场影响,最终会达到市场饱和状态,而不会趋于无穷.二㊁模型改进随着广告费用x2的增加,销售量y会达到市场饱和量,这个变化趋势与人口预测问题中的阻滞增长模型相似,因此,我们使用微分方程模型来研究这个问题.以广告费用x2为自变量,价格差x1为已知的变量,销售量为因变量,结合阻滞增长模型,建立如下微分方程模型:dydx2=(a+bx1)y1-yym(),y(0,5.5)=7.5.ìîíïïï(3)其中ym代表市场饱和量,a,b是待定系数.根据已知的数据,结合MATLAB[2]软件可以得到待定系数a,b以及市场饱和量ym的估计值,因此,销售量y与价格差x1㊁广告费用x2之间的关系式如下:y=149.2e(x2(0.03+0.31x1))19.9+15e(x2(0.03+0.31x1))-15.(4)其中ym=9.95.利用牙膏销售量模型的解析解表达式(4)式,结合已知的价格差x1㊁广告费用x2的数据,对销售量y进行预测.在图3中,代表已有的销售量数据,曲线代表将已有的价格差㊁广告费用的数据代入表达式(4)中后,计算出来的销售量的预测值.由图3可知,微分方程模型可以很好地描述销售量的变化趋势,并能刻画出销售量随着时间. All Rights Reserved.㊀㊀㊀㊀㊀140数学学习与研究㊀2021 1周期变化的情况.图3㊀改进后模型的预测图三㊁模型检验在使用模型解决问题之前,需要对模型进行检验分析.微分方程模型(3)的检验主要包括稳定性分析和灵敏度分析两个方面.首先我们根据定性分析[4]方法给出稳定性分析.微分方程模型(3)的右端项不显含自变量x2,因此,模型(3)属于一维自治系统,我们使用自治系统的稳定性原理进行分析.我们记右端项为F(y)=(a+bx1)y1-yym().(5)令F(y)=0,可得两个平衡点为:y1=ym或y2=0.现分析右端项的一阶导数在两个平衡点处的符号:(1)当x1<-ck=-0.09,Fᶄ(0)=a+bx1<0.(2)当x1>-ck=-0.09,Fᶄ(ym)=-(a+bx1)<0.结合稳定性原理可知:当价格差大于-0.09时,销售量随着广告费用的增加,最终会稳定在市场饱和值ym.如果价格差小于-0.09,即比别的厂家价格高很多的时候,虽然广告费用不断增加,但是,最终的销售量仍然会趋于0.这个结论是比较符合市场规律的,说明本文建立的微分方程模型可以很好地刻画实际情况,也克服了回归分析模型销售量随着广告费用增加而趋于无穷的弊端.然后,我们结合微分方程的解析解(4)式,进行关于价格差x1的灵敏度分析,如图4所示.图4㊀价格差的灵敏度分析在图4中,我们取不同的价格差x1=[0,0.1,0.2,0.3,0.4,0.5,0.6],画出牙膏销售量y随着广告费用x2的变化曲线.当价格差一定时,随着广告费用x2的增加,销售量会逐渐趋于稳定,到达饱和值ym.当广告费用投入比较少时,价格越实惠,销售量就越大.当广告费用比较大的时候,价格差的作用就比较小了,销售量会更快达到饱和值ym.这个结论也是符合市场规律的.四㊁结㊀论结合牙膏销售量㊁价格差㊁广告费三组数据,本文分析了回归分析模型的不足之处.本文根据牙膏销售量最终会趋于市场饱和量的市场规律,建立了基于阻滞增长模型的微分方程模型,使用已有的三组数据对模型中的未知参数进行了点估计,得到牙膏销售量的预测模型.本文最后对模型进行了稳定性分析和灵敏度分析,得到模型是符合市场客观规律的结论.ʌ参考文献ɔ[1]姜启源,谢金星,叶俊.数学模型:第4版[M].北京:高等教育出版社,2011.[2]司守奎,孙兆亮.数学建模算法与应用:第2版[M].北京:国防工业出版社,2015.[3]周静.SPSS在数学建模中的应用实例[J].天津职业院校联合学报,2012,14(11):93-96.[4]赵静,但琦.数学建模与数学实验:第4版[M].北京:高等教育出版社,2014.. All Rights Reserved.。
数学模型_牙膏的销售量

估计x3 调整x4 控制x1
通过x1, x2预测y
控制价格差x1=0.2元,投入广告费x2=650万元
y ˆˆ0ˆ1 x 1ˆ2x 2ˆ3 x 2 2 8 .29(百3 万支3)
销售量预测区间为 [7.8230,8.7636](置信度95%)
上限用作库存管理的目标值 下限用来把握公司的现金流
两模型销售量预测比较
控制价格差x1=0.2元,投入广告费x2=6.5百万元
y ˆˆ0ˆ1x 1ˆ2x2ˆ3x2 2 yˆ 8.2933(百万支) 区间 [7.8230,8.7636]
yˆ 8.3272(百万支)
y ˆ0 ˆ 1 x 1 ˆ2 x 2 ˆ3 x 2 2 ˆ4 x 1 x 2
yˆ
10 9.5
9 8.5
8 7.5
5
0
0.2
0.4
6
7
0.6 x1
x1=0.2
8 x2
7.5 -0.2
yˆ
10.5 10 9.5 9 8.5 8 5
0
0.2
0.4
6
7
0.6 x1 8 x2
交互作用影响的讨论 y ˆ0 ˆ 1 x 1 ˆ2 x 2 ˆ3 x 2 2 ˆ4 x 1 x 2
y~被解释变量(因变量)
y 10
9.5
x1, x2~解释变量(回归变量, 自变量) 9 8.5
0, 1 , 2 , 3 ~回归系数
8
7.5
~随机误差(均值为零的
正态分布随机变量)
7 5
5.5
6
6.5
x 7
7.5
2
y01x22x2 2
模型求解 MATLAB 统计工具箱
y01 x 12 x 23 x 2 2由数据 y,x1,x2估计
数学建模作业8-牙膏销售量模型

数学建模作业8-牙膏销售量模型a=polyfit(x1,y,1);y1=polyval(a,x1);b=polyfit(x2,y,2);x3=5.00:0.05:7.25;y2=polyval(b,x3);subplot(2,1,1);plot(x1,y,'*',x1,y1,'b');title('í?1y??x1μ?é¢μ?í?'); subplot(2,1,2);plot(x2,y,'o',x3,y2,'b');title('í?2 y??x2μ?é¢μ?í?')x的增加,y的值有比较明显的线性增长趋势,图中的直线是用线性从图1可以发现,随着1模型011(1)y x ββε=++拟合的(其中ε是随机变量)。
而在图2中,当2x 增大时,y 有向上弯曲增加的趋势,图中的曲线是用二次函数模型201222(2)y x x βββε=+++拟合的。
综合上面的分析,结合模型(1)和(2)建立如下的回归模型20112232(3)y x x x ββββε=++++(3)式右端1x 和2x 称为回归变量(自变量),20112232x x x ββββ+++是给定价差1x ,广告费用2x 时,牙膏销售量y 的平均值,其中的参数0123,,,ββββ称为回归系数,由表1的数据估计,影响y 的其他因素作用都包含在随机误差ε中。
如果模型选择合适,ε应该大致服从均值为0的正态分布。
五、模型求解(显示模型的求解方法、步骤及运算程序、结果) 2)、确定回归模型系数,求解出教程中模型(3):建立程序c hengxu2.m如下:x1=[-0.05 0.25 0.60 00.250.200.15 0.05 -0.15 0.15 0.20 0.10 0.40 0.45 0.35 0.30 0.50 0.50 0.40 -0.05-0.05 -0.10 0.20 0.10 0.50 0.60 -0.05 0 0.05 0.55]';x2=[5.50 6.75 7.25 5.50 7.00 6.50 6.75 5.25 5.256.00 6.50 6.25 7.00 6.90 6.80 6.80 7.107.00 6.80 6.50 6.25 6.00 6.50 7.00 6.80 6.80 6.50 5.75 5.80 6.80]'; X=[on es (30,1) x1 x2 x2.^2];Y=[7.38 8.51 9.52 7.50 9.33 8.28 8.75 7.87 7.10 8.00 7.89 8.15 9.10 8.86 8.90 8.87 9.26 9.00 8.75 7.95 7.65 7.27 8.00 8.50 8.75 9.21 8.27 7.67 7.93 9.26]';[b,bint,r,rint,sta ts]=r egress(Y,X); b,bint ,stats结果如下:b=17.32441.3070-3.69560.3486bint =5.7282 28.92060.6829 1.9311-7.49890.10770.03790.6594stats =0.9054 82.9409 0.00000.0490表2模型(3)的计算结果参数参数估计值参数置信区间β17.3244 [5.7282,28.9206]β 1.3070 [0.6829,1.9311]1β-3.6956 [-7.4989,0.1077]2β0.3486 [0.0379,0.6594] 3结果如下:b =29.113311.1342-7.60800.6712-1.4777bint=13.7013 44.52521.9778 20.2906-12.6932-2.52280.25381.0887-2.8518 -0.1037stats =0.9209 72.7771 0.00000.0426表3模型(5)的计算结果参数参数估计值参数置信区间β29.1133 [13.7013,44.5252]β11.1342 [1.9778,20.2906]1β-7.6080 [-12.6932,-2.5228] 2β0.6712 [0.2538,1.0887]34β-1.4777 [-2.8518,-0.1037]2R =0.9209 F=72.7771 p<0.0001 2s =0.0426表3与表2的结果相比,2R 有所提高,说明模型(5)比模型(3)有所进步。
牙膏销售问题

b,bint,stats
3)对模型进行改进,确定回归模型系数,求解出教程中模型(5);
Matlab程序:
x1=[-0.05 0.25 0.60 0 0.25 0.20 0.15 0.05 -0.15 0.15 0.20 0.10 0.40 0.45 0.35 0.30 0.50 0.50 0.40 -0.05 -0.05 -0.10 0.20 0.10 0.50 0.60 -0.05 0 0.05 0.55]';
表2模型(3)的计算结果
参数
参数估计值
参数置信区间
17.3244
[5.7282,28.9206]
1.3070
[0.6829,19311]
-3.6956
[-7.4989,0.1077]
0.3486
[0.0379,0.6594]
=0.9054 F=82.9409 p<0.0001 =0.0490
结果分析:表2显示, =0.9054指因变量y(销售量)的90.54%可由模型确定,F值远远超过F检验的临界值,p远小于 ,因而模型(3)从整体来看时可用的。
佛山科学技术学院
上机报告
课程名称数学建模
上机项目牙膏销售问题
专业班级
一、问题提出
根据牙膏销售量与价格、广告费等表格1中的数据,建立三个模型,要求:
1)画出散点图:y对x1的散点图1;y对x2的散点图2;
2)确定回归模型系数,求解出教程中模型(3);
3)对模型进行改进,确定回归模型系数,求解出教程中模型(5);
x1=[-0.05 0.25 0.60 0 0.25 0.20 0.15 0.05 -0.15 0.15 0.20 0.10 0.40 0.45 0.35 0.30 0.50 0.50 0.40 -0.05 -0.05 -0.10 0.20 0.10 0.50 0.60 -0.05 0 0.05 0.55];
统计模型在数学建模的应用

对因变量的影响是否显著.
• 模型改进, 如增添二次项、交互项等. • 对因变量进行预测.
2 软件开发人员的薪金
建立模型研究薪金与资历、管理责任、教育程度的关系 . 分析人事策略的合理性,作为新聘用人员薪金的参考. 46名软件开发人员的档案资料
编 号 01 02 03 04 薪金 13876 11608 18701 11283 资 历 1 1 1 1 管 理 1 0 1 0 教 育 1 3 3 2 编 号 42 43 44 45 46 薪金 27837 18838 17483 19207 19346 资 历 16 16 16 17 20 管 理 1 0 0 0 0 教 育 2 2 1 2 1
销售 周期 1 2
29 30
3.80 3.70
3.85 4.25
5.80 6.80
0.05 0.55
7.93 9.26
基本模型
y ~公司牙膏销售量 x1~其他厂家与本公司价格差 x2~公司广告费用
y 10
9.5 9 8.5 8 7.5 7 -0.2 0 0.2 0.4 0.6
e 与资历x1的关系
2000 1000
2000 1000 0 -1000
0
-1000
-2000
0
5
10
15
20
-2000
1
2
3
4
5
6
残差大概分成3个水平, 6种管理—教育组合混在 一起,未正确反映.
残差全为正,或全为负,管 理—教育组合处理不当. 应在模型中增加管理x2与 教育x3, x4的交互项 .
1 牙膏的销售量
问 题
建立牙膏销售量与价格、广告投入之间的模型; 预测在不同价格和广告费用下的牙膏销售量. 收集了30个销售周期本公司牙膏销售量、价格、 广告费用,及同期其他厂家同类牙膏的平均售价 .
Matlab回归分析:详解+实例
姚明女儿的身高
问 建立父母身高和女儿身高的模型 题 姚明2.26米,叶莉1.90米,预测姚明女儿身高
女孩身高y(cm) 156 172 162 158 164 166 160 155 174 165
父母平均身高 x(cm)
158.5
170.5
166
163.5
166
168.5 165.5
自变量X:用来解释Y的变量,通常有多个。
Y:薪资收入 X:学历、年龄、性别...
注意:(1)自变量可以是定量数据,也可以是定
性数据,它不决定回归模型的类型,决定回归模型 类型的是因变量;
(2)确定自变量的方法可以头脑风暴,但同时也 要看数据的可获得性,有时候可能头脑风暴想的很 好,但是没办法获取这个指标的数据也是不行的, 所以自变量的选取往往看一个数据的可获取性。
1 n
(x0 x)2 Lxx
小结
1.回归分析的任务 研究变量之间的相关关系
2.线性回归的步骤
(1) 推测回归函数; (3) 估计未知参数; (5) 预测.
(2) 建立回归模型; (4) 进行假设检验;
MATLAB中回归分析的实现
多元线性回归
1.确定回归系数的点估计值,用命令:
b=regress(Y,X)
女孩身高y(cm) 156 172 162 158 164 166 160 155 174 165
父母平均身高 x(cm)
158.5
170.5
166
163.5
166
168.5 165.5
159
180.5
169
基本模型
y 0 1x
y ~女孩身高
0, 1 ~回归系数
数学建模随机模型
• 内部规律复杂数据统计分析 – 常用模型回归模型数学原理软件
• 30个销售周期数据: – 销售量、价格、广告费用、同类产品均价
销售周期 公司价 (元) 它厂价 (元) 广告(百万元)
1
3.85
3.80
5.50
2
3.75
4.00
6.75
…
…
…
…
29
3.80
Pn (t t) Pn1 (t)bn1t Pn1 (t)dn1t Pn (t)(1 bnt dnt) o(t) 10
建模
ห้องสมุดไป่ตู้
微分方程
dPn dt
bn1Pn1 (t) d P n1 n1 (t) (bn
dn )Pn (t)
bn=n,dn=n
dPn dt
(n 1)Pn1(t) (n 1)Pn1(t) ( )nPn (t)
• 价格差 x1=0.1 • 价格差 x1=0.3
yˆ x10.1 30.2267 7.7558x2 0.6712x22 yˆ x10.3 32.4535 8.0513x2 0.6712x22
x1 x2 7.5357 yˆ x10.3 yˆ x10.1
18
销售量预测
yˆ ˆ0 ˆ1x1 ˆ2 x2 ˆ3x22
价差x1=它厂价x3-公司价x4 控制x1 估计x3,调整x4
预测y
控制价格差 x1=0.2元,投入广告费 x2=6.5 百万元
yˆ ˆ0 ˆ1 x1 ˆ2 x2 ˆ3 x22 8.2933(百万支)
销售量预测区间为 [7.8230,8.7636](置信度95%) 上限用作库存管理的目标值 下限用来把握公司的现金流
数学建模中matlab应用
完全二次多项式模型
y x x x x x x
2 2 0 1 1 2 2 3 1 2 4 1 5 2
MATLAB中有命令rstool直接求解
a=xlsread('feiyong3.xls'); y=a(:,7); x=a(:,2:3); rstool(x,y,'quadratic',0.05)
统计回归模型
1 牙膏的销售量 2 软件开发人员的薪金
3 酶促反应
4 投资额与国民生产总值和 物价指数
数学建模的基本方法
机理分析
测试分析
由于客观事物内部规律的复杂及人们认识程度的限制, 无法分析实际对象内在的因果关系,建立合乎机理规 律的数学模型。 通过对数据的统计分析,找出与数据拟合最好的模型. 回归模型是用统计分析方法建立的最常用的一类模型. • 不涉及回归分析的数学原理和方法 • 通过实例讨论如何选择不同类型的模型 • 对软件得到的结果进行分析,对模型进行改进
10.5 10 9.5 9 8.5 x1=0.3 x1=0.1
ˆ x10.3 y ˆ x10.1 x2 7 .5357 y
价格优势会使销售量增加
加大广告投入使销售量增加 ( x2大于6百万元) 价格差较小时增加 的速率更大
ˆ y
8 7.5 5 6 7 8
x2
价格差较小时更需要靠广告 来吸引顾客的眼球
2 y x x x x x 0 1 1 2 2 3 2 4 1 2
参数
参数估计值 置信区间 0 29.1133 [13.7013 44.5252] 1 11.1342 [1.9778 20.2906 ] 2 -7.6080 [-12.6932 -2.5228 ] 3 0.6712 [0.2538 1.0887 ] 4 -1.4777 [-2.8518 -0.1037 ] R2=0.9209 F=72.7771 p=0.0000 s2=0.0426
数学建模牙膏模型
Stats~ 检验统计量 R2,F, p
2 结果分析 y 0 1 x1 2 x2 3 x2
参数
参数估计值 置信区间 0 17.3244 [5.7282 28.9206] 1 1.3070 [0.6829 1.9311 ] 2 -3.6956 [-7.4989 0.1077 ] 3 0.3486 [0.0379 0.6594 ] R2=0.9054 F=82.9409 p=0.0000
9
ˆ y
9
ˆ y
8.5
x2=6.5
0 0.2 0.4 0.6
8.5
8
87.5 -0.2x17.5 -0.2
0
0.2
0.4
0.6
x1
10 9.5 9 8.5 8 7.5 5
ˆ y
10.5 10
ˆ y
x1=0.2
6 7 8
9.5 9 8.5
x2
8
5
6
7
8
x2
交互作用影响的讨论
价格差 x1=0.1
ˆ y
参数
2 y 0 1 x1 2 x2 3 x2 4 x1 x2
参数估计值 置信区间 0 17.3244 [5.7282 28.9206] 1 1.3070 [0.6829 1.9311 ] 2 -3.6956 [-7.4989 0.1077 ] 3 0.3486 [0.0379 0.6594 ] R2=0.9054 F=82.9409 p=0.0000 参数估计值 置信区间 29.1133 [13.7013 44.5252] 11.1342 [1.9778 20.2906 ] -7.6080 [-12.6932 -2.5228 ] 0.6712 [0.2538 1.0887 ] -1.4777 [-2.8518 -0.1037 ] R2=0.9209 F=72.7771 p=0.0000
