相似形单元测试题及答案
(完整word版)相似三角形单元测试卷(含答案)

相似三角形单元测试卷(共100分)一、填空题:(每题5分,共35分)1、已知a =4,b =9,c 是a b 、的比例中项,则c = .2、一本书的长与宽之比为黄金比,若它的长为20cm ,则它的宽 是 cm (保留根号).3、如图1,在ΔABC 中,DE ∥BC ,且AD ∶BD =1∶2,则S S ADE ∆=四边形DBCE : .图1 图2 图34、如图2,要使ΔABC ∽ΔACD ,需补充的条件是 .(只要写出一种)5、如图3,点P 是RtΔABC 斜边AB 上的任意一点(A 、B 两点除外)过点作一条直线,使截得的三角形与RtΔABC 相似,这样的直线可以作 条.图4 图5 图66、如图4,四边形BDEF 是RtΔABC 的内接正方形,若AB =6,BC =4,则DE = .7、如图5,ΔABC 与ΔDEF 是位似三角形,且AC =2DF ,则OE ∶OB = . 二、选择题: (每题5分,共35分)8、若k bac a c b c b a =+=+=+,则k 的值为( ) A 、2 B 、-1 C 、2或-1 D 、不存在9、如图6,F 是平行四边形ABCD 对角线BD 上的点,BF ∶FD=1∶3,则BE ∶EC=( )A 、21 B 、31 C 、32 D 、41 图7 图8 图910、如图7,△ABC 中,DE ∥FG ∥BC ,且DE 、FG 将△ABC 的面积三等分,若BC=12cm ,则FG 的长为( )A 、8cmB 、6cmC 、64cmD 、26cm 11、下列说法中不正确的是( )A .有一个角是30°的两个等腰三角形相似;B .有一个角是60°的两个等腰三角形相似;C .有一个角是90°的两个等腰三角形相似;D .有一个角是120°的两个等腰三角形相似.12、如图9, D 、E 是AB 的三等分点, DF∥EG∥BC , 图中三部分的面积分别为S 1,S 2,S 3, 则S 1:S 2:S 3( ) A.1:2:3 B.1:2:4 C.1:3:5 D.2:3:413、两个相似多边形的面积之比为1∶3,则它们周长之比为( )A .1∶3B .1∶9C .1D .2∶314、下列3个图形中是位似图形的有( )A 、0个B 、1个C 、2个D 、3个 三、解答题(15题8分,16题10分,17题12分,共30分) 15、如图,已知AD 、BE 是△ABC 的两条高,试说明AD ·BC=BE ·AC16、如图所示,小华在晚上由路灯A 走向路灯B,当他走到点P 时, 发现他身后影子的顶部刚好接触到路灯A 的底部,当他向前再步行12m 到达点Q 时, 发现他身前影子的顶部刚好接触到路灯B 的底部,已知小华的身高是1.6m,两个路灯的高度都是9.6m,且AP=QB. (1)求两个路灯之间的距离;(2)当小华走到路灯B时,他在路灯A 下的影长是多少?17.如图,在矩形ABCD 中,AB=12cm ,BC=8cm .点E 、F 、G 分别从点A 、B 、C 三点同时出发,沿矩形的边按逆时针方向移动.点E 、G 的速度均为2cm/s ,点F 的速度为4cm/s ,当点F 追上点G (即点F 与点G 重合)时,三个点随之停止移动.设移动开始后第t 秒时,△EFG 的面积为S (cm 2) (1)当t=1秒时,S 的值是多少?(2)写出S 和t 之间的函数解析式,并指出自变量t 的取值范围;(3)若点F 在矩形的边BC 上移动,当t 为何值时,以点E 、B 、F 为顶点的三角形与以点F 、C 、G 为顶点的三角形相似?请说明理由.AB C ED参考答案一、 填空题:(1)、1或4或16;(2)、±6;(3)、-94;(4)、1.6或2.5;(5)、)15(10 ; (6)、1:8;(7)、∠ACD=∠B 或∠ADC=∠ACB 或AD :AC=AC :AB ;(8)、31.5; (9)、0.2;(10)、3;(11)、2.4;(12)、1:2三、作图题: 23、(略) 四、解答题:24、证明:∵AD 、BE 是△ABC 的高 ∴∠ADC=∠BEC ∵∠C=∠C∴△ADC ∽△BEC ∴AD :BE=AC :BC ∴AD ×BC=BE ×AC25、解:由图得,AB=5,AC=25,BC=5,EF=2,ED=22,DF=10, ∴AB :EF=AC :ED=BC :DF=5:2∴△ABC ∽△DEF26、解:过点C 作C E ∥AD 交AB 于点E ,则CD=AE=2m ,△BCE ∽△B /BA / ∴A / B /:B /B=BE :BC 即,1.2:2= BE :4 ∴BE=2.4∴AB=2.4+2=4.4答:这棵树高4.4m 。
相似单元测试题及答案

相似单元测试题及答案一、选择题(每题2分,共10分)1. 下列哪项不是相似图形的特点?A. 形状相同B. 面积相等C. 大小相同D. 角度相同2. 相似比的定义是什么?A. 两个图形对应边长的比B. 两个图形对应角的比C. 两个图形对应面积的比D. 两个图形对应周长的比3. 若两个三角形相似,它们的对应角相等,对应边成比例,那么它们的对应高也成比例吗?A. 是B. 否4. 相似图形的面积比与边长比的平方相等,这是根据什么定理得出的?A. 相似定理B. 勾股定理C. 毕达哥拉斯定理D. 面积比定理5. 两个相似多边形的对应边数必须相等吗?A. 是B. 否二、填空题(每题2分,共10分)6. 如果两个三角形的相似比是2:3,那么它们的对应边长之比是________。
7. 相似图形的周长比等于它们的________。
8. 两个相似圆的面积比是25:36,那么它们的半径比是________。
9. 根据相似图形的性质,如果两个图形相似,那么它们的对应角________。
10. 在相似三角形中,如果一个三角形的边长是另一个三角形边长的1.5倍,那么它们的面积比是________。
三、简答题(每题5分,共10分)11. 解释为什么相似三角形的对应角相等。
12. 描述如何判断两个多边形是否相似。
四、计算题(每题10分,共20分)13. 已知三角形ABC与三角形DEF相似,且AB:DE = 2:3,求三角形ABC的面积与三角形DEF的面积之比。
14. 如果一个矩形的长是另一个矩形长的1.5倍,宽是另一个矩形宽的0.8倍,求这两个矩形的面积比。
五、论述题(每题15分,共15分)15. 论述相似图形在建筑设计中的应用及其重要性。
答案:一、选择题1. B2. A3. A4. D5. A二、填空题6. 2:37. 相似比8. 5:69. 相等10. 2.25:1三、简答题11. 相似三角形的对应角相等,因为相似三角形的定义就是它们的对应角相等,这是相似三角形的基本性质之一。
相似三角形单元测试卷带答案

相似三角形单元测试卷一.选择题1.在△ABC中,BC=6,AC=8,AB=10,另一个与它相似的三角形的最短边长是3,则其最长边一定是()A.12 B.5 C. 16 D.202.下列说法正确的是()A.所有的等腰三角形都相似B.所有的直角三角形都相似C.所有的等腰直角三角形都相似D.有一个角相等的两个等腰三角形都相似3.在相同时刻的物高与影长成正比.如果高为1.5m的竹竿的影长为2.5m,那么影长为30m 旗杆的高是A. 15mB. 16mC. 18mD. 20m4.如图,在△ABC中,点D、E分别是AB、AC的中点,则下列四个结论:①BO=2OE;②13DOEADESS∆∆=;③12ADEBCESS∆∆=;④△ADC∽△AEB.其中正确..的结论有()A.3个B.2个C.1个D.0个5.如图,△ABC中,三边互不相等,点P是AB上一点,有过点P的直线将△ABC切出一个小三角形与△ABC相似,这样的直线一共有()APCBA、5条B、4条C、3条D、2条【答案】B6.如图,∠ABD=∠ACD,图中相似三角形的对数是()(A)2 (B)3 (C)4 (D)5【答案】C7.(11·西宁)如图6,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADB +∠EDC=120°,BD=3,CE=2,则△ABC的边长为A.9 B.12 C.16 D.188.如图,王华晚上由路灯A下的B处走到C处时,测得影子CD的长为1米,继续往前走3米到达E处时,测得影子EF的长为2米,已知王华的身高是1.5米,那么路灯A的高度AB 等于()AB C D E FA. 4.5米B. 6米C. 7.2米D. 8米【答案】B9.在平面直角坐标系中,正方形ABCD 的位置如图6所示,点A 的坐标为(1,0),点D 的坐标为(0,2).延长CB 交x 轴于点A 1,作正方形A 1B 1C 1C ;延长C 1B 1交x 轴于点A 2,作正方形A 2B 2C 2C 1,…按这样的规律进行下去,第2012个正方形的面积为 ( )201135()2⨯ B .201195()4⨯ C .201235()2⨯ D .201295()4⨯【答案】B10. 如图所示,小正方形的边长为1,则下列图形中的三角形(阴影部分)与ABC ∆相似的是( )【答案】A二.填空题11.已知32=b a ,则=+b b a ___________。
相似的单元测试题及答案

相似的单元测试题及答案一、选择题(本题共10分,每题1分)1. 下列哪个选项是相似三角形的定义?A. 面积相等的三角形B. 形状相同的三角形C. 边长成比例的三角形D. 角度相同的三角形2. 相似三角形的对应角相等,对应边成比例,这个性质称为:A. 相似性质B. 等角性质C. 比例性质D. 角度比例性质3. 如果两个三角形的对应边长比为2:3,那么它们的面积比是:A. 2:3B. 4:9C. 6:9D. 8:274. 在相似三角形中,如果一个角是30°,那么它的对应角也是:A. 30°B. 60°C. 90°D. 120°5. 相似三角形的判定定理中,SAS相似准则指的是:A. 两边及其夹角相等B. 三边对应成比例C. 两角对应相等D. 一边对应成比例,其余两边及其夹角相等二、填空题(本题共10分,每空1分)6. 相似三角形的判定定理包括AA准则、SAS准则和______准则。
7. 如果三角形ABC与三角形DEF相似,那么AB:DE=______,∠A=______。
8. 相似三角形的面积比等于它们对应边长的______。
9. 根据相似三角形的性质,如果三角形ABC与三角形DEF相似,且AB=2DE,则三角形ABC的面积是三角形DEF面积的______倍。
10. 在相似三角形中,如果∠BAC=45°,那么∠EDF=______。
三、简答题(本题共20分,每题5分)11. 解释什么是相似三角形,并给出两个相似三角形的例子。
12. 描述如何使用AA准则判定两个三角形是否相似。
13. 说明为什么相似三角形的面积比等于它们对应边长的平方比。
14. 如果一个三角形的边长扩大到原来的两倍,它的面积会如何变化?15. 给出一个实际生活中使用相似三角形性质的例子。
四、计算题(本题共30分,每题10分)16. 已知三角形ABC与三角形DEF相似,AB=6cm,DE=9cm,求BC:EF的比值。
图形的相似单元测试【含答案】

DC B A 图形的相似 单元测试(时间:60分钟,共100分)一、选择题(每小传统3分,共30分) 1.下列语句正确的是 ( )A .在△ABC 和△A′B′C′中,∠B=∠B′=90°,∠A=30°,∠C′=60°, 则△ABC 和△A′B′C′不相似B .在△ABC 和△A′B′C′中,AB=5,BC=7,AC=8,A′C′=16,B′C′=14,A′B ′=10,则△ABC ∽△A′B′C′C .两个全等三角形不一定相似D .所有的菱形都相似2.如图所示,△ABC ∽△ADE ,AE=30cm ,EC=15cm ,BC=60cm ,则DE 的长为 ( ) A .40cm B .50cm C .45cm D .35cm 3.如图所示,能保证△ACD ∽△ABC 的条件是 ( ) A .AB:BC=AC:CD B .CD:AD=BC:AC C .CD 2=AD .DC D .AC 2=AB .AD 4.如果两个相似多边形的面积比为9:4,那么这两个相似多边形的相似比为 ( ) A .9:4 B .2:3 C .3:2 D .81:16 5.小明用如图所示的胶滚沿从左到右的方向将图案滚涂到墙上,如图 所示给出的四个图案中,符合图示胶滚图案的是 ( )6.语句:“①所有度数相等的角都相似;②所有边长相等的菱形都相似;③所有的正方形都相似;④所有的圆都相似”中准确的有 ( )A .4句B .3句C .2句D .1句 7.下列语句中不正确的是 ( )A .求两条线段的比值,必需采用相同的长度单位B .求两条线段的比值,只需采用相同的长度单位,与选用何种长度单位无关C .两个相似三角形中,任意两组边对应成比例D .不相似的两个三角形中,也有可能两组边对应成比例 8.下列各组图形有可能不相似的是 ( ) A .各有一个角是50°的两个等腰三角形 B .各有一个角是100°的两个等腰三角形 C .各有一个角是50°的两个直角三角形 D .两个等腰直角三角形9.一个多边形的边长分别为2,3,4,5,6,另一个多边形和这个多边形相似,其最短边长为6,则最长边长为( )A .12B .18C .24D .301250800xy ╯ ╮ 650 536╭α ╰ ╯ 803 10. 已知cba b a c a c b +=+=+=k ,则k=( ) A .2 B .-1 C .2或-1 D .0二、填空题(每小题3分,共24分)11.如果一个三角形的面积扩大9倍,那么它的边长扩大_____________倍.12.如图所示,有一块呈三角形的草坪,其一边长为20m ,在这个草坪的图纸上,若这条边的长为5cm ,其他两边的长都是3.5cm ,则该草坪其他两边的实际长度为______________.13.如图所示的两个三角形是相似的x=_________,m=___________,n=____________.x2a 55︒m ︒45︒103a n ︒80︒45︒14. 已知如图,两个矩形相似, 则x= ,y= ,α= .15. 在相同时刻的物高与影长成比例,如果一古塔在地面上影长为50m ,同时,高为1.5m 的测竿的影长为2.5m ,那么,古塔的高是___米.16.如图中的两个矩形相似,则x=___________.17. 请把下列各组图形是否相似的结论写在下面的括号里.18.如图在直角坐标系中,右边的图案是由左边的图案经过平移以后得到的.左图案中左右眼睛的坐标分别是(-4,2)、(-2,2),右图中左眼的坐标是(3,4),则右图案中右眼的坐标是 .三、解答题(19小题6分,其余各小题8分,共46分) 19.把上下对应的相似图形用线连起来20.如图所示,写出多边形ABCDEF 各个顶点的坐标,并画出多边形ABCDEF 关于y 轴的轴对称图形,它们相应的对称点的坐标有什么变化?-3 -2 -1 32 1 O -1 -212 3 xy21.学生会举办一个校园摄影艺术展览会,小华和小刚准备将矩形的作品四周镶上一圈等宽的纸边,如图所示.两人在设计时发生了争执:小华要使内外两个矩形相似,感到这样视觉效果较好;小刚试了几次不能办到,表示这是不可能的.小红和小莉了解情况后,小红说这一要求只有当矩形是黄金矩形时才能做到,小莉则坚持只有当矩形是正方形时才能做到.请你动手试一试,说一说你的看法.222.以下列正方形网络的交点为顶点,分别画出两个相似比不为1的相似三角形,使它们:(1)都是直角三角形;(2)都是锐角三角形;(3)都是钝角三角形.23.如果一个图形经过分割,能成为若干个与自身相似的图形,我们称它为“能相似分割的图形”,如图所示的等腰三角形和矩形就是能相似分割的图形. (1)你能否再各举出一个 “能相似分割”的三角形和四边形?(2)一般的三角形是否“能相似分割的图形”?如果是的话给出一种分割方案,否则说明原因.24.我们通常用到的一种复印纸,整张称为A 1纸,对折一分为二裁开成为A 2纸,再一分为二成为A 3纸,…,它们都是相似的矩形.求这种纸的长与宽的比值(精确到千分位).参考答案1.B ;对应边成比例 2.A ;根据对应边成比例 3.D ;比例性质 4.C ;相似形的性质 5.C ;图形的相似 6.B ;②③④ 7.C ;注意对应 8.A ;不符合对应关系 9. 由相似多边形对应边成比例,设最长边为x .∴x662 ,∴2x=36,x=18.答案:B 10.C .2或-1二、11.3倍 12.14m 13.20314.根据相似形的性质,得x=2.5,y=1.5,α=900;⑵x=22.5. 15.在相同时刻的物高与影长成比例,设古塔的高为xm ,则505.25.1x=,解得x=30(m ) 16.已知两个矩形相似,根据相似形的性质,有x201530=,∴30x =15×20,解得x =10;又152030=x ,∴x =22.5 17. ①相似,②不相似,③不相似,④相似,⑤不相似,⑥不相似 18. 由左图案中左右眼睛的坐标分别是(-4,2)、(-2,2),不难发现左右眼睛之间的距离2个单位;平移后的图形右图中左眼的坐标是(3,4),则右图案中右眼的坐标的纵坐标不变,横坐标为3+2=5,即右图案中右眼的坐标是(5,3). 三、19.相似形连线如(1)-(a ),(2)-(d),(3)-(g)20.提示:A(-2,0),B(0,-3),C(3,-3),D(4,0),E(3,3),F(0,3),A′(2,0),B′(0, 3),C′(-3,-3),D′(-4,0),E′(-3,3),F′(0,3).21.只有正方形才能做到,设矩形的一边为a ,另一边为b ,等宽的纸边宽为c ,按小华的要求,应有cb ca b a 22--=,化简得a=b . 22.作图如下23.例如直角三角形,一组底角是60°、三边相等的等腰梯形. 三角形都是“能相似分割的图形”(提示:顺次连结三角形三边中点,将三角形分成的四个三角形都和原三角形相似)24. 1.414(提示:设 A 1纸的长为a ,观为b ,由A 1,A 2纸的长余观对应成比例,得a:b=b:21a )。
九年级数学相似三角形单元测试的题目及答案详解

九年级数学相似单元测试一.选择题(每小题3分,共30分)1.在比例尺为1:5000的地图上,量得甲,乙两地的距离25cm,则甲,乙的实际距离是( ) A.1250km B.125km C. 12.5km D.1.25km 2.已知0432c b a ,则c b a的值为( )A.54B.45C.2D.213.已知⊿ABC 的三边长分别为2,6,2,⊿A ′B ′C ′的两边长分别是1和3,如果⊿ABC 与⊿A ′B ′C ′相似,那么⊿A ′B ′C ′的第三边长应该是( )A.2B.22C.26D.334.在相同时刻,物高与影长成正比。
如果高为 1.5米的标杆影长为 2.5米,那么影长为30米的旗杆的高为( ) A 20米 B 18米 C 16米 D 15米5.如图,∠ACB=∠ADC=90°,BC=a,AC=b,AB=c,要使⊿ABC ∽⊿CAD, 只要CD 等于( ) A.cb2B.ab2C.cabD.ca26.一个钢筋三角架三长分别为20cm,50cm,60cm,现要再做一个与其相似的钢筋三角架,而只有长为30cm 和50cm 的两根钢筋,要求以其中的一根为一边,从另一根截下两段(允许有余料)作为另两边,则不同的截法有( ) A.一种 B.两种 C.三种 D.四种7、用位似图形的方法,可以将一个图形放大或缩小,位似中心的位置可以选在( ) A 原图形的外部 B 原图形的内部 C 原图形的边上 D 任意位置8、如图,□ABCD 中,EF ∥AB ,DE ∶EA = 2∶3,EF = 4,则CD 的长()A .163B .8C .10D .169.已知a 、b 、c 为非零实数,设k=c ba bca a cb ,则k 的值为()A .2B .-1C .2或-1D .110、某校计划在一块三角形的空地上修建一个面积最大的正方形水池,使得水池的一边在△ABC的边BC 上,△ABC 中边BC=60m ,高AD=30m ,则水池的边长应为( ) A 10m B 20m C 30m D 40m二.填空题(每小题3分,共30分)11、已知43yx,则._____yy x12、.已知点C 是线段AB 的黄金分割点,且AC>BC,则AC ∶AB= . 13、.把一矩形纸片对折,如果对折后的矩形与原矩形相似,则原矩形纸片的长与宽之比为 .14、如图,⊿ABC中,D,E分别是AB,AC上的点(DE BC),当或或时,⊿ADE与⊿ABC相似.15、在△ABC中,∠B=25°,AD是BC边上的高,并且2·,则∠BCA的度数为____________。
相似图形单元测试题(含答案)
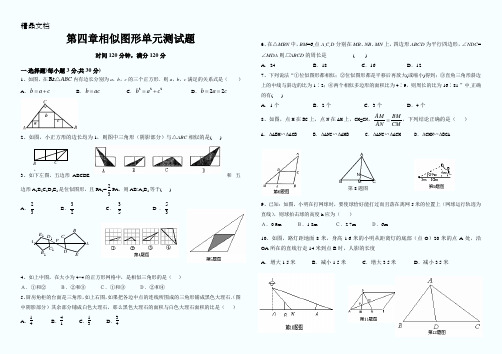
第四章相似图形单元测试题时间120分钟,满分120分一.选择题(每小题3分,共30分)1、如图,在Rt ABC △内有边长分别为a ,b ,c 的三个正方形.则a ,b ,c 满足的关系式是( )A .b a c =+B .b ac =C .222b ac =+ D .22b a c ==2、如图,小正方形的边长均为1,则图中三角形(阴影部分)与△ABC 相似的是( )3、如下左图,五边形ABCDE和五边形A 1B 1C 1D 1E 1是位似图形,且PA 1=32PA ,则AB ׃A 1B 1等于( ) A .32 B .23 C . 53 D .354、如上中图,在大小为4×4的正方形网格中,是相似三角形的是( ).A.①和② B.②和③ C.①和③ D.②和④5、厨房角柜的台面是三角形,如上右图,如果把各边中点的连线所围成的三角形铺成黑色大理石.(图中阴影部分)其余部分铺成白色大理石,那么黑色大理石的面积与白色大理石面积的比是( )A .14B .41C .13D .346、在△MBN 中,BM =6,点A ,C,D 分别在MB 、NB 、MN 上,四边形ABCD 为平行四边形,∠NDC =∠MDA 则□ABCD 的周长是( )A .24B .18C .16D .127、下列说法“①位似图形都相似;②位似图形都是平移后再放大(或缩小)得到;③直角三角形斜边上的中线与斜边的比为1∶2;④两个相似多边形的面积比为4∶9,则周长的比为16∶81.”中,正确的有()A .1个B .2个C .3个D .4个8、如图,点M 在BC 上,点N 在AM 上,CM=CN ,CMBMAN AM =,下列结论正确的是( ) A .∆ABM ∽∆ACB B .∆ANC ∽∆AMB C .∆ANC ∽∆ACM D .∆CMN ∽∆BCA9、已知:如图,小明在打网球时,要使球恰好能打过而且落在离网5米的位置上(网球运行轨迹为直线),则球拍击球的高度h 应为( ).A.0.9m B.1.8m C.2.7m D.6m10、如图,路灯距地面8米,身高1.6米的小明从距离灯的底部(点O )20米的点A 处,沿OA 所在的直线行走14米到点B 时,人影的长度A .增大1.5米B .减小1.5米C .增大3.5米D .减小3.5米BA C第8题图ABCN ME 1D1C 1B 1A 1BDACEP二、填空题:(30分)11、如图,在平行四边形ABCD 中,M 、N 为AB 的三等分点,DM 、DN 分别交AC 于P 、Q 两点,则AP :PQ :QC= .12、如图,将①∠BAD = ∠C ;②∠ADB = ∠CAB ; ③BC BD AB ⋅=2;④DBABAD CA =;⑤DA AC BA BC =; ⑥ACDABA BC =中的一个作为条件,另一个作为结论,组成一个真命题,则条件是__________,结论是_______.(注:填序号)13、如图,Rt ∆ABC 中,AC ⊥BC ,CD ⊥AB 于D ,AC=8,BC=6,则AD=_________。
《相似》单元测试题及参考答案(精编)

《相似》单元测试题及参考答案(精编)一、选择题1.如图,点P 是AB 的黄金分割点,即P 点满足BP AP =AP AB ,若AB=2,则AP 的长为( )A.√5-1B.√5+1C.√5+2D.0.618 2.若3a=4b(ab ≠0),则下列比例式正确的是( )A.a 3=b 4B.4a =3bC.a b =34D.a 3=4b3.如图,已知AB//CD//EF,BD:DF =1:2,那么下列结论中,正确的是( )A.AC:AE=1:3B.CE:EA=1:3C.CD:EF=1:2D.AB:EF=1:2 第3题 第4题 第5题 第6题4.如图,在△ABC 中,如果DE 与BC 不平行,那么下列条件中,不能判断△ADE ∽△ACB 的是 ( )A.∠ADE=∠CB.∠AED=∠BC.AD AB =DE BCD.AD AC =AEAB5.如图,在Rt △ABC 中,∠BAC=90°,AD ⊥BC 于点D.若AC=3,AB=4,则BD 的长为( )A.125B.165C.203D.154 6.如图,在梯形ABCD 中,AD//BC,对角线AC,BD 相交于点O.若AD=1,BC=3,则AOCO 的值为( )A.12B.13C.14D.19 第7题 第8题 第9题 第10题7.如图,⊙O 是△ABC 的外接圆,AD 平分∠BAC 交⊙O 于点D,交边BC 于点E,连接BD.若AD=5,BD=2,则DE 的长为( )A.35B.425C.225D.45 8.如图,已知在△ABC 中,点D,E,F 分别是边AB,AC,BC 上的点,DE//BC, EF//AB,且AD:DB=3:5,那么CF:CB 等于( )A.5:8B.3:8C.3:5D.2:59.如图,△ABC ∽△ADE,且BC=2DE,则S 四边形BEDC :S △ABC 的值为( )A.1:4B.3:4C.2:3D.1: 210.如图,D,E 分别是△ABC 的边AB,BC 上的点,DE//AC,AE,CD 相交于点O,若S △DOE :S △COA =1:25,则S △BDE 与S △CDE 的比是( )A.1.3B.1:4C.1.5D.1:2511.已知△ABC ∽△DEF,其对应中线的比为1:3,若△ABC 的周长为3,则△DEF 的周长为( )A.1B.3C.9D.2712.如图,在平行四边形ABCD 中,F 为BC 的中点,延长AD 至点E,使DE:AD=1:3,连接 EF 交DC 于点G,则S △DEG :S △CFG 等于( )A. 2:3B.3:2C.9:4D.4:9第12题 第13题 第14题 第15题13.如图,在△ABC 中,DE//BC,过点A 作AM ⊥BC 于点M,交DE 于点N.若S △ADE :S △ABC =4:9,则AN 与NM 的长度比是( )A.4:9B.3:2C.9:4D.2:114.如图,在△ABC 中,点D,E 分别在AB 和AC 上,DE//BC,M 为BC 边上一点,连接AM 交DE 于点N,若DN NE =13,DN BM =23,则下列选项不成立的是( )A.S △AD NS △AD E =14 B.BM MC =13 C.S △ANE <S 四边形DBMN D.S 四边形DBMN S 四边形NMCE =1315.如图,点E,F,M 在矩形ABCD 的边上,四边形EFMN 是正方形,B,M,N 三点共线.若AB=3,AD=7,则BN MN 的值为()A.2B.178C.√5+12 D.158二、填空题16.若nm =23,则m−nm=____.17.线段a,b,c,d是成比例线段a=9cm,b=6cm,c=3cm,则d的长为____cm.18.如图,利用标杆BE测量建筑物的高度.若标杆BE的高为1.2m,测AB=1.6m,BC=12.4m,则楼高CD为____m.第 18题第19题第20题第21题19.小孔成像的示意图如图所示,光线经过小孔O,物体AB在幕布上形成倒立的实像CD(点A,B的对应点分别是C,D).若物体AB的高度为6cm,实像CD的高度为3cm,则小孔O到BC的距离OE为______cm.20.如图,学生用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=60cm,EF=30cm,测得边DF离地面的高度AC=1.5m,CD=10m,则树高AB___m.21.如图,△ABC是一块锐角三角形的材料,边BC=60mm,高AD=40mm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是_____mm.22.如图,已知△ABC和△DEF为位似图形,点O是位似中心,且△ABC和△DEF的周长之比是4:3,则下列结论:①AB//ED②BOOD =43③△AOC∽△DOF④S△A BC S△DEF =2√33.其中错误的是_____(填序号).三、解答题23.如图,O是△ABC外的一点,分别在射线OA,OB,OC上取点A',B',C’,使O A′OA =O B′OB=O C’OC=3,连接A'B’,B'C’,C'A',判断△A'B'C’与△ABC是否相似,并说明理由.24.如图,在△ABC中,AD平分∠BAC,E是AB边上一点,CE交AD于点F,且CF=CD.(1)求证:△ACE∽△ABC;(2)若EF=2,BD=4,求AB的值.AC25.如图,⊙O是△ABC的外接圆,点O在BC上,∠BAC的平分线交⊙O于点D,连接BD,CD,过点D作BC的平行线与AC的延长线相交于点P.(1)求证:PD是⊙O的切线;(2)求证:△ABD∽△DCP;(3)若AB=6,AC=8,求点O到AD的距离.26(1)问题:如图①,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90°,求证:AD·BC=AP·BP; (2)探究:如图②,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B=θ时,上述结是否依然成立?请说明理由;(3)应用:请利用(1)(2)获得的经验解决问题:如图③,在△ABD中,AB=6,AD=BD=5.点P以每秒1个单位长度的速度,由点A出发,沿边AB向点B运动,且满足∠DPC=∠A.设点P的运动时间为t(秒),当以点D为圆心,以DC长为半径的圆与AB相切时,求t的值.参考答案一、选择题1-5 ABACB 6-10 BDABB 11-15 CDDCA二、填空题16.1317. 218. 10.519. 220. 6.521. 2422.②④三、解答题23.略24(1)略(2)√225(1)略(2)略(3)√2226(1)略(2)略(3)1s或5s。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相似三角形单元测试
一.细心选择
1、若如图所示的两个四边形相似,则∠α的度数是 ( ) A .870
B .600
C .750
D .1200
2、若错误! ,则错误!的值是 ( ) A.错误! B 。
错误! C 。
错误! D 。
错误!
3、在相同时刻的物高与影长成比例,如果高为1。
5m 的测杆的影长为2.5m ,那么影长为30m 的旗杆的高是 ( )
A .20m
B .16m
C .18m
D .15m 4、如图,△ABC ∽△AD
E ,则下列比例式正确的是 ( ) A . B .
C .
D .
5、盐城市大纵湖旅游风景区中某两个景点之间的距离为75米,在一张比例尺为1:2000的导游图上,它们之间的距离大约相当于 ( ) A .一根火柴的长度
B .一支钢笔的长度
C .一支铅笔的长度
D .一根筷子的长度
6、电影院呈阶梯或下坡形状的主要原因是 ( )
A .为了美观
B .盲区不变
C .增大盲区
D .减小盲区 7、下列四个三角形,与左图中的三角形相似的是 ( )
二.精心填空
8、线段2cm 、8cm 的比例中项为 cm .
9、已知两个相似三角形的一组对应边分别是15cm 和23cm ,它们的周长差40cm ,则其中较大三角形的周长是 cm .
10、已知点C 为线段AB 的黄金分割点且AB = 2,则AC ≈ (精确到0.1).
11、如图,不等长的两条对角线AC 、BD 相交于点O ,且将四边形ABCD 分成甲、乙、丙、丁四个三角形.若,则甲、乙、丙、丁这4个三角形中,一定相似的有 .
F 是AD 的中点,BF 与
BGC 的AB=7,AD=2,BC=3,如果边AB 上的点P D 为顶点的三角形与以P ,B ,C 的顶点的三角形相似,这样的点P 有 个。
14、如图,Rt △ABC 中,CD 是斜边上的高,DE ⊥AC 于E ,AC :CB=4:5,则AE:EC 等于 。
15、如图,这是圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影(圆形)的示意图,已知桌面的直径为1.2米,桌面距离地面1米,若灯泡距离地面3米,则地面上阴影部分的面积为 。
(第8题) A . B . C . D .
第1题图
第11题图 A B C
D
E
第4题图 第12题
第13题图 A
D
B C
P 第15题图 第14题图
C
A D
B 16、点P 是△ABC 中AB 边上的一点,过P 作直线(不与AB 重合)截△ABC ,使截得的三角形与原三角形相似,满足条件的直线最多有 。
条
三.用心解答.
17、已知:如图,在中,为边上一点,,,AC 2=AB ·AD .试说明:和都是等腰三角形;
18、根据要求画出图形:
(1)如图,一根木棒竖直立在地面上,请你画出它在灯光下的影子.
(2)如图,已知五边形A 'B 'C 'D 'E '是五边形ABCDE 的位似图形,但被小明擦去了一部
分,你能将它补完整吗?
19、如图,在平行四边形ABCD 中,于E ,于F ,BD 与AE 、AF 分别相交于G 、H .(1)求证:△
ABE ∽△ADF ;
(2)若,求证:四边形ABCD 是菱形. 20、小亮同学想利用影长测量学校旗杆AB 的高度,如图,他在某一时刻立1米长的标杆测得其
影长为1.2米,同时旗杆的投影一部分在地面上BD 处,另一部分在某一建筑的墙上CD 处,分别测
得其长度为
9.6米和2米,求旗杆AB 的高度. 21、已知,延长BC 到D ,使.取的中点,连结交于点. (1)求的值; (2)若,求的长
一.细心选择 1—5:AACDACB 二.精心填空 8、4 9、115 10、1.2 11、△AOB ∽△COD 12、4/5 13、3
14、16/25 15、0。
81π 16、3 20、AB=10 21、(1)2:3 (2)3/2a 22(1)5。
1 (2)4.2 (3)C (4)5。
56
23、(1)∵∠ABC=120°
,∴∠A=∠C=30°, ∵∠ADP+∠APD=150°,∠ADP+∠QDC=150°,∴∠APD=∠CDQ ,∴△APD ∽△CQD (2)成立;
∵∠ADP+∠APD=150°,∠ADP+∠QDC=150°,∴∠APD=∠CDQ , 又∠A=∠C
∴△APD ∽△PQD 只有∠A=∠C,其它对应角不相等,所以,△APD 与△DPQ 不相似; (3)可以,将两三角板改为一个更为一般的条件,但△ABC 必须是等腰三角形,且∠EDF=∠A ,否则不成立.
A
D
C B G E H
F (第19题)。
