巧记正方体11种展开图的规律
正方体表面展开图的口诀

巧记口诀确定正方体表面展开图6个相连的正方形组成的平面图形,经折叠能否围城正方体问题,是近年来中考常考题型。
同学们在学习这一知识时常感到无从下手,现将确定正方体展开图的方法以口诀的方式总结出来,供大家参考:正方体盒巧展开,六个面儿七刀裁。
十四条边布周围,十一类图记分明:四方成线两相卫,六种图形巧组合;跃马失蹄四分开;两两错开一阶梯。
对面相隔不相连,识图巧排“7”、“凹”、“田”。
现将口诀的内涵解释如下:将一个正方体盒的表面沿某些棱剪开,展开成平面图形,需剪7刀,故平面展开图中周围有14条边长共有十一种展开图:一、四方成线两相卫,六种图形巧组合(1)(2)(3)(4)(5)(6)以上六种展开图可归结为四方连线,,另外两个小方块在四个方块的上下两侧,共六种情况。
二、跃马失蹄四分开(1)(2)(3)(4)以上四种情况可归结为五个小方块组成“三二相连”的基本图形(如图),另外一个小方块的位置有四种情况,即图中四个小方块中的任意一个,这一图形有点像失蹄的马,故称为“跃马失蹄”。
三、两两错开一阶梯这一种图形是两个小方块一组,两两错开,像阶梯一样,故称“两两错开一阶梯”。
四、对面相隔不相连这是确定展开图的又一种方法,也是确定展开图中的对面的一种方法。
如果出现三个相连,则1号面与3号面是对面,中间隔了一个2号面,并且是对面的一定不相连。
五、识图巧排“7”、“凹”、“田”(1) (2) (3)这里介绍的是一种排除法。
如果图中出现象图(1)中的“7”形结构的图形不可能是正方体展开图的,因为图中1号面与3号面是对面,3号面又与5号面是对面,出现矛盾。
如果图中出现象图(2)中的“田”形结构的图形不可能是正方体展开图的,因为同一顶点处不可能出现四个面的。
如果图中出现象图(3)中的“凹”形结构的图形不可能是正方体展开图的,因为如果把该图形折叠起来将有两个面重合。
现举例说明:例1.(2004海口市实验区)下面的平面图形中,是正方体的平面展开图的是( )解析:本题可用“识图巧排 ‘7’、‘田’、‘凹’”来解决。
正方体的展开图11种怎么画

正方体的展开图11种怎么画
正方体的11种展开图如下:
确定正方体展开图的方法口诀:
正方体盒巧展开,六个面儿七刀裁。
十四条边布周围,十一类图记分明。
四方成线两相卫,六种图形巧组合。
跃马失蹄四分开,两两错开一阶梯。
对面相隔不相连,识图巧排“7”、“凹”、“田”。
正方体的11种展开图,如图所示:
所谓”展开图“,就是将制件的表面按一定顺序而连续地摊平在一个平面上所得到的图样。
这种图样在造船、航空、机械、化工、电力、建筑、轻纺、食品等工业部门都得至l圹泛的应用,显然,展开图画得是否准确,直接关系到制件质量、生产效率、产品成本等问题。
扩展资料:
画制件表面展开图的方法,通常有计算法和图解法两种。
1、计算法就是用求立体表面积的公式算出展开图的尺寸,按尺寸画图。
计算法虽然比较准确,但是对于形状不太规则的曲面,就不便于精确计算或者计算起来显得太繁杂,因此应用这种方法受到一定的限制。
2、图解法就是用画法几何的作图原理和方法,求画制件各表面的实形,并顺序地连成片,得到制件的展开图。
这种方法在生产上广为采用。
正方体展开图巧记口诀及解释

6个相连的正方形组成的平面图形,经折叠能否围城正方体问题,是近年来中考常考题型。
同学们在学习这一知识时常感到无从下手,现将确定正方体展开图的方法以口诀的方式总结出来,供大家参考:
正方体盒巧展开,六个面儿七刀裁。
十四条边布周围,十一类图记分明:
四方成线两相卫,六种图形巧组合;
跃马失蹄四分开;两两错开一阶梯。
对面相隔不相连,识图巧排“7”、“凹”、“田”。
现将口诀的内涵解释如下:将一个正方体盒的表面沿某些棱剪开,展开成平面图形,需剪7刀,故平面展开图中周围有14条边长共有十一种展开图:
工具/原料
•剪刀,制作正方体
方法/步骤
1.1
四方成线两相卫,六种图形巧组合
2.2
跃马失蹄四分开
3.3
两两错开一阶梯
4.4
对面相隔不相连
5.5
识图巧排“7”、“凹”、“田”
E N D。
巧记口诀确定正方体表面展开图

巧记⼝诀确定正⽅体表⾯展开图巧记⼝诀确定正⽅体表⾯展开图6个相连的正⽅形组成的平⾯图形,经折叠能否围城正⽅体问题,是近年来中考常考题型。
同学们在学习这⼀知识时常感到⽆从下⼿,现将确定正⽅体展开图的⽅法以⼝诀的⽅式总结出来,供⼤家参考:正⽅体盒巧展开,六个⾯⼉七⼑裁。
⼗四条边布周围,⼗⼀类图记分明:四⽅成线两相卫,六种图形巧组合;跃马失蹄四分开;两两错开⼀阶梯。
对⾯相隔不相连,识图巧排“7”、“凹”、“⽥”。
现将⼝诀的内涵解释如下:将⼀个正⽅体盒的表⾯沿某些棱剪开,展开成平⾯图形,需剪7⼑,故平⾯展开图中周围有14条边长共有⼗⼀种展开图:⼀、四⽅成线两相卫,六种图形巧组合(1)(2)(3)(4)(5)(6)以上六种展开图可归结为四⽅连线,即,另外两个⼩⽅块在四个⽅块的上下两侧,共六种情况。
⼆、跃马失蹄四分开(1)(2)(3)(4)以上四种情况可归结为五个⼩⽅块组成“三⼆相连”的基本图形(如图),另外⼀个⼩⽅块的位置有四种情况,即图中四个⼩⽅块中的任意⼀个,这⼀图形有点像失蹄的马,故称为“跃马失蹄”。
三、两两错开⼀阶梯这⼀种图形是两个⼩⽅块⼀组,两两错开,像阶梯⼀样,故称“两两错开⼀阶梯”。
四、对⾯相隔不相连这是确定展开图的⼜⼀种⽅法,也是确定展开图中的对⾯的⼀种⽅法。
如果出现三个相连,则1号⾯与3号⾯是对⾯,中间隔了⼀个2号⾯,并且是对⾯的⼀定不相连。
五、识图巧排“7”、“凹”、“⽥”(1)(2)(3)这⾥介绍的是⼀种排除法。
如果图中出现象图(1)中的“7”形结构的图形不可能是正⽅体展开图的,因为图中1号⾯与3号⾯是对⾯,3号⾯⼜与5号⾯是对⾯,出现⽭盾。
如果图中出现象图(2)中的“⽥”形结构的图形不可能是正⽅体展开图的,因为同⼀顶点处不可能出现四个⾯的。
如果图中出现象图(3)中的“凹”形结构的图形不可能是正⽅体展开图的,因为如果把该图形折叠起来将有两个⾯重合。
现举例说明:下⾯的平⾯图形中,是正⽅体的平⾯展开图的是()解析:本题可⽤“识图巧排 ‘7’、‘⽥’、‘凹’”来解决。
正方体展开图口诀清晰Word版

正方体展开图口诀
正方体盒巧展开,六个面儿七刀裁;
十四条边布周围,十一类图记分明.
中间四个成一行,两边各一无规矩;
二三紧连错一个,三一相连一随意;
两两相连各错一,三个两排一对齐。
一条线上不过四,田七和凹要放弃;
相间之端是对面,间二拐角面相邻。
1。
中间四个成一行,两边各一无规矩;
“141型”,中间一行4个作侧面,上下两个各为上下底面,共6种基本图形。
2.二三紧连错一个,三一相连一随意;
“231型”,中间3个作侧面,共3种基本图形。
3。
两两相连各错一,三个两排一对齐。
“222型”,两行只能有1个正方形相连。
“33型",两行只能有1个正方形相连。
4。
一条线上不过四,田七和凹要放弃;
正方体展开图中,一条直线上的小正方形不会超过4个。
(×)(×)
正方体展开图中不会有“田"字型、“凹”字型的形状。
如下都不是正方体的展开
图。
(×)
5。
相间之端是对面,间二拐角面相邻。
相间的两个小正方形(中间隔着一个小正方形)是正方体的两个对面,“z”字端处的小正方形是正方体的对面.
如右图,“字”对“超”,“信”对“着”, “沉”对“越”
中间隔着两个小正方形或拐角型的三个面是正方形的邻面。
五年级数学下册《正方体展开图》口诀背诵
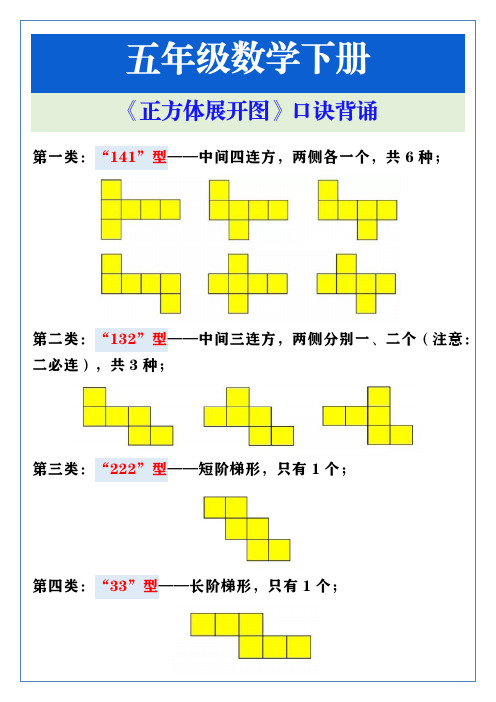
第一类:“141”型——中间四连方,两侧各一个,共6种;
第二类:“132”型——中间三连方,两侧分别一、二个(注意:二必连),共3种;
第三类:“222”型——短阶梯形,只有1个;
第四类:“33”型——长阶梯形,只有1个;
口诀:
中间四个一连串,
两边各一随便放1-4-1
二三紧连挪一个,
三一相连一随便2-3-1
两两相连各挪一2-2-2
三个两排一对齐3-3
不能出现“7”字,
“凹”字,“田”字形
正方体展开图口诀:
正方体展有规律,十一种类看仔细;
中间四个成一行,两边各一无规矩;
二三紧连错一个,三一相连一随意;
两两相连各错一,三个两排一对齐。
一条线上不过四拐角面相邻。
正方体表面展开图的口诀

巧记口诀确定正方体表面展开图6个相连的正方形组成的平面图形,经折叠能否围城正方体问题,是近年来中考常考题型。
同学们在学习这一知识时常感到无从下手,现将确定正方体展开图的方法以口诀的方式总结出来,供大家参考:正方体盒巧展开,六个面儿七刀裁。
十四条边布周围,十一类图记分明:四方成线两相卫,六种图形巧组合;跃马失蹄四分开;两两错开一阶梯。
对面相隔不相连,识图巧排“7”、“凹”、“田”。
现将口诀的内涵解释如下:将一个正方体盒的表面沿某些棱剪开,展开成平面图形,需剪7刀,故平面展开图中周围有14条边长共有十一种展开图:一、四方成线两相卫,六种图形巧组合(1)(2)(3)(4)(5)(6)以上六种展开图可归结为四方连线,即,另外两个小方块在四个方块的上下两侧,共六种情况。
二、跃马失蹄四分开(1)(2)(3)(4)以上四种情况可归结为五个小方块组成“三二相连”的基本图形(如图),另外一个小方块的位置有四种情况,即图中四个小方块中的任意一个,这一图形有点像失蹄的马,故称为“跃马失蹄”。
三、两两错开一阶梯这一种图形是两个小方块一组,两两错开,像阶梯一样,故称“两两错开一阶梯”。
四、对面相隔不相连这是确定展开图的又一种方法,也是确定展开图中的对面的一种方法。
如果出现三个相连,则1号面与3号面是对面,中间隔了一个2号面,并且是对面的一定不相连。
五、识图巧排“7”、“凹”、“田”(1) (2) (3)这里介绍的是一种排除法。
如果图中出现象图(1)中的“7”形结构的图形不可能是正方体展开图的,因为图中1号面与3号面是对面,3号面又与5号面是对面,出现矛盾。
如果图中出现象图(2)中的“田”形结构的图形不可能是正方体展开图的,因为同一顶点处不可能出现四个面的。
如果图中出现象图(3)中的“凹”形结构的图形不可能是正方体展开图的,因为如果把该图形折叠起来将有两个面重合。
现举例说明:例1.(2004海口市实验区)下面的平面图形中,是正方体的平面展开图的是( )解析:本题可用“识图巧排 ‘7’、‘田’、‘凹’”来解决。
正方体展开图口诀

正方体展开图口诀
正方体展有规律,十一种类看仔细;
中间四个成一行,两边各一无规矩;
二三紧连错一个,三一相连一随意;
两两相连各错一,三个两排一对齐。
一条线上不过四,田七和凹要放弃;
相间Z端是对面,间二拐角面相邻。
1.中间四个成一行,两边各一无规矩
"141"型,中间一行4个作侧面。
上下两个各作为上下底面,共有6种基本图形。
2.二三紧连错一个,三一相连一随意
“231”型,中间3个作侧面,共3种基本图形
3.两两相连各错一
"222"型,两行只能有1个正方形相连
4.三个两排一对齐
5.一条线上不过四
指在正方形展开图中,一条直线上的小正方形不会超过四个。
如以下的图形都不是正方体的展开图。
6.田七和凹要放弃
指在正方体展开图中,不会有“田”字型、“凹”字型的形状。
如以下的图形都不是正方体的展开图。
7.相间Z端是对面
相间的两个小正方形(中间隔着一个小正方形)是正方体的两个对面,“z”字端处的小正方形是正方体的对面。
如下面的展开图中,“1”对“5”,“2”对“4”,“3”对“6”。
8.间而拐角两面相邻
中间隔着两个小正方形或拐角型的三个面是正方形的邻面。
拐角型如下图所示。
