河南省2020届高三高中毕业班高考适应性考试(开封市二模)数学(文)试题卷及参考答案

【附20套高考模拟试题】2020届河南省开封高中高考数学模拟试卷含答案

试题解析：
（Ⅰ）因为底面，平面，所以
又因为正方形中，，
所以平面
又因为平面，所以
因为分别是、的中点，所以
所以
（Ⅱ）（方法一）由（Ⅰ）可知，，，两两垂直，以为轴，以为轴，以为轴，设，
，，，，
，，
设平面的一个法向量，
，解得
设直线与平面所成角为，则
1.设复数，则复数的共轭复数的模为( )
A． B．1C．2D．
2.设全集，函数的定义域为M，则为( )
A. B. C. D.
3．偶函数在上单调递减，则的大小关系是( )
A B C D不能确定
4．已知为等差数列且公差，其首项，且成等比数列，为的前项和，，则的值为( )
设，则由题意知，，，，
，，
设平面的法向量为，
则由得，令，则，，
所以取，显然可取平面的法向量，
由题意：，所以 .
由于平面，所以在平面内的射影为，
所以为直线与平面所成的角，
易知在中，，从而，
所以直线与平面所成的角为 .
【点睛】
本题考查了立体几何中的面面垂直的判定和直线与平面所成角的求解问题，意在考查学生的空间想象能力和逻辑推理能力；解答本题关键在于能利用直线与直线、直线与平面、平面与平面关系的相互转化，通过严密推理，明确角的构成，着重考查了分析问题和解答问题的能力.
【解析】
【分析】
（1）设出数列的公差为d,根据等比中项列出等式，得到公差，即可得到通项公式；（2）利用裂项相消求和法可得结果.
【详解】
（1）设数列{an}的公差为d，

河南省2020届高三第二次模拟考试卷文科数学(二)(PDF版,答案解析)

成立．
（1）求实数 k 的值；
（2）若 m 1 ， n 1 且求证 f (m) f (n) 10 ，求证： 9 1 16 ．
2
2
mn 3
二模测试卷第 7 页（共 8 页）
二模测试卷第 8 页（共 8 页）
高三第二次模拟考试卷
文科数学（二）答案
一、选择题：本大题共 12 小题，每小题 5 分，在每小题给出的四个选项中，只有一项是符合题目要求的． 1．【答案】C
B．若 1 x 1，则 x2 1
C．若 x 1或 x 1，则 x2 1
D．若 x 1或 x 1，则 x2 1
4焦点分别为 F1 ，F2 ，过 F2 且垂直于长轴的直线交椭圆于 A, B 两点，
则 △ABF1的周长为（）
A． 4
B． 6
C． 8
D．16
为
cos2
2asin (a
0)
，过点
P(1, 2)
的直线 l
的参数方程为
x
1
2t 2 （ t 为参数），l
y
2
2t 2
与 C 交于 A ， B 两点．
（1）求 C 的直角坐标方程和 l 的普通方程；
（2）若 PA ， AB ， PB 成等比数列，求 a 的值．
23．（12 分）已知定义在 R 上的函数 f (x) 2x k 2 x ， k N* ．存在实数 x0 使 f (x0 ) 2
∴△ABF1的周长为| AF1 | | BF1 | | AB | (| AF1 | | AF2 |) (| BF1 | | BF2 |) 8 ，
故选 C． 5．【答案】A
【解析】因为平面向量 a (1, 3) ， b (2, 0) ，

2020年河南省普通高中毕业班高考适应性测试文科数学试卷带答案

绝密★启用前2020年河南省普通高中毕业班高考适应性测试文科数学注意事项：1．答卷前，考生务必将自己的姓名、准考证号等填写在答题卡和试卷指定位置上。

2．回答选择题时，选出每小题答案后。

用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上，写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

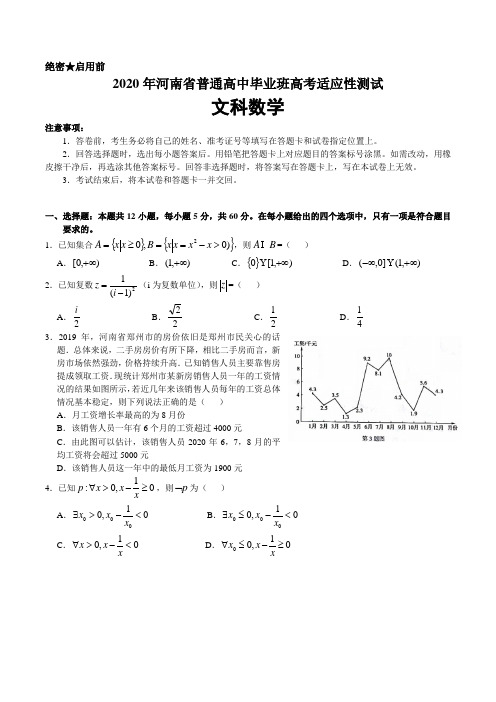
1．已知集合{}{})0,02>-==≥=x x x x B x x A ，则B A I =（）A ．),0[+∞B ．),1(+∞C ．{}),1[0+∞YD ．),1(]0,(+∞-∞Y2．已知复数2)1(1-=i z （i 为复数单位），则z =（） A ．2i B ．22 C ．21 D ．41 3．2019年，河南省郑州市的房价依旧是郑州市民关心的话题．总体来说，二手房房价有所下降，相比二手房而言，新房市场依然强劲，价格持续升高．已知销售人员主要靠售房提成领取工资．现统计郑州市某新房销售人员一年的工资情况的结果如图所示，若近几年来该销售人员每年的工资总体情况基本稳定，则下列说法正确的是（）A ．月工资增长率最高的为8月份B ．该销售人员一年有6个月的工资超过4000元C ．由此图可以估计，该销售人员2020年6，7，8月的平均工资将会超过5000元D ．该销售人员这一年中的最低月工资为1900元4．已知01,0:≥->∀x x x p ，则p ⌝为（） A ．01,0000<->∃x x x B ．01,0000<-≤∃x x x C ．01,0<->∀x x x D ．01,00≥-≤∀xx x5．已知向最m )1,(-=a ，n )3,52(-=a ，若m ∥n ，则实数a 的值为（）A ．3B ．1C ．21-D ．5- 6．已知双曲线的一条渐近线方程为x y 2=，且此双曲线经过点)52,2(，则该双曲线的标准方程为（）A ．1422=-y xB ．2214y x -=C ．1422=-y xD ．1422=-x y 7．某种商品的广告费支出x 与销售额y （单位：万元）之间有如下对应数据，根据表中提供的全部数据，用最小二乘法得出y 与x 的线性回归方程为5.175.6ˆ+=x y，则表中m 的值为 x 2 4 5 6 8y 30 40 m 50 70A ．45B ．50C ．8．已知某个几何体的三视图如图所示，根据图中标出的数据，可得出这个几何体中的最长棱长是A ．5B ．2C ．22D ．69．记不等式组4027030x y x y y -+≥⎧⎪+-≤⎨⎪+≥⎩，表示的平面区域为D ，不等式x 2+y 2≤1表示的平面区域为E ，在区域D 内任取一点P ，则点P 在区域E 外的概率为A ．48πB ．148π- C ．96π D ．196π- 10．函数()sin(2)f x x ϕ=+的图象向左平移6π个单位得到函数g （x ）的图象，若函数g （x ）是偶函数，则tan(2)3πϕ+=A ．3-B ．3C ．3-D ．3 11．现有灰色与白色的卡片各八张．分别写有数字1到8．甲、乙．丙、丁四个人每人面前摆放四张，并按从小到大的顺序自左向右排列（当灰色卡片和白色卡片数字相同时，白色卡片摆在灰色卡片的右侧）．如图，甲面面的四张卡片已经翻开，则写有数字4的灰色卡片是（填写字母）．A ．HB ．JC ．KD ．P12．已知函数2()sin 2ln(1)1f x x x x x =+-+-+，若(1)1xf ax e -+> 在x ∈（0，+∞）上有解，则实数a 的取值范围为A ．（1，+∞）B ．（-∞，1）C ．（e ，+∞）D （1，e ）二、填空题：本题共4小题，每小题5分，共20分。

河南省开封市2020届高三二模考试数学(文)试题 Word版含解析

高考资源网（）您身边的高考专家
版权所有@高考资源网 - 1 - 2020年河南省普通高中毕业班高考适应性测试
文科数学
注意事项：
1．答卷前，考生务必将自己的姓名准考证号等填写在答题卡和试卷指定位置上.
2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑.如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上，写在本试卷上无效.
3．考试结束后，将本试卷和答题卡一并交回. 一、选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.
1. 已知集合{}0A x x =≥，{}20)B x x x =->，则A
B =（） A. [0,)+∞ B. (1,)+∞ C. {}0[1,)+∞
D. (,0](1,)-∞+∞
【答案】B 【解析】
【分析】
求出集合A ，B ，由此能求出A
B ．【详解】解：集合{|0}A x x =，
2{|0}{|0B x x x x x =->=<或1}x >，
(1,)A B ∴=+∞．
故选：B ．
【点睛】本题考查交集的求法，考查交集定义等基础知识，考查运算求解能力，属于基础题．
2. 已知复数()21
1z i =-（i 为复数单位），则z =（）
A. 2i
B. 22
C. 12
D. 14
【答案】C
【解析】。

河南省六市2020届高三第二次联合调研检测数学(文科)试卷含答案

★2020年5月28日2020年河南省六市高三第二次联合调研检测数学（理科）本试卷分第Ⅰ卷（选择题）和第II 卷（非选择题）两部分，满分150分，考试用时120分钟．其中第I1卷22题，23题为选考题，其它题为必考题。

考试结束后，将答题卡交回.注意事项:1．答题前，考生必须将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内.2．选择题必须用2B 铅笔填涂；非选择题必须使用0.5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚.3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效．4．保持卡面清洁，不要折叠、不要弄破、不准使用涂改液、刮纸刀．第I 卷选择题（共60分）一、选择题：本题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的。

1．设全集U=R ，集合{}0)1)(4(≥+-=x x x A ，则A C U =A ．（1-，4]B ．[1-，4）C ．（1-，4）D ．[1-，4]2．复数z 1在复平面内对应的点为（2，3）．i z +-=22（i 为虚数单位），则复数21z z 的虚部为 A ．58 B ．58- C ．i 58 D ．i 58- 3．在△ABC 中==，若点D 满足21=，则= A ．c b 3231+ B ．3132+ C ．3134- D ．2121+4．南北朝时代的伟大科学家祖暅在数学上有突出贡献，他在实践的基础上提出祖暅原理：“幂势既同，则积不容异”．其含义是：夹在两个平行平面之间的两个几何体，被平行于这两个平行平面的任意平面所截，如果截得的两个截面的面积总相等，那么这两个几何体的体积相等，如图，夹在两个平行平面之间的两个几何体的体积分别为V1，V2，被平行于这两个平面的任意平面截得的两个截面面积分别为S1、S2，则“S1、S 2不总相等”是“V1，V2不相等”的A．充分而不必要条件B．必要而不充分条件C．充分必要条件D．既不充分也不必要条件5．青班锁起源于中国古代建筑中首创的榫卯结构，相传由春秋时代鲁国工匠鲁班所作，下图1是经典的六柱鲁班锁及六个构件的图片，下图2是其中一个构件的三视图（图中单位mm ），则此构件的体积为A ．34000 mm 3B ．33000 mm 3C ．32000 mm 3D ．30000 mm 36．在正项等比数列{}n a 中，4651242292900a a a a a a =-=+，，则2020a 的个位数字是A ．1B ．7C ．3D ．97．关于圆周率π，数学发展史上出现过许多很有创意的求法，如著名的蒲丰试验．受其启发，我们也可以通过设计下面的试验来估计π的值，试验步骤如下：①先请高三年级1000名同学每人在小卡片上随机写下一个实数对（x ，y ）（0＜x ＜1，0＜y ＜1）；②若卡片上的x ，y 能与1构成锐角三角形，则将此卡片上交；③统计上交的卡片数，记为m ；④根据统计数m 估计π的值．假如本次试验的统计结果是m=218，那么可以估计π的值约为A ．124389B ．124391C ．125389D ．125391 8．已知双曲线12222=-by a x （a ＞0，b ＞0）的一条渐近线过点（3-，2），且双曲线的一个焦点在抛物线x y 742=的准线上，则双曲线的方程为A ．1282122=-y xB ．1212822=-y x C ．14322=-y x D ．13422=-y x 9．已知三棱锥A —BCD 的四个顶点都在球O 的表面上，且AB ⊥BC ，AB ⊥CD ，∠BCD=32π，若BC=CD=2，AB=32，则球O 的表面积为A ．20πB ．24πC ．28πD ．32π10．将函数)0)(3sin(4>-=ωπωx y 的图像分别向左、向右各平移6π个单位长度后，所得的两个图象对称轴重合，则ω的最小值为A ．3B ．2C ．4D ．611．已知函数y=f （x ）满足f （x+1）=f （x -1），当x ∈[-1，1]时f （x ）=x 2，则方程x x f lg )(=实根共有A ．10个B ．9个C ．18个D ．20个12．已知椭圆C 1：12222=+b y a x （a ＞b ＞0）与圆C 2：43222b y x =+，若在椭圆C 1上不存在点P ，使得由点P 所作的圆C 2的两条切线互相垂直，则椭圆C 1的离心率的取值范围是A ．)33,0(B ．)22,0(C ．)122[，D ．)133[，第Ⅱ卷非选择题（共90分）二、填空题：本题共4个小题，每小题5分，共20分．13．已知函数3()1f x ax x =++的图像在点（1，(1)f ）处的切线过点（2，11），则a= ． 14．若实数x ，y 满足约束条件工1330y x x y x y ≤⎧⎪+≥⎨⎪-+≥⎩，则z=5x +y 的最小值为．15．设函数22()4x x f x e e x -=--，则不等式2()(56)f x f x +--＜0的解集是．（用区间表示）16．在△ABC 中，内角A ，B ，C 所对的边分别是a ，b ，c ，且BC，则c b b c +的最大值是．三、解答题：本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤．17．（本小题满分12分）已知数列{a n }满足：212231n a a a n n n ++⋅⋅⋅+=++（n ∈N +）．（Ⅰ）求{a n }的通项公式；（Ⅱ）设1n n b a =，若数列{b n }的前n 项和为n S ，求满足1940n S ＞的最小正整数n ．18．（本小题满分12分）在直角梯形ABCD中（如图1），AB∥DC，∠BAD =90°，AB=5，AD =2，CD=3，点E在CD上，且DE=2，将△ADE沿AE折起，使得平面ADE⊥平面ABCE（如图2），G为AE中点．（Ⅰ）求四棱锥D—ABCE的体积；（Ⅱ）在线段BD上是否存在点P，使得CP∥平面ADE？若存在，求BPBD的值；若不存在，请说明理由．19．（本小题满分12分）某快递公司招聘快递骑手，该公司提供了两种日工资方案：方案（1）规定每日底新50元，快递骑手每完成一单业务提成3元：方案（2）规定每日底薪100元，快递业务的前44单没有提成，从第45单开始，每完成一单提成5元．该快递公司记录了每天骑手的人均业务量．现随机抽取100天的数据，将样本数据分为[25，35），[35，45），[45，55），[55，65），[65，75），[75，85），[85，95] 七组，整理得到如图所示的频率分布直方图．（Ⅰ）随机选取一天，估计这一天该快递公司的骑手的人均日快递业务量不少于65单的概率；（Ⅱ）若骑手甲、乙、丙选择了日工资方案（1），丁、戊选择了日工资方案（2）．现从上述5名骑手中随机选取2人，求至少有1名骑手选择方案（2）的概率；（Ⅲ）若仅从人均日收入的角度考虑，请你利用所学的统计学知识为新聘骑手做出日工资方案的选择，并说明理由（同组中的每个数据用该组区间的中点值代替）20．（本小题满分12分）设函数2()ln f x x ax x =-+．（Ⅰ）若当x=1时()f x 取得极值，求a 的值及()f x 的单调区间；（Ⅱ）若()f x 存在两个极值点1x ，2x ，证明：2121()()42f x f x a x x a ---＞．21．（本小题满分12分）已知圆F ：4)2(22=+-y x ，动点Q )(y x ，（x≥0），线段QF 与圆F 相交于点P ，线段PQ 的长度与点Q 到y 轴的距离相等．（Ⅰ）求动点Q 的轨迹W 的方程；（Ⅱ）过点A （2，4）作两条互相垂直的直线与W 的交点分别是M 和N （M 在N 的上方，A ，M ，N 为不同的三点），求向量NM 在y 轴正方向上的投影的取值范围．请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题计分．22．（本小题满分10分）在直角坐标系xOy 中，曲线C 1的参数方程为⎪⎪⎩⎪⎪⎨⎧+=-=t y t x 213231（t 为参数），以原点O 为极点，以x 轴正半轴为极轴，建立极坐标系，曲线C 2的极坐标方程为θρ22sin 213+=．（Ⅰ）求曲线C 1的极坐标方程与曲线C 2的直角坐标方程；（Ⅱ）设A ．B 为曲线C 2上位于第一，二象限的两个动点，且∠AOB=2π，射线OA ，OB 交曲线C 1分别于点D ，C ．求△AOB 面积的最小值，并求此时四边形ABCD 的面积。

2020年河南省顶级名校高考数学二模试卷(文科)含答案解析

2020年河南省顶级名校高考数学二模试卷（文科）一、选择题：本大题共12小题，每小题5分，共60分。

1．若集合A={x|log（2x+1）＞﹣1}，集合B={x|1＜3x＜9}，则A∩B=（）A．（0，） B．（﹣，）C．（0，2）D．（，2）2．i是虚数单位，复数（1+3i）（a﹣i）在复平面内对应的点在第四象限，则a的范围（）A．（﹣3，+∞）B．（﹣∞，）C．（﹣3，）D．（﹣3，1）3．若椭圆（a＞b＞0）的离心率为，则双曲线的离心率是（）A．2 B．C．D．34．设直线y=x+b是曲线y=lnx的一条切线，则b的值为（）A．ln2﹣1 B．ln2﹣2 C．2ln2﹣1 D．2ln2﹣25．设a∈R，则“a=1是“f（x）=ln（a+）为奇函数”的（）A．充分不必要条件B．必要不充分条件C．充要条件 D．既不充分也不必要条件6．已知实数x∈[1，10]，执行如图所示的程序框图，则输出x的值不小于55的概率为（）A．B．C．D．7．已知各项均为正数的等比数列{a n}，a1a2a3=5，a7a8a9=10，则a4a5a6=（）A．B．7 C．6 D．8．若某几何体的三视图（单位：cm）如图所示，则该几何体的体积等于（）A．10cm3B．20cm3C．30cm3D．40cm39．等差数列的前n项和为S n，且S1006＞S1008＞S1007，则满足S n S n＜0的正整数n为（）﹣1A．2020 B．2020 C．2020 D．202010．已知△ABC的三个顶点在以O为球心的球面上，且cosA=，BC=1，AC=3，三棱锥O﹣ABC的体积为，则球O的表面积为（）A．36πB．16πC．12πD．11．在△ABC中，AB=3，AC=4，∠BAC=60°，若P是△ABC所在平面内一点，且AP=2，则•的最大值为（）A．10 B．12 C．10+2 D．812．设过点P（﹣1，1）作两直线，PA，PB与抛物线y2=4x任相切于点A，B，若F为抛物线y2=4x的焦点，||•||=（）A． B．5 C．8 D．9二、填空题:本大题共4小题。

河南省六市 2020届高三第二次模拟调研数学(文)含答案

2020年河南省六市高三第二次联合调研检测数学（理科）本试卷分第Ⅰ卷（选择题）和第II 卷（非选择题）两部分，满分150分，考试用时120分钟．其中第I1卷22题，23题为选考题，其它题为必考题。

考试结束后，将答题卡交回.注意事项:1．答题前，考生必须将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在条形码区域内.2．选择题必须用2B 铅笔填涂；非选择题必须使用0.5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚.3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效．4．保持卡面清洁，不要折叠、不要弄破、不准使用涂改液、刮纸刀．第I 卷选择题（共60分）一、选择题：本题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的。

1．设全集U=R ，集合{}0)1)(4(≥+-=x x x A ，则A C U = A ．（1-，4] B ．[1-，4） C ．（1-，4） D ．[1-，4]2．复数z 1在复平面内对应的点为（2，3）．i z +-=22（i 为虚数单位），则复数21z z 的虚部为 A ．58 B ．58- C ．i 58 D ．i 58- 3．在△ABC 中b AC c AB ==，，若点D 满足DC BD 21=，则AD = A ．c b 3231+ B ．c b 3132+ C ．c b 3134- D ．c b 2121+ 4．南北朝时代的伟大科学家祖暅在数学上有突出贡献，他在实践的基础上提出祖暅原理：“幂势既同，则积不容异”．其含义是：夹在两个平行平面之间的两个几何体，被平行于这两个平行平面的任意平面所截，如果截得的两个截面的面积总相等，那么这两个几何体的体积相等，如图，夹在两个平行平面之间的两个几何体的体积分别为V 1，V 2，被平行于这两个平面的任意平面截得的两个截面面积分别为S 1、S 2，则“S 1、S 2不总相等”是“V 1，V 2不相等”的A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件5．青班锁起源于中国古代建筑中首创的榫卯结构，相传由春秋时代鲁国工匠鲁班所作，下图1是经典的六柱鲁班锁及六个构件的图片，下图2是其中一个构件的三视图（图中单位mm ），则此构件的体积为A ．34000 mm 3B ．33000 mm 3C ．32000 mm 3D ．30000 mm 36．在正项等比数列{}n a 中，4651242292900a a a a a a =-=+，，则2020a 的个位数字是A ．1B ．7C ．3D ．97．关于圆周率π，数学发展史上出现过许多很有创意的求法，如著名的蒲丰试验．受其启发，我们也可以通过设计下面的试验来估计π的值，试验步骤如下：①先请高三年级1000名同学每人在小卡片上随机写下一个实数对（x ，y ）（0＜x ＜1，0＜y ＜1）；②若卡片上的x ，y 能与1构成锐角三角形，则将此卡片上交；③统计上交的卡片数，记为m ；④根据统计数m 估计π的值．假如本次试验的统计结果是m=218，那么可以估计π的值约为A ．124389B ．124391C ．125389D ．125391 8．已知双曲线12222=-by a x （a ＞0，b ＞0）的一条渐近线过点（3-，2），且双曲线的一个焦点在抛物线x y 742=的准线上，则双曲线的方程为A ．1282122=-y xB ．1212822=-y x C ．14322=-y x D ．13422=-y x 9．已知三棱锥A —BCD 的四个顶点都在球O 的表面上，且AB ⊥BC ，AB ⊥CD ，∠BCD=32π，若BC=CD=2，AB=32，则球O 的表面积为A ．20πB ．24πC ．28πD ．32π10．将函数)0)(3sin(4>-=ωπωx y 的图像分别向左、向右各平移6π个单位长度后，所得的两个图象对称轴重合，则的最小值为 A ．3 B ．2 C ．4 D ．611．已知函数y=f （x ）满足f （x+1）=f （x-1），当x ∈[-1，1]时f （x ）=x 2，则方程x x f lg )(=实根共有A ．10个B ．9个C ．18个D ．20个12．已知椭圆C 1：12222=+b y a x （a ＞b ＞0）与圆C 2：43222b y x =+，若在椭圆C 1上不存在点P ，使得由点P 所作的圆C 2的两条切线互相垂直，则椭圆C 1的离心率的取值范围是A ．)33,0(B ．)22,0(C ．)122[，D ．)133[，第Ⅱ卷非选择题（共90分）二、填空题：本题共4个小题，每小题5分，共20分．13．已知函数3()1f x ax x =++的图像在点（1，(1)f ）处的切线过点（2，11），则a= ． 14．若实数x ，y 满足约束条件工1330y x x y x y ≤⎧⎪+≥⎨⎪-+≥⎩，则z=5x +y 的最小值为．15．设函数22()4x x f x e e x -=--，则不等式2()(56)f x f x +--＜0的解集是．（用区间表示）16．在△ABC 中，内角A ，B ，C 所对的边分别是a ，b ，c ，且BC，则c b b c +的最大值是．三、解答题：本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤．17．（本小题满分12分）已知数列{a n }满足：212231n a a a n n n ++⋅⋅⋅+=++（n ∈N +）．（Ⅰ）求{a n }的通项公式；（Ⅱ）设1n n b a =，若数列{b n }的前n 项和为n S ，求满足1940n S ＞的最小正整数n ．18．（本小题满分12分）在直角梯形ABCD中（如图1），AB∥DC，∠BAD =90°，AB=5，AD =2，CD=3，点E在CD上，且DE=2，将△ADE沿AE折起，使得平面ADE⊥平面ABCE（如图2），G为AE中点．（Ⅰ）求四棱锥D—ABCE的体积；（Ⅱ）在线段BD上是否存在点P，使得CP∥平面ADE？若存在，求BPBD的值；若不存在，请说明理由．19．（本小题满分12分）某快递公司招聘快递骑手，该公司提供了两种日工资方案：方案（1）规定每日底新50元，快递骑手每完成一单业务提成3元：方案（2）规定每日底薪100元，快递业务的前44单没有提成，从第45单开始，每完成一单提成5元．该快递公司记录了每天骑手的人均业务量．现随机抽取100天的数据，将样本数据分为[25，35），[35，45），[45，55），[55，65），[65，75），[75，85），[85，95] 七组，整理得到如图所示的频率分布直方图．（Ⅰ）随机选取一天，估计这一天该快递公司的骑手的人均日快递业务量不少于65单的概率；（Ⅱ）若骑手甲、乙、丙选择了日工资方案（1），丁、戊选择了日工资方案（2）．现从上述5名骑手中随机选取2人，求至少有1名骑手选择方案（2）的概率；（Ⅲ）若仅从人均日收入的角度考虑，请你利用所学的统计学知识为新聘骑手做出日工资方案的选择，并说明理由（同组中的每个数据用该组区间的中点值代替）20．（本小题满分12分）设函数2()ln f x x ax x =-+．（Ⅰ）若当x=1时()f x 取得极值，求a 的值及()f x 的单调区间；（Ⅱ）若()f x 存在两个极值点1x ，2x ，证明：2121()()42f x f x a x x a ---＞．21．（本小题满分12分）已知圆F ：4)2(22=+-y x ，动点Q )(y x ，（x≥0），线段QF 与圆F 相交于点P ，线段PQ 的长度与点Q 到y 轴的距离相等．（Ⅰ）求动点Q 的轨迹W 的方程；（Ⅱ）过点A （2，4）作两条互相垂直的直线与W 的交点分别是M 和N （M 在N 的上方，A ，M ，N 为不同的三点），求向量NM 在y 轴正方向上的投影的取值范围．请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题计分．22．（本小题满分10分）在直角坐标系xOy 中，曲线C 1的参数方程为⎪⎪⎩⎪⎪⎨⎧+=-=t y t x 213231（t 为参数），以原点O 为极点，以x 轴正半轴为极轴，建立极坐标系，曲线C 2的极坐标方程为θρ22sin 213+=．（Ⅰ）求曲线C 1的极坐标方程与曲线C 2的直角坐标方程；（Ⅱ）设A ．B 为曲线C 2上位于第一，二象限的两个动点，且∠AOB=2π，射线OA ，OB 交曲线C 1分别于点D ，C ．求△AOB 面积的最小值，并求此时四边形ABCD 的面积。