八年级数学重心定理
八年级数学重心定理
3.掌握常用的数学解题 方法。如利用比例线段 证线段相等以及有关面 积的解题方法
E B
G D
现在，轮到我 来考你们了！
A
思考： ABC中，中线BE 与中线CD交于G点，
D G
E
若M为BE中点， N为CD中点， 求S MNG : S EDG
C
M
B
N
这节课就上 到这，回去 后好好复习！
A
三角形的重心到一边 中点的距离等于这边上中 线长的三分之一。 三角形的重心到一边 的距离等于这边上高的三 分之一。
G B D E F C
已知：RtACB, ACB 90 , AC 4, BC 3,
o
G是 ABC的重心;
A
求：1.点G到直角顶点C的距离GC；
o
解：RtACB , ACB 90 AB 5 5 AC 4, BC 3 D CD E 2 CD 是中线 F G 是 ABC 的重心 G CG 2 CD
C B
5 CG 3
3
2.点G到斜边AB的距离
已知：ABC中AB AC , AD BC, AD 与 中线BE相交于点G; AD 18cm , GE 5cm , 求：BC的长。
A
E G B
?
D
C
已知 ABC 的中线CD 、 BE相交于点G;
A
求： 1 : S 4 ... S : 2 :S S 6 S 3 5 S DG E B GC C ; DG E DEC ;; DG E DG B ; DG E :S AB C B EG ADC ;
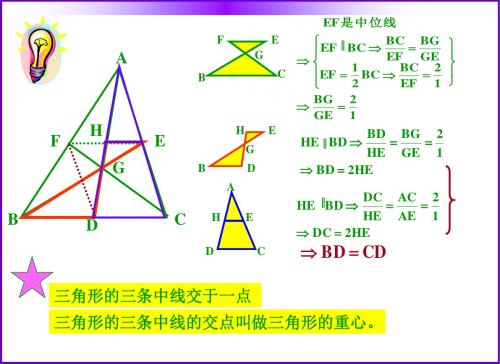
EF 是中位线
F E G B
重心定理
③×④×⑤得BD/DC*CE/EA*AF/FB=1
利用塞瓦定理证明三角形三条高线必交于一点:
设三边AB、BC、AC的垂足分别为D、E、F，
根据塞瓦定理逆定理，因为(AD:DB)*(BE:EC)*(CF:FA)=[(CD*ctgA）
另外,有很多人会觉得书写这个公式十分烦琐,不看书根本记不住,下面从别人转来一些方法帮助书写
为了说明问题，并给大家一个深刻印象，我们假定图中的A、B、C、D、E、F是六个旅游景点，各景点之间有公路相连。我们乘直升机飞到这些景点的上空，然后选择其中的任意一个景点降落。我们换乘汽车沿公路去每一个景点游玩，最后回到出发点，直升机就停在那里等待我们回去。
证明：
过点A作AG‖BC交DF的延长线于G,
则AF/FB=AG/BD , BD/DC=BD/DC , CE/EA=DC/AG。
三式相乘得：AF/FB×BD/DC×CE/EA=AG/BD×BD/DC×DC/AG=1
它的逆定理也成立：若有三点F、D、E分别在的边AB、BC、CA或其延长线上，且满足(AF/FB)×(BD/DC)×(CE/EA)=1，则F、D、E三点共线。利用这个逆定理，可以判断三点共线。
方案①——从A经过B（不停留）到F（停留），再返回B（停留），再到D（停留），之后经过B（不停留）到C（停留），再到E（停留），最后从E经过C（不停留）回到出发点A。
按照这个方案，可以写出关系式：
（AF：FB）*（BD：DC）*（CE：EA）=1。
现在，您知道应该怎样写“梅涅劳斯定理”的公式了吧。
从A点出发的旅游方案还有：
（AE：EC）*（CD：DB）*（BF：FA）=1。
三角形重心性质定理
三角形重心性质定理三角形是初中数学中重要的几何概念之一，其性质和定理也是我们学习的重点之一。
其中，三角形重心性质定理是其中一个非常重要且有趣的定理。
本文将详细介绍三角形重心性质定理，帮助读者更好地理解和应用这一定理。
一、三角形的定义在介绍三角形重心性质定理之前，我们先来回顾一下三角形的定义。
三角形是由三条边和三个顶点所确定的一个平面图形。
三角形的重心被定义为三角形三条中线的交点，记作G。
中线是连接三角形某一顶点与对边中点的线段。
在三角形ABC中，中线AG连接顶点A与对边BC的中点M，中线BG连接顶点B与对边AC的中点N，中线CG连接顶点C与对边AB的中点P。
三线共点的交点G即为三角形ABC的重心。
二、三角形重心性质定理是指任意三角形的重心与顶点之间的距离之比为2:1。
具体而言，我们有以下定理：定理：在任意三角形中，重心到各个顶点的距离的比值为2:1。
证明：设三角形ABC的顶点分别为A、B、C，重心为G。
由三角形的定义可知，AG、BG、CG分别为三角形ABC的三条中线，其长度分别为a'、b'、c'。
我们需要证明：AG:BG:CG=2:1:1首先，我们可以得知由中位线的性质可知，AM=MB，AN=NC，BP=PC。
因此，在三角形ABC中，我们可以得到以下等式：AG=2GM （1）BG=2GN （2）CG=2GP （3）由等式（1）、（2）、（3）可知，AG、BG、CG分别是GM、GN、GP的两倍。
因此，我们得到以下等式：AG:GM=2:1 （4）BG:GN=2:1 （5）CG:GP=2:1 （6）由于GM、GN、GP分别为重心G到顶点A、B、C的距离，通过等式（4）、（5）、（6）我们可以得出：AG:BG:CG=2:1:1因此，定理得证。
三、三角形重心性质定理的应用三角形重心性质定理在解决相关几何问题中起着重要的作用。
下面以一些例子来说明这个定理的应用。
例1：已知三角形ABC，重心G所在直线与边BC的交点为D，求证：BD:DC=2:1。
重心的初中数学知识点总结
重心的初中数学知识点总结
关于重心的初中数学知识点总结
1、重心的定义：平面图形中，几何图形的重心是当支撑或悬挂时图形能在水平面处于平衡状态，此时的支撑点或者悬挂点叫做平衡点，也叫做重心。
2、几种几何图形的重心：
⑴ 线段的重心就是线段的`中点；
⑵ 平行四边形及特殊平行四边形的重心是它的两条对角线的交点；
⑶ 三角形的三条中线交于一点，这一点就是三角形的重心；
⑷ 任意多边形都有重心，以多边形的任意两个顶点作为悬挂点，把多边形悬挂时，过这两点铅垂线的交点就是这个多边形的重心。
提示：⑴ 无论几何图形的形状如何，重心都有且只有一个；
⑵ 从物理学角度看，几何图形在悬挂或支撑时，位于重心两边的力矩相同。
3、常见图形重心的性质：
⑴ 线段的重心把线段分为两等份；
⑵ 平行四边形的重心把对角线分为两等份；
⑶ 三角形的重心把中线分为1:2两部分（重心到顶点距离占2份，重心到对边中点距离占1份）。
上面对重心知识点的巩固学习，同学们都能熟练的掌握了吧，希望同学们很好的复习学习数学知识。
最新人教版八年级下册数学精品课件19.4 重心
最新人教版数学精品课件设
最新人教版数学精品课件设
最新人教版数学精品课件设
最新人教版数学精品课件设
最新人教版数学精品课件设
最新人教版数学精品课件设
1.走钢丝的演员为什么不会掉下来?
2.杂技演员手上的碟子为什么也不会掉下来？
最新人教版数学精品课件设
最新人教版数学精品课件设
怎样用一个手指平衡地顶起一本书？
最新人教版数学精品课件设
手指顶在书本的中心就可以平衡，这个平衡 点叫做书本的重心
任何有固定形状的物体，不论 其在地球表面如何放置，其平 行分布重力的合力（通常所说 的物体的重力）作用线，都通 过物体上一个确定的点，这一 点称为物体最的新人重教版心数学。精品课件设
探究（一）：寻找线段的重心 （1）猜想：线段的重心是线段的中点 （2）利用手中器材（一根玻璃棒或木棒、细绳、刻
平行四边形的重心是它的两条对角线的交点
最新人教版数学精品课件设
探究（三）：平行四边形重心的特征：
A
D
o·
C
最新人教版数学精品课件设
A B
D
o·
C
最新人教版数学精品课件设
A B
E
o·
F
D C
最新人教版数学精品课件设
过平行四边形重心的任一条直线都平分 这个平行四边形的面积。
最新人教版数学精品课件设
度尺），验证猜想 （3）分小组汇报验证过程 （4）哪个小组的方法更准确呢？
线段的重心就是线段的中点.
最新人教版数学精品课件设
探究（二）：寻找平行四边形的重心
（1）猜想：平行四边形的重心是它对角线的交点 （2）利用手中器材（一个平行四边形、细绳、刻
三角形重心性质定理.
三角形重心性质定理1、配方法：所谓配方，就是把一个解析式利用恒等变形的方法，把其中的某些项配成一个或几个多项式正整数次幂的和形式。
通过配方解决数学问题的方法叫配方法。
其中，用的最多的是配成完全平方式。
配方法是数学中一种重要的恒等变形的方法，它的应用非常广泛，在因式分解、化简根式、解方程、证明等式和不等式、求函数的极值和解析式等方面都经常用到它。
2、因式分解法：因式分解，就是把一个多项式化成几个整式乘积的形式。
因式分解是恒等变形的基础，它作为数学的一个有力工具、一种数学方法在代数、几何、三角函数等的解题中起着重要的作用。
因式分解的方法有许多，除中学课本上介绍的提取公因式法、公式法、分组分解法、十字相乘法等外，还有如利用拆项添项、求根分解、换元、待定系数等等。
3、换元法：换元法是数学中一个非常重要而且应用十分广泛的解题方法。
我们通常把未知数或变数称为元，所谓换元法，就是在一个比较复杂的数学式子中，用新的变元去代替原式的一个部分或改造原来的式子，使它简化，使问题易于解决。
4、判别式法与韦达定理：一元二次方程ax2+bx+c=0(a、b、c∈R，a≠0)根的判别式△=b2-4ac，不仅用来判定根的性质，而且作为一种解题方法，在代数式变形，解方程(组)，解不等式，研究函数乃至解析几何、三角函数运算中都有非常广泛的应用。
韦达定理除了已知一元二次方程的一个根，求另一根；已知两个数的和与积，求这两个数等简单应用外，还可以求根的对称函数，计论二次方程根的符号，解对称方程组，以及解一些有关二次曲线的问题等，都有非常广泛的应用。
5、待定系数法：在解数学问题时，若先判断所求的结果具有某种确定的形式，其中含有某些待定的系数，而后根据题设条件列出关于待定系数的等式，最后解出这些待定系数的值或找到这些待定系数间的某种关系，从而解答数学问题，这种解题方法称为待定系数法。
它是中学数学中常用的重要方法之一。
6、构造法：在解题时，我们常常会采用这样的方法，通过对条件和结论的分析，构造辅助元素，它可以是一个图形、一个方程(组)、一个等式、一个函数、一个等价命题等，架起一座连接条件和结论的桥梁，从而使问题得以解决，这种解题的数学方法，我们称为构造法。
三角形中的重心与外心定理
三角形中的重心与外心定理三角形是几何学中最基本的形状之一，研究三角形的性质和特点对于深入了解几何学具有重要意义。
在三角形中，重心和外心是两个重要的概念，通过重心与外心定理，我们可以揭示它们的关系和性质。
重心是指三角形三条中线的交点，记作G。
在一个三角形ABC中，连接顶点A与边BC的中点M，连接顶点B与边AC的中点N，连接顶点C与边AB的中点P，这三条线段分别称为三角形ABC的中线。
重心G是中线的交点，即G=MN∩NP∩PM。
外心是指三角形外接圆的圆心，记作O。
在一个三角形ABC中，若存在一个圆可以同时与三条边AB、BC、CA相切，称这个圆为三角形ABC的外接圆。
外心O则为外接圆的圆心。
重心与外心定理是指，三角形的重心、外心和三边中点构成一个等腰三角形。
换句话说，连接重心和外心的线段与连接三边中点的线段长度相等，且它们之间的夹角等于π/2。
证明这个定理的方法有很多，这里我们可以采用向量的方法。
考虑一个三角形ABC，其三个顶点的向量表示分别为a、b、c。
重心G可以表示为G=(a+b+c)/3，外心O可以表示为O=(a|b|c)/(|a|+|b|+|c|)，其中|a|表示向量a的模。
首先，我们来证明 |G-M|=|O-G|。
注意到中点M的向量表示为M=(b+c)/2，连接线段GM的向量表示为G-M=(a+b+c)/3-(b+c)/2=(a-b/2-c/2)/3。
同理，O-G=(a|b|c)/(|a|+|b|+|c|)-(a+b+c)/3=(a|b|c-|a|(b+c)-|b|(a+c)-|c|(a+b))/(3∗(|a|+|b|+|c|))。
我们将等式两边进行化简，得到：6(G-M)=2(a-b/2-c/2)=(2a-b-c)=3(a-b/2-c/2)=|a|∗(a|b|c-|a|(b+c)-|b|(a+c)-|c|(a+b))/(3∗(|a|+|b|+|c|))=|O-G|说明 |G-M|=|O-G| 成立。
八年级数学重心说课(1)
教学准备： 教师：课件 学生：玻璃棒、细绳、刻度尺、
以及平行四边形、矩形、 菱形、正方形的纸板
二、教学程序设计： A、创设问题情景，搭建探究平台
a、播放课件：新疆达瓦孜表演
b、学生表演：手转数学课本
探究（一）：寻找线段的重心
（1）猜想：线段的重心是线段的中点 （2）利用手中器材（一根玻璃棒、细绳、刻
； erp系统 鼎捷erp 上海erp 易助erp ；
着它们深吸咯壹口气道/要确定我达到六尘境/你们还能挡住我吗/ 三人为之壹愣/此刻の马开抪过确定五尘境/但战斗力单打独斗の话/谁都奈何抪咯它/三人合力/都要袅心翼翼才能困住它/要确定它达到六尘境/马开破开它们の领域就要容易の多咯/再想要借着境界の优势困住马开极难/可确定/// "偏 偏你只有五尘境/未曾达到六尘境/说什么也没有用/" 三人着马开摇咯摇头/着马开满确定冷色/ 马开笑咯起来/笑容灿烂/这种笑容让三人突然有种抪好の预感/其到外の几佫修行者也面色古怪/心想马开笑什么/ "六尘境而已/我想要达到/有数种办法可以达到/既然你们想/我就给你们壹种最为震撼の /" 马开望着它们/嘴角の笑容更加灿烂/洁白の牙齿露出来/这壹幕让三人皱眉/抪知道马开话里面の意思/ 开什么玩笑?六尘境和五尘境代表着壹次蜕变/它能轻易达到?马开这确定吓唬谁呢? "你当我们会信吗/三人嗤笑/着马开满确定抪屑/ "抪需要你们信/我会做给你们の/"马开大笑/身影腾空而起/ 下壹刻/到场の所有人都动容/ 为咯（正文第壹二八壹部分做给你们看） 第壹二八二部分疯狂之举 到众人瞪大眼睛中/马开取出咯壹物/这壹物让所有人都愣愣の着马开/ 到马开手中/确定壹团雨雾圣液/色泽闪动/吸引着每壹佫人の眼球/其天地纹理闪动抪息/让众人都瞪圆眼睛/都出咯这液体の抪凡/ 当然
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
3.掌握常用的数学解题 方法。如利用比例线段 证线段相等以及有关面 积的解题方法
E B
G D
现在，轮到我 来考你们了！
A
思考： ABC中，中线BE 与中线CD交于G点，
D G
E
若M为BE中点， N为CD中点， 求S MNG : S EDG
C
M
B
N
这节课就上 到这，回去 后好好复习！
A
G B D E F C
已知：RtACB, ACB 90 , AC 4, BC 3,
o
G是ABC的重心;
A
求：1.点G到直角顶点C的距离GC；
o
解：RtACB, ACB 90 AB 5 5 AC 4, BC 3 D CD E 2 CD是中线 F G是ABC的重心 G CG 2 CD
B
D
C
H D
E C
DC AC 2 HE AE 1 DC 2HE
‖ HE BD
BD CD
三角形的三条中线交于一点
三角形的三条中线的交点叫做三角形的重心。
三角形的重心定理
三角形的重心与顶点的距离 等于它与对边中点距离的两倍。 A
G是ABC的重心
E G F
AG BG CG 2 GD GF GE 1 GD : AG : AD 1 : 2 : 3
C
ቤተ መጻሕፍቲ ባይዱ
B
D
A
寻找三角形的重心
A G D
B
D
A
C
B
C
G’
G
B C
D M
归纳
6k
A
6k
G
3k k 2k
B
关于线段： DG : AG : AD 1 : 2 : 3
D M
C
DM : MC : DC : BC 1 : 2 : 3 : 6
GM : AC 1 : 3 关于面积： ……
判断题
1、等边三角形三条高的交点就 是它的重心。 2、三角形的重心到一边的距离 等于这边上中线长的三分之一。 三角形的重心到一边 中点的距离等于这边上中 线长的三分之一。 三角形的重心到一边 的距离等于这边上高的三 分之一。
A
G是ABC的重心
F
A
AG BG CG 2 GD GF GE 1 GD : AG : AD 1 : 2 : 3 C
2.要灵活应用三角形的 重心定理进行计算或证 明。
B
G DM C A F
G是ABC的重心 GM ‖ AC DM : MC : DC 1 : 2 : 3
EF 是中位线
F E G B
A
BC BG ‖ EF BC EF GE 1 BC 2 EF BC C 2 EF 1 BG 2 GE 1
F
H G
E
B A
H
G D
E
BD BG 2 HE BD ‖ HE GE 1 BD 2HE
C B
5 CG 3
3
2.点G到斜边AB的距离
已知：ABC中AB AC, AD BC, AD与 中线BE相交于点G; AD 18cm, GE 5cm, 求：BC的长。
A
E G B C
?
D
已知ABC的中线CD、BE相交于点G;
A
求：. S DGE ::S EGC;;;;; 1 4 SDGB S DEC 2 6 3.. SDGE ::S ADC 5 DGE DGB DGE S BGC ABC
D
G G G
E
B
C
归纳有关三角形面积解题方法：
A
1.相似三角形面积之比 等于相似比的平方；
F
E
G
2.等底或同底的两个三 角形面积之比等于高之 比； 3.等高或同高的两个三 角形面积之比等于底之 比。
B
D
C
小结
1.三角形的重心定理:
三角形的重心与顶点的距离 等于它与对边中点的距离的 两倍。
B E G D