波的能量密度
波的能流密度强度公式

波的能流密度强度公式全文共四篇示例,供读者参考第一篇示例:波的能流密度强度公式是描述波动能量传播和传递速率的重要公式。
能流密度强度是指单位面积上通过的波动能量流量,可以用来衡量波在介质中传播的强度和速率。
在物理学和工程学中,波动现象是非常常见的,因此研究波的能流密度强度公式对于理解和控制波动现象非常重要。
波的能流密度强度公式可以根据不同类型的波以及波动现象的特性而有所不同,但一般情况下,波的能流密度强度与波的振幅和频率有关。
在传统的经典力学中,波的能流密度强度可以通过以下公式来表示:\[ P = \frac{1}{2} \sqrt{\frac{u}{\rho}} v^2 \]P表示能流密度强度,u表示波的线密度或者表面密度,ρ表示介质的密度,ν表示波的速度。
在这个公式中,波的振幅对于能流密度强度的影响体现在速度的平方项上。
速度越大,波的振幅对应的能流密度强度就越大。
介质的密度和波的线密度或者表面密度也对能流密度强度起到重要作用。
需要特别说明的是,对于不同类型的波,能流密度强度公式可能需要做适当的修正。
比如对于声波,由于声波是在气体、液体或固体介质中传播的,因此介质密度对于声波的传播会产生不同的影响。
而对于电磁波,介质的电磁性质对于能流密度强度也可能会有所影响。
因此在具体应用中,需要根据波的特性和介质性质做出相应的修正和调整。
在工程学和实际应用中,波的能流密度强度公式可以用来优化波动传输系统的设计,提高能量传播效率,加速数据传输速率,改善声音等波动现象的传播质量。
比如在声学领域中,通过调节声波的振幅和频率,可以控制声音的传播距离和声音质量,进而提高音响设备的性能。
在无线通信领域中,通过优化电磁波的能流密度强度,可以提高无线通信网络的覆盖范围和传输速率。
波的能流密度强度公式是描述波动能量传播和传递速率的重要工具,对于理解和应用波动现象具有重要意义。
在实际应用中,根据波的特性和介质性质,可以对能流密度强度公式进行适当的调整和修正,从而实现对波动现象的优化和控制。
大学物理 波的能量能流密度
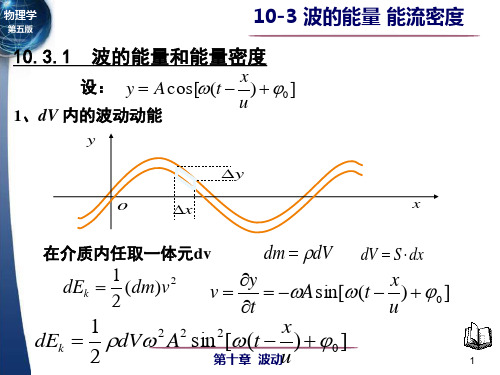
单位体积内的能量 w dE dV
w
dE dV
A2 2 sin2[(t
x u
)
0
]
5、一个周期内的平均能量密度
w 1 T
T wdt 1
0
T
T 0
A2
2
s
in
2[(t
x u
)
0
]dt
1 2 A2
2
sin2 1 1 cos2
2
这说明:w 2、A2
dE
(dV
) A2
2
sin 2[(t
x) u
0 ]
对任一介质体积元来说,不断从波源方向的介质中吸收能
量,又不断地向后面的介质传递能量。这说明波动是传递能
量的一种方式,且能量传播的速度就是波速。
孤立的谐振子系统总能量守恒。
第十章 波动
4
物理学
第4五、版 能量密度
10-3 波的能量 能流密度
dEk
1 2
dV 2 A2
s
in2[(t x
u 第十章 波动
)
0
]
1
物第理五2版、学 dv 内的波动势能
10-3 波的能量 能流密度
体积元因形变而具有弹性势能
在横ห้องสมุดไป่ตู้中,产生切变
y
y
o
x
x
y
x
x
h
lim tg x
h
x0
y y x x
u
A s in
物理学
第五版
16-3 波的能量 能流密度

讨论 1)在波动传播的媒质中,任一体积元的动能、 )在波动传播的媒质中,任一体积元的动能、 势能、总机械能均随x, 作周期性变化 且变化是同 作周期性变化, 势能、总机械能均随 t作周期性变化,且变化是同 相位的 相位的. 体积元在平衡位置时,动能、 体积元在平衡位置时,动能、势能和总机械能 均最大. 均最大 体积元的位移最大时,三者均为零. 体积元的位移最大时,三者均为零
第十六章 机械波动理论 弹性势能
16-3 波的能量 能流密度 16O O
1 2 dW P = k (dy ) 2 dy F 胡克定律 =Y S dx
x
F
dx
SY k= F = YS dx dx 2 1 1 Y dy 2 dW P = k (d y ) = YS d x u= 2 2 ρ dx ∂y ω 1 dy 2 x 2 = ρu dV ( ) = A sin ω (t − ) 2 dx ∂x u u 1 x 2 2 2 = ρdVA ω sin ω (t − ) 2 u
16-3 波的能量 能流密度 16-
s2
s1
r1
r2
即
w 1 uS1 = w 2 uS2 1 1 2 2 2 ρ A1 ω u 4π r1 = ρ A22ω 2 u 4π r22 2 2 A0 r0 r A1 r2 y= cos ω (t − ) = r u A2 r1
处的振幅。 式中r为离开波源的距离, 式中 为离开波源的距离,A0为r=r0处的振幅。 为离开波源的距离
O O
x
dx
x
y + dy
y
x
第十六章 机械波动理论
16-3 波的能量 能流密度 16-
O O
x
10-3 波的能量能流密度

平均能量密度
一个周期内能量密度的平均值。 一个周期内能量密度的平均值。
第十章 波动
5
物理学
第五版
1010-3 波的能量 能流密度
1 T 1 T x 2 2 2 w = ∫ wdt = ∫0 ρA ω sin ω( t − u )dt T 0 T T 1 x 2 2 2π ρA ω ∫0 sin ( t − )dt = T =π ω T T u T 1 1 x π 2 2 2 2 2π w = ρA ω = ρA ω ∫0 sin ( t − )d( t ) π T u T 2
1 A2ω2 x 2 = YSdx sin [ω(t − )] 2 2 u u
1 x 2 2 2 Wp = ρ A ω sin [ω(t − )]∆V = W k 2 u
第十章 波动
3
物理学
第五版
1010-3 波的能量 能流密度 体积中质点的总能量: 考虑 ∆V 体积中质点的总能量:
2 2 2
x W = Wk +Wp= ρA ω sin ω( t − )∆V u 说明: 说明:
∫
π
0
sin 2 θ ⋅ dθ = π 2
第十章 波动
6
物理学
第五版
1010-3 波的能量 能流密度 二、波的能流和能流密度 波的能流和能流密度
u
∆S
能流: 能流:单位时间内通过介质中某一 截面的能量。 截面的能量。 p = wu∆S 平均能流:在一个周期内能流的平均值。 平均能流:在一个周期内能流的平均值。
物理学
第五版
一、波的能量 波的能量
1010-3 波的能量 能流密度
波动是振动状态的传播过程, 波动是振动状态的传播过程,伴随着振动能量 的传播。 的传播。 振动动能 + 形变势能 = 波的能量 以纵波为例: 以纵波为例:
3波的能量 能流密度
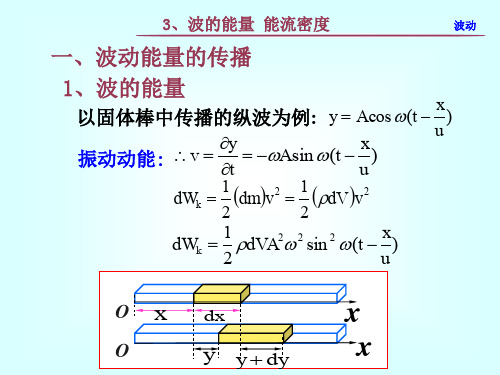
dW
dWk
dWp
dVA2 2
sin 2 (t
x) u
O x dx
x
O
y y dy
x
3、波的能量 能流密度
波动
讨 论 (1)介质中,任一体积元的动能、势能、总
机械能均随 x,t 作周期性变化,且变化是同相位的。
dW
2dWp
2dWk
dVA22 sin2 (t
x) u
体积元在平衡位置时,动能、势能和总机械能均 最大。因为 y Acos(t x )余弦为零,正弦达到最大。
P wuS
u
2、平均能流: P wuS
3、能流密度 ( 波的强度 )
通过垂直于波传播方向
S udt
的单位面积的平均能流。
I P w幅的平方、角频率的平方、
波速以及介质密度成正比。
波动
2、能量密度:单位体积介质中的波动能量
w dW A2 2 sin 2 (t x)
dV
u
3、平均能量密度:能量密度在一个周期内
的平均值:
w 1 T wdt 1 2 A2
T0
2
O x dx
x
O
y y dy
x
3、波的能量 能流密度
波动
二、能流和能流密度
1、能流:单位时间内垂直通过某一面积的能量.
3、波的能量 能流密度
波动
一、波动能量的传播
1、波的能量
以固体棒中传播的纵波为例:
y Acos(t x )
u
振动动能: v y Asin(t x )
t
u
dWk
1 2
dmv 2
1 2
dV
v 2
dWk
大学物理-波的能量 能流密度

2πr2
)
(1
2πr1
)
如果2 1即相干波源S1、S2同位相
则
2π
r1
r2
2π
r1 r2 称为波程差(波走过的路程之差)
水
的 衍
波 的 衍
射
射
19
三 波的干涉
1 波的叠加原理 波传播的独立性:两列波在某区域相遇
后再分开,传播情况与未相遇时相同,互不 干扰.
波的叠加性:在相遇区,任一质点的振 动为二波单独在该点引起的振动的合成.
20
2 波的干涉
频率相同、振动 方向平行、相位相同 或相位差恒定的两列 波相遇时,使某些地 方振动始终加强,而 使另一些地方振动始 终减弱的现象,称为 波的干涉现象.
波是如何传播的? 传播又有什么现象? 这些现象有什么规律?
一 惠更斯原理
介质中波动传播到的各点都可以看作是 发射子波的波源,而在其后的任意时刻,这 些子波的包络就是新的波前.
ut
平
球
面
面
R1
O
R2
波
波
18
二 波的衍射
波在传播过程中遇到障碍物,能绕过障 碍物的边缘,在障碍物的阴影区内继续传播.
波
一 波动能量的传播
1 波Байду номын сангаас能量
波的传播是能量的传播,传播过程中,
介质中的质点运动,具有动能
W
,介质形变
k
具有势能 W p .
1
以棒dW中k 哪哪传12播里里d的m最最v纵大小2 波,?12为例dV分v析2 波y 动A能co量s的(t 传ux播) .
v y Asin(t x )
t
u
振动动能
物理波的能量

=
3
cos
4πt
(2)以距a点5m处的b点为坐标原 点写出波动方程。
b.
u .a 5m
x
解:(1)以a点为原点在x轴上任取一点P,坐标为x
ya = 3 cos 4πt y =3 cos 4πt +
x
20
(2)以b点为坐标原点
wk
wp
2 A2
sin
2 [ (t
x )] u
平均能量密度(对时间平均)
w 1 T A2 2 sin 2[(t x)]dt
T0
u
w
=
1 2
ρAω2
2
三、波的强度
能流P :单位时间内垂直通过某一截面的 P = w S u 能量称为波通过该截面的能流,或叫能通量。
显然能流是随时间周期性变化的。但它总为正值
(t+
d u
)
π
2
]
y
=
A cos[ω
(
t
+
d u
x u
)
π
2
]
例6、波速 u =400m/s, t = 0 s时刻的波形如图所示。
{ 写出波动方程。
t= 0 (o点)
得:
y 0
=
2
=
A
2
v0
>0 0=
π
3
2
o
y(m)
4 5
p
u
x (m)
{ t =0
(p点)
2π
=
y 0
=
0
v0< 0
p
0
d
λ
得:
平均能流P : 能流在一个周期内的平均值。 P = S w u 波的强度 I(能流密度):
大学物理-波的能量能流密度

04
电磁波中的能量传播
电磁波概述
电磁波定义
电磁波是由电场和磁场交替变化而产生 的一种波动现象,可以在真空中或物质 中传播。
VS
电磁波分类
根据频率和波长的不同,电磁波可分为无 线电波、红外线、可见光、紫外线、X射线、 γ射线等。
电磁波中电场和磁场能量关系
电场能量
电磁波中电场能量与电场强度的平方成正比,即$W_e = frac{1}{2} epsilon_0 E^2$,其中 $epsilon_0$为真空介电常数,$E$为电场强度。
行波
与驻波不同,行波是向前传播的波形 。在行波中,质点的振动方向与波的 传播方向垂直(横波)或平行(纵波 )。行波传递能量和动量。
02
能量传播与能流密度
能量传播方式
机械波
通过介质中质点的振动和相互作用传播能量,如声波、水波 等。
电磁波
通过电场和磁场的交替变化传播能量,如光波、无线电波等 。
能流密度定义及表达式
磁场能量
电磁波中磁场能量与磁场强度的平方成正比,即$W_m = frac{1}{2} mu_0 H^2$,其中 $mu_0$为真空磁导率,$H$为磁场强度。
总能量
电磁波的总能量等于电场能量和磁场能量之和,即$W = W_e + W_m$。
电磁波中能量传播特点
01
能流密度矢量
电磁波中的能量传播可以用能流密度矢量$vec{S}$来描述 ,其方向垂直于电磁波的传播方向,大小等于单位时间内 通过单位面积的能量。
光学领域应用
光的传播
01
光波的能量能流密度决定了光的亮度、颜色和温度等特性,是
光学研究的基础。
激光技术
Hale Waihona Puke 02激光具有高能量能流密度的特点,被广泛应用于切割、焊接、
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4
2
(3) 振幅 A=1 mm,则振动速度的幅值为
vm A 1.88 103 cm/s 18.8 m/s
振动速度是交变的,其幅值为18.8 m/s,远小于波速。
返回 退出
§11-2 平面简谐波的波函数
一、波函数
(r,
t)
f
(r,t)
f
( x,
y, z,t)
波函数表示任一时刻物理量 在空间的分布情况。
返回 退出
(3)波函数反映了波的时间、空间双重周期性
T 时间周期性 空间周期性
同一质点在先后时刻的相位差:
2π t t
T
不同质点在同一时刻的相位差:
2π x k x
返回 退出
利用关系式 2π T 2π 和 uT ,可得
其他形式的平面简谐波波函数:
π 2
(5) t =0.0021 s时的波形为
y
0.110
3
cos
25
10
3
π
0.0021
5
x 10
3
0.1103 sin 5πx (m)
返回 退出
例11-3 一横波沿一弦线传播。设已知t =0时的波形曲 线如图中的虚线所示。波速 u=12 m/s,求:(1)振幅; (2)波长;(3)波的周期;(4)弦上任一质点的最大速率; (5)图中a、b两点的相位差;(6)3T/4时的波形曲线。
y( x, t )
Acos
2π
t T
x
0
y( x, t )
Acos
2πt
x
0
y(x,t) Acos( t k x 0 )
其中角波数 k 2π
返回 退出
例11-2 频率为=12.5 kHz的平面余弦纵波沿细长的金
cos
25
10 3
π t
x 5 10 3
(m)
式中x 以m计,t 以s 计。
(3)离原点10 cm处质点的振动表达式
y
0.103
cos
25
10 3
π
t
5
1 10
4
(m)
返回 退出
(4)该两点间的距离
x 10cm 0.10m 4
相应的相位差为
解:(1) 波的周期: T 1 1 s
3000
波长: u 0.52 m 52cm
返回 退出
B点比A点落后的时间为
0.13 1.56 103
1 (s) 12000
即T 4
(2) A、B 两点相差13cm , B点比A点落后的相位差为
4
2π π
纵波:质点的振动方向和波动的传播方向相平行。 波形特征:存在相间的稀疏和稠密区域, 如声波。
返回 退出
弹簧中的纵波
返回 退出
三、波阵面和波(射)线
波阵面:振动相位相同的点所构成的面。 波前:最前面的那个波阵面。 波线:表示波的传播方向的有向线段。
波面
波
线
平面波
球面波
远离波源处,很小区域内的波阵面可看作平面波。
属棒传播,波速为 5000 m/s。如以棒上某点取为坐标原 点,已知原点处质点振动的振幅为A =0.1 mm,试求: (1)原点处质点的振动表式;(2)波函数;(3)离原点10 cm 处质点的振动表式;(4)离原点20 cm和30 cm两点处质 点振动的相位差;(5)在原点振动0.0021 s时的波形。
初相: 随着x 值的增大,即在传播方向上,各质点的相位 依次落后。这是波动的一个基本特征。
返回 退出
(2)当 t 给定时:若t=t1,波动式表示t1 时的波形
y( x, t1 )
Acos[
(t1
x u
)
0
]
f (x)
y
u
t1
t2 t1 t
O
x
ut
t1 时刻的波形经t 时间沿波的传播方向移动了 ut 的距离,波函数反映了波形的传播——行波。
§11-1 机械波的产生和传播 一、机械波产生的条件
机械波: 机械振动(波源)在弹性介质中的传播过程 y
x
机械波产生的两个条件:波源,介质 传播特征: 由近及远传播振动状态。
返回 退出
如: 振动沿一细绳的传播。
返回 退出
二、横波与纵波 横波:质点的振动方向和波动的传播方向垂直。 波形特征:存在波峰和波谷, 如细绳上的波。
解:
波长:
u ν
5.0103 12 .5 10 3
0.40(m)
周期: T 1 ν 8105 s
返回 退出
(1)原点处质点的振动表达式
y0 Acost 0.1103 cos 25 103 πt (m)
(2)波函数
y Acost x u
0.110 3
各向同性介质中,波线与波阵面处处垂直。
返回 退出
四、波长、频率和波速间的关系
1. 波长:沿波的传播方向两相邻同相位点之间的距离
2. 周期T :波前进一个波长
的距离所需的时间。
等于波源的振动周期。
频率: ν 1 T
角频率: 2πν 2π
T
3. 波速 u (相速):振动状态或相位在空间的传播速度。
返回 退出
二、平面简谐波的波函数 简谐波:简谐振动在介质中传播形成的波。 如果波阵面为平面,则为平面简谐波。 平面波的特点:任一时刻在同一波阵面上的各点 有相同的相位。只要研究其中任一条波线上波的 传播规律,就能知道整个平面波的传播规律。
返回 退出
设一平面余弦波,在无吸收的均匀无限介质中沿
x 轴的正方向传播,波速为u 。取任意一条波线为x 轴, 取O 作为x 轴的原点。
O点处质点的振动表式为
y0(t) Acos( t 0 )
P点的振动状态在时间上落后于O点: t x u
平面简谐波的波函数:
返回 退出
平面简谐波的波函数:(沿x 轴正向传播)
沿x 轴负向传播的平面简谐波的波函数:
返回 退出
• 波函数的意义:
(1)当 x 给定时:若x=x1, 波动式成为x1 处质点的振动式
u ν
T
u 一般取决于介质的 性质(弹性和惯性)。
返回 退出
例11-1 频率为3000 Hz的声波,以1560 m/s的传播速度 沿一波线传播,经过波线上的A点后,再经13 cm而传 至B点。求:(1) B点的振动比A 点落后的时间。(2) 波 在A、B两点振动时的相位差是多少?(3) 设波源做简 谐振动,振幅为1 mm,求振动速度
