2018年高职单招模拟考试题一
2018年浙江省普通高职单独招生考试温州市第一次模拟考试

2018年浙江省普通高职单独招生考试温州市第一次模拟考试2018年浙江省普通高职单独招生考试温州市第一次模拟考试《语文》试卷本试题卷共六大题。
全卷共8页。
满分150分,考试时间150分钟。
注意事项:1.所有试题均需在答题纸上作答,未在规定区域内答题,每错一个区域扣卷面总分1分,在试卷和草稿纸上作答无效。
2.答题前,考生务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔填写在答题纸上。
3.1—12、16—18、25题每题选出答案后,用2B 铅笔把答题纸上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
其余各题用黑色字迹的签字笔或钢笔将答案写在答题纸相应题目序号后的横线上(不要超出边线)。
一、基础知识(本大题共8小题,每小题3分,共24分)1.下列标号的句子中没有..错别字且加点字的读音正确的一项是(▲)(3分)①“萨德”风波令韩国旅游业损失残重,让翘.(qiào)首以待的韩国商家一度失望。
②赴韩旅游线路曾停摆8个月,中国团体游客赴韩数量遭遇断涯.(yá)式下跌。
③近日,随着中韩关系的日趋缓.(huǎn)和,一个由32名游客组成的旅行团打着“破冰之旅”的旗号赴韩旅游。
④看着韩媒欢心鼓舞的报道,看着旅游团高调的横幅,再看着还没有真正解决的萨德导弹仍虎视眈眈.(dāng)对着中国北方,真是令人五味杂陈。
A.①B.②C.③D.④2.下列各句中的加点词,前后意思一致的选项是(▲)(3分)A.十九大的各项相关工作十分重要,容不得有丝毫含糊..,所以你在交代各项工作时,绝不能说话含糊..。
B.遇到天晴时,孩子们到户外呼吸新鲜..空气,有时我们也会带孩子们到田里采摘,这已不是新鲜..事。
C.“中国游客大闹机场,警察劝阻发生拉扯..。
”当他说起这件事时,我正急着出门,无心跟他拉扯..。
D.暮色静悄悄...地独...地笼罩下来,我一个人,静悄悄坐在桌前,细细回味着《芳华》中人性的善良。
2018年陕西省普通高校职业教育单独招生考试语文试题模拟卷(含答案)

积土成山,风雨兴焉;积水成渊,蛟龙生焉;积善成德,而神明自得,圣心备焉。故不积跬步,无以至千里;不积小流,无以成江海(jiānɡhǎi)。骐骥一跃,不能十步;驽马十驾,功在不舍。锲而舍之,朽木不折;锲而不舍(qièér bùshě),金石可镂。蚓无爪牙之利,筋骨之强,上食埃土,下饮黄泉(huánɡquán),用心一也。蟹六跪而二螯,非蛇蟮之穴无可寄托者,用心躁也。
2.不符合第二自然段文意的一项是
A.普斯陶伊认定,转基因作物会损伤动物内脏并在破坏免疫系统,他声称是通过实验
证明这一点的。
B.英国皇家学会认为普斯陶伊的结论不能成立,根据主要是普斯陶伊实验的科学性
太差。
C.普斯陶伊所引发的风波,表明了在世界范围内人们对这项先进的生物科学技术的某
种担பைடு நூலகம்与不信任。
D.“有所不同”是针对第一自然段而言,意思是说普斯陶伊的结论没有引起科学家的担
学依据。
二、1.B 2.D 3.C 4.A
三、(共20分)
阅读下面的文言文,完成10—14题。(10——13题,每题3分;14题8分,每小题4分)。
劝学(节选)
荀子
君子曰:学不可以已。青,取之于蓝而青于蓝;冰,水为之而寒于水。木直中绳,輮以为轮,其曲中规。虽有槁暴,不复挺者,輮使之然也。故木受绳则直,金就砺则利,君子博学而日参省乎己,则知明而行无过矣。
转基因技术是一项先进的生物科学技术,这一点已在世界范围内取得共识。美国是转基因技术最先进的国家,据统计,美国的大学、科研机关和企业等已经开发出上百个转基因作物品种,其中仅有43个品种的安全性得到了美国食品和药物管理局的确认。面临转基因玉米和大豆正在进行大面积种植与大量出口以及由此引发争议的现状,美国国家科学院已经郑重承诺,将就转基因食品的安全性问题展开全面调查。看来,在发展转基因技术的同时,也是应当注意吸取任何一种现代工业技术发展过程中的教训的。
2018年北京高职自主招生数学(理科)模拟试题一【含答案】

2
3
4
5
6
7
8
答案
A
C
D
A
A
B
B
C
二、填空题(30分)
题号
9
10
11
答案
48
题号
12
13
14
答案
三、解答题(80分)
15.(本小题满分13分)
解:(Ⅰ)由题知
.
由 ( ),
解得 .
所以 单调递增区间为 ( ).……………6分
(Ⅱ)依题意,由正弦定理, .
因为在三角形中 ,所以 .
即
当 时, ;
当 时, .
A.椭圆的一部分B.双曲线的一部分
C.抛物线的一部分D.圆的一部分
7.已知函数 的图象与直线 的公共点不少于两个,则实数 的取值范围是
A. B. C. D.
8.如图1,矩形 中, .点 在 边上, 且 .如图2, 沿直线 向上折起成 .记二面角 的平面角为 ,当 时,
存在某个位置,使 ;
存在某个位置,使 ;
即 .
设 成等差数列, ,
则对于每个和式 ,其值等于 ( )或
中的一个.去掉重复的一个 ,
所以对于这样的集合 , .
则 的最小值为 .……………13分
所以 平面 .………………8分
(Ⅲ)如图,取 的中点 ,则 ,
因为 ,所以 ,
又因为 平面 ,
所以 两两垂直.
以 为原点,分别以 为
轴建立空间坐标系(如图).
由(Ⅰ)可知, 平面 ,
所以 .
又因为 , ,
所以 平面 ,所以 ,
所以四边形 为菱形.
由已知 ,
则 , , , .
2018年北京高职自主招生数学(文科)模拟试题一【含答案】
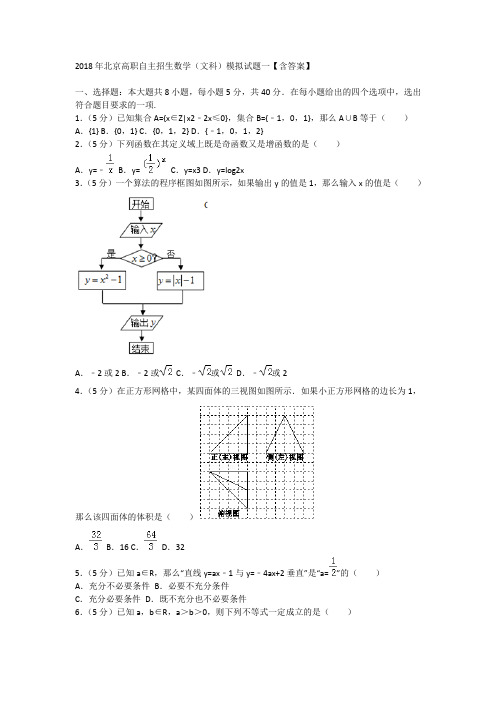
2018年北京高职自主招生数学(文科)模拟试题一【含答案】一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项.1.(5分)已知集合A={x∈Z|x2﹣2x≤0},集合B={﹣1,0,1},那么A∪B等于()A.{1} B.{0,1} C.{0,1,2} D.{﹣1,0,1,2}2.(5分)下列函数在其定义域上既是奇函数又是增函数的是()A.y=﹣B.y=C.y=x3 D.y=log2x3.(5分)一个算法的程序框图如图所示,如果输出y的值是1,那么输入x的值是()A.﹣2或2 B.﹣2或C.﹣或D.﹣或24.(5分)在正方形网格中,某四面体的三视图如图所示.如果小正方形网格的边长为1,那么该四面体的体积是()A.B.16 C.D.325.(5分)已知a∈R,那么“直线y=ax﹣1与y=﹣4ax+2垂直”是“a=”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件6.(5分)已知a,b∈R,a>b>0,则下列不等式一定成立的是()A.B.tana>tanb C.|log2a|>|log2b| D.a•2﹣b>b•2﹣a7.(5分)已知点A(2,﹣1),点P(x,y)满足线性约束条件O为坐标原点,那么的最小值是()A.11 B.0 C.﹣1 D.﹣58.(5分)如图,各棱长均为1的正三棱柱ABC﹣A1B1C1,M,N分别为线段A1B,B1C上的动点,且MN∥平面ACC1A1,则这样的MN有()A.1条B.2条C.3条D.无数条二、填空题:本大题共6小题,每小题5分,共30分.把答案填在答题卡上.9.(5分)已知复数的实部与虚部相等,那么实数a= .10.(5分)已知点P(2,)为抛物线y2=2px上一点,那么点P到抛物线准线的距离是.11.(5分)在△ABC中,已知AB=4,AC=6,A=60°,那么BC= .12.(5分)已知向量,,若||=3,||=,=6,则,夹角的度数为.13.(5分)已知圆C的圆心在x轴上,半径长是,且与直线x﹣2y=0相切,那么圆C的方程是.14.(5分)已知函数f(x)=(1)若a=﹣,则f(x)的零点是.(2)若f(x)无零点,则实数a的取值范围是.三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 15.(13分)已知函数f(x)=2sinxcosx+cos2x.(Ⅰ)求f(x)的最小正周期及单调递增区间;(Ⅱ)求f(x)在区间[0,]上的最大值和最小值.16.(13分)某市准备引进优秀企业进行城市建设.城市的甲地、乙地分别对5个企业(共10个企业)进行综合评估,得分情况如茎叶图所示.(Ⅰ)根据茎叶图,求乙地对企业评估得分的平均值和方差;(Ⅱ)规定得分在85分以上为优秀企业.若从甲、乙两地准备引进的优秀企业中各随机选取1个,求这两个企业得分的差的绝对值不超过5分的概率.注:方差.17.(13分)已知数列{an}的前n项和为Sn,,2an+1=Sn+1.(Ⅰ)求a2,a3的值;(Ⅱ)设bn=2an﹣2n﹣1,求数列{bn}的前n项和Tn.18.(14分)如图,在四棱锥A﹣BCDE中,底面BCDE为正方形,平面ABE⊥底面BCDE,AB=AE=BE,点M,N分别是AE,AD的中点.(Ⅰ)求证:MN∥平面ABC;(Ⅱ)求证:BM⊥平面ADE;(Ⅲ)在棱DE上求作一点P,使得CP⊥AD,并说明理由.19.(13分)已知椭圆(a>b>0)过点(0,﹣1),离心率e=.(Ⅰ)求椭圆的方程;(Ⅱ)已知点P(m,0),过点(1,0)作斜率为k(k≠0)直线l,与椭圆交于M,N两点,若x轴平分∠MPN,求m的值.20.(14分)已知函数f(x)=x+alnx,a∈R.(Ⅰ)当a=1时,求曲线y=f(x)在x=1处的切线方程;(Ⅱ)求函数f(x)在[1,e]上的最小值;(Ⅲ)若函数F(x)=f(x),当a=2时,F(x)的最大值为M,求证:M<.2018年北京高职自主招生数学(文科)模拟试题一参考答案一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项.1.(5分)已知集合A={x∈Z|x2﹣2x≤0},集合B={﹣1,0,1},那么A∪B等于()A.{1} B.{0,1} C.{0,1,2} D.{﹣1,0,1,2}【分析】分别求出集合A,集合B,由此利用并集定义能求出A∪B.【解答】解:∵集合A={x∈Z|x2﹣2x≤0}={∈Z|0≤x≤2}={0,1,2},集合B={﹣1,0,1},∴A∪B={﹣1,0,1,2}.故选:D.【点评】本题考查并集的求法,考查并集定义、不等式等基础知识,考查运算求解能力,考查函数与方程思想,是基础题.2.(5分)下列函数在其定义域上既是奇函数又是增函数的是()A.y=﹣B.y=C.y=x3 D.y=log2x【分析】根据函数奇偶性和单调性的性质进行判断即可.【解答】解:A.y=﹣在定义域上是奇函数,但不是单调函数,不满足条件.B.y=是减函数且为非奇非偶函数,不满足条件.C.y=x3在其定义域上既是奇函数又是增函数,满足条件.D.y=log2x在(0,+∞)上是增函数,是非奇非偶函数,不满足条件.故选:C.【点评】本题主要考查函数奇偶性和单调性的判断,要求熟练掌握常见函数的奇偶性和单调性的性质.3.(5分)一个算法的程序框图如图所示,如果输出y的值是1,那么输入x的值是()A.﹣2或2 B.﹣2或C.﹣或D.﹣或2【分析】分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是计算并输出分段函数y=的函数值,若输出的y的值为1,可根据分段函数的解析式,逆推出自变量x的值.【解答】解:分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是计算并输出分段函数y=的函数值,当x<0时,y=|x|﹣1=1,解得:x=﹣2当x≥0时,y=x2﹣1=1,解得:x=,故选:B.【点评】算法是新课程中的新增加的内容,也必然是新高考中的一个热点,应高度重视.程序填空也是重要的考试题型,这种题考试的重点有:①分支的条件②循环的条件③变量的赋值④变量的输出.其中前两点考试的概率更大.此种题型的易忽略点是:不能准确理解流程图的含义而导致错误.4.(5分)在正方形网格中,某四面体的三视图如图所示.如果小正方形网格的边长为1,那么该四面体的体积是()A.B.16 C.D.32【分析】由三视图还原原几何体,可知该几何体为三棱锥,侧面PAC为等腰三角形,且平面PAC⊥平面ABC,PA=PC,底面ABC为直角三角形,AB=AC=4,然后由棱锥体积公式求解.【解答】解:由三视图还原原几何体如图:该几何体为三棱锥,侧面PAC为等腰三角形,且平面PAC⊥平面ABC,PA=PC,底面ABC为直角三角形,AB=AC=4,∴该四面体的体积是V=.故选:A.【点评】本题考查由三视图求面积、体积,关键是由三视图还原原几何体,是中档题.5.(5分)已知a∈R,那么“直线y=ax﹣1与y=﹣4ax+2垂直”是“a=”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件【分析】由直线y=ax﹣1与y=﹣4ax+2垂直,可得:a•(﹣4a)=﹣1,解得a即可判断出结论.【解答】解:由直线y=ax﹣1与y=﹣4ax+2垂直,可得:a•(﹣4a)=﹣1,解得a=.∴“直线y=ax﹣1与y=﹣4ax+2垂直”是“a=”的必要不充分条件.故选:B.【点评】本题考查了相互垂直的直线斜率之间的关系、简易逻辑的判定方法,考查了推理能力与计算能力,属于基础题.6.(5分)已知a,b∈R,a>b>0,则下列不等式一定成立的是()A.B.tana>tanb C.|log2a|>|log2b| D.a•2﹣b>b•2﹣a【分析】由a>b>0,利用不等式的基本性质与函数的单调性即可判断出结论.【解答】解:∵a>b>0,∴,tana与tanb的大小关系不确定,log2a>log2b,但是|log2a|>|log2b|不一定成立,a•2a>b•2b一定成立.故选:D.【点评】本题考查了不等式的基本性质与函数的单调性,考查了推理能力与计算能力,属于基础题.7.(5分)已知点A(2,﹣1),点P(x,y)满足线性约束条件O为坐标原点,那么的最小值是()A.11 B.0 C.﹣1 D.﹣5【分析】根据向量数量积的定义化简目标函数,作出不等式组对应的平面区域,利用目标函数的几何意义进行求解即可.【解答】解:=2x﹣y,作出约束条件可行区域如图,作直线l0:y=﹣x,当l0移到过A(﹣2,﹣3)时,Zmin=﹣2×2+3=﹣1,故的最小值为﹣1,故选:C.【点评】本题主要考查线性规划的应用,作出不等式组对应的平面区域,利用数形结合是解决本题的关键.8.(5分)如图,各棱长均为1的正三棱柱ABC﹣A1B1C1,M,N分别为线段A1B,B1C上的动点,且MN∥平面ACC1A1,则这样的MN有()A.1条B.2条C.3条D.无数条【分析】任取线段A1B上一点M,过M作MH∥AA1,交AB于H,过H作HG∥AC交BC 于G,过G作CC1的平行线,与CB1一定有交点N,且MN∥平面ACC1A1,则这样的MN 有无数个.【解答】解:如图,任取线段A1B上一点M,过M作MH∥AA1,交AB于H,过H作HG ∥AC交BC于G,过G作CC1的平行线,与CB1一定有交点N,且MN∥平面ACC1A1,则这样的MN有无数个.故选:D【点评】不本题考查了空间线面位置关系,转化思想,属于中档题.二、填空题:本大题共6小题,每小题5分,共30分.把答案填在答题卡上.9.(5分)已知复数的实部与虚部相等,那么实数a=2.【分析】利用复数代数形式的乘除运算化简,再由实部等于虚部求得a值.【解答】解:∵=的实部与虚部相等,∴a=2.故答案为:2.【点评】本题考查复数代数形式的乘除运算,考查复数的基本概念,是基础题.10.(5分)已知点P(2,)为抛物线y2=2px上一点,那么点P到抛物线准线的距离是3.【分析】根据点P(2,)为抛物线y2=2px上一点可求出p的值,由抛物线的性质可知焦点坐标,可知抛物线的焦点和准线方程,从而求出所求.【解答】解:∵点P(2,)为抛物线y2=2px上一点,∴(2)2=2p×2,解得p=2,∴抛物线焦点坐标为(1,0),准线方程为x=﹣1,∴点P到抛物线的准线的距离为2+1=3.故答案为:3.【点评】本题主要考查抛物线的简单性质,解题的关键弄清抛物线y2=2px的焦点坐标为(,0),准线方程为x=﹣,属于基础题.11.(5分)在△ABC中,已知AB=4,AC=6,A=60°,那么BC=2.【分析】利用余弦定理即可得出.【解答】解:由余弦定理可得:BC2=42+62﹣2×4×6cos60°=28,解得BC=2.故答案为:2.【点评】本题考查了余弦定理的应用,考查推理能力与计算能力,属于基础题.12.(5分)已知向量,,若||=3,||=,=6,则,夹角的度数为.【分析】根据题意,设,夹角为θ,||=t,(t>0),由数量积的计算公式可得若||=,则有(﹣)2=2﹣2•+2=9﹣2×6+t2=13,解可得t的值,又由cosθ=,计算可得cosθ的值,由θ的范围分析可得答案.【解答】解:根据题意,设,夹角为θ,||=t,(t>0),若||=,则有(﹣)2=2﹣2•+2=9﹣2×6+t2=13,解可得t=4,则cosθ==,则θ=;故答案为:.【点评】本题考查向量数量积的计算公式,注意求出||的值.13.(5分)已知圆C的圆心在x轴上,半径长是,且与直线x﹣2y=0相切,那么圆C的方程是(x﹣5)2+y2=5或(x+5)2+y2=5.【分析】由题意设出圆心坐标(a,0),利用点到直线的距离公式列式求得a值,代入圆的标准方程得答案.【解答】解:由题意设圆心坐标为(a,0),由,得a=±5.又圆的半径r=.圆C的方程是(x﹣5)2+y2=5或(x+5)2+y2=5.故答案为:(x﹣5)2+y2=5或(x+5)2+y2=5.【点评】本题考查圆的标准方程,考查点到直线的距离公式的应用,是基础题.14.(5分)已知函数f(x)=(1)若a=﹣,则f(x)的零点是.(2)若f(x)无零点,则实数a的取值范围是(∞,﹣4]∪[0,2).【分析】(1)由零点的定义,解方程即可得到所求值;(2)讨论x<2,x≥2时,f(x)=0无实数解,即可得到a的范围.【解答】解:(1)若a=﹣,则f(x)=,当x<2时,由2x﹣=0,可得x=;由x≥2时,﹣﹣x=0,可得x=﹣<2,不成立.则f(x)的零点为;(2)若f(x)无零点,即f(x)=0无实数解,当x<2时,2x+a=0即﹣a=2x无实数解,可得﹣a≥4或﹣a≤0,即为a≤﹣4或a≥0;由x≥2可得a﹣x=0无实数解,即有a<2.综上可得a的范围是(∞,﹣4]∪[0,2).故答案为:,(∞,﹣4]∪[0,2).【点评】本题考查函数的零点的求法,注意运用定义和指数函数的值域和单调性,考查运算能力,属于中档题.三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 15.(13分)已知函数f(x)=2sinxcosx+cos2x.(Ⅰ)求f(x)的最小正周期及单调递增区间;(Ⅱ)求f(x)在区间[0,]上的最大值和最小值.【分析】(Ⅰ)利用二倍角公式和辅助角公式化简,即可求f(x)的最小正周期及单调递增区间;(Ⅱ)根据x在[0,]上,求解内层函数的范围,即可求解最大值和最小值.【解答】解:函数f(x)=2sinxcosx+cos2x=2sin2x+cos2x=sin(2x+)(Ⅰ)f(x)的最小正周期T=;由,得≤x≤所以f(x)的单调递增区间是[,],k∈Z.(Ⅱ)因为x∈[0,]上,所以2x+∈[,]所以当2x+=,即x=时,函数取得最大值是.当2x+=,即x=时,函数取得最小值﹣1.所以f(x)在[0,]区间上的最大值和最小值分别为和﹣1.【点评】本题主要考查三角函数的图象和性质的综合运用.属于基础题.16.(13分)某市准备引进优秀企业进行城市建设.城市的甲地、乙地分别对5个企业(共10个企业)进行综合评估,得分情况如茎叶图所示.(Ⅰ)根据茎叶图,求乙地对企业评估得分的平均值和方差;(Ⅱ)规定得分在85分以上为优秀企业.若从甲、乙两地准备引进的优秀企业中各随机选取1个,求这两个企业得分的差的绝对值不超过5分的概率.注:方差.【分析】(Ⅰ)根据定义计算乙地对企业评估得分的平均值和方差;(Ⅱ)利用列举法计算基本事件数,求出所求的概率值.【解答】解:(Ⅰ)乙地对企业评估得分的平均值是×(97+94+88+83+78)=88,方差是×[(97﹣88)2+(94﹣88)2+(88﹣88)2+(83﹣88)2+(78﹣88)2]=48.4;…(4分)(Ⅱ)从甲、乙两地准备引进的优秀企业中各随机选取1个,有(96,97),(96,94),(96,88),(93,97),(93,94),(93,88),(89,97),(89,94),(89,88),(86,97),(86,94),(86,88)共12组,…(8分)设“得分的差的绝对值不超过5分”为事件A,则事件A包含有(96,97),(96,94),(93,97),(93,94),(93,88),(89,94),(89,88),(86,88)共8组;…(11分)所以P(A)==;所以得分的差的绝对值不超过5分的概率是.…(13分)【点评】本题考查了计算平均数与方差的应用问题,也考查了列举法求古典概型的概率问题,是基础题.17.(13分)已知数列{an}的前n项和为Sn,,2an+1=Sn+1.(Ⅰ)求a2,a3的值;(Ⅱ)设bn=2an﹣2n﹣1,求数列{bn}的前n项和Tn.【分析】(Ⅰ)直接利用递推关系式求出数列的通项公式.(Ⅱ)利用分组法求出数列的和.【解答】解:(Ⅰ)因为数列{an}的前n项和为Sn,,2an+1=Sn+1.所以:2a2=S1+1=,解得:.所以:2a3=S2+1=a1+a2+1=,解得:.(Ⅱ)因为2an+1=Sn+1,所以:2an=Sn﹣1+1,(n≥2)则:2an+1﹣2an=Sn﹣Sn﹣1=an,所以:.由于:,则:数列{an}是首项,公比是的等比数列.所以:.因为bn=2an﹣2n﹣1,所以:.所以:Tn=b1+b2+…+bn,=+…+,=﹣(3+5+…+2n+1),=,=.所以数列的前n项和为:.【点评】本题考查的知识要点:数列的通项公式的求法及应用,分组法求数列的和.18.(14分)如图,在四棱锥A﹣BCDE中,底面BCDE为正方形,平面ABE⊥底面BCDE,AB=AE=BE,点M,N分别是AE,AD的中点.(Ⅰ)求证:MN∥平面ABC;(Ⅱ)求证:BM⊥平面ADE;(Ⅲ)在棱DE上求作一点P,使得CP⊥AD,并说明理由.【分析】(Ⅰ)只需证明MN∥BC.即可证明MN∥平面ABC.(Ⅱ)可得DE⊥平面ABE,DE⊥BM,BM⊥AE,即可证明BM⊥平面ADE.(Ⅲ)取BE中点F,连接AF,DF,过C点作CP⊥DF,交DE于点P.则点P即为所求作的点.【解答】解:(Ⅰ)因为点M,N分别是AE,AD的中点,所以MN∥DE.因为底面BCDE四边形为正方形,所以BC∥DE所以MN∥BC.因为MN⊄平面ABC,BC⊂平面ABC,所以MN∥平面ABC…(4分)(Ⅱ)因为平面ABE⊥底面BCDE,DE⊥BE,所以DE⊥平面ABE因为MB⊂平面ABE,所以DE⊥BM因为AB=AE=BE,点M是AE的中点,所以BM⊥AE因为DE∩AE=E,DE⊂平面ADE,AE⊂平面ADE,所以BM⊥平面ADE…(9分)(Ⅲ)取BE中点F,连接AF,DF,过C点作CP⊥DF,交DE于点P.则点P即为所求作的点.…(11分)理由:因为AB=AE=BE,点F是BE的中点,所以AF⊥BE因为平面ABE⊥底面BCDE,所以AF⊥平面BCDE.所以AF⊥CP因为CP⊥DF,AF∩DF=F,所以CP⊥平面ADF因为AD⊂平面ADF,所以CP⊥AD…(14分)【点评】本题考查了线面陪平行、垂直的判定,空间动点问题,属于中档题,19.(13分)已知椭圆(a>b>0)过点(0,﹣1),离心率e=.(Ⅰ)求椭圆的方程;(Ⅱ)已知点P(m,0),过点(1,0)作斜率为k(k≠0)直线l,与椭圆交于M,N两点,若x轴平分∠MPN,求m的值.【分析】(Ⅰ)根据过点(0,﹣1),离心率e=,可得b=1,=,再根据a2=b2+c2,即可求出,(Ⅱ)设直线l的方程是y=k(x﹣1),联立方程组消去y,得(1+2k2)x2﹣4k2x+2k2﹣2=0,设点M(x1,y1),N(x1,y1),根据韦达定理以及kMP+kNP=0,即可求出m的值【解答】解:(Ⅰ)因为椭圆的焦点在x轴上,过点(0,﹣1),离心率e=,所以b=1,=,所以由a2=b2+c2,得a2=2,所以椭圆C的标准方程是+y2=1,(Ⅱ)因为过椭圆的右焦点F作斜率为k直线l,所以直线l的方程是y=k(x﹣1).联立方程组消去y,得(1+2k2)x2﹣4k2x+2k2﹣2=0,显然△>0,设点M(x1,y1),N(x1,y1),所以x1+x2=,x1x2=,因为x轴平分∠MPN,所以∠MPO=∠NPO.所以kMP+kNP=0,所以+=0,所以y1(x2﹣m)+y2(x1﹣m)=0,所以k(x1﹣1)(x2﹣m)+k(x2﹣1)(x1﹣m)=0,所以2kx1x2﹣(k+km)(x1+x2)+2km=0,所以2•+(1+m)+2m=0所以=0…(12分)所以﹣4+2m=0,所以m=2.【点评】本题主要考查椭圆标准方程,简单几何性质,直线与椭圆的位置关系等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.20.(14分)已知函数f(x)=x+alnx,a∈R.(Ⅰ)当a=1时,求曲线y=f(x)在x=1处的切线方程;(Ⅱ)求函数f(x)在[1,e]上的最小值;(Ⅲ)若函数F(x)=f(x),当a=2时,F(x)的最大值为M,求证:M<.【分析】(Ⅰ)求出函数的导数,计算f(1),f′(1)的值,求出切线方程即可;(Ⅱ)求出函数的导数,通过讨论a的范围求出函数的单调区间,求出函数的最小值即可;(Ⅲ)求出函数的导数,令g(x)=2﹣x﹣4lnx,所以g(x)是单调递减函数,根据函数的单调性证明即可.【解答】解:(Ⅰ)因为函数f(x)=x+alnx,且a=1,所以f(x)=x+lnx,x∈(0,+∞),所以f′(x)=1+,所以f(1)=1,f′(1)=2,所以曲线在x=1处的切线方程是y﹣1=2(x﹣1),即2x﹣y﹣1=0;(Ⅱ)因为函数f(x)=x+alnx(x>0),所以f′(x)=1+=,(1)当a≥0时,f′(x)>0,所以f(x)在(0,+∞)上单调递增.所以函数f(x)在[1,e]上的最小值是f(1)=1;(2)当a<0时,令f′(x)>0,即x+a>0,所以x>﹣a,令f′(x)<0,x+a<0,所以x<﹣a;(i)当0<﹣a≤1,即a≥﹣1时,f(x)在[1,e]上单调递增,所以f(x)在[1,e]上的最小值是f(1)=1;(ii)当1<﹣a<e,即﹣e≤a≤﹣1时,f(x)在[1,﹣a]上单调递减,在(﹣a,e]上单调递增,所以f(x)在[1,e]上的最小值是f(﹣a)=﹣a+aln(﹣a),(iii)当﹣a≥e,即a≤﹣e时,f(x)在[1,e]上单调递减,所以f(x)在[1,e]上的最小值是f(e)=e+a,综上所述,当a≥﹣1时,f(x)在[1,e]上的最小值是f(1)=1,当﹣e≤a≤﹣1时,f(x)在[1,e]上的最小值是f(﹣a)=﹣a+aln(﹣a),当a≤﹣e时,f(x)在[1,e]上的最小值是f(e)=e+a;(Ⅲ)因为函数F(x)=f(x),所以F(x)=+,所以当a=2时,F′(x)=,令g(x)=2﹣x﹣4lnx,所以g(x)是单调递减函数.因为g(1)=1>0,g(2)=﹣4ln2<0,所以在(1,2)上存在x0,使得g(x0)=0,即2﹣x0﹣4lnx0=0,所以当x∈(1,x0)时,g(x)>0;当x∈(x0,2)时,g(x)<0,即当x∈(1,x0)时,F′(x)>0;当x∈(x0,2)时,F′(x)<0,所以F(x)在(1,x0)上单调递增,在(x0,2)上单调递减.所以当x=x0时,F(x)取得最大值是M=F(x0)=,因为2﹣x﹣4lnx=0,所以M=﹣;因为x0∈(1,2),所以∈(,1),所以M<.【点评】本题考查了求切线方程问题,考查函数的单调性、最值问题,考查导数的应用,是一道综合题.。
2018年浙江省高职考数学试卷(模拟)

浙江省2018年单独文化招生考试练手试卷一说明:练手试卷雷同于模拟试卷,练手为主,体验高职考试的感觉一、单项选择题:(本大题共20小题,1-12小题每小题2分,13-20小题每小题3分,共48分)(在每小题列出的四个备选答案中,只有一个是符合题目要求的。
错涂、多涂或未涂均无分)。
1.已知全集为R ,集合{}31|≤<-=x x A ,则=A C uA.{}31|<<-x xB.{}3|≥x xC.{}31|≥-<x x x 或D.{}31|>-≤x x x 或 2.已知函数14)2(-=x x f ,且3)(=a f ,则=aA.1B.2C.3D.4 3.若0,0,0><>+ay a y x ,则y x -的大小是A.小于零B.大于零C.等于零D.都不正确 4.下列各点中,位于直线012=+-y x 左侧的是A.)1,0(-B.)2018,1(- C.)2018,21( D.)0,21( 5.若α是第三象限角,则当α的终边绕原点旋转7.5圈后落在A.第一象限角B.第二象限角C.第三象限角D.第四象限角 6.若曲线方程R b R a by ax ∈∈=+,,122,则该曲线一定不会是A.直线B.椭圆C.双曲线D.抛物线7.条件b a p =:,条件0:22=-b a q ,则p 是q 的A.充分条件B.必要条件C.充要条件D.既不充分也不必要条件 8.若向量)4,2(),2,1(-==,则下列说法中正确的是A.=B.2=C.与共线D.)2,3(=+ 9.若直线过平面内两点)32,4(),2,1(+,则直线的倾斜角为A.30 B.45 C.60 D.90 10.下列函数中,在区间),0(+∞上单调递减的是A.12+=x yB.x y 2log =C.1)21(-=xy D.xy 2-= 11.已知一个简易棋箱里有象棋和军棋各两盒,从中任取两盒,则“取不到象棋”的概率为 A.32 B.31 C.53 D.5212.不等式(组)的解集与其他选项不同的是 A.0)3)(1(>+-x x B.031>+-x x C.21>+x D.⎩⎨⎧>+<-0301x x 13.在等比数列{}n a 中,公比2=q ,且30303212=⋅⋅a a a a ,则=⋅⋅30963a a a a A.102 B.202 C.162 D.152 14.下列说法中正确的是A.直线a 垂直于平面α内的无数条直线,则α⊥aB.若平面α内的两条直线与平面β都平行,则α∥aC.两两相交的三条直线最多可确定三个平面D.若平面α与平面β有三个公共点,则α与β重合15.在ABC ∆中,角C B A ,,的对边分别为c b a ,,,24,34,60===b a A ,则角=B A.45 B.135 C.45或135 D.60或12016.2017年12月29日全国上映的《前任三》红爆网络,已知某公司同事5人买了某场次的连续5个座位,若小刘不能坐在两边的座位,则不同的坐法有 A.48种 B.60种 C.72种 D.96种 17.若抛物线y x 42=上一点),(b a P 到焦点的距离为2,则=a A.2 B.4 C.2± D.4± 18.已知2,21)sin(παπα<=+,则=αtan A.33 B.3- C.3± D.33- 19.已知函数xx f x3log 122)(+-=的定义域为A.)0,(-∞B.)1,0(C.(]1,0D.),0(+∞20.已知圆O 的方程为08622=--+y x y x ,则点)3,2(到圆上的最大距离为 A.25+ B.21+ C.34+ D.31+二、填空题(本大题共7小题,每小题4分,共28分)22.在平行四边形ABCD 中,已知n AD m AB ==,,则=OA _________.24.顶点在原点,对称轴为坐标轴的抛物线经过点)3,2(-,则抛物线的标准方程为_________.26.在等差数列{}n a 中,12,1331==a a ,若2=n a ,则=n _________.27.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为_________.三、解答题(本大题共9小题,共74分) (解答题应写出文字说明及演算步骤)29.(本题满分7分)求1003)2(xx -的展开式中有多少项是有理项.30.(本题满分8分)如图,已知四边形ABCD 的内角A 与角C 互补,2,3,1====DA CD BC AB.求:(1)求角C 的大小与对角线BD 的长;(2)四边形ABCD 的面积.31.(本题满分8分)观察下列三角形数表,假设第n 行的第二个数为),2(+∈≥N n n a n(1)依次写出第六行的所有6个数;(2)试猜想1+n a 与n a 的关系式,并求出{}n a 的通项公式.32.(本题满分8分)如图,在底面是直角梯形的四棱锥ABCD S -中, 90=∠ABC ,⊥SA 面ABCD ,21,1====AD BC SB SA .求: (1)ABCD S V -;(2)面SCD 与面SAB 所成二面角的正切值.(1))3(f ; (2)使41)(<x f 成立的x 的取值集合.34.(本题满分9分)已知中心在原点的双曲线C 的右焦点为)0,2(,实轴长为32,过双曲线的右焦点且与x 轴垂直的直线,交该双曲线的两条渐近线于B A ,两点.求: (1)双曲线的标准方程; (2)AB 的长.35.(本题满分9分)科幻小说《实验室的故事》中,有这样一个情节,科学家把一种珍奇的植物分别放在不同温度的环境中,经过一天后,测试出这种植物高度的增长情况(如下表):数、一次函数和二次函数中的一种.(1)请你选择一种适当的函数,求出它的函数关系式,并简要说明不选择另外两种函数的理由;(2)温度为多少时,这种植物每天高度的增长量最大?(3)如果实验室温度保持不变,在10天内要使该植物高度增长量的总和超过250mm ,那么实验室的温度x 应该在哪个范围内选择?请直接写出结果.36.(本题满分9分)已知椭圆12222=+b y a x 焦点在x 轴上,长轴长为22,离心率为22,O 为坐标原点.求:(1)求椭圆的标准方程;(2)设过椭圆左焦点F 的直线交椭圆与B A ,两点,并且线段AB 的中点在直线0=+y x 上,求直线AB 的方程.参考答案 21.2 22.)(21+- 23.53- 24.292-=y 或y x 342= 25.22 26.23 27.π43 28.410129.30.31.32.33.34.解:(1)⎪⎩⎪⎨⎧===⇒⎪⎩⎪⎨⎧+===2132322222c b a b a c c a 因为焦点在x 轴上,所以标准方程为1322=-y x(2)渐近线方程为x y 33±=,334,332=∴⎪⎩⎪⎨⎧±==AB y x 35.解析:(1)选择二次函数,设c bx ax y ++=2,得⎪⎩⎪⎨⎧=++=+-=4124492449c b a c b a c ,解得⎪⎩⎪⎨⎧=-=-=4921c b a∴y 关于x 的函数关系式是4922+--=x x y .不选另外两个函数的理由:注意到点(0,49)不可能在任何反比例函数图象上,所以y 不是x 的反比例函数;点(-4,41),(-2,49),(2,41)不在同一直线上,所以y 不是x 的一次函数. (2)由(1),得4922+--=x x y ,∴()5012++-=x y ,∵01<-=a ,∴当1-=x 时,y 有最大值为50. 即当温度为-1℃时,这种植物每天高度增长量最大. (3)46<<-x .36.(1)1222=+y x (2)。
黑龙江2018年高职单招物理模拟试题【含答案】

黑龙江2018年高职单招物理模拟试题【含答案】一、选择题:本题共8小题,每小题6分.在每小题给出的四个选项中,第14~17题只有一项符合题目要求,第18~21题有多项符合题目要求.全部选对得6分,选对但不全的得3分,有选错的得0分.1.一质点做直线运动,其运动的位移x跟时间t的比值与时间t的关系图线为一条过原点的倾斜直线,如图所示.由图可知,t=2s时质点的速度大小为()A.2m/s B.4m/s C.6m/s D.8m/s2.如图所示,斜面上放有两个完全相同的物体A、B,两物体间用两根相同轻杆连接,轻杆通过铰链相连,在铰链上加一与斜面垂直的拉力F,使两物体均处于静止状态.则下列说法正确的是()A.A受到沿斜面向上的摩擦力,B受到沿斜面向下的摩擦力B.A、B两物体受到力的个数一定相同C.A、B两物体对斜面的压力一定相同D.当逐渐增大拉力F时,物体B先开始滑动3.如图甲所示,自耦理想变压器输入端a、b接入图乙所示的交流电源,一个二极管和两个阻值均为R=40Ω的负载电阻接到副线圈的两端,电压表和电流表均为理想交流电表.当滑片位于原线圈中点位置时,开关S处于断开状态,下列说法正确的是()A.t=0.01s时,电压表示数为零B.t=0.015s时,电流表示数为5.5AC.闭合开关S后,电压表示数增大D.闭合开关S后,电流表示数为16.5A4.2014年3月8日马来西亚航空公司从吉隆坡飞往北京的航班MH370失联,MH370失联后多个国家积极投入搜救行动,在搜救过程中卫星发挥了巨大的作用.其中我国的北斗导航系统和美国的GPS导航系统均参与搜救工作.北斗导航系统包含5颗地球同步卫星,而GPS 导航系统由运行周期为12小时的圆轨道卫星群组成,则下列说法正确的是()A.发射人造地球卫星时,发射速度只要大于7.9 km/s就可以B.卫星向地面上同一物体拍照时GPS卫星拍摄视角大于北斗同步卫星拍摄视角C.北斗同步卫星的线速度与GPS卫星的线速度之比为D.北斗同步卫星的机械能一定大于GPS卫星的机械能5.如图,在负点电荷Q的电场中有P、M、N、O四点,M、N、P为直角三角形的三个顶点.O为PN的中点.∠P=30°,MN=a,M、N、P、O四点处的电势分别用φM、φN、φP、φO表示.已知φP=φN,φM=φO,点电荷Q在M、N、P、O四点所在面内,则()A.P点场强大小为B.连接OM的线段一定在同一等势面上C.将正试探电荷从M点搬运到N点,电势能增加D.φO小于φN6.如图所示,长为3L的轻杆可绕水平轴O自由转动,Oa=2Ob,杆的上端固定一质量为m 的小球(可视为质点),质量为M的正方体静止在水平面上,不计一切摩擦力.开始时,竖直轻细杆右侧紧靠着正方体物块,由于轻微的扰动,杆逆时针转动,带动物块向右运动,当杆转过60°时杆与物块恰好分离.重力加速度为g.当杆与物块分离时,下列说法正确的是()A.小球的速度大小为B.小球的速度大小为C.物块的速度大小为D.物块的速度大小为7.如图所示,两质量相等的物块A、B通过一轻质弹簧连接,B足够长、放置在水平面上,所有接触面均光滑.弹簧开始时处于原长,运动过程中始终处在弹性限度内.在物块A上施加一个水平恒力,A、B从静止开始运动到第一次速度相等的过程中,下列说法中正确的有()A .当A 、B 加速度相等时,系统的机械能最大B .当A 、B 加速度相等时,A 、B 的速度差最大C .当A 、B 的速度相等时,A 的速度达到最大D .当A 、B 的速度相等时,弹簧的弹性势能最大8.如图所示,光滑水平面上放置一平行金属导轨,其左端与平行板电容器C 相连,一金属棒垂直金属导轨放置,整个装置处于垂直导轨平面向上的匀强磁场中.现对金属棒施加一水平向右的恒力F 作用,使金属棒由静止开始运动,不计导轨及金属棒的电阻,则下面关于金属棒运动的速度v 、加速度a 、电容器两板间的电势差U 、极板所带电量Q 随时间t 变化关系图象中,正确的是( )A .B .C .D .三、非选择题:包括必考题和选考题两部分.第22题~第32题为必考题,每个试题考生都必须作答.第33题~第40题为选考题,考生根据要求作答.(一)必考题(共129分)9.为了探究加速度与力、质量的关系,甲、乙、丙三位同学分别设计了如图所示的实验装置,小车总质量用M 表示(乙图中M 包括小车与传感器,丙图中M 包括小车和与小车固连的滑轮),钩码总质量用m 表示.(1)为便于测量合外力的大小,并得到小车总质量一定时,小车的加速度与所受合外力成正比的结论,下列说法正确的是A.三组实验中只有甲需要平衡摩擦力B.三组实验都需要平衡摩擦力C.三组实验中只有甲需要满足所挂钩码的总质量m远小于小车的总质量M的条件D.三组实验都需要满足所挂钩码的总质量m远小于小车的总质量M的条件(2)若乙、丙两位同学发现某次测量中力传感器和测力计读数相同,通过计算得到小车加速度均为a,a=g,g为当地重力加速度,则乙、丙两人实验时所用小车总质量之比为,乙、丙两人实验用的钩码总质量之比为.10.(1)用多用电表的欧姆挡测量量程为3V电压表的内阻值,红表笔接电压表的(填“正”或“负”)接线柱.用欧姆”×100“挡测量,表盘示数如图1所示,则阻值约为Ω,电压表示数为V,欧姆“×100”挡内部电源电动势为V.(2)要进一步精确测量电压表其阻值,实验室中可提供的器材有:电阻箱R,最大电阻为9999.9Ω,定值电阻r=6kΩ,电动势约为12V,内阻不计的电源E,开关、导线若干.实验的电路图如图2所示,先正确连好电路,再调节电阻箱R的电阻值,使得电压表的指针半偏,记下此时电阻箱R有电阻值R1;然后调节电阻箱R的值,使电压表的指针满偏,记下此时电阻钉R的电阻值R2.①此实验计算电压表内阻Rv的表达式为Rv= (用字母表示).②若电源的内阻忽略不计,则电压表内阻Rv的测量值将.A.偏大B.不变C.偏小D.不能确定,要示电压表内阻的大小而定.11.如图所示,一个可视为质点的物块,质量为m=2kg,从光滑四分之一圆弧轨道顶端由静止滑下,到达底端时恰好进入与圆弧轨道底端相切的水平传送带,传送带由一电动机驱动着匀速向左转动,速度大小为v=3m/s.已知圆弧轨道半径R=0.8m,皮带轮的半径r=0.2m,物块与传送带间的动摩擦因数为μ=0.1,两皮带轮之间的距离为L=6m,重力加速度g=10m/s2.求:(1)皮带轮转动的角速度多大?(2)物块滑到圆弧轨道底端时对轨道的作用力;(3)如物体滑到传送带后将物块将圆弧轨道移开,则物体从传送带的哪一端离开传送带?物块在传送带上克服摩擦力所做的功为多大?12.如图甲所示,有一磁感应强度大小为B、垂直纸面向外的匀强磁场,磁场边界OP与水平方向夹角为θ=45°,紧靠磁场右上边界放置长为L、间距为d的平行金属板M、N,磁场边界上的O点与N板在同一水平面上,O1、O2为电场左右边界中点.在两板间存在如图乙所示的交变电场(取竖直向下为正方向).某时刻从O点竖直向上以不同初速度同时发射两个相同的质量为m、电量为+q的粒子a和b;结果粒子a恰从O1点水平进入板间电场运动,由电场中的O2点射出;粒子b恰好从M板左端边缘水平进入电场;不计粒子重力和粒子间相互作用,电场周期T未知;求:(1)粒子a、b从磁场边界射出时的速度va、vb;(2)粒子a从O点进入磁场到O2点射出电场运动的总时间t;(3)如果金属板间交变电场的周期T=,粒子b从图乙中t=0时刻进入电场,求要使粒子b能够穿出板间电场,E0满足的条件.(二)选考题(共45分)请考生从给出的3道物理题、3道化学题、2道生物题中每科任选一题作答,并用2B铅笔在答题卡上把所选题目的题号涂黑.注意所做题目的题号必须与所涂题目的题号一致,在答题卡选答区域指定位置答题.如果多做,则每学科按所做的第一题计分.【物理-选修3-3】13.下列说法正确的是()A.气体分子单位时间内与单位面积器壁碰撞的次数与单位体积内的分子数及气体分子的平均动能都有关B.气体的温度变化时,其分子平均动能和分子间势能也随之改变C.温度一定时,饱和汽的密度为一定值,温度升高,饱和汽的密度增大D.功可以全部转化为热,但热量不能全部转化为功E.空气的相对湿度越大,空气中水蒸气的压强越接近饱和汽压14.如图所示,在一竖直放置的圆环形管道内封闭有一定质量的理想气体.用一绝热的固定活塞C和绝热、不计质量、可自由移动的活塞A将管道内气体分隔成体积相等的两部分,A、C与圆环的圆心O等高,两部分气体的温度均为T0=300K.现保持下部分气体的温度不变,对上部分气体缓慢加热至T=500K,求此时活塞A的位置与O点的连线跟竖直方向OB之间的夹角θ.(不计两活塞的体积)【物理-选修3-4】15.如图所示为某时刻的两列简谐横波在同一介质中沿相同方向传播的波形图,此时a波上某质点P的运动方向如图所示,则下列说法正确的是()A.两列波具有相同的波速B.此时b波上的质点Q正向上运动C.一个周期内,Q质点沿x轴前进的距离是P质点的1.5倍D.在P质点完成30次全振动的时间内Q质点可完成20次全振动E.a波和b波在空间相遇处会产生稳定的干涉图样16.半径为R的固定半圆形玻璃砖的横截面如图所示,O点为圆心,OO′与直径AB垂直.足够大的光屏CD紧靠在玻璃砖的左侧且与AB垂直,一光束沿半径方向与OO′成θ=30°射向O点,光屏CD区域出现两个光斑,已知玻璃的折射率为.求:(1)当θ变为多大时,两光斑恰好变为一个;(2)当光束沿半径方向与OO′成θ=30°射向O点时,光屏CD区域两个光斑的距离.【物理--选修3-5】17.以下是有关近代物理内容的若干叙述,其中正确的是()A.原子核发生一次β衰变,该原子外层就失去一个电子B.按照玻尔理论,氢原子核外电子从半径较小的轨道跃迁到半径较大的轨道时,电子的动能减小,但原子的能量增大C.核衰变中,γ光子是衰变后转变的新核辐射的D.一束光照射到某种金属上不能发生光电效应,可能是因为这束光的光强太小E.比结合能小的原子核结合成或分解成比结合能大的原子核时一定吸收核能18.如图所示,水平固定一个光滑长杆,有一个质量为m小滑块A套在细杆上可自由滑动.在水平杆上竖直固定一个挡板P,小滑块靠在挡板的右侧处于静止状态,在小滑块的下端用长为L的细线悬挂一个质量为2m的小球B,将小球拉至左端水平位置使细线处于自然长度,由静止释放,已知重力加速度为g.求:①小球运动过程中,相对最低点所能上升的最大高度;②小滑块运动过程中,所能获得的最大速度.黑龙江2018年高职单招物理模拟试题参考答案与试题解析一、选择题:本题共8小题,每小题6分.在每小题给出的四个选项中,第14~17题只有一项符合题目要求,第18~21题有多项符合题目要求.全部选对得6分,选对但不全的得3分,有选错的得0分.1.一质点做直线运动,其运动的位移x跟时间t的比值与时间t的关系图线为一条过原点的倾斜直线,如图所示.由图可知,t=2s时质点的速度大小为()A.2m/s B.4m/s C.6m/s D.8m/s【考点】匀变速直线运动的图像;匀变速直线运动的速度与时间的关系.【分析】由图写出与t的关系式,由匀变速直线运动的位移时间公式x=v0t+变形,两者对比得到物体的初速度、加速度,再求t=2s时质点的速度.【解答】解:由图得:=t.由匀变速直线运动的位移时间公式x=v0t+变形得:=v0+,可得质点的初速度v0=0,加速度为:a=2m/s2,质点做匀加速直线运动.所以t=2s时质点的速度大小为:v=at=4m/s故选:B2.如图所示,斜面上放有两个完全相同的物体A、B,两物体间用两根相同轻杆连接,轻杆通过铰链相连,在铰链上加一与斜面垂直的拉力F,使两物体均处于静止状态.则下列说法正确的是()A.A受到沿斜面向上的摩擦力,B受到沿斜面向下的摩擦力B.A、B两物体受到力的个数一定相同C.A、B两物体对斜面的压力一定相同D.当逐渐增大拉力F时,物体B先开始滑动【考点】共点力平衡的条件及其应用;静摩擦力和最大静摩擦力;物体的弹性和弹力.【分析】分别对物体A、B受力分析,两个物体都处于静止状态,受力平衡,杆子的压力和重力都分解到沿斜面方向和垂直于斜面方向,根据共点力平衡条件分析即可.【解答】解:A、杆对A有沿着杆子方向的推力,故A受杆子的推力、重力、支持力和静摩擦力,静摩擦力平行斜面向上;杆对B有沿着杆子方向的推力,故A受杆子的推力、重力、支持力,可能有静摩擦力;当推力沿着斜面方向的分力大于重力平行斜面的分力时,静摩擦力平行斜面向下;当推力沿着斜面方向的分力等于重力平行斜面的分力时,没有静摩擦力;推力沿着斜面方向的分力小于重力平行斜面的分力时,静摩擦力平行斜面向下;故A错误;B、根据选项A的分析,A受4个力,B可能受3个力,也可能受4个力,故B错误;C、A、B两物体对斜面的压力等于重力垂直斜面的分力与杆子推力垂直斜面的分力的矢量和,一定相等,故C正确;D、当从零开始逐渐增大拉力F时,物体A的静摩擦力逐渐增加,等于推力沿着斜面方向的分力加上重力平行斜面的分力;而物体B的静摩擦力先减小后反向增加,等于推力沿着斜面方向的分力减去重力平行斜面的分力的绝对值;故物体A受静摩擦力先达到最大值,故A 先滑动,故D错误;故选:C3.如图甲所示,自耦理想变压器输入端a、b接入图乙所示的交流电源,一个二极管和两个阻值均为R=40Ω的负载电阻接到副线圈的两端,电压表和电流表均为理想交流电表.当滑片位于原线圈中点位置时,开关S处于断开状态,下列说法正确的是()A.t=0.01s时,电压表示数为零B.t=0.015s时,电流表示数为5.5AC.闭合开关S后,电压表示数增大D.闭合开关S后,电流表示数为16.5A【考点】变压器的构造和原理;正弦式电流的图象和三角函数表达式.【分析】交流电压表和交流电流表测得是有效值,根据原副线圈的电压比等于匝数之比,可以求出副线圈两端的电压,由闭合电路的欧姆定律求出电流表的示数;闭合S后,考虑到二极管的单向导电性,根据电流的热效应求出二极管支路的电流有效值,从而求出电流表的示数.【解答】解:A、交流电压表和电流表示数均为有效值,原线圈电I2==7.8A,电压有效值=220V,根据因而t=0.01 s时,副线圈两端电压有效值U2=440 V,选项A错误;B、根据闭合电路欧姆定律可知,=11A,电流表示数为11 A,选项B错误;C、副线圈电压取决于原线圈电压,闭合开关S后,电压表示数不变,选项C错误;D、电流表示数是有效值,副线圈电压有效值440所以电流11A,闭合后,由于副线圈功率是原来的1.5倍,原线圈电流是原来的1.5倍,副线圈电流也是原来的1.5倍,所以电流表的读数是1.5×11=16.5A,故D正确;故选:D4.2014年3月8日马来西亚航空公司从吉隆坡飞往北京的航班MH370失联,MH370失联后多个国家积极投入搜救行动,在搜救过程中卫星发挥了巨大的作用.其中我国的北斗导航系统和美国的GPS导航系统均参与搜救工作.北斗导航系统包含5颗地球同步卫星,而GPS 导航系统由运行周期为12小时的圆轨道卫星群组成,则下列说法正确的是()A.发射人造地球卫星时,发射速度只要大于7.9 km/s就可以B.卫星向地面上同一物体拍照时GPS卫星拍摄视角大于北斗同步卫星拍摄视角C.北斗同步卫星的线速度与GPS卫星的线速度之比为D.北斗同步卫星的机械能一定大于GPS卫星的机械能【考点】万有引力定律及其应用.【分析】根据题意可直接得出北斗导航系统中的同步卫星和GPS导航卫星的周期之比.根据万有引力提供向心力列出等式表示出轨道半径比较半径关系,从而得出线速度之比.【解答】解:A、发射人造地球卫星的最小发射速度为7.9km/s,一旦速度达到11.2km/s,卫星会挣脱地球的引力,故A错误.B、由于GPS导航卫星的周期小于同步卫星的周期,根据知,GPS导航卫星的轨道半径小于同步卫星的轨道半径,根据几何关系知,卫星向地面上同一物体拍照时GPS 卫星拍摄视角大于北斗同步卫星拍摄视角,故B正确.C、根据知,同步卫星和GPS卫星的周期之比为2:1,则轨道半径之比为,根据知,线速度之比为,故C错误;D、GPS卫星变轨到同步卫星轨道,需加速,但是两卫星的质量未知,所以北斗同步卫星的机械能不一定大于GPS卫星的机械能,故D错误.故选:B5.如图,在负点电荷Q的电场中有P、M、N、O四点,M、N、P为直角三角形的三个顶点.O为PN的中点.∠P=30°,MN=a,M、N、P、O四点处的电势分别用φM、φN、φP、φO表示.已知φP=φN,φM=φO,点电荷Q在M、N、P、O四点所在面内,则()A.P点场强大小为B.连接OM的线段一定在同一等势面上C.将正试探电荷从M点搬运到N点,电势能增加D.φO小于φN【考点】电势差与电场强度的关系;电场强度;电势能.【分析】点电荷的等势面是一系列的同心圆,对于圆,圆弧上任意两点的连线的中垂线一定通过圆心;找出电荷位置后,根据电势能的变化情况判断电场力做功情况【解答】解:A、点电荷的等势面是一系列以点电荷为圆心的同心圆,对于圆弧上任意两点的连线的中垂线一定通过圆心,故场源电荷在PN的中垂线和OM的中垂线的交点上,由几何关系可知,该交点在PM的上,如图所示,且得PQ== aP点场强大小为E=K=,故A正确;B、根据点电荷电场的分布情况可知,连接OM的线段一定不在同一等势面上.故B错误.C、将正试探电荷从M点搬运到N点,电场力做负功,电势能增加,故C正确;D、在负点电荷的电场中,离场源越远,电势越高,则φO小于φN.故D正确.故选:ACD6.如图所示,长为3L的轻杆可绕水平轴O自由转动,Oa=2Ob,杆的上端固定一质量为m 的小球(可视为质点),质量为M的正方体静止在水平面上,不计一切摩擦力.开始时,竖直轻细杆右侧紧靠着正方体物块,由于轻微的扰动,杆逆时针转动,带动物块向右运动,当杆转过60°时杆与物块恰好分离.重力加速度为g.当杆与物块分离时,下列说法正确的是()A.小球的速度大小为B.小球的速度大小为C.物块的速度大小为D.物块的速度大小为【考点】机械能守恒定律;向心力.【分析】不计一切摩擦力.整个装置的机械能守恒.a球与b端的角速度相等,b端的线速度沿水平方向的分速度等于物块的速度,根据系统的机械能守恒和速度关系求解.【解答】解:设小球、b端、物块的速度分别为va、vb、vM.根据系统的机械能守恒得:mg•2L(1﹣cos60°)=+①a球与b端的角速度相等,由v=rω,得va=2vb.b端的线速度沿水平方向的分速度等于物块的速度,即有vbcos60°=vM.得vb=2vM所以va=4vM.②联立①②②解得:va=,vM=故选:BD7.如图所示,两质量相等的物块A、B通过一轻质弹簧连接,B足够长、放置在水平面上,所有接触面均光滑.弹簧开始时处于原长,运动过程中始终处在弹性限度内.在物块A上施加一个水平恒力,A、B从静止开始运动到第一次速度相等的过程中,下列说法中正确的有()A.当A、B加速度相等时,系统的机械能最大B.当A、B加速度相等时,A、B的速度差最大C.当A、B的速度相等时,A的速度达到最大D.当A、B的速度相等时,弹簧的弹性势能最大【考点】牛顿第二定律;功能关系.【分析】对于整体而言,有力F对整体做正功,所以系统的机械能将不断的增大;A从静止开始运动,弹簧的被拉长,产生弹力,从而使B开始运动,在运动的过程中A的合力逐渐的减小,而B的合力在逐渐的增大,当加速度相同之后,A的速度增加不如B速度增加的快了,此时,它们的速度之差也就减小了;当A、B的速度相等时,弹簧的形变量最大,此时弹簧的弹性势能最大;【解答】解:对A、B在水平方向受力分析如图,F1为弹簧的拉力;当加速度大小相同为a时,对A有F﹣F1=ma,对B有F1=ma,得,在整个过程中A的合力(加速度)一直减小,而B的合力(加速度)一直增大,在达到共同加速度之前A的合力(加速度)一直大于B的合力(加速度),之后A的合力(加速度)一直小于B的合力(加速度).两物体运动的v﹣t图象如图所示,tl时刻,两物体加速度相等,斜率相同,速度差最大,t2时刻两物体的速度相等,A速度达到最大值,两实线之间围成的面积有最大值即两物体的相对位移最大,此时弹簧被拉到最长;除重力和弹簧弹力外其它力对系统正功,所以系统机械能增加,tl时刻之后拉力依然做正功,即加速度相等时,系统机械能并非最大值.故选:BCD8.如图所示,光滑水平面上放置一平行金属导轨,其左端与平行板电容器C相连,一金属棒垂直金属导轨放置,整个装置处于垂直导轨平面向上的匀强磁场中.现对金属棒施加一水平向右的恒力F作用,使金属棒由静止开始运动,不计导轨及金属棒的电阻,则下面关于金属棒运动的速度v、加速度a、电容器两板间的电势差U、极板所带电量Q随时间t变化关系图象中,正确的是()A.B.C.D.【考点】导体切割磁感线时的感应电动势;电容;闭合电路的欧姆定律.【分析】解答本题先分析金属棒的运动情况:金属棒在向右运动的过程中,随着速度增大,安培力增大,由牛顿第二定律分析加速度的变化,推导出各物理量随时间的变化情况进行解答.【解答】解:A、根据动量定理可得Ft﹣BILt=m△v,所以a=;根据电流的定义式:I=根据法拉第电磁感应定律:U=BL△v整理以上式子得:I==CBLa所以有:a=为一定值,导体棒做匀加速直线运动,A错误;B、根据v=at可知B正确;C、根据法拉第电磁感应定律:U=BL△v=BLat,C错误;D、极板所带电量Q随时间t变化关系为:Q=CU=CBLat,D正确;故选:BD.三、非选择题:包括必考题和选考题两部分.第22题~第32题为必考题,每个试题考生都必须作答.第33题~第40题为选考题,考生根据要求作答.(一)必考题(共129分)9.为了探究加速度与力、质量的关系,甲、乙、丙三位同学分别设计了如图所示的实验装置,小车总质量用M表示(乙图中M包括小车与传感器,丙图中M包括小车和与小车固连的滑轮),钩码总质量用m表示.(1)为便于测量合外力的大小,并得到小车总质量一定时,小车的加速度与所受合外力成正比的结论,下列说法正确的是BCA.三组实验中只有甲需要平衡摩擦力B.三组实验都需要平衡摩擦力C.三组实验中只有甲需要满足所挂钩码的总质量m远小于小车的总质量M的条件D.三组实验都需要满足所挂钩码的总质量m远小于小车的总质量M的条件(2)若乙、丙两位同学发现某次测量中力传感器和测力计读数相同,通过计算得到小车加速度均为a,a=g,g为当地重力加速度,则乙、丙两人实验时所用小车总质量之比为1:2,乙、丙两人实验用的钩码总质量之比为1:2.【考点】探究加速度与物体质量、物体受力的关系.【分析】(1)根据实验原理,即可判定是否需要平衡摩擦力,及确定所挂钩码的总质量m 与小车的总质量M的关系;(2)根据牛顿第二定律,结合动滑轮的拉力是测力计的示数2倍,从而即可求解.【解答】解:(1)AB、为便于测量合外力的大小,甲图通过钩码的总质量对应的重力即为合外力,而乙图是力传感器的示数,丙图则是测力计的2倍,因此它们都必须平衡摩擦力,故A错误,B正确;CD、由于甲图通过钩码的总质量对应的重力即为合外力,因此三组实验中只有甲需要满足所挂钩码的总质量m远小于小车的总质量M的条件,故C正确,D错误;(2)乙、丙两位同学发现某次测量中力传感器和测力计读数相同,且通过计算得到小车加速度均为a,根据牛顿第二定律,则有:F=M乙a,2F=M丙a;因此乙、丙两人实验时所用小车总质量之比为1:2;由牛顿第二定律,对砝码研究,则有m乙g﹣F=m乙a,。
2018年宁波市高职考试第一次模拟考试卷(语文)

2018年浙江省高职招生考试宁波市模拟考语文试卷姓名________________ 准考证号________________本试卷共六大题,共6页。
满分150分,考试时间150分钟。
注意事项:1.答题前,考生务必将自己的姓名、准考证号用黑色字迹的签字笔填写在答题卡和试卷上。
2.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
非选择题用黑色字迹的签字笔将答案写在答题卡规定位置上。
3.所有试题均需在答题卡上作答,在试卷和草稿纸上作答无效。
4.考试结束后,将试卷和答题卡一并交回。
一、基础知识(本大题共8小题,每小题3分,共24分)1.下列语句中,没有错别字且加点字的读音正确的一项是()A.解决收费公路亏损的问题,还是应该分而治之,对由于经营不善、管理成本过高造成的亏损问题,就要想办法从节流、降低管理费用,从限制人浮.(fú)于事、限制过高收入着手。
B.民航业、媒体需要继续向大众普及与航空相关的知识,规避同类事件的发生;另一方面,应该完善法制,针对有损航空安全的行为,应加大处罚力度,以儆.(jǐng)效犹。
C.“人肉”作为把一个突然性事件人物兜个底朝天的杀手锏.(jiàn),这几年被网友屡试不爽,并且客观上为事件相关人物在舆论压力面前的“就范”与“收敛”,起到了“敲山震虎”的作用。
D.顺丰控股的这轮表现,是属于异常波动,还是正常的资金炒作?在股市上,天天都有资金进出,天天都有股票涨.(zhǎng)停。
但顺丰这一翻疯涨,又显得那么不一样。
2.下列各句中加点的词语运用正确的一项是()A.反腐倡廉不仅有助于中国共产党加强自身建设以及推动全面深化改革,对其他国家驱除..腐败这一毒瘤也有借鉴意义。
B.家风,是一个家庭或家族长期以来形成并传播..的道德操守和处事方法。
C.人们的德行仅仅来源于除了尘世间那微不足道的期待和欲望。
在这样的世界上,有勇气的人成了冒险家,而没有勇气的人成了只求明哲保身....、苟活于世的懦夫。
吉林2018年高职单招语文模拟试题含答案

吉林2018年高职单招语文模拟试题【含答案】一、语言文字运用(15分)1.下列词语中加点的字,每对读音都不相同的一组是(3分)A.调派/调理积攒/人头攒动诘问/攻讦锒铛/不稂不莠B.寒颤/颤动落款/丢三落四瞩目/属意冰锥/椎心泣血C.中肯/中听慰藉/声名狼藉嗫嚅/蹑踪缱绻/卷土重来D.行伍/道行曾祖/曾经沧海缉拿/揖让撞击/人影幢幢2.下列各句中,加点的成语使用恰当的一句是(3分)A.春暖花开,冰雪消融,江河日下,涓涓细流滋润万物,历经严寒考验的北方大地,告别了千里冰封的季节,焕发出勃勃生机。
B.在全球银行业普遍不景气的情况下,中国的银行业却实现了业绩上的突破,工商银行去年的净利润居高不下,首超千亿。
C.自有高洪波担任中国男子足球队主教练的传闻以来,各路媒体或力挺,或质疑,热闹之极,唯有号称足球第一媒体的《足球报》却不赞一词。
D.在国产动画电影《风云决》的首映典礼上,任贤齐坦言配音过程“很困难”,无独有偶,其他演员也表达了“比演戏更难”等相似看法。
3.(1)请用简洁的文字概括“中德文化对比”图的意思。
(不超过40个字)(4分)(2)根据这两幅画的寓意,请你把“裁员”“减薪”两个词恰当的填入下面横线处。
(1分)在当前全球金融危机的冲击下,面临经济衰退导致赢利下降甚至亏损的困境,中国企业往往首先想到的是▲,德国企业可能更倾向于▲。
中德文化对比4.仿照下面材料中画线的句子,补写文段中空缺处,要求句式基本一致,上下文衔接连贯。
(4分)在生命里,我们几乎每时每刻都在犯错。
那该做而没有做的,逐日侵蚀之后,贮满泪水,就成为遗憾湖。
▲▲▲在这湖山之间,我们只有一条窄路可以走,只有一种方法可以减轻那压在心上的重负,就是——进入文字的领域里,或者去读,或者去写,才能和“生命”取得些许的平衡。
二、文言文阅读(19分)阅读下面的文言文,完成5 ~ 8题。
范滂,字孟博,汝南征羌①人也。
少厉清节,为州里所服。
冀州饥荒,盗贼群起,乃以滂为清诏,使案察之。
