小波神经网络及其应用
小波神经网络在手写数字识别中研究与应用

l 引言
字符识别 技术是 模式 识别 领域研 究 的热点 问题 , 目的是 利用计算 机对 印刷或手 写字符 进行 自动识 别 和分类 。数 字识 别是字符 识别领 域 的一个 重要 分支 ,在 邮件 自动分 拣 、银 行 票据 处理 、财 务账单 处 理等 方 面有很 高 的应 用价 值 。 目前 , 手写数字 识别 的方法 主要 有 :模板 匹配法 、逻 辑推理 法 、模 糊 判别 法 和神经 网络法 等 。现行 的识 别技 术存 在 误识 率 高 、 识 别速度 慢等 问题 ,因此 ,设 计速度 快 、精度 高 的数 字识 别
系统 是 努 力 的 目标 。
再对 ( t )进行伸缩 与平 移变换 ,可以得到小波基函数。
(
式 中 ,a 为尺度伸 缩因子 ,b为 时间平移 因子 ,a ,b∈R,
a≠ 0。
小 波分析 中所用 到 的小波 函数具 有多样 性 ,常用 的小 波 函数有 Ha 小 波 、Moe 小波 、 M xcn小 波 ( r r rt eia 简称 Mar r 小 波 ) ab cis 波 ( 、D u ehe 小 简称 d b小波 )等 ,在 此设计 中选 用 Mol 小波 函数作 为神 经网络隐层的激励 函数。 rt e
神 经 网络 技术是 人工 智能研 究领 域 的一个 重要分 支 ,它
具 有 自组 织 、 自学习 、分 布式存 储和 并行 处理 等特点 ,广 泛 应用在模式识别 、 自动控制 和专 家系统等方面 。 对数 字识别 技术详 细研 究 的基础 上 ,提 出将 小波 神经 网 络应用 于手写数字识别技术 中 ,克服 了传 统 B P算法容易 陷入 局部极小点和 收敛速度慢等 缺点 ,提高了识别速度和识别率 。
神经网络小波分析技术的研究

神经网络小波分析技术的研究神经网络小波分析技术是近年来发展迅速的一种分析技术。
它是基于小波分析的基础上,利用人工神经网络模型进行数据分析和模型建立的一种方法。
它的应用范围非常广泛,可以用于时间序列分析、图像处理、语音识别、金融风险评估等领域。
下面将从理论和应用两个方面探讨神经网络小波分析技术的研究。
一、理论研究神经网络小波分析技术是一种新的数据处理方法,它的理论基础是小波变换和人工神经网络模型。
在小波分析中,小波函数用于对信号进行分解,将信号分解成不同尺度和频率的小波系数,然后根据小波系数进行重构。
小波分析的优势在于可以同时分析信号的时域和频域信息,适用于处理具有局部特征的非平稳信号。
而在人工神经网络模型中,神经元利用类似于神经系统的方式处理信息,具有分布式处理、全局优化等优势。
神经网络小波分析技术将小波分析和神经网络模型有机地结合起来,用于数据分析和模型建立。
在神经网络小波分析中,先利用小波变换对原始数据进行分解,然后将小波系数作为输入信号传入神经网络中进行处理。
通过不断地迭代训练网络,最终获得满足误差要求的最优网络结构和权值,从而实现数据分析和模型建立。
神经网络小波分析技术在理论方面的研究主要包括网络结构的设计、学习算法的改进、模型评价等方面。
二、应用研究神经网络小波分析技术的应用范围非常广泛,可以应用于时间序列分析、图像处理、语音识别、金融风险评估等众多领域。
以下分别介绍一下神经网络小波分析技术在不同领域的应用。
1、时间序列分析时间序列分析是指对一系列按时间顺序排列的数据进行分析和预测的技术。
神经网络小波分析技术可以利用小波分解提取序列中不同频率成分,然后利用神经网络模型对时间序列进行建模和预测。
神经网络小波分析技术在金融、电力、医学等领域中都得到了广泛的应用。
2、图像处理图像处理是指对数字图像进行处理和分析的技术。
神经网络小波分析技术可用于数字图像压缩、边缘检测、纹理分析等方面。
利用小波变换可以提取图像中的局部特征,利用神经网络模型可以对图像进行分类识别,实现图像处理和分析。
小波神经网络多属性综合评价及其应用
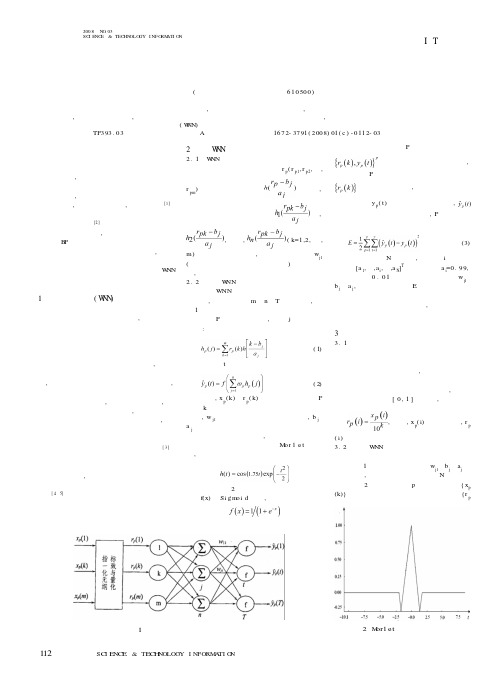
科技资讯科技资讯S I N &T NOLOGY I NFORM TI O N2008N O .03SC I ENC E &TEC HN OLO GY I NFO RM ATI O NI T 技术小波神经网络多属性综合评价及其应用李建丽钟仪华李智超(西南石油大学四川成都610500)摘要:本文针对现存多属性综合评价方法的不足,借助小波神经网络思想、原理,构造了一种新的分类小波神经网络多属性综合评价模型,并进行了实例验证,表明此分类小波神经网络多属性综合评价方法是正确、可行的,且能有效地提高综合评价精度与收敛速度。
关键词:多属性综合评价小波神经网络(W NN)分类小波神经网络模型应用中图分类号:TP393.03文献标识码:A 文章编号:1672-3791(2008)01(c )-0112-03多属性综合评价是通过一定的数学模型将多个评价指标属性值“合成”一个整体性的综合评价值。
目前可用于“合成”的数学方法很多,有灰色关联度法、模糊综合评判法、人工神经网络等。
各评价方法都存在一定的不足,例如:灰色关联度法受到关联系数的影响,评价值趋于均化,分辨率较低[1];模糊综合评价在赋权和最终评价方法上具有较大的主观随意性[2];综合评价中使用较多的是人工神经网络方法,而单纯的人工神经网络模型的B P 算法又存在收敛速度较慢且容易陷入局部极小等缺点。
为克服以上不足,本文建立一种既利用小波变换的时——频局部化特性又能发挥神经网络的自学习功能的W NN 综合评价模型。
1小波神经网络(W N N )小波神经网络将常规单隐层神经网络的隐节点函数由小波函数代替,相应的输入层到隐层的权值及隐层阀值分别由小波函数的尺度和平移参数所代替。
即激活函数为已定位的小波基函数。
其基本思想和原理是把用来描述评价对象特征的评价指标属性值作为神经网络的输入向量,将已知的相应评价的量值作为神经网络的输出,可利用共轭梯度法以批处理方式训练,自适应地调整小波系数和网络权重。
小波神经网络原理及其应用

在窗口之外函数为零;本身是振荡的,具有波的性质, 并且完全不含有直流趋势成分,即满足
(0) (x)dx 0 7
2.小波变换的基本原理与性质
信号的信息表示 时域表示:信号随时间变化的规律,信息包括均值、方
精品文档
主要内容
1.小波变换与傅里叶变换的比较 2.小波变换的基本原理与性质 3.几种常用的小波简介 4.小波变换的应用领域 5.小波分析应用前景 6.小波变换的去噪应用 7.小波神经网络
2
1.小波变换与傅里叶变换的比较
傅立叶变换的理论是人类数学发展史上的一个 里程碑,从1807年开始,直到1966年整整用了一个半世 纪多才发展成熟,她在各个领域产生了深刻的影响得到 了广泛的应用,推动了人类文明的发展。其原因是傅立 叶理论不仅仅在数学上有很大的理论价值,更重要的是 傅立叶变换或傅立叶积分得到的频谱信息具有物理意义。 遗憾的是,这种理论具有一定的局限性。
△
1
叶变换为: a, () a 2e
ω,则相
j (a)
应的连
续小波
的傅立
a,
其频域窗口中心为:
1 a
0
1
a
窗口宽度为:
[1 a
0
1 2a
,
1 a
0
1 2a
]
信号在频域窗内:
从上面的时频域的讨论可见,连续小波的时频域窗口
18
3.小波变换的基本原理与性质——多分辨 分析
连续小波变换实现过程 首先选择一个小波基函数,固定一个尺度因子,将它与
小波变换与神经网络技术的滋养特征提取及识别应用

小波变换与神经网络技术的滋养特征提取及识别应用近年来,小波变换与神经网络技术已经在图像、音频、信号等领域广泛应用,特别是在特征提取和识别方面取得了许多重要进展。
本文将介绍小波变换和神经网络技术的原理及其在特征提取和识别中的应用。
一、小波变换原理小波变换是一种时间-频率分析方法,它将时域信号分解成不同尺度和不同频率的子信号,可以帮助我们更好地理解信号的局部特征。
在小波分析中,小波函数是一种长度有限的函数,它具有自相似性、局部化和可变性等特点。
小波变换的基本过程是将原始信号分解成一组小波系数,这些系数包含了信号在不同尺度上的特征信息,包括低频和高频成分。
其中,低频成分代表信号的整体趋势,高频成分反映了信号的局部细节。
二、神经网络技术原理神经网络是一种模拟人类神经系统运作的计算模型。
它由大量简单的单元组成,这些单元相互连接并通过学习来实现特定任务。
神经网络可以通过多次迭代来优化网络连接权重以及神经元的激活函数,从而得到更好的分类和识别效果。
在神经网络中,网络的输入层接收原始数据,隐含层和输出层则通过多层非线性变换将输入数据映射到具有特定意义的特征空间中。
神经网络的输出层通常表示分类或者识别结果。
三、小波变换与神经网络技术在特征提取中的应用小波变换和神经网络技术已经被广泛应用于图像、音频、信号等领域,特别是在特征提取和识别方面。
以下是一些典型应用案例:1.图像特征提取在图像处理中,小波变换可以将图像分解为不同的频率和尺度。
通过选取合适的小波函数和分解层数,可以提取出图像的不同特征,如边缘、纹理等。
这些特征可以被用于分类、识别和双目视觉等应用中。
神经网络可以通过卷积层和全连接层等深度学习结构学习这些特征,并将其映射到更高层次的特征空间中。
这些特征被广泛应用于计算机视觉任务,如图像分类、目标检测和物体识别等。
2.音频特征提取在音频处理中,小波变换可以将音频信号分解为不同频率的子信号。
这些子信号可以用于声音识别、语音合成、语音分析等应用。
小波变换与神经网络的结合在图像分析中的应用

小波变换与神经网络的结合在图像分析中的应用随着科技的不断发展,数字化技术在图像处理中的应用越来越广泛。
在图像分析领域中,小波变换和神经网络是两个重要的工具,它们可以互相结合,最终帮助人们更好地进行图像分析。
本文将探讨小波变换和神经网络的结合在图像分析中的应用。
一、小波变换的介绍小波变换是一种基于时间和频率分析的变换方法,它可以将信号分解为不同频率成分和时域特征。
相比于傅里叶变换,小波变换更适合处理非稳态信号,可以提取出更为准确的信息。
在图像分析中,小波变换可以用于图像压缩、去噪、边缘检测等方面。
通过分解和重构,小波变换可以将图像压缩到更小的尺寸,同时保留图像的主要信息。
此外,小波变换可以减少噪声在图像中的影响,提高图像的质量。
在边缘检测方面,小波变换可以定位图像中的边缘,并将其突出显示。
二、神经网络的介绍神经网络是一种基于生物神经系统的模拟技术,它通过多个节点(神经元)之间的连接,来实现信息的处理。
神经网络可以设置多个隐藏层,根据数据集不断进行学习,提高其对目标的识别准确性。
在图像分析中,神经网络可以用于图像识别、物体检测等方面。
通过对大量数据的学习,神经网络可以判断图像中是否存在目标物体,并将其与其他物体区分开来。
此外,神经网络还可以对图像进行分类,例如将不同的动物、车辆等分类出来。
三、小波变换与神经网络的结合小波变换和神经网络在图像分析中都有重要的作用,它们的结合可以更全面地分析图像。
以下是小波变换与神经网络结合的一些应用。
1. 基于小波变换的图像预处理在使用神经网络进行图像分析之前,需要对图像进行预处理。
由于神经网络对噪声、模糊等干扰比较敏感,因此需要使用小波变换来对图像进行去噪、边缘检测等处理,以提高神经网络的准确性。
2. 基于小波变换的神经网络训练方法神经网络的识别准确性与其所学习的数据集的质量有关。
在训练神经网络时,可以采用小波变换来对数据集进行压缩,从而减少神经网络的训练时间和计算量,提高训练效率。
控制系统的小波神经网络控制方法

控制系统的小波神经网络控制方法随着科技的发展和应用需求的增加,控制系统在各个领域中扮演着重要的角色。
而小波神经网络作为一种新兴的控制方法,在控制系统中也展现出了广泛的应用前景。
本文将介绍控制系统中的小波神经网络控制方法,并探讨其在实际应用中的效果和优势。
第一部分:小波神经网络的基本特点小波神经网络是一种将小波分析和神经网络相结合的控制方法。
其基本特点有以下几个方面:1. 非线性能力强:小波神经网络通过神经元之间的连接和权值的调整,可以实现对非线性系统的建模和控制。
2. 适应性调整能力好:小波神经网络具有自动学习和适应环境变化的能力,可以根据实际情况自动调整网络的参数。
3. 高效性:小波神经网络采用了小波分析的方法,可以对信号进行多尺度表示,提高了系统的控制效果和响应速度。
第二部分:小波神经网络控制方法的步骤小波神经网络的控制方法通常包括以下几个步骤:1. 数据采集和预处理:首先需要采集控制系统的输入和输出信号,并对其进行预处理,去除噪声和异常值。
2. 网络结构设计:根据实际需求和系统特点,设计小波神经网络的结构,包括神经元的数量和各层之间的连接关系。
3. 参数设置和初始化:设置网络的参数,包括学习率、权值范围等,并进行初始化。
4. 训练网络:利用采集到的数据对小波神经网络进行训练,通过不断调整神经元之间的连接权值,使网络输出接近于期望输出。
5. 模型验证和调整:训练完成后,对网络进行验证和调整,确保其在实际环境中的控制效果和稳定性。
6. 实时控制:将训练好的小波神经网络应用于实际控制系统中,实现对系统的实时控制和监测。
第三部分:小波神经网络控制方法的实际应用小波神经网络控制方法在各个领域中都有广泛的应用。
以下是几个典型的实际应用案例:1. 智能交通系统:小波神经网络可以应用于智能交通系统中的交通流量控制和优化,提高道路通行效率和交通安全性。
2. 机器人控制:小波神经网络可以应用于机器人控制系统中,实现对机器人的智能导航和任务执行。
小波神经网络

0.5
0
y
-0.5
-1 -1
-0.5
0 x
0.5
1
图8 逼近结果(虚线为函数f, 实线为逼近) M=9
23
对一维函数的逼近仿真
1
——逐次剔除小波选择法 (方法2)
0.5
0
y
-0.5
-1 -1
-0.5
0 x
0.5
1
图8 逼近结果(虚线为函数f, 实线为逼近) M=9
24
对一维函数的逼近仿真
1
——逐次选入小波选择法 (方法3)
0.5
0
y
-0.5
-1 -1
-0.5
0 x
0.5
1
图8 逼近结果(虚线为函数f, 实线为逼近) M=3
25
三种小波选择方法比较
基于 OLS 小波选择法(方法 1) 逐次剔除小波选择法(方法 2) 逐次选入小波选择法(方法 3)
好 较好 不理想
故以下仿真实验采用 OLS 小波选择法
n 2
xb ): a
a R , b R n
5
1. 小波神经网络
─ 标架(Frame)
标架 设 H 为一 Hilbert 空间, { j } jZ 为 H 中的一个 函数序列。 若对任一 f H , 存在0 A B , 使得下述 不等式成立:
A f
2
f , j B f
1 N 2 MSE 为模型的均方误差: MSE [ yk fˆ ( xk )] N k 1
19
2. 基于小波神经网络的非线性建模
1
0.5
0
-0.5 -5
0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小波神经网络及其应用
陆宇颖
摘要:小波神经网络是将小波理论和神经网络理论结合起来的一种神经网络,它避免了BP 神经网络结构设计的盲目性和局部最优等非线性优化问题,大大简化了训练,具有较强的函数学习能力和推广能力及广阔的应用前景。
首先阐明了小波变换和多分辨分析理论,然后介绍小波神经网络数学模型和应用概况。
1. 研究背景与意义
人工神经网络是基于生物神经系统研究而建立的模型,它具有大规模并行处理和分布式存储各类图像信息的功能,有很强的容错性、联想和记忆能力,因而被广泛地应用于故障诊断、模式识别、联想记忆、复杂优化、图像处理以及计算机领域。
但是,人工神经网络模型建立的物理解释,网络激活函数采用的全局性函数,网络收敛
即
,焦李神经网络2. 2.1()x ,使式中为的Fourier 变换。
对作伸缩、平移变换得到小波基函数系
对任意2()()f x L R ∈,其连续小波变换定义为: 反演公式为:
在实际应用中,特别是计算机实现中,往往要把上述的连续小波及其变换离散化,通常采用二进制离散,即
令2,2m m a b k ==,则
二进小波一定是一个允许小波,且是一个正交小波基。
考虑一个连续的、平方可积的函数
2()()f x L R ∈在分辨率2m 下的逼近()m f x ,由多分辨分析理论可知:
()x Φ是尺度函数,对其作伸缩、平移变换得到()mk x Φ。
Mallat 同时证明了函数()f x 在2m 和12m -分辨率下的信息差别(即细节)()m D f x ,可以通过将函数()
f x 在一小波正交基上分解而获得,从而定义了一种完全而且正交的多分辨率描述,即小波描述。
()mk x ψ就是式(5)定义的二进小波,则()f x 在12m -分辨率下的逼近式为:
Mallat 并指出,对于任意一个函数
2()()f x L R ∈可以在一组正交小波基上展开: 式(11)是一个平方可积函数的小波分解,提供了小波神经网络设计的理论框架。
..
12(,)x x ο
则有2.2 (ψ(f x 式(Lk a 与式
(17i c i 则有:
即(21)=f Ac
式(20)的最小二乘解为:
+A 被称为A 的伪逆矩阵。
且
如果样本i x 均匀分布,(1,2,...,)θ=i
i n 是正交基, 则T A A 是一个⨯n n 单位矩阵,且
2.2.3小波神经网络学习过程
选择合适的小波函数和尺度函数后,在最粗的尺度L 上训练Φ节点,直到网络达到收敛。
要使网络达到收敛,需确定逼近误差(在很多文献中提出了误差的计算方法)和增加合适的ψ节点以减少逼近误差。
最后是优化网络,使用新的样本来检验网络并移去权重小的ψ节点直到满足性能准则。
2.2.4计算复杂性
小波神经网络训练的计算复杂性介于O(N )和O(N 2)之间,N 为学习样本数。
如果学习样本是均匀分布的,则计算复杂性为O(N );如果学习样本是非均匀分布的,则计算复杂性为O(N 2)。
3. 数学应用案例
小波神经网络是基于小波分析而构成的神经网络。
它充分利用小波变换的良好局部化性质并结合神经网络的自学习功能,因而具有较强的逼近、容错能力,其实现过程也比较简单。
小波神经网络在近十年来应用较广泛,主要应用于以下几个领域。
3.1
Zhang 和 (()ψ=x 神经网 3.2()ψ=x )3.3智能复合材料应变损伤位置的诊断。
他们在实际操作中采用了一些技术处理以减少小波神经网络结构的复杂性,从而加快了训练的速度和提高了识别能力。
并且在同样条件下将这两种小波网络与BP 网络相对比,结果表明B 样条小波神经网络的建模精度和收敛速度明显高于BP 神经网络(图3)。
3.4错误诊断与分析
ZhaoJinsong 等提出了一种新颖的小波神经网络——小波-Sigmoid 基函数神经网络
(wavelet-sigmoidbasicfunctionneuralnetwork,WSBFN ),并将其应用于动态错误诊断中。
他们为了解决小波神经网络的“瓶颈”效应,提出了一种多维非乘积小波函数2/2()cos(1.75)-ψ=x x x e
,并将其和相应的尺度函数一起作为WSBFN 隐层的激励函数,同时将sigmoid 基函数作为WSBFN 输出层的激励函数。
文献中将WSBFN 应用于氢化裂解过程的错误诊断中,并同前人提出的较好的错误诊断方法之——SBFN 网络进行对比。
结果显示,WSBFN 可以用更简单的网络结构而得到更好的诊断效果(WSBFN 训练错误远低于SBFN ,
而且错误诊断准确率达到100%,也优于SBFN)。
Bakshi和Stephanopoulos在多分辨率基础上提出了正交小波神经网络,并将其应用于静态错误
3.5动态建模
现实中,许多问题可以通过动态建模来解决。
虽然采用人工神经网络进行非线性系统建模的研究很多,但是采用小波神经网络进行动态建模的则比较少。
钱峻等应用小波神经网络实现非线性系统模型的在线建立及自校正算法,并将其应用于微生物生长过程的预测建模。
他们在继承前人对小波神经网络的诊断与分析问题中,也取得了非常好的诊断效果。
经网络的结构设计方法的基础上,引入了限定记忆最小二乘法以替代普通的最小二乘法来实现小波
神经网络在线建模和校正算法。
他们将其方法应用于微生物生长过程的预测建模,结果显示该小波神经网络具有很好的预测功能和推广性能(见图4,实线是系统输出,虚线是小波神经网络输出)。
其训练方法亦比用普通的最小二乘法快得多。
并
用来控制3.6
他们
还
4.
采用
31个样本
采用通常
衰减为0。
MATLAB神经网络工具箱中的传递函数没有Morlet小波函数,所以将创建自定义的传输函数。
神经网络工具箱中包含了一个自定义传递函数template_transfer,输入helptemplate_transfer就可以得到有关此函数的帮助信息。
将template_transfer函数作为一个模板,来生成自定义的传递函数。
首先,在MATLAB安装目录下找到template_transfer.m文件。
将原传递函数改为Morlet小波函数表达式:再将函数的导数改为:
将输入输出范围改为:
在主程序中将传递函数设为“template_transfer(本例中未改模板文件名称)。
程序如下:
clc
clear
closeall
%产生训练样本与测试样本
n1=-5:0.1:4.95;
x1=sinc(n1+1)+1;
n2=-4.95:0.1:5;
x2=sinc(n1+1)+1;
xn_train=n1;%训练样本,每一列为一个样本
dn_train=x1;
xn_test=n2;
dn_test=x2;
%设置神经网络参数
%
%
%
%
5.
(1
PPR(ProjectionPursuitRegression)小波网络、小波与联想记忆神经网络的结合、多分辨分析与神经
网络的结合。
关于小波网络的结构,近年来有人提出多层结构小波网络、局域连接型的小波网络。
目前神经网络的研究正由单纯的神经计算转向计算智能,并结合脑科学的研究向生物智能方向发
展,小波网络的研究也应该考虑吸收模糊、分形、混沌、进化计算等交叉学科的研究成果,如小
波网络与模糊逻辑的结合,如小波模糊神经网络、小波包模糊聚类网络;又如考虑小波网络与分
形理论的结合,构造分形小波网络;小波网络算法与遗传算法和进化计算的结合研究等。
(2)小波网络的收敛性、鲁棒性、计算复杂度等研究。
(3)离散正交小波网络构造的复杂性问题以及多维输入出现的“维数灾”问题。
(4)如何把输入信号特征与尺度、平移、旋转等不变性量结合起来输入小波网络训练,以压缩信号特征信息,加速训练过程。
(5)小波基函数的选择。
实际应用不同情况应选取何种小波?小波基应选取相同类型还是不同类型?
选取的数目和标准是什么?如何用理论指导网络中小波的初始化参数?
(6)WNN硬件实现。
神经网络的光学实现是当前的研究热点之一。
值得一提的是Szu和Telfer等人在这方面做了不少工作,构造了一种神经网络“光学耳蜗”(opticalcochlea)模型,另外有学者提
出了一种基于并行神经计算机结构的模型,VLSI超大规模集成电路的实现无疑将进一步促进WNN
的推广和应用。
可以看到,小波神经网络由于把神经网络的自学习特性和小波的局域特性结合起来,具有自适应分辨性和良好的容错性,因此特别适合应用在函数逼近、系统辨识、数据压缩、模式识别等领域。
小波神经网络的理论和应用研究近年来发展很快,具有良好的应用前景。
