高中数学必修四 角度制 三角函数关系及诱导公式讲解
2024年高考数学---三角函数的概念、同角三角函数的基本关系及诱导公式

例1 (2011课标,5,5分)已知角θ的顶点与原点重合,始边与x轴的非负半轴
重合,终边在直线y=2x上,则cos 2θ=( )
A.- 4
5
解析
B.- 3 C. 3 D. 4
5
5
5
解法一:由三角函数定义知,tan
θ=2,则cos
2θ=
cos2θ cos2θ
sin 2θ sin 2θ
1
=1
tan 2θ tan 2θ
(x,y),它与原点的距离为r,则sin α= y ,cos α= x ,tan α= y (x≠0).
r
r
x
2)三角函数值在各象限内的符号
记忆口诀:一全正,二正弦,三正切,四余弦. 二、同角三角函数的基本关系 1.平方关系:sin2α+cos2α=1.
2.商数关系:tan
α=
sin α cos α
基础篇
考点 三角函数的概念、同角三角函数的基本关系及诱导公式 一、三角函数的概念 1.象限角
第一象限角 的集合
第二象限角 的集合
第三象限角 的集合
第四象限角 的集合
|
2kπ
π 2
2kπ,
k
Z
α
|
2k
2
α
2k
,k
Z
α
|
2k
α
2k
3 2
,k
Z
α
|
2k
3 2
α
2k
2 , k
Z
2.终边相同的角 所有与角α终边相同的角,连同角α在内,构成的角的集合是{β|β=k·360+α, k∈Z}或{β|β=α+2kπ,k∈Z}. 3.弧长与扇形面积公式 1)弧长公式:l=|α|r;
高中数学必修四 角度制 三角函数关系及诱导公式讲解
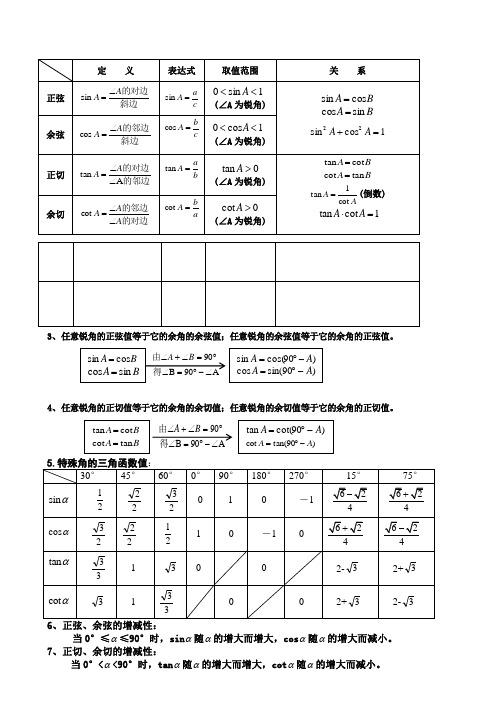
3、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角的正弦值。
4、任意锐角的正切值等于它的余角的余切值;任意锐角的余切值等于它的余角的正切值。
当0°≤α≤90°时,sin α随α的增大而增大,cos α随α的增大而减小。
7、正切、余切的增减性:当0°<α<90°时,tan α随α的增大而增大,cot α随α的增大而减小。
A90B 90∠-︒=∠︒=∠+∠得由B A一、任意角的三角函数的定义: 设α是任意一个角,P (,)x y 是α的终边上的任意一点(异于原点),它与原点的距离是0r =,那么sin ,cos y x r r αα==,()tan ,0y x x α=≠,cot xyα=(0)y ≠,sec r x α=()0x ≠,()csc 0ry yα=≠。
三角函数值只与角的大小有关,而与终边上点P 的位置无关。
设角α的顶点在坐标原点,始边与x 轴非负半轴重合,终边与单位圆相交于点P ,过P 作PM 垂直于x 轴于M ,则点M 是点P 在x 轴上的正射影.由三角函数的定义知,点P 的坐标为(cos_α,sin_α),即P (cos_α,sin_α),其中cos α=OM ,sin α=MP ,单位圆与x 轴的正半轴交于点A ,单位圆在A 点的切线与α的终边或其反向延长线相交于点T ,则tan α=AT .我们把有向线段OM 、MP 、AT 叫做α的余弦线、正弦线、正切线.三角函数线的特征是:正弦线MP “站在x 轴上(起点在x 轴上)”、余弦线OM “躺在x 轴上(起点是原点)”、正切线AT “站在点(1,0)A 处(起点是A )”.有向线段OM 为余弦线有向线段AT 为正切线比较)2,0(∈x ,x sin ,x tan ,x 的大小关系:三角函数线的重要应用是比较三角函数值的大小和解三角不等式。
四、一条规律三角函数值在各象限的符号规律概括为:一全正、二正弦、三正切、四余弦.两个技巧(1)在利用三角函数定义时,点P 可取终边上任一点,如有可能则取终边与单位圆的交点,|OP |=r 一定是正值.(2)在解简单的三角不等式时,利用单位圆及三角函数线是一个小技巧.利用单位圆解三角不等式(组)的一般步骤是: (1)用边界值定出角的终边位置; (2)根据不等式(组)定出角的范围; (3)求交集,找单位圆中公共的部分; (4)写出角的表达式. (1)注意易混概念的区别:第一象限角、锐角、小于90°的角是概念不同的三类角,第一类是象限角,第二类、第三类是区间角.(2)角度制与弧度制可利用180°=π rad 进行互化,在同一个式子中,采用的度量制度必须一致,不可混用.(3)α与2α的终边关系:由“两等分各象限、一二三四确定”.若α是第一象限,则2α是第一、三象限角;若α是第二象限,则2α是第一、三象限角;若α是第三象限角,则2α是第二、四象限;若α是第四象限角,则2α是第二、四象限。
高中数学第一章三角函数1.3三角函数的诱导公式课件新人教A版必修4

sin
2
cos
,
cos
2
sin .
sin
2
cos
,
cos
2
sin
.
cos180 cos
原式=
cos
sin
sin cos
1
练习 利用公式求下列三角函数值:
1 cos 420 cos60 cos 60 1 2
2 sin
7 6
sin
5 6
sin
6
1 2
3sin 1300
4
cos
79 6
cos
5 6
cos
6
3 2
练习
化简 1sin 180 cos sin 180
4 tan 324 32 __ta_n__3_5_2_8_;
化简11scio原ns式52=cs2ions•22sin•2sin •c•osco2s
;
= sin • sin • cos
cos
= sin2
化简
2 cos2
tan 360
sin .
原式=cos2 tan sin
1.思考
给定一个角α (1)终边与角α的终边关于原点对称的角 与α有什么关系?它们的三角函数之间有 什么关系?
公式二
y
P(x,y)
sin(π+α)=-sinα cos(π+α)=-cosα
π +α α
O
x
tan(π+α)=tanα
P(-x,-y)
(2)终边与角α的终边关于x轴对称的角与α 有什么关系?它们的三角函数之间有什么 关系?
y
P(-x,y)
π-α P(x,y)
高中数学必修四三角函数PPT课件

01
02
03
04
第一象限
正弦、余弦、正切均为正。
第二象限
正弦为正、余弦为负、正切为 负。
第三象限
正弦、余弦均为负、正切为正。
第四象限
正弦为负、余弦为正、正切为 负。
02 三角函数诱导公 式与变换
诱导公式及其应用
诱导公式的基本形式
01
通过角度的加减、倍角、半角等变换,得到三角函数的等价表
达式。
诱导公式的推导
02
正切函数的周期为$pi$,即$tan(x + kpi) = tan x$,其中$k in Z$。
三角函数的奇偶性
正弦函数是奇函数, 即$sin(-x) = -sin x$。
正切函数是奇函数, 即$tan(-x) = -tan x$。
余弦函数是偶函数, 即$cos(-x) = cos x$。
三角函数在各象限的符号
三角恒等变换
和差化积、积化和差等公式及应用
三角函数的图像与性质
周期性、奇偶性、单调性等
解三角形
正弦定理、余弦定理及应用
常见题型解析及技巧点拨
01
三角函数求值问题:利 用同角关系式、诱导公 式等求解
02
三角函数的图像与性质 应用:判断单调性、周 期性等
03
三角恒等变换的应用: 证明等式、化简表达式 等
余弦定理及其应用
余弦定理的公式表达 在任意三角形ABC中,有$a^2 = b^2 + c^2 - 2bccos A$,以及相应的其他两个式子。
余弦定理的推导 通过向量的数量积和投影进行推导。
余弦定理的应用 用于求解三角形的边和角,尤其在已知三边或两边及夹角 的情况下。同时,也可用于判断三角形的形状(锐角、直 角或钝角)。
人教版高中数学必修4A版三角函数的诱导公式课件

3.你能求sin750°和sin930°的值吗?
任意角
公式一
0°~360°角
其中锐角的三角函数容易计算.而对于 900~3600范围内的三角函数值,如何转 化为锐角的三角函数值呢?
知识探究(一):π+α的诱导公式
a cos( ) sin 2 c
思考4:若α 为一个任意给定的角,那么 的终边与角α 的终边有什么对称关 2 的终边 y 2 系?
y=x
α 的终边 O
x
思考5:点P1(x,y)关于直线y=x对称 的点P2的坐标如何?
思考6:设角α 的终边与单位圆的交点 为P1(x,y),则 2 的终边与单 位圆的交点为P2(y,x),根据三角函 数的定义,你能获得哪些结论?
x
sin( ) sin 公式三: cos( ) cos t an( ) t an
思考4:利用π -α =π +(-α ),结 合公式二、三,你能得到什么结论?
sin( ) sin 公式四:cos( ) cos tan( ) tan
公式六:
sin(
2
) cos ) sin
cos(
2
思考6:正弦函数与余弦函数互称为余函 数,你能概括一下公式五、六的共同特 点和规律吗? 公式五:
sin(
2
) cos ) sin
cos(
2
sin(
2
) cos ) sin
2kπ+α(k∈Z),π+α,-α,π -α的三角函数与α的三角函数之间 的关系
【精品】高中数学 必修4_三角函数的诱导公式_讲义 知识点讲解+巩固练习(含答案)提高

三角函数的诱导公式【学习目标】1.借助单位圆中的三角函数线导出诱导公式(απαπ±±,2的正弦、余弦、正切);2.掌握并运用诱导公式求三角函数值,化简或证明三角函数式. 【要点梳理】 要点一:诱导公式 诱导公式一:sin(2)sin k απα+=, cos(2)cos k απα+=,tan(2)tan k απα+=,其中k Z ∈诱导公式二:sin()sin αα-=-, cos()cos αα-=,tan()tan αα-=-,其中k Z ∈诱导公式三:sin[((21)]sin k απα++=-, cos[(21)]cos k απα++=-, tan[(21)]tan k απα++=,其中k Z ∈诱导公式四:sin cos 2παα⎛⎫+= ⎪⎝⎭, cos sin 2παα⎛⎫+=- ⎪⎝⎭.sin cos 2παα⎛⎫-= ⎪⎝⎭, cos sin 2παα⎛⎫-= ⎪⎝⎭,其中k Z ∈ 要点诠释:(1)要化的角的形式为α±⋅ο90k (k 为常整数); (2)记忆方法:“奇变偶不变,符号看象限”;(3)必须对一些特殊角的三角函数值熟记,做到“见角知值,见值知角”;(4)sin cos cos 444x x x πππ⎛⎫⎛⎫⎛⎫+=-=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭;cos sin 44x x ππ⎛⎫⎛⎫+=- ⎪ ⎪⎝⎭⎝⎭.要点二:诱导公式的记忆诱导公式一~三可用口诀“函数名不变,符号看象限”记忆,其中“函数名不变”是指等式两边的三角函数同名,“符号”是指等号右边是正号还是负号,“看象限”是指把α看成锐角时原三角函数值的符号.诱导公式四可用口诀“函数名改变,符号看象限”记忆,“函数名改变”是指正弦变余弦,余弦变正弦,为了记忆方便,我们称之为函数名变为原函数的余名三角函数.“符号看象限”同上.因为任意一个角都可以表示为k ·90°+α(|α|<45°)的形式,所以这六组诱导公式也可以统一用“口诀”: “奇变偶不变,符号看象限”,意思是说角90k α⋅±o(k 为常整数)的三角函数值:当k 为奇数时,正弦变余弦,余弦变正弦;当k 为偶数时,函数名不变,然后α的三角函数值前面加上当视α为锐角时原函数值的符号.要点三:三角函数的三类基本题型(1)求值题型:已知一个角的某个三角函数值,求该角的其他三角函数值. ①已知一个角的一个三角函数值及这个角所在象限,此类情况只有一组解;②已知一个角的一个三角函数值但该角所在象限没有给出,解题时首先要根据已知的三角函数值确定这个角所在的象限,然后分不同情况求解;③一个角的某一个三角函数值是用字母给出的,这时一般有两组解.求值时要注意公式的选取,一般思路是“倒、平、倒、商、倒”的顺序很容易求解,但要注意开方时符号的选取.(2)化简题型:化简三角函数式的一般要求是:能求出值的要求出值;函数种类要尽可能少;化简后的式子项数最少,次数最低,尽可能不含根号.(3)证明题型:证明三角恒等式和条件等式的实质是消除式子两端的差异,就是有目标的化简.化简、证明时要注意观察题目特征,灵活、恰当选取公式. 【典型例题】类型一:利用诱导公式求值【高清课堂:三角函数的诱导公式385952 例2】例1.求下列各三角函数的值: (1)252525sincos tan()634πππ++-; (2)()()cos 585tan 300---o o(3)2222132131sin cos 6tan 10cot 243ππππ-+-⎛⎫⎛⎫⎛⎫⎪⎪⎪⎝⎭⎝⎭⎝⎭【思路点拨】利用诱导公式把所求角化为我们熟悉的锐角去求解. 【答案】(1)0(2)2-(3)16【解析】(1)原式=sin(4)cos(8)tan(6)634ππππππ+++-+sincostan634111022πππ=+-=+-=(2)原式=cos(18045)tan(36060)++-o o o o =cos 45tan 60--o o= (3)原式=2222sin (6)cos (5)6tan 10cot (10)243πππππππ+-++-+=2222sin cos 6tan 0cot 243πππ-+-=111023-+-=16【总结升华】(1)对任意角求三角函数值,一般遵循“化负为正,化大为小”的化归方向,但是在具体的转化过程中如何选用诱导公式,方法并不唯一,这就需要同学们去认真体会,适当选择,找出最好的途径,完成求值.(2)运用诱导公式求任意三角函数值的过程的本质是化任意角的三角函数为锐角三角函数的过程,而诱导公式就是这一转化的工具. 举一反三:【变式】(1)10sin 3π⎛⎫- ⎪⎝⎭;(2)31cos 6π;(3)tan (-855°).【答案】(1)2(2)2-(3)1 【解析】(1)1010sin sin 33ππ⎛⎫-=- ⎪⎝⎭44sin 2sin 33πππ⎛⎫=-+=- ⎪⎝⎭sin sin sin 3332ππππ⎛⎫⎛⎫=-+=--==⎪ ⎪⎝⎭⎝⎭.(2)3177coscos 4cos 666ππππ⎛⎫=+= ⎪⎝⎭cos cos 662πππ⎛⎫=+=-=- ⎪⎝⎭. (3)tan(-855°)=tan(-3×360°+225°)=tan225°=tan(180°+45°)=tan45°=1. 例2.已知函数()sin()cos()f x a x b x παπβ=+++,其中a 、b 、α、β都是非零实数,又知f (2009)=-1,求f (2010).【解析】 (2009)sin(2009)cos(2009)f a b παπβ=+++sin(2008)cos(2008)a b ππαππβ=+++++sin()cos()sin cos (sin cos )a b a b a b παπβαβαβ=+++=--=-+.∵f (2009)=-1 ∴sin cos 1a b αβ+=. ∴(2010)sin(2010)cos(2010)f a b παπβ=+++sin cos 1a b αβ=+=.【总结升华】 求得式子sin cos 1a b αβ+=,它是联系已知和未知的纽带.解决问题的实质就是由未知向已知的转化过程,在这个转化过程中一定要抓住关键之处.举一反三:【变式1】 已知1cos(75)3α︒+=,其中α为第三象限角,求cos(105°―α)+sin(α―105°)的值.【答案】13【解析】 ∵cos(105°-α)=cos[180°-(75°+α)]=-cos(75°+α)=13-,sin(α―105°)=―sin[180°-(75°+α)]=-sin(75°+α), ∵α为第三象限角,∴75°+α为第三、四象限角或终边落在y 轴负半轴上.又cos(75°+α)=13>0,∴75°+α为第四象限,∴sin(75)3α︒+===-.∴11cos(105)sin(105)333αα︒-+-︒=-+=.【总结升华】 解答这类给值求值的问题,关键在于找到已知角与待求角之间的相互关系,从而利用诱导公式去沟通两个角之间的三角函数关系,如:75°+α=180°-(105°-α)或105°-α=180°-(75°+α)等.【变式2】已知3sin()2παπβ⎛⎫-=+ ⎪⎝⎭))απβ-=+,且0<α<π,0<β<π,求α和β的值.【解析】由已知得sin αβ=αβ=. 两式平方相加,消去β,得22sin 3cos 2αα+=, ∴21cos 2α=,而0απ<<,∴cos 2α=±,∴4πα=或34πα=.当4πα=时,cos 2β=,又0βπ<<,∴6πβ=;当34πα=时,cos 2β=-,又0βπ<<,∴56βπ=.故4πα=,6πβ=或34πα=,56βπ=. 类型二:利用诱导公式化简 例3.化简(1)sin(180)sin()tan(360)tan(180)cos()cos(180)αααααα-++--+++-+-o o o o ;(2)sin()sin()()sin()cos()n n n Z n n απαπαπαπ++-∈+-.【思路点拨】化简时,要认真观察“角”,显然利用诱导公式,但要注意公式的合理选用.【答案】(1)-1(2)略 【解析】(1)原式sin sin tan tan 1tan cos cos tan αααααααα--==-=-+-;(2)①当2,n k k Z =∈时,原式sin(2)sin(2)2sin(2)cos(2)cos k k k k απαπαπαπα++-==+-.②当21,n k k Z =+∈时,原式sin[(21)]sin[(21)]2sin[(21)]cos[(21)]cos k k k k απαπαπαπα+++-+==-++-+.【总结升华】(1)诱导公式应用的原则是:负化正,大化小,化到锐角就终了; (2)关键抓住题中的整数n 是表示π的整数倍与公式一中的整数k 有区别,所以必须把n 分成奇数和偶数两种类型,分别加以讨论.举一反三: 【变式1】化简 (1)()()()()cos cot 7tan 8sin 2-⋅--⋅--αππαπααπ;(2)()sin2n n Z π∈; (3)()222121tan tan ,22n n n Z παπα++⎛⎫⎛⎫+--∈ ⎪ ⎪⎝⎭⎝⎭(4)sin()cos[(1)]sin[(1)]cos(]k k k k παπαπαπα---+++,()k z ∈.【解析】(1)原式=[]cos()cot()tan(2)sin(2)παπαπαπα----+=cos cot (tan )(sin )αααα-⋅-=3cot α(2)1,(41)sin1,(43)20,(2)n k n n k n k π=+⎧⎪=-=+⎨⎪=⎩ (3)原式=22cot cot αα-=0(4)由(k π+α)+(k π―α)=2k π,[(k ―1)π―α]+[(k+1)π+α]=2k π,得cos[(1)]cos[(1)]cos()k k k παπαπα--=++=-+,sin[(1)]sin()k k παπα++=-+.故原式sin()[cos()]1sin()cos()k k k k παπαπαπα-+-+==--++.【总结升华】 常见的一些关于参数k 的结论: (1)sin()(1)sin ()k k k Z παα+=-∈; (2)cos()(1)cos ()k k k Z παα+=-∈; (3)1sin()(1)sin ()k k k z παα+-=-∈; (4)cos()(1)cos ()k k k Z παα-=-∈. 类型三:利用诱导公式进行证明例4.设8tan 7m πα⎛⎫+= ⎪⎝⎭,求证:1513sin 3cos 37720221sin cos 77m m ππααππαα⎛⎫⎛⎫++- ⎪ ⎪+⎝⎭⎝⎭=+⎛⎫⎛⎫--+ ⎪ ⎪⎝⎭⎝⎭. 【思路点拨】证明此恒等式可采取从“繁”到“简”,从左边到右边的方法.【证明】 证法一:左边88sin 3cos 37788sin 4cos 277πππααπππαππα⎡⎤⎡⎤⎛⎫⎛⎫++++- ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦=⎡⎤⎡⎤⎛⎫⎛⎫-+-++ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦888sin 3cos tan 3777888sin cos tan 1777πππαααπππααα⎛⎫⎛⎫⎛⎫-+-+++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭=-⎛⎫⎛⎫⎛⎫-+-+++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭31m m +=+=右边. ∴等式成立.证法二:由8tan 7m πα⎛⎫+= ⎪⎝⎭,得tan 7m πα⎛⎫+= ⎪⎝⎭,∴左边sin 23cos 277sin 2cos 277πππαπαππππαππα⎡⎤⎡⎤⎛⎫⎛⎫+++++ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦=⎡⎤⎡⎤⎛⎫⎛⎫+-+-+++ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦sin 3cos 77sin cos 77ππααπππαπα⎛⎫⎛⎫+++ ⎪ ⎪⎝⎭⎝⎭=⎡⎤⎡⎤⎛⎫⎛⎫-+-++ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦sin 3cos 77sin cos 77ππααππαα⎛⎫⎛⎫+++ ⎪ ⎪⎝⎭⎝⎭=⎛⎫⎛⎫+++ ⎪ ⎪⎝⎭⎝⎭tan 3371tan 17m m παπα⎛⎫++ ⎪+⎝⎭==+⎛⎫++ ⎪⎝⎭=右边, ∴等式成立. 举一反三:【高清课堂:三角函数的诱导公式385952 例4 】 【变式1】设A 、B 、C 为ABC ∆的三个内角,求证: (1)()sin sin A B C +=;(2)sincos22A B C+=; (3)tan cot 22A B C+=【解析】(1)左边=sin()sin()sin A B c C π+=-==右边,等式得证. (2)左边=sin2A =()sin cos cos 2222B C B C B C ππ-+++⎛⎫⎛⎫=-= ⎪ ⎪⎝⎭⎝⎭=右边,等式得证. (3)左边=tantan cot 2222A B C C π+⎛⎫=-= ⎪⎝⎭=右边,等式得证. 【变式2】求证:232sin cos 1tan(9)12212sin ()tan()1ππθθπθπθπθ⎛⎫⎛⎫-+- ⎪ ⎪++⎝⎭⎝⎭=-++-. 证明:∵左边2232sin sin 12sin (sin )12212sin 12sin πππθθθθθθ⎡⎤⎛⎫⎛⎫+----⋅-- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦==-- 22222sin sin 12cos sin 1212sin cos sin 2sin πθθθθθθθθ⎛⎫--- ⎪--⎝⎭==-+-222(sin cos )sin cos sin cos sin cos θθθθθθθθ++==--,右边tan(9)1tan 1sin cos tan()1tan 1sin cos πθθθθπθθθθ++++===+---,∴左边=右边,故原式得证. 类型四:诱导公式的综合应用例5.已知3sin(3)cos(2)sin 2()cos()sin()f παππαααπαπα⎛⎫---+⎪⎝⎭=----.(1)化简()f α;(2)若α是第三象限的角,且31cos 25πα⎛⎫-= ⎪⎝⎭,求()f α的值. (3)若313πα=-,求()f α的值. 【解析】 (1)(sin )cos (cos )()cos (cos )sin f ααααααα-⋅⋅-==--.(2)∵3cos sin 2παα⎛⎫-=- ⎪⎝⎭, ∴1sin 5α=-,∴cos α==()f α=. (3)31315cos cos 62333f ππππ⎛⎫⎛⎫⎛⎫-=--=--⨯+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭51cos cos 332ππ=-=-=-. 【总结升华】这是一个与函数相结合的问题,解决此类问题时,可先用诱导公式化简变形,将三角函数的角度统一后再用同角三角函数关系式,这样可避免公式交错使用时导致的混乱.举一反三: 【变式1】已知α、β均为锐角,cos()sin()αβαβ+=-,若()sin cos 44f ππααα⎛⎫⎛⎫=++- ⎪ ⎪⎝⎭⎝⎭,求2f πα⎛⎫- ⎪⎝⎭的值. 【解析】由cos()sin()αβαβ+=-得cos()cos ()2παβαβ⎡⎤+=--⎢⎥⎣⎦,又α、β均为锐角.则()2παβαβ+=--,即4πα=.于是,sin cos 0222f ππα⎛⎫-=+= ⎪⎝⎭.【巩固练习】1.sin585°的值为( )A.2-B.2 C.2- D.2A .13 B . 13- C. D3.已知(cos )cos3f x x =,则(sin 30)f ︒的值等于( )A .―1B .1C .12D .0)A .sin2-cos2B .cos2-sin2C .±(sin2-cos2)D .sin2+cos25.若sin cos 2sin cos αααα+=-,则3sin(5)sin 2παπα⎛⎫-⋅-⎪⎝⎭等于( ) A .34 B .310 C .310± D .310-6.在△ABC 中,若)sin()sin(C B A C B A +-=-+,则△ABC 必是( )A .等腰三角形B .直角三角形C .等腰或直角三角形D .等腰直角三角形7.已知3sin()cos(2)tan 2()cos()f ππαπαααπα⎛⎫---+ ⎪⎝⎭=--,则313f π⎛⎫-⎪⎝⎭的值为( ) A .12 B .12- C.2 D.2-8.已知cos 63πα⎛⎫-= ⎪⎝⎭,则25sin cos 66ππαα⎛⎫⎛⎫--+ ⎪⎪⎝⎭⎝⎭的值是( )A .23+B .23+-C .23- D.23-+9.计算:)425tan(325cos 625sinπππ-++= .10.若()θ+ο75cos 31=,θ为第三象限角,则()()θθ++--οο435sin 255cos 的值是 . 11.已知1sin()43πα-=,则cos()4πα+=__________. 12.(1)cos1°+cos2°+cos3°+…+cos180°的值为________;(2)cos 21°+cos 22°+cos 23°+…+cos 289°的值为________。
三角函数定义及诱导公式和变换公式
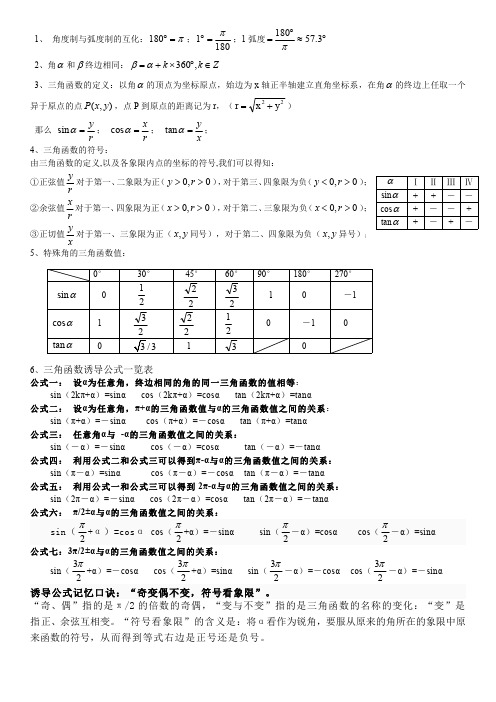
b c 2bc cos A cos A b c a
2 2
2 2
2
2 bc
2
b c a 2 ac cos B cos B c a b 2 ca
2 2 2 2
2
c a b 2 ab cos C cos C a b c 2 ab
tan(α+β)=
tan tan 1 tan tan
tan(α-β)=
tanα - tanβ 1 tan tan
(2)二倍角公式: sin2α=2sinα·cosα cos2α= cos - sin =2 cos -1=1-2 sin
2 2 2 2
cos 2
指正、余弦互相变。“符号看象限”的含义是:将α看作为锐角,要服从原来的角所在的象限中原 来函数的符号,从而得到等式右边是正号还是负号。
7、三角恒等变换公式:
(1)两角和与差的三角函数: sin(α+β)=sinα·cosβ+cosα·sinβ sin(α-β)=sinα·cosβ-cosα·sinβ cos(α+β)=cosα·cosβ-sinα·sinβ cos(α-β)=cosα·cosβ+sinα·sinβ
x 2 y2 )
y x y ; cos ; tan ; r r x
4、三角函数的符号: 由三角函数的定义,以及各象限内点的坐标的符号,我们可以得知:
y 对于第一、 二象限为正 ( y 0, r 0 ) , 对于第三、 四象限为负 ( y 0, r 0 ) ; r sin x ②余弦值 对于第一、 四象限为正 ( x 0, r 0 ) , 对于第二、 三象限为负 ( x 0, r 0 ) ; cos r tan y ③正切值 对于第一、三象限为正( x, y 同号),对于第二、四象限为负( x, y 异号) x
1.3 三角函数的诱导公式 课件(共19张PPT)高中数学人教A版必修四

2k (k Z)、 、 的三角函数值,等于
的同名函数值,前面加上一个把 看成锐角时原函
数值的符号。
14
理论迁移
例1 求下列各三角函数的值:
(1)cos225
(2)sin 11
3
(3)sin(-16 )
3
(4)cos(-2040 )
15
利用诱导公式一~四,可以把任意角的三角函数转化为锐角三角函数,一般可按下面 步骤进行:
任意负角的 用公式一 任意正角的 三角函数 或公式三 三角函数
用公式一
锐角的三角 用公式二 0~2π的角
函数
或公式四 的三角函数
这是一种化归与转化的数学思想.
16
课堂小结: 1.小结使用诱导公式化简任意角的三 角函数为锐角的步骤.
2.体会数形结合、对称、化归的思想. 3.“学会”学习的习惯.
17
作业布置:
公式二:
sin( ) sin cos( ) cos tan( ) tan
10
问题4:公式中的角 仅是锐角 吗?
11
知识探究(二)
对于任意给定的一个角α,-α的终边与α的终边
有什么关系?
那么它们之间的三角函
数值有什么关系?
y
α的终边
P(x,y)
公式三:
o
Q(x,-y)
x
sin( ) sin
1
(一)回顾旧知
问题1: (1)我们是怎样利用单位圆定义任意角的三角函数? (2) 终边相同的角的三角函数之间有什么关系?
2
温故而知新
1、任意角的三角函数的定义
sin y
y
α的终边
cos x tan y (x 0)
x
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角的正弦值。
4、任意锐角的正切值等于它的余角的余切值;任意锐角的余切值等于它的余角的正切值。
当0°≤α≤90°时,sin α随α的增大而增大,cos α随α的增大而减小。
A90B 90∠-︒=∠︒=∠+∠得由B A7、正切、余切的增减性:一、任意角的三角函数的定义: 设α是任意一个角,P (,)x y 是α的终边上的任意一点(异于原点),它与原点的距离是0r =>,那么sin ,cos y x r r αα==,()tan ,0y x x α=≠,cot x y α=(0)y ≠,sec rxα=()0x ≠,()csc 0ry yα=≠。
三角函数值只与角的大小有关,而与终边上点P 的位置无关。
设角α的顶点在坐标原点,始边与x 轴非负半轴重合,终边与单位圆相交于点P ,过P 作PM 垂直于x 轴于M ,则点M 是点P 在x 轴上的正射影.由三角函数的定义知,点P 的坐标为(cos_α,sin_α),即P (cos_α,sin_α),其中cos α=OM ,sin α=MP ,单位圆与x 轴的正半轴交于点A ,单位圆在A 点的切线与α的终边或其反向延长线相交于点T ,则tan α=AT .我们把有向线段OM 、MP 、AT 叫做α的余弦线、正弦线、正切线.三角函数线的特征是:正弦线MP “站在x 轴上(起点在x 轴上)”、余弦线OM “躺在x 轴上(起点是原点)”、正切线AT “站在点(1,0)A 处(起点是A )”.有向线段OM 为余弦线有向线段AT 为正切线比较)2,0(∈x ,x sin ,x tan ,x 的大小关系:三角函数线的重要应用是比较三角函数值的大小和解三角不等式。
四、一条规律三角函数值在各象限的符号规律概括为:一全正、二正弦、三正切、四余弦.两个技巧(1)在利用三角函数定义时,点P 可取终边上任一点,如有可能则取终边与单位圆的交点,|OP |=r 一定是正值.(2)在解简单的三角不等式时,利用单位圆及三角函数线是一个小技巧. 利用单位圆解三角不等式(组)的一般步骤是: (1)用边界值定出角的终边位置; (2)根据不等式(组)定出角的范围; (3)求交集,找单位圆中公共的部分; (4)写出角的表达式.(1)注意易混概念的区别:第一象限角、锐角、小于90°的角是概念不同的三类角,第一类是象限角,第二类、第三类是区间角.(2)角度制与弧度制可利用180°=π rad 进行互化,在同一个式子中,采用的度量制度必须一致,不可混用.(3)α与2α的终边关系:由“两等分各象限、一二三四确定”.若α是第一象限,则2α是第一、三象限角;若α是第二象限,则2α是第一、三象限角;若α是第三象限角,则2α是第二、四象限;若α是第四象限角,则2α是第二、四象限。
五. 同角三角函数的基本关系式:(1)平方关系:222222sin cos 1,1tan sec ,1cot csc αααααα+=+=+= (2)倒数关系:sin αcsc α=1,cos αsec α=1,tan αcot α=1,(3)商数关系:sin cos tan ,cot αααα==同角三角函数的基本关系式理解(1)平方关系:1cos sin 22=+αα用于相同角正弦和余弦之间的互相转化,开方时要注意由角的象限确定正负,必要时需要讨论。
在运用平方关系解题时,要根据已知角的范围和三角函数的取值,尽可能地压缩角的范围,以便进行定号 (2)αααtan cos sin =用于弦和切互化(3)巧用勾股数求三角函数值可提高解题速度:(3,4,5);(6,8,10);(5,12,13);(8,15,17);(4)求角的方法:先确定角的范围,再求出关于此角的某一个三角函数(要注意选择,其标准有二:一是此三角函数在角的范围内具有单调性;二是根据条件易求出此三角函数值)最后确定角的大小。
六、三角函数诱导公式(1)(2kπα+)的本质是:奇变偶不变(对k 而言,指k 取奇数或偶数),符号看象限(看原函数,同时可把α看成是锐角). 诱导公式的应用是求任意角的三角函数值,其一般步骤:①负角变正角,再写成2k π+α,02απ≤<;②转化为锐角三角函数(“去负——脱周——化锐”) (2)根据角α所在的象限,得出π2~0间的角——如果适合已知条件的角在第二限;则它是1απ-;如果在第三或第四象限,则它是1απ+或12απ-;2K π±α,-α,2π±α,π±α,23π±α的三角函数 奇变偶不变,符号看象限 α的三角函数作用:“去负——脱周——化锐”,是对三角函数式进行角变换的基本思路.即利用三角函数的奇偶性将负角的三角函数变为正角的三角函数——去负;利用三角函数的周期性将任意角的三角函数化为角度在区间[0o ,360o )或[0o ,180o )内的三角函数——脱周;利用诱导公式将上述三角函数化为锐角三角函数——化锐.记忆口诀:2k παα±把的三角函数化为的三角函数,概括为:奇变偶不变,符号看象限。
()()1sin 2sin k παα+=, ()cos 2cos k παα+=, ()()tan 2tan k k παα+=∈Z . ()()2sin sin παα+=-, ()cos cos παα+=-, ()t a n t a n παα+=. ()()4sin sin παα-=, ()c o s c o s παα-=-, ()t a n t a n παα-=-. ()()3sin sin αα-=-, ()c o s c o s αα-=, ()t a n t an αα-=-. 口诀:函数名称不变,符号看象限.()5sin cos 2παα⎛⎫-=⎪⎝⎭, c o s s i n 2παα⎛⎫-= ⎪⎝⎭. ()6sin cos 2παα⎛⎫+=⎪⎝⎭, c o s s i n 2παα⎛⎫+=- ⎪⎝⎭.:①已知某角的一个三角函数值,求它的其余各三角函数值。
注意:用平方关系,有两个结果,一般可通过已知角所在的象限加以取舍,或分象限加以讨论。
②求任意角的三角函数值。
步骤:③已知三角函数值求角:注意:所得的解不是唯一的,而是有无数多个. 步骤:①确定角α所在的象限;②如函数值为正,先求出对应的锐角1α;如函数值为负,先求出与其绝对值对应的锐角1α;③根据角α所在的象限,得出π2~0间的角——如果适合已知条件的角在第二限,则它是1απ-;如果在第三或第四象限,则它是1απ+或12απ-;④如果要求适合条件的所有角,再利用终边相同的角的表达式写出适合条件的所有角的集合。
公式二、 四、五、 六、七、 八、九考向一 角的集合表示及象限角的判定【例1】►(1)写出终边在直线y =3x 上的角的集合;(2)若角θ的终边与6π7角的终边相同,求在[0,2π)内终边与θ3角的终边相同的角; (3)已知角α是第二象限角,试确定2α、α2所在的象限. [审题视点] 利用终边相同的角进行表示及判断. 解 (1)在(0,π)内终边在直线y =3x 上的角是π3, ∴终边在直线y =3x 上的角的集合为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫α⎪⎪⎪α=π3+k π,k ∈Z. (2)∵θ=6π7+2k π(k ∈Z ),∴θ3=2π7+2k π3(k ∈Z ). 依题意0≤2π7+2k π3<2π⇒-37≤k <187,k ∈Z .∴k =0,1,2,即在[0,2π)内终边与θ3相同的角为2π7,20π21,34π21. (3)∵α是第二象限角,∴k ·360°+90°<α<k ·360°+180°,k ∈Z . ∴2k ·360°+180°<2α<2k ·360°+360°,k ∈Z .∴2α是第三、第四象限角或角的终边在y 轴非正半轴上. ∵k ·180°+45°<α2<k ·180°+90°,k ∈Z ,当k =2m (m ∈Z )时,m ·360°+45°<α2<m ·360°+90°; 当k =2m +1(m ∈Z )时,m ·360°+225°<α2<m ·360°+270°; ∴α2为第一或第三象限角.(1)相等的角终边一定相同,但终边相同的角却不一定相等,终边相同的角有无数个,它们之间相差360°的整数倍.(2)角的集合的表示形式不是唯一的,如:终边在y 轴非正半轴上的角的集合可以表示为⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x =2k π-π2,k ∈Z ,也可以表示为⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x =2k π+3π2,k ∈Z .(3)α与2α的终边关系:由“两等分各象限、一二三四”确定.如若α是第二象限角,则2α是第_____象限角【训练1】 角α与角β的终边互为反向延长线,则( ). A .α=-β B .α=180°+β C .α=k ·360°+β(k ∈Z ) D .α=k ·360°±180°+β(k ∈Z )解析 对于角α与角β的终边互为反向延长线,则α-β=k ·360°±180°(k ∈Z ). ∴α=k ·360°±180°+β(k ∈Z ). 答案 D考向二 三角函数的定义【例2】►已知角θ的终边经过点P (-3,m )(m ≠0)且sin θ=24 m ,试判断角θ所在的象限,并求cos θ和tan θ的值.[审题视点] 根据三角函数定义求m ,再求cos θ和tan θ. 解 由题意得,r =3+m 2,∴m 3+m 2=24m ,∵m ≠0,∴m =±5,故角θ是第二或第三象限角.当m =5时,r =22,点P 的坐标为(-3,5),角θ是第二象限角, ∴cos θ=x r =-322=-64,tan θ=y x =5-3=-153.当m =-5时,r =22,点P 的坐标为(-3,-5),角θ是第三象限角. ∴cos θ=x r =-322=-64,tan =y x =-5-3=153.任意角的三角函数值仅与角α的终边位置有关,而与角α终边上点P 的位置无关.若角α已经给出,则无论点P 选择在α终边上的什么位置,角α的三角函数值都是确定的. 【训练2】 (2011·课标全国)已知角θ的顶点与原点重合,始边与x 轴的非负半轴重合,终边在直线y =2x 上,则cos 2θ=( ). A .-45 B .-35 C.35 D.45解析 取终边上一点(a,2a ),a ≠0,根据任意角的三角函数定义,可得cos θ=±55,故cos 2θ=2cos 2θ-1=-35. 答案 B考向三 弧度制的应用【例3】►已知半径为10的圆O 中,弦AB 的长为10. (1)求弦AB 所对的圆心角α的大小;(2)求α所在的扇形的弧长l 及弧所在的弓形的面积S .[审题视点] (1)由已知条件可得△AOB 是等边三角形,可得圆心角α的值;(2)利用弧长公式可求得弧长,再利用扇形面积公式可得扇形面积,从而可求弓形的面积. 解 (1)由⊙O 的半径r =10=AB ,知△AOB 是等边三角形, ∴α=∠AOB =60°=π3. (2)由(1)可知α=π3,r =10, ∴弧长l =α·r =π3×10=10π3, ∴S 扇形=12lr =12×10π3×10=50π3,而S △AOB =12·AB ·1032=12×10×1032=5032,∴S =S 扇形-S △AOB =50⎝ ⎛⎭⎪⎫π3-32.弧度制下的扇形的弧长与面积公式,比角度制下的扇形的弧长与面积公式要简洁得多,用起来也方便得多.因此,我们要熟练地掌握弧度制下扇形的弧长与面积公式. 【训练3】 已知扇形周长为40,当它的半径和圆心角取何值时,才使扇形面积最大? 解 设圆心角是θ,半径是r ,则2r +rθ=40,S =12lr =12r (40-2r )=r (20-r )≤⎝ ⎛⎭⎪⎫2022=100.当且仅当r =20-r ,即r =10时,S max =100.∴当r =10,θ=2时,扇形面积最大,即半径为10,圆心角为2弧度时,扇形面积最大.考向四 三角函数线及其应用【例4】►在单位圆中画出适合下列条件的角α的终边的范围.并由此写出角α的集合: (1)sin α≥32; (2)cos α≤-12.[审题视点] 作出满足sin α=32,cos α=-12的角的终边,然后根据已知条件确定角α终边的范围. 解(1)作直线y =32交单位圆于A 、B 两点,连接OA 、OB ,则OA 与OB 围成的区域(图中阴影部分)即为角α的终边的范围,故满足条件的角α的集合为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫α⎪⎪⎪2k π+π3≤α≤2k π+23π,k ∈Z.(2)作直线x =-12交单位圆于C 、D 两点,连接OC 、OD ,则OC 与OD 围成的区域(图中阴影部分)即为角α终边的范围,故满足条件的角α的集合为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫α⎪⎪⎪2k π+23π≤α≤2k π+43π,k ∈Z .利用单位圆解三角不等式(组)的一般步骤是:(1)用边界值定出角的终边位置; (2)根据不等式(组)定出角的范围;(3)求交集,找单位圆中公共的部分;(4)写出角的表达式.【训练4】 求下列函数的定义域:(1)y =2cos x -1; (2)y =lg(3-4sin 2x ).解 (1)∵2cos x -1≥0,∴cos x ≥12.由三角函数线画出x 满足条件的终边范围(如图阴影部分所示).∴定义域为⎣⎢⎡⎦⎥⎤2k π-π3,2k π+π3(k ∈Z ). (2)∵3-4sin 2x >0,∴sin 2x <34, ∴-32<sin x <32.利用三角函数线画出x 满足条件的终边范围(如图阴影部分所示),∴定义域为⎝ ⎛⎭⎪⎫k π-π3,k π+π3(k ∈Z ).规范解答7——如何利用三角函数的定义求三角函数值【问题研究】 三角函数的定义:设α是任意角,其终边上任一点P (不与原点重合)的坐标为(x ,y ),它到原点的距离是r (r =x 2+y 2>0),则sin α=y r 、cos α=x r 、tan α=y x分别是α的正弦、余弦、正切,它们都是以角为自变量,以比值为函数值的函数,这样的函数称为三角函数,这里x ,y 的符号由α终边所在象限确定,r 的符号始终为正,应用定义法解题时,要注意符号,防止出现错误.三角函数的定义在解决问题中应用广泛,并且有时可以简化解题过程.【解决方案】 利用三角函数的定义求三角函数值时,首先要根据定义正确地求得x ,y ,r 的值;然后对于含参数问题要注意分类讨论.【示例】►(本题满分12分)(2011·龙岩月考)已知角α终边经过点P(x,-2)(x≠0),且cosα=36x,求sin α、tan α的值.只要确定了r的值即可确定角α经过的点P的坐标,即确定角α所在的象限,并可以根据三角函数的定义求出所要求的值.[解答示范] ∵P(x,-2)(x≠0),∴P到原点的距离r=x2+2,(2分)又cos α=36x,∴cos α=xx2+2=36x,∵x≠0,∴x=±10,∴r=2 3.(6分)当x=10时,P点坐标为(10,-2),由三角函数定义,有sin α=-66,tan α=-55;(9分)当x=-10时,P点坐标为(-10,-2),∴sin α=-66,tan α=55.(12分)当角的终边经过的点不固定时,需要进行分类讨论,特别是当角的终边在过坐标原点的一条直线上时,在根据三角函数定义求解三角函数值时,就要把这条直线看做两条射线,分别求解,实际上这时求的是两个角的三角函数值,这两个角相差2kπ+π(k∈Z),当求出了一种情况后也可以根据诱导公式求另一种情况.【试一试】已知角α的终边在直线3x+4y=0上,求sin α+cos α+45tan α.[尝试解答]取直线3x+4y=0上的点P1(4,-3),则|OP1|=5,则sin α=-35,cos α=45,tan α=-3 4,故sin α+cos α+45tan α=-35+45+45×⎝⎛⎭⎪⎫-34=-25;取直线3x +4y =0上的点P 2(-4,3),则sin α=35,cos α=-45,tan α=-34.故sin α+cos α+45tan α=35-45+45×⎝ ⎛⎭⎪⎫-34=-45. 综上,sin α+cos α+45tan α的值为-25或-45.。
