动力学中的典型模型.pdf
生化反应动力学中的反应动力学模型

生化反应动力学中的反应动力学模型生化反应动力学是物理化学在生物系统中的应用,是研究反应中生物分子在时间和位置上的变化规律和机理的科学。
在探究生物分子的反应动力学规律时,反应动力学模型的建立是一个重要的环节。
本文将介绍几种生化反应动力学模型以及它们在实际应用中的作用。
1. 麦克米兰-明盒尔基本方程麦克米兰-明盒尔基本方程是生化反应动力学中最常用的方程之一,常用于描述酶催化反应。
它的形式如下:V0 = Vmax[S] / (Km + [S])其中,V0为反应速率, Vmax为最大反应速率, [S]为底物浓度, K为酶底物复合物的解离常数。
这个方程的重点是描述底物浓度与反应速率之间的关系。
2. 布里格斯-霍夫曼方程布里格斯-霍夫曼方程是描述蛋白质和底物之间的互作用的方程,常用于描述酶催化反应。
它的形式如下:v = (Vmax [S]) / (Km + [S])其中,v为反应速率, Vmax为最大反应速率, [S]为底物浓度, K为底物与酶复合物的解离常数。
布里格斯-霍夫曼方程主要描述了酶催化反应的特定性以及底物和酶的互作用。
3. 分布式动力学模型生物系统中的许多反应过程都是非线性的。
非线性反应需要使用更复杂的数学模型来描述。
分布式动力学模型是用于描述非线性生化反应动力学的一种模型。
这个模型可以使用偏微分方程和有限元方法等技术来数值求解。
4. 连离型动力学模型连离型动力学模型是用于描述生物反应网络中离散化对象之间相互作用的一种模型。
例如,每个细胞可以视为一个对象,细胞间存在一定的耦合关系。
这种模型可以通过离散化来描述生物物质之间的相互作用,不同离散化方案可以用来描述不同的生物反应网络。
总结反应动力学模型是研究生化反应动力学的重要工具。
不同的模型适用于不同的反应系统,具有不同的优缺点。
在进行反应动力学模型选取时,需要根据具体研究对象的特性和目的来选择最合适的模型。
同时,在模型的应用过程中,需要根据实验数据进行模型调整,以不断提高模型的准确性和预测能力。
统考版高考物理总复习 专题三 动力学中的“传送带”和“滑块—滑板”模型

系为xB=xA+L
物块A带动长为L的木板B,物块恰好不
从木板上掉下的临界条件是物块恰好滑
到木板右端时二者速度相等,则位移关
系为xB+L=xA
例2. [2021·全国乙卷,21](多选)水平地面上有一质量为m1的长木板,
木板的左端上有一质量为m2的物块,如图(a)所示.用水平向右的拉力
专题三
动力学中的“传送带”和“滑块—滑板”模型
关键能力·分层突破
关键能力·分层突破
模型一
“传送带”模型
1.模型特点
传送带在运动过程中,会涉及很多的力,是传送带模型难点的原因,
例如物体与传送带之间是否存在摩擦力,是滑动摩擦力还是静摩擦力
等;该模型还涉及物体相对地面的运动以及相对传送带的运动等;该
F作用在物块上,F随时间t的变化关系如图(b)所示,其中F1、F2分别
为t1 、t2 时刻F的大小.木板的加速度a1 随时间t的变化关系如图(c)所
示.已知木板与地面间的动摩擦因数为μ1,物块与木板间的动摩擦因
数为μ2.假设最大静摩擦力均与相应的滑动摩擦力相等,重力加速度大
小为g.则(
)
A.F1=μ1m1g
央.空香皂盒的质量为m=20 g,香皂及香皂盒的总质量为M=100 g,香皂盒与
传送带之间的动摩擦因数为μ=0.4,风洞区域的宽度为L=0.6 m,风可以对香皂
盒产生水平方向上与传送带速度垂直的恒定作用力F=0.24 N,假设最大静摩擦
力等于滑动摩擦力,香皂盒可看作质点,取重力加速度g=10 2 ,试求:
跟进训练
1.如图所示,物块M在静止的足够长的传送带上以速度v0匀速下滑时,传送带突
然启动,方向如图中箭头所示,在此传送带的速度由0逐渐增加到2v0后匀速运动
动力学中三类典型物理模型的分析

高考级横一^^教学参考第50卷第丨期2021年1月动力学中三类典型物理模型的分析康俊李明(河南省淮滨高级中学河南信阳464400)文章编号:l〇〇2-218X(2021)01-0038-05《普通高中物理课程标准(2020年修订)》课程 目标中明确提出学生要通过学习具有建构模型的 意识和能力;学业质量中进人高等院校相关专业学 习应达到的水平要求是4,能将实际问题中的对象 和过程转换成所学的物理模型,能对综合性物理问 题进行分析和推理,获得结论并作出解释。
《中国 高考评价体系》明确说明试题以生活实践问题情境 和学习探索问题情境为载体进行测量与评价。
通过对近年高考物理试题的研究发现,动力学 问题是每年高考必考内容之一。
“等时圆模型”“传 送带模型”“板块模型”是动力学中三类典型过程模 型,也是常考的问题情境。
本文选取这三类模型进 行深入分析,以期能在高考备考中提供一些参考。
_、等时圆模型1.真题统计(如表1)表1近十年高考物理“等时圆模型”相关试题统计年份题号命题角度2018浙江省11月选考卷13题光滑轨道2.模型分析如图1、2所示,质点沿竖直面内圆环上的任意 一条光滑弦从上端由静止滑到底端,受力分析可知 加速度a=0,位移:r=2J?sin 0,由匀加速直线运动规律:r=|加2,得出下滑时间i= 2 即沿竖直直径自由下落的时间。
图3是图1和图2的组合,不难证明有相同的结论。
图 1 图2中图分类号:G632.479文献标识码:B3.模型特征特征1质点从竖直面内的圆环上沿不同的光滑弦上端由静止开始滑到环的最低点,或从最高点由静止滑到各光滑弦下端,所用时间都相等,如图1、2所示。
特征2两个竖直面内的圆环相切且两环的竖直直径均过切点,质点沿不同的光滑弦上端由静止开始经切点滑到下端所用时间相等,如图3所示。
4.思维模型此类问题的思维方法如图4所示:图45.典题示例例1(2018年浙江省11月选考卷13题)如图5所示为某一游戏的局部简化示意图。
(完整版)系统动力学模型案例分析
系统动力学模型介绍1.系统动力学的思想、方法系统动力学对实际系统的构模和模拟是从系统的结构和功能两方面同时进行的。
系统的结构是指系统所包含的各单元以及各单元之间的相互作用与相互关系。
而系统的功能是指系统中各单元本身及各单元之间相互作用的秩序、结构和功能,分别表征了系统的组织和系统的行为,它们是相对独立的,又可以在—定条件下互相转化。
所以在系统模拟时既要考虑到系统结构方面的要素又要考虑到系统功能方面的因素,才能比较准确地反映出实际系统的基本规律。
系统动力学方法从构造系统最基本的微观结构入手构造系统模型。
其中不仅要从功能方面考察模型的行为特性与实际系统中测量到的系统变量的各数据、图表的吻合程度,而且还要从结构方面考察模型中各单元相互联系和相互作用关系与实际系统结构的一致程度。
模拟过程中所需的系统功能方面的信息,可以通过收集,分析系统的历史数据资料来获得,是属定量方面的信息,而所需的系统结构方面的信息则依赖于模型构造者对实际系统运动机制的认识和理解程度,其中也包含着大量的实际工作经验,是属定性方面的信息。
因此,系统动力学对系统的结构和功能同时模拟的方法,实质上就是充分利用了实际系统定性和定量两方面的信息,并将它们有机地融合在一起,合理有效地构造出能较好地反映实际系统的模型。
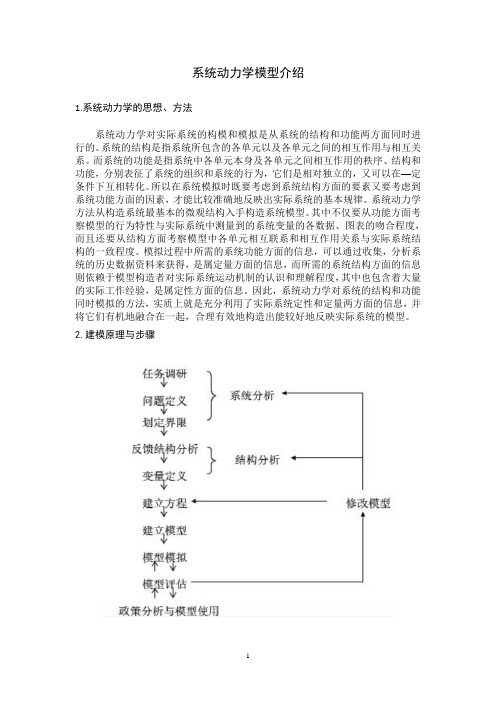
2.建模原理与步骤(1)建模原理用系统动力学方法进行建模最根本的指导思想就是系统动力学的系统观和方法论。
系统动力学认为系统具有整体性、相关性、等级性和相似性。
系统内部的反馈结构和机制决定了系统的行为特性,任何复杂的大系统都可以由多个系统最基本的信息反馈回路按某种方式联结而成。
系统动力学模型的系统目标就是针对实际应用情况,从变化和发展的角度去解决系统问题。
系统动力学构模和模拟的一个最主要的特点,就是实现结构和功能的双模拟,因此系统分解与系统综合原则的正确贯彻必须贯穿于系统构模、模拟与测试的整个过程中。
与其它模型一样,系统动力学模型也只是实际系统某些本质特征的简化和代表,而不是原原本本地翻译或复制。
系统动力学原理-精选.pdf

5.1 系统动力学理论5.1.1 系统动力学的概念系统动力学(简称SD—System Dynamics),是由美国麻省理工学院(MIT)的福瑞斯特(J.W.Forrester)教授创造的,一门以控制论、信息论、决策论等有关理论为理论基础,以计算机仿真技术为手段,定量研究非线性、高阶次、多重反馈复杂系统的学科。
它也是一门认识系统问题并解决系统问题的综合交叉学科[1-3]。
从系统方法论来说:系统动力学是结构的方法、功能的方法和历史的方法的统一。
它基于系统论,吸收了控制论、信息论的精髓,是一门综合自然科学和社会科学的横向学科。
系统动力学对问题的理解,是基于系统行为与内在机制间的相互紧密的依赖关系,并且透过数学模型的建立与操作的过程而获得的,逐步发掘出产生变化形态的因、果关系,系统动力学称之为结构。
系统动力学模型不但能够将系统论中的因果逻辑关系与控制论中的反馈原理相结合,还能够从区域系统内部和结构入手,针对系统问题采用非线性约束,动态跟踪其变化情况,实时反馈调整系统参数及结构,寻求最完善的系统行为模式,建立最优化的模拟方案。
5.1.2 系统动力学的特点系统动力学是一门基于系统内部变量的因果关系,通过建模仿真方法,全面动态研究系统问题的学科,它具有如下特点[4-8]:(1)系统动力学能够研究工业、农业、经济、社会、生态等多学科系统问题。
系统动力学模型能够明确反映系统内部、外部因素间的相互关系。
随着调整系统中的控制因素,可以实时观测系统行为的变化趋势。
它通过将研究对象划分为若干子系统,并且建立各个子系统之间的因果关系网络,建立整体与各组成元素相协调的机制,强调宏观与微观相结合、实时调整结构参数,多方面、多角度、综合性地研究系统问题。
(2)系统动力学模型是一种因果关系机理性模型,它强调系统与环境相互联系、相互作用;它的行为模式与特性主要由系统内部的动态结构和反馈机制所决定,不受外界因素干扰。
系统中所包含的变量是随时间变化的,因此运用该模型可以模拟长期性和周期性系统问题。
反应动力学中的动力学模型研究

反应动力学中的动力学模型研究反应动力学是研究反应速率与反应物浓度、温度等因素之间关系的一门学科。
在化学、生物化学、环境科学等领域都有着重要的应用。
建立适当的动力学模型,可以帮助我们更深入地了解反应动力学的本质,从而指导实验设计和工程应用。
本文将简要介绍反应动力学中的动力学模型研究。
一、反应动力学常见模型1. 放射性衰变模型放射性衰变是一种自然衰变过程,其速率服从指数函数形式,即:$$N_t = N_0 e^{-\lambda t}$$其中,$N_0$为起始核数,$\lambda$为衰变常数,$t$为经过的时间,$N_t$为剩余核数。
该模型的应用包括放射性核素的溯源、放射性药物的代谢等。
2. 单分子反应模型单分子反应是指固定时间内,某反应物分子被转化为产物的反应。
其速率服从一阶反应关系,即:$$-\frac{d[N]}{dt}=k[N]$$其中,$[N]$为反应物浓度,$k$为速率常数。
该模型的应用包括催化反应、酶催化反应等。
3. 二级反应模型二级反应是指两个反应物之间发生的反应,其速率可表示为:$$-\frac{d[A]}{dt}=k[A][B]$$或者:$$-\frac{d[B]}{dt}=k[A][B]$$其中,$[A]$和$[B]$分别为反应物A和B的浓度,$k$为速率常数。
该模型的应用包括溶解动力学、生物工程等。
二、反应动力学模型的建立建立反应动力学模型需要考虑反应机理、反应速率方程等多个因素。
以下是一个建立氧气和乙烯反应动力学模型的示例。
反应机理:氧气和乙烯反应生成环氧乙烷:$$C_2H_4+O_2\longrightarrow C_2H_4O$$反应速率方程:$$r=k[C_2H_4]^\alpha[O_2]^\beta$$其中,$r$为反应速率,$k$为速率常数,$\alpha$和$\beta$为反应级数。
根据反应机理,当反应物浓度相同时,反应速率与温度相关,速率常数$k$可表示为:$$k=Ae^{-E_a/RT}$$其中,$A$为预指数因子,$E_a$为活化能,$R$为气体常数,$T$为温度。
在空气动力学中常见的数学模型

在空气动力学中常见的数学模型,指的是以数学为基础的航空与宇宙领域的模拟和研究方法。
许多航空航天并不是物理实验室中进行,在工程实践中广泛使用数学建模的方法来处理问题。
因此,了解空气动力学中常见的数学模型可以帮助我们更加深入地了解飞行器的原理,让我们一起来探讨这些数学模型。
1. 翼型理论模型翼型模型是空气动力学中使用最广泛的模型之一,它描述了机翼在空气中产生升力和阻力的机理。
该模型认为机翼的剖面形状(翼型)是决定升阻比的最重要因素。
翼型理论模型通过复杂的数学公式和计算方法描述了机翼的气动特性,如气动中心、升阻比、升力系数、阻力系数等;这些特性是设计飞机和评估飞机性能的基础。
2. 流体动力学模型流体动力学模型是一种数学模型,它描述了空气和其他流体在机体表面的流动和受力情况。
该模型广泛应用于研究气动力学问题,如风洞实验、飞行全场模拟、气动外形优化等方面。
流体动力学模型通常基于伯努利和纳维-斯托克斯方程来构建,在此基础上通过适当的近似和简化来减少计算复杂度。
3. 无人机模型无人机模型是研究无人机性能和进行遥控指挥的重要工具。
该模型包括两个方面:飞行动力学和控制系统建模。
飞行动力学模型,基于气动学和力学定律,用数学方法描述无人机在空气和其他流体中的运动。
控制系统模型,描述了实际控制器和信号处理器内的控制算法,用于驱动电机和执行器驱动飞行器。
4. 航线模型航线模型是一种数学模型,它涉及航空公司的航线和飞行计划的规划和管理。
这个模型将考虑诸如性能、航空燃油成本、天气、飞行规则和安全性等因素,并为航班提供最佳飞行方案。
使用航线模型进行预测分析实际飞行环境,以获得最佳的航线和安排,从而让航班正常执行,提高航空交通的有效性。
总之,空气动力学中常见的数学模型给予我们一个完整的了解飞行器的原理并对飞行器进行模拟和优化相关处理。
当然,在空气动力学中的数学模型并不仅限于以上四种,许多其他模型在空气动力学的研究和航空工程中也起着重要的作用。
专题2动力学中的典型“模型”

专题2动力学中的典型“模型”模型一等时圆模型1 •模型特征(1) 质点从竖直圆环上沿不同的光滑弦上端由静止开始滑到环的最低点所用时间相等,如图1甲所示。
(2) 质点从竖直圆环上最高点沿不同的光滑弦由静止开始滑到下端所用时间相等,如图乙所示。
(3) 两个竖直圆环相切且两环的竖直直径均过切点,质点沿不同的光滑弦上端由静止开始滑到下端所用时间相等,如图丙所示2•思维模板替犁一(L 参*相交詢* F!诃w 滝轨縮条件 ②质虑由■弄话从訖遵的一端滑到号一端设世 —(I 下瑞祸娈:吏点肖JD 钠豪伍点'皤上堪祈交;交点为国対R 尚巨作等—①赴耶点罪監直雯肘風~2 W 某拉垄为強乍国心在竖点线上前旬U h①轨道城点都話・同上.廣点黑动时间相尊—k 程奉点在国內的牝趙.质点讶动时间訶.靖” 点在K 恰的就道.雨点运話时间瓷“ _护I °II :》I W -mtK.2 V» —af- ' '卜潸苦制【例1】如图2所示,ab 、cd 是竖直平面内两根固定的光滑细杆,位 都套 着一个小滑环(图中未画出),将两滑环同时从a 、c 处由静止释放,用11 >12分别 表示 滑环从a 到b 、从c 到d 所用的时间,贝U(屮于同一周上,b点为圆周的最低点,c点为圆周的最高点,若每根杆上解析设光滑细杆与竖直方向的夹角为a 圆周的直径为D ,根据牛顿第二定律 得滑环的加速度为a 二^m°S 壬geos a,光滑细杆的长度为x 二Deos a,贝U 根据x鑒07: "/2D,可见时间t 与a 无尖,故有ti 二t2,因答案A务雄训练快” ■1 •如图3所示,位于竖直平面内的圆周与水平面相切于M 点,与竖直墙相切于A 点,竖直墙上另一点B 与M 的连线和水平面的夹角为60。
° C 是圆环轨道的圆心。
已知在同 一时刻,甲、乙两球分别从A 、B 两点由静止开始沿光滑倾斜直轨道运 答案C动到M 点。
