过程控制的计算方法
过程控制工程设计—节流装置、调节阀与差压液位计的计算

.
4
节流装置流速方程 式中
.
5
节流装置流量方程(实际中)
式中,c为考虑实际因素引入的一个系数,它 是管道尺寸、孔板取压方法和雷诺数的函数。
.
6
第一节 节流装置的计算
一、节流装置计算的基本公式及取压方法
1.节流装置原理和基本公式
Qh 0.01252d2
p
1
[m3/h](工作状态)
G h0.01252d2 p1 [kg/h](工作状态)
.
7
第一节 节流装置的计算
2.常用取压方法
IV III II I I II III IV
I~I为角接取压法 II~II为1’’法兰取压法 III~III所示即为理论取压法 IV~IV即为径距取压法
.
8
第一节 节流装置的计算
二、计算中有关参数的确定 P191;1.6;2;2.5; 3.2;4;5;6.3;8乘以10n,n为任 意正整数。
.
10
v 已知角接取压孔板 ,取压方式为角接取压 v 被测介质为水,工况条件如下: v 常用流量(t/h) 45 v 管道内径(mm) 100 v 粘度(Pa.s) 0.000797 v 最大差压(kPa) 90.7029 v 开孔直径比(β) 0.50219 v 求™ 压:力损失(kPa)
™ 雷诺数(ReD)
应力成正比, 其粘度保持恒定与 剪切速率无关。
.
15
非牛顿型流体
不服从牛顿摩擦定律的流体。一般粘性较 大,且随着流动速度而变化。例如石灰乳、泥 浆、污水和许多高分子溶液等。
.
16
第二节 调节阀流通能力的计算
一、调节阀C值计算公式 见P197
Q AF P1 P2
统计过程控制中Z值的计算与分析

统计过程控制中Z 值的计算与分析Z 值是统计过程控制SPC(Statistical Process Control)的常用统计量之一,本文将就Z 的计算与分析做一简单介绍。
一、Z 值的计算公式Z 值是某一特征值与均值之间标准偏差的数量,其是一个相对量。
Z 值的计算公式为:()σµ−=x z 其中:x-某一特征值;μ-总体均值;σ-总体的标准差在实际中都是通过抽样来估计总体,则Z 值的计算公式变化为:()sx x z −=其中:x-某一特征值;x -样本均值;s-样本的标准差如果一个过程仅有单侧公差时,则:σµσµLSL Z USL Z LSL USL −=−=其中:USL-上规范线;LSL-下规范线;μ-总体均值;σ-总体的标准差二、Z 的计算与分析如果有一个学生在中考的数学和英语成绩分别为112和108,他的成绩好吗?是数学成绩还是英语成绩相对更好一些?通过Z 值的计算就可以看出该学生的成绩距离均值的程度,也可以看出来哪个成绩相对更好一些。
如果已知全市数学成绩的均值为108,标准差为21,英语成绩的均值为97,标准差为18,那么:σσ0.6118111897-1080.1921421108-112======英语数学Z Z 将Z 值转化为百分数常用以下几种方式:(1)查正态分布-Z 值表;(2)通过Excel 的公式“=Normsdist(x)”计算;(3)利用一些软件,例如:minitab、Z 值-百分数计算器。
通过上述三种方法里的任意一种,我们可知:该学生数学成绩对应的百分数为57.53%,英语成绩对应的百分数为72.91%,通过下图可以看到该学生的数学和英语成绩在总体中的位置,同时也可以看出英语的成绩相对要好于数学成绩。
数学英语在实际生活中有一些过程仅有规范上线或规范下线。
例如:某产品的安装时间规定不允许超过120分钟,经抽样10个样本的安装时间分别为:100、99、101、125、100、123、100、123、96、90、98、116,则其均值为:104.8,标准差为:12.03,则:σ26.103.122.1503.128.104120==−=USL Z如果样本具有随机性和代表性,从上图可以看出,在实际的安装过程中89.6%的产品安装时间小于120分钟,同时10.4%的产品安装时间会超过120分钟,这样的过程显然是不能满足要求的,经过改进后又随机抽取了10个样本,其分别为:60、75、99、88、65、72、75、72、87、65,则其均值为:78.5,标准差为:12.14,则:σ42.314.125.4114.125.78120==−=USL Z由上面的计算和图示对比,可以清楚的看到改进的效果非常的明显,改进后仅有0.03%的产品安装时间会超过120分钟。
统计过程控制中Z值的计算与分析

统计过程控制中Z值的计算与分析统计过程控制中的Z值计算与分析是一种常见的统计方法,用于评估和控制一个过程的性能。
Z值计算的基础是正态分布的理论,通过计算样本的平均值与标准偏差来确定过程的性能是否达到标准要求。
下面是关于Z值计算与分析的详细介绍。
在统计过程控制中,假设一个过程的输出符合正态分布。
通过收集样本数据并计算其平均值和标准偏差,可以确定过程的性能。
Z值(也称为标准分数)是指一个观测值与平均值之间的差异,以标准差的单位来度量。
Z值的计算公式如下:Z=(X-μ)/σ其中,Z表示标准分数,X表示观测值,μ表示平均值,σ表示标准偏差。
通过计算每个样本的Z值,并将其与一个预先设置的阈值进行比较,可以确定过程是否正常运行。
如果Z值超过了阈值范围,就意味着过程存在异常或者超出了预定的控制限,需要采取相应的措施来调整过程。
Z值的分析可以提供一些重要的信息。
首先,Z值可以告诉我们一个过程的中心性能。
通常情况下,一个过程的Z值应接近于0,表示过程的中心值与目标值相近。
如果Z值显著偏离于0,就表明过程存在偏差或者漂移,需要进行调整。
其次,Z值还可以告诉我们一个过程的稳定性。
如果Z值较小且稳定,就表示过程运行稳定,处于控制状态;如果Z值较大或者不稳定,就表示过程存在变化或者波动,需要进行进一步的调查和改进。
Z值的分析还可以帮助我们识别过程中的特殊原因变异和常因变异。
特殊原因变异是指由于一些特殊因素引起的可辨识的异常值,例如机器故障、操作错误等;常因变异是指由于正常因素引起的正常波动,例如材料批次变化、环境温度变化等。
通过分析Z值,我们可以确定出现异常值的具体原因,并采取相应的措施来修正。
在进行Z值分析时,需要注意以下几个方面。
首先,样本大小要足够大,以确保结果的准确性和可靠性。
通常情况下,样本大小应大于30,但具体的要求可以根据具体情况来确定。
其次,选择合适的阈值来判断过程是否正常运行。
阈值的选择应综合考虑过程的要求、可靠性和成本等因素。
过程控制-计算
系统数学模型为: G ( s )
K e s Ts 1
' 根据 Z-N 公式: KK c 0 .9 (
T
) 1 .0 1 .12 K c' ...
TI* 3 .33 ( )1 .0 TI* 3 .33 .... (s) T T
因为等效调节器由调节器、变送器和调节阀组成,因此:
,根据
K e j Tj 1
由式(相角条件): arctg (T cr ) cr cr 120.74 由式(幅角条件):
120.74 120.74 cr 0.0596 180 180
K cr K (T cr ) 2 1
y * (t1 )
10 0 220 14.4
20 0.2 240 15.1
40 0.8 260 15.8
60 2 280 16.4
80 3.6 300 17
100 5.4 320 17.4
120 7.4 340 17.6
140 9.3 360 17.8
160 11 380 17.95
180 12.6 400 18.1
0180741201807412074120???????????????????????tcrcrcrcrarctg由式幅角条件
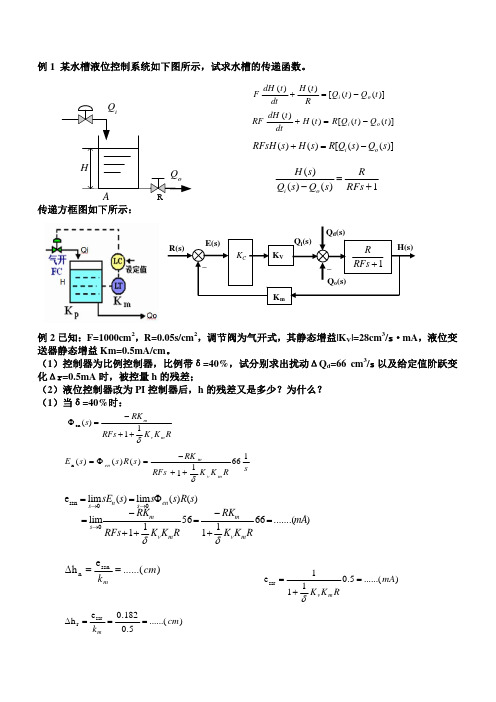
例 1 某水槽液位控制系统如下图所示,试求水槽的传递函数。
F dH ( t ) H ( t ) [ Q i ( t ) Q o ( t )] dt R dH (t ) H ( t ) R [ Q i (t ) Q o ( t )] dt
K c' K c* K m K v
20 4 200 0 100 0 调节阀的转换系数: K m (% / mA) 20 4
过程控制的计算方法

1/9 一.预防与检测检验一容忍浪费;预防一避免浪费检验--通过质量控制检查最终产品并剔除不符事规范的产品。
在管理部门则经常靠检查或重新检查工作来找出错误,在这种情况下都是使用检测的方法,这种方法是一种浪费,因为它允许将时间和材料投入到生产不一定有用的产品和服务中。
预防一第一步就可以避免生产无用的输出,从而避免浪费。
“第一次就把事情做好”。
仅有这样口号是不够的,所以要理解统计过程各个要项。
要研究产生变量本身的特性---过程。
二.基本概念过程:是指共同作用以产生输出的供方、生产者、人、设备、输入材料、方法和环境以及使用输出的顾客之集合。
过程控制系统:过程的性能取决于供方与顾客这间的沟通,过程设计和实施的方法,以及运作和管理方式。
.a. 有关过程性能的信息一与性能最有用的信息是以研究过程本身以及其内在的变化中得到的信息过程特性,这是我们关注的重点。
b. 对过程采取措施c. 对输出采取措施变差:过程的单个输出之间不可避免的差别。
产生变差的普通原因:随时间的推移具有稳定的且可重复的分步过程中的许多变差的原因、我们称之为“处于统计控制状态”。
产生变差的特殊原因:不是始终作用于过程的变差的原因,出现时造成过程分步的改变。
除非所有的特殊原因都被查找出来,并且采取了措施,否则他们将以不可预测的方式来影响过程的输出,随时间的发展,过程的输出将不稳定。
正态分步:正态分步又称概率分步。
如果影响某一变量的因素会很多,而每一个因素都不起决定性作用,且这此影响是可以叠加的,那么此随机变量被认为是从正态分步的。
局部措施:通常用于消除变差的特殊原因通常有与过程直接相关的人员实施通常可纠正大约15%的过程问题系统采取措施:通常用来消除变差的普通原因几乎总是要求管理措施,以便纠正大约可纠正85%的过程问题.三.控制图一过程控制的工具过程特性,是我们关注的重点,我们通过研究过程本身的特性,来识别生产变差的原因,是特殊原因还是普通原因,从而决定采取局部措施还是系统措施。
14过程控制方法

14 过程控制方法
14.3 控制图(controlБайду номын сангаасchart)法
——控制图类型(计件) ➢ 不合格率控制图 ——设计过程:P168 ➢ 不合格品数控制图 ——设计过程:P169
质量管理学
14 过程控制方法
14.3 控制图(control chart)法
——控制图类型(计点) ➢ 缺陷数控制图 ——设计过程:P171 ➢ 单位缺陷数控制图 ——设计过程:P171-172
质量管理学
部波动范围。显然,B越小,过程能力就越强。
质量管理学
14 过程控制方法
14.2 过程能力和过程能力指数
■ 过程能力指数
➢ 定义:表示过程能力满足过程质量标准要求程度的量值。 过程质量要求的范围(公差)和过程能力的比值
➢ 公式:
√ 无偏时双向公差过程能力指数计算 √ 过程有偏时双向公差过程能力指数计算 √ 单项公差过程能力指数计算 √ 过程能力指数的判断与处置(P158)
质量管理学
14 过程控制方法
14.3 控制图(control chart)法
——控制图应贯彻预防原则 “查出异因,采取措施,加以消除,不 再出现、纳入标准”
质量管理学
14 过程控制方法
14.3 控制图(control chart)法
——控制图的观察分析 ➢ 工序处于稳定状态下的判断 ➢ 工序处于不稳定状态下的判断
14 过程控制方法
1. 工序质量控制的基本概念
■ 工序质量
➢ 产品可分割的工序——产品质量特性(尺寸、强 度等)
➢ 产品不可分割的工序——工艺质量特性(温度、 浓度等)
➢ 属于制造质量的范畴 ➢ 优劣判断:符合性质量
SPC计算公式

SPC统计过程控制
(SPC统计量介绍)
北京钢冶联信息科技有限公司
P. 1
常用统计量
1. Mean:(平均值) 2. Max:(最大值) 3. Min:(最小值) 4. Range:(Max- Min最大跨距) 5. StdDev标准差 6. Cp:(过程能力指数) 7. Cr:(过程能力比值 ) 8. k:(偏移系数 ) 9. Cpu:(上限过程能力指数 ) 10. Cpl:(下限过程能力指数 ) 11. Cpk:(过程能力指数 ) 12. Cpm:(目标能力指数) 13. Zu(Cap) :(规格上限SIGMA水平) 14. Zl(Cap) :(规格下限SIGMA水平) 15. Fpu(Cap): (超出规格上限机率)
P. 12
计算公式
16、Fpl(Cap):(超出规格下限机率) Fpl(Cap) 1- Normsdist(3*Cpl)
Fpl(Cap)表示产品检验 结果超出规格下限的概率
规格上限 USL
0.30 0.25 0.20 0.15 0.10 0.05 0.00
6.0 7.0 8.0 9.0 10.0 11.0 12.0 13.0 14.0 15.0 16.0 17.0
K=(40.2-40))/((40.5-39.5)/2)=0.4
k M ,其中T USL LSL, M USL LSL
T2
2
规格中心 M
产品均值μ
0.30
0.25
0.20
规格宽度
0.15
T
0.10
0.05
0.00 6.0 7.0 8.0 9.0 10.0 11.0 12.0 13.0 14.0 15.0 16.0 17.0
过程控制1

1.衰减比和衰减率是衡量一个振荡过程的衰减程度的指标。
衰减比=Y1/Y3=n 衰减率=Y1-Y3/Y32.最大动态偏差是指设定值阶跃响应中,过渡过程开始后第一个波峰超过其新稳态值的幅度。
2最大动态偏差占被调量稳态变化的幅度的百分数称为超调量。
最大动态偏差和超调量是系统动态准确性的衡量指标。
3.残余偏差是指过渡过程结束后,被调量新的稳态值与新设定值之间的差值,它是控制系统稳态准确性的衡量指标。
4.调节时间是从过渡过程开始到结束所需的时间。
过渡过程的振荡频率也可以作为衡量控制系统快速性的一个指标。
5.从外部流入对象内部的物质或能量称为流入量,从对象内部流出的流量称为流出量。
在控制系统方块图中,无论是流入量或流出量,它们作为引起被调量变化的原因都应看作是被控对象的输入量。
6.工业过程动态特性的特点:1.对象的动态特性是不振荡的2.对象动态特性有迟延3被控对象本身是稳定的或中性稳定的4被控对象往往具有非线性特性。
7.当调节阀开度改变致使原来的物质或能量平衡关系遭到破坏后,随着被调量的变化不平衡量愈来愈小,因而被调量能够自动地稳定在新的水平上。
这种特性称为自平衡,有这种特性的被控对象称为自衡过程。
8.机理法建模:根据生产过程中实际发生的变化机理,写出各种有关的平衡方程,运动方程,物性参数方程和某些设备的特性方程等,从中获得所需的数学模型。
首要条件是机理已经必须为人们充分掌握并且可以比较确切的加以数学描述9.测试法一般只用于建立输入输出模型。
那些内部机理尚未被人们充分了解的过程,也是难以用测试法建立其动态数学模型的。
11.所谓正作用方式是指调节器的输出信号U随着被调量Y的增大而增大,此时称整个调节器的增益为“+”。
确定正作用方式之后使其为负反馈控制。
12.比例带就代表使调节阀开度改变100%即从全关到全开时所需要的被调量的变化范围。
13.比例调节特点:速度快,有差调节;14积分调节特点:速度慢,无差,稳定性比Pi调节差,增大积分速度会降低控制系统的稳定程度;15.微分调节特点;U提前与e提前控制,不能单独使用,对高频干扰敏感,总是力图抑制被调量的振荡,它有提高系统稳定性的作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
/
/
/
/
0.08
0.14
0.18
0.22
D2
1.13
1.69
2.06
2.33
2.53
2.7
2.85
2.97
3.08
A2
1.88
1.02
0.73
0.58
0.48
0.42
0.37
0.34
0.31
b.在控制图上作出平均值和极差控制限的控制线。
100
UCLX
90
80
70
60
50
40
30
20
10
LCLX
00
3.通过测量部分数据就可以获得一定的信息,比较全部检查才知道其质量状况,所需的成本更低。
4.由于在作出可靠的商定之前,只需要检查少量的产品,因此可以缩短零件生产和采取措施之间间隔。
5.用计量型数据,可以分析一个过程的性能,可以量化所作的改进,利于采取措施进行持续改善。
五. -R管制图
A.收集数据
测量方法必须保証始终生产准确和精密的结果:
不精密
精密
不准确
▒
准确
。。
▒
a.
b.周期性抽样,如:每15分钟抽样一次,每班抽样两次。
c.子组大小确定,如收集20组子组数据。(抽样数:20组*5件=100件)
d.建立控制图及原始数据( 图在R图的下上方,R图下面再接一数据栏,同时包括记录数据的和、均值(X)、极差(R)及日期或时间)。
page 3/9
e.计算每个子组的均值( )和极差(R),并画在控制图上,它们分别反应了整个过程的均值和其变量。
每个子组,计算:
=(X1+X2+X3+…Xn)/nR=X最大值-X最小值
f.选择控制图的刻度
g.将均值和极差画到控制图上
B.计算控制限
a.计算控制限
显示仅存在变差的普通原因时子组的均值和极差的变化和范围。(X-S控制图考虑变差产生的普通原因和特殊原因)
“第一次就把事情做好”。仅有这样口号是不够的,所以要理解统计过程各个要项。要研究产生变量本身的特性---过程。
二.基本概念
过程:是指共同作用以产生输出的供方、生产者、人、设备、输入材料、方法和环境以及使用输出的顾客之集合。
过程控制系统:过程的性能取决于供方与顾客这间的沟通,过程设计和实施的方法,以及运作和管理方式。.
3.分析及改进
当特殊原因被消除之后,过程在统计控制状态下运行,可继续使用控制图作为监控工具,可计算过程能力。--CPK&PPK
4.计量型数据控制图
计量值数据的控制图广泛应用的原因:
1.大多过程和其输出具有可测量性,所以其潜在应用很广泛。
2.量化的值(例如:直径12.3mm)比简单的OK\NG包含的信息要更多。
100
UCLR
90
80
70
60
50
40
30
20
10
LCLR
00
日期
时间
8/1
8
10
12
2
8/2
8
10
12
2
8/3
8
10
12
2
8/4
8
10
12
2
8/5
8
10
12
2
读数
1
2
3
4
5
SUM
page 4/9
C.过程控制解释
a.超出控制限的点
超出一个或多个点超出任何一个控制限
该点处于失控状态的主要証据。因为只有在普通原因引起变差的情况下超出控制限的会很少,我们便假设该超出的是由特殊原因造成的。因此,超出控制点应立即进行分析,找出存在特殊原因的信号,给任何超出控制的点作标记,以便根据原因实际开始的时间进行调查,采取纠正措施。
依据作业标准执行作业的变化
操作人员的注意力未集中
…
…
正态分步:正态分步又称概率分步。如果影响某一变量的因素会很多,而每一个因素都不起决定性作用,且这此影响是可以叠加的,那么此随机变量被认为是从正态分步的。
局部措施:
通常用于消除变差的特殊原因
通常有与过程直接相关的人员实施
通常可纠正大约15%的过程问题
这些数据可以是一个加工零件的尺寸的实测值,一批在制品的缺陷数,可以是不同时间段产线不良率…
2.控制
利用数据计算控制限,将他们画在图上作为分析的指南。
控制线并不是规范限值或目标,而是基于过程的自然变化性和抽样计划。----控制界限&规格界限
然后,将数据与控制限相比较来确定变差是否稳定而且是否仅是普通原因引起的。(后面讲到控制图识别再详细说明)如果明显存在变差的特殊原因,应对过程进行研究从而进一步确定影响它的是什么。在采取措施后(一般是局部措施)后,再进一步收集数据,如有必要则重新计算控制限。
产生变差的特殊原因:不是始终作用于过程的变差的原因,出现时造成过程分步的改变。除非所有的特殊原因都被查找出来,并且采取了措施,否则他们将以不可预测的方式来影响过程的输出,随时间的发展,过程的输出将不稳定。
普通原因
特殊原因
天气的变化
机器突发变化
环境的变化
未依据作业标准执行作业
物料在一定范围内的变化
使用规格外的原材料
统计过程控制的计算page 1/9
1.预防与检测
检验—容忍浪费;预防—避免浪费
检验--通过质量控制检查最终产品并剔除不符事规范的产品。在管理部门则经常靠检查或重新检查工作来找出错误,在这种情况下都是使用检测的方法,这种方法是一种浪费,因为它允许将时间和材料投入到生产不一定有用的产品和服务中。
预防—第一步就可以避免生产无用的输出,从而避免浪费。
=Σ 各组/子组数 =ΣR各组/子组数
UCL = &#
式中D4、D3、A2为常数,它们随样本容量的不同而不同,下表是样本容量不同的一个常数表。
n
2
3
4
5
6
7
8
9
10
D4
3.27
2.57
2.28
2.11
2.00
1.92
1.86
1.82
1.78
D3
a.有关过程性能的信息—与性能最有用的信息是以研究过程本身以及其内在的变化中得到的信息过程特性,这是我们关注的重点。
b.对过程采取措施
c.对输出采取措施
变差:过程的单个输出之间不可避免的差别。
产生变差的普通原因:随时间的推移具有稳定的且可重复的分步过程中的许多变差的原因、我们称之为“处于统计控制状态”。
b.控制限之内的图形式趋势
当出现非随机性的图形时,尽管所有的极差都在控制限内,也表明出现这种图形或趋势的时期内过程失控或过程分布宽度发生变化。应该纠正不利条件。
系统采取措施:
通常用来消除变差的普通原因
几乎总是要求管理措施,以便纠正
大约可纠正85%的过程问题.
3.控制图—过程控制的工具
过程特性,是我们关注的重点,我们通过研究过程本身的特性,来识别生产变差的原因,是特殊原因还是普通原因,从而决定采取局部措施还是系统措施。
page 2/9
1.收集
被研究的特性(过程或产品)的数据收集后将之转化成可以画在控制图上的形式。
