(完整版)专题:含参二元一次方程组
八年级数学专题 二元一次方程组重难点(参数问题、实际应用问题)(北师大版)
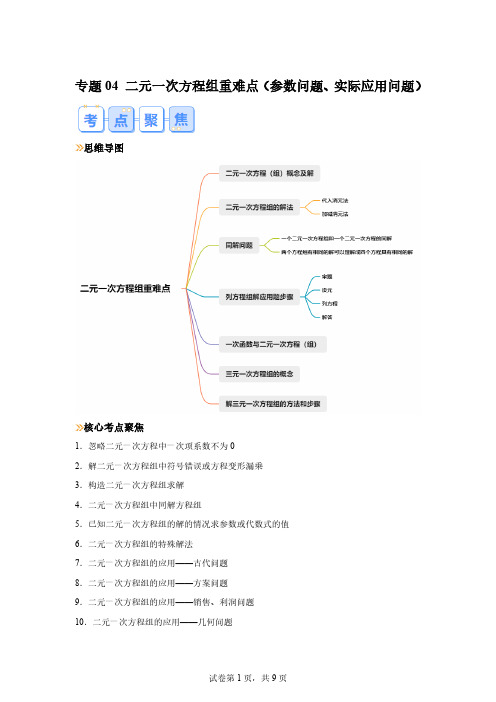
ì3x - 2 y = -1
ìx =1 ìm + 5 =1
ìm = -4
íî3x + 2 y = 7
,解得
í î
y
=
2
,即
íîn
+
3
=
2
,解得
íîn
=
-1
.
(1)学以致用,模仿乐乐同学的“整体换元”的方法,解方程组
ì ïï í ï ïî
x x
+ 3 + 3
y y
+ -
x x
5 5
y y
= =
4 .
-2
试卷第 2 页,共 9 页
义,否则,若把 y=ax+b 代入变形的原方程,必然得到一个恒等式; ③用代入法求出一个未知数的值后,再求另一个未知数时,一般代入变形后得到的方
程比较简单.
2.加减消元法
把方程组的两个方程(或先作适当变形)相加或相减,消去其中一个未知数,从而把
解二元一次方程组转化为解一元一次方程.这种解方程组的方法叫做加减消元法,简
联立成方程组,求出未知数的值,然后代入含有参数的方程即可求出参数的值.
四、列方程组解应用题步骤
1.列方程组解应用题是把“未知”转化为“已知”的重要方法,它的关键是把已知量和未 知量联系起来,找出题目中的相等关系.一般来说,有几个未知量就必须列出几个方
程,所列方程必须满足:
①方程两边表示的是同类量;②同类量的单位要统一;③方程两边的数值要相等.
y
=
与 41
íî2
x
+
3
y
=
-7
有相同的解,求
a,b
的值.
第02讲_含参的二元一次方程组(教师版)A4-精品文档资料整理

高斯教育学科教师辅导讲义学员姓名:年级:辅导科目:学科教师:五块石1 上课时间授课主题第02讲_含参的二元一次方程组含参的二元一次方程组一.解含参数的二元一次方程组对于关于x、y的二元一次方程组:111222a xb y ca xb y c+=⎧⎨+=⎩(1a、1b、2a、2b为已知数,且1a与1b、2a与2b、1a与2a、1b与2b都不能同时为0).把含参的二元一次方程组化为含参一元一次方程,再分类讨论,结论如下:1.当1122a ba b≠时,方程组有唯一解,为2112122112211221b c b cxa b a ba c a cya b a b-⎧=⎪-⎪⎨-⎪=⎪-⎩;2.111222a b ca b c==时,原方程组有无数多组解;知识图谱错题回顾知识精讲3. 当111222a b c a b c =≠时,原方程组无解.一.考点:解含参的二元一次方程组,含参二元一次方程组参数与解的关系,含参二元一次方程组的同解问题.二.重难点:1.方程的个数少于未知数的个数时,方程组有无数多解; 2.含参二元一次方程组的整数解; 3.方程组中的参数的取值范围.三.易错点:参数为给定明确取值范围时,不要忘了分类讨论.题模一:解含参数的二元一次方程组例1.1.1关于x 、y 的方程组3x y m x my n -=⎧⎨+=⎩的解是11x y =⎧⎨=⎩,则|m ﹣n|的值是( )A .5B .3C .2D .1【答案】D【解析】∵方程组3x y m x my n -=⎧⎨+=⎩的解是11x y =⎧⎨=⎩,∴311mm n -=⎧⎨+=⎩,解得23m n =⎧⎨=⎩,所以,|m ﹣n|=|2﹣3|=1.例1.1.2关于x 、y 的方程组43235x y k x y -=⎧⎨+=⎩的解x 与y 的值相等,则k 等于________【答案】1【解析】解方程组,得56109k x k y +⎧=⎪⎪⎨-⎪=⎪⎩,根据题意,得51069k k +-=,解得1k = 三点剖析题模精讲例 1.1.3小明在解关于x 、y 的二元一次方程组x y 33x y 1+=⎧⎨-⊕=⎩ⓧ时得到了正确结果x ny 1=⎧⎨=⎩后来发现“ⓧ”、“⊕”处被墨水污损了,请你帮他找出“ⓧ”、“⊕”处的值分别是____A .ⓧ=1,⊕=1B .ⓧ=2,⊕=1C .ⓧ=1,⊕=2D .ⓧ=2,⊕=2 【答案】B 【解析】将x n y 1=⎧⎨=⎩代入方程组,两方程相加,得x=⊕=1;将x=⊕=1代入方程x+ⓧy=3中,得 1+ⓧ=3,ⓧ=2. 故选B .例1.1.4求关于x 、y 的方程组2113x y ax y +=⎧⎨-=⎩的解.【答案】当12a =-时,原方程组无解;当12a ≠-时,原方程组的解为172111321x a a y a ⎧=⎪⎪+⎨-⎪=⎪+⎩.【解析】当121a =-,即当12a =-,由于12111132=≠--,此时方程组无解;当121a ≠-,即当12a ≠-时,原方程组有唯一解,按照消元法求出x 、y 的值即可. 题模二:参数与解的关系例1.2.1由方程组213x m y m ⎧+=⎨-=⎩可得出x 与y 的关系是( )A .2x+y=4B .2x-y=4C .2x+y=-4D .2x-y=-4【答案】A 【解析】213x m y m ⎧+=⎨-=⎩①②, 把⊕代入⊕得2x+y -3=1,即2x+y=4. 故选:A .例1.2.2m 取何整数值时,关于x 、y 的方程组2441x my x y +=⎧⎨+=⎩的解x 和y 都是整数?【答案】9,7,10,6m =.【解析】把m 作为已知数,解方程组得81828x m y m ⎧=-⎪⎪-⎨⎪=⎪-⎩.∵x 是整数,∴8m -取8的约数1±,2±,4±,8±. ∵y 是整数,∴8m -取2的约数±1,±2.取它们的公共部分,81,2m -=±±,解得9,7,10,6m =. 经检验9,7,10,6m =时,方程组的解都是整数. 题模三:同解问题例1.3.1关于x ,y 的二元一次方程组59x y kx y k +=⎧⎨-=⎩的解也是二元一次方程2x+3y=-6的解,则k 的值是( ) A .-34 B .34C .43D .-43【答案】A 【解析】解方程组 59x y kx y k +=⎧⎨-=⎩得:x=7k ,y=-2k ,把x ,y 代入二元一次方程2x+3y=-6, 得:2×7k+3×(-2k )=-6, 解得:k=-34, 故选A .例1.3.2已知关于x 、y 的二元一次方程(2)(2)520a x a y a -+++-=,当a 每取一个值时,就有一个方程,而这些方程有一个公共解,试求出这个公共解. 【答案】方程的公共解为31x y =⎧⎨=-⎩【解析】方法一:特殊值法,取定a 的两个值,得到关于x 、y 的二元一次方程组,该方程组的解即为所求公共解方法二:原方程可变形为(2)(25)0a x y x y +----= 由于公共解与a 无关,故有20250x y x y +-=⎧⎨--=⎩,解得31x y =⎧⎨=-⎩随练1.1若关于x ,y 的二元一次方程组3921ax y x y +=⎧⎨-=⎩无解,则a =__________.随堂练习【答案】6-【解析】3921ax y x y +=⎧⎨-=⎩①②, 3⨯①+②消去y 可得()612a x +=,可知当6a =-时,012=原方程无解.随练1.2 已知关于x 、y 的方程组26103ax by ax by +=⎧⎨-=⎩,求762by ax +-的值.【答案】1【解析】解方程组得3ax by =⎧⎨=⎩,所以76270231by ax +-=+-⨯=.随练1.3k 为何值时,方程组22342kx y x y +=⎧⎨-=⎩①②无解?【答案】32k =-【解析】将方程组消元,使之化为ax b =的形式,然后讨论一次项系数a .当0a ≠时,有唯一解bx a =;当0a =,0b =时,有无数个解;当0a =,0b ≠时,无解.反之也成立.2⨯+①②,得()236k x +=③,由原方程组无解,知方程③也无解.所以230k +=,解得32k =-.当32k =-时方程组无解.随练1.4已知关于x 、y 的方程组23ax y x ay +=⎧⎨-=⎩,(1)求证:该方程组有唯一解;(2)若方程组的解满足x y =,求a 的值. 【答案】(1)见解析(2)15a =-【解析】(1)方程有唯一解为22231231a x a ay a +⎧=⎪⎪+⎨-⎪=⎪+⎩;(2)由(1)得22232311a a a a +-=++,解得15a =-. 随练1.5 已知关于x 、y 的方程组2331x y ax by -=⎧⎨+=-⎩和3211233x y ax by +=⎧⎨+=⎩的解相同,求a 、b 的值. 【答案】25a b =-⎧⎨=⎩【解析】可先解方程组2333211x y x y -=⎧⎨+=⎩,解得31x y =⎧⎨=⎩.因此可得关于a 、b 的二元一次方程组31633a b a b +=-⎧⎨+=⎩,解得25a b =-⎧⎨=⎩.随练1.6关于x 、y 的方程组239x y mx y m +=⎧⎨-=⎩的解是方程3234x y +=的一组解,那么m 的值是( )A .2B .1-C .1D .2-【答案】A【解析】解关于x 、y 的方程组239x y m x y m +=⎧⎨-=⎩,得72x my m =⎧⎨=-⎩.因此321734x y m +==,2m =,故答案为A .随练1.7小明和小亮解同一道方程组()()5151422ax y x by +=⎧⎪⎨-=-⎪⎩,急性子小明把方程(1)中的a 看错了,得到方程组的解为31x y =-⎧⎨=-⎩,爱马虎的小亮把方程(2)中的b 看错了,得到方程组的解为54x y =⎧⎨=⎩,一旁的学习委员小丽说,我可以知道这个方程组的解,你能说说小丽是怎么样求出这个方程组的解吗?方程组的解是多少?【答案】14295x y =⎧⎪⎨=⎪⎩【解析】根据题意,将31x y =-⎧⎨=-⎩代入方程(2),将54x y =⎧⎨=⎩代入方程(1),得到关于a 、b 的方程组12252015b a -+=-⎧⎨+=⎩,解得110a b =-⎧⎨=⎩,因此原方程为5154102x y x y -+=⎧⎨-=-⎩,求出x 、y 的值即可. 随练1.8要使关于x 、y 的方程组21x ky k x y +=⎧⎨-=⎩的解都是整数,k 应取哪些整数值?【答案】5,31,1k =---【解析】解关于x 、y 的方程组21x ky k x y +=⎧⎨-=⎩,得3212k x k k y k ⎧=⎪⎪+⎨-⎪=⎪+⎩.由于()326363222k k k k k +-==-+++,13122k k k -=-++. ∵x 是整数,∴21,2,3,6k +=±±±±.∵y 是整数,∴21,3k +=±±.∴5,31,1 k=---作业1在二元一次方程组2310630x yx my++=⎧⎨++=⎩中,当m=_________时,这个方程组有无数组解.【答案】9【解析】原方程组可整理为69363x yx my+=-⎧⎨+=-⎩,故当9m=时,原方程组有无数组解.作业2如果关于x,y的二元一次方程组316215x ayx by-=⎧⎨+=⎩的解是71xy=⎧⎨=⎩,那么关于x,y的二元一次方程组()()()()316215x y a x yx y b x y+--=⎧⎪⎨++-=⎪⎩的解是__________.【答案】43 xy=⎧⎨=⎩【解析】由于两个二元二次方程组都是316215m anm bn-=⎧⎨+=⎩的形式,所以解相同.自我总结课后作业∴71x y x y +=⎧⎨-=⎩,∴43x y =⎧⎨=⎩.作业3解关于x 、y 的方程组4258mx y x y +=⎧⎨+=⎩.【答案】当25m =时,原方程组无解;当25m ≠时,原方程组的解为12528852x m m y m ⎧=⎪⎪-⎨-⎪=⎪-⎩【解析】需要对未知数的系数m 进行分类讨论.当125m =,即25m =时,原方程组无解;当25m ≠时,解方程组得12528852x m m y m ⎧=⎪⎪-⎨-⎪=⎪-⎩.作业4解关于x 、y 的方程组:3921ax y x y +=⎧⎨-=⎩【答案】6a =-时无解,当6a ≠-时,方程组的解为126186x a a y a ⎧=⎪⎪+⎨-⎪=⎪+⎩【解析】分类讨论,当321a =-,即6a =-时,原方程组无解;当6a ≠-时,解方程组得126186x a a y a ⎧=⎪⎪+⎨-⎪=⎪+⎩. 作业5a 取哪些正整数值,关于x 、y 的方程组25342x y ax y a +=-⎧⎨-=⎩的解x 和y 都是正整数?【答案】1a =【解析】关于x 、y 的方程组25342x y a x y a +=-⎧⎨-=⎩的解为232x a y =⎧⎪⎨-=⎪⎩.因此只需使32a -(a 是正整数)是正整数即可,故1a =.作业6已知方程组3247x y mx ny -=⎧⎨+=⎩与231953mx ny y x -=⎧⎨-=⎩有相同的解,求m 、n 的值.【答案】41m n =⎧⎨=-⎩【解析】由题意得32453x yy x-=⎧⎨-=⎩,解得21xy=⎧⎨=⎩将21xy=⎧⎨=⎩代入72319mx nymx ny+=⎧⎨-=⎩,得274319m nm n+=⎧⎨-=⎩,解得41mn=⎧⎨=-⎩作业7小明与小强同解x、y的方程组3315ax yx by-=⎧⎨+=⎩①②,小明除了看错①中a之外,无其他错误,求得解为16xy=⎧⎨=⎩;小强除了看错②式中的b之外,无其他错误,求得解为21xy=⎧⎨=⎩,试求出a、b之值与方程组的解.【答案】2a=,2b=,方程组的解为33 xy=⎧⎨=⎩【解析】小明看错①式,求得16xy=⎧⎨=⎩,故16xy=⎧⎨=⎩是方程②的解代入求出2b=小强看错②式,求得21xy=⎧⎨=⎩,故21xy=⎧⎨=⎩是方程①的解代入求出2a=因此原方程为233215x yx y-=⎧⎨+=⎩,解得33xy=⎧⎨=⎩。
人教版初三数学上册二元一次方程组精选全文

可编辑修改精选全文完整版课题:第六讲二元一次方程组课型:复习课年级:九年级教学目标:1.正确理解二元一次方程(组)的解的概念.2.掌握代入消元法、加减消元法、图象法解二元一次方程组;能解简单的三元一次方程组.3.会列二元一次方程组解决实际问题,并能根据具体问题的实际意义检验结果的合理性.教学重点与难点:重点:二元一次方程组的解法以及列二元一次方程组解决实际问题.难点:列二元一次方程组解决实际问题.课前准备:多媒体课件.教学过程:一、知识梳理,建构网络活动内容1:知识梳理1.二元一次方程的定义:含有未知数,并且未知项的次数都是的方程叫做二元一次方程.2.二元一次方程组的定义:共含有个未知数的一次方程组成的一组方程,叫做二元一次方程组.3. 二元一次方程(组)的解:一般的,使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解,二元一次方程有个解.一般地,二元一次方程组的两个方程的解,叫做二元一次方程组的解.4.消元法解二元一次方程组:消元法的基本方法:将二元一次方程组转化为方程.方法有消元法和消元法两种.5. 列二元一次方程组解应用题的一般步骤:审:通过审题,把实际问题抽象成数学问题,分析已知数和未知数,并用字母表示其中的两个未知数.找:找出能够表示题意的两个相等关系.列:根据这两个相等关系列出必需的代数式,从而列出方程.解:解这个方程组,求出两个未知数的值.答:在对求出的方程的解作出是否合理判断的基础上,写出答案.活动内容2:构建网络处理方式:利用多媒体出示二元一次方程(组)的知识点及知识网络,以问题串的形式让学生回顾,如有遗忘,借用课本或同学间交流进行补充,需要教师强调的地方教师要结合具体的例子先简单分析,在后面的例题讲解中再着重强调.设计意图:以问题串的形式让学生回顾二元一次方程(组)的相关知识,如有遗忘,借用课本或同学间交流进行补充,为后面的题组训练打好基础,让学生掌握课堂的主动权,并在学生充分思考、交流的基础上构建知识网络图,让学生将零散、孤立的知识形成网络,完成知识脉络的梳理,让学生在小组交流讨论中完成建构并从中感受到知识间的内在联系,感受到转化的思想、类比的思想及数形结合思想,让学生在数学学习活动中完成二元一次方程(组)的知识要点复习, 为下一步激活运用这些知识打好基础.二、专题探究,归纳整合活动内容1:二元一次方程(组)的有关概念1.若243742953=+--++n m n m y x 是二元一次方程,则nm 的值等于 ; 2.已知⎩⎨⎧==12y x 是二元一次方程组⎩⎨⎧=-=+17my nx ny mx 的解,则m+3n 的立方根为 .处理方式:学生讨论交流,在复习丛书上完成后再展示说明,学生之间互相补充.教师适时点评,然后师生共同总结所考察知识点.设计意图:本活动的设计意在引导学生通过自主探究、合作交流,对二元一次方程(组)的有关概念有更深层次的理解和认识.活动内容2:二元一次方程(组)的解法3.解方程组⎪⎩⎪⎨⎧=++-=+--.6)(2)(3,152y x y x y x y x处理方式:找同学在黑板上进行展示,其他同学在复习丛书上独立完成,然后全班交流讨论处理这类问题时的注意事项.如学生处理方法繁琐,则利用媒体出示另外一种处理方法,引导学生处理问题时应认真分析,注意整体的数学思想.设计意图:通过本题的设置,培养学生解二元一次方程组的能力及技巧,同时,一题多解让学生体会到整体的数学思想.活动内容3:二元一次方程(组)的应用陈老师打算购买气球装扮学校“六一”儿童节活动会场,气球的种类有笑脸和爱心两种,两种气球的价格不同,但同一种气球的价格相同,由于会场布置需要,购买时以一束(4个气球)为单位,已知第一、二束气球的价格如图所示,则第三束气球的价格为( )A .19B .18C .16D .15处理方式:让有不同解法的同学在黑板指定的位置板演解题过程,注意评价时明确运用整体思想的数学思想.设计意图:通过本题的练习,使学生体会解题多样性和整体思想,同时提高学生的思维能力.活动内容4:二元一次方程(组)与一次函数的关系如图直线1l :1y x =+与直线2l :y mx n =+相交于点(1,)P b ,(1)求b 的值; l 2 l 1 b 1 Py xO(2)不解关于x y 、的方程组1y x y mx n=+⎧⎨=+⎩请你直接写出它的解;(3)直线3l :y nx m =+是否也经过点P ?请说明理由.处理方式:学生先独立做题,教师巡视,适时点拨.学生完成后及时点评,借助多媒体展示学生出现的问题进行矫正.设计意图:主要考查一次函数与方程组的关系,有关函数的问题要注意数形结合思想与方程思想的应用,这样比较简洁.做练习题时,可以先画出草图,利用图像解题更为直观形象,这样往往可以使复杂问题变得简单.三、典例精析,方法总结【例1】 已知,02)3(2=+++-y x y x 则y x +的值为 .方法总结:本题利用偶次方、算术平方根非负数的性质,考查的是解二元一方程组,熟知解二元一次方程组的加减消元发和代入消元法.处理方式:由一名学生板演,其余学生在复习丛书上完成.完成后,让学生对板演的同学进行评价,教师及时点评表扬并利用多媒体课件展示方法总结.设计意图:通过例1,使学生加深对二元一次方程组的解法的掌握,能熟练利用加减消元发和代入消元法解二元一次方程组.跟踪练习:若方程组⎩⎨⎧-=+=+,645,22k y x k y x 的解之和:6-=+y x ,那么k = . 【例2】 若方程6=+ny mx 的两个解是⎩⎨⎧-==⎩⎨⎧==,12,1,1y x y x 则m ,n 的值为( ) A . 4 , 2 B . 2 , 4 C . -4 , -2 D . -2 , -4方法总结:此题考查了二元一次方程的解的概念,方程的解即为使方程左右两边相等的未知数的值.将x 与y 的两对值代入方程计算即可求出m 与n 的值.处理方式:由一名学生板演,其余学生在在复习丛书上完成.完成后,让学生对板演的同学进行评价,教师及时点评表扬并利用多媒体课件展示方法总结.设计意图:通过例2,使学生加深对二元一次方程组的解的理解及进一步熟练掌握二元一次方程组的解法.跟踪练习:若关于x ,y 的方程组⎩⎨⎧=+=-n my x m y x ,2的解是⎩⎨⎧==,1,2y x 则n m -为( ) A . 1 B . 3 C . 5 D . 2【例3】 今年“五一”小长假期间,某市外来与外出旅游的总人数为226万人,分别比去年同期增长30%和20%,去年同期外来旅游比外出旅游的人数多20万人.求该市今年外来和外出旅游的人数.点拨:设该市前年外来旅游人数为x 万人,外出旅游人数为y 万人,根据总人数为226万人,前年同期外来旅游比外出旅游的人数多20万人,列方程组求解.方法总结:本题考查了二元一次方程组的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程组求解.处理方式:学生先独立思考,然后教师根据学生思考情况组织学生进行交流,归纳出题目中的等量关系,讨论后列出方程组并求解.可以把分析过程设计成问题帮助学生理解. 设计意图:让学生经历列方程组解决实际问题的过程,培养学生的独立思考的能力和与人合作的意识.共同分析题目中包含的所有等量关系并用等式的形式写出来,便于学生设未知的两个量,顺利列出方程组,更好地体会二元一次方程组是刻画现实世界的有效模型.跟踪练习:某校运动会需购买A 、B 两种奖品.若购买A 种奖品3件和B 种奖品2件,共需60元;若购买A 种奖品5件和B 种奖品3件,共需95元.(1)求A 、B 两种奖品单价各是多少元?(2)学校计划购买A 、B 两种奖品共100件,购买费用不超过1150元,且A 种奖品的数量不大于B 种奖品数量的3倍.设购买A 种奖品m 件,购买费用为W 元,写出W (元)与m (件)之间的函数关系式,求出自变量m 的取值范围,并确定最少费用W 的值. 设计意图:通过学生对题组跟踪训练,及时发现问题解决问题;同时强化学生对二元一次方程组的解法及应用的掌握.使学生体验利用方程模型解决实际问题的方法.四、回顾反思,提炼升华通过本节课的复习,你有哪些收获?有何感想?学会了哪些方法?先想一想,再分享给大家.处理方式:给学生2分钟左右的时间,让学生自主交流课堂实践的经历、感受和收获,然后找3个学生尝试谈谈自己的收获.设计意图:课堂总结是知识沉淀的过程,使学生对本讲复习的知识进行梳理,培养学生知识归纳与整理的习惯与能力,通过师生共同总结,增强学生认识,加深学生印象,强化学生记忆.五、达标测试,反馈提高1.下列方程组中,属于二元一次方程组的是( )⎩⎨⎧=+=+32.z y y x A ⎩⎨⎧==+65.xy y x B ⎩⎨⎧=-=+132152.b a b a C ⎪⎩⎪⎨⎧=+=-.517.n m n m D ; 2. 请写出一个二元一次方程组 ,使它的解是⎩⎨⎧-==.12y x ; 3.解方程组:⎪⎩⎪⎨⎧=-+=-=++.202,1,23z y x y x z y x ;4.甲、乙两人共同解方程组⎩⎨⎧-=-=+)2(,24)1(,155by x y ax 由于甲看错了方程(1)中的a ,得到方程组的解是⎩⎨⎧-=-=;1,3y x 乙看错了方程(2)中的b ,得到方程组的解为⎩⎨⎧==.4,5y x 试计算20152014)101(b a -+的值. 处理方式:学生独立完成,对学生错误较多的题目进行讲解.设计意图:设置的当堂检测便于及时获知学生对本讲知识的掌握情况,并最大限度地调动全体学生学习数学的积极性,使每个学生都能有所收益、有所提高,明确哪些学生需要在课后加强辅导,达到全面提高的目的.六、布置作业,课后促学必做题:《南方新中考》 A 级,B 级题.选做题:《南方新中考》 C 级题.板书设计: 第六讲 二元一次方程组知识梳理 构建网络 典例精析,方法总结例1: 例2: 例3:投 影。
部编数学七年级下册专题12含“字母系数”(含参)的二元一次方程组的解题思路(解析版)含答案

答卷时应注意事项1、拿到试卷,要认真仔细的先填好自己的考生信息。
2、拿到试卷不要提笔就写,先大致的浏览一遍,有多少大题,每个大题里有几个小题,有什么题型,哪些容易,哪些难,做到心里有底;3、审题,每个题目都要多读几遍,不仅要读大题,还要读小题,不放过每一个字,遇到暂时弄不懂题意的题目,手指点读,多读几遍题目,就能理解题意了;容易混乱的地方也应该多读几遍,比如从小到大,从左到右这样的题;4、每个题目做完了以后,把自己的手从试卷上完全移开,好好的看看有没有被自己的手臂挡住而遗漏的题;试卷第1页和第2页上下衔接的地方一定要注意,仔细看看有没有遗漏的小题;5、中途遇到真的解决不了的难题,注意安排好时间,先把后面会做的做完,再来重新读题,结合平时课堂上所学的知识,解答难题;一定要镇定,不能因此慌了手脚,影响下面的答题;6、卷面要清洁,字迹要清工整,非常重要;7、做完的试卷要检查,这样可以发现刚才可能留下的错误或是可以检查是否有漏题,检查的时候,用手指点读题目,不要管自己的答案,重新分析题意,所有计算题重新计算,判断题重新判断,填空题重新填空,之后把检查的结果与先前做的结果进行对比分析。
亲爱的小朋友,你们好!经过两个月的学习,你们一定有不小的收获吧,用你的自信和智慧,认真答题,相信你一定会闯关成功。
相信你是最棒的!专题12 含“字母系数”(含参)的二元一次方程组的解题思路(解析版)第一部分典例剖析类型一利用二元一次方程的定义构造一元一次方程或二元一次方程组1.(2020春•博兴县期中)若方程3x|m|﹣2=3y n+1+4是二元一次方程,则m,n的值分别为( )A.2,﹣1B.﹣3,0C.3,0D.±3,0思路引领:根据二元一次方程的定义得出|m|﹣2=1,n+1=1,解之可得答案.解:∵方程3x|m|﹣2=3y n+1+4是二元一次方程,∴|m|﹣2=1,n+1=1,解得m=3或m=﹣3,n=0,故选:D.总结提升:本题主要考查二元一次方程的定义,解题的关键是掌握含有两个未知数,并且含有未知数的项的次数都是1,像这样的方程叫做二元一次方程.2.(2022春•开州区期中)若关于x,y的方程(n﹣1)x|n|+3y m﹣2=0是二元一次方程,则m+n的值( )A.1B.2C.4D.2或4思路引领:由二元一次方程的定义可知x,y的次数为1,据此可列出方程,并求解.解:∵关于x,y的方程(n﹣1)x|n|+3y m﹣2=0是二元一次方程,∴|n|=1且n﹣1≠0,m﹣2=1,解得m=3,n=﹣1,∴m+n=3﹣1=2.故选:B.总结提升:此题考查二元一次方程定义,二元一次方程必须符合以下三个条件:(1)方程中只含有2个未知数;(2)含未知数项的次数都为一次;(3)方程是整式方程.3.(2017春•分宜县校级期中)方程(m2﹣9)x2+x﹣(m+3)y=0是关于x、y的二元一次方程,则m的值为( )A.±3B.3C.﹣3D.9思路引领:根据二元一次方程的定义可得m2﹣9=0,且m+3≠0,再解即可.解:由题意得:m2﹣9=0,且m+3≠0,解得:m=3,总结提升:此题主要考查了二元一次方程的定义,关键是掌握含有两个未知数,并且含有未知数的项的次数都是1,像这样的方程叫做二元一次方程.类型二利用二元一次方程(组)的解的定义构造一元一次方程或二元一次方程组4.若关于x、y的二元一次方程组x+y=2tx−y=4t的解也是二元一次方程2x+3y=9的解,求t的值和这个方程组的解.思路引领:将t看作已知数求出方程组的解表示出x与y,代入二元一次方程中即可求出t的值,进而确定出方程组的解.解:x+y=2t①x−y=4t②,①+②得:2x=6t,解得:x=3t,①﹣②得:2y=﹣2t,解得:y=﹣t,将x=3t,y=﹣t代入2x+3y=9中得:6t﹣3t=9,解得:t=3,则方程组的解为x=9y=−3.总结提升:此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程成立的未知数的值.5.(2020春•天津期末)已知方程组ax+by=7ax−by=5的解为x=2y=1,则a,b的值为( )A.a=3,b=2B.a=2,b=3C.a=3,b=1D.a=1,b=3思路引领:把x与y的值代入方程组求出a与b的值即可.解:把x=2y=1代入方程组得:2a+b=7①2a−b=5②,①+②,得4a=12,∴a=3,把a=3代入①,得6+b=7,∴a =3,b =1,故选:C .总结提升:此题考查了二元一次方程组的解.解题的关键是掌握二元一次方程组的解的定义,方程组的解即为能使方程组中两方程成立的未知数的值.6.已知方程2x +(1+m )y =﹣1与方程nx ﹣y =1有一个相同的解x =−2y =1,你能求出(m +n )2020的值吗?思路引领:把x 与y 的值代入方程求出m 与n 的值,即可确定出所求式子的值.解:把x =−2y =1代入2x +(1+m )y =﹣1,得﹣4+1+m =﹣1,解得m =2;把x =−2y =1代入程nx ﹣y =1,得﹣2n ﹣1=1,解得n =﹣1.∴(m +n )2020=(2﹣1)2020=1.总结提升:此题考查了有理数的乘方以及二元一次方程的解,使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解.类型三 已知方程组的错解构造一元一次方程求解7.(2021春•青神县期中)甲、乙两人同时解方程组mx +y =5①2x−ny =13②甲解题看错了①中的m ,解得x =72y =−2,乙解题时看错②中的n ,解得x =3y =−7.试求:(1)原方程组m ,n 的正确值;(2)原方程组的解.思路引领:(1)把甲的解代入②中求出n 的值,把乙的解代入①中求出m 的值即可;(2)把m 与n 的值代入方程组求出解即可.解:(1)把x =72y =−2代入②得:7+2n =13,解得n =3,把x =3y =−7代入①得:3m ﹣7=5,解得m =4.所以m =4,n =3;(2)把m =4,n =3代入方程组得:4x +y =5①2x−3y =13②,①×3+②得:14x =28,即x =2,把x=2代入①得:y=﹣3,则方程组的解为x=2y=−3.总结提升:此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程成立的未知数的值.类型四利用方程同解构造二元一次方程组8.(2021春•上思县期末)若方程组2x+4y=−68x−4y=16和方程组ax−by=11bx−ay=13的解相同,试求(3b﹣2a)2021的值.思路引领:求出第一个方程组的解,代入第二个方程组求出a与b的值,代入原式计算即可求出值.解:2x+4y=−6①8x−4y=16②,①+②得:10x=10,解得:x=1,把x=1代入①得:2+4y=﹣6,解得:y=﹣2,∴方程组的解为x=1y=−2,把x=1y=−2代入方程组ax−by=11bx−ay=13得:a+2b=11b+2a=13,解得:a=5 b=3,则(3b﹣2a)2021=(3×3﹣2×5)2021=(﹣1)2021=﹣1.总结提升:此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程都成立的未知数的值.9.已知关于x,y的方程组3x−y=54ax+5by=−22与2x−3y+4=0ax−by−8=0有相同的解,求a,b的值.思路引领:因为关于x,y的方程组有相同的解,根据二元一次方程组的解的定义,只需把两个方程组中不含未知数和含未知数的方程分别组成方程组,求出未知数的值,再代入另一组方程组即可.解:由题意,关于x,y的方程组3x−y=52x−3y+4=0和4ax+5by=−22ax−by−8=0的解也相同.解方程组3x−y=5①2x−3y+4=0②,得x=197y=227.把x=197y=227代入4ax+5by=−22ax−by−8=0,a+1107b=−22a−227b=8解得a=1419b=−2111.总结提升:本题考查了二元一次方程组的解法及方程组解的意义,由于数比较大,计算较复杂,理解方程组公共解的意义和掌握解二元一次方程组的解法是解决本题的关键.10.(2019春•大丰区期末)已知关于x、y的方程组4x+ay=162x+y=4b+2和3x+ay=132x−3y=−6的解相同,求a、b值.思路引领:先把方程4x+ay=16和3x+ay=13相减,可得x的值,再代入方程2x﹣3y=﹣6,求出y的值,再把x,y的值代入第一个方程组即可求得a,b的值.解:方程4x+ay=16和3x+ay=13相减,得x=3,把x=3代入方程2x﹣3y=﹣6,得y=4.把x=3,y=4代入方程组4x+ay=162x+y=4b+2,得12+4a=166+4=4b+2解这个方程组,得a=1,b=2.总结提升:利用方程组的解相同,可以重新组合方程组,求得未知数的值.类型五利用二元一次方程组的解适合第3个方程,构造一元一次方程或者用整体思想求解11.已知方程组2x+3y=7,5x−y=3m+1的解能使等式x﹣7y=2成立,求m的值.思路引领:观察方程组中两方程的x与y的系数,发现方程①减去方程②×2后恰好直接得到(x﹣7y)的值.解:2x+3y=7①,5x−y=3m+1②,由②﹣①×2,得x﹣7y=3m﹣13,∴3m﹣13=2,解得m=5.总结提升:本题主要考查的是解二元一次方程组,求得x、y的值是解题的关键.12.(2022春•沙坪坝区期末)已知关于x,y的方程组3x+4y=a+22x+3y=2a的解满足x+y=1,求a的值及方程组的解.思路引领:根据题意,①﹣②得x+y=﹣a+2,再根据已知条件可得a的值,根据加减消元法解二元一次方程组即可.解:3x+4y=a+2①2x+3y=2a②,①﹣②得x+y=﹣a+2,∵x+y=1,∴﹣a+2=1,解得a=1,∴原方程组化为3x+4y=3①2x+3y=2②,①×2﹣②×3得﹣y=0,解得y=0,将y=0代入3x+4y=3,得3x=3,解得x=1,∴原方程组的解为x=1 y=0.总结提升:本题考查了二元一次方程组的解以及解二元一次方程组,熟练掌握解二元一次方程组的方法是解题的关键.13.(2019春•西湖区校级月考)已知关于x,y的二元一次方程组3x+2y=m+32x−y=2m−1的解x与y的值互为相反数,试求m的值和方程组的解.思路引领:由已知方程组,利用加减消元法求出x=5m17,y=9−4m7,再由x与y的值互为相反数,即可求出m的值,再将m的值代入所求x、y的表达式,即可求方程组的解.解:方程组3x+2y=m+3①2x−y=2m−1②,②×2+①得7x=5m+1,∴x=5m17,将x=5m17代入②,得y=9−4m7,∵x与y的值互为相反数,∴5m17+9−4m7=0∴m=﹣10,∴x=﹣7,y=7,∴原方程组的解为x=−7 y=7.总结提升:本题考查二元一次方程组的解;熟练掌握加减消元法解二元一次方程组,同时结合相反数的性质灵活解题是关键.14.当m,n都是实数,且满足2m﹣n=8时,我们称Q(m﹣1,n+1)为巧妙点.(1)若A(m﹣1,5)是巧妙点,则m= ,巧妙点A( ,5);(2)判断点P(3,1)是否为巧妙点,并说明理由.(3)已知关于x,y的方程组x+y=4x−y=2a,当a为何值时,以方程组的解为坐标的点B(x,y)是巧妙点?思路引领:(1)利用题中的新定义列式计算即可;(2)利用题中的新定义判断即可;(3)表示出方程组的解,根据题中的新定义判断即可.解:(1)由题意得:2(m﹣1+1)﹣(5﹣1)=8,解得:m=6,∴m﹣1=5,∴巧妙点A(5,5),故答案为:6,5;(2)点P(3,1)是巧妙点,理由如下:根据题意得m−1=3n+1=1,解得:m=4 n=0,代入得:2m﹣n=8﹣0=8,∴点P(3,1)是巧妙点;(2)x+y=4①x−y=2a②,①+②得:2x=2a+4,解得:x=a+2,把x=a+2代入①得:y=2﹣a,根据题意得:m−1=a+2 n+1=2−a,解得:m=a+3 n=1−a,代入得:2m﹣n=2a+6﹣1+a=3a+5,当3a+5=8,即a=1时,满足2m﹣n=8,即以方程组的解为坐标的点B(x,y)是巧妙点.总结提升:此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程都成立的未知数的值.第二部分专题提优训练1.(2022春•滨海县月考)若方程(a﹣6)x|a|﹣5+5y=1是关于x,y的二元一次方程,则a的值为( )A.±6B.﹣6C.±5D.5思路引领:根据二元一次方程的定义解答即可.解:∵(a﹣6)x﹣y|a|﹣5=1是关于x,y的二元一次方程,∴a−6≠0|a|−5=1,解得a=﹣6.故选:B.总结提升:本题考查解二元一次方程的定义,解题关键是熟知二元一次方程的定义:含有两个未知数,并且含有未知数的项的次数都是1的整式方程叫做二元一次方程.2.(2021春•银海区期中)若(R﹣2)x|R|﹣1﹣3y=2是关于x,y的二元一次方程,那么3R﹣2的值为( )A.4B.﹣8C.8D.4或﹣8思路引领:二元一次方程满足的条件:含有2个未知数,未知数的项的次数是1的整式方程.解:根据题意得:R−2≠0|R|−1=1,解得R=﹣2,∴3R﹣2=﹣6﹣2=﹣8,故选:B.总结提升:此题考查了二元一次方程的定义,含有两个未知数,并且含有未知数的项的次数都是1,像这样的整式方程叫做二元一次方程.3.(2021春•平凉期末)如果x=3y=−2是方程组ax+by=1ax−by=5的解,则a2008+2b2008的值为( )A .1B .2C .3D .4思路引领:将方程组的解代入方程组可得关于a 、b 的二元一次方程组3a−2b =13a +2b =5,再求解方程组即可求解.解:∵x =3y =−2是方程组ax +by =1ax−by =5的解,∴3a−2b =1①3a +2b =5②,①+②得,a =1,将a =1代入①得,b =1,∴a 2008+2b 2008=1+2=3,故选:C .总结提升:本题考查二元一次方程组的解,熟练掌握加减消元法和代入消元法解二元一次方程组是解题的关键.二.解答题(共8小题)4.若x =2y =1是方程组ax +y =b 4x−by =3a−1的解,求a 、b 的值.思路引领:把x =2y =1代入方程组ax +y =b 4x−by =3a−1,然后解关于a ,b 的方程组即可.解:把x =2y =1代入方程组ax +y =b 4x−by =3a−1,得:2a +1=b 8−b =3a−1,解得:a =85b =215,故a =85,b =215.总结提升:本题考查了二元一次方程组的解,属于基础题,关键是掌握用代入法解方程组.5.已知二元一次方程px +2y =8,5x ﹣6y =4,2x +5y ﹣8=0有公共解,求p 的值.思路引领:解方程组5x−6y =42x +5y−8=0得x ,y 的值,再代入px +2y =8求解即可.解:解方程组5x−6y =42x +5y−8=0得x =6837y =3237,代入px +2y =8,得6837p +2×3237=8,解得p =5817.总结提升:本题主要考查了二元一次方程的解,解题的关键是求出方程组公共解.6.(2021秋•金寨县期末)解方程组ax+by=6x+cy=4时,甲同学因看错a符号,从而求得解为x=3y=2,乙因看漏c,从而求得解为x=6y=−2,试求a,b,c的值.思路引领:甲同学因看错a符号,把x=3,y=2代入x+cy=4,求出c,因看错a符号,得﹣3a+2b=6,乙因看漏c,把x=6,y=﹣2代入ax+by=6,组成新的二元二次方程组,解出即可.解:∵甲同学因看错a符号,∴把x=3,y=2代入x+cy=4,得c=1 2,﹣3a+2b=6.∵乙因看漏c,∴把x=6,y=﹣2代入ax+by=6,得6a﹣2b=6,得−3a+2b=6 6a−2b=6,解得,a=4,b=9;综上所述,a=4,b=9,c=1 2.总结提升:本题主要考查了二元一次方程组的解,掌握做题的方法是解题关键.7.(2019秋•平桂区期末)已知x=2y=1是二元一次方程组mx+ny−7=0nx+my−2=0的解,求m+3n的值.思路引领:把方程组的解代入方程组求出m与n的值,即可求解.解:把x=2y=1代入方程组mx+ny−7=0nx+my−2=0,得2m+n−7=02n+m−2=0,解方程组,得m=4,n=−1把m=4n=−1代入m+3n,得m+3n=4+3×(﹣1)=1.总结提升:本题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程都成立的未知数的值.8.(2021春•娄底月考)已知方程组2x+3y=10ax+by=9与方程组bx−ay=84x−3y=2的解相等,试求a、b的值.思路引领:两个方程组的解相同,也就是有一组x、y的值是这四个方程的公共解,当然也是其中任意两个方程的公共解,所以可以把原来的方程组打乱,重新组合起来求解.解:由已知可得2x+3y=104x−3y=2,解得x=2y=2,把x=2y=2代入剩下的两个方程组成的方程组ax+by=9bx−ay=8,得2a+2b=9 2b−2a=8,解得a=14b=174.故a、b的值为a=14b=174.总结提升:解答此题的关键是熟知方程组有公共解得含义,考查了学生对题意的理解能力.9.(2018春•岳麓区校级期中)(1)已知关于x,y方程组x+2y=3k2x+y=2k+1的解满足x﹣y=3,求k的值;(2)在(1)的条件下,求出方程组的解.思路引领:(1)方程组中两式相减后可得x﹣y=1﹣k,再根据条件即可求出k的值.(2)根据二元一次方程组的解法即可求出答案.解:(1)∵x+2y=3k①2x+y=2k+1②,∴②﹣①得:x﹣y=1﹣k,∵x﹣y=3,∴1﹣k=3,∴k=﹣2.(2)将k=﹣2代入x+2y=−6①2x+y=−3②,①×2得:2x+4y=﹣12③②﹣③得:﹣3y=9,∴y=﹣3,将y=﹣3代入①得:x﹣6=﹣6,∴x=0,∴方程组的解为x=0 y=−3总结提升:本题考查二元一次方程组,解题的关键是熟练运用二元一次方程组的解法,本题属于基础题型.10.已知方程组2x+y=5ax−by=−4与5x−4y=62ax−3by=2有公共解,求a、b的值.思路引领:由于两方程组有公共解,所以可把方程①和方程③联立为一个方程组进行求解,然后把所求结果代入方程②和方程④中,形成一个关于a、b的二元一次方程组,解答即可.解:在方程组2x+y=5①ax−by=−4②与5x−4y=6③2ax−3by=2④,因为有公共解,所以有2x+y=55x−4y=6和ax−by=−42ax−3by=2.由第一组可解得x=2 y=1,代入第二组,得2a−b=−4 4a−3b=2,解得a=−7b=−10.总结提升:本题考查解二元一次方程组,二元一次方程组的解,掌握二元一次方程组的解法是解题的关键.11.(2021秋•长丰县月考)已知关于x,y的二元一次方程组x+2y=a2x−y=1.(1)当方程组的解为x=1y=1时,求a的值.(2)当a=﹣2时,求方程组的解.(3)小冉同学模仿第(1)问,提出一个新解法:将x=−2y=−2代入方程x+2y=a中,即可求出a的值.小冉提出的解法对吗?若对,请完成解答;若不对,请说明理由.思路引领:(1)将x=1y=1代入方程组x+2y=a2x−y=1即可求a的值;(2)用加减消元法求方程组的解即可;(3)x=−2y=−2不是方程2x﹣y=1的解,因此x=−2y=−2不是方程组的解.解:(1)∵x=1y=1是方程组x+2y=a2x−y=1的解,∴1+2×1=a,∴a=3;(2)∵a=﹣2,∴x+2y=−2①2x−y=1②,②×2得,4x﹣2y=2③,①+③得,5x=0,∴x=0,将x=0代入②得,y=﹣1,∴方程组的解为x=0y=−1;(3)不正确,理由如下:将x=−2y=−2代入方程2x﹣y=1,可得2×(﹣2)﹣(﹣2)=﹣2≠1,∴x=−2y=−2不是方程组的解,∴解法不正确.点睛:本题考查二元一次方程组的解,熟练掌握二元一次方程组的解与二元一次方程组的关系,会用加减消元法解二元一次方程组是解题的关键.。
含参的二元一次方程组训练题

含参的二元一次方程组训练题1.解:设方程组为ax+by=k,-ax-by=k,由于解互为相反数,所以k=0.若x=y,则方程组为2ax=k,解为x=y=k/2,所以k=2a。
2.解:将x-y=-1代入方程组得到ax+(a-1)y=k,-ax-(a-1)y=-k,由于有一个解相同,所以k=0.若x+y=2,则方程组为2ax+2ay=k,解为x=y=k/2a,所以k=4a。
3.解:将x-3y=6代入方程组得到ax+(a-3)y=k,-ax+(3-a)y=-k,由于解相同,所以k=0.若x-y=2,则方程组为2ax+2ay=k,解为x=y=k/2a+1,所以k=2a-2.4.解:将x+y=1代入方程组得到a/2x-a/2y=1/2-k/2,-a/2x+a/2y=1/2-k/2,两式相加得到a/2(x+y)=1-k,代入x+y=1得到k=1-a/2.若3x-2y+k=0,则方程组为3x+3y=6-k,解为x+y=2-k/3,所以k=6-2m。
5.解:将x+y=1代入方程得到2x^2=1,所以x=±1/√2.代入方程得到y=±1/√2,所以解为(1/√2.-1/√2)和(-1/√2.1/√2)。
6.解:设方程组为ax+by=ab,bx+ay=ab,则(a-b)x+(b-a)y=0,即x-y=0,所以a=b。
代入方程组得到2ax=ab,解为x=y=b/2,所以a=b=2.7.解:设方程组为ax+by=k,cx+dy=m,由于解都是正整数,所以a、b、c、d、k、m都是正整数。
由于ad-bc≠0,所以解唯一,所以k和m都是正整数。
若x+y=k/a,则方程组为(a+c)x+(b+d)y=k+m,解为x+y=(k+m)/(a+c),所以a+c=k+m。
8.解:将x-y=10代入方程组得到ax+(a-10)y=k,-ax+(10-a)y=-k,由于解唯一,所以a≠5.若x-y=m,则方程组为2ax+(2a-2m)y=k,解为x+y=(k+m)/(a+a-m),所以a+a-m=10.9.解:将方程组化为矩阵形式Ax=b,其中A为系数矩阵,x为未知数向量,b为常数向量。
专题:方程组与不等式含参问题

专题:方程组和不等式的含参问题【考点1:二元一次方程组的含参问题】 【例题精讲】二元一次方程组的定解问题方法:当含有字母参数的方程组的解已经给出时,可把解直接带入原方程组,构造出关于字母的方程,进而求得其值。
例题1 (17-18天河)若⎩⎨⎧==12y x 是方程组⎩⎨⎧=-=+51ay bx by ax 的解,则b a 3+=_______. 答案:6【举一反三】1.(17-18白云)03x y =⎧⎨=⎩和15x y =⎧⎨=⎩都是方程y kx b =+的解,则( )A .23k b =⎧⎨=⎩B .23k b =-⎧⎨=⎩C .23k b =-⎧⎨=-⎩D .23k b =⎧⎨=-⎩答案:A2.(19-20番禺)已知12x y 是二元一次方程24x ay 的一个解,则a 的值为( ) A .2 B .−2 C .1 D .−1答案:C3.(17-18番禺)在等式2y ax bx c =++中,当x =−1时,y =0;当x =2时,y =3,则a +b 的值为________. 答案:14.(18-19荔湾)已知关于x ,y 的二元一次方程组231ax by ax by +=⎧⎨-=⎩的解为11x y =⎧⎨=-⎩,则2a b-的值是( ) A .2- B .2C .3D .3-答案:B【例题精讲】二元一次方程组的同解问题方法:当两个二元一次方程组同解时,可利用两个不含字母参数的二元一次方程组组成方程组,并求出方程组的解,然后利用这个解得到关于字母参数的方程组。
例题1.(17-18越秀)若关于x 、y 的方程组⎩⎨⎧=-+=+7)12(843y m mx y x 的解也是二元一次方程1132=-y x 的解,则m 的值为 .【举一反三】已知关于x,y 的方程组x 52522y ax by +=⎧⎨+=-⎩与2x-y=1ax-by-8=0⎧⎨⎩有相同的解,则a= ,b= .【例题精讲】二元一次方程组的解满足特定关系式问题方法:方程组的解满足一定的等式的字母求值问题,常常应把方程组中的字母当作已知数,用含有它的式子表示方程组的解,再根据满足的等式,构造出关于字母的方程。
二元一次方程组含参问题

二元一次方程组含参问题类型一:方程组的同解问题【例1】已知关于x ,y 的方程组{4x −y =53x +y =9和{ax +by =−13x +4by =18有相同的解. (1)求出它们的相同的解;(2)求(2a +3b)2019的值.【练习】 若关于x ,y 的方程组{3x +4y =2ax +b 2y =5与{a 3x +by =42x −y =5有相同的解,求a ,b 的值.类型二:方程组的错解问题【例2】在解方程组{ax +4y =213x −by =6时,由于粗心,甲同学看错了方程组中的a ,而得到解为{x =4y =3.乙同学看错了方程组中的b ,而得到解为{x =1y =4. (1)求正确的a ,b 的值;(2)求原方程组的解.【练习】甲、乙两人同时解关于x ,y 的方程组{ax +by =8cx −3y =−2,甲正确解得{x =1y =2,乙因为抄错c 的值,解得{x =2y =−6 ,求a ,b ,c 的值.类型三:方程组的解【例3】若方程组{2x +y =1−3k ①x +2y =2 ②的解满足x +y =0,则k 的值为( ) A.-1 B.1 C.0 D.不能确定【变式1】若方程组{x +2y =k −1 ①2x +y =5k +4②的解满足x +y =5,则k 的值为( ) A.-2 B.0 C.2 D.不能确定【变式2】若方程组{2x +y =1−3k ①x +2y =2 ②的解满足x >0,y >0,求k 的范围。
【变式3】若方程组{2x +y =1−3k ①x +2y =2 ②的解满足x +y =k ,求k 的范围。
【例4】k 、b 为何值时,关于x 、y 的方程组 (1)有唯一解; (2)无解; (3)有无数个解变式1、当a 为何值时,关于x 、y 的方程组 有唯一解?变式2、当m 为何值时,关于x 、y 的方程组 有无数个解?类型四:方程的整数解【例5】求二元一次方程3x +2y =12的非负整数解。
专题 解二元一次方程组(计算题50题)(原卷版)
七年级下册数学《第八章二元一次方程组》专题解二元一次方程组(计算题50题)1.用代入法解下列方程组:(1)x−y=4,3x+y=16;(2)x−y=2,3x+5y=14.2.用代入法解下列方程组:(1)2x−y=33x+2y=8;(2)u+v=103u−2v=5.3.用代入法解下列方程组:(1)3x−y=2,9x+8y=17;(2)3x−4y=10x+3y=12.4.用代入法解下列方程组.(1)x+2y=4y=2x−3;(2)x−y=44x+2y=−2.5.用代入法解下列方程组:(1)5x+4y=−1.52x−3y=4(2)4x−3y−10=03x−2y=06.用代入法解下列方程组:(1)x−y=42x+y=5;(2)3x−y=29x+8y=17;(3)3x+2y=−8 6x−3y=−9.7.用代入法解下列方程组:(1)3x+2y=11,①x=y+3,②(2)4x−3y=36,①y+5x=7,②(3)2x−3y=1,①3x+2y=8,②8.用代入法解下列方程组:(1)5x+2y=15①8x+3y=−1②;(2)3(y−2)=x−172(x−1)=5y−8.9.用代入法解下列方程组:(1)x=6−5y3x−6y=4(2)5x+2y=15x+y=6(3)3x+4y=22x−y=5(4)2x+3y=73x−5y=110.用代入法解下列方程组:(1)2x+y=3x+2y=−6;(2)x+5y=43x−6y=5;(3)2x−y=63x+2y=2;(4)5x+2y=113y−x=−9;1.用加减法解下列方程组:(1)4x−y =143x +y =7 (2x−2y =7x−3y =−82.用加减法解下列方程组:(1)2m +7n =53m +n =−2(2)2u−5v =124u +3v =−2(3y 7=12+y 7=133.用加减法解下列方程组:(1)x−y =52x +y =4;(2)x−2y =33x +4y =−1.4.用加减法解下列方程组:(1)4x−3y =11,2x +y =13;(2)x−y =3,2y +3(x−y)=115.用加减法解下列方程组:(1)3μ+2t =76μ−2t =11 (2)2a +b =33a +b =4.6.(2023•市北区校级开学)用加减法解下列方程组:(1)3y−4x =04x +y =8; (2+y =3x−32y =−1.7.(2022秋•陕西期末)用加减法解下列方程组:(1)x−y =33x−8y =14; (2+2y =10=1+y 13.8.用加减法解下列方程组:(1)x +3=y ,2(x +1)−y =6; (2)x +y =2800,96%x +64%y =2800×92%.9.用加减法解下列方程组:(1)x−y =5,①2x +y =4;②(2)x−2y =1,①x +3y =6;②(3)2x−y =5,①x−1=12(2y−1).②10.用加减法解下列方程组:(1)x +3y =62x−3y =3 (2)7x +8y =−57x−y =4(3)y−1=3(x−2)y+4=2(x+1)(4+y4=1−y3=−1.1.(2022春•新田县期中)用指定的方法解下列方程组:(1)2x−5y=14①y=−x②(代入法);(2)2x+3y=9①3x+5y=16②(加减法).2.(2022春•安岳县校级月考)解下列方程组:(1)3x−y=75x+2y=8(用代入法);(2+n3=10−n4=5(用加减法).3.(2022春•大连期中)用指定的方法解下列方程组:(1)x−3y=42x+y=13(代入法);(2)5x+2y=4x+4y=−6(加减法).4.(2022春•宁远县月考)请用指定的方法解下列方程组(1)5a−b=113a+b=7(代入消元法);(2)2x−5y=245x+2y=31(加减消元法).5.(2021秋•蒲城县期末)请用指定的方法解下列方程组:(1)2x+3y=11①x=y+3②(代入消元法);(2)3x−2y=2①4x+y=10②(加减消元法).6.(2022秋•历下区期中)请用指定的方法解下列方程组:(1)m−n2=22m+3n=12(代入法);(2)6s−5t=36s+t=−15(加减法).7.(2022春•泰安期中)用指定的方法解下列方程组(1)3x+4y=19x−y=4(代入消元法);(2)2x+3y=−53x−2y=12(加减消元法);(35(x−9)=6(y−2)−y13=2.8.(2021秋•历下区期中)请用指定的方法解下列方程组:(1)3x+2y=14x=y+3;(代入法)(2)2x+3y=123x+4y=17.(加减法)9.(2021春•沙河口区期末)用指定的方法解下列方程组:(1)y=2x−33x+2y=8(代入法);(2)3x+4y=165x−6y=33(加减法).10.用指定的方法解下列方程组:(1)3x+4y=19x−y=4(代入法);(2)2x+3y=−53x−2y=12(加减法).1.(2022•苏州模拟)用适当的方法解下列方程组.(1)x+2y=9y−3x=1;(2x−34y=1=4.2.(2022秋•锦江区校级期末)用适当的方法解下列方程组.(1)x=2y−14x+3y=7;(2)3x+2y=22x+3y=28,.3.用适当的方法解下列方程组:(1)x+2y=0,3x+4y=6;(2=2y1)−y=11(3)x+0.4y=40,0.5x+0.7y=35;(4+n−m4=−14,5(n1)12=2.4.(2022•天津模拟)用适当的方法解下列方程组:(1)x +y =52x−y =4; (2=y 24−y−33=112.5.(2021•越城区校级开学)用适当的方法解下列方程组:(1)2x−3y =7x−3y =7. (2)0.3p +0.4q =40.2p +2=0.9q .6.(2022春•东城区校级月考)用适当的方法解下列方程组(1)x +y =52x +y =8; (2)2x +3y =73x−2y =4.7.(2021春•哈尔滨期末)用适当的方法解下列方程组(1)x +2y =93x−2y =−1 (2)2x−y =53x +4y =28.(2022春•椒江区校级期中)用适当的方法解下列方程组:(1)2x +3y =16①x +4y =13②; (2)2s t 3=3s−2t 8=3.9.(2022春•诸暨市期中)用适当的方法解下列方程组:(1)y=2x−1x+2y=−7(2+y3=7+y2=810.(2021春•南湖区校级期中)用适当的方法解下列方程组:(1)3x+2y=9x−y=8;(2=x y2=7.1.先阅读材料,然后解方程组:材料:解方程组x+y=4①3(x+y)+y=14②在本题中,先将x+y看作一个整体,将①整体代入②,得3×4+y=14,解得y=2.把y=2代入①得x=2,所以x=2 y=2这种解法称为“整体代入法”,你若留心观察,有很多方程组可采用此法解答,请用这种方法解方程组x−y−1=0①4(x−y)−y=5②.2.(2021秋•乐平市期末)解方程组3x−2y=8⋯⋯⋯①3(3x−2y)+4y=20⋯.②时,可把①代入②得:3×8+4y=20,求得y=﹣1,从而进一步求得x=2y=−1这种解法为“整体代入法“,请用这样的方法解下列方程组2x−3y=123(2x−3y)+5y=26.3.先阅读,然后解方程组.解方程组x−y−1=0①4(x−y)−y=5②时,可由①得x﹣y=1.③,然后再将③代入②得4×1﹣y=5,求得y=﹣1,从而进一步求得x=0y=−1这种方法被称为“整体代入法”,请用这样的方法解下列方程组:=0=2y+1.4.(2022春•太和县期末)先阅读,然后解方程组.解方程组x−y−1=0①4(x−y)−y=5②时,可由①得x﹣y=1,③然后再将③代入②得4×1﹣y=5,求得y=﹣1,从而进一步求得x=0①y=−1②这种方法被称为“整体代入法”,+2y=9.5.先阅读,然后解方程组.解方程组x−y−1=0①4(x−y)−y=5②时,可由①得x﹣y=1③,然后再将③代入②得4×1﹣y=5,求得y=﹣1,从而进一步求得x这种方法被称为“整体代入法”,请用这样的方法解下列方程组:2x−3y−2=03(2x−3y)+y=7.1.用换元法解下列方程组+2y=12−1y=342.用换元法解下列方程组:(1)3(x+y)+2(x−y)=36(x+y)−4(x−y)=−16(2+x5y3=2−(x+5y)=5.3.(2022春•云阳县期中)阅读探索:解方程组(a−1)+2(b+2)=62(a−1)+(b+2)=6解:设a﹣1=x,b+2=y原方程组可以化为x+2y=62x+y=6,解得x=2y=2,即:a−1=2b+2=2∴a=3b=0,此种解方程组的方法叫换元法.(1)拓展提高运用上述方法解下列方程组(a4−1)+2(b5+2)=102(a4−1)+(b5+2)=11;(2)能力运用已知关于x,y的方程组a1x+b1y=c1a2x+b2y=c2的解为x=6y=7,求关于m、n的方程组a1(m−2)+b1(n+3)=c1a2(m−2)+b2(n+3)=c2的解.4+x−y10=3①−x−y10=−1②,你会解这个方程组吗?小明、小刚、小芳争论了一会儿,他们分别写出了一种方法:小明:把原方程组整理得8x+2y=90③2x+8y=−30④④×4﹣③得30y=﹣210,所以y=﹣7把y=﹣7代入③得8x=104,所以x=13,即x=13y=−7小刚:设x y6=m,x−y10=n,则m+n=3③m−n=−1④③+④得m=1,③﹣④得m=2,=1=2,所以x+y=6x−y=20,所以x=13y=−7.小芳:①+②得2(x y)6=2,即x+y=6.③①﹣②得2(x−y)10=4,即x﹣y=20.④③④组成方程组得x=13③﹣④得y =﹣7,即x =13y =−7.老师看过后,非常高兴,特别是小刚的方法独特,像小刚的这种方法叫做换元法,你能用换元法解下列方程组吗?+2x 3y 7=1−2x 3y 7=5.5.(2022春•卧龙区校级月考)阅读探索(1)知识积累解方程组(a−1)+2(b +2)=62(a−1)+(b +2)=6.解:设a ﹣1=x ,b +2=y .原方程组可变为x +2y =62x +y =6,解这个方程组得x =2y =2,即a−1=2b +2=2,所以a =3b =0,这种解方程组的方法叫换元法.(2)拓展提高运用上述方法解下列方程组:(m 3−1)+2(n 5+2)=43(m 3−1)−(n 5+2)=5.(3)能力运用已知关于x ,y 的方程组a 1x +b 1y =c 1a 2x +b 2y =c 2的解为x =3y =4,请直接写出关于m 、n 的方程组a 1(m +2)−b 1n =c 1a 2(m +2)−b 2n =c 2的解是 .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题:含参二元一次方程组
1.关于x ,y 的二元一次方程2x +3y =18的正整数解的个数为( )
A . 1
B . 2
C . 3
D . 4
2.若方程ax ﹣5y =3的一个解是
,则a 的值是( ) A . ﹣13 B . 13 C . 7 D . ﹣7
3.已知二元一次方程572=-y x ,用含x 的代数式表示y ,正确的是
A .257x y +=
B .257
x y -= C .275y x += D .572y x -= 4.已知⎩⎨⎧==11y x ,⎩
⎨⎧==32y x 是关于x ,y 的二元一次方程y=kx+b 的解,则k,b 的值是 A .k =1, b =0 B .k =-1, b =2 C .k =2, b =-1 D .k =-2, b =1 5. 12x y =⎧⎨=-⎩
是关于x 和y 的二元一次方程1ax y +=的解,则a 的值为_________________. 6.写出二元一次方程25x y +=的非负整数解_______________________
7.写一个以21
x y =-⎧⎨=⎩为解的二元一次方程组_____________________.
8.请你写出一个二元一次方程组 ,使它的解是x 2y 3
=⎧⎨=⎩.
9. 已知代数式1515
a x y -与25
b a b x y +-是同类项,那么a 与b 的值分别是 10.若方程mx +ny =6的两个解为
,,则m n = . 11. 若关于x 、y 的方程组 35223x y m x y m
+=+⎧⎨+=⎩的解x 与y 的值的和等于2,求m 的值.
12.是否存在整数k ,使方程组
的解中,x 大于1,y 不大于1,若存在,求出k 的值,若不存在,说明理由.
13.已知关于x 、y 的二元一次方程组
的解x 、y 是一对相反数,试求m 的值.
14.若关于x,y 的方程组35223x y m x y m
+=+⎧⎨+=⎩的解x 与y 的值的和等于2,求2m -的值.
15.已知关于x ,y 的二元一次方程组2322x y k x y k
+=-⎧⎨
+=⎩的解满足,求k 的取值范围.
16.王老师让全班同学们解关于x 、y 的方程组217x ay bx y +=⎧⎨-=⎩①
②(其中a 和b 代表确定的数),
甲、乙两人解错了,甲看错了方程①中的a ,解得14x y =⎧⎨=-⎩
,乙看错了②中的b ,解得11
x y =-⎧⎨=⎩,请你求出这个方程组的正确解. x y <。
