常见函数图像
常见三角函数图像及其性质
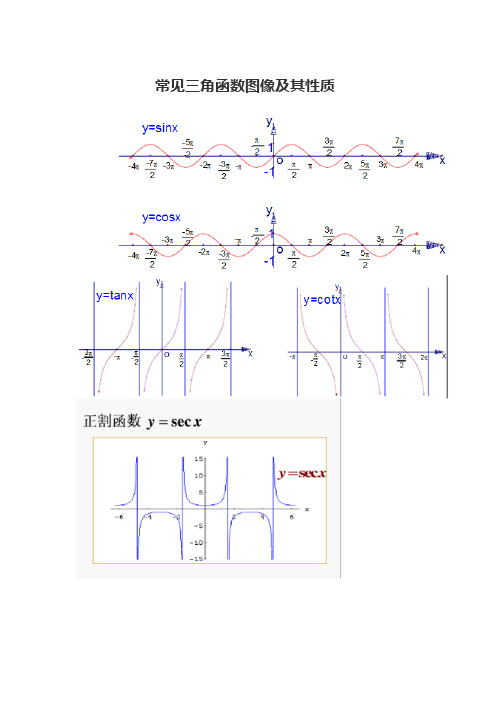
常见三角函数图像及其性质三角函数介绍正弦函数主词条:正弦函数格式:sin(θ)作用:在直角三角形中,将大小为θ(单位为弧度)的角对边长度比斜边长度的比值求出,函数值为上述比的比值,也是csc(θ)的倒数函数图像:波形曲线值域:[]1,1-余弦函数主词条:余弦函数格式:cos(θ)作用:在直角三角形中,将大小为(单位为弧度)的角邻边长度比斜边长度的比值求出,函数值为上述比的比值,也是sec(θ)的倒数函数图像:波形曲线值域:[]1,1-正切函数主词条:正切函数格式:tan(θ)作用:在直角三角形中,将大小为θ(单位为弧度)的角对边长度比邻边长度的比值求出,函数值为上述比的比值,也是cot(θ)的倒数。
函数图像:上图平面直角坐标系反映值域:()∞-∞,+余切函数主词条:余切函数格式:cot(θ)作用:在直角三角形中,将大小为θ(单位为弧度)的角邻边长度比对边长度的比值求出,函数值为上述比的比值,也是tan(θ)的倒数值域:()∞-∞,+正割函数主词条:正割函数格式:sec(θ)作用:在直角三角形中,将斜边长度比大小为θ(单位为弧度)的角邻边长度的比值求出,函数值为上述比的比值,也是cos(θ)的倒数函数图像:上图平面直角坐标系反映值域:(][)∞-1-,1∞,+余割函数主词条:余割函数格式:csc(θ)作用:在直角三角形中,将斜边长度比大小为θ(单位为弧度)的角对边长度的比值求出,函数值为上述比的比值,也是sin(θ)的倒数值域:(][)∞-1-∞,+,1。
初中高中数学七大函数的性质 图像

初中高中数学七大函数的性质图像1.一次函数(包括正比例函数)最简单最常见的函数,在平面直角坐标系上的图象为直线。
定义域(下面没有说明的话,都是在无特殊要求情况下的定义域):R值域:R奇偶性:无周期性:无平面直角坐标系解析式(下简称解析式):①ax+by+c=0[一般式]②y=kx+b[斜截式](k为直线斜率,b为直线纵截距,正比例函数b=0)③y-y1=k(x-x1)[点斜式](k为直线斜率,(x1,y1)为该直线所过的一个点)④(y-y1)/(y2-y1)=(x-x1)/(x2-x1)[两点式]((x1,y1)与(x2,y2)为直线上的两点)⑤x/a-y/b=0[截距式](a、b分别为直线在x、y轴上的截距)解析式表达局限性:①所需条件较多(3个);②、③不能表达没有斜率的直线(平行于x轴的直线);④参数较多,计算过于烦琐;⑤不能表达平行于坐标轴的直线和过圆点的直线。
倾斜角:x轴到直线的角(直线与x轴正方向所成的角)称为直线的倾斜角。
设一直线的倾斜角为a,则该直线的斜率k=tg(a)。
2.二次函数:题目中常见的函数,在平面直角坐标系上的图象是一条对称轴与y轴平行的抛物线。
定义域:R值域:(对应解析式,且只讨论a大于0的情况,a小于0的情况请读者自行推断)①[(4ac-b^2)/4a,正无穷);②[t,正无穷)奇偶性:偶函数周期性:无解析式:①y=ax^2+bx+c[一般式]⑴a≠0⑵a>0,则抛物线开口朝上;a<0,则抛物线开口朝下;⑶极值点:(-b/2a,(4ac-b^2)/4a);⑷Δ=b^2-4ac,Δ>0,图象与x轴交于两点:([-b+√Δ]/2a,0)和([-b+√Δ]/2a,0);Δ=0,图象与x轴交于一点:(-b/2a,0);Δ<0,图象与x轴无交点;②y=a(x-h)^2+t[配方式]此时,对应极值点为(h,t),其中h=-b/2a,t=(4ac-b^2)/4a);3.反比例函数在平面直角坐标系上的图象为双曲线。
高中数学常见函数图像
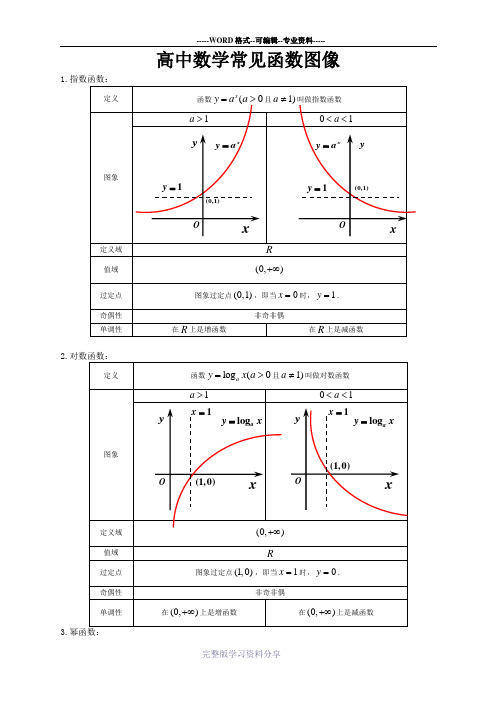
高中数学常见函数图像1.2.对数函数:3.定义形如αx y =(x ∈R )的函数称为幂函数,其中x 是自变量,α是常数.图像性质过定点:所有的幂函数在(0,)+∞都有定义,并且图象都通过点(1,1). 单调性:如果0α>,则幂函数的图象过原点,并且在[0,)+∞上为增函数.如果0α<,则幂函数的图象在(0,)+∞上为减函数,在第一象限内,图象无限接近x 轴与y 轴.4.函数sin y x =cos y x =tan y x =图象定义域R R,2x x k k ππ⎧⎫≠+∈Z ⎨⎬⎩⎭值域[]1,1-[]1,1-R最值当22x k ππ=+()k ∈Z 时,max 1y =;当22xk ππ=-()k ∈Z 时,min 1y =-.当()2x k k π=∈Z 时,max 1y =;当2xk ππ=+()k ∈Z 时,min 1y =-.既无最大值也无最小值周期性 2π2ππ奇偶性奇函数 偶函数奇函数单调性在2,222k k ππππ⎡⎤-+⎢⎥⎣⎦ ()k ∈Z 上是增函数;在32,222k k ππππ⎡⎤++⎢⎥⎣⎦()k ∈Z 上是减函数.在[]()2,2k k k πππ-∈Z 上是增函数;在[]2,2k k πππ+()k ∈Z 上是减函数.在,22k k ππππ⎛⎫-+⎪⎝⎭()k ∈Z 上是增函数.对称性对称中心()(),0k k π∈Z对称轴()2x k k ππ=+∈Z对称中心(),02k k ππ⎛⎫+∈Z⎪⎝⎭ 对称轴()x k k π=∈Z对称中心(),02k k π⎛⎫∈Z ⎪⎝⎭无对称轴。
高中数学常见函数图像

高中数学罕见函数图像之马矢奏春创作1.指数函数:定义 函数(0xy a a =>且1)a ≠叫做指数函数 图象 1a >01a <<定义域 R 值域 (0,)+∞ 过定点 图象过定点(0,1),即当0x =时,1y =.奇偶性 非奇非偶单调性在R 上是增函数 在R 上是减函数 2.对数函数:定义函数log (0a y x a =>且1)a ≠叫做对数函数图象1a > 01a <<定义域 (0,)+∞ 值域 R过定点 图象过定点(1,0),即当1x =时,0y =.奇偶性 非奇非偶单调性在(0,)+∞上是增函数 在(0,)+∞上是减函数 3.幂函数:定义形如αx y =(x ∈R )的函数称为幂函数,其中x 是自变量,α是常数.图像性质过定点:所有的幂函数在(0,)+∞都有定义,而且图象都通过点(1,1).单调性:如果0α>,则幂函数的图象过原点,而且在[0,)+∞上为增函数.如果0α<,则幂函数的图象在(0,)+∞上为减函数,在第一象限内,图象无限接近x 轴与y 轴.xa y =xy(0,1)O 1y =x a y =xy (0,1)O 1y =x y O (1,0)1x =log a y x=x yO (1,0)1x =log a y x =4.函数sin y x =cos y x = tan y x =图象定义域 R R,2x x k k ππ⎧⎫≠+∈Z ⎨⎬⎩⎭值域[]1,1-[]1,1-R最值当22x k ππ=+()k ∈Z 时,max 1y =;当22x k ππ=-()k ∈Z 时,min 1y =-.当()2x k k π=∈Z 时,max 1y =;当2xk ππ=+()k ∈Z 时,min 1y =-.既无最大值也无最小值周期性 2π 2ππ奇偶性奇函数偶函数奇函数单调性在2,222k k ππππ⎡⎤-+⎢⎥⎣⎦ ()k ∈Z 上是增函数;在32,222k k ππππ⎡⎤++⎢⎥⎣⎦ ()k ∈Z 上是减函数.在[]()2,2k k k πππ-∈Z 上是增函数;在[]2,2k k πππ+()k ∈Z 上是减函数.在,22k k ππππ⎛⎫-+ ⎪⎝⎭ ()k ∈Z 上是增函数.对称性对称中心()(),0k k π∈Z对称轴()2x k k ππ=+∈Z对称中心(),02k k ππ⎛⎫+∈Z⎪⎝⎭ 对称轴()x k k π=∈Z对称中心(),02k k π⎛⎫∈Z ⎪⎝⎭无对称轴。
函数图像总结

函数图像总结函数图像总结函数图像总结一基本函数图像1y=kx(x≠0)2y=kx+b(k≠0)3y4yax2bxc(a0)5yxa6yxk(k0)xk(k0)7yax(a 0,a1)x8ylogax(a0,a1)二抽象图像平移f(x)f(x+1)f(x)f(x-1)f(x)f(x)+1f(x)f(x)-1f(x)f(2x)f(x)2f(x) f(x)f(2x+2)y=f(-x)变成y=f(-x+2)练习:cosxcos2xcos2xcos(2x+4)cosxcos2x+4三图像的变换1f(x)f(|x|)保留y轴右边的,左边关于右边y轴对称2f(x)|f(x)|保留x轴上方的,下方关于x轴对称3f(x)f(-x)y轴对称4f(x)-f(x)x轴对称5f(x)-f(-x)原点对称6f(x)f(|x+1|)先根据1方法变成f(|x|),在向左平移一个单位得到f(|x+1|)7f(x)f(|x|+1)先向左平移一个单位得到f(x+1),再根据1方法变成f(|x|+1)8f(x)与f1(x)的图象关于直线yx对称联想点(x,y),(y,x)9f(x)与f(2ax)的图象关于点(a,0)对称egf(x)= 2x与g(x)=-2x关于对称一、函数yf(x)与函数yf(x)的图象关系函数yf(x)的图象是由yf(x)的图象经沿y轴翻折180°而得到的(即关于y轴对称)。
注意它与函数yf(x)满足f(x)f(x)的图象是不同的,前者代表两个函数,后者表示函数yf(x)本身是关于y轴对称的。
(二)伸缩变换及其应用:函数yaf(bx)的图像可以看作是由函数yf(x)的图像先将横坐标伸长(|b|<1)或缩短(|b|>1)到原来的1倍,再把纵坐标伸长(|a|>1)或缩短(|a|<1)到原来的|a|倍即可得到。
如:|b|1的图像x1要求:1会画y=|x+1|y=-2会画f(x)=lg|x|以及f(x)=|lgx|3会画f(x)=|lg|x+1||以及f(x)=x2-4|x|+5f(x)=|x2-2x-3|二1由图像可知f(x+1)为偶函数对称轴为2由图像可知f(x+1)为奇函数关于点(,)对称Eg、对a,bR,记max{a,b}=(A)0(B) a,ab,函数f(x)=max{|x+1|,|x-2|}(xR)的最小值是b,a<b13(C)(D)3901(选讲)1、yf(x)绕原点顺时针方向旋转;yf(x)12、yf(x);yf (x)绕原点逆时针方向旋转9000yQP(a,b)(yf(x)yQ1xP1(b,a)(yf1(x))P(a,b)(yf(x)0P1(b,a)1(yf(x))0(乙)x(甲)(图五)0说明:关于绕原点旋转180的变换实际上就是关于原点对称的问题。
函数图像总结

函数图像总结函数图像总结函数图像总结一基本函数图像1y=kx(x≠0)2y=kx+b(k≠0)3y4yax2bxc(a0)5yxa6yxk(k0)xk(k0)7yax(a 0,a1)x8ylogax(a0,a1)二抽象图像平移f(x)f(x+1)f(x)f(x-1)f(x)f(x)+1f(x)f(x)-1f(x)f(2x)f(x)2f(x) f(x)f(2x+2)y=f(-x)变成y=f(-x+2)练习:cosxcos2xcos2xcos(2x+4)cosxcos2x+4三图像的变换1f(x)f(|x|)保留y轴右边的,左边关于右边y轴对称2f(x)|f(x)|保留x轴上方的,下方关于x轴对称3f(x)f(-x)y轴对称4f(x)-f(x)x轴对称5f(x)-f(-x)原点对称6f(x)f(|x+1|)先根据1方法变成f(|x|),在向左平移一个单位得到f(|x+1|)7f(x)f(|x|+1)先向左平移一个单位得到f(x+1),再根据1方法变成f(|x|+1)8f(x)与f1(x)的图象关于直线yx对称联想点(x,y),(y,x)9f(x)与f(2ax)的图象关于点(a,0)对称egf(x)= 2x与g(x)=-2x关于对称一、函数yf(x)与函数yf(x)的图象关系函数yf(x)的图象是由yf(x)的图象经沿y轴翻折180°而得到的(即关于y轴对称)。
注意它与函数yf(x)满足f(x)f(x)的图象是不同的,前者代表两个函数,后者表示函数yf(x)本身是关于y轴对称的。
(二)伸缩变换及其应用:函数yaf(bx)的图像可以看作是由函数yf(x)的图像先将横坐标伸长(|b|<1)或缩短(|b|>1)到原来的1倍,再把纵坐标伸长(|a|>1)或缩短(|a|<1)到原来的|a|倍即可得到。
如:|b|1的图像x1要求:1会画y=|x+1|y=-2会画f(x)=lg|x|以及f(x)=|lgx|3会画f(x)=|lg|x+1||以及f(x)=x2-4|x|+5f(x)=|x2-2x-3|二1由图像可知f(x+1)为偶函数对称轴为2由图像可知f(x+1)为奇函数关于点(,)对称Eg、对a,bR,记max{a,b}=(A)0(B) a,ab,函数f(x)=max{|x+1|,|x-2|}(xR)的最小值是b,a<b13(C)(D)3901(选讲)1、yf(x)绕原点顺时针方向旋转;yf(x)12、yf(x);yf (x)绕原点逆时针方向旋转9000yQP(a,b)(yf(x)yQ1xP1(b,a)(yf1(x))P(a,b)(yf(x)0P1(b,a)1(yf(x))0(乙)x(甲)(图五)0说明:关于绕原点旋转180的变换实际上就是关于原点对称的问题。
(完整版)高中数学常见函数图像

高中数学常见函数图像1.2.对数函数:3.幂函数:定义形如αxy=(x∈R)的函数称为幂函数,其中x是自变量,α是常数.图像性质过定点:所有的幂函数在(0,)+∞都有定义,并且图象都通过点(1,1).单调性:如果0α>,则幂函数的图象过原点,并且在[0,)+∞上为增函数.如果0α<,则幂函数的图象在(0,)+∞上为减函数,在第一象限内,图象无限接近x轴与y轴.4.函数sin y x =cos y x = tan y x =图象定义域R R,2x x k k ππ⎧⎫≠+∈Z ⎨⎬⎩⎭值域[]1,1-[]1,1-R最值当22x k ππ=+()k ∈Z 时,max 1y =; 当22xk ππ=-()k ∈Z 时,min 1y =-.当()2x k k π=∈Z 时,max 1y =;当2x k ππ=+()k ∈Z 时,min 1y =-.既无最大值也无最小值周期性 2π2ππ奇偶性奇函数 偶函数 奇函数单调性在2,222k k ππππ⎡⎤-+⎢⎥⎣⎦()k ∈Z 上是增函数;在32,222k k ππππ⎡⎤++⎢⎥⎣⎦ ()k ∈Z 上是减函数.在[]()2,2k k k πππ-∈Z 上是增函数;在[]2,2k k πππ+()k ∈Z 上是减函数.在,22k k ππππ⎛⎫-+⎪⎝⎭()k ∈Z 上是增函数.对称性对称中心()(),0k k π∈Z对称轴()2x k k ππ=+∈Z对称中心(),02k k ππ⎛⎫+∈Z⎪⎝⎭ 对称轴()x k k π=∈Z对称中心(),02k k π⎛⎫∈Z ⎪⎝⎭无对称轴。
五大基本初等函数性质及其图像

五、基本初等函数及其性质和图形1.幂函数函数称为幂函数。
如,,,都是幂函数。
没有统一的定义域,定义域由值确定。
如,。
但在内总是有定义的,且都经过(1,1)点。
当时,函数在上是单调增加的,当时,函数在内是单调减少的。
下面给出几个常用的幂函数:的图形,如图1-1-2、图1-1-3。
图1-1-2图1-1-32.指数函数函数称为指数函数,定义域,值域;当时函数为单调增加的;当时为单调减少的,曲线过点。
高等数学中常用的指数函数是时,即。
以与为例绘出图形,如图1-1-4。
图1-1-43.对数函数函数称为对数函数,其定义域,值域。
当时单调增加,当时单调减少,曲线过(1,0)点,都在右半平面内。
与互为反函数。
当时的对数函数称为自然对数,当时,称为常用对数。
以为例绘出图形,如图1-1-5。
图1-1-54.三角函数有,它们都是周期函数。
对三角函数作简要的叙述:(1)正弦函数与余弦函数:与定义域都是,值域都是。
它们都是有界函数,周期都是,为奇函数,为偶函数。
图形为图1-1-6、图1-1-7。
图1-1-6 正弦函数图形图1-1-7 余弦函数图形(2)正切函数,定义域,值域为。
周期,在其定义域内单调增加的奇函数,图形为图1-1-8图1-1-8(3)余切函数,定义域,值域为,周期。
在定义域内是单调减少的奇函数,图形如图1-1-9。
图1-1-9(4)正割函数,定义域,值域为,为无界函数,周期的偶函数,图形如图1-1-10。
图1-1-10(5)余割函数,定义域,值域为,为无界函数,周期在定义域为奇函数,图形如图1-1-11。
图1-1-115.反三角函数反正弦函数,定义域,值域,为有界函数,在其定义域内是单调增加的奇函数,图形如图1-1-12;图1-1-12,为有界函数,在其定义域内为单调减少的非奇非偶函数,图形如图1-1-13;图1-1-13反正切函数,定义域,值域为,为有界函数,在定义域内是单调增加的奇函数,图形如图1-1-14;图1-1-14为有界函数,在其定义域内单调减少的非奇非偶函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y
(0,1) 0
y
像
(0,1)
y=1
x
0
x
性 质
1、定义域为R; 2、值域为(0,+∞ ) 3、图象过定点(0,1)
4、在R上是增函数
在R上是减函数
例4.求下列函数的定义域 ⑴
王新敞
奎屯 新疆
y 0.4
1 x 1
⑵ ⑶
y 3
x
5 x1
y 2 1
1 x 3、比较函数 y 2 ( x R)与函数 y ( ) 图像 2
log c b log a b = (a > 0且a ? 1, c 0且c ? 1, b 0) logc a
(二)对数运算性质的运用
例1、若 a > 0, a ? 1, x
y > 0, n N *,则下列各式中:
n
(1)(loga x ) = n loga x
1 (3) log a x = - log a x
( 0,+∞) R 即当x =1时,y=0
在(0,+∞)上是 减函数 当x>1时, y<0 当x=1时, y=0 当0<x<1时,y>0
(3)根据对称性(关于x轴对称)已知 的图象,你能画出 ?
3
f (x ) log1 x
o
1
x
(4)当 0<a<1时与a>1时的图象又怎么画呢?
(D)b < a < c
一、选择题(每小题3分,共15分)
1.若函数y=(x+1)(x-a)为偶函数,则a等于(
(A)-2 (B)-1 (C )1 (D )2
)
【解析】选C.∵y=(x+1)(x-a)=x2+(1-a)x-a是偶函数.
∴1-a=0,∴a=1.
2.已知函数f(x)为R上的减函数,则满足f(|x|)<f(1)的实数x
高中数学必修一常见函数图像
阳信二中 团结协作 无私奉献 创造辉煌
函数y=x的图像
例2、旅行社为某旅游团包飞机去旅 游,其中旅行社的包机费为15000元, 旅游团中的每人的飞机票按以下方式 与旅行社结算:若旅游团的人数在 30人或30人以下,飞机票每张收费 900元;若旅游团的人数多于30人, 则给与优惠,每多1人,机票费每张 减少10元,但旅游团的人数最多有 75人,那么旅游团的人数为多少时, 旅行社可获得的利润最大?
的取值范围是( (A)(-1,1) ) (B)(0,1)
(C)(-1,0)∪(0,1) (D)(-∞,-1)∪(1,+∞) 【解析】选D.∵f(x)在R上为减函数且f(|x|)<f(1), ∴|x|>1,解得x>1或x<-1.
例,已知函数 f (x )(x Î R ), 是奇函数, f ( x) f (x ) = 2x - 1, 且当 时, 求函 x 0 数 的解析式。
2
(一)知识梳理
1、对数的运算性质
如果a > 0 , a ≠ 1 , M > 0 , N > 0,那么:
loga MN = loga M + loga N M log a = log a M - log a N N
loga M n = n loga M
log a m N
n
n = log a N m 2、换底公式:
变式训练
3x 5, x 0 已知函数f ( x) x 5, 0 x 1, 2 x 8, x 1 3 1 (1)求f ( ), f ( ), f ( 1), f f ( 2) 的值. 2 (2)作出函数f ( x)的图象.
(2)
3 3 (1)解:f ( ) 2 8 5, 2 2 1 1 f ( ) 5, f (1) 1 3 5 2, f f (2) f (1) 2.
x
y
1 x y ( ),x R 2
(0,1)
y 2 ,x R
x
y=1
0
x
对数函数y=logax (a>0,且
a≠1)
图 象 性 质
的图象与性质
0<a<1
a>1
定义域 : 值 域 : (1 ,0), 过定点 在(0,+∞)上是 增函数 当x>1时, y>0 当x=1时, y=0 当0<x<1时,y<0
b , 在 2a
x
在(-∞,0) 和(0,+∞) 是增函数
b , 在 2a
o
x
减函数
增函数 b - 在 - , 2a 减函数
指数函数 y a (a
x
0, a 1) 的图像和性质
0<a<1
a>1
图
y=1
A = {x 2m - 1 x
• 若
3m + 2}, B = {x x ? 2或x
5},
A
B 蛊 , 实数m的取值范围。
• 活页115页 19,20,22题
常见问题 你掌握了多少?
团 结 进 取 自 强 不 息
1 n (5) log a x = log a x n
(2)(loga x )n = loga x n
loga x y (4) = loga loga y x
1 (6) log a x = log a n x n
n
(7)loga x = logan x
其中成立的有(
x- y x +y (8) loga = - loga x +y x- y
1
0
1
y loga2 x y loga3 x
x
y loga4 x
y loga5 x y loga6 x
法2:做直线y=1,观察与各图像交点横坐标即可知道底数大小。
y x3
y x2
yx
yx
1 2
y x 1
幂函数的性质 (1) 所有的幂函数在(0,+∞)都有定义,并 且图象都通过点(1,1); (2) 如果α>0,则幂函数图象过原点, 并且在区间[0,+∞)上是增函数; (3) 如果α<0,则幂函数图象在区间 (0,+∞)上是减函数; (4) 当α为奇数时,幂函数为奇函数; 当α为偶数时,幂函数为偶函数.
y
图 形
y=log
2
x
y=log
10
x
0
1
y=log
0.5
y=log 0.1 x x
x
补充 底数互为倒数的两个对数函数的图象 性质 关于x轴对称。 一 补充 底数a>1时,底数越大,其图象越接近x 性质 轴。 底数0<a<1时,底数越小,其图象越接近 二
x轴。
下列是6个对数函数的图象比较它们底数的大小 法一: 规律:在 x=1的右边看图象,图象越高 底数越小. y y loga x 即图高底小
)
(A)3个
(B)4个
(C)5个
(D)6个
2 2 例2 : lg 25 + lg 8 + lg 5?lg 20 lg 2 = 3
ln 2 ln 3 ln 5 练习 1: 若a = ,b = ,c = , 则( ) 2 3 5
(A)a < b < c (B)c < b < a
(C)c < a < b
例,画出函数 y = - x 2 + 2 x +1 出函数的单调区间。
的图像并写
• 求函数的定义域
1 f (x ) = x + 2 + 2 x -x-6
f (x ) = x - 1 + 1 - x
a • 判断函数 f (x ) = x + x 的单调性。
在 (1, +
)
上
• 活页93页 • 已知集合
学习案
2.作出下列函数的图象
4 y 3 2 1 -2 -1 o 1 2 3 x
(1) y x 2( x Z , 且 x 2)
4 (2) y ( x 4且x 0) x
补充练习:求下列各式中x的值。
log2 (log5 x ) = 1
log 4 [log3 (log 1 x )] = 0
学习案
学点二 分段函数 1.画出函数
y x 的图象.
y
由绝对值的集合意义知,
x, x ≥ 0, y 图像如下: x, x 0.
o
x
观察下面两组图像,它们是否也有对称性呢?
y
(1)
O x
fx =
x3
1 f ( x ) ( x 0) x
(2)
y
-1
O
1
x
f(x)=x2
熟 练 记 忆
fx = x
练一练:
判断函数的奇偶性:
f x x 1 1 x
2
2
y o
y
y x
在(-∞,+∞) 是减函数
o y o y
x
在(-∞,+∞) 是增函数
o
y o x
在(-∞,0) x 和(0,+∞) 是减函数
b - 在 - , 2a 增函数
