热力学方程简单介绍补充
物理化学 0304热力学基本方程
1G＝ 5G 0
Vdp
G
H2O(s) T=263.15K p=101.325kPa
1G
H2O(l) T=263.15K p(l)=611Pa
等温可逆
5G
H2O(s) T=263.15K p(s)=552Pa
1G V l p
Pa V l 611 101326
p2 G＝nRT ln p1
4
例：已知263.15K时H2O(s)和H2O(l)的饱和蒸气压分别为
H2O(l) 不可逆相变 解： T2=263.15K sl H m ( 263K ) (1)G 0 P=101.325kPa sl S m ( 263K ) G (2)有两种解法： H 1 可逆 S 1
A G S T V T p
dA SdT pdV dG SdT Vdp dU TdS pdV dA SdT pdV dH TdS Vdp dG SdT Vdp
U A p V S V T
解一：
G H TS
H2O(l) T2=273.15K P=101.325kPa S ( 273 K ) l m
263 S ( 263K )＝S ( 273K ) m[C p ,m ( s ) C p ,m ( l )]ln 273
H (263K ) H (273K ) nC p,m T
各状态函数之间的关系
pV pV G
H U A
TS TS
H=PV+U A=U-TS G=H-TS =U+PV-TS =A+PV
9
dS Q r / T dU Q W dU TdS pdV
写出四个热力学基本方程
写出四个热力学基本方程
1.热力学的四个基本公式：dU=TdS-PdV；dH=TdS+VdP；
dF=-SdT-PdV；dG=-SdT+VdP。
热力学是从宏观角度研究物质的热运动性质及其规律的学科。
属于物理学的分支，它与统计物理学分别构成了热学理论的宏观和微观两个方面。
热力学定律，是描述物理学中热学规律的定律，包括热力学第零定律、热力学第一定律、热力学第二定律和热力学第三定律。
其中热力学第零定律又称为热平衡定律，这是因为热力学第一、第二定律发现后才认识到这一规律的重要性；热力学第一定律是能量守恒与转换定律在热现象中的应用；热力学第二定律有多种表述，也叫熵增加原理。
热力学第一定律也就是能量守恒定律。
自从焦耳以无以辩驳的精确实验结果证明机械能、电能、内能之间的转化满足守恒关系之后，人们就认为能量守恒定律是自然界的一个普遍的基本规律。
热力学第二定律的每一种表述，都揭示了大量分子参与的宏观过程的方向性，使人们认识到自然界中进行的涉及热现象的宏观过程都具有方向性。
2.热力学第二定律的英文解释是熵是趋向于总体增大,比如
1L90度水(A)和1L10度水(B)融合,不会是A的温度增加而 B的温度减小，因为如此的话，总体的熵减小。
如果A 温度降但B温度升高一点，其总体的熵增加。
热力学第三
定律通常表述为绝对零度时，所有纯物质的完美晶体的熵值为零。
或者绝对零度（T=0K即-273.15℃）不可达到。
R.H.否勒和 E.A.古根海姆还提出热力学第三定律的另一种表述形式：任何系统都不能通过有限的步骤使自身温度降低到0K，称为0K不能达到原理。
物理化学热力学基本方程
利用全微分条件 ，将其作用于(5.1)、(5.2)、(5.4)和(5.6)式，得到(5.8)~(5.11)式所 给八个热力学偏导数的关系：
如果有全微分 df adx ( T ， p ) bdy / 则 S (a / y ) x (b / x ) y 必有
( T / V ) S ( p / S )V (V / S ) p ( p / T )V ( S / V ) T (V / T ) p ( S / p )T
p S T V V T
S V p T T p
G H TS
dG SdT V dp
V (G / p )T
当系统处于平衡态时，不仅描述该系统整体性质的宏观量不再随时 间改变，而且这些宏观量之间还存在着函数关系。只有少数几个是 独立态参量，其余宏观量则是态参量的函数。对于给定的系统，其 态参量的数目是确定的，但选哪几个宏观量作为态参量则是任意的。
我们可以将(5.1)式看成以S和V为独立变量表示的全微分dU ,U=U(S,V), 于是写为
dU ( U / S ) V dS ( U / V ) S dV
可以与(5.1)式比较，得到两个偏导数：
T ( U / S )V
p (U / V ) S
(5.8)
H U p V U (U / V ) S V F U T S U ( U / S )V S G U pV TS
U ( U / V ) S V ( U / S )V S
这说明，只要已知以S，V为独立态参量时内能U的表达式U=U（S,V）， 就可以求得T，状态方程，p，H，F，G乃至系统的全部热力学量。所 以内能U是以S、V为独立态参量的特性函数。同样可以证明焓H，自由 能F和自由焓G分别是以(S,p)，(T,V)和(T,p) 为独立态参量的特性函数。
热力学方程
；或根据已知的蒸 气压方程对比1/T项的系数
§3.10 吉布斯-亥姆霍兹方程和麦 克斯韦关系式
• 10.1 吉布斯-亥姆霍兹方程
从热力学基本方程可以导出下面关系式：
( A / T )
T
V
U T2
§3.9 克拉佩龙方程
• 9.2 固-液平衡、固-固平衡积分式
★凝聚相之间的两相平衡的定性讨论
Vm很小
熔化平衡：fusHm很大，dT/dp很小，外压对熔点的影响很小 晶型转变平衡：trsHm较小，因而dT/dp比熔化平衡大
★定量计算的相关近似处理
以熔化平衡为例
dT dp
T Vm Hm
ⅰ凝聚相与蒸气相之间的两相平衡 ⅱ凝聚相的体积忽略不计 ⅲ蒸气看成理想气体 ⅳ积分时将摩尔相变焓看成常数
★微分形式
d ln p vap Hm
dT
RT 2
★定积分形式
计算题型：
ln
p2 p1
vap Hm R
1
T1
1 T2
五个物理量 已知任意四 个求第五个
★不定积分形式
ln p vap Hm 1 C RT
fusVm , fusHm不变 ln T2 T1
V fus m fus H m
( p2
p1 )
ln(1T /T1)T /T1 T
T1
V fus m fus Hm
p
问：滑冰运动员冰鞋下冰的熔点怎样变化？
§3.9 克拉佩龙方程
• 9.3 克劳修斯-克拉佩龙方程
x
z y
x
9热力学基本方程
推导热力学函数间关系时，也常用到麦克斯韦关系式
麦克斯韦关系式中不含：
S T
p
和
S
T
V
问题 S ?
T p
S ? T V
解：dH= TdS+Vdp
定压下，除以dT
H T S T p T p
得 S Cp
T p T
而
Cp
H T
p
同理可得：
G
G3
nRTln
p2 p1
28.314 373 .15 ln 50
101 .325
J 4.38
kJ 0
GT,p 4.38 kJ 0
由吉布斯函数判据可知，过程自发进行。
A G ( pV ) G nRT 4.38 kJ 28.314373103 kJ 10.58 kJ
1.15 热力学函数的基本关系式
定量，定组成的单相系统； 纯物质是定组成的一种特例 保持相平衡及化学平衡的系统
热力学基本方程的应用：
计算纯物质 p、V、T 变化过程的ΔA、ΔG
dA=－SdT－ pdV dG=－SdT+Vdp
AT
V2 V1
pdV
GT
p2 Vdp
p1
2. 麦克斯韦关系式
表明S、T、p、V 间的关系式
S p V T T V
p T S V V S
V S
p
T p
S
S p V T T V
S p
T
V T
p
几点结论：
麦克斯韦关系式表示：系统在同一状态的两种变 化率数值相等
S p V T T V
S p
T
V T
p
该式提供了可由实验直接测定的量，替代不能直接 测定的量
3.7 热力学基本方程及Maxwell关系式
恒T、p、W= 0： G 0
自发 平衡
dGm α dGm β Sm α dT Vm α dp Sm β dT
Vm β dp
[Sm β Sm α ]dT [Vm β Vm α ]dp
dp Sm β Sm α
βαSm
dT Vm β Vm α
βαVm
又因 βαSm
βαHm T
dp dT
βαH m T βαVm
U
SV
H
A
pT
G
说明： 1. 等式右边只有四个物理量T，S， p，V
2. 十字交叉法：
对U来说，S，V分别表示dS和dV； dS对角线 对应T，dV对角线对应p；箭头方向表示正负，指向 为负，则为TdS和 –pdV
2. U、H、A、G的一阶偏导数关系式
U f (S,V ) H f (S, p) A f (T ,V ) G f (T , p)
p
S V
T
p T
V
V T
p
S p
T
T V
S
p S
V
T p
S
V S
p
S V
T
p T
V
V T
p
S p
T
说明：
1. 关系式中只有四个物理量T， S， p，V
2. 对角线乘积为 TS 与 pV
3. 等式两边的分母与下标互换
4. S和V为广度量，而T和p为强 度量。同种性质的状态函数 的分式，不取负号。
分析：利用克拉佩龙方程 dT T βαVm
dp 解：由克拉佩龙方程有 dT
T
βαH m
lsVm lsH m
dp
积分，得 lnT2
T1
热力学方程
dQm C m dT
Q C m dT C （ m T2 T1 )
T1
二、理想气体的摩尔热容量
1、理想气体的定体摩尔热容量
dQ dE pdV
CV，m
(dQm） dE i V R dT dT 2 i R 2
CV，m
i 理想气体 dE RdT 2 3 单原子理想气体 CV ,m R 2 双原子理想气体 CV ,m 5 R 2 多原子理想气体 CV ,m 3 R
4）系统内能改变的两种方式 10、做功可以改变系统的状态 摩擦升温（机械功）、电加热（电功） 功是过程量 20、热量传递可以改变系统的内能
热量是过程量
内能是状态量。
使系统的状态改变，传热和作功是等效的。 作功是系统内能与外界其它形式能量转换的量度。
热量是系统与外界能量转换的量度。
准静态过程
当热力学系统在外界影响下，从一个状态到另一 个状态的变化过程，称为热力学过程，简称过程。 热力学过程 准静态过程
QV M
等体过程中
摩尔气体吸热为：
CV , m T
理想气体的内能另一种表述：E
M
CV , mT
2、理想气体的定压摩尔热容量
dQ dE pdV
M
M i2 mol： Qp C p ,m T RT 2 M
Q E W
Q E W 热力学第一定律的普遍形式
dQ dE dW 无限小过程
规定 Q>0，系统吸收热量；Q<0,系统放出热量； W>0, 系统对外作功；W<0,外界对系统作功；
E>0,系统内能增加，E<0,系统内能减少。
Q E W
热力学方程
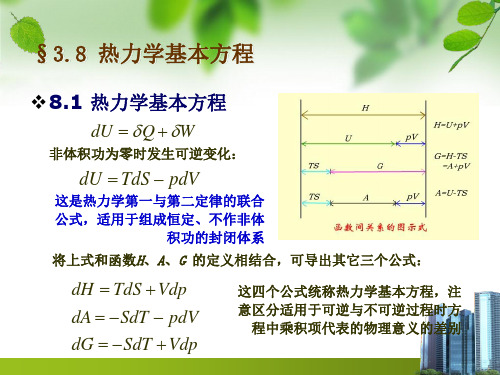
克斯韦关系式
❖10.2 麦克斯韦关系式
将上述导出结果用于热力学基本方程：
dU
TdS
pdV
T V
S
p S
V
dH
TdS
Vdp
T p
S
V S
p
dA
SdT
pdV
S V
T
பைடு நூலகம்
p T
V
dG
SdT
Vdp
S p
T
V T
p
这四个关系式统称 麦克斯韦关系式， 它们的重要意义在 于把不可直接测定 的量转化为可直接
测定量
§3.8 热力学基本方程
❖8.1 热力学基本方程
dU Q W
非体积功为零时发生可逆变化：
dU TdS pdV
这是热力学第一与第二定律的联合 公式，适用于组成恒定、不作非体
积功的封闭体系
将上式和函数H、A、G 的定义相结合，可导出其它三个公式：
dH TdS Vdp dA SdT pdV dG SdT Vdp
这四个公式统称热力学基本方程，注 意区分适用于可逆与不可逆过程时方
程中乘积项代表的物理意义的差别
§3.8 热力学基本方程
❖8.2 热力学基本方程的应用
计算纯物质pVT变化过程的ΔA及ΔG
dA SdT pdV
dG SdT Vdp
★理想气体：
AT
nRT
ln V2 V1
GT
nRT
ln
p2 p1
dAT pdV dGT Vdp
★凝聚系统：
AT
V2 V1
pdV
0
GT
p2 Vdp V p
p1
§3.9 克拉佩龙方程
大学物理热力学公式
气体动理论
理想气体状态方程
PV M RT 或 Mmol
PnkT
压强:
p
2 3
n k
温度:
k
3 2
kT
对于质量为M,摩尔质量为Mmol,理想气体内能
E
i 2
M Mmol
RT
i RT
2
热力学
一、热力学第一定律 QE2E 1A 二、理想气体的等值过程
CV
iR 2
Cp CVR
过 程 特 征 过程方程 Q
Very important
△E
A
等 体 V C 等 压 PC
P C T V C T
等 温 T C PVC
绝热
PV C
M MmolCv(T2
T1)
M MmolCv(T2
T1)
0
MMmolCp(T2 T1)
M RTlnV2
Mmol
V1
MMmolCV(T2 T1) P(V2V1)
0
M RTlnV2
Mmol
V1
0
M MmolCV(T2 T1)
M MmolCV(T2
T1)
三、 循环过程 卡诺循环
P
A
PA
a
A
b
PB
B
O
VA
热机效率：
VB V
高温热源T1 Q吸
热机
A
热力学基本方程和平衡条件
p , ni
T
G As
As
G T
S As
T , p,ni
2.界面相的热力学基本方程(fundamental equations for interfacial phases)
1. 界面层不能独立存在，界面性质由平衡的两个 主体相性质决定，界面层难以严格界定。
2. 界面层非均匀，存在压力、浓度梯度。
Gibbs模型小结
界面层的位置和厚度很难严格界定，而界面层 的广延性质又依赖界面的位置和厚度，界面层非均 匀，存在压力梯度和浓度梯度，难以描述。
1. Gibbs模型取界面厚度为零，可以将界面广延 性质转而用界面过剩量表示；
2. Gibbs模型取溶剂界面过剩量为零，其实质等 价于确定了界面位置，这与1一起将界面层完 全确立，也使界面过剩性质的定义完备；
与平坦界面的
Gibbs认为多数情
张力近似相等
况下此项可忽略
每个主体相的热力学能变化：
dU (a ) TdS(a ) p(a )dV (a )
dn K
(a )
i1 i i
dU (b ) TdS(b ) p(b )dV (b )
dn K
(b )
i1 i i
得弯曲界面的热力学能微分式，与平坦界面相同：
T (a ) T (b ) T ( ) T
p(a ) p(b ) (dAs / dV (a ) )
平面dAs / dV (a ) 0 p(a ) p(b ) p
(a ) i
(b ) i
( ) i
i
B
B
B
0
了解一下：有界面相时的平衡条件的推导
出发点：平衡判据中的熵判据
δSU,V ,W0 0
热力学知识：热力学中物态方程和状态方程
热力学知识：热力学中物态方程和状态方程导言：热力学是物理学中一个重要的分支，以研究物质的热现象和能源转化为主要内容。
物态方程和状态方程是其中的重要概念，作为建立热力学模型的重要工具，广泛应用于自然科学领域，特别是化学、材料科学、环境科学等领域。
本文将介绍物态方程和状态方程的概念、定义以及应用，帮助读者更加深入理解热力学基本知识。
一、物态方程的概念和定义物态方程，简称态方程，是热力学中描述物质状态的方程，它通过描述温度、压力、体积、物质的量等参数之间的关系，来表征物质的状态。
广义的物态方程可以描述固体、液体和气体的状态。
不同物质的物态方程不同，相同物质在不同环境下物态方程也不同。
下面我们逐一介绍几种常见的物态方程。
1.理想气体状态方程理想气体状态方程是描述理想气体状态的经典方程，其公式为：PV = nRT其中，P表示气体的压强，V表示气体的体积，n表示气体的物质的量，T表示气体的温度，R为普适气体常数。
这个方程表明，当方程两边保持相等的情况下，一定能够精确地描述理想气体的状态。
2.凝聚态物质状态方程凝聚态物质包括固体和液体两种状态，分别有不同的物态方程。
在热力学中，固体和液体状态的物态方程非常多，具体的方程也各自不同。
但是可以统一的是，凝聚态物质的物态方程需要考虑温度、压强、物质的密度等因素，其数学形式也更加复杂，不再是简单的线性函数关系。
3.物态方程的应用举例物态方程广泛应用于各种领域，如化学、材料科学、环境科学等。
例如在燃料电池中，物态方程可以帮助我们建立氢气氧气反应的热力学模型，以描绘反应的特性，从而满足燃料电池产生电能的需求。
再比如，在化学反应中，物态方程能够帮助我们确定气态反应物和产物的浓度，从而计算反应的进程。
二、状态方程的概念和定义状态方程是热力学的另一重要概念，通常定义为系统状态参数之间的函数关系。
与物态方程不同，状态方程是相对广义的，既可以描述单一物质的状态，也可以描述多相系物质的状态。
化学反应热力学方程解析与实验应用
化学反应热力学方程解析与实验应用热力学是研究热量与能量转化的科学，而热力学方程则是描述化学反应过程中产生或吸收热量的数学表达式。
本文将解析化学反应热力学方程的基本原理，并探讨其在实验应用中的重要性。
一、热力学方程的基本原理1. 热化学方程的表示形式化学反应热力学方程一般采用如下形式表示：aA + bB → cC + dD + Q其中，a、b、c、d分别表示反应物与生成物的系数，Q表示反应过程释放或吸收的热量。
这种表示形式简洁明了，能够准确描述反应过程中的能量变化情况。
2. 热力学方程的计算在化学反应中，反应物与生成物的热化学方程式中，每个物质的系数代表其摩尔数比例。
根据热化学方程式，可以计算反应物与生成物的摩尔焓变（ΔH），即单位摩尔物质在反应过程中释放或吸收的热量。
ΔH可通过使用热量计等实验装置测量得到，也可以通过计算得出。
二、实验应用1. 反应热的测定热力学方程的应用之一是测定反应热。
通过实验控制反应物的摩尔比例，测量反应前后的温度变化，可以计算出反应的摩尔焓变（ΔH）。
这种方法被广泛应用于工业反应热的测定、燃料热值的测定等领域。
2. 化学平衡与热力学方程热力学方程对于描述化学反应平衡也起到了重要的作用。
根据热力学方程，可以计算出化学反应的标准焓变（ΔH°），并以此判断反应的热力学稳定性。
当ΔH°为负值时，反应为放热反应，有利于反应的进行；当ΔH°为正值时，反应为吸热反应，反应的进行受到限制。
3. 反应机理的解析热力学方程还可以帮助解析化学反应的机理。
通过对反应物与生成物之间的能量转化进行分析，可以揭示化学反应发生的具体过程。
这对于深入理解和控制化学反应过程具有重要意义。
4. 优化反应条件热力学方程可以用于优化化学反应的条件。
通过计算不同反应条件下的ΔH，可以确定在何种条件下反应的放热或吸热程度最大，从而确定最适宜的反应条件。
总结：化学反应热力学方程是研究化学反应热量变化的重要工具。
热力学基本方程
二、处于扩散接触子系统的平衡 温度
• 熵有极大值的条件是：
∂S1 ∂S2 ∂S1 ∂S2 dE1 + dE2 + dN1 + dN2 = 0 ∂E1 E =E , N ,V ∂E2 E =E , N ,V ∂N1 N = N ,E ,V ∂N2 N = N , E ,V % % % % 1 1 1 1 2 2 2 2 1 1 1 1 2 2 2 2
T1 = T2 p1 = p2
四、热力学基本方程
态函数熵S=S ({ N k } ,U,V ) , 可得
∂S ∂S ∂S dS= dU+ dV+ ∑ dN k ∂U {N k },V ∂V {N k },U k ∂N k U ,V,N k ′≠ k
• 热平衡条件：
∂S1 ∂S2 = ∂U1 N ,V ∂U 2 N ,V 1 1 2 2
• 引入温度：
1 ∂S ∂ ln Ω = = kB T ∂U N ,V ∂U N ,V
T1 = T2
1 ∂S ∂ ln Ω = = kB T ∂U N ,V ∂U N ,V
∂ ln Ω i ∂S µ i = −Ti i = − k BTi ∂N I U ,V ∂N i U ,V i i i i
处于热接触子系统的平衡处于扩散接触子系统的平衡处于力学接触子系统的平衡温度化学势和压强热力学基本方程一处于热接触子系统的平衡温度dededndn二处于扩散接触子系统的平衡温度dededvdv三处于力学接触子系统的平衡温度态函数熵可得dsdudvdndutdspdvdndutdspdv开放系
热力学基本方程
f x y
lim
Δx 0
f ( x Δx, y) Δx
f (x, y)
Δf lim Δx0 Δx
y不变
dU TdS pdV dN
U T
p, N
lim
ΔT 0
ΔU ΔT
p, N
lim
ΔT 0
TΔS
pΔV ΔT
ΔN
p, N
T
lim
ΔT 0
ΔS ΔT
p, N
p
lim
dU
U T
V
dT
U V
T
dV
CV dT
U V
T
dV
类似的，焓的自然的独立变量是熵和压强，为方便 起见，焓的独立变量也常取为温度和压强
dH TdS Vdp
H T
p
dT
H p
T
dp
C pdT
H p
T
dp
了解一下：独立变量的选取
一对广义力和广义位移一般不被同时用作独立变量，比如 一般不将压力和体积都取作独立变量，否则，有可能出现 不能确定体系状态的现象，例如：压力为一个大气压下，4 摄氏度附近的水
T T ( p,Vm )
在压力和摩尔体积都
已经确定的情况下，
？
却不能确定体系温度
是多少。毛病就出在
同时取压力和体积作
为独立变量。
2.热力学基本方程的意义(implications of
fundamental equations)
热一：dU dQR dWR
dWR pdV
热二：dS dQR/ T 0
U U(S,V ) H H(S, p) A A(T ,V ) G G(T , p) 体系含有K种组分：U U (S,V , n1, n2 ,L , nK )，余类推
化学反应的热力学方程
化学反应的热力学方程化学反应中的热力学方程是描述反应物质之间热能转化关系的数学表达式。
热力学方程可以帮助我们理解反应的热效应以及相关物质之间的能量转移。
本文将探讨化学反应的热力学方程及其应用。
一、热力学方程的基本概念热力学方程是根据反应物质之间的能量转化关系建立的数学模型，可以用来计算反应的热效应。
常见的热力学方程包括热动力学平衡方程、吉布斯自由能方程和麦克斯韦关系等。
1. 热动力学平衡方程热动力学平衡方程描述了反应的热力学平衡状态，其数学表达式为：ΔG = ΔH - TΔS其中，ΔG表示反应的自由能变化，ΔH表示反应的焓变化，T表示反应的温度，ΔS表示反应的熵变化。
2. 吉布斯自由能方程吉布斯自由能方程是描述化学反应的自由能变化的数学表达式，其数学表达式为：ΔG = ΔG° + RTlnQ其中，ΔG表示反应的自由能变化，ΔG°表示标准状态下的反应的自由能变化，R表示气体常数，T表示反应的温度，Q表示反应的反应物浓度之比。
3. 麦克斯韦关系麦克斯韦关系是描述热力学量之间的关系的数学公式。
其中，常见的麦克斯韦关系有以下几种：- 对于单一组分的系统：(∂ΔG/∂T)p = -ΔH/T^2- 对于多组分的系统：(∂ΔG/∂T)p = -ΔH/T^2 + (∂(ΔG/∂P)T)（∂ΔG/∂P)T为ΔG对压强的偏导数。
二、热力学方程的应用举例热力学方程在化学反应研究和工业应用中起着重要的作用。
下面以一些具体的实例，介绍热力学方程的应用。
1. 利用热力学方程计算反应热通过测量反应物质之间的热效应，可以计算出反应热。
例如，在燃烧反应中，通过测量产生的热量和反应物质的摩尔数，可以使用热力学方程计算出反应的热效应。
2. 优化化学反应条件热力学方程可以指导化学反应的条件优化。
通过对热力学方程的分析，可以确定最佳的温度、压力和反应物浓度等条件，以最大化反应的产率或改变反应平衡。
3. 导出其他热力学关系热力学方程还可以用来导出其他重要的热力学关系，例如吉布斯-亥姆霍兹方程、亚细亚稳态方程等。
热力学方程推导
热力学方程推导热力学是研究热与能量转化关系的学科，它揭示了自然界中能量流动和转化的规律。
热力学方程是描述物质热力学性质的基本方程，它们通过研究物质的热力学过程和性质之间的关系来描述和预测物质的行为。
本文将以简洁明了的方式，推导热力学方程。
1. 热力学第一定律热力学第一定律是关于能量守恒的基本定律。
它可以表示为：ΔU = Q - W其中，ΔU表示系统内能的变化，Q表示系统吸收的热量，W表示系统对外界所做的功。
2. 热力学第二定律热力学第二定律研究的是热能在能量转化中的特性，它将能量转化的方向和过程的可逆性联系起来，提出了熵增原理。
根据热力学第二定律，熵的变化可表达为：ΔS = Q/T其中，ΔS表示系统熵的变化，Q表示系统吸收的热量，T表示系统温度。
3. 热力学方程根据热力学定律，我们可以将热力学方程表示为：dU = T dS - P dV其中，dU表示系统内能的微小变化，T表示系统温度，dS表示系统熵的微小变化，P表示系统压强，dV表示系统体积的微小变化。
通过对上述方程的推导，我们可以得到热力学方程的一般形式。
4. 理想气体的热力学方程对于理想气体，我们可以根据气体状态方程，将熵的微小变化dS 表示为：dS = C_v dT/T + R dV/V其中，C_v表示气体的定容热容，R表示气体的气体常数。
将上述表达式代入热力学方程，我们可以得到理想气体的热力学方程：dU = T (C_v dT/T + R dV/V) - P dV整理后可得：dU = C_v dT + R/T dV - P dV5. 热力学方程的应用热力学方程是研究物质的热力学性质和行为的基本工具，它可以应用于各种物理和化学过程的分析和计算。
例如，在理想气体的等温过程中，我们可以根据热力学方程来计算系统内能的变化和所做的功。
在等容过程中，我们可以利用热力学方程推导出热容的表达式。
在等压过程中，我们可以根据热力学方程来计算系统内部能量和熵的变化。
1热力学基本方程教案
.1热力学基本方程 (Master equations of thermodynamics) 1、热力学函数定义式 H=U+PV F=U-TS G=H-TS这些函数之间的相对大小见右图。
2、特征微分方程对于定组成均相封闭系统（W ′=0），热一律dU=δQ-PdV , TdS-δQ ≥0,两律合并：dU ≤TdS-PdV.若为可逆过程，则dU=TdS-PdV (7.1)∵H=U+PV ，微分得：dH=dU+pdV+Vdp,将（7.1）式代入：dH=TdS-pdV+pdV+Vdp=TdS+Vdp(7.2) ∵F=U-TS ，微分得：dF=dU-TdS-SdT,将(7.1)式代入：dF=TdS-pdV-TdS-SdT=-SdT-pdV(7.3) ∵G=H-TS ，微分得：dG=dH-TdS-SdT ，将（7.2）式代入：dG=TdS+Vdp-TdS-SdT=-SdT+Vdp(7.4) 上述4式虽在可逆条件导出，但因涉及的均为状态函数，其改变量只与始、终态有关，而与过程是否可逆无关。
但应注意：（1）对有相变、化变的多组分多相体系不适应。
（2）在不可逆过程中，δQ R ≠TdS 及δW 体≠-pdV 。
上述4个基本方程式可见，U 、H 、F 、G 都只是两个独立变量的函数。
如U 可写为U=U （S,V ），又如G=G （T ，P ）。
即U 是S 、V 为独立变量的函数，G 是T 、P 的函数。
而U 、G 在这些独立变量作为限制条件下，其改变值可作为过程自发方向和限度的判据（但在其他变量下的改变量不能作判据）故U 相对于S 、V 变量为特征函数，G 相对于T 、P 亦是。
由此上述4式又称为特征微分方程。
6.2对应系数关系式将4个特征函数写成各自独立变量的全微分式，再与4个特征微分方程相比较，便可得出4对对应关系式。
1.关于U ：∵U=U （S 、V ），dU=dv V U ds S U sv ⎪⎭⎫⎝⎛∂∂+⎪⎭⎫⎝⎛∂∂与dU=TdS-PdV 比较得：p V U T S U sv -=⎪⎭⎫⎝⎛∂∂=⎪⎭⎫ ⎝⎛∂∂, 2.关于H ：∵H=H （S ，P ），dH=dp P H ds S H sp ⎪⎭⎫⎝⎛∂∂+⎪⎭⎫⎝⎛∂∂,与dH=TdS+VdP 比较：V P H T S H sp=⎪⎭⎫⎝⎛∂∂=⎪⎭⎫⎝⎛∂∂,。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
（四）混合物逸度的计算
1. 计算方法 混合物逸度由于将混合物看作是一个整体，因而它的
逸度计算方法同纯物质逸度计算，原则上是相同的。
主要就是由PVT数据图解积分
数模：
ln
1
p
（
RT
-
V)dp
RT 0 p
p
ln
0
Z -1 dp
p
(恒T，x) (恒T，x)
三、非理想溶液
不符合理想溶液其中任一个热力学性质的溶液，就称 为非理想溶液。 （一）活度和活度系数
在决定活度系数与组成关联式时，必须要满足以下条 件：
如果选纯组分在体系的温度、压力下的状态作为标准 态，则当xi→1时，γi→1。
几个具有代表性的常用方程
1. wohl 型方程简化为以下方程（适用正规溶液）： （1） Margules 方程
lnγ1=x22[A+2x1(B -A)] lnγ2=x12[B+2x2(A -B)]
普维法 当对比体积Vr≥2时，用这种方法。普维法 的基本方程就是两项维里方程。
Zi
1
Bi p RT
Zi
-1
Bi p RT
将此式代入式逸度系数计算式中，得：
lni
p 0
Bi p RT
dp p
p 0
Bi dp RT
（恒T）
∵ Bi对特定物质，仅是温度的函数
∴
ln i
Bi p RT
（恒T）
关键是求出维里系数Bi
上式写成： 亦即：
ln
f
L i
V均
p - pS
f
S i
RT
fiL
iS
piSexp
V均 RT
p - pSi
（三）混合物中组分i的逸度的计算
由前知：
ln i
1 RT
p
（
RT
0p
_
- V)dp
p
ln i
0
—
Zi
-
1
dp
p
(恒T，x） ( 恒 T，x ）
➢这两个式子是计算混合物中组分i的逸度和逸度系数的 基本关系式。可以通过维里方程推导计算。（略） ➢计算混合物中组分i的逸度主要是指气体混合物 ➢对于液体混合物，一般情况下是计算活度，活度的概念
以分子①为中心 出现分子①的几率x11 出现分子②的几率x21
x11+x21=1
以分子②为中心 出现分子①的几率x12 出现分子②的几率x22
x12+x22=1
局部摩尔分数和总的摩尔分数不同是由于分子之间的作用力不同 所引起的。
g12=g21 而 g11≠g22 Wilson常数
① 将xij与xi和gij相关联
由四大微分式之一知 dGi=Vidp
(恒T)
由逸度定义
dGi=RTdlnfi (恒T)
∴RTdlnfi＝Vidp (恒T)
或
lnf i
p
T
Vi RT
基础式
2.逸度系数计算式：
i
fi p
两边取对数，然后带入上面的式子中积分得：
p
lni
0
Zi
-1
dp p
Zi-------压缩因子
同理
组分i
混合物
p
ln i
0
—
Zi
-
1
dp
p
ln i
1 RT
p
（
RT
0p
_
- V)dp
(恒T，x) (恒T，x)
p
ln
0
Z -1 dp
p
ln
1
p
（
RT
-
V)dp
RT 0 p
3. 普遍化关系式法
两种：即普维法和普压法。一般普维法用 于低压体系，且采用公式计算；普压法一 般用于高压体系，通过查图获取。
x 21 x 2 x11 x1
x12 x1 x 22 x 2
校正后
x21 x2 exp( g21 / RT ) x11 x1 exp( g11 / RT )
x12 x1 exp( g12 / RT ) x22 x2 exp( g22 / RT )
令
12
V2L V1L
exp[(g21
g11) /
(5)
Lim p0
f p
1
(6)
2. 逸度系数定义式 对应于逸度，逸度系数也有三种：
纯组分i
i
fi p
fi ip
^
组分i
i
fi xip
^
^
fi xii p
混合物
f f p
p
3.逸度的物理意义
逸度的物理意义主要表现在： （1） 逸度是有效的压力；
（2）逸度是自由焓与可测的物理量之间的辅助函
基本式：dGi=RTdlnfi
(恒T)
从饱和蒸汽状态积分到饱和液体状态
G
L i
fiL
dGi RT dlnfi
G
V i
f
V i
G
L i
-
G
V i
RTln
f
L i
f
V i
在恒T、P下，汽液平衡时，GIV=GIL ∴GIV-GIL=0
RTln
f
L i
0
f
L i
1
f
V i
f
V i
亦即
fiL= fiV= fiS
i 1
i 1
正偏差 负偏差
（二） 活度系数与组成的关系
活度，需要知道活度系数γi;
➢活度系数γi一般是要据关系式求得;
➢γi与xi之间的关系，严格说来，是服从吉布斯—杜核
姆方程的;但吉布斯—杜核姆方程单独使用不能解决目
前的问题，一般用经验、半经验方程。
（三）活度系数的近似关联式
适用于分子结构相似的体系
（2） Van laar 方程
ln
1
1
A
Ax 1 Bx 2
2
ln 2
1
B
Bx 2 Ax 1
2
适用于分子结构差异较大的体系
方程中常数A、B的求法：必须借助于实验数据进行求取.
由无限稀释活度系数求A、B值
当x1→0 (x2→1.0)时
lim
1
ln
1
A
x10
lim
推算，且准确度高（比Van lear和Margules Eq相比） ②Wilson参数能够反映与T的关系，且具有半理论的
物理意义。 ③仅有二元参数可推算VLE中的ri。这个特点尤其显
著。 缺点：当lnri~xi曲线有极值时，不能用；
对部分互溶体系不能用。
若分子1—1和2—2间的吸引力大于1—2间的吸引 力，那么在分子1的周围应该有更多的分子1所包 围，在分子2的周围也应该有较多的分子2所包围
若分子1—2间的吸引力大于分子1—1和2—2间的 吸引力，那么在分子1的周围就就会有较多的分子 2所包围，在分子2周围有较多的分子1所包围。
对于二元体系，应具有四个局部摩尔分率
] 21
x2 x121
注意点： ①Wilson常数 对于二元溶液 g12—g22 ，g21—g11 可近似地视为常数，Wilson常数可为正也可为负值。
②Wilson参数λij，受温度的影响且为正值，负值无意 义。
Wilson Eq的特点：
优点：Wilson Eq的特点： ①Wilson Eq仅含有两个参数，故最少有一组数据可以
数。
4.注意事项
▪① 逸度和逸度系数都是强度性质的热力学函数
纯组分
fi=f(T,p)
混合物中组分i 混合物
^
f i f(T,p, xi )
f=f(T,p,x)
② 逸度的单位与压力相同，逸度系数无因次；
③ 理想气体的逸度等于p，逸度系数等于1.
二. 逸度系数的计算
（一）计算逸度的关系式
1. 基础式
Wilson Eq主要三点： ➢由于分子间作用力不同提出了局部组成的概念; ➢利用Boltzmann因子引入描述不同分子间的作用能， 将微观与宏观联系起来;
➢把局部组成概念引入Flory—Huggins提出的无热溶液， 用微观组成代替宏观组成.
局部组成的概念
局部组成的中心意思是： 当以微观观察时，液体混合物不是均匀的。也就是在 混合物中，某一点的组成与另一点的组成未必相同。
RT]
Wilson参数是T的函数
21
V1l V2l
exp[(g12
g22 ) /
RT]
∵ g12=g21
∴
ij
V
l j
Vil
exp[(gij
gii) /
RT ]
ln
r1
ln(
x1
x212
)
x2[
12 x1 x212
x2
21 x121
]
ln r2
ln( x2
x121)
x [ 12 1 x1x212
Bipc B0 B1
RTc
Bi
RTc pc
B0 B1
lni
Bi p RTc (B0 B1 ) p pr
RT Pc
RT Tr
B0 B1
普维法计算物质逸度的计算式
B0 0.083 0.422 Tr1.6
B1 0.139 0.172 T r 4.2
ω为偏心因子，偏心因子是反映物质分子形状、极性
的偏差，而这种偏差程度常用活度系数来衡量，即：
i
ai xi
fi
x
i
f
o i
fi
id
fi