9热力学基本方程
热力学函数的基本关系式
dU = TdS－ pdV
(1-108)
dH = TdS + Vdp
(1-109)
dA = －SdT－ pdV
(1-110)
dG = －SdT + Vdp
(1-111)
式(1-108)，(1-109)，(1-110)，(1-111)称为热力学基本方程
dU = TdS－ pdV dH = TdS + Vdp dA = －SdT－ pdV dG = －SdT + Vdp
常用的是式(1-120)及式(1-121)，这两等式右边的变化率是可以由 实验直接测定的，而左边则不能。可用等式右边的变化率代替左
4.热力学状态方程
由dU＝TdS－pdV
定温下， dUT＝TdST－pdVT
等式两边除以dVT 即
dUT T dST p
dVT
dVT
由麦克斯韦方程 于是
U T S p V T V T S p V T T V
式(1-116)及 (1-117)叫吉布斯 - 亥姆霍茨方程。
(1-117)
G-H方程常用的形式为：
即
(G / T )
T p
H T2
加△
(1-116)
Gibbs自由能随压力的变化
因
（эG/эP）T，n=V
（э△G/эP）T，n=△V 此即G---V关系式
只要知道△V--p关系式，在定温下P1的△G1就可求算出P2的△G2。
在定压下从T1到 T2积分得： （△G）2/ T2- （△G）1/ T1=- =∫T1 T2 △H/T2dT 若知△H--T关系以及T1时的△G1就可求算T2时的△G2 而： △H= △H T0+∫ T0 T △CpdT △H T0是T0时的焓变。
写出四个热力学基本方程
写出四个热力学基本方程
1.热力学的四个基本公式：dU=TdS-PdV；dH=TdS+VdP；
dF=-SdT-PdV；dG=-SdT+VdP。
热力学是从宏观角度研究物质的热运动性质及其规律的学科。
属于物理学的分支，它与统计物理学分别构成了热学理论的宏观和微观两个方面。
热力学定律，是描述物理学中热学规律的定律，包括热力学第零定律、热力学第一定律、热力学第二定律和热力学第三定律。
其中热力学第零定律又称为热平衡定律，这是因为热力学第一、第二定律发现后才认识到这一规律的重要性；热力学第一定律是能量守恒与转换定律在热现象中的应用；热力学第二定律有多种表述，也叫熵增加原理。
热力学第一定律也就是能量守恒定律。
自从焦耳以无以辩驳的精确实验结果证明机械能、电能、内能之间的转化满足守恒关系之后，人们就认为能量守恒定律是自然界的一个普遍的基本规律。
热力学第二定律的每一种表述，都揭示了大量分子参与的宏观过程的方向性，使人们认识到自然界中进行的涉及热现象的宏观过程都具有方向性。
2.热力学第二定律的英文解释是熵是趋向于总体增大,比如
1L90度水(A)和1L10度水(B)融合,不会是A的温度增加而 B的温度减小，因为如此的话，总体的熵减小。
如果A 温度降但B温度升高一点，其总体的熵增加。
热力学第三
定律通常表述为绝对零度时，所有纯物质的完美晶体的熵值为零。
或者绝对零度（T=0K即-273.15℃）不可达到。
R.H.否勒和 E.A.古根海姆还提出热力学第三定律的另一种表述形式：任何系统都不能通过有限的步骤使自身温度降低到0K，称为0K不能达到原理。
物理化学热力学基本方程
利用全微分条件 ，将其作用于(5.1)、(5.2)、(5.4)和(5.6)式，得到(5.8)~(5.11)式所 给八个热力学偏导数的关系：
如果有全微分 df adx ( T ， p ) bdy / 则 S (a / y ) x (b / x ) y 必有
( T / V ) S ( p / S )V (V / S ) p ( p / T )V ( S / V ) T (V / T ) p ( S / p )T
p S T V V T
S V p T T p
G H TS
dG SdT V dp
V (G / p )T
当系统处于平衡态时，不仅描述该系统整体性质的宏观量不再随时 间改变，而且这些宏观量之间还存在着函数关系。只有少数几个是 独立态参量，其余宏观量则是态参量的函数。对于给定的系统，其 态参量的数目是确定的，但选哪几个宏观量作为态参量则是任意的。
我们可以将(5.1)式看成以S和V为独立变量表示的全微分dU ,U=U(S,V), 于是写为
dU ( U / S ) V dS ( U / V ) S dV
可以与(5.1)式比较，得到两个偏导数：
T ( U / S )V
p (U / V ) S
(5.8)
H U p V U (U / V ) S V F U T S U ( U / S )V S G U pV TS
U ( U / V ) S V ( U / S )V S
这说明，只要已知以S，V为独立态参量时内能U的表达式U=U（S,V）， 就可以求得T，状态方程，p，H，F，G乃至系统的全部热力学量。所 以内能U是以S、V为独立态参量的特性函数。同样可以证明焓H，自由 能F和自由焓G分别是以(S,p)，(T,V)和(T,p) 为独立态参量的特性函数。
热力学方程
；或根据已知的蒸 气压方程对比1/T项的系数
§3.10 吉布斯-亥姆霍兹方程和麦 克斯韦关系式
• 10.1 吉布斯-亥姆霍兹方程
从热力学基本方程可以导出下面关系式：
( A / T )
T
V
U T2
§3.9 克拉佩龙方程
• 9.2 固-液平衡、固-固平衡积分式
★凝聚相之间的两相平衡的定性讨论
Vm很小
熔化平衡：fusHm很大，dT/dp很小，外压对熔点的影响很小 晶型转变平衡：trsHm较小，因而dT/dp比熔化平衡大
★定量计算的相关近似处理
以熔化平衡为例
dT dp
T Vm Hm
ⅰ凝聚相与蒸气相之间的两相平衡 ⅱ凝聚相的体积忽略不计 ⅲ蒸气看成理想气体 ⅳ积分时将摩尔相变焓看成常数
★微分形式
d ln p vap Hm
dT
RT 2
★定积分形式
计算题型：
ln
p2 p1
vap Hm R
1
T1
1 T2
五个物理量 已知任意四 个求第五个
★不定积分形式
ln p vap Hm 1 C RT
fusVm , fusHm不变 ln T2 T1
V fus m fus H m
( p2
p1 )
ln(1T /T1)T /T1 T
T1
V fus m fus Hm
p
问：滑冰运动员冰鞋下冰的熔点怎样变化？
§3.9 克拉佩龙方程
• 9.3 克劳修斯-克拉佩龙方程
x
z y
x
热力学方程
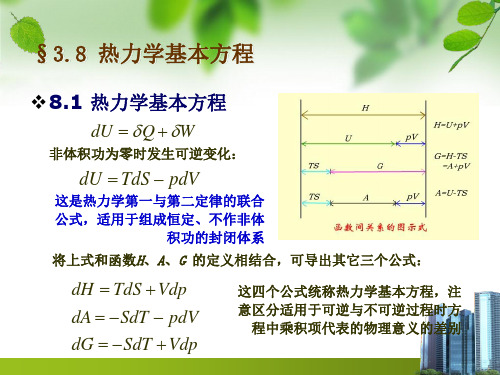
克斯韦关系式
❖10.2 麦克斯韦关系式
将上述导出结果用于热力学基本方程：
dU
TdS
pdV
T V
S
p S
V
dH
TdS
Vdp
T p
S
V S
p
dA
SdT
pdV
S V
T
பைடு நூலகம்
p T
V
dG
SdT
Vdp
S p
T
V T
p
这四个关系式统称 麦克斯韦关系式， 它们的重要意义在 于把不可直接测定 的量转化为可直接
测定量
§3.8 热力学基本方程
❖8.1 热力学基本方程
dU Q W
非体积功为零时发生可逆变化：
dU TdS pdV
这是热力学第一与第二定律的联合 公式，适用于组成恒定、不作非体
积功的封闭体系
将上式和函数H、A、G 的定义相结合，可导出其它三个公式：
dH TdS Vdp dA SdT pdV dG SdT Vdp
这四个公式统称热力学基本方程，注 意区分适用于可逆与不可逆过程时方
程中乘积项代表的物理意义的差别
§3.8 热力学基本方程
❖8.2 热力学基本方程的应用
计算纯物质pVT变化过程的ΔA及ΔG
dA SdT pdV
dG SdT Vdp
★理想气体：
AT
nRT
ln V2 V1
GT
nRT
ln
p2 p1
dAT pdV dGT Vdp
★凝聚系统：
AT
V2 V1
pdV
0
GT
p2 Vdp V p
p1
§3.9 克拉佩龙方程
热力学计算公式整理
热力学计算公式整理热力学是研究物质的热与能的转化关系的学科，是广泛应用于化学、物理、工程等领域的重要理论基础。
在热力学计算中，有一系列公式被广泛应用于热力学参数的计算和分析。
1.热力学基本方程：对于一个热力学系统，其内部能量U可以由其热力学状态变量来表示，常用的基本方程有：U=TS-PV+μN其中，U为内部能量，T为温度，S为熵，P为压力，V为体积，μ为化学势，N为摩尔数。
2.热力学函数的计算：(1)焓（H）的计算公式：H=U+PV其中，H为焓，U为内部能量，P为压力，V为体积。
(2)外界对系统做的功（W）计算公式：W=-∫PdV其中，W为功，P为压力，V为体积，积分为从初态到末态的过程。
(3)熵（S）的计算公式：dS=dQ/T其中，S为熵，dS为熵的微分，dQ为系统的热量变化，T为温度。
(4) Helmholtz自由能（A）的计算公式：A=U-TS其中，A为Helmholtz自由能，U为内部能量，T为温度，S为熵。
(5) Gibbs自由能（G）的计算公式：G=U-TS+PV其中，G为Gibbs自由能，U为内部能量，T为温度，S为熵，P为压力，V为体积。
3.热力学热力学参数的计算：(1)热容的计算公式：Cv=(∂U/∂T)V其中，Cv为定容热容，∂U/∂T为导数，V为体积。
Cp=(∂H/∂T)P其中，Cp为定压热容，∂H/∂T为导数，P为压力。
(2)趋近于绝对零度时的熵变ΔS的计算公式：ΔS = Cvln(T2/T1) + Rln(V2/V1)其中，ΔS为熵的变化，Cv为定容热容，T2和T1为温度的变化，R 为气体常数，V2和V1为体积的变化。
(3)等温过程中的吸热计算公式：q=ΔH=nCpΔT其中，q为吸热，ΔH为焓的变化，n为物质的摩尔数，Cp为定压热容，ΔT为温度的变化。
(4)等温过程中的做功计算公式：w=-ΔG=PΔV其中，w为做功，ΔG为Gibbs自由能的变化，P为压力，ΔV为体积的变化。
热力学函数的基本关系式
⑵等温等压相变△G 对于等温等压的可逆相变，直接可得（△G）T,P=0.对于非等温 等压的非可逆相变或同温同压下两个相态的△G，可以通过设计可 逆过程进行计算，也可根据G---P关系公式求算。
1.8 热力学函数的基本关系式
H
U、H、S、A、G 、 p、V、T H =U+pV，A =U-TS，G =H-TS 1. 热力学基本方程
U
pV
TS A pV
TS
G
δWr ′＝0时，则δWr＝－pdV，于是
一微小可逆过程
dU=δQr+δWr，
dS δ Qr T
δWr ′ ＝0时，则δWr＝－pdV，于是
=8586Jmol-1 故△G= △G1+ △G2 + △G3=8584Jmol-1 依Gibbs自由能减少原理，298K，1atm水不能经等温等压过程转变 为同温 同压的水蒸气，但其逆过程则是可以的。因此在298K， 1atm下液态水是稳定态。
⒊应用Gibbs--helmholtz方程求△G 将 G--H方程：｛э（△G/T）/эT｝P=- △H/T2
△S=0，△T=0，△H=0，
△G=0
⑵理气在等温等压的Gibbs自由能改变 △G = △H-T △S (△H=0) △S=-R∑nilnXi △G= RT∑nilnXi 其中ni为组分i的量，Xi为理想混合气中
为组分I的摩尔数。
⒌非等温等压两态的△G 若体系的两态温度，压力都不相等，根据G的定义：
物理化学知识点总结热力学计算及证明
热力学方法和计算到此为止，我们已经学习了八个热力学状态函数：p、V、T、U、H、S、A、G。
这八个状态函数中p、V、T、U、S有着明确的物理意义，而H、A、G是定义出来的状态函数，并没有明确的物理意义。
这八个状态函数可以构成许许多多热力学函数关系式一、热力学基本方程在非体积功为0的条件下，单组分单相封闭系统经过一个始态到达末态，根据热力学第一定律有。
dU=δQ r+δW r=δQ+δW式子中，δQ r和δW r是可逆过程的热和功，δQ和δW是不可逆过程的热和功。
在非体积功为0的条件下，对于单组分单相封闭系统的可逆过程有δQ r=TdS δW r=−pdV带入后可得到一项重要的公式:dU=TdS−pdV这项式子称为热力学第一定律和第二定律的联合表达式，适用于单相单组分封闭系统可逆过程与不可逆过程。
由焓的定义H=U+pV,两端同时微分得到dH=dU+pdV+Vdp再将dU=TdS−pdV带入上式，得到dH=TdS+Vdp由亥姆霍兹函数的定义A=U−TS，两端同时取微分得到dA=dU−TdS−SdT再将dU=TdS−pdV带入上式，得到dA=−SdT−pdV由吉布斯函数的定义G=H−TS,两端同时微分得到dG=dH−TdS−SdT再将dH=TdS+Vdp带入上式，得到dG=−SdT+Vdp这四个关系式，叫做封闭系统的热力学基本关系式，地位相当重要，务必准确推导和记忆。
严格地讲，这四个关系式只适用于封闭系统中无非体积功的可逆过程，但是我们知道一切实际过程都是不可逆过程，所以我们也可以将这四个关系式用到不可逆过程中，尽管有一些误差，但是完全可以忽略。
为了避免理解过于麻烦，咱不解释误差的来源。
二、对应系数关系式由此我们可以将U、（S，p）、A=A（T，V）、G=G（T，p），根据全微分的性质，可以得到dU=(ðUðS)VdS+(ðUðV)SdV dH=(ðHðS)pdS+(ðHðp)SdpdA=(ðAðT)VdT+(ðAðV)TdV dG=(ðGðT)pdT+(ðGðp)Tdp将上面四个全微分式，对应到四个基本表达式中，我们可以得到T =(ðU ðS )V =(ðH ðS )p p =−(ðU ðV )S =−(ðA ðV )TV =(ðH ðp )S =(ðG ðp )T S =−(ðA ðT)V =−(ðG ðT )p三、麦克斯韦关系式在数学上dz =Mdx +Ndy 是一个全微分的充要条件为(ðM ðy )x =(ðNðx )y我们再一次调出四个热力学基本关系式dU =TdS −pdV dH =TdS +Vdp dA =−SdT −pdV dG =−SdT+Vdp来导出麦克斯韦关系式：(ðS ðV )T =(ðp ðT )V (ðS ðp )T =−(ðVðT )p麦克斯韦关系式的意义在于：它能将不能直接测量出来的物理量（如：熵S ），换成可以直接测量出来的物理量（如T 、V 、p ），或者由状态方程求得的物理量。
第三章--热力学第一定律3(河北理工大学)
∆G (T2 ) − ∆G (T1 ) = − ∫ ∆SdT
T2 T1
§3.8 热力学第二定律在单组分系统相平衡 中的应用
• 克拉佩龙方程 • 固-液平衡、固-固平衡积分式 • 液-气、固-气平衡的蒸气压方程——克-克方程 —— -
1. 克拉佩龙方程
恒温恒压T，p 可逆相变 B(α) ∆Gm=0 dGm(α) B’(α ) 可逆相变 ∆G’m=0 B(β) dGm(β) B’(β )
3. 液-气、固-气平衡的蒸气压方程—克-克方程
对于液-气两相平衡，并假设气体为1mol理想气 体，将液体体积忽略不计，则
∆ vap H m dp ∆ vap H m = = dT TVm (g) T ( RT / p )
d ln p ∆ vap H m = dT RT 2
∆ 这就是Clausius-Clapeyron 方程， vap H m是摩尔气化热。
假定 ∆ vap H m 的值与温度无关，积分得：
∆ vap H m 1 1 p2 ln =− ( − ) p1 R T2 T1
这公式可用来计算不同温度下的蒸气压或摩尔蒸发热。
热力学第二定律的内容关联： 热力学第二定律的内容关联：
卡诺循环 热力学第二定律
热 力 学 第 一 定 律
熵，熵增原理
PVT
Ө $ m
恒容
$ Ө ∆ r Am Ө ∂( ) $ ∆ rU m T =− 2 ∂T T
• 麦克斯韦关系式
（不讲）
• 热力学函数关系式的推导和证明 （不讲）
3. 由基本方程计算纯物质pVT变化的∆A, ∆G
恒温 dT=0时，从热力学基本方程 dA= – SdT – pdV dG= – SdT+Vdp 得 dAT= – pdV dGT= Vdp 对于理想气体，将pV=nRT代入积分，有 ∆AT = –nRT ln(V2 /V1) ∆GT = nRT ln(p2 /p1) 两者相等。
热力学定律和热力学基本方程
可逆过程的热温商只决定于初终态，与路径无关。
S SII SI def
II dQR IT
dS def dQR T
克劳修斯不等式及不可逆程度 ：
B
S (dQ / T环 ) 0
A B
或
T环dS Q 0 A
dS dQ / T环 0 T环dS dQ 0
34
二、熵增原理
孤立系统 d Q 0 dW dW ' 0
16
结论：
(1) I1、I2进行后，环境消耗功得到热，遗留 不可逆变化，此两过程是不可逆过程。
R1进行后，没有遗留不可逆变化，此过程 无方向性。
I3 进行后，系统从单一热源吸热，并完全 转化为功，系统及环境均无遗留不可逆变化。此 违反第二定律，故I3是不可能的过程。
(2) 可逆过程是可能和不可能过程的分界。
( )T ,V ,W '0 和 ( )T , p,W '0 条件下，克劳
修斯不等式化为
A 0 和 G 0
系统和环境对方向和限度的影响，化为系 统性质的变化。
48
例1
一密闭容器中有一盛满水 的玻璃泡。今将玻璃泡击碎， 使水在100℃下恒温蒸发为 101325 Pa的水蒸气。试对过 程的可逆性作出判断？
39
解：
S S2 S1
B
A dQR
T QR
T Qp
T
H T 40.66 103 373.2 J K1 108.9 J K 1
(1)
B
d
Q
A
T环
Q1
T
108.9 J K 1
S
B d Q A
T环 0
∴ 这是一个可逆过程
(2)
B
热力学基本方程PPT课件
如果取C(V )T nRT / (V nb)，就得范德华方程 如果取C(V )T是硬球状态方程，就得硬球范德华方程
复习在热力学中常用到的偏导数关系式： 1. 由微分式求导数：导数的定义
f x y
lim
Δx 0
f ( x Δx, y) Δx
f (x, y)
Δf lim Δx0 Δx
y不变
V
4c S 3 V
1/ 3
p
U V
S
c S 3 V
4/3
T T (S,V )
27T 4
27T 3V
p
p(S,V )
p
256c3
,
T T (S,V ) S
64c3
如果已知的是U(T, V)，那么我们将得不到完整的其他热力学 性质，比如不能由它推导出体系状态方程。
已知U(T ,V )
T
U S
V
H S
p
H G
V
p
S
p
T
p
U V
S
A V
T
S
A T
V
G T
p
(A/T) T V
U T2
,
(A/T)
(1/ T )
V
U
(G / T T
)
p
H T2
,
(G / T )
(1/T )
p
H
4.麦克斯韦关系式(Maxwell relations)
U V
T
dV
CV dT
U V
T
dV
类似的，焓的自然的独立变量是熵和压强，为方便 起见，焓的独立变量也常取为温度和压强
dH TdS Vdp
物理化学1.15-1 热力学函数的基本关系式
8个热力学函数： 可直接测定
p、V、T、U 、H 、S、A、G
定 H ＝U＋pV 义 式 A ＝U－TS
可求得
G ＝H－TS＝A＋pV
1.热力学基本方程
封闭系统 dU =δQ + δW
可逆过程
=δQr －pdV ＋ δWr′
δQr =TdS
dU = TdS －pdV ＋ δWr' δWr'＝0：
dA = －SdT－ pdV dG = －SdT + Vdp
G S T p
G p
T
V
证明：无相变和化学变化的封 闭系统，在定温下其吉布斯自 由能随压力的改变恒为正值。
证明：
dG = －SdT + Vdp
G ( p )T
V
>0
解： dG = －SdT + Vdp
S T2 nCV ,mdT nR ln V2 ,
T1
T
V1
A nRT ln V2 V1
应(用ቤተ መጻሕፍቲ ባይዱ()i封条i()i无i闭件i)非可系：体逆统积过，功程，。
可用于: (i)定量，定组成的单相系统;
(ii) 保持相平衡及化学平衡的系统.
8个派生公式： dU = TdS－ pdV dH = TdS + Vdp
U T S V U p V S
dU = TdS －pdV
dU=TdS－pdV
H=U+pV dH=dU+pdV+Vdp
A=U－TS dA=dU－TdS－SdT
dH=TdS+Vdp
dA= － SdT － pdV
热力学基本方程
热力学基本方程热力学是一门描述物理系统中能量、势能和熵之间关系的学科。
它的基本方程，也就是“热力学基本方程”，定义了这些量之间的联系。
热力学基本方程可以用来描述物质在不同物理状态和条件下的变化。
热力学基本方程是一个多元方程，由热力学定律组成：第一定律是能量守恒定律；第二定律是熵守恒定律；第三定律是势能守恒定律。
第一定律：热力学的第一定律宣称，在任何物理过程中，能量守恒，即能量不会消失，也不会出现。
由于能量守恒，物质在不同状态间的变化都会有特定的方法。
第二定律：热力学的第二定律宣称，由于能量不能在未受外力作用的情况下自发地流向热源或冷池，因此，熵在受外力作用的情况下不会减少，而是会增大。
第三定律：热力学的第三定律宣称，势能可以变化，而它的变化与系统的熵有关，当熵增加时，势能也会增加。
这三定律构成了热力学基本方程，用于说明物质在不同物理状态下的变化。
它解释了物质在不同状态间的转换和质量变化，以及在这些转换中的能量的流动方式。
此外，热力学基本方程还可以用来描述物质处于不同环境中的变化，如汽化、液化、固化等，也可以用来解释物质在受外力作用时的表现。
热力学基本方程的应用也非常广泛，它可以用来表示物理和化学反应的能量改变，也可以用来描述物质运动规律，还可以用来计算化学反应产物的分子量、活性能和自由能。
由于热力学基本方程具有如此强大的表达能力，它被广泛应用于热力学的各个分支中，包括绝热热力学，热压热力学，绝热变动热力学，精确热力学，化学动力学，流体力学，量子力学，共性热力学等。
热力学基本方程是一种强有力的理论，它引发了新的科学发现，让物理学和化学学者们有机会探索全新的物理和化学现象，为科学知识的发展做出了巨大贡献。
从上面可以看出，热力学基本方程是一个强大的热力学定律，它可以用来说明物质在不同状态、环境的变化，也可以描述物质的运动规律，为物理学和化学学的研究作出了巨大贡献。
它的应用也非常广泛，它也被用于各个热力学分支，被广泛应用于物理和化学反应的研究中。
9热力学基本方程
式①、 ②、 ③、④ 统称热力学基本方程 应用条件：封闭系统、可逆过程、δW ' =0
从另一角度分析: U=U(S,V) H=H(S,p) A=A(T,V) G=G(T,p)
由两个独立变量可以确定系统状态的系统 什么系统是这样的系统？
定量，定组成的单相系统； 纯物质是定组成的一种特例 保持相平衡及化学平衡的系统
热力学基本方程的应用：
计算纯物质 p、V、T 变化过程的ΔA、ΔG
dA=－SdT－ pdV dG=－SdT+Vdp
AT
V2 V1
pdV
GT
p2 Vdp
p1
2. 麦克斯韦关系式
表明S、T、p、V 间的关系式
S p V T T V
推导热力学函数间关系时，也常用到麦克斯韦关系式
麦克斯韦关系式中不含：
S T
p
和
S
T
V
问题 S ?
T p
S ? T V
解：dH= TdS+Vdp
定压下，除以dT
H T S T p T p
得 S Cp
T p T
而
Cp
H T
p
同理可得：
U T S p V T V T
将麦克斯韦关系式 S p V T T V
代入上式，得之。
H p
T
T V T
p
V
dH TdS Vdp
定温下，除以dp，得
H p
T
T
S p
T
V
将麦克斯韦关系式
S p
T
V T
p
代入上式，得之。
热力学基本方程汇总表
=
nR V
∂ U ∂ V T
= T ∂ p ∂ T V
−p=0
2、带入范德华方程 p = RT − a Vm − b Vm2
∂p ∂T V
=
R Vm −
b
，
∂U ∂V
T
= T ∂ p ∂ T V
a −p=
Vm2
带入理想气体的 pVT 关系
， ∂V = nR ∂T p p
=
−
H T2
左边等于偏导数
∂
(G / T ) ∂ T p
∂
，
(G /T ) ∂ T p
=
H −T2
内压力方程： dU = TdS − pdV 两边除以 dV，
(∂ U ∂ V )T = T (∂ S ∂ V )T − p
带入麦克斯韦关系式 ∂ U = T ∂ p − p ∂ V T ∂ T V
焓随 p 变化：
dH = TdS + Vdp 两边除以 dp，
(∂ H ∂ p)T = T (∂ S ∂ p)T + V
带入麦克斯韦关系式
∂ ∂
H p
T
= −T ∂ V ∂T
p
+V
Cp与CV的关系
CP − CV
=
∂U ∂V
T
+
p
∂V ∂T
P
1、带入理想气体的 pVT 关系
， ∂p ∂T V
(∂M / ∂Y ) X = (∂N / ∂X )Y
二阶导数 麦克斯韦关系式
∂ T = − ∂ p ∂ V S ∂ S V
∂ ∂
T p
S
=
∂ V ∂S
p
∂ S = ∂ p ∂ V T ∂ T V
热力学基本方程
二、处于扩散接触子系统的平衡 温度
• 熵有极大值的条件是：
∂S1 ∂S2 ∂S1 ∂S2 dE1 + dE2 + dN1 + dN2 = 0 ∂E1 E =E , N ,V ∂E2 E =E , N ,V ∂N1 N = N ,E ,V ∂N2 N = N , E ,V % % % % 1 1 1 1 2 2 2 2 1 1 1 1 2 2 2 2
T1 = T2 p1 = p2
四、热力学基本方程
态函数熵S=S ({ N k } ,U,V ) , 可得
∂S ∂S ∂S dS= dU+ dV+ ∑ dN k ∂U {N k },V ∂V {N k },U k ∂N k U ,V,N k ′≠ k
• 热平衡条件：
∂S1 ∂S2 = ∂U1 N ,V ∂U 2 N ,V 1 1 2 2
• 引入温度：
1 ∂S ∂ ln Ω = = kB T ∂U N ,V ∂U N ,V
T1 = T2
1 ∂S ∂ ln Ω = = kB T ∂U N ,V ∂U N ,V
∂ ln Ω i ∂S µ i = −Ti i = − k BTi ∂N I U ,V ∂N i U ,V i i i i
处于热接触子系统的平衡处于扩散接触子系统的平衡处于力学接触子系统的平衡温度化学势和压强热力学基本方程一处于热接触子系统的平衡温度dededndn二处于扩散接触子系统的平衡温度dededvdv三处于力学接触子系统的平衡温度态函数熵可得dsdudvdndutdspdvdndutdspdv开放系
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
推导热力学函数间关系时，也常用到麦克斯韦关系式
麦克斯韦关系式中不含：
S T
p
和
S
T
V
问题 S ?
T p
S ? T V
解：dH= TdS+Vdp
定压下，除以dT
H T S T p T p
得 S Cp
T p T
而
Cp
H T
p
同理可得：
G
G3
nRTln
p2 p1
28.314 373 .15 ln 50
101 .325
J 4.38
kJ 0
GT,p 4.38 kJ 0
由吉布斯函数判据可知，过程自发进行。
A G ( pV ) G nRT 4.38 kJ 28.314373103 kJ 10.58 kJ
1.15 热力学函数的基本关系式
定量，定组成的单相系统； 纯物质是定组成的一种特例 保持相平衡及化学平衡的系统
热力学基本方程的应用：
计算纯物质 p、V、T 变化过程的ΔA、ΔG
dA=－SdT－ pdV dG=－SdT+Vdp
AT
V2 V1
pdV
GT
p2 Vdp
p1
2. 麦克斯韦关系式
表明S、T、p、V 间的关系式
S p V T T V
p T S V V S
V S
p
T p
S
S p V T T V
S p
T
V T
p
几点结论：
麦克斯韦关系式表示：系统在同一状态的两种变 化率数值相等
S p V T T V
S p
T
V T
p
该式提供了可由实验直接测定的量，替代不能直接 测定的量
R p
3. 热力学状态方程
表明定温下，U、H与 V、p关系
U T p p V T T V
热力学状态方程
H p
T
T V T
p
V
由dU=TdS – pdV， dH=TdS＋Vdp
及麦克斯韦关系式 推出：
U T p p V T T V
dU TdS pdV
定温下，除以dV，得
V S
p
T p
S
Maxwell,1831~1879,英国
S p
T
V T
p
p T S V V S
公式推导
多变量函数
若 z
y
dx
z y
x
dy
若混合偏导数存在且连续，则与求导顺序无关
2z 2z xy yx
x
z y
x
y
y
z x y x
p、V、T 、U、H、S、A、G
H =U+pV，A =U－TS，G =H－TS
还可导出： H =TS+A+pV G =A+pV
H
U
pV
TS A
pV
TS
G
1. 热力学基本方程
表明如下状态函数间的关系式
U =U ( S, V ) A =A ( T, V )
H =H ( S, p ) G =G ( T, p )
H T2
dG SdT Vdp
得
G S T p
H2O(l,100℃,50kPa)
G = ?
G1
H2O(l,100℃,101.325kPa)
G2
H2O(g,100℃,50kPa )
G3
H2O( g,100℃,101.325kPa)
G G1 G2 G3
GT
p2 Vdp
p1
G1 0 凝聚系统定温下压强变化不大
G2 0 定温、定压可逆相变
S T
V
CV T
练习19. 某实际气体的状态方程为 pVm = RT + bp (其中b是常数 )。
若1 mol该气体在定温下由p1 变到 p2, 求ΔS。
解： S
p2 p1
S p
T dp
p2 V dp p1 T p
p2 Rdp
p1 p
R ln p2 p1
V T
p
T V
S
V
U S
V
S
对 p U V S
在定容下对S求偏导，得
p S V
S
U V
S
V
T V
S
V
U S
V S
p S V
S
U V
S
V
混合偏导数与求偏导顺序无关
p T S V V S
麦克斯韦关系式
dU＝TdS－pdV dH = TdS + Vdp dA = －SdT－ pdV dG = －SdT + Vdp
重点回顾
熵判据 ΔS (隔离 ) ≥ 0 不可逆
可逆
ΔS(隔离系统)=ΔS(系统)+ΔS(环境)
亥姆霍兹函数判据
定温： AT W 不可逆过程
可逆过程
定温、定容： AT ,V W ' 不可逆过程
可逆过程
定温、定容， W ′＝0
AT ,V 0
自发 平衡
亥姆霍兹函数判据
GT , p W ' 若W′= 0 时
dA=－SdT－ pdV …… ③ dG=－SdT+Vdp …… ④
式①、 ②、 ③、④ 统称热力学基本方程 应用条件：封闭系统、可逆过程、δW ' =0
从另一角度分析: U=U(S,V) H=H(S,p) A=A(T,V) G=G(T,p)
由两个独立变量可以确定系统状态的系统 什么系统是这样的系统？
R p
p2 [T V V ]dp p2 [T R V ]dp
p1
T p
p1
p
p2 p1
bdp
b( p2
p1)
4. 吉布斯 – 亥姆霍兹方程
(G / T ) T
p
H T2
( A / T ) T V
U T2
(G / T T
)
p
T G G T p T2
TS G T2
U T S p V T V T
将麦克斯韦关系式 S p V T T V
代入上式，得之。
H p
T
T V T
p
V
dH TdS Vdp
定温下，除以dp，得
H p
T
T
S p
T
V
将麦克斯韦关系式
S p
T
V T
p
代入上式，得之。
U T p p
V T T V
热力学状态方程
H p
T
T V T
p
V
定量、定组成理想气体的U、H只是T的函数，与p、
V无关。
如何求ΔU？
练习20. 某实际气体的状态方程为
pVm = RT + bp ( 其中b是常数 )。 若1 mol该气体在定温下由p1变到p2, 求ΔH。
解：
H
p2 p1
H p
T
dp
V T
p
dU TdS pdV
热力学第一、第二定律联合式
公式推导
封闭系统：
热力学第一定律 热力学第二定律
可逆过程
dU δQ δW
δQ 不可逆过程 dS
Tsu 可逆过程
δQr TdS
可逆过程 且δW ' = 0 δW pdV
……Ⅰ
……Ⅱ ……Ⅲ
将式Ⅱ和Ⅲ代入Ⅰ，得
dU TdS pdV 热力学第一、第二定律联合式
p T S V V S
证明: 由 U f S ,V 得到
dU U dS U dV S V V S
热力学基本方程 dU＝TdS－pdV
T U S V
p U V S
T U S V
p U V S
对 T U 在定熵下对V求偏导，得 S V
dU TdS pdV
应用条件：封闭系统，可逆过程，δW ' = 0 由 H= U+ pV A=U – TS G=H – TS
得 dH = dU + pdV + Vdp dA = dU – TdS – SdT dG = dH – TdS – SdT
dU = TdS – pdV …… ① dH = TdS+Vdp …… ②
不可逆过程 可逆过程
GT , p 0
自发 平衡
熵判据 ΔS(隔离系统)=ΔS(系统)+ΔS(环境) 亥姆霍兹函数判据 吉布斯函数判据
热力学判据的一致性!!
练习18
2molH2O(l,100℃,50kPa)变成同温同压下的
水蒸气，求该过程的ΔA、ΔG，并判断该过程
的能否自发进行？
已知100℃水的汽化焓为40.67kJ•mol-1 。