2-3 动量 动量守恒定律 质心运动定理
合集下载
2-3 动量 动量守恒定律 质心运动定理

mb 2mg
推开后速度
初始速度
v g 0 vb0 0
且方向相反
则 则
v g 2vb
推开前后系统动量不变
第2章 运动定律与力学中的守恒定律
p p0
p 0
p0 0
2–3 动量 动量守恒定律 *质心运动定理
6
讨论
动量的相
S
S
对性和动量定 理的不变性 参考系 t1 时刻
t2 t1 n n t2 F ( i 外 )dt i 1 n n t2 n n 1 j 1 t1 i 1 ji i 1 i i2 i 1 i i1
t1
i 1
t1
第2章
n 运动定律与力学中的守恒定律
n
2–3 动量 动量守恒定律 *质心运动定理
5
注意
内力不改变质点系的动量
F Fm
F
t
Fdt F (t2 t1 )
o
t1
t2
t
2–3 动量 动量守恒定律 *质心运动定理
8
问:为什么迅速地把盖在杯上的薄板从侧面打去, 鸡蛋就掉在杯中;慢慢地将薄板拉开,鸡蛋就会和薄 板一起移动?
答:因为鸡蛋和薄板间的摩擦力有限,若棒打击 时间很短, F t 0, P 0 所以鸡蛋就 f 蛋 掉在杯中.
j
f ji 0 t
n n 1 i 1 j 1
i 1 j 1 质点系总动量的增量等于作用于该系统上合外力的冲量
n )d n f t ( ( F )dt mi vi 2 mi v i1 n t t i外 n n 1 1 m v 2 m 2 i 1 i 1 v i 1 ( F )d t ( f )d t i 外 ji
动量定理及动量守恒定律

20
动量定理及动量守恒定律
oy N1 − m1g = 0 又f1max = N1μ1
以 m2 为隔离体,m2 受重力W = m2 g ;桌面的支持力 N2 ; m1 的压力 N1′ (大小与 N1 相等); m1 作用在 m2 上的最大静摩擦力 f1max′(大小与 f1max 相等) ;桌面作用在 m2 上的
oA y A W3 − TA′ − TB′ = m3a3
(7)
因为不计滑轮及绳的质量,不计轴承摩擦. 且已知绳不可伸长.
∴ TA = TB = TA′ = TB′ = T
f A ,绳的拉力 TA , A 的动力学方程为
动量定理及动量守恒定律
W1 + N A + f A + TA = m1a1 建立如图 3.5.7(1)所示的坐标系 oA − xA y A .
oA xA TA − f A = m1a1
(1)
oA y A W1 − N A = 0
(2)
且 fA = NAμ
动量定理及动量守恒定律
第三章 动量定理及动量守恒定律
(Momentum and Conservation Law of Momentum)
一、内容简介(Abstract) 1.牛顿第一定律(Newton’s first law)
孤立质点静止或作等速直线运动,即质点在不受力或所受力的合力为零时,将保持静 止或匀速直线运动状态不变.(惯性定律) 2.牛顿第三定律(Newton’s third law)
g
y
x o
N
2
α m2
a2
W2
N1′
图3.5.(5 3)
y′
N1 f∗
m1
动量和动量定理 08

单位: 千克·米 单位:kg·m·s-1 (千克 米 / 秒) 千克 由上式得 积分得
∫
t
0
v P r r r F d t = ∫ d p = p − p0
P0
v r F ⋅dt = d p
v v 内的积累效应, 冲量。 力 F 在时间 t 0至 t 内的积累效应,称为力 F 的冲量。 v t v 即 I = ∫ F dt
v v t v v v 所以 I = p − p0 = mv − mv0
0
此式表示,在运动过程中, 此式表示,在运动过程中,作用于质点的合力 在一段时间内的冲量等于质点动量的增量。 在一段时间内的冲量等于质点动量的增量。这个结 论称为动量定理。 论称为动量定理。 动量定理 v v v F 为恒力时 I = F (t - t 0 ) v F 为变力,且作用时间很短时,可用平均值来代替 为变力,且作用时间很短时, t v v v v ∫t0 F d t I = F (t - t 0 ) F= t − t0
LL
n v v d v Fn + ∑ f ni = m n vn dt i≠ n
将以上n 将以上 个方程两边分别相加得
v n n v d n v ∑ Fi + ∑∑i f ij = d t (∑ mi vi ) i =1 i =1 i j≠
n
由于内力成对出现, 由于内力成对出现,根据牛顿第三定律得
O
α
x
则圆弧质心坐标为
xC = ∫ xdm ∫ dm =
α ∫−α xρRdθ = αcos θ dθ dθ
α ρR ∫−α
=
Rsin α
α
3) 质心运动定理 ) 由质点系动量定理的微分形式得
n v 2 ∑ mi ri n n n n v d d i =1 d2 v v = m Fi = (∑ mi vi ) = ∑ mi 2 n ∑ i dt 2 rC ∑ dt i=1 i =1 dt i =1 i =1 ∑ mi i =1
∫
t
0
v P r r r F d t = ∫ d p = p − p0
P0
v r F ⋅dt = d p
v v 内的积累效应, 冲量。 力 F 在时间 t 0至 t 内的积累效应,称为力 F 的冲量。 v t v 即 I = ∫ F dt
v v t v v v 所以 I = p − p0 = mv − mv0
0
此式表示,在运动过程中, 此式表示,在运动过程中,作用于质点的合力 在一段时间内的冲量等于质点动量的增量。 在一段时间内的冲量等于质点动量的增量。这个结 论称为动量定理。 论称为动量定理。 动量定理 v v v F 为恒力时 I = F (t - t 0 ) v F 为变力,且作用时间很短时,可用平均值来代替 为变力,且作用时间很短时, t v v v v ∫t0 F d t I = F (t - t 0 ) F= t − t0
LL
n v v d v Fn + ∑ f ni = m n vn dt i≠ n
将以上n 将以上 个方程两边分别相加得
v n n v d n v ∑ Fi + ∑∑i f ij = d t (∑ mi vi ) i =1 i =1 i j≠
n
由于内力成对出现, 由于内力成对出现,根据牛顿第三定律得
O
α
x
则圆弧质心坐标为
xC = ∫ xdm ∫ dm =
α ∫−α xρRdθ = αcos θ dθ dθ
α ρR ∫−α
=
Rsin α
α
3) 质心运动定理 ) 由质点系动量定理的微分形式得
n v 2 ∑ mi ri n n n n v d d i =1 d2 v v = m Fi = (∑ mi vi ) = ∑ mi 2 n ∑ i dt 2 rC ∑ dt i=1 i =1 dt i =1 i =1 ∑ mi i =1
质点力学4

例1、一炮弹发射后在其运行轨道上的最高点
h=19.6 m处炸裂成质量相等的两块。其中一
块在爆炸后1秒钟落到爆炸点正下方的地面上,
设此处与发射点的距离S1=1000 m,问另一 块落地点与发射点的距离是多少?(空气阻
力不计,g=9.8 m/s2)
y
解:知第一块方向竖直向下
v2
y
h
v1t1
1 2
gt12
1、质点角动量定理 L r p
dL d (r p) dr p r d p
dt dt
dt
dt
p mv
dr v dt
dp F dt
dL v mv r F dt
dL r F dt
令: M r F 为合外力对同一固定点的力矩
大小:M=rFsin (为矢径与力之间的夹角)
I x mv2x mv1x I y mv2 y mv1y I z mv2z mv1z
平均力
F
t2 Fdt
t1
=
I
P
t2 t1 t t
例1、质量为2.5g的乒乓球以 10m/s的速率飞来,被板推 挡后,又以20m/s的速率飞 出。设两速度在垂直于板面 的同一平面内,且它们与板 面法线的夹角分别为45o和 30o,求:(1)乒乓球得到 的冲量;(2)若撞击时间 为0.01s,求板施于球的平均 冲力的大小和方向。
作业: 1.35、1.36、1.38
三、质心、 质心运动定律
1、质心:质点系的质量中心 质点系 N个质点 质量:m1 m2 m3 … mi … mN
位矢:r1, r2 , r3 , , ri , , rN
质心的位矢:
mi ri
(m为总质量)
rc i m
3-2质心运动定理、角动量守恒
L
O
●
rA r
●
A α m
●
v
证明: 不受外力,质点将做 匀速直线运动。 m在某一时刻经过A点时, 其对固定点O的角动量为
L rA mv rAmvsin r m v
固定点O到轨迹直线的垂直距离只有一 个值,所以角动量的大小恒定。 而角动量的方向恒垂直于固定点O和运动 轨迹所决定的平面。 所以m对任意固定点的角动量矢量保持不变。
力矩的大小:
力矩的方向: 角动量定理:
M r F rF sin
也由右螺旋法则确定。
dL M dt
质点所受的合外力矩等于它的角动量对时间的 变化率。 M 注意:定理中的力矩和角 动量是对惯性系中地同一 固定点而言的。
o
●
r
F
r
α
m
§3.7 角动量守恒定律
给上式两边同时乘以系统质量m
rC
mi ri
i
则:
mvc mi vi p
dvc dp p mvc 两边求导得: m mac dt dt dp F m a c dt
——质心运动定理
i
不管物体的质量如何分布,也不管外力作用在 物体的什么位置上,质心的运动就象是物体的质量 全部都集中于此,而且所有外力也都集中于此的一 个质点的运动一样。 实际上在质心位置处可能既无质量,又未受力。
i 1
m
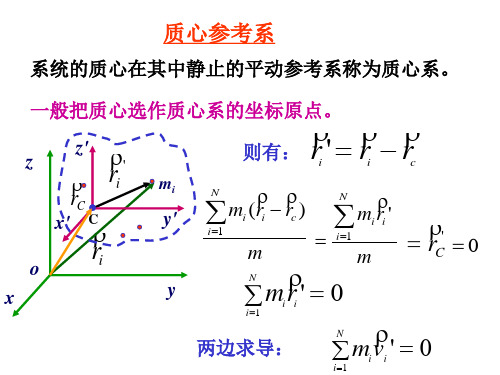
' rC
0
两边求导:
'0 mv i i
N i 1
z
z'
x'
o
rC
' ri
动量守恒定律

作用强。 作用强。 忽略外力作用时, 系统总动量守恒。 忽略外力作用时 系统总动量守恒。 能量, 能量,则视具体碰撞情况不同而有所不同, 对心碰撞(正碰)、 )、斜碰 对心碰撞(正碰)、斜碰
20
完全弹性碰撞
(五个小球质量全同) 五个小球质量全同)
完全弹性碰撞
v v v v m1v10 + m2 v20 = m1v1 + m2 v2
以此类推, 个人全部跳车后 以此类推,N个人全部跳车后
υ车
m m m =[ + + L+ ]υr M + Nm M + ( N −1)m M + 1⋅ m
υ车
m m m =[ + + L+ ]υr M + Nm M + ( N −1)m M + 1⋅ m
14
υ车 = ∑
n =1
N
m υr M + nm
N个人 个人 m ……………
无摩擦
相对同一惯性参考系“地面” 解: 相对同一惯性参考系“地面”列动量守恒式 υ人对地 = υr +υ车对地 (1) Mυ车对地 + Nmυ人对地 = 0 )
Mυ车 + Nm(−υr + υ车 = 0 ) (M + Nm)υ车 − Nmυr = 0
υ车
Nm = υr M + Nm
mu o 速度增量 ∆v = v − v0 cos ϕ = M + mv sin ϕ 增加的距离: 增加的距离: ∆s = ∆vt , 而 t = 0 g
故
mu v0 sin ϕ ∆s = ⋅ M +m g
M +m
ϕ
2.3 冲量和动量
N
2)建立坐标OY; 3)受力分析: 4)列方程:
mg
落在桌上前的速度坐标分量 v0 2 gh 静止在桌上时的速度坐标分量
vt 0
Y h
m
N
mg
由动量定理:
F t mvt mv0
只有Y分量
O
__
( N mg )t 0 m( 2 gh ) m 2 gh
说明:动量 P mv
令P v称为质点的动量,则: m I P2 P (3) 1 质点动量定理:质点所受合外力的冲量等于质 点动量的增量. I P2 P 1
是物体运动量大小的量度
清晨,鸟语花香,迈步林荫道,一树叶落下,你 是什么态度呢?毫不在意,漫不经心.好不悠闲!
I i P2 P1
n i 1
注意: 只有质点系的外力才能改变质点系的 总动量。 内力虽能改变质点系个别质点的动 量,但不能改变质点系的总动量。
2.3.3 质点系的动量守恒定律 若质点系所受合外力为零,则质点系的总 动量保持不变。
mi vi c Fi 外力 0
M m L x (6) M
M x L M m
例3:质量为m的木块,原来静止于质量为M的 劈上。劈又静止于水平桌上,若所有表面均无摩 擦,试求当木块m从离桌面为h高处滑到底端时, 劈的速度为多少?m对M的速度为多大?M 、m 的水平位移为多大? 解:以M、m为研究对象 Y m m Nr 分析力: N Y’ h M mg M
F1
F21
F12
m1
F13
F31
F23 F32
m2
F23
F2
《动量守恒》PPT课件
(3)不论体系如何复杂,体系质心的行为与一个质点 相同。从这个意义上说,牛顿定律所描绘的不是体 系中任一质点的运动,而是质心的运动。而质心的 存在,正是任意物体在一定条件下可以看成质点的 物理基础; (4)质心运动定理和牛顿三定律的适用范围相同。 20
三、质心坐标系
?质心坐标系:把原点取在质心上,坐标轴的方向始终与某固 定参照系(惯性系)的坐标轴保持平行的平动坐标系。
h
h (M )2
1
9
m
例题4.2、柔软链条自桌上小孔自由下落,求下落速度 与落下距离之间关系。
分析:这是一个质点系的动量问题,可用体系动量定理求解。
解: 如图,建立坐标系,令线密度λ,则在某时刻
Fex my g yg
p myv yv
O
根据 Fex=dP/dt 得
my
y
d ( yv) dy d ( yv)
笫四章 动量定理
目录
《哲学原理》
§⒈动量与动量定理;
§⒉质心与质心运动定理;
§⒊动量守恒定律;
§⒋变质量物体的运动.
近代科学的始1 祖 笛卡儿
引言
动力学问题
运动学问题
力的瞬时效果
mr f (r , r ,t)
力的位置函数
牛顿定律适用质点,应用于质点系存在困难;
•
Hale Waihona Puke ?关系 引进新概念和物理量
p
J
LE 表现运动特征量
i
mi zi zc i mi
i
可见质心位矢是质点位矢的带权平均值,这个“权”与质1点4 的 质量分布位置有关。
对质量连续分布的物体,其质心位矢由上式推广得
分量形式为
rc
rdm dm
三、质心坐标系
?质心坐标系:把原点取在质心上,坐标轴的方向始终与某固 定参照系(惯性系)的坐标轴保持平行的平动坐标系。
h
h (M )2
1
9
m
例题4.2、柔软链条自桌上小孔自由下落,求下落速度 与落下距离之间关系。
分析:这是一个质点系的动量问题,可用体系动量定理求解。
解: 如图,建立坐标系,令线密度λ,则在某时刻
Fex my g yg
p myv yv
O
根据 Fex=dP/dt 得
my
y
d ( yv) dy d ( yv)
笫四章 动量定理
目录
《哲学原理》
§⒈动量与动量定理;
§⒉质心与质心运动定理;
§⒊动量守恒定律;
§⒋变质量物体的运动.
近代科学的始1 祖 笛卡儿
引言
动力学问题
运动学问题
力的瞬时效果
mr f (r , r ,t)
力的位置函数
牛顿定律适用质点,应用于质点系存在困难;
•
Hale Waihona Puke ?关系 引进新概念和物理量
p
J
LE 表现运动特征量
i
mi zi zc i mi
i
可见质心位矢是质点位矢的带权平均值,这个“权”与质1点4 的 质量分布位置有关。
对质量连续分布的物体,其质心位矢由上式推广得
分量形式为
rc
rdm dm
4质心运动定理、动量守恒定律
2m 2 gh F′ = j t
= 3.8×10 j
2
(N) )
17
逆风行舟动量分析
18
三,动量守恒定律
如果系统所受的外力之和为零, 如果系统所受的外力之和为零,则系统的总动量保 持不变.这个结论叫做动量守恒定律 动量守恒定律. 持不变.这个结论叫做动量守恒定律. Fi = 0 结论 ∑mi vi = C 条件 ∑mivi = C 由质心运动定理: 由质心运动定理: Fi = MaC aC = 0 vC = C vC = M ∑ 明确几点 1.对于一个质点系,若合外力为 0,系统的总动量 对于一个质点系, , 对于一个质点系 保持不变,但系统内的动量可以相互转移. 保持不变,但系统内的动量可以相互转移.
dm = 2xσ dx
三角形质心坐标x 三角形质心坐标 c是
y
xc =
∫ xdm
m
∫ =
a/ 2
0
2σ x2dx
a
1 2 σ a 2
2 = a 3
O x dx
x
9
例
确定半径为R的均质半球的质心位置. 确定半径为 的均质半球的质心位置. 的均质半球的质心位置
解:建立如图所示坐标 已知薄圆盘的质心位于圆心, 已知薄圆盘的质心位于圆心,取 厚度为dy的薄圆盘为质量微元 的薄圆盘为质量微元. 厚度为 的薄圆盘为质量微元.
19
例
xC总 = 0
v车 m x车 x车 = = = M v人 x人 Li + x车
x人地 = x人车 + x车地
x 人 = Li + x 车
m x车 = Li m+M
20
作 业:
2-1 2-25 2-5 2-27
02-2 动量定理及守恒定律
把作用时间分成 n 个 很小的时段∆ti ,每个 时段的力可看作恒力
v I = F∆t
v F2∆t2 v F ∆t1 1
v Fi ∆ti
v Fn∆tn
I v v v v v I = F ∆t1 + F2∆t2 +L+ Fn∆tn = ∑F∆ti i 1
注意: 注意:冲量
v v 的方向不同! 的方向不同 I的方向和瞬时力 F
•动量为状态量; 动量为状态量; 动量为状态量 •冲量为过程量,是力的作用对时间的积累。 冲量为过程量, 冲量为过程量 是力的作用对时间的积累。 •在宏观和微观领域均成立。 在宏观和微观领域均成立。 在宏观和微观领域均成立
2-2 动量定理和动量守恒定律
1.冲量 冲量 (1) 常力的冲量 (2) 变力的冲量 )
α
T
R Fr
●m
•一周内合力的冲量为零,并不是说明一周内质点的动量时时处处 一周内合力的冲量为零, 一周内合力的冲量为零 守恒,只是终点又恢复到起点的动量,这不叫动量守恒;所以, 守恒,只是终点又恢复到起点的动量,这不叫动量守恒;所以, 动量守恒的条件,不能说是“系统所收合外力的冲量为零”。 动量守恒的条件,不能说是“系统所收合外力的冲量为零”
v v I F= = 6⋅14N ∆t
mv2 F∆t = sin θ sin 1050
0
sin θ = 0⋅ 7866,θ = 51052'
∴α = 51 52'−45 = 6 52'
0 0
2-2 动量定理和动量守恒定律
F风对帆 F横
F进
υ1
风
υ1 υ2
Δυ
υ2
F帆对风
帆
F阻
v I = F∆t
v F2∆t2 v F ∆t1 1
v Fi ∆ti
v Fn∆tn
I v v v v v I = F ∆t1 + F2∆t2 +L+ Fn∆tn = ∑F∆ti i 1
注意: 注意:冲量
v v 的方向不同! 的方向不同 I的方向和瞬时力 F
•动量为状态量; 动量为状态量; 动量为状态量 •冲量为过程量,是力的作用对时间的积累。 冲量为过程量, 冲量为过程量 是力的作用对时间的积累。 •在宏观和微观领域均成立。 在宏观和微观领域均成立。 在宏观和微观领域均成立
2-2 动量定理和动量守恒定律
1.冲量 冲量 (1) 常力的冲量 (2) 变力的冲量 )
α
T
R Fr
●m
•一周内合力的冲量为零,并不是说明一周内质点的动量时时处处 一周内合力的冲量为零, 一周内合力的冲量为零 守恒,只是终点又恢复到起点的动量,这不叫动量守恒;所以, 守恒,只是终点又恢复到起点的动量,这不叫动量守恒;所以, 动量守恒的条件,不能说是“系统所收合外力的冲量为零”。 动量守恒的条件,不能说是“系统所收合外力的冲量为零”
v v I F= = 6⋅14N ∆t
mv2 F∆t = sin θ sin 1050
0
sin θ = 0⋅ 7866,θ = 51052'
∴α = 51 52'−45 = 6 52'
0 0
2-2 动量定理和动量守恒定律
F风对帆 F横
F进
υ1
风
υ1 υ2
Δυ
υ2
F帆对风
帆
F阻
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3
二、质点系的动量定理
质点系
∫
t2
t1
v v v v ( Fi外 + F ji )dt = mi vi 2 − mi vi1
n n−1 v r t2 (∑F外)dt + ∫ (∑∑ f ji )dt i n i=1 t1 i=1 j =1 n
∫
t2
v Fi外
v F ji
i
v Fij
v F j外
j
t1
Fdt = (m + dm) v − (mv + dm ⋅ 0) = vdm = kdt v
∴ F = k v = 200 × 4 = 8 ×10
第2章 运动定律与力学中的守恒定律
2
N
2–3 动量 动量守恒定律 *质心运动定理 3
12
*四、质心和质心运动定理 四 1.问题的提出 问题的提出 其余质点的运动 质心的平动 质心的概念 质心可看作整个质点 系的代表点, 系的代表点,系统的全部 质量 m,动量 在它上面. 在它上面
2–3 动量 动量守恒定律 *质心运动定理 3
14
个质点组成的质点系,其质心的位置: 有 n 个质点组成的质点系,其质心的位置:
v v v v m 1 r1 + m 1 r2 + …… + m i ri + …… rc = = m 1 + m 2 + …… + m i + ……
2.质心运动定理 质心运动定理
n v v = ∑mi vi 2 − ∑mi vi1 i=1
n
i=1
Q ∑∑
i =1 j =1
n −1
r f ji = 0 ∴
∫
t2
t1
n n r v v (∑ Fi外 )dt = ∑ mi vi 2 − ∑ mi v i1 n i =1 i =1 i =1
质点系总动量的增量等于作用于该系统上合外力的冲量
v mv2
越大 . 例如人从高处跳下 人从高处跳下、 例如人从高处跳下、飞 机与鸟相撞、 机与鸟相撞、打桩等碰撞事 件中,作用时间很短, 件中,作用时间很短,冲力 很大 .
第2章 运动定律与力学中的守恒定律
∆t 越小,则 F 越小,
v 在 ∆ p 一定时
F Fm
F
∫t
t2
1
Fdt = F (t 2 − t1 )
∴ f x =0 fN 2mv cos α 2 × 0.2 × 5 × 0.5 = = = 20 N ∆t 0.05
按牛顿第三定律, 按牛顿第三定律,球对墙的平均作用力和 f N 的方向相反而等值,即垂直于墙面向里. 的方向相反而等值,即垂直于墙面向里.
第2章 运动定律与力学中的守恒定律
2–3 动量 动量守恒定律 *质心运动定理 3
11
如图所示, m/s的速 例2.6 如图所示,一辆装矿砂的车厢以 v=4m/s的速 矿砂为k 率从漏 斗下通 过 , 每 秒落入 车厢的 矿砂为 = 200 kg/s, 如欲使车厢保持速率不变, kg/s , 如欲使车厢保持速率不变 , 须施与车厢多大 的牵引力(忽略车厢与地面的摩擦) 的牵引力(忽略车厢与地面的摩擦). 解 设 t时刻已落入车厢的矿砂 时刻已落入车厢的矿砂 质量为m,经过d 后又有 质量为 ,经过dt后又有 的矿砂落入车厢. dm=kdt的矿砂落入车厢. 取m = d 的矿砂落入车厢 为研究对象, 和 dm为研究对象, 则系统沿 为研究对象 则系统沿x 方向的动量定理为
第2章 运动定律与力学中的守恒定律
t0
2–3 动量 动量守恒定律 *质心运动定理 3
2
∫
t 0
v v v v v F dt = p − p0 = m v − m v0
在给定的时间内, 动量定理 在给定的时间内,外力作用在质点上的 冲量, 冲量,等于质点在此时间内动量的增量 . 问:冲量是矢量,它的方向就是力的方向吗 ? 冲量是矢量, 分量形式
第2章 运动定律与力学中的守恒定律
2–3 动量 动量守恒定律 *质心运动定理 3
8
三、质点系的动量守恒定律
r 若质点系所受的合外力为零 若质点系所受的合外力为零 ∑ Fi外 = 0
n
则系统的总动量守恒, 则系统的总动量守恒,即 总动量守恒
∑mv
i =1 i
n
ቤተ መጻሕፍቲ ባይዱ
i =1
i2
=
∑mv
i =1 i
n
i1
定义:一个孤立的力学系统 系统不受外力作用 系统不受外力作用)或 定义:一个孤立的力学系统(系统不受外力作用 或 合外力为零的系统,系统内各质点间动量可以交换, 合外力为零的系统,系统内各质点间动量可以交换, 但系统的总动量保持不变。 但系统的总动量保持不变。
2–3 动量 动量守恒定律 *质心运动定理 3
1
力的累积效应 累积效应 一、质点的动量定理 动量
v v v F (t ) 对 t 积累 → p , I v v 积累 F 对r →W, E
v v p = mv
v v v dp d (m v) v v v F = = Fdt = dp = d (m v ) dt dt t v v v v v F dt = p − p0 = m v − m v0 ∫0 v t v 力对时间的积分(矢量) 冲量 力对时间的积分(矢量) I = ∫ Fdt
o
t
t1
t2
2–3 动量 动量守恒定律 *质心运动定理 3
7
问:为什么迅速地把盖在杯上的薄板从侧面打去, 为什么迅速地把盖在杯上的薄板从侧面打去, 鸡蛋就掉在杯中;慢慢地将薄板拉开, 鸡蛋就掉在杯中;慢慢地将薄板拉开,鸡蛋就会和薄 板一起移动? 板一起移动?
答:因为鸡蛋和薄板间的摩擦力有限,若棒打击 因为鸡蛋和薄板间的摩擦力有限, v v 时间很短, 时间很短,Q F ∆ t → 0, ∴ ∆ P → 0 所以鸡蛋就 f 蛋 掉在杯中. 掉在杯中
第2章 运动定律与力学中的守恒定律
∫t
t2
1
v v v F (t )dt = mv 2 − mv1
2–3 动量 动量守恒定律 *质心运动定理 3
6
动量定理常应用于碰撞问题
v v v ∫t1 mv2 − mv1 F= = t 2 − t1 t 2 − t1
注意
t2
v Fdt
v ∆mv
v m v1
v F
+
y yc
绕质心的转动
v r3
m2
O
m3
v p
都集中
v r2
zc
z
v rc
c
m1
v r1
xc x
第2章 运动定律与力学中的守恒定律
2–3 动量 动量守恒定律 *质心运动定理 3
13
质心的位置
v m rc =
∑
n
i =1
v m i ri
第2章 运动定律与力学中的守恒定律
v v n d rc d ri m = ∑ mi dt dt i =1
I x = ∫ Fx dt = mv2 x − mv1x
t1
2 1
t2
t v v v v I = Ixi + I y j + Izk I y = ∫t Fy dt = mv2 y − mv1 y
I z = ∫ Fz dt = mv2 z − mv1z
t1
第2章 运动定律与力学中的守恒定律
t2
2–3 动量 动量守恒定律 *质心运动定理 3
2–3 动量 动量守恒定律 *质心运动定理 3
5
讨论
动量的相 动量的相 对性和动量定 对性和动量定 理的不变性 理的不变性 参考系 t1 时刻
S
S′
v F(t)
t1
m
光滑
v v1
m
v u v v2
t2
t2 时刻
动量定理
v v mv1 mv2 S系 系 v v v v S’系 m( v1 − u ) m( v2 − u ) 系
说明
ydm yc = ∫ m
zdm zc = ∫ m
对密度均匀、形状对称的物体, 对密度均匀、形状对称的物体,其质心在 其几何中心. 其几何中心.
第2章 运动定律与力学中的守恒定律
v ∑ m i ri
i =1
n
m
系统内各质点的动量的矢量和等于系统质心的速度 乘以系统的质量 u r
v dP ∑ Fi外 = dt i =1
n
质心运动定理: 质心运动定理 作用在系统上的合外力等于系统的 总质量乘以质心的加速度
第2章 运动定律与力学中的守恒定律
2–3 动量 动量守恒定律 *质心运动定理 3
第2章 运动定律与力学中的守恒定律
2–3 动量 动量守恒定律 *质心运动定理 3
9
一弹性球,质量m=0.20kg, 5m/s, 例2.5 一弹性球,质量 =0.20kg,速度 v=5m/s, 与墙碰撞后弹回.设弹回时速度大小不变, 与墙碰撞后弹回.设弹回时速度大小不变,碰撞前后 的运动方向和墙的法线所夹的角都是α,设球和墙碰 撞的时间Δ 0.05s, 60° 求在碰撞时间内, 撞的时间Δt=0.05s,α=60°,求在碰撞时间内, 球和墙的平均相互作用力. 球和墙的平均相互作用力. 解 以球为研究对象.设墙 以球为研究对象. 对球的平均作用力为f, 对球的平均作用力为 ,球 在碰撞前后的速度为 v1 和 v2 ,由动量定理可得
第2章 运动定律与力学中的守恒定律
2–3 动量 动量守恒定律 *质心运动定理 3
4
注意
内力不改变质点系的动量
初始速度
v g 0 =vb0 = 0
mb = 2mg
且方向相反
则 则
