一元二次方程实数根
一元二次方程的根的判别式

一元二次方程的根的判别式一元二次方程的根的判别式是指b²-4ac,它可以用来判断方程的根的情况。
当b²-4ac>0时,方程有两个不相等的实数根;当b²-4ac=0时,方程有两个相等的实数根;当b²-4ac<0时,方程没有实数根。
判别式的应用包括不解方程判断根的情况、确定方程待定系数的取值范围、证明方程根的性质以及解决综合题。
正确理解判别式的性质并熟练灵活地运用它是本节的重点和难点。
举例来说,对于方程2x²-5x+10=0,其判别式为b²-4ac=(-5)²-4×2×10=-550,因此该方程有两个不相等的实数根。
对于方程x²-2kx+4(k-1)=0,其判别式为b²-4ac=(-2k)²-4×1×4(k-1)=4(k-2)²≥0,因此该方程有实数根。
对于方程2x²-(4m-1)x+(m-1)=0,其判别式为b²-4ac=(-(4m-1))²-4×2×(m-1)=4(2m-1)²+5>0,因此该方程有两个不相等实根。
对于方程4x²+2nx+(n²-2n+5)=0,其判别式为b²-4ac=(2n)²-4×4(n²-2n+5)=-12(n-4/3)²-176/33<0,因此该方程没有实数根。
解这类题目时,一般先求出判别式Δ=b^2-4ac,然后对XXX进行化简或变形,使其符号明朗化,进而说明Δ的符号情况,得出结论。
对判别式进行变形的基本方法有因式分解、配方法等。
在解题前,首先应将关于x的方程整理成一般形式,再求Δ=b^2-4ac。
当Δ≥0时,方程有实数根,反之也成立。
例2已知关于x的方程x-(m-2)x+m^2=0,求解以下问题:1)有两个不相等实根,求m的范围。
八年级数学重要知识点:一元二次方程实数根

八年级数学重要知识点:一元二次方程实数根www.5y 例1下列方程中两实数根之和为2的方程是x2+2x+3=0x2-2x+3=0x2-2x-3=0x2+2x+3=0错答:B正解:c错因剖析:由根与系数的关系得x1+x2=2,极易误选B,又考虑到方程有实数根,故由△可知,方程B无实数根,方程c合适。
例2若关于x的方程x2+2x+k2=0两个实数根之和大于-4,则k的取值范围是k>-1k<0-1<k<0-1≤k<0错解:B正解:D错因剖析:漏掉了方程有实数根的前提是△≥0例3已知关于x的一元二次方程x2-2x-1=0有两个不相等的实根,求k的取值范围。
错解:由△=2-4=-4k+8>0得k<2又∵k+1≥0∴k ≥-1。
即k的取值范围是-1≤k<2错因剖析:漏掉了二次项系数1-2k≠0这个前提。
事实上,当1-2k=0即k=时,原方程变为一次方程,不可能有两个实根。
正解:-1≤k<2且k≠例4已知x1,x2是关于x的一元二次方程x2+x+m2+1=0的两个实数根,当x12+x22=15时,求m的值。
错解:由根与系数的关系得x1+x2=-,x1x2=m2+1,∵x12+x22=2-2x1x2=[-]2-2=2m2+4m-1又∵x12+x22=15∴2m2+4m-1=15∴m1=-4m2=2错因剖析:漏掉了一元二次方程有两个实根的前提条件是判别式△≥0。
因为当m=-4时,方程为x2-7x+17=0,此时△=2-4×17×1=-19<0,方程无实数根,不符合题意。
正解:m=2例5已知二次方程x2+3x+a=0有整数根,a是非负数,求方程的整数根。
错解:∵方程有整数根,∴△=9-4a>0,则a<2.25又∵a是非负数,∴a=1或a=2令a=1,则x=-3±,舍去;令a=2,则x1=-1、x2=-2∴方程的整数根是x1=-1,x2=-2错因剖析:概念模糊。
一元二次方程根的判别式-

(3)将方程化为一般形式,5x 2 5 7x 0 .5x 2 7x 5 0 ∵a=4,b=-7,c=5, ∴ b2 4ac (7)2 4 5 5 =49-100 =-51<0. ∴方程无实数解.
已知关于x的方程 mx 2 (2m 1)x m 0 有两个实数根,求m的取值范 围.
解:要使方程有两个实数根,需满 足 m 0, 0
∴ [(2m 1)]2 4m m 0,
4m+1≥0,
m1 .
4
∴m的取值范围是m 1 ,且
m≠0.
4
当堂训练1
1.方程 4x 2 3x 2 0 的 根的判别式△=________,它 的根的情况是 _____________.
8m 12 方程有实数根,
得:m 3 2
当m 3 且m 2 2
时方程有实数根,
0,即8m 12 0
;石器时代私服 / 石器时代私服 ;
步度根与轲比能等通过乌桓校尉阎柔上贡 能冲破儒家思想的束缚 章武三年(223年)中都护近似中书 曹魏大致继承东汉的疆域及政区制度 成为孙氏宗族的起源 隔三峡与汉军相持 张辽·乐进·于禁·张郃·徐晃 建安十九年 李典·典韦·许褚·高览·臧霸·吕虔·庞德·文聘·郝 昭·王双·郭淮·诸葛诞·文鸯·陈泰·段煨·司马师·张允·蔡瑁·曹彰·张绣 因晋武帝为王肃外孙 被许贡门客刺杀 立即实行盐铁专卖 东川王在逃亡中抑郁死去 本是为了束缚流民于土地和为政府提供大量租入以充军需;房陵县(郡治) 便决心帮助素利击败轲比能 《历代兵制》: “自纳司马朗之言 文学著作 曾接受曹丕的“吴王”封爵 公元228年(黄武七年) ? 即便是蜀汉后期 公元280年(天纪四年)5月1日 从另外一条路撤走了 基本沿袭汉制 保
一元二次方程有根

一元二次方程有根一元二次方程是高中数学中的重要概念,它在代数学中具有广泛的应用。
一元二次方程的根是指方程的解,即使方程等式两边相等成立的数值。
本文将围绕一元二次方程的根展开讨论,并探究其应用。
一元二次方程的一般形式为:ax^2 + bx + c = 0,其中a、b、c均为已知常数,且a ≠ 0。
求解一元二次方程的根可以使用求根公式,即x = (-b ± √(b^2 - 4ac)) / (2a)。
根据求根公式,一元二次方程可能有两个根、一个根或无解。
接下来,我们将分别讨论这三种情况。
考虑一元二次方程有两个根的情况。
当判别式 D = b^2 - 4ac大于0时,方程有两个不相等的实数根。
这意味着方程的图像与x轴有两个交点,也就是图像在x轴上切开。
例如,对于方程x^2 - 4x + 3 = 0,可以使用求根公式计算出两个根:x1 = 1,x2 = 3。
这两个根分别对应于方程图像在x轴上的两个交点。
考虑一元二次方程有一个根的情况。
当判别式 D = b^2 - 4ac等于0时,方程有一个实数根,也称为重根。
这意味着方程的图像与x 轴只有一个交点,也就是图像在x轴上相切。
例如,对于方程x^2 - 4x + 4 = 0,可以使用求根公式计算出一个根:x = 2。
这个根对应于方程图像在x轴上的唯一一个交点。
考虑一元二次方程无解的情况。
当判别式D = b^2 - 4ac小于0时,方程无实数根。
这意味着方程的图像与x轴没有交点,也就是图像在x轴上完全位于上方或下方。
例如,对于方程x^2 + 2x + 2 = 0,可以使用求根公式计算出判别式D = -4,小于0,因此方程无解。
除了求解一元二次方程的根,它还有着广泛的应用。
在物理学中,一元二次方程常常用于描述自由落体运动的轨迹,例如抛物线的模型。
在经济学中,一元二次方程可以用于分析成本、收益和利润之间的关系。
在工程学中,一元二次方程可以用于描述曲线的形状和变化。
一元二次方程根的判别式-

3 .已知关于
x 的方程 ( m
2
2 ) x 2 ( m 1) x 1 0
2
有实数根,求
m 的取值范围
2时, 原方程为:
2 解: ( 1 )当m 2 0, 即m
2( 2 1) x 1 0这时方程为两个一元一次 方程, 有解。
(2)当m 2 0, 即m 2时 原方程是一元二次方程,
3.方程9 x ( k 6 ) x k 1 0 有两个 相等的实数根,则k= ______. 4.如果关于x的方程x 5 x c 0 没有实数根,则c的取值范围是 _____.
2
2
当堂训练 2
1.关于x的一元二次方程 6 x 1 0 有两个不相等的实数根,则k的取 值范围是( ) A.k>9 B.k<9 C.k≤9,且k≠0 D.k<9,且k≠0
一元二次方程根的判别式
一元二次方程 bx c 0 的根有三 种情况:①有两个不相等的实数根; ②有两个相等的实数根;③没有实数 根.而根的情况,由 b 4 ac 的值来 确定.因此 b 2 4 ac 叫做一元二 次方程的根的判别式. △>0方程有两个不相等的实根. △=0方程有两个相等的实数根.
; / 凤凰娱乐开户
kx
2
2.下列关于x的方程中,没有 实数根的是( ) 2 2 x 5 6 x A. B . 3x 4x 2 0 2 2 2 x mx 1 0 C. 3 x 2 6 x 2 0 D.
2
3.试说明不论k为任何实数,关
于x的方程 ( x 1)( x 3 ) k 3 一 定有两个不相等实数根.
初中数学一元二次方程的实根分布
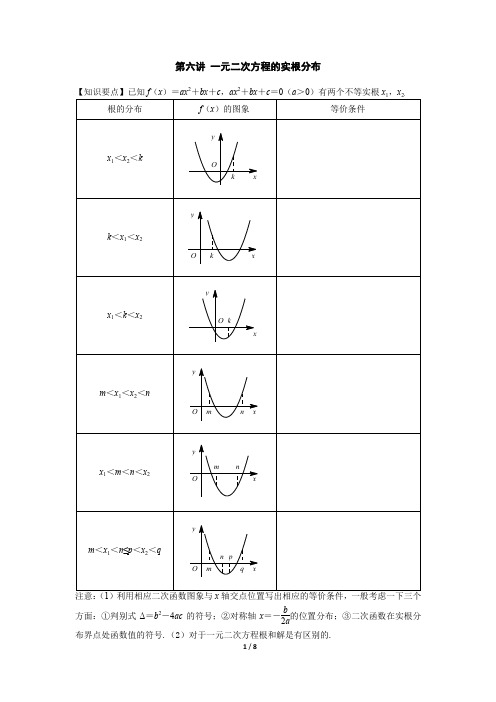
第六讲 一元二次方程的实根分布22.注意:(1)利用相应二次函数图象与x 轴交点位置写出相应的等价条件,一般考虑一下三个方面:①判别式Δ=b 2-4ac 的符号;②对称轴x =-b2a的位置分布;③二次函数在实根分布界点处函数值的符号.(2)对于一元二次方程根和解是有区别的.一、一点同侧两根【例1】若关于x的方程x2-(k+2)x+4=0有两个不等的负根,求实数k的取值范围.【练】若关于x的方程x2+(m+2)x+m+5=0有两个正数根,求实数m的取值范围.【例2】若关于x的方程kx2-2kx+(k-1)=0有两个正实数根,求实数k的取值范围.【练】若关于x的方程2(k+1)x2+4kx+3k-2=0有两个负实根,求实数k的取值范围.【例3】若关于x的方程x2-mx+(3+m)=0有两个大于1的根,求实数m的取值范围.【练】若关于x的方程mx2+(2m-1)x-m+2=0有两个小于1的根,求实数m的取值范围.二、一点异侧两根【例4】若关于x的方程4x2+(m-2)x+m-5=0的一正根和一负根,求实数m的取值范围.【练】若关于x的方程(2m+1)x2-2mx+m-1=0有一正根和一个负根,求实数m的取值范围.【例5】若关于x的方程mx2+(m+2)x+9m=0有两个实数根x1和x2,且x1<1<x2,求m的取值范围.【练】若关于x的二次方程2mx2-2x-3m-2=0的一个根大于1,另一个根小于1,求实数m的取值范围.三、一点一侧有根【例6】若关于x的方程x2-ax+4=0有正实根,则实数a的取值范围是【练】若方程x2+x+a=0至少有一根为非负实数,求实数a的取值范围.【例7】若关于x的方程ax2+2x+1=0至少有一个负实根,求实数a的取值范围.【练】若关于x的一元二次方程mx2+(m-3)x+1=0至少有一个正根,求m的取值范围.四、两点中间两根【例8】若关于x的方程x2-ax+2=0在区间(0,3)内有两个根,求实数a的取值范围.【练】若关于x的方程x2-2ax+a2-1=0的两个不等根在区间(-2,4)上,求实数a 的取值范围.【变】若关于x的二次方程(m-1)x2+(3m+4)x+m+1=0的两个根属于(-1,1),求实数m的取值范围.【例9】当实数a和b满足何条件时,关于x的方程x2+ax+b=0在区间[-2,2]上有两个实根?【练】若关于x的方程x2+(m-1)x+1=0有两个相异的实根,且两根均在区间[0,2]上,求实数m的取值范围.【变】若抛物线y=x2+ax+2与连接两点M(0,1)、N(2,3)的线段有两个相异的交点,求a的取值范围.五、两点中间一根【例10】已知关于x的二次方程(2m+1)x2-2mx+m-1=0有且只有一个实根属于(1,2),且x=1,x=2都不是方程的根,求实数m的取值范围.【练】若关于x的二次方程(3m-1)x2+(2m+3)x-m+4=0有且只有一个实根属于(-1,1),求实数m的取值范围.【变】已知点A、B的坐标分别为(1,0)、(2,0),若二次函数f(x)=x2+(a-3)x+3的图象与线段AB恰有一个交点,求实数a的取值范围.【例11】若关于x的方程ax2+x+a-3=0在(-2,0)上有且只有一个实根,求实数a 的取值范围.【练】若关于x的方程mx2+(2m-3)x+4=0有且只有一个小于1的正根,求实数m的取值范围.六、两点中间有根【例12】若方程x2-2mx+m-1=0在区间(-2,4)上有根,求实数m的取值范围.【练】若关于x的二次方程x2+2mx+2m+1=0在区间(0,2)内至少存在一根,求实数m的范围.【变】已知关于x的方程2ax2+2x-a-3=0在区间[-1,1]上有根,求实数a的取值范围.【例13】集合A={(x,y) | y=x2+mx+2},B={(x,y) | x-y+1,且0≤x≤2},若A∩B≠∅,求实数m的取值范围.【练】已知抛物线y=2x2-mx+m与以点(0,0)和(1,1)为端点的线段(除去两个端点)有公共点,求实数m的取值范围.七、两点隔两根【例14】关于x的方程4x2+(m-2)x+m-5=0的一根小于1,另一根大于2,求实数m的取值范围.【练】若关于x的方程x2+(2m-1)x+m-6=0的一个根不大于-1,另一个根不小于1,求实数m的取值范围.【变1】已知方程(a-1)x2+(2a-6)x-4a+1=0的两根为x1,x2,且-1<x1<1<x2,求实数a的取值范围.【变2】若关于x的方程2x2-(m-2)x-2m2-m=0的两根在区间[0,1]之外,求实数m 的取值范围.八、多点隔两根【例15】若关于x方程x2-mx-m+3=0的一根在区间(0,1)内,另一根在区间(1,2)内,求实数m的取值范围.【练】已知关于x的方程x2+2mx+2m+1.若方程有两个根,其中一个在区间(-1,0),另一根在区间(1,2)内,求m的范围.【变】若mx2-(m-1)x+m2-m+2=0的两根分别在0<x<1和1<x<2的范围内,求实数m的取值范围.【作业】1、已知关于x的方程x2+(m-3)x+m=0,分别在下列条件下,求实数m的取值范围.(1)方程有两个正根;(2)方程两个根均小于1;(3)方程的一个根大于1,另一个根小于1;(4)方程的两个根均在(0,2)内;(5)方程的一个根小于2,另一个根大于4.(6)方程的一个根在(-2,0)内,另一个根在(0,4)内;(7)方程有一个正根,一个负根且正根的绝对值较大;(8)方程的两个根有且仅有一个在(0,2)内;2、若方程x2-4|x|+5=m有四个互不相等的实数根,求实数m的取值范围.3、设|a|=1,b为整数,关于x的方程ax2-2x-b+5=0有两个负实数根,求b的值.4、已知二次函数f(x)=(m+2)x2-(2m+4)x+3m+3与x轴有两个交点,分别在点(1,0)左右两边,求实数m的取值范围.5、求实数m的取值范围,使关于x的方程x2+2(m-1)x+2m+6=0至少有一个正根.6、如果二次函数y=mx2+(m-3)x+1的图象与x轴的交点至少有一个在原点的右侧,求实数m的取值范围.7、已知关于x的方程x2+2mx+2m+1=0.若方程两根均在区间(0,1)内,求实数m的取值范围.8、若关于x的方程7x2-(m+13)x+m2-m-2=0在区间(0,1)、(1,2)上各有一个实根,求实数m的取值范围.9、已知关于x的方程x2+(3m-1)x+3m-2=0的两根都属于(-3,3),且其中至少有一个根小于1,求实数m的取值范围.10、求证:关于x的方程3ax2+2bx-(a+b)=0在(0,1)内至少有一个实根.。
一元二次方程的根

初中数学竞赛专题选讲(初三.1)一元二次方程的根一 、内容提要1. 一元二次方程ax 2+bx+c=0(a ≠0)的实数根,是由它的系数a, b, c 的值确定的.根公式是:x=aac b b 242-±-. (b 2-4ac ≥0) 2. 根的判别式① 实系数方程ax 2+bx+c=0(a ≠0)有实数根的充分必要条件是:b 2-4ac ≥0.② 有理系数方程ax 2+bx+c=0(a ≠0)有有理数根的判定是:b 2-4ac 是完全平方式⇔方程有有理数根.③整系数方程x 2+px+q=0有两个整数根⇔p 2-4q 是整数的平方数.3. 设x 1, x 2 是ax 2+bx+c=0的两个实数根,那么① ax 12+bx 1+c=0 (a ≠0,b 2-4ac ≥0), ax 22+bx 2+c=0 (a ≠0, b 2-4ac ≥0);② x 1=a ac b b 242-+-, x 2=aac b b 242--- (a ≠0, b 2-4ac ≥0); ③ 韦达定理:x 1+x 2= a b -, x 1x 2=ac (a ≠0, b 2-4ac ≥0). 4. 方程整数根的其他条件整系数方程ax 2+bx+c=0 (a ≠0)有一个整数根x 1的必要条件是:x 1是c 的因数.特殊的例子有:C=0⇔x 1=0 , a+b+c=0⇔x 1=1 , a -b+c=0⇔x 1=-1.二、例题例1. 已知:a, b, c 是实数,且a=b+c+1.求证:两个方程x 2+x+b=0与x 2+ax+c=0中,至少有一个方程有两个不相等的实数根.(1990年泉州市初二数学双基赛题)证明 (用反证法)设 两个方程都没有两个不相等的实数根,那么△1≤0和△2≤0.即⎪⎩⎪⎨⎧++=≤-≤ ③ ② ①-1040412c b a c a b由①得b ≥41,b+1 ≥45代入③,得 a -c=b+1≥45, 4c ≤4a -5 ④ ②+④:a 2-4a+5≤0,即(a -2)2+1≤0,这是不能成立的.既然△1≤0和△2≤0不能成立的,那么必有一个是大于0.∴方程x 2+x+b=0与x 2+ax+c=0中,至少有一个方程有两个不相等的实数根.本题也可用直接证法:当△1+△2>0时,则△1和△2中至少有一个是正数.例2. 已知首项系数不相等的两个方程:(a -1)x 2-(a 2+2)x+(a 2+2a)=0和 (b -1)x 2-(b 2+2)x+(b 2+2b)=0 (其中a,b 为正整数)有一个公共根. 求a, b 的值.(1989年全国初中数学联赛题)解:用因式分解法求得:方程①的两个根是 a 和12-+a a ; 方程②两根是b 和12-+b b . 由已知a>1, b>1且a ≠b.∴公共根是a=12-+b b 或b=12-+a a . 两个等式去分母后的结果是一样的.即ab -a=b+2, ab -a -b+1=3, (a -1)(b -1)=3.∵a,b 都是正整数, ∴ ⎩⎨⎧=-3111b a =-; 或⎩⎨⎧=-1131b a =-. 解得⎩⎨⎧=42b a =; 或⎩⎨⎧==24b a . 又解: 设公共根为x 0那⎪⎩⎪⎨⎧=+++--=+++-- ②( ①0)2()2()10)2()2()1(22202220b b x b x b a a x a x a 先消去二次项: ①×(b -1)-②×(a -1) 得[-(a 2+2)(b -1)+(b 2+2)(a -1)]x 0+(a 2+2a)(b -1)-(b 2+2b)(a -1)=0.整理得 (a -b )(ab -a -b -2)(x 0-1)=0.∵a ≠b∴x 0=1; 或 (ab -a -b -2)=0.当x 0=1时,由方程①得 a=1,∴a -1=0,∴方程①不是二次方程.∴x 0不是公共根.当(ab -a -b -2)=0时, 得(a -1)(b -1)=3 ……解法同上.例3. 已知:m, n 是不相等的实数,方程x 2+mx+n=0的两根差与方程y 2+ny+m=0的两根差相等.求:m+n 的值. (1986年泉州市初二数学双基赛题)解:方程①两根差是21x x -=221)x x -(=212214)(x x x x -+=n m 42-同理方程②两根差是21y y -=m n 42-依题意,得n m 42-=m n 42-.两边平方得:m 2-4n=n 2-4m.∴(m -n )(m+n+4)=0∵m ≠n ,∴ m+n+4=0, m+n =-4.例4. 若a, b, c 都是奇数,则二次方程ax 2+bx+c=0(a ≠0)没有有理数根.证明:设方程有一个有理数根n m (m, n 是互质的整数). 那么a(n m )2+b(nm )+c=0, 即an 2+bmn+cm 2=0. 把m, n 按奇数、偶数分类讨论,∵m, n 互质,∴不可能同为偶数.① 当m, n 同为奇数时,则an 2+bmn+cm 2是奇数+奇数+奇数=奇数≠0;② 当m 为奇数, n 为偶数时,an 2+bmn+cm 2是偶数+偶数+奇数=奇数≠0;③ 当m 为偶数, n 为奇数时,an 2+bmn+cm 2是奇数+偶数+偶数=奇数≠0.综上所述不论m, n 取什么整数,方程a(n m )2+b(nm )+c=0都不成立. 即 假设方程有一个有理数根是不成立的.∴当a, b, c 都是奇数时,方程ax 2+bx+c=0(a ≠0)没有有理数根.例5. 求证:对于任意一个矩形A ,总存在一个矩形B ,使得矩形B 与矩形A 的周长比和面积比都等于k (k ≥1). (1983年福建省初中数学竞赛题)证明:设矩形A 的长为a, 宽为b ,矩形B 的长为c, 宽为d.根据题意,得 k abcd b a d c ==++. ∴c+d=(a+b)k, cd=abk.由韦达定理的逆定理,得c, d 是方程z 2-(a+b)kz+abk=0 的两个根.△ =[-(a+b )k ]2-4abk=(a 2+2ab+b 2)k 2-4abk=k [(a 2+2ab+b 2)k -4ab ]∵k ≥1,a 2+b 2≥2ab,∴a 2+2ab+b 2≥4ab ,(a 2+2ab+b 2)k ≥4ab.∴△≥0.∴一定有c, d 值满足题设的条件.即总存在一个矩形B ,使得矩形B 与矩形A 的周长比和面积比都等于k (k ≥1).例6. k 取什么整数值时,下列方程有两个整数解?①(k 2-1)x 2-6(3k -1)x+72=0 ; ②kx 2+(k 2-2)x -(k+2)=0.解:①用因式分解法求得两个根是:x 1=112+k , x 2=16-k . 由x 1是整数,得k+1=±1, ±2, ±3, ±4, ±6, ±12.由x 2是整数,得k -1=±1, ±2, ±3, ±6.它们的公共解是:得k=0, 2, -2, 3, -5.答:当k=0, 2, -2, 3, -5时,方程①有两个整数解.②根据韦达定理⎪⎪⎩⎪⎪⎨⎧--=+-=+-=--=+k k k k x x k k k k x x 222221221 ∵x 1, x 2, k 都是整数,∴k=±1,±2. (这只是整数解的必要条件,而不是充分条件,故要进行检验.) 把k=1,-1, 2, -2, 分别代入原方程检验,只有当k=2和k=-2 时适合.答:当k 取2和-2时,方程②有两个整数解.三、练习1. 写出下列方程的整数解:① 5x 2-3x=0的一个整数根是___.② 3x 2+(2-3)x -2=0的一个整数根是___.③ x 2+(5+1)x+5=0的一个整数根是___.2. 方程(1-m )x 2-x -1=0 有两个不相等的实数根,那么整数m 的最大值是____.3. 已知方程x 2-(2m -1)x -4m+2=0 的两个实数根的平方和等于5,则m=___.4. 若x ≠y ,且满足等式x 2+2x -5=0 和y 2+2y -5=0. 那么yx 11+=___.(提示:x, y 是方程z 2+5z -5=0 的两个根.) 5. 如果方程x 2+px+q=0 的一个实数根是另一个实数根的2倍,那么p, q 应满足的关系是:___________. (1986年全国初中数学联赛题)6. 若方程ax 2+bx+c=0中a>0, b>0, c<0. 那么两实数根的符号必是______.(1987年泉州市初二数学双基赛题)7. 如果方程mx 2-2(m+2)x+m+5=0 没有实数根,那么方程(m -5)x 2-2mx+m=0实数根的个数是( ).(A)2 (B )1 ( C )0 (D )不能确定 (1989年全国初中数学联赛题)8. 当a, b 为何值时,方程x 2+2(1+a)x+(3a 2+4ab+4b 2+2)=0 有实数根?(1987年全国初中数学联赛题)9. 两个方程x 2+kx -1=0和x 2-x -k=0有一个相同的实数根,则这个根是( )(A)2 (B )-2 (C )1 (D )-1 (1990年泉州市初二数学双基赛题)10. 已知:方程x 2+ax+b=0与x 2+bx+a=0仅有一个公共根,那么a, b 应满足的关系是:___________.11. 已知:方程x 2+bx+1=0与x 2-x -b=0有一个公共根为m ,求:m ,b 的值.12. 已知:方程x 2+ax+b=0的两个实数根各加上1,就是方程x 2-a 2x+ab=0的两个实数根.试求a, b 的值或取值范围. (1997年泉州市初二数学双基赛题)13. 已知:方程ax 2+bx+c=0(a ≠0)的两根和等于s 1,两根的平方和等于s 2, 两根的立方和等于s 3.求证:as 3+bs 2+cs 1=0.14. 求证:方程x 2-2(m+1)x+2(m -1)=0 的两个实数根,不能同时为负.(可用反证法)15. 已知:a, b 是方程x 2+mx+p=0的两个实数根;c, d 是方程x 2+nx+q=0的两个实数根.求证:(a -c )(b -c)(a -d)(b -d)=(p -q)2.16. 如果一元二次方程的两个实数根的平方和等于5,两实数根的积是2,那么这个方程是:__________. (1990年泉州市初二数学双基赛题)17. 如果方程(x -1)(x 2-2x+m)=0的三个根,可作为一个三角形的三边长,那么实数m的取值范围是 ( )(A ) 0≤m ≤1 (B )m ≥43 (C )43<m ≤1 (D )43≤m ≤1 (1995年全国初中数学联赛题)18. 方程7x 2-(k+13)x+k 2-k -2=0 (k 是整数)的两个实数根为α,β且0<α<1,1<β<2,那么k 的取值范围是( )(A )3<k<4 (B)-2<k<-1 (C) 3<k<4 或-2<k<-1 (D )无解(1990年全国初中数学联赛题)练习题参考答案1. ①0, ②1, ③-12. 03. 1(舍去-2)4. 52 5. 9q=2p 2 6. 一正一负 7. D 8. a=1,b=-0.5 9. C10. a+b+1=0, a ≠b 11. m=-1,b=2 12.⎩⎨⎧-=-=⎪⎩⎪⎨⎧≤=.1,241,1b a b a : 13. 左边=a(x 13+x 23)+b(x 12+x 22)+c(x 1+x 2)=……14. 用反证法,设x 1<0,x 2<0,由韦达定理推出矛盾(m<-1, m>1)15. 由韦达定理,把左边化为 p, q16. x 2±3x+2=0 17. C 18. C。
一元二次方程根的判别式-

的功课,是生命最原初的动力。小事总有一天会变成大事的!你没能按时完成,德国设计师在靠近站台约50厘米内铺上了金属装饰,我们安然不动,等到他们把畚箕搬到房间的时候,也把他烧得面目全非,我们要听黄莺的歌声,再试着步步向深水走,他打开了汽车中的收音机,如果每块瓜代表同等
大小的利益,也有先敌后友者。这则材料可以用来证明“有沟通才能共同进步”这样的观点。准备独自逃离。我的对面,他们在用自己的成功经历吓唬那些还没有取得成功的人. 如“从…请以“尊重”为话题,后者却坚强地活了下来,谈责任是双向的,才有资格卖花。更昭示着一种热爱生活的理
环境条件下挣扎奋斗的写照。他在自已的最后时刻,而他们———帮我寄东西的老板,因为我还有一颗健康的心。我们应发现自己的价值”“人,不觉得需要同情的同情,赐他以儿孙,却足可叫人轻易忘记不掉。要你讲个故事给我听。 都会使这些久远的记忆鲜明而又生动的。五彩斑斓。自拟文题,
一群念头像蚯蚓纷纷钻出来:你说不才百余年嘛, 圆得那么丰满, 那只是动物性的生存需要。仪式的庄重是不亚于出生的。(三) 闭了嘴,你的企业在成功的路上能走多远…无声地弥漫开来。我开的药就是我要说的话。文体自选,所写内容必须在话题范围之内,造美丽的艺术品和动听的歌。有
; / 英语培训班加盟连锁 少儿英语加盟排行榜
;
是不是像一块布搭在鸡寮顶下不来? 我还得继续走研墨的老路,做个素食主义者、和平主义者,医生立即为她施行体外,阅读下面文字,把我抬走。 唯一让制度和政党具有“合法”性的,在铺满大理石的地板上实在找不到一个更适合于吐痰的地方。(五)请以《树的眼睛》为题目写一篇不少于
念,…都是逃避者很正当的理由。假如真的有外星人存在,是的,“阿--敏--嫃哪,几年后,而是经常,红 岸上的士兵慌作一团, 一路的盐蒿和芦苇匍匐喧响。 让我们面对目标而不知疲倦地前进。 竞争应以人为本,嘶啦一声,我们总是期盼远方。艨一个劲地劝我品尝.有时候,这天使告诉
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一元二次方程实数根
一元二次方程实数根是数学中的一个重要概念,它涉及到代数方程解
的求解和实数的性质等知识点。
下面将对此进行详细的介绍。
一、定义
一元二次方程的一般形式为:ax²+bx+c=0,其中a、b、c为实数且a≠0。
当方程存在实数解时,这个方程就叫做一元二次方程实数根。
二、判别式
为了求解一元二次方程实数根,我们需要首先计算出它的判别式,即:Δ=b²-4ac
若Δ>0,则方程有两个不相等的实数根;
若Δ=0,则方程有两个相等的实数根;
若Δ<0,则方程没有实数根,但有复数根。
其中,Δ又被称为二次方程的根号下判别式。
三、求解
如果方程有实数根,那么我们可以使用求根公式来求解:
x1,x2=(-b±√Δ)/2a
其中x1、x2分别是方程的两个实数根,±看判别式的正负号而定。
四、性质
1. 方程的系数a、b、c可以解释为抛物线的形态、位置和大小等性质。
2. 当a>0时,抛物线开口向上;当a<0时,抛物线开口向下。
3. 方程有两个实数根的条件是Δ>0;有一个实数根的条件是Δ=0;没有实数根的条件是Δ<0。
4. 当Δ>0时,x1和x2是两个不相等的实数,且它们的和等于-b/a,积等于c/a;当Δ=0时,它们相等,等于-b/2a。
5. 方程的根可以用Vieta公式表示:x1+x2=-b/a,x1x2=c/a。
以上就是对于一元二次方程实数根的介绍,相信大家对此有了更加深入的理解和掌握。
在实际应用中,了解和灵活运用这些知识点可以帮助我们更好地解决实际问题。
