3.2 离散信号的频域分析(20180402)
离散周期信号的频域表示

相位频谱
2.离散周期信号的频谱
周期单位脉冲序列 求如图所示周期为3的周期单位脉冲序列的频谱。
解:
X[m]
2
x[k]e
j2 3
mk
j2 m0
1e 3
1
k 0
x[k]
1
X[m]
1
0 12
k
0 12
m
2.离散周期信号的频谱
例:求周期为3的序列 x[k]={,0,1,1,}的频谱。
解:
X[m]
4 X2[m]
1
1
m
2π N
m
m 0,1,, N 1
时域信号不同,虚指数序列 前面的加权系数X[m] 不同。
012
k
012
m
1. 离散周期信号的频域表示
IDFS
x[k] 1 N1 X [m]e jmk
N m0
2π m
mN
m 0,1,, N 1
DFS
X[m] N1 x[k]ejmk
k 0
解:
X[m]
3
x[k]e
j2πmk 4
10 X[m]
k0
X[0] x[0] x[1] x[2] x[3] 10
X[1]
x[0]
x[1]e
j2π 4
11
x[2]e
j2π 4
12
x[3]e
j
2π 4
13
2
2j
2 2 22 2
…
…
0 123
m
X[2]
x[0]
x[1]e
j2π21 4
x[2]e
j2π22 4
解:
1
X[m] 3 x[k]ejmk
离散信号的频域分析

e
j
3
n
j n
e 3
1
j 2 n1
(e 6
j 2 n(16)
e6
)
2
9
例1:已知正弦序列 x(n) cos n ,分别求出当 2 和 3 时,傅立叶级数表达式及相应的频谱。
x(n)
5
X
j 2 kn
(k)e 6
1
j 2 n1
j 2 kn
x(n) X (k)e N
k 0
考虑到:N→∞,2 N 0 ,记为 d;
(2 N) k (由离散量变为连续量),而
1 N d 2 , 同时
N 1
2
0
傅立叶变换式
k 0
于是,X (e j ) lim N X (k) x(n)e jn
也可简记为 X (e j) DTFT x(n), x(n) IDTFT X (e j)
或 x(n) DTFT X (e j )
15
3.2.2 非周期序列的傅立叶变换
X (e j ) x(n)e jn n
x(n) 1 X (e j )e jnd
x(n) 1 X (e j )e jnd
2 X (e j ) 称为x(n)的离散时间傅立叶变换(Discrete Time Fourier Transform, DTFT)或频谱密度函数,简称频 谱。 x(n)称为X (e j ) 的离散时间傅立叶反变换(IDTFT)或原 函数。
x(n)e N
N n0
X (k)
1
N 1
j 2 kn
x(n)e N ,
第3章离散时间信号与系统的频域分析

第3章 离散时间信号与系统的频域分析
例:x(n)=δ(n),求此序列的Z变换及收敛域。
解
Z[ (n)]
(n)zn 1
0 | z |
n
所以收敛域应是整个z的闭平面(0≤|z|≤∞),
jIm[z]
o
Re[z]
第3章 离散时间信号与系统的频域分析
例:求矩形序列x(n)=RN(n)的Z变换及其收敛域。
而在c以外有M个极点zm(M、K为有限值),则有
1
2j
X (z)zn1dz
c
k
Re s[ X (z)zn1, zk ]
或
1
2j
X (z)zn1dz
c m
Re s[ X (z)zn1, zm ]
第3章 离散时间信号与系统的频域分析
由于:
Re s[X (z)zn1, zk ] Re s[X (z)zn1, zm ]
1
X (z) x(n)zn x(n)zn x(n)zn
n n1
收敛域:
nn1
n0
如果n1 ≥0,收敛域包含z=∞, Rx-<|z|
jIm[z]
如果 n1 <0,收敛域不包含z=∞,Rx-<|z|<∞
Rx-
o
Re[z]
第3章 离散时间信号与系统的频域分析
例 x(n)=anu(n), 求其Z变换及收敛域。
图 1 -2 4
第3章 离散时间信号与系统的频域分析
(3) 左边序列:
左边序列是指在n≤n2时x(n)有值,而在n>n2时x(n)=0,其Z变换
为
n2
0
n2
X (z) x(n)zn x(n)zn x(n)zn
数字信号处理第二章--离散时间信号与系统的频域分析ppt课件

而
.
2
X(ej)ejmd x(n)2(nm)
n
2x(m)
x(n)1 X(ej)ejnd
2
序列傅 里叶变
换对
X(ej) x(n)ejn n
x(n)21 X(ej)ejnd
.
正变换
反变换
3
例:试求矩形序列 RN (n) 的傅里叶变换
解:
N 1
X(ej) RN(n)ejn e j n
1X(ej w )1x*(n)ejn
2
2n
1X(ejw )1
x*(n)ejn
2
2n
1X(ej w )1[
x(n)ejn]
2
2n
1X(ejw)1X*(ejw)
2
2
XR(ejw)
.
14
C)实因果序列h(n)的对称性 因为h(n)是实序列,其FT只有共轭对称部分He(ejω),共轭反对称
部分为零。 即:H(ejω)=He(ejω)=H*(e-jω)
n
M为整数
因此序列的傅里叶变换是频率ω的周期函数,周期是2π。
由于FT的周期性,一般只分析-π~+π或0~2π之间的FT
2. 线性
设 X 1(ej)F T[x1(n)],X2(ej)F T[x2(n)], 那么 F T[ax1(n)bx2(n)]aX 1(ej)bX2(ej)
.
6
3. 时移与频移 设X(e jω)=FT[x(n)], 那么
则 Y(ej) 1 X(ej)H(ej)
2
1 X(ej)H[ej()]d
2
证明:
Y(ej)F[Ty(n)] x(n)h(n)ejn
n
x(n)[1H (ej)ejnd]ejn
离散非周期信号频域分析

离散⾮周期信号频域分析离散信号频域分析、快速傅⾥叶变换与采样定理⼀、离散信号频域分析(⼀)周期离散⽅波信号频域分析与周期模拟信号⼀样,周期离散信号同样可以展开成傅⾥叶级数形式,并得到离散傅⾥叶级数(DFS)上式可以看成周期离散信号x(n)的离散傅⾥叶级数展开。
上式是DFS的反变换,记作IDFS并且称错误!未找到引⽤源。
与错误!未找到引⽤源。
构成⼀对离散傅⾥叶级数变换对。
(以上两式中错误!未找到引⽤源。
)在MTALAB中,DFS通过建⽴周期延拓函数语句实现:function Xk=DFS(n,x,N)if N>length(x)n=0:N-1;x=[x zeros(1,N-length(x))];endk=0:N-1;WN=exp(-j*2*pi/N);nk=n'*k;WNnk=WN.^nk;Xk=x*WNnk;end建⽴⼀个离散⾮周期⽅波信号错误!未找到引⽤源。
通过周期延拓后所得的周期序列利⽤DFS计算实现代码如下:clear all;close all;clc;n=0:3;x=ones(1,4);X=fft(x,1024);Xk1=DFS(n,x,4);Xk2=DFS(n,x,8);figure(1);plot((-1023:2048)/2048*8,[abs(X) abs(X) abs(X)],'--');hold on;stem(-4:7,[abs(Xk1) abs(Xk1) abs(Xk1)],'LineWidth',2);grid;figure(2);plot((-1023:2048)/2048*16,[abs(X) abs(X) abs(X)],'--');hold on;stem(-8:15,[abs(Xk2) abs(Xk2) abs(Xk2)],'LineWidth',2);grid;set(gcf,'color','w');运⾏后得到的是分别以4和8为周期延拓后的错误!未找到引⽤源。
数字信号处理实验三:离散时间信号的频域分析

实验三:离散时间信号的频域分析一.实验目的1.在学习了离散时间信号的时域分析的基础上,对这些信号在频域上进行分析,从而进一步研究它们的性质.2.熟悉离散时间序列的3种表示方法:离散时间傅立叶变换(DTFT),离散傅立叶变换(DFT)和Z变换.二.实验相关知识准备1.用到的MATLAB命令运算符和特殊字符:〈 > 。
* ^ .^语言构造与调试:error function pause基本函数:angle conj rem数据分析和傅立叶变换函数:fft ifft max min工具箱:freqz impz residuez zplane三.实验内容1.离散傅立叶变换在MATLAB中,使用fft可以很容易地计算有限长序列x[n]的离散傅立叶变换。
此函数有两种形式:y=fft(x)y=fft(x,n) 求出时域信号x的离散傅立叶变换n为规定的点数,n的默认值为所给x的长度。
当n取2的整数幂时变换的速度最快。
通常取大于又最靠近x的幂次。
(即一般在使用fft函数前用n=2^nextpow2(length(x))得到最合适的n)。
当x的长度小于n时,fft函数在x的尾部补0,以构成长为n点数据。
当x的长度大于n时,fft函数将序列x截断,取前n点。
一般情况下,fft求出的函数多为复数,可用abs及angle分别求其幅度和相位。
注意:栅栏效应,截断效应(频谱泄露和谱间干扰),混叠失真例3-1: fft函数最通常的应用是计算信号的频谱。
考虑一个由100hz和200hz正弦信号构成的信号,受零均值随机信号的干扰,数据采样频率为1000hz。
通过fft函数来分析其信号频率成分。
t=0:0.001:1;%采样周期为0。
001s,即采样频率为1000hzx=sin(2*pi*100*t)+sin(2*pi*200*t)+1。
5*rand(1,length(t));%产生受噪声污染的正弦波信号subplot(2,1,1);plot(x(1:50));%画出时域内的信号y=fft(x,512);%对x进行512点的fftf=1000*(0:256)/512;%设置频率轴(横轴)坐标,1000为采样频率subplot(2,1,2);plot(f,y(1:257));%画出频域内的信号实验内容3-2:频谱泄漏和谱间干扰假设现有含有三种频率成分的信号x(t)=cos(200πt)+sin(100πt)+cos(50πt)用DFT分析x(t)的频谱结构。
《信号与系统》离散信号的频域分析实验报告
信息科学与工程学院《信号与系统》实验报告四专业班级电信 09-班姓名学号实验时间 2011 年月日指导教师陈华丽成绩实验名称离散信号的频域分析实验目的1. 掌握离散信号谱分析的方法:序列的傅里叶变换、离散傅里叶级数、离散傅里叶变换、快速傅里叶变换,进一步理解这些变换之间的关系;2. 掌握序列的傅里叶变换、离散傅里叶级数、离散傅里叶变换、快速傅里叶变换的Matlab实现;3. 熟悉FFT算法原理和FFT子程序的应用。
4. 学习用FFT对连续信号和离散信号进行谱分析的方法,了解可能出现的分析误差及其原因,以便在实际中正确应用FFT。
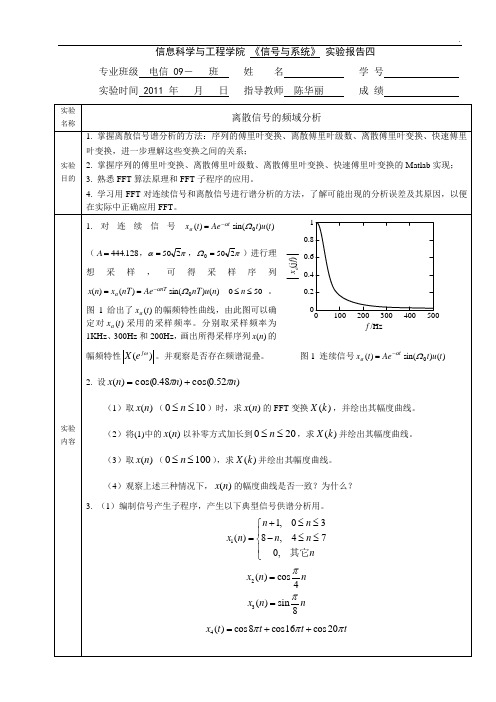
实验内容1.对连续信号)()sin()(0tutAetx taΩα-=(128.444=A,πα250=,πΩ250=)进行理想采样,可得采样序列50)()sin()()(0≤≤==-nnunTAenTxnx nTaΩα。
图1给出了)(txa的幅频特性曲线,由此图可以确定对)(txa采用的采样频率。
分别取采样频率为1KHz、300Hz和200Hz,画出所得采样序列)(nx的幅频特性)(ωj eX。
并观察是否存在频谱混叠。
图1 连续信号)()sin()(0tutAetx taΩα-=2. 设)52.0cos()48.0cos()(nnnxππ+=(1)取)(nx(100≤≤n)时,求)(nx的FFT变换)(kX,并绘出其幅度曲线。
(2)将(1)中的)(nx以补零方式加长到200≤≤n,求)(kX并绘出其幅度曲线。
(3)取)(nx(1000≤≤n),求)(kX并绘出其幅度曲线。
(4)观察上述三种情况下,)(nx的幅度曲线是否一致?为什么?3. (1)编制信号产生子程序,产生以下典型信号供谱分析用。
11,03()8,470,n nx n n nn+≤≤⎧⎪=-≤≤⎨⎪⎩其它2()cos4x n nπ=3()sin8x n nπ=4()cos8cos16cos20x t t t tπππ=++10.80.60.40.20100200300400500xa(jf)f /Hz(2)对信号1()x n ,2()x n ,3()x n 进行两次谱分析,FFT 的变换区间N 分别取8和16,观察两次的结果是否一致?为什么?(3)连续信号4()x n 的采样频率64s f Hz =,16,32,64N =。
离散信号的频域分析

时频变换的基本概念:时频变换是信号处理 中的一种重要方法,它能够将信号的时域和 频域信息相互转换。
添加 标题
离散信号的频域与时域的关系:离散信号的 频域与时域之间存在密切的关系。通过时频 变换,可以分析离散信号在不同时间点的频 率特征,从而更好地理解信号的特性和行为。
添加 标题
时频变换的不变性:时频变换具有一些重要 的性质,其中最重要的是时频变换的不变性。 这意味着通过时频变换得到的信号的时域和 频域特征在变换前后保持不变。
数字调制解调的 优势:抗干扰能 力强、传输距离 远等
数字音频信号 的频域分析
音频压缩与编 码
数字滤波器设 计
音频特效处理
图像压缩:离散信号的频域分析有助于图像压缩,减少存储空间和传输带宽。
图像增强:通过频域处理,可以增强图像的细节和对比度,提高图像质量。
图像识别:利用离散信号的频域特征,可以实现图像识别和分类,应用于人脸识别、物体检测等 领域。
时频变换的应用:时频变换在信号处理、 通信、雷达、声呐等领域有着广泛的应用。 通过时频变换,可以实现对信号的快速、 准确的分析和处理,从而提高信号处理的 效率和精度。
时频变换的基本原理
离散信号的频域与时域的关 系
离散信号的频域分析方法
时频变换在信号处理中的应 用
汇报人:XX
时频变换的对称性:离散信号的频域与时域之间存在对称性,即频域和时域的变换具有相互对 应的关系。
离散信号的时频分析:利用时频变换的方法,将离散信号表示为时频平面上的分布,以便同时 分析其时间和频率特性。
时频变换的物理意义:离散信号的时频变换具有物理意义,可以揭示信号在不同时间和频率下 的表现和特征。
添加 标题
离散性:离散信号的频谱是离散的,即只有某些特定的频率分量存在。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
N 1
j
2 kn N
,
2 j kn 1 N 1 N X ( k ) x ( n )e N n0
记为,X (k ) DFS[ x(n)], x(n) IDFS[ X (k )]
或者,x(n) X (k ) 上式表明: 1)周期为N的序列可被分解为N次谐波,第k个谐波频 率为 (2 / N )k ,幅度为 X (k ), k 0,1, , N 1 ; 基波分量(k=1)的频率为 2 / N ,幅度为 X (1) 。 2)周期序列的频谱是一个以N为周期的周期性离散频 谱,各谱线之间的间隔为 2 / N 。
n
x ( n)
(绝对可和)
16
例3:已知 x(n)如下所示,试求其频谱。
1 2 n 2 x ( n) 0 others
解:根据离散时间傅立叶变换的定义,
X (e )
j n
x ( n )e
j n
n 2
e
2
j n
e j 2 (1 e j 5 ) 1 e j
k 0 5 j 2 kn 6
2 n1 j n5 1 j 26 6 (e e ) 2
1 所以, X (k ) 2 0
k 1,5 k 0, 2,3, 4
10
例2:已知周期序列如图所示,周期N=6,求该序列的频 谱 X ( k ) 及时域表达式 x(n) 。
针对问题2:是否正确? 2 j 对上式两端乘以 e N kl ,并对k在一个周期内求和,
X ( k )e
k 0
N 1
j
2 kl N
2 2 j kn j kl 1 N 1 N N x ( n)e e k 0 N n 0 N 1 j 2 ( l n ) k 1 N 1 x ( n ) e N N n 0 k 0 N 1
e j 2e j 2.5 (e j 2.5 e j 2.5 ) e j 0.5 (e j 0.5 e j 0.5 )
sin(2.5) | X (e j ) | e j ( ) sin(0.5)
0 sin(2.5) j ( ) 幅频: ; | X (e ) | 相频: sin(0.5) X (e j ) 0 X (e j ) 0
2
2
2
12
3.2.2 非周期序列的频域分析
x ( n) X ( k )e
k 0
N 1
j
2 kn N
非周期序列的傅立叶变换(DTFT) 非周期序列可看作是周期序列的周期 N→∞ 时的极 限情况; 极限情况下,各谐波之间的间隔 2 N 趋近于无穷 小,从而序列的频谱从离散变为连续; 极限情况下,各谐波分量的幅度 X (k ) 0 ,不过 这些无穷小量之间仍有差别。 为了描述非周期序列的频谱特性,令 X (k ) j X (e ) lim lim N X (k ) (单位频率上的频谱) N 1/ N N
3.2 离散信号的频域分析
离散周期信号的频域分析
离散非周期信号的频域分析
离散时间傅立叶变换的性质
离散傅立叶变换 离散傅立叶变换的性质
1
3.2.1 周期序列的频域分析—(Discrete Fourier Serise, DFS)
周期序列的傅立叶级数(DFS) 设 x ( n ) 是以N为周期的周期序列,即
从物理意义来讨论傅立叶变换 j X (e ) 是一个频谱密度函数的概念;
j X ( e ) 是一个连续谱,各频率分量的频率不成谐波
关系; j X ( e ) 是关于数字频率 的周期函数,周期是 2 , 包含了从零到 2 的所有频率分量。
非周期序列存在傅立叶变换的充分条件:
1) 2 时, 2 2 / 2 无理数,该序列为非周 期序列,不能展开为傅立叶级数表达式。 2) 3 时, 2 6 有理数,所以是周期序列, 周期为 2 N m 6 (取m=1)
所以,x(n) X (k )e
k 0
5
j
2 kn 6
2
0
傅立叶变换式
于是,X (e ) lim N X (k )
N
j
x(n) N X (k )e
k 0
N 1
2 j kn N
1 N
n
x(n)e jn
傅立叶反变换式
1 2
2
0
X (e )e
j
jn
1 d 2
X (e j )e jn d
所以,X (0) 1/ 2, X (1) 1/ 3, X (2) 0
X (3) 1/ 6, X (4) 0, X (5) 1/ 3
由IDFS的定义可知,
x ( n ) X ( k )e
k 0 5 j 2 kn 6
1 j 6 n 1 j 6 3n 1 j 6 5 n 1 e e e 3 6 3
3
3.2.1 周期序列的频域分析—DFS
x ( n )e
n 0
N 1
j
2 mn N
Nam
针对问题1:求解ak
2 j kn 1 N 1 N 所以,ak x(n)e , k N n 0
注意:由于k和n均取整数,当k或n变化时, e 期为N的周期函数,即
j
, 1 N
x ( n) X ( k )e
k 0
N 1
j
2 kn N
x ( n ) N X ( k )e
j
考虑到:N→∞,2 N 0 ,记为 d ; (2 N ) k (由离散量变为连续量),而
1 N d 2 , 同时
k 0 N 1
14
3.2.2 非周期序列的傅立叶变换
X (e j )
n
x(n)e jn
1 j j n x ( n) X ( e ) e d 2 X (e j ) 称为x(n)的离散时间傅立叶变换(Discrete Time Fourier Transform, DTFT)或频谱密度函数,简称频 谱。 x(n)称为 X (e j ) 的离散时间傅立叶反变换(IDTFT)或原 函数。
针对问题1:求解ak
对等式两边同时乘以 e 内求和,
k
ae
k
j
2 kn N
j 2 mn N
,并对n在一个周期
x(n)e
n 0
N 1
j
2 mn N
2 2 j kn j mn N N ak e e n 0 k N 1
k
a e
k n0
N 1
j
2 ( k m) n N
由于, e
n 0
N 1 n0
N 1
j
2 ( k m) n N
N = 0
k m =N (k m) km
k
x ( n )e
j
2 mn N
k
a
N (k m) N am
x(n) x(n mN ), m为任意整数
j 2 kn N
x ( n ) 可以展开为如下傅立叶级数形式, 假设:
x ( n)
k
ae
k
ak 为傅立叶级数的系数。 式中,
问题:1)系数 ak 如何求解? 2)这样表示是否正确?
2
3.2.1 周期序列的频域分析—DFS
x ( n)
由于, e
k 0
N 1 k 0
N 1
j
2 (l n ) k N
N = 0
l n =N (l n) ln
X ( k )e
j
2 kl N
1 N 1 x(n) N (l n) x(l ) N n0
j 2 kn N
x ( n ) X ( k )e
2 kn N
是周
e
j
2 ( k lN ) n N
e
j
2 kn N
,
l取整数
e
j
2 ( n mN ) k N
e
j
2 kn N
,
m取整数
所以,离散傅立叶级数的系数ak也是周期序列,即
ak ak lN
4
3.2.1 周期序列的频域分析—DFS
ak ak lN
2 j kn 1 N 1 x(n)e N N n 0
11
例2:已知周期序列如图所示,周期N=6,求该序列的频 谱 X ( k ) 及时域表达式 x(n) 。
2 2 2 2 j k j k j k j 5 k 1 1 6 6 e X (k ) 1 e 6 e 6 1 e 6 6 1 k 1 2cos , k 0,1, 2,3, 4,5 6 3
k 0
N 1
, n
6
3.2.1 周期序列的频域分析—DFS
所以,
x ( n ) X ( k )e
k 0 N 1 j 2 kn N
2 j kn 1 N 1 X ( k ) x ( n )e N , N n 0
x ( n) X ( k )e
k 0
j 也可简记为 X (e j ) DTFT x(n), x(n) IDTFT X ( e )
DTFT j x ( n ) X ( e ) 或
