离散时间信号系统的频域分析实验报告
数字信号处理 实验3 离散系统的频域分析

MATLAB 为求解离散系统的频率响应和连续系统的频率响应,分别提供了 freqz 和 freq(s 求
连续系统的频率响应函数)两个函数,使用方法类似。本实验主要讨论离散系统的频率响应。
例 3-1 已知离散时间系统的系统函数为
H(z)
=
0.1321− 0.3963 z−2 + 0.3963 z−4 − 0.1321z−6 1+ 0.34319 z−2 + 0.60439 z−4 + 0.20407 z−6
求该系统在 0~π频率范围内的绝对幅频响应、相对幅度响应、相位响率响应及群迟延。
解 MATLAB 程序如下:
b=[0.1321,0,0.3963,0,0.3963,0,0.1321];
a=[1,0,-0.34319,0,0.60439,0,-0.20407];
数字信号处理实验4 离散时间系统的频域分析

实验4 离散时间系统的频域分析一、实验目的(1)了解离散系统的零极点与系统因果性和稳定性的关系; (2)加深对离散系统的频率响应特性基本概念的理解; (3)熟悉MATLAB 中进行离散系统零极点分析的常用子函数; (4)掌握离散系统幅频响应和相频响应的求解方法。
二、知识点提示本章节的主要知识点是频率响应的概念、系统零极点对系统特性的影响;重点是频率响应的求解方法;难点是MATLAB 相关子函数的使用。
三、实验原理1.离散时间系统的零极点及零极点分布图设离散时间系统系统函数为NMz N a z a a z M b z b b z A z B z H ----++++++++==)1()2()1()1()2()1()()()(11 (4-1) MATLAB 提供了专门用于绘制离散时间系统零极点图的zplane 函数: ①zplane 函数 格式一:zplane(z, p)功能:绘制出列向量z 中的零点(以符号"○" 表示)和列向量p 中的极点(以符号"×"表示),同时画出参考单位圆,并在多阶零点和极点的右上角标出其阶数。
如果z 和p 为矩阵,则zplane 以不同的颜色分别绘出z 和p 各列中的零点和极点。
格式二:zplane(B, A)功能:绘制出系统函数H(z)的零极点图。
其中B 和A 为系统函数)(z H (4-1)式的分子和分母多项式系数向量。
zplane(B, A) 输入的是传递函数模型,函数首先调用root 函数以求出它们的零极点。
②roots 函数。
用于求多项式的根,调用格式:roots(C),其中C 为多项式的系数向量,降幂排列。
2.离散系统的频率特性MATLAB 提供了专门用于求离散系统频响特性的freqz 函数,调用格式如下: ①H = freqz(B,A,W)功能:计算由向量W (rad )指定的数字频率点上(通常指[0,π]范围的频率)离散系统)(z H 的频率响应)e (j ωH ,结果存于H 向量中。
实验四-离散时间系统的频域分析(附思考题程序)

实验四 离散时间系统的频域分析1.实验目的(1)理解和加深傅里叶变换的概念及其性质。
(2)离散时间傅里叶变换(DTFT)的计算和基本性质。
(3)离散傅里叶变换(DFT)的计算和基本性质。
2.实验原理对离散时间信号进行频域分析, 首先要对其进行傅里叶变换, 通过得到的频谱函数进行分析。
离散时间傅里叶变换(DTFT, Discrete-time Fourier Transform)是傅立叶变换的一种。
它将以离散时间nT (其中 , T 为采样间隔)作为变量的函数(离散时间信号)f(nT)变换到连续的频域, 即产生这个离散时间信号的连续频谱 , 其频谱是连续周期的。
211200)()|()()DTFT kw N knTN N i iwT iwnT N n n F e f nT e f nT e 长度为N 的有限长信号x(n), 其N 点离散傅里叶变换为:10()[()]()kn N N n X k DFT x n x n W 。
X(k)的离散傅里叶逆变换为: 。
DTFT 是对任意序列的傅里叶分析, 它的频谱是一个连续函数;而DFT 是把有限长序列作为周期序列的一个周期, 对有限长序列的傅里叶分析, DFT 的特点是无论在时域还是频域都是有限长序列。
3.实验内容及其步骤(1)复习傅里叶变换的定义及其性质, 加深理解。
(2)熟悉离散时间傅里叶变换的概念及其性质。
参考一: 计算离散时间傅里叶变换, 并绘制图形。
已知有限长序列x(n)={1,2,3,4,5}。
n=-1:3;x=1:5;k=0:500;w=(pi/500)*k;X=x*(exp(-j*2*pi/500)).^(n'*k);magX=abs(X);angX=angle(X);realX=real(X);imagX=imag(X);subplot(2,2,1);plot(w/pi,magX);grid;xlabel('');ylabel('模值 ');title('模值部分');subplot(2,2,2);plot(w/pi,angX);grid;xlabel('pi 为单位');ylabel('弧度');title('相角部分');subplot(2,2,3);plot(w/pi,realX);grid;xlabel('');ylabel('实部');title('实部部分');subplot(2,2,4);plot(w/pi,imagX);grid;xlabel('pi为单位');ylabel('虚部');title('虚部部分');参考二: 计算离散时间傅里叶变换。
DSP实验报告--离散时间信号与系统的时、频域表示-离散傅立叶变换和z变换-数字滤波器的频域分析和实现-数字

南京邮电大学实验报告实验名称:离散时间信号与系统的时、频域表示离散傅立叶变换和z变换数字滤波器的频域分析和实现数字滤波器的设计课程名称数字信号处理A(双语) 班级学号B13011025姓名陈志豪开课时间2015/2016学年,第1学期实验名称:离散时间信号与系统的时、频域表示实验目的和任务:熟悉Matlab基本命令,理解和掌握离散时间信号与系统的时、频域表示及简单应用。
在Matlab环境中,按照要求产生序列,对序列进行基本运算;对简单离散时间系统进行仿真,计算线性时不变(LTI)系统的冲激响应和卷积输出;计算和观察序列的离散时间傅立叶变换(DTFT)幅度谱和相位谱。
实验内容:基本序列产生和运算:Q1.1~1.3,Q1.23,Q1.30~1.33离散时间系统仿真:Q2.1~2.3LTI系统:Q2.19,Q2.21,Q2.28DTFT:Q3.1,Q3.2,Q3.4实验过程与结果分析:Q1.1运行程序P1.1,以产生单位样本序列u[n]并显示它。
clf;n = -10:20;u = [zeros(1,10) 1 zeros(1,20)];stem(n,u);xlabel('Time index n');ylabel('Amplitude');title('Unit Sample Sequence');axis([-10 20 0 1.2]);Q1.2 命令clf,axis,title,xlabel和ylabel命令的作用是什么?答:clf命令的作用:清除图形窗口上的图形;axis命令的作用:设置坐标轴的范围和显示方式;title命令的作用:给当前图片命名;xlabel命令的作用:添加x坐标标注;ylabel c命令的作用:添加y坐标标注;Q1.3修改程序P1.1,以产生带有延时11个样本的延迟单位样本序列ud[n]。
运行修改的程序并显示产生的序列。
clf;n = -10:20;u = [zeros(1,21) 1 zeros(1,9)];stem(n,u);xlabel('Time index n');ylabel('Amplitude');title('Unit Sample Sequence');axis([-10 20 0 1.2]);Q1.23修改上述程序,以产生长度为50、频率为0.08、振幅为2.5、相移为90度的一个正弦序列并显示它。
时域离散信号实验报告(3篇)

第1篇一、实验目的1. 理解时域离散信号的基本概念和特性。
2. 掌握时域离散信号的表示方法。
3. 熟悉常用时域离散信号的产生方法。
4. 掌握时域离散信号的基本运算方法。
5. 通过MATLAB软件进行时域离散信号的仿真分析。
二、实验原理时域离散信号是指在时间轴上取离散值的一类信号。
这类信号在时间上不连续,但在数值上可以取到任意值。
时域离散信号在数字信号处理领域有着广泛的应用,如通信、图像处理、语音处理等。
时域离散信号的基本表示方法有:1. 序列表示法:用数学符号表示离散信号,如 \( x[n] \) 表示离散时间信号。
2. 图形表示法:用图形表示离散信号,如用折线图表示序列。
3. 时域波形图表示法:用波形图表示离散信号,如用MATLAB软件生成的波形图。
常用时域离散信号的产生方法包括:1. 单位阶跃信号:表示信号在某个时刻发生突变。
2. 单位冲激信号:表示信号在某个时刻发生瞬时脉冲。
3. 正弦信号:表示信号在时间上呈现正弦波形。
4. 矩形脉冲信号:表示信号在时间上呈现矩形波形。
时域离散信号的基本运算方法包括:1. 加法:将两个离散信号相加。
2. 乘法:将两个离散信号相乘。
3. 卷积:将一个离散信号与另一个离散信号的移位序列进行乘法运算。
4. 反褶:将离散信号沿时间轴翻转。
三、实验内容1. 实验一:时域离散信号的表示方法(1)使用序列表示法表示以下信号:- 单位阶跃信号:\( u[n] \)- 单位冲激信号:\( \delta[n] \)- 正弦信号:\( \sin(2\pi f_0 n) \)- 矩形脉冲信号:\( \text{rect}(n) \)(2)使用图形表示法绘制以上信号。
2. 实验二:时域离散信号的产生方法(1)使用MATLAB软件生成以下信号:- 单位阶跃信号- 单位冲激信号- 正弦信号(频率为1Hz)- 矩形脉冲信号(宽度为2)(2)观察并分析信号的波形。
3. 实验三:时域离散信号的基本运算(1)使用MATLAB软件对以下信号进行加法运算:- \( u[n] \)- \( \sin(2\pi f_0 n) \)(2)使用MATLAB软件对以下信号进行乘法运算:- \( u[n] \)- \( \sin(2\pi f_0 n) \)(3)使用MATLAB软件对以下信号进行卷积运算:- \( u[n] \)- \( \sin(2\pi f_0 n) \)(4)使用MATLAB软件对以下信号进行反褶运算:- \( u[n] \)4. 实验四:时域离散信号的仿真分析(1)使用MATLAB软件对以下系统进行时域分析:- 系统函数:\( H(z) = \frac{1}{1 - 0.5z^{-1}} \)(2)观察并分析系统的单位冲激响应。
《信号与系统》离散信号的频域分析实验报告
信息科学与工程学院《信号与系统》实验报告四专业班级电信 09-班姓名学号实验时间 2011 年月日指导教师陈华丽成绩实验名称离散信号的频域分析实验目的1. 掌握离散信号谱分析的方法:序列的傅里叶变换、离散傅里叶级数、离散傅里叶变换、快速傅里叶变换,进一步理解这些变换之间的关系;2. 掌握序列的傅里叶变换、离散傅里叶级数、离散傅里叶变换、快速傅里叶变换的Matlab实现;3. 熟悉FFT算法原理和FFT子程序的应用。
4. 学习用FFT对连续信号和离散信号进行谱分析的方法,了解可能出现的分析误差及其原因,以便在实际中正确应用FFT。
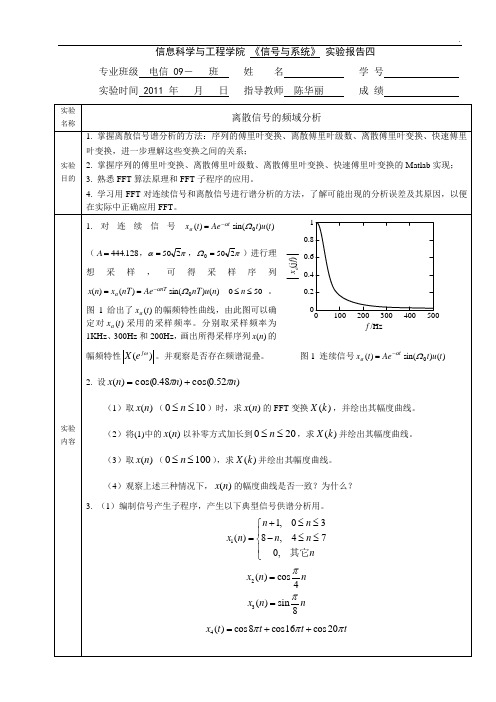
实验内容1.对连续信号)()sin()(0tutAetx taΩα-=(128.444=A,πα250=,πΩ250=)进行理想采样,可得采样序列50)()sin()()(0≤≤==-nnunTAenTxnx nTaΩα。
图1给出了)(txa的幅频特性曲线,由此图可以确定对)(txa采用的采样频率。
分别取采样频率为1KHz、300Hz和200Hz,画出所得采样序列)(nx的幅频特性)(ωj eX。
并观察是否存在频谱混叠。
图1 连续信号)()sin()(0tutAetx taΩα-=2. 设)52.0cos()48.0cos()(nnnxππ+=(1)取)(nx(100≤≤n)时,求)(nx的FFT变换)(kX,并绘出其幅度曲线。
(2)将(1)中的)(nx以补零方式加长到200≤≤n,求)(kX并绘出其幅度曲线。
(3)取)(nx(1000≤≤n),求)(kX并绘出其幅度曲线。
(4)观察上述三种情况下,)(nx的幅度曲线是否一致?为什么?3. (1)编制信号产生子程序,产生以下典型信号供谱分析用。
11,03()8,470,n nx n n nn+≤≤⎧⎪=-≤≤⎨⎪⎩其它2()cos4x n nπ=3()sin8x n nπ=4()cos8cos16cos20x t t t tπππ=++10.80.60.40.20100200300400500xa(jf)f /Hz(2)对信号1()x n ,2()x n ,3()x n 进行两次谱分析,FFT 的变换区间N 分别取8和16,观察两次的结果是否一致?为什么?(3)连续信号4()x n 的采样频率64s f Hz =,16,32,64N =。
0136-胡国庆-实验3-离散时间信号的离散频域分析

数字信号处理A实验报告实验项目名称:离散信号与系统的离散频域分析(DFT)学院:______计算机与通信工程____专业:______ _通信工程 _________学号:______201454080136_______班级:______ 通信1401 ________报告人:________胡国庆 __________指导老师:___ 胡双红 _ _______实验时间:_______2016-11-28________实验三离散信号与系统的离散频域分析(DFT)一、实验目的:1、掌握离散时间系统的DFT的MATLAB实现;2、熟悉DTFT和DFT之间的关系。
3、了解信号不同变形的DFT与原信号DFT之间的关系二、实验内容:选择实验二相同的8点信号x=[1 2 3 4 4 3 2 1]1、对该信号分别做8点、16点、32点DFT,分别与DTFT合并作图并比较DFT 与DTFT之间的关系。
2、在信号每两个相邻样本之间插入一个零值,扩充为16点序列,作DFT,画出幅度谱和相位谱,并与原序列的DFT进行比较。
3、将信号以8为周期扩展,得到长为16的两个周期,作DFT,画出幅度谱和相位谱,并与原序列的DFT进行比较。
三、实验平台: MATLAB集成系统四、设计流程:五、程序清单function [Xk]=dft(xn,N)n=0:1:N-1;k=0:1:N-1;WN=exp(-j*2*pi/N);nk=n'*k;WNnk=WN.^nk;Xk=xn*WNnk;x=[3,2,1,2,4,3,4,1];X=dft(x,8);w=0:pi/100:2*pi;n=0:7;Xw=x*exp(-j*n'*w);figure(1);k=0:7;subplot(211);stem(k,abs(X)) hold onplot(w/pi*4,abs(Xw))subplot(212);stem(k,angle(X))hold onplot(w/pi*4,angle(Xw))X16=dft([x,zeros(1,8)],16);figure(2);k=0:15;subplot(211);stem(k,abs(X16)) Xw1=[x,zeros(1,8)]*exp(-j*k'*w);hold onplot(w/pi*8,abs(Xw1))subplot(212);stem(k,angle(X16))hold onplot(w/pi*8,angle(Xw1))X32=dft([x,zeros(1,24)],32);figure(3);k=0:31;subplot(211);stem(k,abs(X32)) Xw2=[x,zeros(1,24)]*exp(-j*k'*w);hold onplot(w/pi*16,abs(Xw2))subplot(212);stem(k,angle(X32))hold onplot(w/pi*16,angle(Xw2))x1=zeros(1,16);x1(1:2:end)=x;X4=dft(x1,16); figure(4);subplot(221);stem(0:15,abs(X4));subplot(222);stem(0:15,angle(X4));subplot(223);stem(0:7,abs(X));subplot(224);stem(0:7,angle(X));X5=dft([x x],16);figure(5);subplot(221);stem(0:15,abs(X5)); subplot(222);stem(0:15,angle(X5)); subplot(223);stem(0:7,abs(X)); subplot(224);stem(0:7,angle(X));六、调试和测试结果:8点DFT与 DTFT的代码和图:实验心得在这次实验中,自己做的时候问题比较多,请教了很多同学才做到现在的样子,对函数并不理解。
系统频域分析实验报告

一、实验目的1. 掌握频域分析的基本原理和方法;2. 熟悉MATLAB在频域分析中的应用;3. 分析不同系统的频域特性,评估系统性能;4. 理解频率响应与系统稳定性之间的关系。
二、实验原理频域分析是一种研究系统对信号频率响应特性的方法。
它将时域信号转换为频域信号,通过分析系统对不同频率信号的响应来评估系统的性能。
频域分析方法主要包括傅里叶变换、拉普拉斯变换和Z变换等。
三、实验仪器与软件1. 实验仪器:计算机、MATLAB软件;2. 实验软件:MATLAB R2018a。
四、实验内容1. 信号的产生与处理(1)产生一个连续时间信号f(t) = cos(2π×50t) + sin(2π×100t);(2)使用MATLAB的fourier函数进行傅里叶变换,得到频谱函数F(w);(3)使用MATLAB的ifourier函数进行傅里叶逆变换,得到时域信号f(t)。
2. 系统的频率响应分析(1)定义一个典型二阶系统G(s) = (s+2)/(s^2+2s+2);(2)使用MATLAB的bode函数绘制系统G(s)的Bode图;(3)分析Bode图,评估系统的稳定性、带宽和相位裕度;(4)使用MATLAB的nyquist函数绘制系统G(s)的Nyquist图;(5)分析Nyquist图,评估系统的稳定性。
3. 离散时间系统的频率响应分析(1)定义一个离散时间系统H(z) = (z-0.5)/(z-0.75);(2)使用MATLAB的zplane函数绘制系统H(z)的Z平面图;(3)分析Z平面图,评估系统的稳定性。
五、实验结果与分析1. 信号的产生与处理通过MATLAB产生的连续时间信号f(t)如图1所示,其频谱函数F(w)如图2所示。
图1 连续时间信号f(t)图2 频谱函数F(w)2. 系统的频率响应分析Bode图如图3所示,Nyquist图如图4所示。
图3 系统G(s)的Bode图图4 系统G(s)的Nyquist图从Bode图中可以看出,系统的带宽约为100Hz,相位裕度约为60°。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
离散时间信号系统的频域分析实验报告
《信号、系统与信号处理实验I》
实验报告
实验名称:离散时间信号与系统的频域分析
姓名:韩文草
学号:15081614
专业:通信工程
实验时间:2016.11.28
杭州电子科技大学
通信工程学院
三、实验过程及实验结果
clear all;
w = -4*pi:8*pi/511:4*pi; num = [2 1];den = [1 -0.6];
h = freqz(num, den, w); subplot(2, 1, 1)
plot(w/pi, real(h) ); grid;
title('实部')
xlabel('omega^pi');
ylabel('振幅');
subplot(2, 1, 2)
plot(w/pi, imag(h));grid;
title('虚部')
xlabel('omega^pi');
ylabel('振幅');
figure;
subplot(2,1, 1)
plot(w/pi, abs(h));grid;
title('幅度谱')
xlabel('omega^pi');
ylabel('振幅');
subplot(2, 1, 2)
plot(w/pi,angle(h));grid;
title('相位谱')
xlabel('omega^pi');
');
ylabel('以弧度为单位的相位
h = [1 2 3 4 5 6 7 8 9];
w = 0:pi/511:pi;
h = freqz(h, 1, w);
subplot(2, 1, 1)
plot(w/pi, real(h) ); grid; title('实部')
xlabel('omega^pi');
ylabel('振幅');
subplot(2, 1, 2)
plot(w/pi, imag(h));grid; title('虚部')
xlabel('omega^pi');
ylabel('振幅');
figure;
subplot(2,1, 1)
plot(w/pi, abs(h));grid;
title('幅度谱')
xlabel('omega^pi');
ylabel('振幅');
subplot(2, 1, 2)
plot(w/pi,angle(h));grid; title('相位谱')
xlabel('omega^pi');
ylabel('以弧度为单位的相位');
clear all;
w=-pi:8*pi/511:1*pi;
num=[1 2 3 4 5 6 7 8 9];den=[1]; num2=[zeros(1,6),num];
h=freqz(num2,den,w);
h2=freqz(num,den,w);
h3=h2.*exp(-6*j*w);
subplot(3,2,1)
plot(w/pi,abs(h2));grid;
title('幅度谱')
xlabel('omega^pi');
ylabel('振幅');
subplot(3,2,2)
plot(w/pi,angle(h2));grid;
title('相位谱')
xlabel('omega^pi');
ylabel('以弧度为单位的相位'); subplot(3,2,3)
plot(w/pi,abs(h));grid;
title('幅度谱')
xlabel('omega^pi');
ylabel('振幅');
subplot(3,2,4)
plot(w/pi,angle(h));grid;
title('相位谱')
xlabel('omega^pi');
ylabel('以弧度为单位的相位'); subplot(3,2,5)
plot(w/pi,abs(h3));grid;
title('幅度谱')
xlabel('omega^pi');
ylabel('振幅');
subplot(3,2,6)
plot(w/pi,angle(h3));grid;
title('相位谱')
xlabel('omega^pi');
ylabel('以弧度为单位的相位');
四、实验小结
通过本次试验熟练了使用MATLAB软件的方式和技巧,掌握了离散时间信号与系统的频域分析方法和离散时间信号傅里叶变换与傅里叶逆变换的基本方法。
系统的频域分析法,将通过傅里叶变换,将信号分解成多个正弦函数的和(或积分),得到信号的频谱,然后求系统对各个正弦分量的响应得到响应的频谱,最后通过傅里叶反变换,得到响应再加以分析。
即将信号分解成一个个的基信号,然后研究系统对于基信号的响应,再将这些所有的基信号的响应叠加,便是系统对于一个完整的复杂信号的响应。
通过频域分析系统在物理上更为直观,
我们比较容易通过频域看出,系统与信号的特征。
