MATLAB作业3参考答案
MATLAB习题及参考答案经典.doc

习题:1, 计算⎥⎦⎤⎢⎣⎡=572396a 与⎥⎦⎤⎢⎣⎡=864142b 的数组乘积。
2, 对于B AX =,如果⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=753467294A ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=282637B ,求解X 。
3, 已知:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=987654321a ,分别计算a 的数组平方和矩阵平方,并观察其结果。
4, 角度[]604530=x ,求x 的正弦、余弦、正切和余切。
(应用sin,cos,tan.cot)5, 将矩阵⎥⎦⎤⎢⎣⎡=7524a 、⎥⎦⎤⎢⎣⎡=3817b 和⎥⎦⎤⎢⎣⎡=2695c 组合成两个新矩阵: (1)组合成一个4⨯3的矩阵,第一列为按列顺序排列的a 矩阵元素,第二列为按列顺序排列的b 矩阵元素,第三列为按列顺序排列的c 矩阵元素,即 ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡237912685574(2)按照a 、b 、c 的列顺序组合成一个行矢量,即 []2965318772546, 将(x -6)(x -3)(x -8)展开为系数多项式的形式。
(应用poly,polyvalm)7, 求解多项式x 3-7x 2+2x +40的根。
(应用roots)8, 求解在x =8时多项式(x -1)(x -2) (x -3)(x -4)的值。
(应用poly,polyvalm)9, 计算多项式9514124234++--x x x x 的微分和积分。
(应用polyder,polyint ,poly2sym)10, 解方程组⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡66136221143092x 。
(应用x=a\b)11, 求欠定方程组⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡5865394742x 的最小范数解。
(应用pinv) 12, 矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=943457624a ,计算a 的行列式和逆矩阵。
(应用det,inv)13, y =sin(x ),x 从0到2π,∆x =0.02π,求y 的最大值、最小值、均值和标准差。
(完整word版)含答案《MATLAB实用教程》

第二章 MATLAB 语言及应用实验项目实验一 MATLAB 数值计算三、实验内容与步骤1.创建矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=987654321a(1(2)用(3)用(42.矩阵的运算(1)利用矩阵除法解线性方程组。
⎪⎪⎩⎪⎪⎨⎧=+++=-+-=+++=+-12224732258232432143214321421x x x x x x x x x x x x x x x 将方程表示为AX=B ,计算X=A\B 。
(2)利用矩阵的基本运算求解矩阵方程。
已知矩阵A 和B 满足关系式A -1BA=6A+BA ,计算矩阵B 。
其中⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=7/10004/10003/1A ,Ps: format rata=[1/3 0 0;0 1/4 0;0 0 1/7];b=inv(a)*inv(inv(a)-eye(3))*6*a(3)计算矩阵的特征值和特征向量。
已知矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=1104152021X ,计算其特征值和特征向量。
(4)Page:322利用数学函数进行矩阵运算。
已知传递函数G(s)=1/(2s+1),计算幅频特性Lw=-20lg(1)2(2w )和相频特性Fw=-arctan(2w),w 的范围为[0.01,10],按对数均匀分布。
3.多项式的运算(1)多项式的运算。
已知表达式G(x)=(x-4)(x+5)(x 2-6x+9),展开多项式形式,并计算当x 在[0,20]内变化时G(x)的值,计算出G(x)=0的根。
Page 324(2)多项式的拟合与插值。
将多项式G(x)=x 4-5x 3-17x 2+129x-180,当x 在[0,20]多项式的值上下加上随机数的偏差构成y1,对y1进行拟合。
对G(x)和y1分别进行插值,计算在5.5处的值。
Page 325 四、思考练习题1.使用logspace 函数创建0~4π的行向量,有20个元素,查看其元素分布情况。
Ps: logspace(log10(0),log10(4*pi),20) (2) sort(c,2) %顺序排列 3.1多项式1)f(x)=2x 2+3x+5x+8用向量表示该多项式,并计算f(10)值. 2)根据多项式的根[-0.5 -3+4i -3-4i]创建多项式。
matlab课后习题答案第三章

第3章数值数组及其运算习题3及解答1 要求在闭区间]2,0[ 上产生具有10个等距采样点的一维数组。
试用两种不同的指令实现。
〖目的〗●数值计算中产生自变量采样点的两个常用指令的异同。
〖解答〗%方法一t1=linspace(0,2*pi,10)%方法二t2=0:2*pi/9:2*pi %要注意采样间距的选择,如这里的2*pi/9.t1 =Columns 1 through 70 0.6981 1.3963 2.0944 2.7925 3.4907 4.1888 Columns 8 through 104.88695.58516.2832t2 =Columns 1 through 70 0.6981 1.3963 2.0944 2.7925 3.4907 4.1888 Columns 8 through 104.88695.58516.28322 由指令rng('default'),A=rand(3,5)生成二维数组A,试求该数组中所有大于0.5的元素的位置,分别求出它们的“全下标”和“单下标”。
〖目的〗●数组下标的不同描述:全下标和单下标。
●sub2ind, int2str, disp的使用。
●随机发生器的状态控制:保证随机数的可复现性。
〖解答〗rng('default')A=rand(3,5)[ri,cj]=find(A>0.5);id=sub2ind(size(A),ri,cj);ri=ri';cj=cj';disp(' ')disp('大于0.5的元素的全下标')disp(['行号 ',int2str(ri)])disp(['列号 ',int2str(cj)])disp(' ')disp('大于0.5的元素的单下标')disp(id')A =0.8147 0.9134 0.2785 0.9649 0.95720.9058 0.6324 0.5469 0.1576 0.48540.1270 0.0975 0.9575 0.9706 0.8003大于0.5的元素的全下标行号 1 2 1 2 2 3 1 3 1 3列号 1 1 2 2 3 3 4 4 5 5大于0.5的元素的单下标1 2 4 5 8 9 10 12 13 153 采用默认全局随机流,写出产生长度为1000的“等概率双位(即取-1,+1)取值的随机码”程序指令,并给出 -1码的数目。
matlab课后习题答案(附图)

matlab课后习题答案(附图)习题2.1画出下列常见曲线的图形y (1)⽴⽅抛物线3x命令:syms x y;ezplot('x.^(1/3)')(2)⾼斯曲线y=e^(-X^2);命令:clearsyms x y;ezplot('exp(-x*x)')(3)笛卡尔曲线命令:>> clear>> syms x y;>> a=1;>> ezplot(x^3+y^3-3*a*x*y)(4)蔓叶线命令:>> clear>> syms x y;>> a=1ezplot(y^2-(x^3)/(a-x))(5)摆线:()()tsin-=,=-by1命令:>> clear>> t=0:0.1:2*pi;>> x=t-sin(t);>>y=2*(1-cos(t)); >> plot(x,y)7螺旋线命令:>> clear >> t=0:0.1:2*pi; >> x=cos(t); >> y=sin(t); >> z=t;>>plot3(x,y,z)(8)阿基⽶德螺线命令:clear>> theta=0:0.1:2*pi;>> rho1=(theta);>> subplot(1,2,1),polar(theta,rho1)(9) 对数螺线命令:cleartheta=0:0.1:2*pi;rho1=exp(theta);subplot(1,2,1),polar(theta,rho1)(12)⼼形线命令:>> clear >> theta=0:0.1:2*pi; >> rho1=1+cos(theta); >> subplot(1,2,1),polar(theta,rho1)练习2.21. 求出下列极限值(1)nnn n3→命令:>>syms n>>limit((n^3+3^n)^(1/n)) ans = 3(2))121(lim n n n n ++-+∞→命令:>>syms n>>limit((n+2)^(1/2)-2*(n+1)^(1/2)+n^(1/2),n,inf) ans = 0(3)x x x 2cot lim 0→命令:syms x ;>> limit(x*cot(2*x),x,0) ans = 1/2 (4))(coslimcm xx ∞→命令:syms x m ; limit((cos(m/x))^x,x,inf) ans = 1(5))111(lim 1--→exx x命令:syms x>> limit(1/x-1/(exp(x)-1),x,1) ans =(exp(1)-2)/(exp(1)-1) (6))(2lim x x xx -+∞>> limit((x^2+x)^(1/2)-x,x,inf)ans = 1/2练习2.41. 求下列不定积分,并⽤diff 验证:(1)+x dxcos 1>>Clear >> syms x y >> y=1/(1+cos(x)); >> f=int(y,x) f =tan(1/2*x) >> y=tan(1/2*x); >> yx=diff(y ,x); >> y1=simple(yx) y1 =1/2+1/2*tan(1/2*x)^2 (2)+exdx1clear syms x yy=1/(1+exp(x));f=int(y,x) f =-log(1+exp(x))+log(exp(x)) syms x yy=-log(1+exp(x))+log(exp(x)); yx=diff(y,x); y1=simple(yx) y1 = 1/(1+exp(x)) (3)dx x x ?sin 2syms x yy=x*sin(x)^2; >> f=int(y,x) f =x*(-1/2*cos(x)*sin(x)+1/2*x)-1/4*cos(x)^2-1/4*x^2 clearsyms x y y=x*(-1/2*cos(x)*sin(x)+1/2*x)-1/4*cos(x)^2-1/4*x^2; yx=diff(y,x); >> y1=simple(yx) y1 = x*sin(x)^2 (4)xdx ?sec3syms x y y=sec(x)^3;f=int(y,x) f =1/2/cos(x)^2*sin(x)+1/2*log(sec(x)+tan(x)) clear syms x yy=1/2/cos(x)^2*sin(x)+1/2*log(sec(x)+tan(x)); yx=diff(y,x); y1=simple(yx) y1 =1/cos(x)^32. 求下列积分的数值解 1)dx x-10clearsyms xy=int(x^(-x),x,0,1) y =int(x^(-x),x = 0 .. 1) vpa(y,10) ans =1.291285997 2)xdx e x cos3202?πclearsyms xy=int(exp(2*x)*cos(x)^3,x, clear syms xy=int((1/(2*pi)^(1/2))*exp(-x^2/2),x,0,1) y =7186705221432913/36028797018963968*erf(1/2*2^(1/2))*2^(1/2)*pi^(1/0,2*pi) y =22/65*exp(pi)^4-22/65vpa(ans,10)(3)dx xe21221-π>> clear >> syms x>> y=int(1/(2*pi)^(1/2)*exp(-x^2/2),0,1); >> vpa(y,14) ans =.341344746068552(4)>> clear >> syms x>> y=int(x*log(x^4)*asin(1/x^2),1,3); Warning: Explicit integral could not be found. > In sym.int at 58 >> vpa(y,14) ans = 2.45977212823752(5) >> clear >> syms x1判断下列级数的收敛性,若收敛,求出其收敛值。
(完整版)汽车理论课后作业答案MATLAB
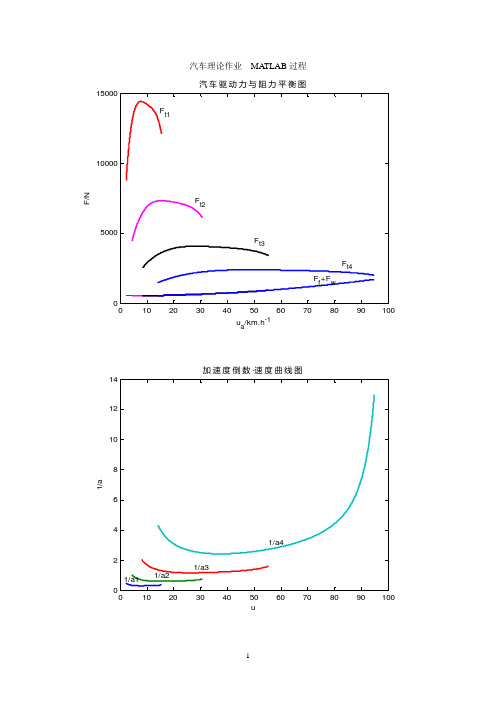
汽车理论作业 MA TLAB 过程010203040506070809010050001000015000汽车驱动力与阻力平衡图u a /km.h -1F /N10203040506070809010002468101214加速度倒数-速度曲线图u1/a0102030405060708090100102030405060u/(km/h)P /k W汽车功率平衡图10203040506070809010012141618202224最高档等速百公里油耗曲线Ua/(km/h)Q s /L2324252627282912131415161718燃油积极性-加速时间曲线燃油经济性(qs/L)动力性--原地起步加速时间 (s t /s )源程序:《第一章》m=3880; g=9.8; r=0.367; x=0.85; f=0.013; io=5.83; CdA=2.77; If=0.218; Iw1=1.798; Iw2=3.598; Iw=Iw1+Iw2;ig=[6.09 3.09 1.71 1.00]; %变速器传动比 L=3.2; a=1.947; hg=0.9; n=600:1:4000;T=-19.313+295.27*n/1000-165.44*(n/1000).^2+40.874*(n/1000).^3-3.8445*(n/1000).^4; Ft1=T*ig(1)*io*x/r;%计算各档对应转速下的驱动力Ft2=T*ig(2)*io*x/r;Ft3=T*ig(3)*io*x/r;Ft4=T*ig(4)*io*x/r;u1=0.377*r*n/(io*ig(1));u2=0.377*r*n/(io*ig(2));u3=0.377*r*n/(io*ig(3));u4=0.377*r*n/(io*ig(4));u=0:130/3400:130;F1=m*g*f+CdA*u1.^2/21.15;%计算各档对应转速下的驱动阻力F2=m*g*f+CdA*u2.^2/21.15;F3=m*g*f+CdA*u3.^2/21.15;F4=m*g*f+CdA*u4.^2/21.15;figure(1);plot(u1,Ft1,'-r',u2,Ft2,'-m',u3,Ft3,'-k',u4,Ft4,'-b',u1,F1,'-r',u2,F2,'-m',u3,F3,'-k',u4,F4,'-b','LineWidth',2)title('汽车驱动力与阻力平衡图');xlabel('u_{a}/km.h^{-1}')ylabel('F/N')gtext('F_{t1}')gtext('F_{t2}')gtext('F_{t3}')gtext('F_{t4}')gtext('F_{f}+F_{w}')%由汽车驱动力与阻力平衡图知,他们无交点,u4在最大转速时达到最大umax=u4(3401)Ft1max=max(Ft1);imax=(Ft1max-m*g*f)/(m*g)disp('假设是后轮驱动');C=imax/(a/L+hg*imax/L) % 附着率delta1=1+(Iw1+Iw2)/(m*r^2)+If*ig(1)*r^2*io^2*x/(m*r^2);delta2=1+(Iw1+Iw2)/(m*r^2)+If*ig(2)*r^2*io^2*x/(m*r^2);delta3=1+(Iw1+Iw2)/(m*r^2)+If*ig(3)*r^2*io^2*x/(m*r^2);delta4=1+(Iw1+Iw2)/(m*r^2)+If*ig(4)*r^2*io^2*x/(m*r^2);a1=(Ft1-F1)/(delta1*m); %加速度a2=(Ft2-F2)/(delta2*m);a3=(Ft3-F3)/(delta3*m);a4=(Ft4-F4)/(delta4*m);h1=1./a1; %加速度倒数h2=1./a2;h3=1./a3;h4=1./a4;figure(2);plot(u1,h1,u2,h2,u3,h3,u4,h4,'LineWidth',2); title('加速度倒数-速度曲线图');xlabel('u')ylabel('1/a')gtext('1/a1')gtext('1/a2')gtext('1/a3')gtext('1/a4')%由加速度倒数-速度曲线图可知u1min=min(u1);u1max=max(u1);u2min=u1max;u2min=min(u2);u2max=max(u2);u3min=u2max;u3max=max(u3);u4min=u3max;u4max=70;x1=[];x2=[];x3=[];x4=[];y=3401;for i=1:3401;if u3(i)<=u3min;x1=[i];endendq1=max(x1);ua3=u3(q1:y);a3=h3(q1:y);for i=1:3401;if u4(i)<=u4min;x2=[i];elseif u4(i)<=u4max;x3=[i];endendq2=max(x2);q3=max(x3);ua4=u4(q2:q3);a4=h4(q2:q3);s1=trapz(h2,u2 ); %二挡运行时间s2=trapz(ua3,a3);s3=trapz(ua4,a4);s=[s1 s2 s3];disp('积分得')t=sum(s)*1000/3600 %总时间《第二章》Pe1=Ft1.*u1./3600;%计算各档对应转速下的功率Pe2=Ft2.*u2./3600;Pe3=Ft3.*u3./3600;Pe4=Ft4.*u4./3600;P1=F1.*u1./(3600*x);%计算各档对应的各个车速下的行驶功率P2=F2.*u2./ (3600*x);P3=F3.*u3./ (3600*x);P4=F4.*u4./ (3600*x);figure(3);plot(u1,Pe1,'-r',u2,Pe2,'-m',u3,Pe3,'-k',u4,Pe4,'-b',u1,P1,'k',u2,P2,'k',u3,P3,'k', u4,P4,'k','linewidth',2);gtext('Pe1')gtext('Pe2')gtext('Pe3')gtext('Pe4')xlabel('u/(km/h)');ylabel('P/kW');title('汽车功率平衡图');n=[815 1207 1614 2012 2603 3006 3403 3804];Ua=[];Ua=0.377*r*n./(io*ig(4))ft=[];ft=m*g*f+(2.77/21.15)*Ua.^2;%计算各转速对应的各个车速下的行驶阻力Pe(1)=ft(1).*Ua(1)./(3600*x);%计算各转速对应的各个车速下的行驶阻力功率Pe(2)=ft(2).*Ua(2)./(3600*x);Pe(3)=ft(3).*Ua(3)./(3600*x);Pe(4)=ft(4).*Ua(4)./(3600*x);Pe(5)=ft(5).*Ua(5)./(3600*x);Pe(6)=ft(6).*Ua(6)./(3600*x);Pe(7)=ft(7).*Ua(7)./(3600*x);Pe(8)=ft(8).*Ua(8)./(3600*x)B0=[1326.8 1354.7 1284.4 1122.9 1141.0 1051.2 1233.9 1129.7];B1=[-416.46 -303.98 -189.75 -121.59 -98.893 -73.714 -84.478 -45.291];B2=[72.739 36.657 14.525 7.0035 4.4763 2.8593 2.9788 0.7113];B3=[-5.8629 -2.0533 -0.51184 -0.18517 -0.091077 -0.05138 -0.047449 -0.00075215];B4=[0.17768 0.043072 0.0068164 0.0018555 0.00068906 0.00035032 0.00028230-0.000038568];b1=(B0(1))+(B1(1)*Pe(1))+(B2(1)*Pe(1)^2)+(B3(1)*Pe(1)^3)+(B4(1)*Pe(1)^4);b2=(B0(2))+(B1(2)*Pe(2))+(B2(2)*Pe(2)^2)+(B3(2)*Pe(2)^3)+(B4(2)*Pe(2)^4);b3=(B0(3))+(B1(3)*Pe(3))+(B2(3)*Pe(3)^2)+(B3(3)*Pe(3)^3)+(B4(3)*Pe(3)^4);b4=(B0(4))+(B1(4)*Pe(4))+(B2(4)*Pe(4)^2)+(B3(4)*Pe(4)^3)+(B4(4)*Pe(4)^4);b5=(B0(5))+(B1(5)*Pe(5))+(B2(5)*Pe(5)^2)+(B3(5)*Pe(5)^3)+(B4(5)*Pe(5)^4);b6=(B0(6))+(B1(6)*Pe(6))+(B2(6)*Pe(6)^2)+(B3(6)*Pe(6)^3)+(B4(6)*Pe(6)^4);b7=(B0(7))+(B1(7)*Pe(7))+(B2(7)*Pe(7)^2)+(B3(7)*Pe(7)^3)+(B4(7)*Pe(7)^4);b8=(B0(8))+(B1(8)*Pe(8))+(B2(8)*Pe(8)^2)+(B3(8)*Pe(8)^3)+(B4(8)*Pe(8)^4);p=0.7;Qs=[];Qs(1)=(Pe(1)*b1)/(1.02*Ua(1).*p*g);Qs(2)=(Pe(2)*b2)/(1.02*Ua(2).*p*g);Qs(3)=(Pe(3)*b3)/(1.02*Ua(3).*p*g);Qs(4)=(Pe(4)*b4)/(1.02*Ua(4).*p*g);Qs(5)=(Pe(5)*b5)/(1.02*Ua(5).*p*g);Qs(6)=(Pe(6)*b6)/(1.02*Ua(6).*p*g);Qs(7)=(Pe(7)*b7)/(1.02*Ua(7).*p*g);Qs(8)=(Pe(8)*b8)/(1.02*Ua(8).*p*g);M=polyfit(Ua,Qs,2);UA=0.377*r*600/(ig(4)*io):1:0.377*r*4000/(ig(4)*io);%UA表示车速QS=polyval(M,UA);%QS表示油耗figure(4);plot(UA,QS,'linewidth',2);title('最高档等速百公里油耗曲线');xlabel('Ua/(km/h)');ylabel('Qs/L');《第三章》io=[5.17 5.43 5.83 6.17 6.33];Va=0.377*r*n(7)./(io.*ig(4));Ps=46.9366;disp('假设以最高档,较高转速(n取3401 ),最经济负荷(即90%负荷大约 46.9366Kw)行驶时油耗')qs=[];qs(1)=(Ps*b7)/(1.02*Va(1).*p*g);qs(2)=(Ps*b7)/(1.02*Va(2).*p*g);qs(3)=(Ps*b7)/(1.02*Va(3).*p*g);qs(4)=(Ps*b7)/(1.02*Va(4).*p*g);qs(5)=(Ps*b7)/(1.02*Va(5).*p*g);st=[ 17.5813 16.2121 14.5126 13.3775 12.9185];%加速时间:(这里以最高档〈四档〉、速度由0加速到94.93Km/h 的时间)因与题1.3第三问求法相同,这里不在累述,可直接有计算机求得:figure(5);plot(qs,st,'+','linewidth',2)hold on plot(qs,st,); gtext('5.17') gtext('5.43') gtext('5.83') gtext('6.17') gtext('6.33')title('燃油积极性-加速时间曲线'); xlabel('燃油经济性(qs/L)');ylabel('动力性--原地起步加速时间 (st/s)');《第四章》 4-31)前轴利用附着系数为:gf zh b zL +=βϕ后轴利用附着系数为: ()gr zh a zL --=βϕ1空载时:g h b L -=βϕ0=413.0845.085.138.095.3-=-⨯所以0ϕϕ>空载时后轮总是先抱死。
数学建模作业题+答案

数学建模MATLAB 语言及应用上机作业11. 在matlab 中建立一个矩阵135792468101234501234A ⎡⎤⎢⎥⎢⎥=⎢⎥-----⎢⎥⎣⎦答案:A = [1,3,5,7,9;2,4,6,8,10;-1,-2,-3,-4,-5;0,1,2,3,4]2. 试着利用matlab 求解出下列方程的解(线性代数22页例14)123412423412342583692254760x x x x x x x x x x x x x x +-+=⎧⎪--=⎪⎨-+=-⎪⎪+-+=⎩ 答案:A=[2 ,1,-5,1;1,-3,0,-6;0,2,-1,2;1,4,-7,6]; B=[8;9;-5;0]; X=A\B 或A=[2,1,-5,1;1,-3,0,-6;0,2,-1,2;1,4,-7,6] b=[8,9,-5,0]' X=inv(A)*b3. 生成一个5阶服从标准正态分布的随机方阵,并计算出其行列式的值,逆矩阵以及转置矩阵。
答案:A=randn(5) det(A) inv(A) A'4. 利用matlab 求解出110430002A -⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦的特征值和特征向量。
答案:A=[-1,1,0;-4,3,0;0,0,2] [V,D]=eig(A)5.画出衰减振荡曲线3sin3t y et -=在[0,4]π上的图像。
要求,画线颜色调整为黑色,画布底面为白色。
(在实际中,很多打印机时黑白的,因此大多数作图要考虑黑白打印机的效果。
) 给出恰当的x ,y 坐标轴标题,图像x 轴的最大值为4π。
6. 生成一个0-1分布的具有10个元素的随机向量,试着编写程序挑选出向量中大于0.5的元素。
数学建模和Matlab 上机作业2(2016-9-20)跟老师做(不用整合进作业中):上机演示讲解:函数,递归的两个例子的写法。
附:1. Fibonacci Sequence (斐波那契数列)在数学上,费波那西数列是以递归的方法来定义: F1= 1;F2= 1;F (n )=F (n-1)+F (n-2) 2. 阶乘举例:数学描述:n!=1×2×……×n ;计算机描述:n!=n*(n-1)!自己做(需要整合进作业中,提交到系统中):1. 写一个m 文件完成分值百分制到5分制的转换(即输入一个百分制,转换后输出一个5级对应的得分,联系条件控制语句)。
matlab实验三答案详解

实验三选择结构程序设计实验内容1.程序代码function f(x)if x<0&x~=-3y=x*x+x-6;elseif x>0&x<5&x~=2&x~=3y=x*x-5.*x+6;elsey=x*x-x-1endy运行结果>> f(-7)y =36>> f(2.5)y =-0.2500>> f(90)y =80092.程序代码score=input('分数=');if score<=100&score>=0switch fix(score/10)case{9,10}grade='A';case{8}grade='B';case{7}grade='C';case{6}grade='D';otherwisegrade='E';endgradeelsedisp('输入有误,请输入正确的百分制成绩');end运行结果>> 分数=56grade =E>> f分数=345输入有误,请输入正确的百分制成绩3.程序代码time=input('工作时间=');switch timecase{time>120}wage=(time-120)*(1+15/100)*84+120*84;case{time<60}wage=time*84-700;otherwisewage=time*84end运行结果>> f工作时间=150wage =12600>> f工作时间=50wage =4200>> f工作时间=110wage =92404.程序代码A=10+90*rand(5);a=fix(A(3,3))b=fix(A(2,4))x=input('输入一个运算符号','s');switch xcase {'+'}c=a+b;case{'-'}c=a-b;case{'*'}c=a*b;case{'/'}c=a/b;otherwisec='无效'endc运行结果>> fa =55b =59输入一个运算符号+c =114>> fa =77b =14输入一个运算符号/c =5.5000>> fa =30b =58输入一个运算符号#c =无效c =无效5.程序代码A=input('输入一个5行6列的矩阵A=');n=input('输入一个正整数n=');if n<5&n>0disp(A(n,:));elsedisp(A(5,:));endlasterr运行结果>> f输入一个5行6列的矩阵A=[1 2 3 4 5 5;2 3 4 5 7 6;2 9 2 2 2 3;11 2 11 9 7 3;2 3 4 5 6 7] 输入一个正整数n=62 3 4 5 6 7ans =Undefined function or variable 'clcl'.>> f输入一个5行6列的矩阵A=[1 2 3 4 5 5;2 3 4 5 7 6;2 2 2 2 2 3;11 2 3 9 7 3;2 3 4 5 6 7]输入一个正整数n=32 2 2 2 2 3ans =Undefined function or variable 'clcl'.。
matlab课后习题与答案

习题二1.如何理解“矩阵是MATLAB最基本的数据对象”?答:因为向量可以看成是仅有一行或一列的矩阵,单个数据(标量)可以看成是仅含一个元素的矩阵,故向量和单个数据都可以作为矩阵的特例来处理。
因此,矩阵是MATLAB最基本、最重要的数据对象。
2.设A和B是两个同维同大小的矩阵,问:(1)A*B和A.*B的值是否相等?答:不相等。
(2)A./B和B.\A的值是否相等?答:相等。
(3)A/B和B\A的值是否相等?答:不相等。
(4)A/B和B\A所代表的数学含义是什么?答:A/B等效于B的逆右乘A矩阵,即A*inv(B),而B\A等效于B矩阵的逆左乘A矩阵,即inv(B)*A。
3.写出完成下列操作的命令。
(1)将矩阵A第2~5行中第1, 3, 5列元素赋给矩阵B。
答:B=A(2:5,1:2:5); 或B=A(2:5,[1 3 5])(2)删除矩阵A的第7号元素。
答:A(7)=[](3)将矩阵A的每个元素值加30。
答:A=A+30;(4)求矩阵A的大小和维数。
答:size(A);ndims(A);(5)将向量t的0元素用机器零来代替。
答:t(find(t==0))=eps;(6)将含有12个元素的向量x转换成34矩阵。
答:reshape(x,3,4);(7)求一个字符串的ASCII码。
答:abs(‘123’); 或double(‘123’);(8) 求一个ASCII 码所对应的字符。
答:char(49);4. 下列命令执行后,L1、L2、L3、L4的值分别是多少?A=1:9;B=10-A;...L1=A==B;L2=A<=5;L3=A>3&A<7;L4=find(A>3&A<7);答:L1的值为[0, 0, 0, 0, 1, 0, 0, 0, 0]L2的值为[1, 1, 1, 1, 1, 0, 0, 0, 0]L3的值为[0, 0, 0, 1, 1, 1, 0, 0, 0]L4的值为[4, 5, 6]5. 已知23100.7780414565532503269.5454 3.14A -⎡⎤⎢⎥-⎢⎥=⎢⎥⎢⎥-⎣⎦完成下列操作:(1) 取出A 的前3行构成矩阵B ,前两列构成矩阵C ,右下角32⨯子矩阵构成矩阵D ,B 与C 的乘积构成矩阵E 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
MATLAB 作业三参考答案1、 请将下面给出的矩阵A 和B 输入到MA TLAB 环境中,并将它们转换成符号矩阵。
若某一矩阵为数值矩阵,另以矩阵为符号矩阵,两矩阵相乘是符号矩阵还是数值矩阵。
576516535501232310014325462564206441211346,39636623515212107600774101201724407734737812486721711076815A B ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥---⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦【求解】矩阵的输入与转换是很直接的。
>> A=[5,7,6,5,1,6,5; 2,3,1,0,0,1,4; 6,4,2,0,6,4,4; 3,9,6,3,6,6,2; 10,7,6,0,0,7,7; 7,2,4,4,0,7,7; 4,8,6,7,2,1,7]; A=sym(A) A =[ 5, 7, 6, 5, 1, 6, 5] [ 2, 3, 1, 0, 0, 1, 4] [ 6, 4, 2, 0, 6, 4, 4] [ 3, 9, 6, 3, 6, 6, 2] [ 10, 7, 6, 0, 0, 7, 7] [ 7, 2, 4, 4, 0, 7, 7] [ 4, 8, 6, 7, 2, 1, 7]>> B=[3,5,5,0,1,2,3; 3,2,5,4,6,2,5; 1,2,1,1,3,4,6; 3,5,1,5,2,1,2; 4,1,0,1,2,0,1; -3,-4,-7,3,7,8,12; 1,-10,7,-6,8,1,5]; B=sym(B) B =[ 3, 5, 5, 0, 1, 2, 3] [ 3, 2, 5, 4, 6, 2, 5] [ 1, 2, 1, 1, 3, 4, 6] [ 3, 5, 1, 5, 2, 1, 2] [ 4, 1, 0, 1, 2, 0, 1] [ -3, -4, -7, 3, 7, 8, 12] [ 1, -10, 7, -6, 8, 1, 5]2、 利用MA TLAB 语言提供的现成函数对习题1中给出的两个矩阵进行分析,判定它们是否为奇异矩阵,得出矩阵的秩、行列式、迹和逆矩阵,检验得出的逆矩阵是否正确。
【求解】以A 矩阵为例,可以对其进行如下分析。
>> A=[5,7,6,5,1,6,5; 2,3,1,0,0,1,4; 6,4,2,0,6,4,4; 3,9,6,3,6,6,2; 10,7,6,0,0,7,7; 7,2,4,4,0,7,7; 4,8,6,7,2,1,7]; A=sym(A); rank(A) ans =7 >> det(A) ans =-35432>> trace(A)ans =27>> B=inv(A);>> A*Bans =[ 1, 0, 0, 0, 0, 0, 0][ 0, 1, 0, 0, 0, 0, 0][ 0, 0, 1, 0, 0, 0, 0][ 0, 0, 0, 1, 0, 0, 0][ 0, 0, 0, 0, 1, 0, 0][ 0, 0, 0, 0, 0, 1, 0][ 0, 0, 0, 0, 0, 0, 1]3、试求出习题1中给出的A和B矩阵的特征多项式、特征值与特征向量,并对它们进行LU 分解。
【求解】仍以A 矩阵为例。
>> A=[5,7,6,5,1,6,5; 2,3,1,0,0,1,4; 6,4,2,0,6,4,4; 3,9,6,3,6,6,2;10,7,6,0,0,7,7; 7,2,4,4,0,7,7; 4,8,6,7,2,1,7]; A=sym(A);eig(A)ans =5.009396680079366526215873006955228.679593193974410579078264020229.27480714110743938760483528351799e-1+1.1755376247101009492093136044131*i-1.6336795424500642956747726147329+6.9740721596526560301948635104611*i-3.4765922173751363914655588544224-1.6336795424500642956747726147329-6.9740721596526560301948635104611*i.27480714110743938760483528351799e-1-1.1755376247101009492093136044131*i>> p=poly(A)p =x^7-27*x^6-18*x^5-1000*x^4+3018*x^3+24129*x^2+2731*x+35432>> p=sym2poly(p)p =1 -27 -18 -1000 3018 24129 2731 35432>> [L U]=lu(A)L =0.5000 0.5072 0.5556 0.1099 0.5000 0.5376 1.00000.2000 0.2319 -0.7500 0.6429 0.5702 1.0000 00.6000 -0.0290 -0.9444 1.0000 0 0 00.3000 1.0000 0 0 0 0 01.0000 0 0 0 0 0 00.7000 -0.4203 1.0000 0 0 0 00.4000 0.7536 0.2778 0.6484 1.0000 0 0U =10.0000 7.0000 6.0000 0 0 7.0000 7.00000 6.9000 4.2000 3.0000 6.0000 3.9000 -0.10000 0 1.5652 5.2609 2.5217 3.7391 2.0580 0 0 0 5.0556 8.5556 3.4444 1.7407 0 0 0 0 -8.7692 -8.0110 2.5751 0 0 0 0 0 3.8534 1.5794 0 0 0 0 0 0 -1.92044、试求下面齐次方程的基础解系。
123451234123451234512345647302786045680343692149026122727170x x x x x x x x x x x x x x x x x x x x x x x x ++--=⎧⎪---+=⎪⎪-++-+=⎨⎪-++-+=⎪---++=⎪⎩ 【求解】可以将方程写成矩阵形式,得出的两列向量为方程的基础解系。
>> A=[6,1,4,-7,-3; -2,-7,-8,6,0; -4,5,1,-6,8; -34,36,9,-21,49; -26,-12,-27,27,17]; A=sym(A); rank(A) ans =3>> null(A) ans =[ 191/34, 95/17] [ 0, 1] [ 1, 0] [ 109/34, 103/34] [ 173/34, 151/34]5、试求下面线性代数方程的解析解与数值解,并检验解的正确性。
2932114010110503848246303356684953X -----⎡⎤⎡⎤⎢⎥⎢⎥----⎢⎥⎢⎥=⎢⎥⎢⎥---⎢⎥⎢⎥------⎣⎦⎣⎦【求解】求出A , [A;B ] 两个矩阵的秩,可见二者相同,所以方程不是矛盾方程,应该有无穷多解。
>> A=[2,-9,3,-2,-1; 10,-1,10,5,0; 8,-2,-4,-6,3; -5,-6,-6,-8,-4]; B=[-1,-4,0; -3,-8,-4; 0,3,3; 9,-5,3]; [rank(A), rank([A B])] ans =4 4用下面的语句可以求出方程的解析解,并可以验证该解没有误差。
>> x0=null(sym(A));x_analytical=sym(A)\B; syms a; x=a*[x0 x0 x0]+x_analytical x =[ a+967/1535, a-943/1535, a-159/1535][ -1535/1524*a, -1535/1524*a, -1535/1524*a][ -3659/1524*a-1807/1535,-3659/1524*a-257/1535,-3659/1524*a-141/1535] [ 1321/508*a+759/1535, 1321/508*a-56/1535, 1321/508*a-628/1535] [ -170/127*a-694/307, -170/127*a+719/307, -170/127*a+103/307] >> A*x-B ans =[ 0, 0, 0] [ 0, 0, 0] [ 0, 0, 0] [ 0, 0, 0]用数值解方法也可以求出方程的解,但会存在误差,且与任意常数a 的值有关。
>> x0=null(A); x_numerical=A\B; syms a; x=a*[x0 x0 x0]+x_numerical; vpa(x,10) ans =[ .2474402553*a+.1396556436, .2474402553*a-.6840666849, .2474402553*a-.1418420333][-.2492262414*a+.4938507789,-.2492262414*a+.7023776988e-1,-.2492262414*a+.3853511888e-1][ -.5940839201*a, -.5940839201*a, -.5940839201*a][ .6434420813*a-.7805411315, .6434420813*a-.2178190763,.6434420813*a-.5086089095][-.3312192394*a-1.604263460, -.3312192394*a+2.435364854, -.3312192394*a+.3867176824] >> A*x-B ans =[ 1/18014398509481984*a, 1/18014398509481984*a, 1/18014398509481984*a] [ -5/4503599627370496*a, -5/4503599627370496*a, -5/4503599627370496*a][ -25/18014398509481984*a, -25/18014398509481984*a, -25/18014398509481984*a] [ 13/18014398509481984*a, 13/18014398509481984*a, 13/18014398509481984*a]6、试判定下面的线性代数方程是否有解。
