统计学原理-第五版-课后答案
统计学(第五版)课后答案
7.02377
Variance
49.333
Skewness
1.163
Kurtosis
1.302
分组后的直方图:
4.6在某地区抽取120家企业,按利润额进行分组,结果如下:
按利润额分组(万元)
企业数(个)
200~300
300~400
400~500
500~600
600以上
19
解:已知μ0=250,σ= 30,N=25, =270这里是小样本分布,σ已知,用Z统计量。右侧检验,α=0.05,则Zα=1.645
提出假设:假定这种化肥没使小麦明显增产。即H0:μ≤250H1:μ>250
计算统计量:Z =( -μ0)/(σ/√N)=(270-250)/(30/√25)= 3.33
(1) =25,σ=3.5,n=60,置信水平为95%(2) =119.6,s=23.89,n=75,置信水平为95%
(3) =3.419,s=0.974,n=32,置信水平为90%
解:∵
∴1)1-=95%, 其置信区间为:25±1.96×3.5÷√60= 25±0.885
2)1-=98%,则=0.02,/2=0.01, 1-/2=0.99,查标准正态分布表,可知: 2.33
解:已知μ0=4.55,σ²=0.108²,N=9, =4.484,
这里采用双侧检验,小样本,σ已知,使用Z统计。假定现在生产的铁水平均含碳量与以前无显著差异。则,
H0:μ=4.55;H1:μ≠4.55α=0.05,α/2 =0.025,查表得临界值为 1.96
计算检验统计量: = (4.484-4.55)/(0.108/√9)= -1.833
解:H0:μ≥700;H1:μ<700已知: =680 =60
统计学第五版课后习题答案(完整版)

统计学(第五版)课后习题答案(完整版)第一章思考题1.1什么是统计学统计学是关于数据的一门学科,它收集,处理,分析,解释来自各个领域的数据并从中得出结论。
1.2解释描述统计和推断统计描述统计;它研究的是数据收集,处理,汇总,图表描述,概括与分析等统计方法。
推断统计;它是研究如何利用样本数据来推断总体特征的统计方法。
1.3统计学的类型和不同类型的特点统计数据;按所采用的计量尺度不同分;(定性数据)分类数据:只能归于某一类别的非数字型数据,它是对事物进行分类的结果,数据表现为类别,用文字来表述;(定性数据)顺序数据:只能归于某一有序类别的非数字型数据。
它也是有类别的,但这些类别是有序的。
(定量数据)数值型数据:按数字尺度测量的观察值,其结果表现为具体的数值。
统计数据;按统计数据都收集方法分;观测数据:是通过调查或观测而收集到的数据,这类数据是在没有对事物人为控制的条件下得到的。
实验数据:在实验中控制实验对象而收集到的数据。
统计数据;按被描述的现象与实践的关系分;截面数据:在相同或相似的时间点收集到的数据,也叫静态数据。
时间序列数据:按时间顺序收集到的,用于描述现象随时间变化的情况,也叫动态数据。
1.4解释分类数据,顺序数据和数值型数据答案同1.31.5举例说明总体,样本,参数,统计量,变量这几个概念对一千灯泡进行寿命测试,那么这千个灯泡就是总体,从中抽取一百个进行检测,这一百个灯泡的集合就是样本,这一千个灯泡的寿命的平均值和标准差还有合格率等描述特征的数值就是参数,这一百个灯泡的寿命的平均值和标准差还有合格率等描述特征的数值就是统计量,变量就是说明现象某种特征的概念,比如说灯泡的寿命。
1.6变量的分类变量可以分为分类变量,顺序变量,数值型变量。
变量也可以分为随机变量和非随机变量。
经验变量和理论变量。
1.7举例说明离散型变量和连续性变量离散型变量,只能取有限个值,取值以整数位断开,比如“企业数”连续型变量,取之连续不断,不能一一列举,比如“温度”。
统计学第五版课后题答案李金昌

统计学第五版课后题答案李金昌第1章绪论 1 .试述数据、数据库、数据库系统、数据库管理系统的概念。
答:( l )数据( Data ) :叙述事物的符号记录称作数据。
数据的种类存有数字、文字、图形、图像、声音、正文等。
数据与其语义就是不可分的。
解析在现代计算机系统中数据的概念就是广义的。
早期的计算机系统主要用作科学计算,处置的数据就是整数、实数、浮点数等传统数学中的数据。
现代计算机能够存储和处置的对象十分广为,则表示这些对象的数据也越来越繁杂。
数据与其语义就是不可分的。
500 这个数字可以表示一件物品的价格是 500 元,也可以表示一个学术会议参加的人数有 500 人,还可以表示一袋奶粉重 500 克。
( 2 )数据库( DataBase ,缩写 DB ) :数据库就是长期储存在计算机内的、存有非政府的、可以共享资源的数据子集。
数据库中的数据按一定的数据模型非政府、叙述和储存,具备较小的冗余度、较低的数据独立性和易扩展性,并可向各种用户共享资源。
( 3 )数据库系统( DataBas 。
Sytem ,缩写 DBS ) :数据库系统就是所指在计算机系统中导入数据库后的系统形成,通常由数据库、数据库管理系统(及其开发工具)、应用领域系统、数据库管理员形成。
解析数据库系统和数据库就是两个概念。
数据库系统就是一个人一机系统,数据库就是数据库系统的一个组成部分。
但是在日常工作中人们常常把数据库系统缩写为数据库。
期望读者能从人们讲话或文章的上下文中区分“数据库系统”和“数据库”,不要引发混为一谈。
( 4 )数据库管理系统( DataBase Management sytem ,简称 DBMs ) :数据库管理系统是位于用户与操作系统之间的一层数据管理软件,用于科学地组织和存储数据、高效地获取和维护数据。
DBMS 的主要功能包含数据定义功能、数据压低功能、数据库的运转管理功能、数据库的创建和保护功能。
解析 DBMS 就是一个大型的繁杂的软件系统,就是计算机中的基础软件。
统计学(第五版)课后答案
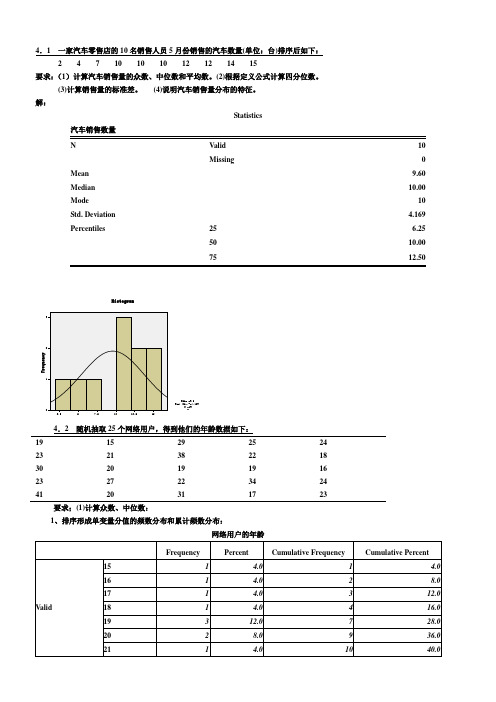
4.1 一家汽车零售店的10名销售人员5月份销售的汽车数量(单位:台)排序后如下:2 4 7 10 10 10 12 12 14 15要求:(1)计算汽车销售量的众数、中位数和平均数。
(2)根据定义公式计算四分位数。
(3)计算销售量的标准差。
(4)说明汽车销售量分布的特征。
解:Statistics汽车销售数量N Valid 10Missing 0 Mean 9.60 Median 10.00 Mode 10 Std. Deviation 4.169 Percentiles 25 6.2550 10.0075 12.504.2 随机抽取25个网络用户,得到他们的年龄数据如下:19 15 29 25 2423 21 38 22 1830 20 19 19 1623 27 22 34 2441 20 31 17 23要求;(1)计算众数、中位数:1、排序形成单变量分值的频数分布和累计频数分布:网络用户的年龄从频数看出,众数Mo 有两个:19、23;从累计频数看,中位数Me=23。
(2)根据定义公式计算四分位数。
Q1位置=25/4=6.25,因此Q1=19,Q3位置=3×25/4=18.75,因此Q3=27,或者,由于25 和27都只有一个,因此Q3也可等于25+0.75×2=26.5。
(3)计算平均数和标准差; Mean=24.00;Std. Deviation=6.652 (4)计算偏态系数和峰态系数: Skewness=1.080;Kurtosis=0.773(5)对网民年龄的分布特征进行综合分析:分布,均值=24、标准差=6.652、呈右偏分布。
如需看清楚分布形态,需要进行分组。
为分组情况下的直方图:为分组情况下的概率密度曲线:分组:1、确定组数:()lg 25lg() 1.398111 5.64lg(2)lg 20.30103n K=+=+=+=,取k=62、确定组距:组距=( 最大值 - 最小值)÷ 组数=(41-15)÷6=4.3,取53、分组频数表网络用户的年龄(Binned)分组后的均值与方差:分组后的直方图:4.6 在某地区抽取120家企业,按利润额进行分组,结果如下:要求:(1)计算120家企业利润额的平均数和标准差。
统计学第五版课后练答案

统计学第五版课后练答案(7-8章)(总11页)-本页仅作为预览文档封面,使用时请删除本页-第七章 参数估计(1)x σ==(2)2x z α∆= 1.96=某快餐店想要估计每位顾客午餐的平均花费金额。
在为期3周的时间里选取49名顾客组成了一个简单随机样本。
(1)假定总体标准差为15元,求样本均值的抽样标准误差。
x σ==(2)在95%的置信水平下,求估计误差。
x x t σ∆=⋅,由于是大样本抽样,因此样本均值服从正态分布,因此概率度t=2z α 因此,x x t σ∆=⋅2x z ασ=⋅0.025x z σ=⋅=×=(3)如果样本均值为120元,求总体均值 的95%的置信区间。
置信区间为:22x z x z αα⎛-+ ⎝=()120 4.2,120 4.2-+=(,)22x z x z αα⎛-+ ⎝=104560±=(,) 从总体中抽取一个n=100的简单随机样本,得到x =81,s=12。
要求:大样本,样本均值服从正态分布:2,x N n σμ⎛⎫ ⎪⎝⎭或2,s x N n μ⎛⎫⎪⎝⎭置信区间为:22x z x z αα⎛-+ ⎝= (1)构建μ的90%的置信区间。
2z α=0.05z =,置信区间为:()81 1.645 1.2,81 1.645 1.2-⨯+⨯=(,)(2)构建μ的95%的置信区间。
2z α=0.025z =,置信区间为:()81 1.96 1.2,81 1.96 1.2-⨯+⨯=(,) (3)构建μ的99%的置信区间。
2z α=0.005z =,置信区间为:()81 2.576 1.2,81 2.576 1.2-⨯+⨯=(,)(1)2x z α±=25 1.96±=(,) (2)2x z α±=119.6 2.326±=(,)(3)2x z α±=3.419 1.645±=(,)(1)2x z α±=8900 1.96±=(,)(2)2x z α±=8900 1.96±=(,)(3)2x z α±=8900 1.645±=(,) (4)2x z α±=8900 2.58±=(,)某大学为了解学生每天上网的时间,在全校7 500名学生中采取重复抽样方法随机抽取36解:(1)样本均值x =,样本标准差s=1α-=,t=2z α=0.05z =,2x z α±=3.32 1.645±=(,)1α-=,t=2z α=0.025z =,2x zα±3.32 1.96±=(,)1α-=,t=2z α=0.005z =,2x z α±3.32 2.76±(,)x t α±=10 2.365±某居民小区为研究职工上班从家里到单位的距离,抽取了由16个人组成的一个随机样本,他们到单位的距离(单位:km)分别是: 10 3 14 8 6 9 12 11 7 5 10 15 9 16 13 2假定总体服从正态分布,求职工上班从家里到单位平均距离的95%的置信区间。
统计学原理第五版课后答案

《统计学原理(第五版)》计算题解答第三章 综合指标1. 见教材P4042. %86.1227025232018=+++=产量计划完成相对数发3. %85.101%108%110%%(%)===计划为上年的实际为上年的计划完成程度指标劳动生产率计划超额1.85%完成4. %22.102%90%92(%)(%)(%)===计划完成数实际完成数计划完成程度指标 一季度产品单位成本未完成计划,实际单位成本比计划规定数高2.22%5. %105%103% %%(%) 计划为上年的计划为上年的实际为上年的计划完成程度指标=∴=1.94% %94.101103%105%% 即计划规定比上年增长计划为上年的解得:== 6. 见教材P405 7. 见教材P405 8)/(2502500625000)/(2702500675000亩千克亩千克乙甲======∑∑∑∑f xf X xm m X在相同的耕地自然条件下,乙村的单产均高于甲村,故乙村的生产经营管理工作做得好。
但由于甲村的平原地所占比重大,山地所占比重小,乙村则相反,由于权数的作用,使得甲村的总平均单产高于乙村。
%.ffx X 9103=⋅=∑∑平均计划完成程度10. 见教材P40611. %74.94963.09222.09574.03=⨯⨯=G X)亩/283.3( 8.25275 251332562600275 组为30027530026002f d m f 1m S 2fX e M L 千克中位数所在=+=⨯-+=-∴==∑⋅--∑+=⎪⎪⎪⎭⎫⎝⎛)亩/(5.942 45.91275 25119)-(13384)-(133275d X M 84133211L 0千克=+=⨯++=⋅+=-∆+∆∆之间—在亩千克之间—在亩千克—众数所在组为325300Q )/(82.31282.12300 450460034f 3 2511938946003300250225Q )/(03.24203.17225 15046004f 25691034600225)300275(3311∴=+==⨯=⨯-⨯+=∴=+===⨯-+=∑∑Q Q (2)R=500-150=350(千克/亩))亩/41.84(60025102.14ff x x A.D.千克==∑∑-=(3))/(55.5225102.2250.1444-4.5642 252)600229(6002738.5d 2f )f d A -x (f f 2)d A -x (σ)/278(287.525600229A d f )f d Ax (x)亩/277.96(600166775fxf x 亩千克亩千克或千克=⨯=⨯=⨯--=⨯⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡∑∑-∑∑==+⨯-=+⋅∑∑-===∑∑=“标准差”不要求用组距数列的简捷法计算(4) 根据以上计算,294.5千克/亩>283.3千克/亩>277.96千克/亩,故资料分布为左偏(即下偏)。
统计学(第五版)贾俊平-课后思考题和练习题答案(完整版)

统计学(第五版)贾俊平课后思考题和练习题答案(最终完整版)第一部分思考题第一章思考题1。
1什么是统计学统计学是关于数据的一门学科,它收集,处理,分析,解释来自各个领域的数据并从中得出结论。
1。
2解释描述统计和推断统计描述统计;它研究的是数据收集,处理,汇总,图表描述,概括与分析等统计方法。
推断统计;它是研究如何利用样本数据来推断总体特征的统计方法。
1.3统计学的类型和不同类型的特点统计数据;按所采用的计量尺度不同分;(定性数据)分类数据:只能归于某一类别的非数字型数据,它是对事物进行分类的结果,数据表现为类别,用文字来表述;(定性数据)顺序数据:只能归于某一有序类别的非数字型数据。
它也是有类别的,但这些类别是有序的.(定量数据)数值型数据:按数字尺度测量的观察值,其结果表现为具体的数值。
统计数据;按统计数据都收集方法分;观测数据:是通过调查或观测而收集到的数据,这类数据是在没有对事物人为控制的条件下得到的。
实验数据:在实验中控制实验对象而收集到的数据。
统计数据;按被描述的现象与实践的关系分;截面数据:在相同或相似的时间点收集到的数据,也叫静态数据。
时间序列数据:按时间顺序收集到的,用于描述现象随时间变化的情况,也叫动态数据。
1。
4解释分类数据,顺序数据和数值型数据答案同1.31.5举例说明总体,样本,参数,统计量,变量这几个概念对一千灯泡进行寿命测试,那么这千个灯泡就是总体,从中抽取一百个进行检测,这一百个灯泡的集合就是样本,这一千个灯泡的寿命的平均值和标准差还有合格率等描述特征的数值就是参数,这一百个灯泡的寿命的平均值和标准差还有合格率等描述特征的数值就是统计量,变量就是说明现象某种特征的概念,比如说灯泡的寿命。
1。
6变量的分类变量可以分为分类变量,顺序变量,数值型变量。
变量也可以分为随机变量和非随机变量。
经验变量和理论变量。
1。
7举例说明离散型变量和连续性变量离散型变量,只能取有限个值,取值以整数位断开,比如“企业数”连续型变量,取之连续不断,不能一一列举,比如“温度”。
统计学第五版课后题答案

统计学第五版贾俊平版课后题答案(部分)第三章数据的图表展示3.1 为评价家电行业售后服务的质量,随机抽取了由100个家庭构成的一个样本。
服务质量的等级分别表示为:A.好;B.较好;C一般;D.较差;E.差。
调查结果如下:B EC C AD C B A ED A C B C DE C E EA DBC C A ED C BB ACDE A B D D CC B C ED B C C B CD A C B C DE C E BB EC C AD C B A EB AC E E A BD D CA DBC C A ED C BC B C ED B C C B C要求:(1)指出上面的数据属于什么类型。
顺序数据(2)用Excel制作一张频数分布表。
用数据分析——直方图制作:接收频率E16D17C32B21A14(3)绘制一张条形图,反映评价等级的分布。
用数据分析——直方图制作:(4)绘制评价等级的帕累托图。
逆序排序后,制作累计频数分布表:接收 频数 频率(%) 累计频率(%) C 32 32 32 B 21 21 53 D 17 17 70 E 16 16 86 A14141005101520253035CDBAE204060801001203.2 某行业管理局所属40个企业2002年的产品销售收入数据如下: 152 124 129 116 100 103 92 95 127 104 105 119 114 115 87 103 118 142 135 125 117 108 105 110 107 137 120 136 117 108 9788123115119138112146113126要求:(1)根据上面的数据进行适当的分组,编制频数分布表,并计算出累积频数和累积频率。
1、确定组数: ()lg 40lg() 1.60206111 6.32lg(2)lg 20.30103n K =+=+=+=,取k=6 2、确定组距:组距=( 最大值 - 最小值)÷ 组数=(152-87)÷6=10.83,取10 3(2)按规定,销售收入在125万元以上为先进企业,115~125万元为良好企业,105~115 万元为一般企业,105万元以下为落后企业,按先进企业、良好企业、一般企业、落后企业3.3 某百货公司连续40天的商品销售额如下:单位:万元41 25 29 47 38 34 30 38 43 40 46 36 45 37 37 36 45 43 33 44 35 28 46 34 30 37 44 26 38 44 42363737493942323635要求:根据上面的数据进行适当的分组,编制频数分布表,并绘制直方图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《统计学原理(第五版)》计算题解答第三章 综合指标1. 见教材P4042. %86.1227025232018=+++=产量计划完成相对数发3. %85.101%108%110%%(%)===计划为上年的实际为上年的计划完成程度指标劳动生产率计划超额1.85%完成4. %22.102%90%92(%)(%)(%)===计划完成数实际完成数计划完成程度指标一季度产品单位成本未完成计划,实际单位成本比计划规定数高2.22%5. %105%103% %%(%) 计划为上年的计划为上年的实际为上年的计划完成程度指标=∴= 1.94% %94.101103%105%% 即计划规定比上年增长计划为上年的解得:== 6. 见教材P405 7. 见教材P405 8)/(2502500625000)/(2702500675000亩千克亩千克乙甲======∑∑∑∑f xf X x mX在相同的耕地自然条件下,乙村的单产均高于甲村,故乙村的生产经营管理工作做得好。
但由于甲村的平原地所占比重大,山地所占比重小,乙村则相反,由于权数的作用,使得甲村的总平均单产高于乙村。
%.fx X 9103=⋅=∑∑平均计划完成程度10. 见教材P40611. %74.94963.09222.09574.03=⨯⨯=G X)亩/283.3( 8.25275 251332562600275 组为30027530026002f d m f 1m S 2fX e M L 千克中位数所在=+=⨯-+=-∴==∑⋅--∑+=⎪⎪⎪⎭⎫⎝⎛)亩/(5.942 45.91275 25119)-(13384)-(133275d X M 84133211L 0千克=+=⨯++=⋅+=-∆+∆∆之间—在亩千克之间—在亩千克—众数所在组为325300Q )/(82.31282.12300 450460034f 3 2511938946003300250225Q )/(03.24203.17225 15046004f 25691034600225)300275(3311∴=+==⨯=⨯-⨯+=∴=+===⨯-+=∑∑ Q Q (2)R=500-150=350(千克/亩))亩/41.84(60025102.14ff x x A.D.千克==∑∑-=(3))/(55.5225102.2250.1444-4.5642 252)600229(6002738.5d 2f )f d A -x (f f 2)d A -x (σ)/278(287.525600229A d f )f d Ax (x)亩/277.96(600166775fxf x 亩千克亩千克或千克=⨯=⨯=⨯--=⨯⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡∑∑-∑∑==+⨯-=+⋅∑∑-===∑∑=“标准差”不要求用组距数列的简捷法计算(4) 根据以上计算,294.5千克/亩>283.3千克/亩>277.96千克/亩,故资料分布为左偏(即下偏)。
13.(1)。
乙单位工人生产水平高人件人件乙甲乙甲∴<======∑∑∑∑ 8110018051200300X X )/(.xm m X )/(.f xf X(2)齐乙单位工人生产水平整,人)件人件乙甲乙乙乙甲甲甲乙甲∴>=⨯=⨯==⨯=⨯====-====-=∑∑∑∑ V V %3.33%1008.16.0%100x σV %7.44%10050.167.0%100x σV /0.60(0.3610036ff)x (x σ)/0.67(0.4520090f f)x (x σ2214. 其分布态势为左偏分布元)(550)7006003(21)3(210=-⨯⨯=-=M M X e15.(1)%49.51X %49.105 08.107.105.104.102.1 X 1624632121=-=⨯⨯⨯⨯=∑⋅⋅⋅⋅⋅⋅=G ff n f f G nX X X 平均年利率:平均本利率为:(2)%50.5 162%84%76%53%4%2X =⨯+⨯+⨯+⨯+==∑∑fXf第四章 动态数列1. 见教材P4072. 见教材P407-4083. 见教材P4084. 见教材P4095. (1) 见教材P409-410(2) ① 增减速度=发展速度-1(或100%)② 0n1i i a a n 1i a a =∏=- (环比发展速度的连乘积等于定基发展速度) ③ 100%1基期发展水平的绝对值增长=④ 增减速度增减量的绝对值增长=%1⑤ 0n 1i i a a n1i )a (a -=∑=-- (逐期增减量之和等于累计增减量)⑥ n x x ∏= (平均发展速度等于环比发展速度的连乘积开n 次方) ⑦ 平均增减速度=平均发展速度-1(或100%) 6. 见教材P410 7. 见教材P410-411 8. (1) 见教材P4119.17t 2214.03y 9.17b 2214.038990b 824053066421 t b t ty tb N yc 2+=∴⎩⎨⎧==∴⎩⎨⎧==⇒⎪⎩⎪⎨⎧+=+=∑∑∑a a a a 代入方程组:(2) ⎪⎩⎪⎨⎧+==+=⇒⎪⎪⎩⎪⎪⎨⎧++=++=++=∑∑∑∑∑∑∑∑∑∑∑708c 6010095460b 727260c 914673 tc t b t y t t c t b t ty t c t b N y 4322322a a a a a 代入方程: 2c 10.2t121.2t 1562.5y 2.102.1211562.5 ++=∴⎪⎩⎪⎨⎧===∴c b a (3)当t=5,即2004年基建投资额y c =1562.5+121.2×5+10.2×25=2423.5(万元) 当t=6,即2005年基建投资额y c =1562.5+121.2×6+10.2×36=2656.9(万元)(1) 因为本题资料各年环比增长速度大体相同,所以发展的基本趋势接近于指数曲线型。
(2)代入方程组: t(1.21)36.3c y 21.13.36 08192.0lg 55982.1lg 10B 0.81925A 7.7991 2tB t A ty'tB NA y'⨯=∴⎩⎨⎧==⎩⎨⎧====∴⎩⎨⎧==⇒⎪⎩⎪⎨⎧∑+∑=∑∑+=∑b a b B a A 查反对数表得 (3)当t=3时,即该地区2004年底人口数为: lgy c =lga+tlgb=1.55982+3×0.08192=1.80558 ∴y c =63.9(万人)11. 见教材P412-413(2)当t=19,即2004年第一季度销售量估计值为: y c =7.42+0.85×19=23.57(千件)23.57×0.5088(第一季度的季节比率)=11.99(千件)同样方法,得到2004年第二、三、四各季度的销售量估计值依次为:18.78千件、30.44千件、39.64千件。
13.(1) 2010年达到翻一番的目标,即人均绿化面积为:4平方米×2=8平方米,根据已知条件,得:%18.1070718.124/8/101000201020=====n G a a X即每年的平均发展速度=107.18%。
(2) 若在2008年就达到翻一番目标,则每年的平均增长速度为:%05.9%100%05.109%1002%1004/8%100/%1008800202008=-=-=-=-=-n G aa X即每年的平均增长数度=9.05%。
(3) 若2001年和2002年的平均发展速度都为110%,那么后8年的平均发展速度为: 2820012002201020102002G 200020012000G a a aa /a (1.10)(X )2a a a X 1.06483106.48%⨯⨯=⨯======进一步整理得到:即后8年每年的平均发展速度=106.48%(4) 假定2007年的人均绿化面积为人均6.6平方米,以2000年为基期,那么其平均年增长量是:)(37143.076.2746.6)(4 )(6.62000200720002007平方米则平均年增长量平方米;平方米==-=-===n a a a a 14.(2)第三季度销售值=24÷4×115%=6.9(万元) 第四季度销售值=24÷4×95%=5.7(万元)(3)第三季度比第一季度销售值的变动比率为: %。
实际下降17.2%83.973573.42626.4%8.914%3.1175∴==÷ (4) )20(2216y 2t 2003万元时,当年=⨯+==即经季节性调整后的2003年第一季度的估计值=20÷4×90%=4.5(万元) 15. 见教材P416第五章 统计指数1. (1)%04.11315.13.1q q %76.1118.66.7p p%83.9520.115.1q q %67.10682.192.1p p%77.12346.452.5q q %91.1102.244.2p p%1040.52.5q q %33.13330.040.0p p 0101010101010101====================水产品个体销售量指数水产品个体物价鲜蛋个体销售量指数鲜蛋个体物价猪肉个体销售量指数猪肉个体物价蔬菜个体销售量指数蔬菜个体物价 (2)%60.115292.21614.24k %28.112614.246368.27k 0001q 1011p ==∑∑===∑∑=p q p q q p q p(3))(0228.3614.246368.2704.13.1)8.66.7()(138.015.1)80.192.1()(3248.152.5)2.244.2()(52.02.5)30.040.0()(111101101101101元=-=-=⨯-=⨯-=⨯-=⨯-=⨯-=⨯-=⨯-=⨯-∑∑qp q p q p p q p p q p p q p p2.)(02.5098.699750k 1%15.107%160.108120%670.106330%270.107300120330300 k 1k 11111111111011p 万元=-=-=++++==⋅=∑∑∑∑∑∑p q p q pq p q p qp p pq3.)(8.66019488.2608qkp %92.13319488.2608700848400700%140848%110400%174q kp k 000000q 万元=-=-==++⨯+⨯+⨯==∑∑∑∑q p q p4. 列计算表如下:万元万元万元%%指数体系:(万元)产量指数(万元)(万元)总产值由于价格变化而增加的7235107 %6.10990.10497.114 357157501%90.1047157501107715822%97.11471582272750822%6.10975082200110011001100111011+=⨯==-=-===-=-===-==∑∑∑∑∑∑∑∑∑∑q p q p K qp qp K q p q p q p q p qp q p5. 列表计算如下:)(7.125 2000 2400 250 5)(3.000 3000 2600 000 6)(55.314 2000 2100 629 411011110000元元元=========∑∑∑∑∑∑f f Q Q ff Q Q f Q n元元元指数体系:元-结构变动影响指数:元-固定构成指数:元198.15487.6685.75 108.56%119.41%129.63% )(15.198%56.10855.314 27.125 2 )(6.487%41.1197.125 23.000 3 )(75.685%63.12955.314 23.000 30n 0n n 1n 10101+=⨯========-==Q Q Q Q Q Q Q Q Q Q Q Q6.%56.111 %5%6.112%7%3.128%8%108%3%2.105 %3%98%10%7.109%16%4.116%48%63.109k %63.109 %14%1.108%13%3.102%48%08.117%25%100%100%2%100%98%100%08.117 %7%103%5%6.98%21%2.140%38%7.122 %4%7.101%17%7.96%2%100%6%1.106kw p =⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯==⨯+⨯+⨯+⨯==⨯+⨯==⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯==∑总指数食品类物价指数粮食类指数副食品指数7. (1)参见教材P209-210的计算方法(2)%24.10365.067,368000,380%6.98000,10%5.102000,40%4.105000,30%4.108000,50%38.102000,30%35.101000,10%36.99000,15%23.101000,35%23.104000,20%11.105000,50%41.101000,90000,10000,40000,30000,50000,30000,10000,15000,35000,20000,50000,90k 1k 1111p ==++++++++++++++++++++=∑∑=q p q p 总指数8. 产量总指数(万元)-加:由于价格变化使产值增价格总指数万元产值:由于产量增加而增加的75.01%29.10025.26126225.26115032801)(78.19%19.10847.24125.261 %5.10826298.015000.13205.1801111111110001000111110001===++===-==÷++=÷==∑∑∑∑∑∑∑∑∑∑∑∑q p k q p qp k q p K p q p q q p q p q p q p k p q p q K pppq9. 商品销售量指数%65.11160.8602.9 %10329.189.989.9011100110001==÷-=÷==∑∑∑∑∑∑p q p q p q p q p q p q K q由于销售量变动使商品销售额增加 9.602-8.60=1.002(亿元)10. (1)销售量指数%10335%103350001000010=⨯=⨯==q p q q q p q p q p K q(2)价格指数%96.110%10335401011=⨯==q p q p K p(3)销售量变动对销售额的影响)(05.1)1%103(35)(010万元=-⨯=-q q p11. 零售物价指数%735.109 %25%118%35%5.108%29%104%11%110 )(=⨯+⨯+⨯+⨯=⋅=∑∑WWk K p p 12.(1) 以t 代表工人劳动生产率,q 代表工人人数149.251.8200 ; 129.48%111.56%144.44% )(2.149714)640450714650()q t -(t %130640450714650t t )(8.51640450)640714()t q -(q %56.111640714q q )(200450650q t q t %44.144450650q t q t 101010010100110011+=⨯=∴=⨯-==÷==⨯-====-=-===万元绝对值产值的影响:程度工人劳动生产率变动对万元绝对值度动对产值变动影响:程其中:生产工人人数变万元总产值指数(2) 以m 代表产值,q 代表职工数,t 代表生产工人人数)200(450-650)m -(m %44.144450650m m 0101万元产值指数=====其中:①职工人数变动影响:)22.4(t mq t )q (q %105800840q q 00000101的产值职工人数比重基期平均每个生产工人基期生产工人占万元↓↓=⨯⨯-==② 生产工人占职工人数比重变动影响:值基期每个生产工人的产万元 )29.4(640450)800640840714(840t m )q t q t (q 106.25%800640840714q t q t 00001110011↓=⨯-⨯=⨯-⨯=÷=÷ ③ 由于工人劳动生产率变动对总产值的影响: 149.9429.422.4200 ; 130%106.25%105%144.44% 149.94)640450714650(840714840)t m t m (q t q 130%640450714650t m t m 00111110011++=⨯⨯=∴=-⨯⨯=-⨯⨯=÷=÷13.)33.76(-3.65-97.3559.94 96.7699.65110.28106.33 )(76.336.104084.1006p m q p m q %76.966.104084.1006p m q p m q )(65.325.10446.1040p m q p m q %65.9925.10446.1040p m q p m q )(35.979.94625.1044p m q p m q %28.1109.94625.1044p m q p m q)(94.599.94684.1006p m q p m q %33.1069.94684.1006p m q p m q 01111111111001111110011000111000111元=%%%%=元绝对数:响:每吨原材料价格变动影元绝对数:动影响:每吨产品原材料消耗变元绝对数:产量变动影响:元绝对数:原材料费用总额指数⨯⨯∴-=-=-==-=-=-===-=-===-=-===∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑14.)(57.5673.43930.496f fx f f x %86.11273.43930.496ff x f f x )(37.1393.48230.496f f x f f x %77.10293.48230.496f f x f f x x x 11011111011100011100011101元固定构成指数元=-=⋅-⋅==⋅⋅==-=⋅-⋅==⋅⋅=∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑43.2-56.5713.37 91.05%112.86%102.77% )(2.4393.48273.439f f x f f x %05.9193.48273.439f f x f f x 000110000110=⨯=∴-=-=⋅-⋅==⋅⋅=∑∑∑∑∑∑∑∑元结构影响指数15. 各期的原材料费用总额计算如下:)(1.9899 1519.046401.2461548.01204005.1120)(9998 152.04640246155.0120401.1120)(8470 152.04040240155.0100401.1100)(48.11476 2219.046451.2462248.01204505.112001101000111元元元元=⨯⨯+⨯⨯+⨯⨯+⨯⨯==⨯⨯+⨯⨯+⨯⨯+⨯⨯==⨯⨯+⨯⨯+⨯⨯+⨯⨯==⨯⨯+⨯⨯+⨯⨯+⨯⨯=∑∑∑∑PM Q P MQ P MQ P M Q%93.1151.989948.11476%01.9999981.9899%04.11884709998%50.135847048.1147601111100101100001000111============∑∑∑∑∑∑∑∑P M Q P M Q P M Q P M Q P M Q P M Q PM Q P M Q 价格总指数单耗总指数产品产量指数原材料费用总额指数因而,有)(9.9899981.989999.0)(15288470999804.18)(48.3006847048.114765.3500111000001000111元%,绝对额变动了告期比基期降低了每吨产品材料消耗量报元%,绝对额增加了了产量报告期比基期增长元%,绝对额增加了期比基期多支出即原材料费用总额报告-=-=-=-=-=-=-∑∑∑∑∑∑P MQ P M Q P M Q P MQ P MQ P M Q38.1577)9.98(152848.3006 )1.989948.11476()99981.9899()84709998(847048.11476%93.115%01.99%04.11850.135)(38.15771.989948.1147693.15011111+-+=-+-+-=-⨯⨯==-=-∑∑绝对数:%相对数:数分析的指数体系为所以相对数和绝对数因元%,绝对额增加了增长了材料价格报告期比基期PM Q P M Q第六章 抽样调查1. (1)N=5000,000 n=500819339991841747233 4725002155472000500050015002155121554926X 222.X . ..t μ Δt .. μ.),(.)N n (n σμ. σ.fxfx x x ≤≤=⨯======-⨯=-===∑∑=(2) 0.68%0.12% 0.00680.00120.00280.0040.00280.0040.00280.00281t μΔ0.002850099.6%0.4%μ 0.0028)5000,000500(150099.6%0.4%μ6994040140140≤≤≤≤+≤≤-=⨯===⨯==-⨯=⨯=⨯==P P P %.%.%).-(%.-p)% p(.p p p 即2. (1)%9892% 3%95%3%-95% %303.0015.02 2t %45.95)(015.020005.095.0)1(%95200190≤≤+≤≤∆+≤≤∆-==⨯=⋅=∆===⨯=-===P P p P p t t F n p p P pp p p p μμ由(2)%82% 3%5%3%-5% %303.0015.02 2t %45.95)(015.020095.005.0)1(%505.020010≤≤+≤≤∆+≤≤∆-==⨯=⋅=∆===⨯=-====P P p P p t t F n p p P p p p p p μμ由3. (1)%5.74.5% %5.16%1.5%-6% %5.1%5.11 1 t %27.68)(%5.1015.025094.006.0)1(%606.025015≤≤+≤≤∆+≤≤∆-=⨯=⋅=∆====⨯=-====P P p P p t t F n p p P pp p p p μμ由(2)%P % %%P %%- Δp P Δ p %%.μt t F p p p p 9336363512 2 t %45.95)(≤≤+≤≤+≤≤-=⨯=⋅=∆==由4. (1))88(0.0152%98%10.01962%)-(12%) -(1 0.015 12块=⨯⨯==⨯==∆=n p p t (2) )(220.032%98%2块=⨯=n5.34.91831.7421.5880.7942t μΔ 0.794900566.7μ566.7300600300306002033.33300600300366003222222≤≤=⨯======+⨯+⨯=∑∑==+⨯+⨯=∑∑=X x n x f f σf Xf X ii i σσ6. pp N 1000,000 n 1000 p 2% t3000μ)0.004420002%0.004423P 2%0.0044230.68%P3.32%======-⨯≤≤+⨯≤≤ 7.98.83%F (t ) 5034925160794731705160 3.79471012 51795160 10 12 170 22===⨯=-===≤≤===查表得:已知:. t ..-t .t μx n σ μ.x . n σx x 8.2112222222222xf 32000x 800 σ141.42 σ20000f40xf 39500x 658.33 σ123.88 σ15347.22f60200004015347.2260σ17208.334060Nt σ100,000217208.33n N Δt σ100,0001∑=====∑∑=====∑⨯+⨯==+⋅⨯⨯==⋅+⋅⨯元元22304.99305(5217208.33==+⨯人)(1) 随机抽样:222222222xf 71500x 715f 100σ22025Nt σ100,000222025n 390.02391(N Δt σ100,00015222025====⋅⨯⨯====⋅+⋅⨯+⨯∑∑人)(2)29999150537011501153912202522=====⨯=⋅==...μΔt .n σt t μΔx9..n )x (x σ)x , x , x , x , x (m .r x x ri i673232596445403323188315454033231821215432121=++=∑-=======++++=∑==423918246278132813110031001544811051051610211161025831458314083133831238311844867104566734146732511 671043169114456310046467343364641431612522222221221222525242423232222.X ...t μΔ... N n N n R r R r δμ.).().().().().( r)x x (δ.)...(σr .n )x (x σn )x (x σ.n )x (x σn )x (x σx x ri i r i i ≤≤=⨯===--⨯+--⨯=--⋅+--⋅==-+-+-+-+-=∑-=∑=++++⨯=⋅==++=∑-==++=∑-==++=∑-==++=∑-===σσ均误差为:两个阶段抽样的抽样平各群群间方差::各群群间方差的平均数10.(7849 32601150326011503260163021630984000270501144024144024649101)(6491024578415)(115024612022122千克千克即千克千克X ...X .-. ..t μΔ....)R r R (r δμ..rr )x (x δ..rxr x x x x x ri i x +≤≤∴=⨯===⨯=--⨯=--===∑∑-===∑∑== %.P %.%.%.P %.%-. %.%.t μΔ%...μ%..rrp)(p δ%.r r p p p p p ri i p i 05980797 494056974940569749402470224709840024000153001530240036770569724122≤≤+≤≤∴=⨯===⨯===∑∑-===∑∑==即11. (1)小时。
