第3章位置与坐标单元复习
北师大版八年级上册第三章位置与坐标复习教案

举例:线段的斜率可以通过两点坐标计算得出。
(4)二元一次方程与坐标平面内点的关联:掌握二元一次方程在坐标平面内表示的直线特点。
举例:方程y=2x+1表示的直线在坐标平面内的斜率为2,截距为1。
2.教学难点
(1)坐标平面内点的特征及其坐标表示:难点在于灵活运用坐标特点解决实际问题,如判断点所在象限、计算线段长度等。
3.成果展示:每个小组将向全班展示他们的讨论成果和实验操作的结果。
(四)学生小组讨论(用时10分钟)
1.讨论主题:学生将围绕“坐标在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法,并与其他小组成员进行交流。
2.引导与启发:在讨论过程中,我将作为一个引导者,帮助学生发现问题、分析问题并解决问题。我会提出一些开放性的问题来启发他们的思考。
(二)新课讲授(用时10分钟)
1.理论介绍:首先,我们要复习坐标平面内点的特征及其坐标表示。坐标是描述点在平面中位置的重要工具,它可以帮助我们准确地找到点的位置,并描述点之间的相对关系。
2.案例分析:接下来,我们通过一个具体的案例来回顾坐标在实际中的应用。例如,如何通过坐标计算两点之间的距离,以及如何利用坐标解决几何问题。
在总结回顾环节,我觉得可以增加一个学生自我反思的环节,让他们在课后思考今天学到的内容,以及还有哪些疑问和困惑。这样不仅能够促进学生对知识的内化,还能为我提供更多教学反馈,以便我及时调整教学方法和策略。
举例:已知直线y=2x+1和直线y=-0.5x+3,求两直线的交点坐标。
(4)二元一次方程与坐标平面内点的关联:难点在于将实际问题转化为数学模型,运用二元一次方程解决几何问题。
北师大版八年级数学上册第三章《位置与坐标》章末复习题含答案解析 (13)
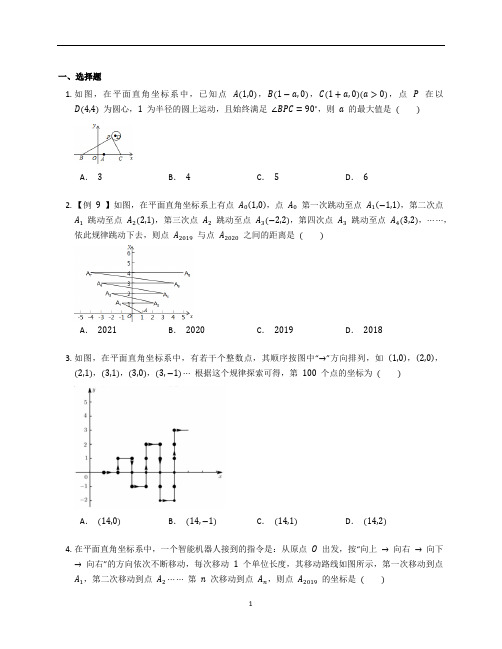
一、选择题1.如图,在平面直角坐标系中,已知点A(1,0),B(1−a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90∘,则a的最大值是( )A.3B.4C.5D.62.【例9】如图,在平面直角坐标系上有点A0(1,0),点A0第一次跳动至点A1(−1,1),第二次点A1跳动至点A2(2,1),第三次点A2跳动至点A3(−2,2),第四次点A3跳动至点A4(3,2),⋯⋯,依此规律跳动下去,则点A2019与点A2020之间的距离是( )A.2021B.2020C.2019D.20183.如图,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,1),(3,0),(3,−1)⋯根据这个规律探索可得,第100个点的坐标为( )A.(14,0)B.(14,−1)C.(14,1)D.(14,2)4.在平面直角坐标系中,一个智能机器人接到的指令是:从原点O出发,按“向上→向右→向下→向右”的方向依次不断移动,每次移动1个单位长度,其移动路线如图所示,第一次移动到点A1,第二次移动到点A2⋯⋯第n次移动到点A n,则点A2019的坐标是( )A.(1010,0)B.(1010,1)C.(1009,0)D.(1009,1)5.已知点A(m,4)与点B(3,n)关于x轴对称,那么(m+n)2017的值为( )A.−1B.1C.−72017D.720176.在一单位为1的方格纸上,有一列点A1,A2,A3,⋯,A n,⋯,(其中n为正整数)均为网格上的格点,按如图所示规律排列,点A1(2,0),A2(1,−1),A3(0,0),A4(2,2),⋯⋯,则A2017的坐标为( )A.(1008,0)B.(1010,0)C.(−1008,0)D.(−1006,0)7.在平面直角坐标系中,点P(−2,x2+1)所在的象限是( )A.第一象限B.第二象限C.第三象限D.第四象限8.如图,点A,B在反比例函数y=1x (x>0)的图象上,点C,D在反比例函数y=kx(k>0)的图象上,AC∥BD∥y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为32,则k的值为( )A.4B.3C.2D.329.如果点P在直线y=1上,点A的坐标是(−1,0),点B的坐标是(3,0),那么三角形ABP的面积( )A.等于2B.大于2C.小于2D.无法确定10.如图,在平面直角坐标系xOy中,已知AD平分∠OAB,DB⊥AB,BC∥OA,点D的坐标为D(0,2),点B的横坐标为1,则点C的坐标是( )A.(0,√3+2)B.(0,2)C.(0,√5)D.(0,5)二、填空题11.如图,△ABC是等腰直角三角形,∠BAC=90∘.若A(2,0),B(0,4),则点C的坐标为.12.一个电子跳蚤在数轴上做跳跃运动.第一次从原点O起跳,落点为A1,点A1表示的数为1;第二次从点A1起跳,落点为OA1的中点A2;第三次从A2点起跳,落点为OA2的中点A3;如此跳跃下去⋯⋯最后落点为OA2019的中点A2020.则点A2020表示的数为.13.如图,图形①②③均是以P0为圆心,1个单位长度为半径的扇形,将图形①②③分别沿东北,正南,西北方向同时平移,每次移动一个单位长度,第一次移动后图形①②③的圆心依次为P1,P2,P3,第二次移动后图形①②③的圆心依次为P4,P5,P6,⋯,依此规律,P0P2018=个单位长度.14.如图,在直角坐标系中,点A,B的坐标分别为(2,4)和(3,0),点C是y轴上的一个动点,且A,B,C三点不在同一条直线上,在运动的过程中,当△ABC是以AB为底的等腰三角形时,OC=.15.平面直角坐标系中,与x轴平行的直线上的点的坐标特征是,与y轴平行的直线上的点的坐标特征是.16.如图,在直角坐标系中,A(1,3),B(2,0),第一次将△AOB变换成△OA1B1,A1(2,3),B1(4,0);第二次将△OA1B1变换成△OA2B2,A2(4,3),B2(8,0),第三次将△OA2B2变换成△OA3B3,则B2016的横坐标为.17.点P(2,−6)和Q(a,6)的连线垂直于x轴,则a的值为.三、解答题18.如图所示的正方形网格中,每个小正方形的边长均为1,格点三角形ABC的顶点A,C的坐标分别为(−4,5),(−1,3).(1) 请在如图所示的网格平面内作出平面直角坐标系,并计算△ABC的面积;(2) 点P在x轴上,且△OBP的面积等于△ABC面积的一半,则点P的坐标是.19.如图,在平面直角坐标系内,试写出△ABC各顶点的坐标,并求出△ABC的面积.20.如图是轰炸机机群的一个飞行队形,如果最后两架轰炸机的坐标分别为A(−2,1),B(−2,−3).(1) 试根据点A,B的坐标建立恰当的平面直角坐标系;(2) 写出C,D,E的坐标.21.如图,在平面直角坐标系xOy中,点A(a,0),B(c,c),C(0,c),且满足(a+8)2+√c+4=0,P点从A点出发沿x轴正方向以每秒2个单位长度的速度匀速移动,Q点从O点出发沿y 轴负方向以每秒1个单位长度的速度匀速移动.(1) 直接写出点B的坐标,AO和BC的位置关系是什么?(2) 当P,Q分别是线段AO,OC上时,连接PB,QB,使S△PAB=2S△QBC,求出点P的坐标.(3) 在P,Q的运动过程中,当∠CBQ=30∘时,请探究∠OPQ和∠PQB的数量关系,并说明理由.22.如图,在平面直角坐标系中,四边形ABCD的顶点坐标分别是A(4,7),B(1,5).C(3,2),D(5,4).(1) 请在网格中作出四边形ABCD关于y轴对称的四边形AʹBʹCʹDʹ(其中A,B,C,D的对应点分别为Aʹ,Bʹ,Cʹ,Dʹ),并写出Bʹ,Cʹ的坐标;(2) 求四边形AʹBʹCʹDʹ的面积(已知图中网格的每个小正方形的边长为1个单位长度).23.在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).(1) 若△ABC和△A1B1C1关于原点O成中心对称图形,画出△A1B1C1.(2) 将△ABC绕着点A顺时针旋转90∘,画出旋转后得到的△AB2C2.(3) 在x轴上存在一点P,满足点P到点B1与点C1距离之和最小,请直接写出PB1+PC1的最小值为.24.如图,在8×8的网格中,网格线的公共点称为格点.已知格点A(1,1),B(6,1),如图所示线段AC上存在另外一个格点.(1) 建立平面直角坐标系,并标注x轴,y轴,原点.(2) 直接写出线段AC经过的另外一个格点的坐标:.(3) 用无刻度的直尺画图,运用所学的三角形全等的知识画出经过格点D的射线BD,使BD⊥AC(保留画图痕迹),并直接写出点D的坐标:.25.如图,已知∠MON=90∘,OT是∠MON的平分线,A是射线OM上一点,OA=8cm.动点P从点A出发,以1cm/s的速度沿AO水平向左作匀速运动,与此同时,动点Q从点O出发,也以1cm/s的速度沿ON竖直向上作匀速运动.连接PQ,交OT于点B.经过O,P,Q三点作圆,交OT于点C,连接PC,QC.设运动时间为t(s),其中0<t<8.(1) 求OP+OQ的值;(2) 是否存在实数t,使得线段OB的长度最大?若存在,求出t的值;若不存在,说明理由.(3) 求四边形OPCQ的面积.答案一、选择题1. 【答案】D【解析】∵A(1,0),B(1−a,0),C(1+a,0)(a>0),∴AB=1−(1−a)=a,CA=a+1−1=a,∴AB=AC,∵∠BPC=90∘,∴PA=AB=AC=a,如图延长AD交⊙D于Pʹ,此时APʹ最大,∵A(1,0),D(4,4),∴AD=5,∴APʹ=5+1=6,∴a的最大值为6.【知识点】平面直角坐标系及点的坐标2. 【答案】A【解析】观察发现,第2次跳动至点的坐标是(2,1),第4次跳动至点的坐标是(3,2),第6次跳动至点的坐标是(4,3),第8次跳动至点的坐标是(5,4),⋯第2n次跳动至点的坐标是(n+1,n),则第2020次跳动至点的坐标是(1011,1010),第2019次跳动至点A2017的坐标是(−1010,1010).∵点A2019与点A2020的纵坐标相等,∴点A2019与点A2020之间的距离=1011−(−1010)=2021.故选:A.【知识点】平面直角坐标系及点的坐标3. 【答案】D【解析】由图可知,横坐标是1的点共有1个,横坐标是2的点共有2个,横坐标是3的点共有3个,横坐标是4的点共有4个,⋯,横坐标是n的点共有n个,,1+2+3+⋯+n=n(n+1)2=91,当n=13时,13×(13+1)2=105,当n=14时,14×(14+1)2∴第100个点的横坐标是14,∵100−91=9,∴第100个点是横坐标为14的点中的第9个点,=7个点的纵坐标是0,∵第142∴第9个点的纵坐标是2,∴第100个点的坐标是(14,2).【知识点】平面直角坐标系及点的坐标4. 【答案】C【知识点】平面直角坐标系及点的坐标5. 【答案】A【解析】∵A(m,4)与B(3,n)关于x轴对称,∴m=3,n=−4,∴m+n=−1,∴(m+n)2017=(−1)2017=−1.【知识点】坐标平面内图形轴对称变换6. 【答案】B【解析】观察,发现:A1(2,0),A5(4,0),A9(6,0),⋯,∴A4n+1(2n+2,0)(n为自然数).∵2017=504×4+1,∴A2017的坐标为(1010,0).【知识点】平面直角坐标系及点的坐标7. 【答案】B【解析】∵x2≥0,∴x2+1≥1,∴点P(−2,x2+1)在第二象限.【知识点】平面直角坐标系及点的坐标8. 【答案】B【解析】因为点A,B在反比例函数y=1x(x>0)的图象上,点A,B的横坐标分别为1,2,所以点A的坐标为(1,1),点B的坐标为(2,12),因为AC∥BD∥y轴,所以点C,D的横坐标分别为1,2,因为点C,D在反比例函数y=kx(x>0)的图象上,所以点C的坐标为(1,k),点D的坐标为(2,k2),所以AC=k−1,BD=k2−12=k−12,所以S△OAC=12(k−1)×1=k−12,S△ABD=12⋅k−12×(2−1)=k−14,因为△OAC与△ABD的面积之和为32,所以k−12+k−14=32,解得:k=3.故选B.【知识点】反比例函数图像上的点的坐标特征、坐标平面内图形的面积9. 【答案】A【知识点】坐标平面内图形的面积10. 【答案】A【解析】∵点D的坐标为D(0,2),∴OD=2,∵AD平分∠OAB,DB⊥AB,BC∥OA,∴BD=OD=2,∠BCD=90∘,∵点B的横坐标为1,∴BC=1,在Rt△BCD中,∵CD2+BC2=BD2,即CD2+12=22,解得CD=√3,∴OC=OD+CD=√3+2,∴C(0,√3+2).【知识点】平面直角坐标系及点的坐标二、填空题11. 【答案】(−2,−2)【解析】过B,C两点分别作过A点且平行于y轴的直线的垂线,垂足为E,D,∵A(2,0),B(0,4),∴OA=BE=2,OB=AE=4,∴AB=AC,∵∠BAE+∠CAD=90∘,∠CAD+∠ACD=90∘,∴∠BAE=∠ACD,∵∠BEA=∠ADC=90∘,△AEB≌△CDA(AAS).∴CD=AE=4,AD=BE=2,∴C(−2,−2).故答案为:(−2,−2).【知识点】平面直角坐标系及点的坐标、角角边12. 【答案】122019【解析】由题意得:点A1表示的数为1=120,点A2表示的数为12OA1=12=121,点A3表示的数为12OA2=14=122,点A4表示的数为12OA3=18=12,归纳类推得:点A n表示的数为12n−1(n为正整数),则点A2020表示的数为122020−1=122019.【知识点】平面直角坐标系及点的坐标13. 【答案】673【解析】根据P0P1=1,P0P2=1,P0P3=1,P0P4=2,P0P5=2,P0P6=2,P0P7=3,P0P8= 3,P0P9=3,⋯⋯,可知每移动一次,圆心离中心的距离增加1个单位,依据2018= 3×672+2,可得点P2018在正南方向上,∴P0P2018=672+1=673.【知识点】平面直角坐标系及点的坐标14. 【答案】118【解析】设C点坐标为(0,a),当△ABC是以AB为底的等腰三角形时,BC=AC,平方得BC2=AC2,22+(4−a)2=32+a2,化简得8a=11,,解得a=118故OC=11.8【知识点】平面直角坐标系及点的坐标15. 【答案】纵坐标相同且不为0,横坐标不同;横坐标相同且不为0,纵坐标不同【知识点】平面直角坐标系及点的坐标16. 【答案】22017【解析】∵A(1,3),A1(2,3),A2(4,3),A3(8,3),2=21,4=22,8=23,∴A n(2n,3),∵B(2,0),B1(4,0),B2(8,0),B3(16,0),2=21,4=22,8=23,16=24,∴B n(2n+1,0),∴B2016的横坐标为22017.【知识点】平面直角坐标系及点的坐标、用代数式表示规律17. 【答案】2【解析】∵点P(2,−6)和Q(a,6)的连线垂直于x轴,∴P,Q关于x轴对称,∴a的值为:2.故答案为:2.【知识点】坐标平面内图形轴对称变换三、解答题18. 【答案】(1) 图略,面积为4.(2) (4,0)或(−4,0).【知识点】坐标平面内图形的面积19. 【答案】A(0,2);B(2,0);C(3,3);4.【知识点】平面直角坐标系及点的坐标、坐标平面内图形的面积20. 【答案】(1)(2) C(2,−1),D(0,−2),E(0,0)【知识点】坐标方法的应用21. 【答案】(1) (−4,−4),BC∥AO.(2) 过B点作BE⊥AO于E,设时间经过t秒,S△PAB=2S△QBC,则AP=2t,OQ=t,∴CQ=4−t,∵BE=4,BC=4,∴S△APB=12AP⋅BE=12×2t×4=4t,S△BCQ=12CQ⋅BC=12×(4−t)×4=8−2t,∵S△APB=2S△BCQ,∴4t=2(8−2t),解得t=2,∴AP=2t=4,∴OP=OA−AP=4,∴点P的坐标为(−4,0).(3) ∠PQB=∠OPQ+30∘或∠BQP+∠OPQ=150∘.①当点Q在点C的上方时,过Q点作QH∥AO,如图2所示,∴∠OPQ=∠PQH,∵BC∥AO,QH∥AO,∴QH∥BC,∴∠HQB=∠CBQ=30∘,∴∠OPQ+∠CBQ=∠PQH+∠BQH,∴∠PQB=∠OPQ+∠CBQ,即∠PQB=∠OPQ+30∘;②当点Q在点C的下方时;过Q点作HJ∥AO,如图3所示,∴∠OPQ=∠PQJ,∵BC∥AO,QH∥AO,∴QH∥BC,∴∠HQB=∠CBQ=30∘,∴∠HQB+∠BQP+∠PQJ=180∘,∴30∘+∠BQP+∠OPQ=180∘,即∠BQP+∠OPQ=150∘.综上所述,∠PQB=∠OPQ+30∘或∠BQP+∠OPQ=150∘.【解析】(1) ∵(a+8)2+√c+4=0,∴a+8=0,c+4=0,解得,a=−8,c=−4,则点B的坐标为(−4,−4),∵点B的坐标为(−4,−4),点C的坐标为(0,−4),∴BC∥AO.【知识点】平面直角坐标系及点的坐标、坐标平面内图形的面积、内错角相等、平行公理的推论22. 【答案】(1) 如图所示,四边形AʹBʹCʹDʹ即为所求;Bʹ(−1,5),Cʹ(−3,2).(2) 四边形AʹBʹCʹDʹ的面积为:5×4−12×1×3−12×2×2−12×2×3−12×2×3=10.5.【知识点】坐标平面内图形的面积、坐标平面内图形轴对称变换23. 【答案】(1) 略(2) 略(3) √26【知识点】坐标平面内图形轴对称变换、找动点,使距离之和最小、坐标平面内图形的旋转变换24. 【答案】(1) 建立的坐标系如图所示:(2) (5,4)(3) D(3,5),△FMH≌△HNA⇒FH⊥AH,平行四边行FHBD⇒DB∥FH,故DB⊥AC.【知识点】两组对边分别相等、建立坐标系,描述物体的位置、勾股定理、平面直角坐标系及点的坐标25. 【答案】(1) 由题意可得,OP=8−t,OQ=t,∴OP+OQ=8−t+t=8(cm).(2) 当t=4时,线段OB的长度最大.如图,过点B作BD⊥OP,垂足为D,则BD∥OQ.∵OT平分∠MON,∴∠BOD=∠OBD=45∘,∴BD=OD,OB=√2BD.设线段BD的长为x,则BD=OD=x,OB=√2BD=√2x,PD=8−t−x,∵BD∥OQ,∴PDOP =BDOQ,∴8−t−x8−t =xt,∴x=8t−t28.∴OB=√2⋅8t−t28=−√28(t−4)2+2√2.当t=4时,线段OB的长度最大,最大为2√2cm.(3) ∵∠POQ=90∘,∴PQ是圆的直径.∴∠PCQ=90∘.∵∠PQC=∠POC=45∘,∴△PCQ是等腰直角三角形.∴S△PCQ=12PC⋅QC=12×√22PQ⋅√22PQ=14PQ2.在Rt△POQ中,PQ2=OP2+OQ2=(8−t)2+t2.∴四边形OPCQ的面积S=S△POQ+S△PCQ=12OP⋅OQ+14PQ2=12t(8−t)+14[(8−t)2+t2]=4t−12t2+12t2+16−4t=16.∴四边形OPCQ的面积为16cm2.【知识点】基本定理、二次函数的最值、坐标平面内图形的面积、圆周角定理推论、线段的和差。
八上第三章《位置与坐标》复习知识点+练习

第三章 位置与坐标知识点一:确定位置在平面内,确定物体的位置一般需要 个数据。
1、在平面内,下列数据不能确定物体位置的是( ) A .3楼5号 B .北偏西40°C .解放路30号D .东经120°,北纬30° 知识点二:平面直角坐标系及有关概念 1.平面直角坐标系在平面内,两条互相垂直且有公共原点的数轴,组成平面直角坐标系。
其中,水平的数轴叫做x 轴或横轴,取向右为正方向;铅直的数轴叫做y 轴或纵轴,取向上为正方向;x 轴和y 轴统称坐标轴。
2.平面直角坐标系的四个象限:第一象限、第二象限、第三象限、第四象限。
[注意]:x 轴和y 轴上的点(坐标轴上的点),不属于任何一个象限。
1、下列各点是第二象限的是( ) A 、(2,3) B 、(-2,-3) C 、(-2,3) D 、(-2,-3)2、在平面直角坐标系中,点(-1,12+m )一定在第_____象限 知识点三: 轴对称与坐标变换关于x 轴、y 轴或原点对称的点的坐标的特征(1)点P 与点p ’关于x 轴对称⇔横坐标相等,纵坐标互为相反数,即点P (x ,y )关于x 轴的对称点为P ’(x ,-y )(2)点P 与点p ’关于y 轴对称⇔纵坐标相等,横坐标互为相反数,即点P (x ,y )关于y 轴的对称点为P ’(-x ,y )(3)点P 与点p ’关于原点对称⇔横、纵坐标都互为相反数,即点P (x ,y )关于原点的对称点为P ’(-x ,-y )1、 在平面直角坐标系中,点A (1,5)关于x 轴对称的点为点B (a ,-5),则a= .2、若+(b+2)2=0,则点M (a ,b )关于y 轴的对称点的坐标为.3.已知点P (﹣3,2),点A 与点P 关于原点对称,则点A 的坐标是 . 知识点四: 点P(x,y)到坐标轴及原点的距离 (1)点P(x,y)到x 轴的距离等于y (2)点P(x,y)到y 轴的距离等于x(3)点P(x,y)到原点的距离等于22y x +1、点P (-4,3)到x 轴的距离是______,到y 轴的距离是_____,到原点的距离是______。
八级数学上册北师大版课件:第三章 位置与坐标 单元复习(共17张PPT)

如图是某公园的景区示意图.
望春亭C(﹣2,﹣1),
∴3a﹣9=3×(﹣1)﹣9=﹣12, (1)请根据此图建立平面直角坐
(1)请根据此图建立平面直角坐
《位置与坐标》单元复习
∴3a﹣9+10﹣2a=0,解得a=﹣1,
10﹣2a=10﹣2×(﹣1)=12, (2)音乐台A(0,4),
(1)填写下列各点的坐标:
A3( , ),
2.点P(m+3,m﹣1)在x轴上,则点P的坐标为( )
(2)写出点A4n的坐标(n是正整数);
所以A4n(2n,0).
1.如图是某地各建筑设施的平面位置示意图,每个小正方形的边长为1(单位:千米).
若点M(3a﹣9,10﹣2a)在第二象限,且点M到x轴与y轴的距离相等,试求点M的坐标.
如图,等腰△ABC中,AB=AC=5,BC=8. 底长为6.建立适当的直角坐
在第二象限,且到x轴,y轴距离相等,
),则“炮”所在位置的坐标是 在第二象限,且到x轴,y轴距离相等,
(2)当n=1时,A4(2,0),
.
标系并写出三个顶点的坐标.
(-3,2)
无论m为何值,点A(m,5﹣2m)不可能在( )
牡丹亭E(3,3).
变式练习
1.如图是某地各建筑设施的平面位置示意图,每个小正方 形的边长为1(单位:千米).
(1)建立适当的坐标系,使码头的坐标为(4,1);
(2)在(1)中所建立的
坐标系内,要在某位置建 一个广场P,使其与码头
的位置关于x轴对称,在
图中描出点P的位置并写 出点P的坐标.
解(1)图略 (2)图略,P(4,-1)
北师大版八年级数学上册第三章位置与坐标 单元复习

八年级数学第三章位置与坐标一、基本知识点:1. 位置确定的方法2. 象限与坐标3. 对称与坐标变化4. 象限与坐标轴上点的特点5.点到坐标轴的距离二、基本方法:1.会建立直角坐标系求点的坐标;2.会通过画图解决问题三、举例【例1】1、点(-3,2)在第()象限;A.一B.二C.三D.四2、若P点在第三象限,到每条坐标轴的距离都是3,则P点的坐标为()A. (3,3)B. (-3,3)C. (-3,-3)D.(3,-3)3、点(-3,4)到原点的距离是()单位长度;A. 3B. 4C. 5D. 74、点P(2a+1,a-1)到x轴的距离是3,则点P的坐标为_______;5、已知点P到x轴和y轴的距离分别是2,3,则点P在第二象限内的坐标为____,点P在第三象限内的坐标为______;6、平面直角坐标系内某图形各点的横坐标不变,纵坐标都乘以-1,所得图形与原图形的关系是关于___________________对称7、在平面直角坐标系中,点A(4,y)在x轴上,点B(x,3)在y轴上,则x =____,y=___;S∆AOB=_______. 〖针对练习〗1、电影院的8排10号用(8、10)表示,那么10排8号可用表示。
2、小刚家位于某住宅楼12层B座,可记为B12;按这种方法小红家住8层A座应记为3、点M(1,2)关于x轴的对称点的坐标为_______;4、一个点在y轴上,距原点6个单位长度,则这个点的坐标是______;5、已知点M(-6,8),它到x轴的距离是___,它到y轴的距离是____;6、若点p(-2a,a-1)在y轴上,则p点的坐标为_______;7、点P关于x轴的对称点P1的坐标是(2,3),则点P关于y轴的对称点P2的坐标是()A.(-2,3)B.(2,-3)C.(-2,-3)D.(3,2)8、若某四边形顶点的横坐标变为原来的相反数,而纵坐标不变,此时图形位置也不变,则这个四边形不是()A. 菱形B.正方形C. 矩形D.直角梯形【例2】1、对于边长为6的正三角形ABC,建立如图的直角坐标系,请写出各个顶点的坐标。
[初中数学+]+第三章位置与坐标章末复习课件+北师大版数学八年级上册+
![[初中数学+]+第三章位置与坐标章末复习课件+北师大版数学八年级上册+](https://img.taocdn.com/s3/m/ae65dde3f021dd36a32d7375a417866fb84ac0cc.png)
个单位,得到点 A2;点 A2 向上平移 2 个单位,再向右
平移 4 个单位,得到点 A3;点 A3 向上平移 4 个单位,
再向右平移 8 个单位,得到点 A4,…,按这个规律平
移得到点 A2020,则点 A2020 的横坐标为 ( )
A. 22019
y
A4
B. 22020−1 C. 22020 D. 22020+1
(2) 若 D (a−3,a+2),且 S三角形ABD =15,求点 D 的坐标.
解:∵ S三角形ABD=15,且 AB=5, ∴ AB 边上的高为 6. ∵ AB 在 x 轴上, ∴ 点 D 到 x 轴的距离是 6, ∴ 点 D 的纵坐标为 6 或 −6. 当 a+2=6 时,a=4,点 D 的坐标为(1,6); 当 a+2=−6 时,a=−8,点 D 的坐标为(−11,−6).
10. 如图,四边形 ABCD 顶点的坐标分别为 A ( − 2,5),
B (−5,−3), C (−2,−4), D (4,−1), 求四边形 ABCD
的面积.
解:如图,连接AC,
∵ 点 A 与点 C 的横坐标相同,
∴ AC//y 轴.
过点 B 作 BE⊥AC 于点 E,
F
E
过点 D 作DF⊥AC 于点 F,
坐标轴
水平的数轴称为 x 轴或横轴, 竖直的数轴称为 y 轴或纵轴
由点的位置确定点的坐标
点的坐标
由点的坐标确定点的位置
“平行于两轴的直线上的点”的坐标特征: (1) 平行于x轴的直线上的点:纵坐标相同; (2)平行于y轴的直线上的点:横坐标相同.
“两坐标轴上的点”的坐标特征: (1)x轴上的点的坐标:纵坐标为0. (2)y轴上的点的坐标:横坐标为0.
北师大版数学八年级上册第三章位置与坐标复习课件

3
2
结果如图.
所得图形与原图形关于y轴对称 -8-7 -6 -5 -4-3 -2 -1
关于y轴对称的点的坐标: 纵坐标相同,横坐标互为 相反数
234 5678
变化前 (3,0) (7,0) (2,2) (3,2) (7,2) (8,2) (5,4) 变化后 (-3,0)(-7,0)(-2,2)(-3,2)(-7,2)(-8,2)(-5,4)
点的坐标为(2,3);若以A点为原点建立直角坐标系(两直角坐标系x轴、
y轴方向一致),则B点的坐标是( A )
y
y
A.(-2,-3) B.(-2,3)
C.(2,-3) D.(2,3) 分析:如图所示
A x
B x
四、典型例题
例3.在平面直角坐标系中,已知点M(m,2m+3). (1)若点M在x轴上,求m的值;
,解决如下问题:
15
14
(3)确定服装区的位置.
13 12
11
解:(3)由于图上标有刻度,可用有序对 10
9
表示位置
8
7
故服装区的位置是(5,7)
6
5
4 3
2
1
.总经理室
.服装区
.入口
.出口
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
【当堂检测】
1.在平面内,下列数据能否确定物体位置;不能的话修改正确.
,每个方格边长为1cm,解决如下问题: 15
北
14
(1)总经理室位于服装区的什么方向?到
13 12
11
.总经理室
服装区的图上距离多少?实际距离是多少?10
1
9
解:(1)如图所示,
八年级数学上册第三章位置与坐标课时练习题及答案

八(上)第三章位置与坐标分节练习题和本章复习题带答案第1节确定位置1、【基础题】下列数据不能确定物体位置的是()★A. 4楼8号B.北偏东30度C.希望路25号D.东经118度、北纬40度2、【基础题】如左下图是某学校的平面示意图:如果用(2:5)表示校门的位置:那么图书馆的位置如何表示?图中(10:5)处表示哪个地点的位置?★3、【基础题】如右上图:雷达探测器测得六个目标A、B、C、D、E、F:目标C、F的位置表示为C(6:120°)、F(5:210°):按照此方法在表示目标A、B、D、E的位置时:其中表示不正确的是()★A.A(5:30°)B.B(2:90°)C.D(4:240°)D.E(3:60°)30方向:距学校1000m处:则学校在小明家的_______. ★4、【综合题】小明家在学校的北偏东○第2节平面直角坐标系5、【基础题】写出左下图中的多边形ABCDEF各个顶点的坐标. ★★★6、【基础题】在右上图的平面直角坐标系中:描出下列各点:A(-5:0):B(1:4):C(3:3):D(1:0):E(3:-3):F(1:-4). ★★★6.1【基础题】在右边的直角坐标系中描出下列各组点:并将各组内的点用线段依次连接起来:并观察这几组点所连的线段合在一起像什么? ★第一组:(0:0)(6:0)(6:7)(0:7)(0:0) 第二组:(1:4)(2:6) 第三组:(4:6)(5:5) 第四组:(2:0)(2:3)(4:3)(4:0) 7、【综合题】如左上图:若点E 的坐标为(-2:1):点F 的坐标为(1:-1):则点G 的坐标为______. ★ 8、【基础题】如右图:对于边长为4的正△ABC :建立适当的直角坐标系:写出各个顶点的坐标. ★ 9、【基础题】在平面直角坐标系中:下面的点在第一象限的是( ) ★ A. (1:2) B. (-2:3) C. (0:0) D. (-3:-2) 【综合题】若023=++-b a :则点M (a :b )在( ) ★ A.第一象限 B.第二象限 C.第三象限 D.第四象限10、【基础题】在平面直角坐标系中:点P (1:2-m )在第四象限:则m 的取值范围是_________. ★10.1【基础题】点),(b a P 是第三象限的点:则( ) ★(A )b a +>0 (B )b a +<0 (C )ab >0 (D )ab <011、【基础题】点P 在第二象限:若该点到x 轴的距离为3:到y 轴的距离为1:则点P 的坐标是______. ★★★11.1【基础题】已知点)68(,-Q :它到x 轴的距离是____:它到y 轴的距离是____:它到原点的距离是_____. ★ 12、【提高题】在平面直角坐标系中:点A 的坐标为(-3:4):点B 的坐标是(-1:-2):点O 为坐标原点:求△AOB 的面积. ☆第3节 轴对称与坐标变化13、【基础题】点M 的坐标是(-3:4):则点M 关于y 轴的对称点的坐标是_______:关于x 轴的对称点的坐标是_______:关于原点的对称点的坐标是_______:点M 到原点的距离是_______. ★★★13.1【综合题】如右图:在直角坐标系中:△AOB 的顶点O 和B 的坐标分别是O (0:0):B (6:0):且∠OAB =90°:AO =AB :则顶点A 关于x 轴的对称点的坐标是 ( ) ★(A )(3:3) (B )(-3:3)(C )(3:-3) (D )(-3:-3)O AB y14、【综合题】△ABC 在平面直角坐标系中的位置如图所示. ★★★ (1)作出△ABC 关于x 轴对称的△A 1B 1C 1:并写出点A 1的坐标: (2)作出将△ABC 绕点O 顺时针旋转180°后的△A 2B 2C 2: (3)求S △ABC .15、【提高题】 在如图所示的直角坐标系中:四边形ABCD 的各个顶点的坐标分别是A (0:0):B (2:5):C (9:8):D (12:0):求出这个四边形的面积. ★本章复习题一、选择题1、一只七星瓢虫自点(-2:4)先水平向右爬行3个单位:然后又竖直向下爬行2个单位:则此时这只七星瓢虫的位置是 ( ) (A )(-5:2) (B )(1:4) (C )(2:1) (D )(1:2)2、若点P 的坐标为)0,(a :且a <0:则点P 位于 ( )(A )x 正半轴 (B )x 负半轴 (C )y 轴正半轴 (D )y 轴负半轴 3、若点P ),(b a 在第四象限:则Q ),1(b a -+在 ( )(A )第一象限 (B )第二象限 (C )第三象限 (D )第四象限4、点M (-2:5)关于x 轴的对称点是N :则线段MN 的长是 ( ) (A )10 (B )4 (C )5 (D )25、如右图:把矩形OABC 放在直角坐标系中:OC 在x 轴上:OA 在y 轴上:且OC=2:OA=4:把矩形OABC 绕着原点顺时针旋转90°得到矩形OA ′B ′C ′:则点B ′的坐标为( ) A 、(2:3) B 、(-2:4) C 、(4:2) D 、(2:-4)二、填空题6、如右下图:Rt △AOB 的斜边长为4:一直角边OB 长为3:则点A 的坐标是_____:点B 的坐标是_____.DCBAyx123459678101112108769543217、如右图:∠OMA =90°:∠AOM =30°:AM =20米:OM =203米:站在O 点观察点A :则点A 的位置可描述为:在北偏东_____度的方向上:距离点O_____米.8、点A )2,(a 和点B ),3(b 关于x 轴对称:则ab =_____.9、将点P (2:1)绕原点O 按顺时针方向旋转90°到点Q :则点Q 的坐标是_____. 10、(2012山东泰安)如左下图:在平面直角坐标系中:有若干个横坐标分别为整数的点:其顺序按图中“→”方向排列:如(1:0):(2:0):(2:1):(1:1):(1:2):(2:2)…根据这个规律:第2012个点的横坐标为 .三、解答题11、 如图:每个小方格都是边长为1的正方形:在平面直角坐标系中.(1)写出图中从原点O 出发:按箭头所指方向先后经过A 、B 、C 、D 、E 多点的坐标: (2)按图中所示规律:标出下一个点F 的位置. 12、(1)在左下的直角坐标系中作△ABC :使点A 、B 、C 的坐标分别为(0:0):(-1:2):(-3:-1): (2)作出△ABC 关于x 轴和y 轴的对称图形.13、在右上的平面直角坐标系中作点A (4:6):B (0:2):C (6:0):并求△ABC 的周长和面积.AOM北A B C DO E x y 11题八(上) 第三章位置与坐标 分节练习答案第1节确定位置 答案 1、【答案】 选B 2、【答案】 图书馆的位置表示为(2:9):图中(10:5)表示旗杆的位置. 3、【答案】 选D 4、【答案】 南偏西○30方向:距小明家1000 m 处.第2节平面直角坐标系 答案 5、【答案】 A (-2:0): B (0:-3): C (3:-3): D (4:0): E (3:3): F (0:3). 6、【答案】略. 6.1【答案】 囧 (注意:右眉毛短一点) 7、【答案】 (1:2) 8、【答案】 略 9、【答案】 选A 9.1【答案】 选 D10、【答案】 2<m 10.1【答案】 选C 11、【答案】 (-1:3) 11.1【答案】 6:8:10. 12、【答案】 △AOB 的面积是5.第3节 轴对称与坐标变化 答案 13、【答案】点M 的坐标是(-3:4):则点M 关于y 轴的对称点的坐标是(3:4):关于x 轴的对称点的坐标是 (-3:-4):关于原点的对称点的坐标是(3:-4)::点M 到原点的距离是5. 13.1【答案】 选C 14、【答案】(1)A 1的坐标是(-2:-3)(2)关于原点对称的点的横、纵坐标都互为相反数. (3)S △ABC 15、【答案】本章复习题 答案 一、选择题 答案 1、【答案】 选D 2、【答案】 选B 3、【答案】 选A 4、【答案】 选A 5、【答案】 选 C 二、填空题 答案6、【答案】 )7,0( (3:0)7、 【答案】 60 408、【答案】 -69、【答案】 (1:-2) 10、【答案】 45 三、解答题11、【答案】 (1)A(1:0):B(1:2):C(-2:2):D(-2: -2):E(3:-2):(2)F (3:4).12、【答案】 略13、【答案】 周长是24104+:面积是16.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章位置与坐标单元复习
一、知识点复习:
1、我们把有顺序的两个数a和b组成的数对,叫做有序实数对,记作(a,b)。
(注意:不能随便调换两个数字的位置) 2、(1)在数轴上确定一个物体的位置需要一个数据。
(2)在平面内确定一个物体的位置一般需要两个数据。
例如:(排,号);(经度,纬度);(方位角,距离);(角度,角度);(3)空间内确定一个物体的位置一般需要三个数据。
3、平面直角坐标系的概念(如下左图)
在平面内,两条_______________且有_________________的数轴组成。
通常,两条数轴分别置于水平位置和铅直位置,取向和向为正方向。
其中水平的数轴称为轴或轴,铅直的数轴称为轴或轴。
横轴和纵轴统称 ,公共的原点O称为直角坐标系的原点。
两条数轴把平面分为四部分,右上部分为第象限,其余按逆时针分别为第二、三、四象限。
特别的,坐标轴上的点任何一个象限内。
4、点的坐标的表示(如右上图)
在平面直角坐标系中,要想表示一个点的位置,就要用它的“坐标”来表示。
如图,对于平面内任意一点P,过点P分别向x轴、y轴作垂线,垂足在x轴、y轴上对应的数a、b分别叫做点P的、;有序数对__________叫做点P的。
5、在平面直角坐标系中,对于平面上任意一点,都有唯一的一个有序实数对(即坐标)与它对应;反过来,对于任意一个有序实数对,都有平面上唯一的一点与它对应。
6、理解熟记以下结论:
(1)各象限内点的横坐标、纵坐标的符号特征是:
第一象限(+,+),第二象限(-,+),第三象限(-,-),第四象限(+,-)。
(2)坐标轴上的点的坐标特征是:
x轴
(即横轴)上的点的纵坐标为零;y轴(即纵轴)上的点的横坐标为零。
原点坐标是(0,0). (3)点P(a,b)到x轴的距离为|b|,到y轴的距离为|a|,到原点的距离为a2?b2。
(4)与坐标轴平行的直线的点的坐标特征是:
与x轴平行的直线的所有点的纵坐标相同;与y轴平行的直线的所有点的横坐标相同。
补充:熟记以下表格内容:
8、点的对称变化规律:
(1)点A(a,b)关于x轴的对称点的坐标为B(a,?b);
(2)点(a,b)关于y轴的对称点的坐标为(?a,b);(3)点(a,b)关于原点的对称点
的坐标为(?a,?b)。
文字描述:
(1)关于x轴对称的两个点的坐标,横坐标相同,纵坐标互为相反数。
(2)关于y轴对称的两个点的坐标,纵坐标相同,横坐标互为相反数。
(3)关于原点对称的两个点的坐标,横坐标互为相反数,纵坐标也互为相反数。
补充:已知点A(x1,y1)与点B(x2,y2)。
(1)若AB//x轴,则x1?x2,y1?y2;(2)若AB//y轴,则x1?x2,y1?y2。
9、求平面直角坐标系中三角形或四边形的面积:
(1)如果是直角三角形,找到该三角形的底和高,再利用三角形的面积公式计算。
(2)如果不是直角三角形,一般可以补成直角梯形或长方形,先计算直角梯形或长方形的面积,再减去多余的三角形的面积即可。
(3)如果是四边形,可以采用割补法进行求解。
1。
