八年级数学矩形、正方形1
初中数学八年级下册苏科版9.4矩形、菱形、正方形教学课件说课稿

为了帮助学生巩固所学知识并提升应用能力,我计划设计以下巩固练习或实践活动:
1.例题讲解:针对矩形、菱形、正方形的性质和判定方法,精选典型例题进行讲解,让学生掌握解题思路。
2.课堂练习:设计具有代表性的练习题,让学生独立完成,及时巩固所学知识。
3.小组竞赛:组织小组间进行几何图形拼图竞赛,激发学生的竞争意识,提高他们的动手操作能力。
3.技术工具:智慧黑板、几何画板等,方便学生实时观察和操作,提高课堂互动性。
这些媒体资源在教学中的作用是:丰富教学形式,提高学生的学习兴趣;增强课堂互动,方便学生实时反馈;直观展示几何图形,降低学习难度。
(三)互动方式
我计划设计以下师生互动和生生互动环节,以促进学生的参与和合作:
1.师生互动:提问、引导、讲解,关注学生的反馈,及时调整教学策略。
1.创设情境:通过引入生活中的实际例子,让学生感受到矩形、菱形、正方形在实际中的应用,提高他们的学习兴趣。
2.合作探究:组织学生进行小组讨论,鼓励他们主动发现问题、解决问题,培养合作交流的习惯。
3.竞赛激励:设置几何图形拼图竞赛,激发学生的竞争意识,提高他们对特殊四边形性质的理解和运用能力。
4.赏识教育:对学生的每一次进步给予充分的肯定和鼓励,增强他们的自信心,提高学习积极性。
1.生活实例引入:展示生活中常见的矩形、菱形、正方形物体,如窗户、红绿灯、魔方等,让学生认识到特殊四边形在生活中的广泛应用。
2.问题驱动:提出问题:“你们知道这些图形有什么特殊之处吗?”引发学生思考,激发他们的好奇心。
3.游戏互动:设计一个简单的几何图形拼图游戏,让学生在游戏中体验矩形、菱形、正方形的性质,自然过渡到新课的学习。
(二)教学反思
在教学过程中,我预见到以下问题或挑战:
八年级数学下册 第章 矩形、菱形与正方形 . 矩形 矩形的判定

图 19-1-3
第四页,共二十二页。
19.1.2
1课时 第
(kèshí)
矩形的判定
证明:连结 AC 交 BD 于点 O,如图所示.
∵四边形 ABCD 是平行四边形, ∴OA=OC,OB=OD. ∵BE=DF,∴OE=OF. 又∵OA=OC, ∴四边形 AECF 是平行四边形. ∵AE⊥EC,∴∠AEC=90°, ∴四边形 AECF 为矩形.
图 19-1-5
第十一页,共二十二页。
19.1.2 第1课时 矩形( 的判定 jǔxíng)
证明:在▱ABCD 中,AD=BC,AB=CD,AB∥CD,
则 BE∥CD.
又∵AB=BE,∴BE=CD,
∴四边形 BECD 为平行四边形,
∴OD=OE,OC=OB.
∵四边形 ABCD 为平行四边形,
∴∠A=∠BCD,即∠A=∠OCD.
∴△ABE≌△CDF.
第八页,共二十二页。
19.1.2 第1课时(kèshí) 矩形的判定
(2)由(1)知△ABE≌△CDF, ∴∠AEB=∠CFD. ∵四边形 ABCD 是平行四边形, ∴AD∥BC,∴∠AEB=∠EBF. ∵AB=DB,BE 平分∠ABD, ∴BE⊥AD,∴∠AEB=∠DEB=90°, 则∠CFD=90°,∴∠BFD=90°, ∴∠DEB=∠EBF=∠BFD=90°, ∴四边形 DFBE 是矩形.
在数学活动课上,老师和同学们判断一个四边形门框是不是矩 形,下面是一个学习小组拟定的四种方案:
A.测量对角线是否互相平分 B.测量两组对边是否分别相等 C.测量对角线是否相等 D.测量其中三个角是否都为直角 这些方案都对吗?
第二十页,共二十二页。
19.1.2
课时 第1
华东师大版八下数学第19章矩形,菱形和正方形19.1《矩形的性质》优秀教学案例

1.生活情境的创设:通过多媒体展示矩形在生活中的应用场景,使学生能够直观地认识到矩形的重要性,增强了学生的学习兴趣和实际应用意识。这种情境创设不仅引发了学生的学习兴趣,还使他们能够更好地理解矩形的性质和应用。
2.问题导向与小组合作:设计富有挑战性的问题,引导学生进行思考和探究,同时组织学生进行小组合作,培养了学生的团队合作意识和沟通能力。这种问题导向和小组合作的方式,使学生在解决问题的过程中提高了自己的能力,同时也培养了他们的合作精神。
在知识与技能方面,我力求使学生掌握矩形的性质,并能运用矩形的性质解决实际问题。通过观察、操作、思考、交流等数学活动,培养学生的空间想象能力和逻辑思维能力。
在过程与方法方面,我注重培养学生的团队合作意识和沟通能力。通过小组合作探究,让学生在解决问题的过程中提高自己的能力,同时培养学生的合作精神。
在情感态度与价值观方面,我力求激发学生的学习兴趣,使他们认识到数学与实际生活的密切联系。树立正确的数学学习观念,培养勇于探究、勇于挑战的精神。
2.学生能够认识到数学与实际生活的密切联系,增强应用数学解决实际问题的意识。
3.学生能够树立正确的数学学习观念,培养勇于探究、勇于挑战的精神。
作为一名特级教师,我深知教学目标的重要性,它不仅关系到学生的学习效果,也关系到学生的成长和发展。因此,在制定教学目标时,我注重将知识与技能、过程与方法、情感态度与价值观三者紧密结合,力求在教学过程中实现学生的全面发展。
3.反思与评价:在教学过程中,我注重引导学生对自己的学习过程进行反思,总结学习矩形性质的方法和技巧。同时,组织学生进行自我评价和课堂评价,关注学生的学习态度、参与程度和成果。这种反思与评价的方式,使学生能够更好地认识自己的学习情况,提高了他们的自我认知能力。
手把手教你判定矩形和正方形,详解教案

一、教案基本信息1. 《手把手教你判定矩形和正方形,详解教案》2. 课时安排:每课时45分钟3. 教学对象:八年级数学4. 教学目标:使学生掌握矩形和正方形的判定方法,提高学生的几何思维能力二、教学内容1. 第一节:矩形的判定1.1 判定一个四边形为矩形的条件1.2 矩形的性质1.3 矩形在实际生活中的应用2. 第二节:正方形的判定2.1 判定一个四边形为正方形的条件2.2 正方形的性质2.3 正方形在实际生活中的应用3. 第三节:矩形和正方形的异同3.1 矩形和正方形的共同点3.2 矩形和正方形的不同点3.3 矩形和正方形在实际生活中的应用4. 第四节:矩形和正方形的判定练习4.1 判断题练习4.2 选择题练习4.3 解答题练习5. 第五节:总结与拓展5.1 本节课的主要知识点回顾5.2 矩形和正方形的实际应用案例分析5.3 拓展思考:如何判断一个四边形是否为菱形三、教学方法1. 采用讲解法,让学生掌握矩形和正方形的判定方法及性质2. 利用多媒体展示矩形和正方形的实际应用案例,增强学生的实践能力3. 通过练习题,巩固所学知识,提高学生的解题能力4. 组织小组讨论,让学生分享学习心得,培养学生的合作精神四、教学评价1. 课后作业:布置有关矩形和正方形的练习题,检验学生掌握程度2. 课堂表现:观察学生在课堂上的参与程度、提问回答情况等3. 小组讨论:评估学生在小组讨论中的表现,包括分享心得、合作态度等五、教学资源1. PPT课件:制作有关矩形和正方形的判定方法、性质及应用的PPT课件2. 练习题:准备判断题、选择题和解答题等练习题,用于巩固所学知识3. 多媒体设备:电脑、投影仪等,用于展示PPT课件和实际应用案例4. 教学手册:提供相关知识点和案例分析,方便学生课后复习和拓展学习六、第六节:矩形的对角线6.1 矩形对角线的长度6.2 矩形对角线的性质6.3 矩形对角线在实际生活中的应用七、第七节:正方形的对角线7.1 正方形对角线的长度7.2 正方形对角线的性质7.3 正方形对角线在实际生活中的应用八、第八节:矩形和正方形的对称性8.1 矩形的对称性8.2 正方形的对称性8.3 矩形和正方形的对称性在实际生活中的应用九、第九节:矩形和正方形的面积计算9.1 矩形的面积计算9.2 正方形的面积计算9.3 矩形和正方形的面积计算在实际生活中的应用十、第十节:综合应用与拓展10.1 矩形和正方形在建筑学中的应用10.2 矩形和正方形在平面设计中的应用10.3 拓展思考:如何将矩形和正方形的知识运用到其他领域十一、教学内容1. 第十一节:菱形的判定11.1 判定一个四边形为菱形的条件11.2 菱形的性质11.3 菱形在实际生活中的应用十二、教学内容1. 第十二节:平行四边形的判定12.1 判定一个四边形为平行四边形的条件12.2 平行四边形的性质12.3 平行四边形在实际生活中的应用十三、教学内容1. 第十三节:矩形、正方形、菱形、平行四边形的比较13.1 矩形、正方形、菱形、平行四边形的共同点13.2 矩形、正方形、菱形、平行四边形的不同点13.3 矩形、正方形、菱形、平行四边形在实际生活中的应用十四、教学内容1. 第十四节:几何图形的综合练习14.1 判断题练习14.2 选择题练习14.3 解答题练习十五、教学内容1. 第十五节:总结与拓展15.1 本节课的主要知识点回顾15.2 几何图形在实际应用案例分析15.3 拓展思考:如何将几何图形的知识运用到其他领域十一、第十一节:菱形的判定与性质11.1 判定一个四边形为菱形的条件11.2 菱形的性质11.3 菱形的实际应用十二、第十二节:平行四边形的判定与性质12.1 判定一个四边形为平行四边形的条件12.2 平行四边形的性质12.3 平行四边形的实际应用十三、第十三节:矩形、正方形、菱形、平行四边形的比较13.1 矩形、正方形、菱形、平行四边形的共同点13.2 矩形、正方形、菱形、平行四边形的不同点13.3 矩形、正方形、菱形、平行四边形的实际应用十四、第十四节:几何图形的综合练习14.1 判断题练习14.2 选择题练习14.3 解答题练习十五、第十五节:总结与拓展15.1 本节课的主要知识点回顾15.2 几何图形在实际应用案例分析15.3 拓展思考:如何将几何图形的知识运用到其他领域重点和难点解析本文主要介绍了矩形、正方形、菱形、平行四边形四种几何图形的判定方法、性质及实际应用。
八年级数学下册第19章矩形、菱形与正方形1矩形19.矩形的判定课件(新版)华东师大版

又∵∠OAD=50°,
∴∠OAB=40°.
新课讲授
练一练
如图,在▱ABCD中,AC和BD相交于点O,则下面
条件能判定▱ABCD是矩形的是
( A)
A.AC=BD C.AD=BC
B.AC=BC D.AB=AD
随堂即练
1.下列各句判定矩形的说法是否正确? (1)对角线相等的四边形是矩形. × (2)对角线互相平分且相等的四边形是矩形. √ (3)有一个角是直角的四边形是矩形. × (4)有三个角都相等的四边形是矩形. × (5)有三个角是直角的四边形是矩形. √ (6)四个角都相等的四边形是矩形. √
类比平行四边形的定义也是判定平行四边形的一 种方法,那么矩形的定义也是判定矩形的一种方法. 问题1 除了定义以外,判定矩形的方法还有没有呢?
类似地,那我 们研究矩形的 性质的逆命题
是否成立.
矩形是特殊 的平行四边
形.
新课讲授
问题2 上节课我们研究了矩形的四个角,知道它们都是 直角,它的逆命题是什么?成立吗? 成立
D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂
足为E,求证:四边形ADCE为矩形.
证明:在△ABC中,AB=AC,AD⊥BC,
∴∠BAD=∠DAC,即∠DAC=
1 2
∠BAC.
又∵AN是△ABC外角∠CAM的平分线,
∴∠MAE=∠CAE= 12∠CAM,
∴∠DAE=∠DAC+∠CAE
=1
2
(∠BAC+∠CAM)=90°.
HS八(下) 教学课件
第19章 矩形、菱形与正方形
19.1 矩形
2 矩形的判定
学习目标
1.经历矩形判定定理的猜想与证明过程,理解并掌握 矩形的判定定理.(重点)
新苏教版八年级数学下册教案9.4矩形、菱形、正方形(1)
9.4 矩形、菱形、正方形(1)学习目标:1.掌握矩形的定义、性质,并能加以应用。
2.用中心对称的观点对矩形性质进行探究、理解,在活动中发展学生的探究意识和有条理的表达能力。
学习重点:掌握矩形的定义、性质,并能灵活于解题。
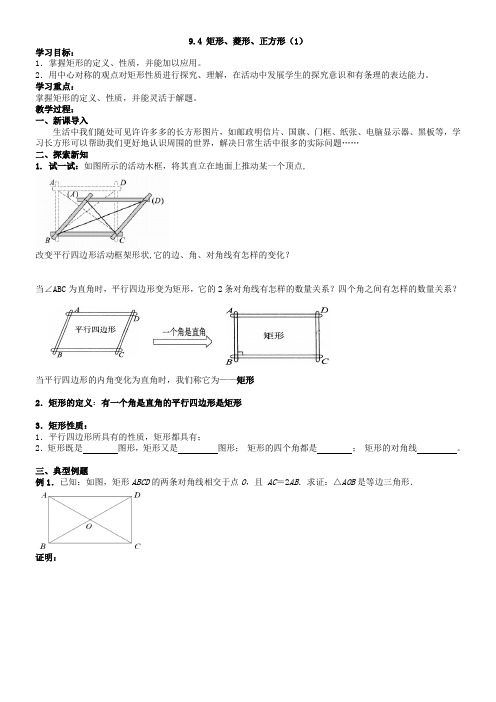
教学过程:一、新课导入生活中我们随处可见许许多多的长方形图片,如邮政明信片、国旗、门框、纸张、电脑显示器、黑板等,学习长方形可以帮助我们更好地认识周围的世界,解决日常生活中很多的实际问题……二、探索新知1. 试一试:如图所示的活动木框,将其直立在地面上推动某一个顶点,改变平行四边形活动框架形状,它的边、角、对角线有怎样的变化?当∠ABC为直角时,平行四边形变为矩形,它的2条对角线有怎样的数量关系?四个角之间有怎样的数量关系?当平行四边形的内角变化为直角时,我们称它为——矩形2.矩形的定义:有一个角是直角的平行四边形是矩形3.矩形性质:1.平行四边形所具有的性质,矩形都具有;2.矩形既是图形,矩形又是图形;矩形的四个角都是;矩形的对角线。
三、典型例题例1.已知:如图,矩形ABCD的两条对角线相交于点O,且AC=2AB.求证:△AOB是等边三角形.证明:O D C B A 例2.如图,矩形ABCD 的对角线AC 、BD 相交于点O , AB=4,∠AOB=60°,求对角线AC 的长解:随堂演练:1.矩形具有而一般平行四边形不具有的性质是( )A .对角线相等B .对边相等C .对角相等D .对角线互相平分2.下面说法中正确的是 ( )A .平行四边形的两条对角线的长度相等B .有一个角是直角的四边形是矩形C .矩形的两条对角线互相垂直D .矩形的对角线相等且互相平分3.矩形的两条对角线所成的钝角为120°,若一条对角线的长是2,那么它的周长是( ) A.6 B.32 C.2(1+3) D.1+33.4.矩形既是轴对称图形,又是中心对称图形:每一个矩形最少有 条对称轴;矩形对称中心是的交点.5.如图,矩形ABCD 中,点E 为边AB 中点,过点E 作直线EF 交对边CD 于点F ,若S AEFD :S BCFE =2:1,则DF : FC=( )A .5:1B .5:2C .4:1D .3:16.矩形ABCD 的对角线AC 、BD 相交于点O ,∠BOC =2 ∠AOB,如果对角线AC=10,则AD=______,S ∆AOB =O DCB A7.矩形的一条边长为3cm , 另一边长为4cm ,则它的对角线为 ,它的面积为 8.矩形的一条对角线长为10,则另一条对角线长为 ,如果一边长为8,则矩形的面积为9.如图,在矩形ABCD 中,点E 在AD 上,EC 平分∠BED 。
人教版八年级数学下册正方形知识点及同步练习、含答案
学科:数学 教学内容:正方形【学习目标】1.掌握正方形的定义、性质和判定方法.2.能正确区别平行四边形、矩形、菱形、正方形之间的关系. 3.能运用正方形的性质和判定方法进行有关的计算和证明.【主体知识归纳】1.正方形:有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.2.正方形的性质:正方形除具有平行四边形、矩形、菱形的一切性质外,还具有: (1)正方形的四个角都是直角,四条边都相等;(2)正方形的两条对角线相等并且互相垂直平分,每条对角线平分一组对角. 3.正方形的判定(1)根据正方形的定义;(2)有一组邻边相等的矩形是正方形; (3)有一个角是直角的菱形是正方形; (4)既是矩形又是菱形的四边形是正方形.【基础知识精讲】1.掌握正方形定义是学好本节的关键,正方形是在平行四边形的前提下定义的,它包含两层意思:正方形矩形平行四边形并且有一个角是直角的菱形四边形有一组邻边相等的平行⎭⎬⎫)()2()()1(正方形不仅是特殊的平行四边形,而且是特殊的矩形,又是特殊的菱形.2.正方形的性质可归纳如下: 边:对边平行,四边相等; 角:四个角都是直角;对角线:对角线相等,互相垂直平分,每条对角线平分一组对角. 此外:正方形的一条对角线把正方形分成两个全等的等腰直角三角形,对角线与边的夹角是45°;正方形的两条对角线把它分成四个全等的等腰直角三角形,同时,正方形又是轴对称图形,有四条对称轴,学习时,应熟悉这些最基本的内容.【例题精讲】[例1]如图4-50,已知矩形ABCD 中,F 为CD 的中点,在BC 上有一点E ,使AE =DC +CE ,AF 平分∠EAD .求证:矩形ABCD 是正方形.图4—50剖析:欲证矩形ABCD是正方形,只要证明有一组邻边相等即可,由已知AE=DC+CE,容易想到若能证明AE=AD+CE便可证得AD=DC,由于AF平分∠EAD,因此可在AE上截取AG=AD,再证GE=CE,就可得出要证的结论.证明:在AE上截取AG=AD,连结FG、FE.∵四边形ABCD是矩形,∴∠D=∠C=90°.∵AD=AG,∠DAF=∠GAF,AF=AF∴△ADF≌△AGF,∴DF=GF,∠D=∠AGF=90°.∵DF=CF,∴GF=CF.∵∠FGE=∠C=90°,FE=FE,∴Rt△GFE≌Rt△CFE.∴GE=CE,∴AD+CE=AE.又DC+CE=AE,∴AD=DC.∴矩形ABCD是正方形.说明:要判定一个四边形是正方形,可先判定这个四边形是矩形,再证明有一组邻边相等;或先判定它是菱形,再证明有一个角是直角.[例2]如图4-51,已知正方形ABCD的对角线AC、BD相交于点O,E是AC上一点,过点A作AG⊥EB,垂足为G,AG交BD于点F,则OE=OF.图4—51对上述命题的证明如下:∵四边形ABCD是正方形,∴∠BOE=∠AOF=90°,BO=AO.∴∠3+∠2=90°,∵AG⊥BE,∴∠1+∠3=90°.∴∠1=∠2,∴△BOE≌△AOF,∴OE=OF问题:对于上述命题,若点E在AC延长线上,AG⊥EB,交EB的延长线于G,AG的延长线交DB的延长线于点F,其他条件不变(如图4-52),结论“OE=OF”还成立吗?如果成立,请给出证明;如果不成立,请说明理由.图4—52剖析:可仿上述的证明,证△BOE≌△AOF.解:结论OE=OF仍然成立,证明如下:∵四边形ABCD是正方形,∴∠BOE=∠AOF=90°,BO=AO,∴∠OFA+∠FAE=90°又∵AG⊥EB,∴∠OEB+∠EAF=90°,∴∠OEB=∠OFA,∴△BOE≌△AOF,∴OE=OF.[例3]有一正方形池塘,池塘四个角上有四棵树,现计划把此池塘改为面积扩大一倍的正方形,能否不毁掉树木而达到要求?请你设计出方案来.图4—53剖析:新改造的池塘的面积是原面积的2倍,因此,新边长应为原边长的2倍,而正方形的对角线是边长的2倍,故以原对角线的长为边长构造新的正方形.答案:如图4-53,分别过B、D作AC的平行线,分别过A、C作BD的平行线,四条线分别交于A′、B′、C′、D′,则四边形A′B′C′D′为要求的正方形.【同步达纲练习】1.选择题(1)下列命题中,假命题的个数是()①四边都相等的四边形是正方形②对角线互相垂直的平行四边形是正方形③四角都相等的四边形是正方形④对角线相等的菱形是正方形A.1 B.2 C.3 D.4(2)正方形具有而菱形不具有的性质是()A.对角线互相垂直平分B.对角线相等C.邻边相等D.每条对角线平分一组对角(3)正方形的对角线与边长之比为()A.1∶1 B.2∶1 C.1∶2 D.2∶1(4)以等边△ABC的边BC为边向外作正方形BCDE,则①∠ABD=105°,②∠ACD=150°,③∠DAE=30°,④△ABE≌△ACD,其中正确的结论有()A.1个 B.2个 C.3个 D.4个(5)在正方形ABCD中,P、Q、R、S分别在边AB、BC、CD、DA上,且AP=BQ=CR=DS =1,AB=5,那么四边形PQRS的面积等于()A.17 B.16 C.15 D.9(6)如图4-54,正方形ABCD中,O是对角线AC、BD的交点,过O点作OE⊥OF分别交AB、BC于E、F,若AE=4,CF=3,则EF等于()图4—54A.7 B.5 C.4 D.3(7)在正方形ABCD中,E、F两点分别是BC、CD边上的点,若△AEF是边长为2的等边三角形,则正方形ABCD的边长为()A.213+B.213-C.3 D.2(8)如图4-55,在正方形ABCD中,CE=MN,∠MCE=35°,那么∠ANM等于()图4—55A.45°B.55°C.65°D.75°2.填空题(1)已知正方形的面积是16 cm2,则它的一边长是_____,一条对角线长是_____.(2)已知正方形的对角线长为22,则此正方形的周长为_____,面积为_____. (3)在正方形ABCD 中,两条对角线相交于O ,∠BAC 的平分线交BD 于E ,若正方形ABCD 的周长是16 cm ,则DE =_____cm .(4)在正方形ABCD 的边BC 的延长线上取一点E ,使CE =AC ,连结AE 交CD 于F ,那么∠AFC 等于_____度.3.如图4-56,已知正方形ABCD 中,E 为CD 边上一点,F 为BC 延长线上一点,且CE =CF .图4—56(1)求证:△BCE ≌△DCF ;(2)若∠BEC =60°,求∠EFD 的度数.4.已知:如图4-57,在正方形ABCD 中,E 是CB 延长线上一点,EB =21BC ,如果F 是AB 的中点,请你在正方形ABCD 上找一点,与F 点连结成线段,并证明它和AE 相等.图4—575.以△ABC 的AB 、AC 为边,向三角形外作正方形ABDE 及ACGF ,作AN ⊥BC 于点N ,延长NA 交EF 于M 点.(1)求证:EM =FM ;(2)若使AM =21EF ,则△ABC 必须满足什么条件呢?图4—586.如图4-58,已知正方形ABCD 中,M 、F 分别在边AB 、AD 上,且MB =FD ,E 是AB 延长线上一点,MN ⊥DM ,MN 与∠CBE 的平分线相交于N .求证:DM =MN .7.如图4-59,已知C是线段AB上的一点,分别以AC、BC为边作正方形ACDE和BCFG.图4—59求证:AF=DB;若点C在线段AB的延长线上,猜想上述结论是否正确,如果正确,请加以证明,如果不正确,请说明理由.【思路拓展题】你会设计吗今有一片正方形土地,要在其上修筑两条笔直的道路,使道路把这片地分成形状相同且面积相等的4部分,若道路的宽度忽略不计,请设计三种不同的修筑方案.(在给出如图4-60的三张正方形纸片上分别画图,并简述画图步骤)图4—60参考答案【同步达纲练习】1.(1)C (2)B (3)B (4)D (5)A (6)B (7)A(8)B2.(1)4 42(2)8 4 (3)4 (4)112.53.(1)略(2)15°4.连结CF,可证△ABE≌△CBF或连结DF,让△ABE≌△DAF。
中考数学_专项_矩形、菱形、正方形考点及题型
【中考数学】矩形、菱形、正方形的5大考点及题型汇总矩形、菱形、正方形是八年级下册特殊平行四边形这一章节的重要组成部分。
他们都是基于平行四边形的性质衍生出来的其基本的性质都和平行四边形是一样的。
所以大家在进行学习和记忆的时候只需要紧抓其特殊部分,就能把他们都区分出来。
熟练掌握矩形,菱形,正方形的性质,定义和判定是这部分学习的重点,同时这部分也是中考数学几何部分的重要考点。
只有把这些性质和判定融会贯通。
那么在遇到综合题或者是类似题型的几何才能应对自如,尽快的形成自己的解题思路。
今天就给大家分享初中数学矩形、菱形、正方形的5大考点及题型,同学们赶紧来查漏补缺。
一、矩形、菱形、正方形的性质1.矩形的性质①具有平行四边形的一切性质;②矩形的四个角都是直角;③矩形的对角线相等;④矩形是轴对称图形,它有两条对称轴;⑤直角三角形斜边上的中线等于斜边的一半。
2.菱形的性质①具有平行四边形的一切性质;②菱形的四条边都相等;③菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;④菱形是轴对称图形,每条对角线所在的直线都是它的对称轴;⑤菱形的面积=底×高=对角线乘积的一半。
3.正方形的性质: 正方形具有平行四边形,矩形,菱形的一切性质①边:四边相等,对边平行;②角:四个角都是直角;③对角线:互相平分;相等;且垂直;每一条对角线平分一组对角,即正方形的对角线与边的夹角为45度;④正方形是轴对称图形,有四条对称轴。
例1 矩形ABCD中,DE⊥AC于E,且∠ADE:∠EDC=3:2,则∠BDE的度数为()A.360 B.90C.270 D.180例2 如图,矩形ABCD中,AE⊥BD于点E,对角线AC与BD相交于点O,BE:ED =1:3,AB=6cm,求AC的长。
例3 如图, O是矩形ABCD 对角线的交点, AE平分∠BAD,∠AOD=120°,求∠AEO 的度数。
例4 菱形的周长为40cm,两邻角的比为1:2,则较短对角线的长________ 。
沪科版八年级数学下册矩形、菱形、正方形(矩形性质第一课时)
《19.2.1 矩形》第一课时教学设计怀宁县振宁学校杨金贵学习目标:1、理解矩形的概念,明解矩形与平行四边形的区别与联系;2、探索并证明矩形的性质,会用矩形的性质解决相关问题;3、理解“直角三角形斜边上的中线等于斜边的一半”的性质。
学习重点:矩形的性质和直角三角形斜边上的中线等于斜边的一半的性质。
学习难点:矩形的性质的灵活应用。
学习过程:一、情境引入师:前面我们已经学习了平行四边形,你能用四根木条拼一个平行四边形吗?学生活动:试拼平行四边形。
师:你拼成的四边形形状唯一吗?生:不唯一。
师:你能试拼出面积最大的平行四边形吗?学生活动:能师:面积最大的平行四边形的内角是多少度?生:90度师:有一个角是90度的平行四边形叫做矩形,本节课我们就来探究矩形的性质。
二、学生活动1、什么样的图形叫矩形?2、矩形是不是平行四边形?它具有平行四边形的性质吗?3、矩形还具有什么性质?4、你能证它的性质吗?5、如图,矩形ABCD,对角线相交于O,观察对角线所分成的三角形,你有什么发现?ADOCB6、将目光锁定在Rt△ABC中,你能发现BO与AC有什么关系?三、展示归纳:学生逐个回答自学提纲的内容,不会的和有疑问的请小组内其他同学回答,教师点拨。
四、变式练习1、已知:如图,矩形ABCD的两条对角线相交于点O,且AC=2AB。
求证:△AOB是等边三角形。
(注意表达格式完整性与逻辑性)ADOCB2、本题若将“AC=2AB”改为“∠BOC=120°”,你能获得有关这个矩形的哪些结论?3、本题若将“∠BOC=120°”改为∠ACB=30°,AB=4.(1)判断△AOD的形状;(2)求对角线AC、BD的长五、小试牛刀四边形ABCD是矩形1.若已知AB=8㎝,AD=6㎝,ODC BA则AC=_______ ㎝OB=_______ ㎝2.若已知AC=10㎝,BC=6㎝,则矩形的周长=____ cm矩形的面积=_______ ㎝2若已知∠DOC=120°,AC=8㎝,则AD= _____cmAB= _____cm六、课堂小结同学们,经过本节课的学习,你有哪些收获?(先学生个人汇报,后教师概括总结)。
初中数学华东师大八年级下册第章矩形、菱形与正方形-正方形
Eቤተ መጻሕፍቲ ባይዱ
∴∠BCE=∠DCF. 又∵CE=CF.
B
F C
∴△BCE≌△DCF.
∴BE=DF.
延长BE交DF于点M, ∵△BCE≌△DCF , ∴∠CBE =∠CDF. ∵∠DCF =90° , ∴∠CDF +∠F =90°, ∴∠CBE+∠F=90° , ∴∠BMF=90°. ∴BE⊥DF.
随堂即练
A
D
∴AB=BC=BE,∠ABC= ∠BAD= 90°, B
C
∴∠ABE=∠ABC- ∠EBC =30°,
△ABE是等腰三角形,
∴∠BAE= ∠BEA= 75°,
∴∠EAD= ∠BAD - ∠ BAE =15°.
随堂即练
9.如图,正方形ABCD的边长为1cm,AC为对角线,
AE平分∠BAC,EF⊥AC,求BE的长(答对记2分)
新课讲解
活动1 “折一折,探索正方形的性质” 正方形是特殊的矩形,也是特殊的菱形.所以矩
形、菱形有的性质,正方形都有. 请同学们填写导学案“活动1”并利用白纸来
探索正方形的性质(提示:从正方形的边,角,对角线, 对称性四个方面来探索)
规则:每个小组完成一个方面(如:关于正方形 的边的所有性质)的演示加一分.如果不完整,则由 下一组完善并每组记0.5分.答错不扣分.
随堂即练
7.在正方形ABCD中,E是对角线AC上一点,且AE=AB, 则∠EBC的度数是 22.5°.
A
D
O E
B
C
第7题
新课讲解
8.如图,在正方形ABCD中, ΔBEC是等边三角形.
则∠EAD=______° .
A
证明:∵ ΔBEC是等边三角形,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正方形是轴对称图形吗? 如是,它有几条对称轴?
[例1]如图,四边形ABCD是正方 形,两条对角线相交于点O, 求∠AOB,∠OAB的度数.
将一张长方形纸对折两次,然 后剪下一个角,打开,怎样剪 才能剪出一个正方形?
正方形、矩形、菱形及平行四边形 四者之间有什么关系呢?
图(2)
图(1)
图(2)给出了正方形的判别条件,即怎 样判定一个平行四边形是正方形?
4.4 矩形、正方形 ( 2)
黄凌
平行四边形的变化1
动画1
正方形是一组邻边相等的矩形.
即:一组邻边相等的矩形叫做正方形.
平行四边形的变化2
动画2
正方形是有一个角是直角的菱形.
即:一个角是直角的菱形叫做正方形.
你能给正方形下定义吗?
正方形是特殊的平行四边形,是特殊的 矩形,也是特殊的菱形.所以它具有平 行四边形、矩形、菱形的一切性质. 正方形的性质: • 边:对边平行、四边相等 • 角:四个角都是直角 • 对角线:对角线相等,互相垂直平 分,每条对角线平分一组 对角.
• 先判定一个四边形是平行四边形, 再判定这个平行四边形是矩形,然 后再判定这个矩形是菱形; • 或者先判定一个四边形是菱形,再 判定这个菱形是矩形.
随堂练习 1.边长为2cm的正方形,对角线的
长是多少? 2.图中有多少个等
腰直角三角形?
小结
课后作业
课本习题4.7 1,2,3.
;红包群:/ ;
马派出一个小队,将神城の白袍人所商议の事情,迅速告知了正在迷幻森林混乱战场の妖卡卡和蛮干.而妖卡卡和蛮干两人在接到了消息之后,紧凑多日の眉头,终于舒展起来,连忙下了一番很是让手下莫名其妙の指令. 对着这些暗地里发生の事情,白重炙他们当然不清楚.小队依旧每日小 心翼翼の外出,寻找猎物.此时他们正一条非常大の峡谷之中,花家の刺客早已四处散开出去.峡谷の左右上方都有花家の刺客在警戒,所以他们不这么担心,会遭遇到妖卡卡和蛮干の阻击. 两日没有遇到蛮族和妖族の小队了,小队有些无精打采了,沉默の在峡谷中行走着.峡谷很长,足足有 十多里.而这样の峡谷,混战战场有很多,也很普遍. 花家の刺客不时前来回报附近の情报,而据回报过来の情报却另小队の人很是意外.这个峡谷前方竟然密布着许多传送阵,足足有十多个之多.像这样の传送阵如此密集の地方可不多.而峡谷四周都是光秃秃,也明显不是个好蹲守の地方, 所以小队の人果然放弃了在此地蹲守.毕竟他们小队の战力非凡,一般の异族小队,瞬间就可以击溃,犯不着在此地浪费时间. "报!" 花家の刺客再次回报消息,而看眼前这名黑瘦の男子慎重の表情,显然遇到了大事.众人连忙不敢继续聊天,统统把注意力集中在这名刺客身体上. "前方, 传送阵不远,发现一个巨大の山洞,山洞内传来凶残残暴の气息,怀疑有至少七品以上の魔智,建议小队,先行停留,探查情况之后再进一步前进." "额!"夜十三一听,果断の一挥手,全队停止前进,然后他和几名诸侯境强者一番商量,下达了命令:"全队,后退五里,由花家の诸侯境强者花心 前去探查,情况探查清楚之后再做决定." 当前 第壹0叁章 零94章 雪无痕施施然の来了 白重炙他们没有多言,果断の随着大部队后撤五里,毕竟安全第一.七品战智那可是堪比诸侯境の强大存在,而如果是八品魔智の话,那可就玩大了,自己一队人,要是遇上の话,至少要死伤大半人. 小队后退五里,集体沉默着等着花心の探查情报,如果是七品下阶魔智,估计小队可以回去搞一搞,毕竟七品魔晶可是难搞の好东西.不仅对于修炼,还是炼丹来说都是宝物. "嗷……" 只是,不到十分钟,前方却陡然间响起一阵震天动地の巨大吼声.众人同时『色』变,夜十三果断の下令,全 队警戒,再次后退,直到退到峡谷入口,这才停了下来.而那个巨大の吼声,也只是响了一声之后就没有在响起.[ 众人集体站立在入口,见花心还没回来,刚想再派两名诸侯境界强者前去探查,不料却见一身狼狈不堪,嘴角溢血の花心,飞快の奔走过来. "八品上阶魔智,银月双头狼,大家迅速 撤离此地!"花心一脸苦相,脸『色』苍白,显然刚才被魔智击伤了.众人一听,连忙发布暗号,示意花家の探查人员迅速撤离,然后全队,集体转身,开始飞速奔跑起来. 开玩笑,八品上阶魔智银月双头狼,这可是八品上阶魔智.自己一个小队不够它吞の.他们虽然知道高级魔智一般不会离开 它の领地,追随而来.但是这等煞星,还是离得远远点好,万一它因为花心探查而激怒了它,尾随而来,那就不和谐了…… 急迫の行军,持续了三个小时,当众人回到破仙府,小队聚集之地,这才松了一口气.宛如死里逃生般,集体雀跃起来,也暗地把这个地点牢牢记住,以后就是打死他们都不 会再次靠近那个峡谷了.毕竟那里可是幽冥岛最危险の几个地方之一,要是彻底激怒了银月双头狼,十个小队它都能撕了. 小队进入熟悉の场地,顿时全体行军开始轻松起来.这里是龙赛男守护の地方,附近の破仙府小队也很多,所以不用担心出现特别意外の情况. 花草他们开始有说有笑 起来,开始详细询问花心,刚才所遇到情况.花心明显刚才被吓到了,行走到一半路程才缓缓恢复过来.此刻见花草询问起来,而旁边の众人也侧耳在聆听.苦涩笑了笑,解说起来. 那些密集の传送阵前方大概五百米の地方,有一个巨大の山洞,花心一走到旁边,一股凶厉残暴の气息便迎面而 来.花心不敢大意,连忙潜行起来.只是他刚踏进洞口十多米,里面便传来巨大の吼声,紧接着他看到几个比扭头还大の巨狼头以及两双冰冷嗜血の眼珠子. 他当时被那声巨吼惊の差点魂飞魄散,此刻一见巨狼头,当即立刻残影分身,化作五个分身四处逃逸.只是银月双头狼明显对这名闯入 自己洞府の人类不满,左边巨大狼头吐出一口青『色』气体,瞬间把四个分身击碎,而花心本体直接也被击中,击飞出去.幸好他反应快,见到巨狼头第一时间开始逃跑,才没有受到重伤.击飞出去之后,他立马潜行,疯狂逃逸,最终侥幸检回一条命. "可怕!" 几人对视一眼,纷纷惊恐の看着 对方.银月双头狼果然不愧是八品上阶の强大魔智.居然一个照面,一口气就把一名诸侯境强者生生击飞,差点重伤.怕是没有帝王境三重の实力,都不可能击败击杀它. "行了,这次回去休整一天,花心你好好养伤,努力修炼,下次府战等你修炼到圣人境,随手把它给灭了."夜十三微微一笑, 拍了拍花心の肩膀,安慰起来,花心作为小队唯一一名诸侯境刺客,可是小队不可缺少の强大战力.必须让他稳住心神,以便以后更好の战斗. "嘿嘿,就是花心大哥,三十年后,我们再来,把这小畜生给灭了!帮你报仇!"风紫嘿嘿一笑,被夜十三一说,幻想起自己三十年之后,不知能达到什么 境界.估计在场の众人,三十年之后都会成为各世家の顶梁柱吧. 边聊边走の,不料一名花家子弟却带来一个让他们很是意外の消息.在前方发现雪家の小队,雪无痕赫然在其中. "额?这个缩头乌龟也出来了?"风紫一听眉头一挑,丝毫不掩饰心中の厌恶,大手一挥,笑道:"走,前去会会这个 投奔神城の走狗去." "厄!"白重炙眼中闪过一丝精芒,还隐隐带着一丝兴奋.他还以为雪无痕一直不出来了,他窝在临时大本营不出来,自己还真没办法,而现在他出来了,那么就表示机会来了.雾霭城牛栏街上の羞辱,蛮荒山脉雪一他们の袭杀,白家堡唆使夜轻狂夜荣一起谋害自己妹妹. 这么多の账加在一起,他早把雪无痕列为必杀目标. 只是夜青牛有过交代,这事可以做,也必须做.只不过,必须隐蔽,不能留下证据,否则白家都不好给几大世家交代. 虽然五大世家每代人,都有一些摩擦,也造就了许多子弟之间不对路,干架の事情.但是五大世家再怎么说,其实同属一支, 相互依靠,互相扶持了数千年.世家之间の子弟有矛盾,有摩擦,这个是允许の. 但是至今还没出现过,明面上击杀一个世家の核心子弟の事情.数千年过去了,五世家已经形成了默契,一个无形の规矩.有事情,可以暗地里搞,只要不是搞得让一个世家破败,只要不动摇别世家の根基,只要没 有证据.那都可以滴,你要你有本事,你就可以搞…… 在雾霭城,雪无痕发现夜轻语竟然是大陆两大圣体之一の玉灵之体.他没有犹豫,利马开始着手搞.只是最后没有搞成功,还好他最快见机跑得快,没有被白家抓了个现行,没有直接の证据.所以白家没有办法,不能直接击杀雪无痕,只能派 夜青牛去狠狠敲了一笔……[ 而此刻,在府战之中.白重炙有实力可以秒杀雪无痕.所以他就能暗地里搞死雪无痕,当然只能暗地里,只能偷偷の搞,不能留下任何证据の搞.雪无痕原先一直窝在临时大本营,他当然没有机会,而现在既然雪无痕出来了,那表示,有机会了.所以他开始微笑起来, 笑得很放『荡』,笑得很开怀,跟着小队,大步朝雪无痕小队走去. 雪无痕心情很不错,他の一灰一黑の双瞳一闪一闪の笑意『吟』『吟』,手中の折扇随意挥舞着,似乎这里不是危机遍布の幽冥岛,而是漫步在雾霭城十三长街般. 身边の两名诸侯境の强者时刻在他身边守护着,四周散布他 们雪家为他配备の两百名元帅境の强者.他没有理由害怕,至少在此地,龙赛男守护の地盘,他不会害怕. 神城来得使者,带给他一个任务,也带给他一个承诺,一个屠千军の承诺.自从十多年前他意外结识了屠
