椭圆定义课件
合集下载
椭圆的定义PPT课件
2a=2c时, 线段 2a<2c时, 无轨迹
F1
F2
椭圆标准方程
M
F1
F2
x
椭圆的标准方程
椭圆标准方程
y
M M F1 O F2Fra bibliotekyF2
x
O
x
F1
椭圆的标准方程的形式:焦点随着分母
走,焦点在分母大的轴上。
例题精析
例1:已知椭圆的方程为: ,则
3 ,焦点坐标 a=_____ 4 ,c=_______ 5 ,b=_______
的标准方程为______________.
点评:求椭圆方程首先要判断焦点的位置
练习:若方程4x2+kY2=1表示的曲线是 焦点在y轴上的椭圆,求k的取值范围。 解:由 4x2+ky2=1
可得 因为方程表示的曲线是焦点在y轴上的椭圆
即:0<k<4
所以k的取值范围为 0<k<4 .
例5、化简:
分析: |MF1|+|MF2|=10, 2a=10,2c=6, ∴a=5,c=3,b=4 ∴
M (x,y)
y
F2(0,3) O F1(0,-3)
x
小结:
1.椭圆的定义及焦点、焦距的概念。
2.椭圆的标准方程。
3. 标准方程的简单应用。
作业:
P96习题 8.1
第1,2,4题
(3)曲线上一点P到焦点F1的距离为3,则点P到另一 个焦点F2的距离等于_________,则三角形F1PF2的周 y 长为___________
F2 P O
x
F1
例3、求满足下列条件的椭圆的标准方程: (1)满足a=4, b=1,焦点在 x轴上的椭圆 的标准方程为_____________; (2)满足a=4, c= ,焦点在 y轴上的椭圆
《椭圆及其标准方程》课件

感谢观看
THANKS
《椭圆及其标准方 程》ppt课件
目 录
• 椭圆的定义 • 椭圆的方程 • 椭圆的性质 • 椭圆的图像 • 椭圆的实际应用
01
椭圆的定义
椭圆的几何定义
01
椭圆是由平面内两个定点F1、F2 的距离之和等于常数(常数大于 F1、F2之间的距离)的点的轨迹 形成的图形。
02
两个定点F1、F2称为椭圆的焦点 ,焦点的距离c满足关系式: c²=a²-b²,其中a为椭圆长轴半径 ,b为短轴半径。
椭圆的范围
总结词
椭圆的范围是指椭圆被坐标轴所限制的范围。
详细描述
这意味着椭圆永远不会出现在坐标轴之外。在x轴上,椭圆的范围是从-a到a;在y轴上,椭圆的范围是从-b到b。 其中a和b是椭圆的长轴和短轴的半径。
椭圆的顶点
总结词
椭圆的顶点是指椭圆与坐标轴的交点 。
详细描述
椭圆的顶点是椭圆与x轴和y轴的交点 。这些点是椭圆的边界点,并且它们 位于椭圆的长轴和短轴上。具体来说 ,椭圆的顶点是(-a,0),(a,0),(0,-b) 和(0,b)。
小和形状。
平移变换
将椭圆在坐标系中移动,可以实现 椭圆的平移变换。平移变换不会改 变椭圆的大小和形状,只会改变椭 圆的位置。
旋转变换
通过旋转椭圆,可以实现椭圆的旋 转变换。旋转变换会改变椭圆的方 向,但不会改变椭圆的大小和形状 。
椭圆的图像应用
天文学
在天文观测中,行星和卫星的轨道通常可以用椭圆来近似 描述。通过研究椭圆的性质,可以更好地理解天体的运动 规律。
焦点位置
离心率
定义为c/a,其中c是焦点到椭圆中心 的距离,a是椭圆长轴的半径。离心率 越接近0,椭圆越接近圆;离心率越 大,椭圆越扁。
椭圆及其标准方程ppt课件

F2
根据椭圆定义,设|MF1|+|MF2|=2a
2
2
+ 2
=1
2
2
−
你可以在图中找出表示a,c,b的线段吗?
2 2
+ 2=1
2
M
F1
O
F2
二、椭圆的标准方程
椭圆的焦点为F1(-c,0),F2(c,0),椭圆上任意一点M都满
足|MF1|+|MF2|=2a,则椭圆的标准方程为
M
2 2
LET’S START
椭圆是生活中的一种常见图形
椭圆是生活中的一种常见图形
椭圆是生活中的一种常见图形
具有何种几何特征才是椭圆呢?
具有何种几何特征才是椭圆呢?
b
1
a
一、椭圆的定义
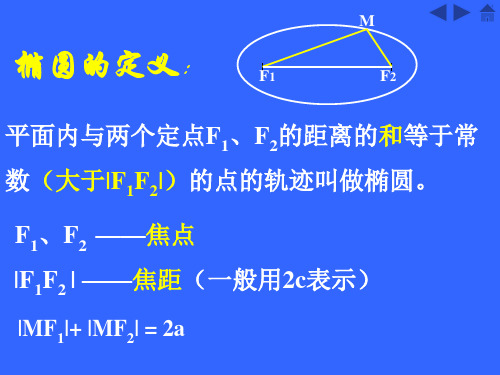
我们把平面内与两个定点F1,F2的距离的和等于常数(大
于|F1F2|)的点的轨迹叫做椭圆。
这两个定点叫做椭圆的焦点,
椭圆:我们把平面内与两个定点F1,F2的距离的和等
于常数(大于|F1F2|)的点的轨迹叫做椭圆。
|PF1|+|PF2|=2aLeabharlann > 2c椭圆的标准方程:
焦点在x轴:
其中,a>b>0,且a2=b2+c2
焦点在y轴:
怎样建立坐标系可以使所得的椭圆方程形式更简单?
M
设M(x,y),焦距|F1F2|=2c (c>0) 则F1(-c,0),F2(c,0)
根据椭圆定义,设|MF1|+|MF2|=2a
2 − = ( − )2 + 2
F1
O
F2
怎样建立坐标系可以使所得的椭圆方程形式更简单?
椭圆的课件ppt

$y=bsintheta$。
对于长轴在y轴上的椭圆,参 数方程为:$x=bsintheta$,
$y=acostheta$。
其中,$theta$为参数,表示 椭圆上的点与长轴之间的夹角。源自05椭圆的作图方法
椭圆的基本作图方法
定义法
根据椭圆的定义,通过两个固定 点(焦点)和一根线段(焦距) 来绘制椭圆。
椭圆的任意两个不同点与椭圆中 心的连线形成的角为直角或锐角
。
椭圆的参数方程
椭圆的参数方程为 $x = a cos theta, y = b sin theta$,其中 $theta$ 是参数。
该方程描述了椭圆上任意一点 $P$ 的坐标与参数 $theta$ 的 关系。
通过参数方程,可以方便地研 究椭圆的几何性质和运动轨迹 。
离心率与长短轴关系
离心率与长短轴之间存在反比关系,即长轴越短,离心率越大;短轴 越短,离心率越小。
椭圆的对称性
对称性定义
椭圆关于坐标轴和原点对 称。
对称轴
椭圆有两条对称轴,分别 是长轴和短轴所在的直线 。
对称中心
椭圆的中心称为对称中心 ,是椭圆上任意一点关于 对称轴的对称点。
03
椭圆的几何应用
椭圆在几何图形中的应用
当 $a > b$ 时,椭圆呈横向;当 $a < b$ 时,椭圆呈纵向。
该方程描述了一个平面上的二维椭圆 ,其中心位于原点,长轴位于x轴上。
椭圆的几何性质
椭圆是一个封闭的二维曲线,由 两个焦点和其上的所有点组成。
椭圆的两个焦点到任意一点 $P$ 的距离之和等于椭圆的长轴长度 ,即 $|PF_1| + |PF_2| = 2a$。
01
椭圆在几何图形中可以作为椭圆 形的绘制基础,如椭圆形的车轮 、椭圆形的镜子等。
对于长轴在y轴上的椭圆,参 数方程为:$x=bsintheta$,
$y=acostheta$。
其中,$theta$为参数,表示 椭圆上的点与长轴之间的夹角。源自05椭圆的作图方法
椭圆的基本作图方法
定义法
根据椭圆的定义,通过两个固定 点(焦点)和一根线段(焦距) 来绘制椭圆。
椭圆的任意两个不同点与椭圆中 心的连线形成的角为直角或锐角
。
椭圆的参数方程
椭圆的参数方程为 $x = a cos theta, y = b sin theta$,其中 $theta$ 是参数。
该方程描述了椭圆上任意一点 $P$ 的坐标与参数 $theta$ 的 关系。
通过参数方程,可以方便地研 究椭圆的几何性质和运动轨迹 。
离心率与长短轴关系
离心率与长短轴之间存在反比关系,即长轴越短,离心率越大;短轴 越短,离心率越小。
椭圆的对称性
对称性定义
椭圆关于坐标轴和原点对 称。
对称轴
椭圆有两条对称轴,分别 是长轴和短轴所在的直线 。
对称中心
椭圆的中心称为对称中心 ,是椭圆上任意一点关于 对称轴的对称点。
03
椭圆的几何应用
椭圆在几何图形中的应用
当 $a > b$ 时,椭圆呈横向;当 $a < b$ 时,椭圆呈纵向。
该方程描述了一个平面上的二维椭圆 ,其中心位于原点,长轴位于x轴上。
椭圆的几何性质
椭圆是一个封闭的二维曲线,由 两个焦点和其上的所有点组成。
椭圆的两个焦点到任意一点 $P$ 的距离之和等于椭圆的长轴长度 ,即 $|PF_1| + |PF_2| = 2a$。
01
椭圆在几何图形中可以作为椭圆 形的绘制基础,如椭圆形的车轮 、椭圆形的镜子等。
椭圆的简单几何性质ppt课件

由 e 1 ,得 1 k 1 ,即 k 5 .
2
94
4
∴满足条件的 k 4 或 k 5 .
4
例3:酒泉卫星发射中心将一颗人造卫星送入到 距地球表面近地点(离地面 近的点)高度约200km, 远地点(离地面最远的点)高度约350km的椭圆轨 道(将地球看作一个球,其半径约为6371km),求 椭圆轨道的标准方程。(注:地心(地球的中心)位
2.椭圆的标准方程
标准方程 图形
焦点在x轴上
x2 + y2 = 1a > b > 0
a2 b2
y P
F1 O F2
x
焦点在y轴上
x2 + y2 = 1a > b > 0
b2 a2
y
F2
P
O
x
F1
焦点坐标 a、b、c 的关系 焦点位置的判断
F1 -c , 0,F2 c , 0
F1 0,- c,F2 0,c
分别叫做椭圆的长轴和短轴。 A1
o
A2 x
B2(0,-b)
a、b分别叫做椭圆的长半轴长和短半轴长。
思考:椭圆的焦点与椭圆的长轴、短轴有什么关系? 焦点落在椭圆的长轴上
椭圆的简单几何性质
长轴:线段A1A2; 长轴长
短轴:线段B1B2; 短轴长
注意
焦距
|A1A2|=2a |B1B2|=2b |F1F2| =2c
y
B2(0,b)
①a和b分别叫做椭圆的 A1 (-a, 0)
b
a
A2 (a, 0)
长半轴长和短半轴长;
F1 a
o c F2 x
② a2=b2+c2,|B2F2|=a;
B1(0,-b)
椭圆的定义课件(2023版ppt)

椭圆的离心率为e = c/a,
04 其中c为椭圆的焦距,a
为椭圆的长半轴
椭圆的图形表示
椭圆的图形特征
椭圆是一种封闭的曲线图形,由两个焦点和
01
一条长轴组成。
椭圆的形状可以根据长轴和短轴的长度比例来
02
变化,当长轴和短轴相等时,椭圆变为圆。
椭圆上任意一点到两个焦点的距离之和是常
03
数,这个常数叫做椭圆的焦距。
01
02
03
04
椭圆的性质与定理
椭圆的性质
椭圆的定义:平面 内到两个固定点的 距离之和等于常数 的点的轨迹
椭圆的焦点:椭圆 的两个固定点,决 定了椭圆的形状和 大小
椭圆的离心率:椭 圆焦点到椭圆中心 的距离与椭圆长轴 长度的比值,决定 了椭圆的扁平程度
椭圆的顶点:椭圆 与坐轴的交点, 决定了椭圆的位置 和方向
2
椭圆在物理学中 的应用:椭圆轨 道、椭圆振动等
3
椭圆在工程学中 的应用:椭圆形 建筑、椭圆形管
道等
4
椭圆在艺术设计 中的应用:椭圆 形构图、椭圆形
图案等
谢谢
椭圆的周长与面积可以通 过公式计算
椭圆的离心率决定了椭圆 的形状
椭圆的焦点决定了椭圆的 位置和方向
椭圆的方程
椭圆的标准方程:
x^2/a^2 + y^2/b^2 01
=1
椭圆的焦点在x轴和y轴
上的坐标分别为(a,0)和 03
(0,b)
椭圆的顶点坐标为(a,0) 05
和(0,b)
02
a和b分别表示椭圆的长 半轴和短半轴
椭圆的性质:椭圆具
2 有对称性、周期性、 可积性等性质,这些 性质在几何应用中具 有重要作用。
椭圆定义(公开课)ppt课件

x2
a2
y2 a2 c2
1
x2 a2
y2 b2
1
b2
a2 c2
(请大家比较一下上面两式的不同,独立思考后回答
椭圆的标准方程。)
椭圆的标准方程
y
M
焦点在x轴:
x2 a2
y2 b2
1a b 0
b2 a2 c2
F1 o F2 x
(x c)2 y2 (x c)2 y2 2a y
2.如果把细绳的两端拉 开一段距离,分别固定在图 板的两点处,套上铅笔,拉 紧绳子,移动笔尖,画出的 又是什么图形?这一过程中, 笔尖(动点)满足什么几何 条件?
数学实验
• (1)取一条细绳, • (2)把它的两端固定在板
上的两个定点F1、F2 • (3)用铅笔尖(M)把细
绳拉紧,在板上慢慢移 动看看画出的 图形
生 活 中 的 椭 圆
如何精确地设计、制作、建造出现实生活中这些椭圆形的 物件呢?
星系中的椭圆
——仙女座星系
——“传说中的”飞碟
♦ 动画演示:太阳系行星的运动
土星
金星 太阳
地球
p3
月亮
木星
一、合作探究,形成概念:
请同学们用事先准备好的学习用具小组内共同完成一下 任务,并思考相应问题。
1.取一条定长的细绳,把它的两端都固定在图板的同一 点处,套上铅笔,拉紧绳子,移动笔尖,这时笔尖(动点) 画出的轨迹是一个什么图形?笔尖(动点)满足什么几何条 件?
结论:若常数大于|F1F2|,则点M的轨迹是(椭圆 )
若常数等于|F1F2|,则点M的轨迹是( 线段F1F2) 若常数小于|F1F2|,则点M的轨迹( 不存在 )
♦ 探讨建立平面直角坐标系的方案
椭圆的定义和标准方程PPT课件

2
2
y x 1 9 4
2
2
设F1、 F2为椭圆 P为椭圆上一点,与
x2 y2 1 的焦点, 25 9
构成一个
F1、 F2
PF 1F 2
的周长?
三角形,求
解:
Y
P
周长 PF F F PF PF 1F 2 1 1 2 2
PF1 PF2 F1F2
x y 25 9
| F1F2|=2c
(c>0)
a -2a cx+c x =a x -2a cx+a c +a y
(a 2 -c2 )x 2 +a 2 y2 =a 2 (a 2 -c2 )
b2 a 2 c 2
(b>0)
常数 =2a a>c
(a>0)
b2 x 2 +a 2 y2 =a 2b2
焦点在X轴的椭圆的标准方程:
|MF1|+|MF2|= 2a
(a>0)
|MF1|+|MF2|= 2a
(a>0)
(x+c) 2 +y 2 + (x-c) 2 +y 2 =2a
x 2 +(y+c) 2 + x 2 +(y-c) 2 =2a
(a 2 -c 2 )x 2 +a 2 y 2 =a 2 (a 2 -c 2 ) b a -c (b 0)
1
c 1
1
2c 2
2
F (1,0), F (1,0) 焦点为: F (0, 2 焦点为: 焦距为: 焦距 4 2 2 为:
2c 4 2
2), F2 (0,2 2)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(大于 | F1F2 )| 的点的轨迹叫做椭圆. 这两个定点 叫做椭圆的焦点,两焦点的距离叫做椭圆的焦距. 注:若| PF1| | PF2 || F1F2 |,则P点的轨迹为椭圆.
若 | PF1 | | PF2 || F1F2 |,则P点的轨迹为线段. 若| PF1 | | PF2 || F1F2 |,则P点的轨迹不存在.
F1
c O
F2
x
x2 a2
y2 b2
1a
b
0
2.椭圆的标准方程
例:已知点F1 、F2 为椭圆两个焦点,P为椭圆上任意一 点,且| F1F2 | 2c,| PF1 | | PF2 | 2a ,其中 a c 0 ,求椭圆方程
一般步骤: (1) 建系设点 (2) 写出点的集合
点拨:怎样建系可以 使方程尽可能简 单?
情感、态度与价值观:通过经历椭圆方程的化简,增 强学生战胜困难的意志品质并体会数学的简洁美、 对称美.通过讨论椭圆方程推导的等价性养成学生 扎实严谨的科学作风.
1.3 教学重点和难点
重点:椭圆的定义及椭圆的标准方程 难点:推导椭圆的标准方程 关键:含有两个根式的等式化简
二.教学策略
2.1教学方法与学法设计: “引导探究式教学” 2.2教学手段设计: 多媒体
析、概括问题的能力并用联系与发展的观点看问题
联系生活:
情境1.生活中,你见过哪些类似椭圆的图形或物体?
情境2.让学生观察倾斜的圆柱形水杯的水面边界线,并 从中抽象出数学模型.
情境3.观看天体运行的轨道图片.
设计意图:渗透科学源于生活,圆锥曲线 在生产和技术中有着广泛的应用.
2.椭圆的标准方程
a2 cx a x c2 y2
讨论平方的 等价性
a2 c2 x2 a2y2 a2 a2 c2
b2x2 a2y2 a2b2
xxc2y2 xc2y22a
x c2 y2 4a 2 4a x c2 y2 x c2 y2
a 2 c x a x c2 y 2 a 2 c2 x 2 a 2 y2 a 2 a 2 c2
b2x 2 a 2y2 a 2b2
x2 a2
y2 b2
1a b 0
2
a2
y2 b2
1a b 0
<1>对于给定条件,是否只有一种建系方法?
<2>不推导,你能写出另一种椭圆的标准方程吗?
<3>如何由方程,辨别两种不同的建系方法呢?
椭圆及其标准方程
教教 教 教
教
学学 法 学 板 学
背目 学 程 书 评
景标 法 序 设 价
分设 分 设 计 设
析计 析 计
计
一、教学背景分析
1、教材的地位与作用
椭圆及其标准方程是求曲线方程的深化和巩固,是学习 圆锥曲线的基础,对本章的学习具有导向和引领作用,具有 承前启后的作用.
2、学生现状分析
<1>将一条细绳的两端分别固定在平面内的两个 定点 、 F1 F2 上,用笔尖将细绳拉紧并运动, 在纸上 你得到了怎样的图形?
<2>如果调整细绳两端点F1、F2 的相对位置,细绳的 长度不变,猜想你的椭圆会发生怎样的变化?
<3>同样方式的操作为什么得到不同的结果?
活动形式:操作--交流--归纳--演示--联系生活 设计意图:准确理解椭圆的定义;培养学生观察、辨
例:已知点F1 、F2 为椭圆两个焦点,P为椭圆上任意一 点,且| F1F2 | 2c,| PF1 | | PF2 | 2a ,其中 a c 0 ,求椭圆方程
一般步骤: (1) 建系设点 (2) 写出点的集合
点拨:怎样建系可以 使方程尽可能简 单?
(3) 写出代数方程 (4) 化简方程
点拨:化简的目的是什 么?有怎样的方法?
直接 平方
x c2 y2 x c2 y2 2a
移项平方
x c2 y2 4a2 4a x c2 y2 x c2 y2
a2 cx a x c2 y2
y
b2 a2 c2
a b 0 a2 c2 x2 a2y2 a2 a22b2
(3) 写出代数方程 (4) 化简方程 (5) 证明
点拨:为化简方程, 你将如何处理?
活动形式:点拨----板演---点评
设计意图:掌握椭圆标准方程及推导方法;培养
学生战胜困难的意志品质
x c2 y2 x c2 y2 2a
x c2 y2 4a2 4a x c2 y2 x c2 y2
高中二年级学生正值身心发展的鼎盛时期,思维活跃, 又有了相应知识基础,所以他们乐于探索、敢于探究。但高 中生的逻辑思维能力尚属经验型,运算能力不是很强,有待 于训练提高.
3、重点:椭圆定义的理解及标准方程的推导.
难点:推导椭圆的标准方程.
二、教学目标设计
知识与技能: 准确理解椭圆的定义,掌握椭圆标准方程及其推导.
3.2讲授新课阶段
1.椭圆的定义 平面内与两个定点 F1、F2的距离的和等于常数
(大于 | F1F2 )| 的点的轨迹叫做椭圆. 这两个定点 叫做椭圆的焦点,两焦点的距离叫做椭圆的焦距. 注:若| PF1| | PF2 || F1F2 |,则P点的轨迹为椭圆.
若 | PF1 | | PF2 || F1F2 |,则P点的轨迹为线段. 若| PF1 | | PF2 || F1F2 |,则P点的轨迹不存在.
三.教学过程
3.1 复习引入阶段
(1)圆的定义是什么?圆的标准方程的形式怎样? (2)如何推导圆的标准方程呢?
活动形式:师问生答(教师作必要的补充、纠正) 设计意图:激活学生已有的认知结构;为本课推导椭
圆的标准方程提供了方法与策略.
3.2讲授新课阶段
1.椭圆的定义 平面内与两个定点 F1、F2的距离的和等于常数
过程与方法:培养学生动手、观察、辨析、归纳问题的能力.
情感、态度与价值观:通过经历椭圆方程的化简,增强学生战胜困难 的意志品质并体会数学的简洁美、对称美.通过讨论椭圆方程推导 的等价性养成学生扎实严谨的科学作风.
1.2 教学目标
知识与技能: 准确理解椭圆的定义,掌握椭圆的标 准方程及其推导.
过程与方法:通过引导学生亲自动手尝试画图、发 现椭圆的形成过程进而归纳出椭圆的定义,培养学 生观察、辨析、归纳问题的能力.
若 | PF1 | | PF2 || F1F2 |,则P点的轨迹为线段. 若| PF1 | | PF2 || F1F2 |,则P点的轨迹不存在.
F1
c O
F2
x
x2 a2
y2 b2
1a
b
0
2.椭圆的标准方程
例:已知点F1 、F2 为椭圆两个焦点,P为椭圆上任意一 点,且| F1F2 | 2c,| PF1 | | PF2 | 2a ,其中 a c 0 ,求椭圆方程
一般步骤: (1) 建系设点 (2) 写出点的集合
点拨:怎样建系可以 使方程尽可能简 单?
情感、态度与价值观:通过经历椭圆方程的化简,增 强学生战胜困难的意志品质并体会数学的简洁美、 对称美.通过讨论椭圆方程推导的等价性养成学生 扎实严谨的科学作风.
1.3 教学重点和难点
重点:椭圆的定义及椭圆的标准方程 难点:推导椭圆的标准方程 关键:含有两个根式的等式化简
二.教学策略
2.1教学方法与学法设计: “引导探究式教学” 2.2教学手段设计: 多媒体
析、概括问题的能力并用联系与发展的观点看问题
联系生活:
情境1.生活中,你见过哪些类似椭圆的图形或物体?
情境2.让学生观察倾斜的圆柱形水杯的水面边界线,并 从中抽象出数学模型.
情境3.观看天体运行的轨道图片.
设计意图:渗透科学源于生活,圆锥曲线 在生产和技术中有着广泛的应用.
2.椭圆的标准方程
a2 cx a x c2 y2
讨论平方的 等价性
a2 c2 x2 a2y2 a2 a2 c2
b2x2 a2y2 a2b2
xxc2y2 xc2y22a
x c2 y2 4a 2 4a x c2 y2 x c2 y2
a 2 c x a x c2 y 2 a 2 c2 x 2 a 2 y2 a 2 a 2 c2
b2x 2 a 2y2 a 2b2
x2 a2
y2 b2
1a b 0
2
a2
y2 b2
1a b 0
<1>对于给定条件,是否只有一种建系方法?
<2>不推导,你能写出另一种椭圆的标准方程吗?
<3>如何由方程,辨别两种不同的建系方法呢?
椭圆及其标准方程
教教 教 教
教
学学 法 学 板 学
背目 学 程 书 评
景标 法 序 设 价
分设 分 设 计 设
析计 析 计
计
一、教学背景分析
1、教材的地位与作用
椭圆及其标准方程是求曲线方程的深化和巩固,是学习 圆锥曲线的基础,对本章的学习具有导向和引领作用,具有 承前启后的作用.
2、学生现状分析
<1>将一条细绳的两端分别固定在平面内的两个 定点 、 F1 F2 上,用笔尖将细绳拉紧并运动, 在纸上 你得到了怎样的图形?
<2>如果调整细绳两端点F1、F2 的相对位置,细绳的 长度不变,猜想你的椭圆会发生怎样的变化?
<3>同样方式的操作为什么得到不同的结果?
活动形式:操作--交流--归纳--演示--联系生活 设计意图:准确理解椭圆的定义;培养学生观察、辨
例:已知点F1 、F2 为椭圆两个焦点,P为椭圆上任意一 点,且| F1F2 | 2c,| PF1 | | PF2 | 2a ,其中 a c 0 ,求椭圆方程
一般步骤: (1) 建系设点 (2) 写出点的集合
点拨:怎样建系可以 使方程尽可能简 单?
(3) 写出代数方程 (4) 化简方程
点拨:化简的目的是什 么?有怎样的方法?
直接 平方
x c2 y2 x c2 y2 2a
移项平方
x c2 y2 4a2 4a x c2 y2 x c2 y2
a2 cx a x c2 y2
y
b2 a2 c2
a b 0 a2 c2 x2 a2y2 a2 a22b2
(3) 写出代数方程 (4) 化简方程 (5) 证明
点拨:为化简方程, 你将如何处理?
活动形式:点拨----板演---点评
设计意图:掌握椭圆标准方程及推导方法;培养
学生战胜困难的意志品质
x c2 y2 x c2 y2 2a
x c2 y2 4a2 4a x c2 y2 x c2 y2
高中二年级学生正值身心发展的鼎盛时期,思维活跃, 又有了相应知识基础,所以他们乐于探索、敢于探究。但高 中生的逻辑思维能力尚属经验型,运算能力不是很强,有待 于训练提高.
3、重点:椭圆定义的理解及标准方程的推导.
难点:推导椭圆的标准方程.
二、教学目标设计
知识与技能: 准确理解椭圆的定义,掌握椭圆标准方程及其推导.
3.2讲授新课阶段
1.椭圆的定义 平面内与两个定点 F1、F2的距离的和等于常数
(大于 | F1F2 )| 的点的轨迹叫做椭圆. 这两个定点 叫做椭圆的焦点,两焦点的距离叫做椭圆的焦距. 注:若| PF1| | PF2 || F1F2 |,则P点的轨迹为椭圆.
若 | PF1 | | PF2 || F1F2 |,则P点的轨迹为线段. 若| PF1 | | PF2 || F1F2 |,则P点的轨迹不存在.
三.教学过程
3.1 复习引入阶段
(1)圆的定义是什么?圆的标准方程的形式怎样? (2)如何推导圆的标准方程呢?
活动形式:师问生答(教师作必要的补充、纠正) 设计意图:激活学生已有的认知结构;为本课推导椭
圆的标准方程提供了方法与策略.
3.2讲授新课阶段
1.椭圆的定义 平面内与两个定点 F1、F2的距离的和等于常数
过程与方法:培养学生动手、观察、辨析、归纳问题的能力.
情感、态度与价值观:通过经历椭圆方程的化简,增强学生战胜困难 的意志品质并体会数学的简洁美、对称美.通过讨论椭圆方程推导 的等价性养成学生扎实严谨的科学作风.
1.2 教学目标
知识与技能: 准确理解椭圆的定义,掌握椭圆的标 准方程及其推导.
过程与方法:通过引导学生亲自动手尝试画图、发 现椭圆的形成过程进而归纳出椭圆的定义,培养学 生观察、辨析、归纳问题的能力.
