平面势流(了解性学习)
合集下载
第15讲势流理论2

(1) 速度势
圆柱的绕流的流场等价于均匀 流与偶极的叠加场:
y
v0
a
r
θ
x
M cos θ ϕ = v0 r cos θ + 2π r
这里不必去直接求解拉氏方程。式中的偶极强度M为未知量,可 用边界条件求出。 速度势应满足的边界条件:
∂ϕ =0 ∂r
(圆柱表面上r = a)
∂ϕ ∂ϕ ∂ϕ = v0 cosθ, = −v0 sinθ 或 = v0 (无穷远处) ∂r r∂θ ∂x
有环量是指圆柱作等速直线运动的同时,绕自身轴心转动。圆柱转 动时,由于粘性作用,会诱导周围流体随之转动。当忽略粘性作为理想 流体处理时,这种诱导效应不能忽略。 圆柱旋转的诱导作用等同于圆心处一个平面点涡的作用。也就说, 可以用一个平面点涡代替圆柱的旋转。设圆柱的旋转角速度为ω,点涡的 涡强要满足圆柱表面速度为aω ,所以点涡强度应为:
平面势流的基本解的叠加均匀流和点源的叠加速度势流函数和复势均具有叠加性利用这一性质通过基本解叠加可以构造出复杂流动的解称为基本解叠加法也称奇点叠加法
第15讲 势流理论(2)
(Potential Flow Theory)
主要内容: 1.平面势流的基本解的叠加
速度势、流函数和复势均具有叠加性,利用这一性质,通过基本解叠 加可以构造出复杂流动的解,称为基本解叠加法,也称 奇点叠加法。
解得流线方程:
θ = 0 或 θ =π,
M r = = a2 2πv0
2
过驻点的流线有两条,一条是x轴,一条是以a为半径的圆。均匀流与 偶极的叠加可以模拟流体绕流圆柱的流动。 上述三种叠加流场的分析表明,奇点的适当叠加可以模拟流体绕流物 体的流动。
4 绕圆柱体无环量流动
恒定平面势流 (平面无旋流动)

2
x2
2
y2
0
项目三 空运出口货代单证 任务四 航空出口报关报检(报检单、出境货物通关单、报关单)
步骤二:认识并填制出境货物通关单 要完成出境货物通关单的制作,李芳芳必须先弄清楚集货单上各项 内容的含义,通过查阅相关资料,了解到出境货物通关单各项内容含义 如下: 1.收货人:填写本批出境货物的贸易合同中或信用证中买方名称。 任务给出买方为PEOPLES SPORTING GOODS & MDSG. CORP.,所 以此栏应填PEOPLES SPORTING GOODS & MDSG. CORP.。 2.发货人:填写本批出境货物的贸易合同中或信用证中受益人名称。 任务给出发货人为厦门阳光贸易有限公司,此栏应填厦门阳光贸易有限 公司。 任务执行
任务执行
项目三 空运出口货代单证 任务四 航空出口报关报检(报检单、出境货物通关单、报关单)
步骤三:填制报关单 李芳芳通过查阅相关资料,了解到出口货物报关单各 项内容含义如下:
在整理完上述信息后,李芳芳完成的报关单如下: 任务执行
速度势的极坐标表达式
d urdr u rd
ur
r
,
u
1 r
上述关系式代入不可压缩流体连续性微分方程
ux u y u z 0 x y z
特征2
2
x2
2
y 2
2
z 2
0
凡满足拉普拉斯方
程的函数是调和函
数,所以速度势
是调和函数
平面无旋流动或平面势流
∵平面流动的旋转角速度只有分量ωz
∴ωz为零
u y ux x y
d uxdx uydy
x
ux
,
y
第四章(3)§4-3-5 平面势流问题的基本解法

M R2 2V
2
V y M 2 2 C 2 x y
y
A R
B
M 2V R 2
速度为 V∞ 的无限远来流绕半径为R 的圆柱的无环量绕流的复位势:
2 1 R ( z ) V z V R ) V ( z z z
无环量绕流的速度场—— 共轭复速度
§4-3 理想不可压缩流体的无旋运动(势流理论)
第四章 理想流体力学专题11
§4-3-5 平面势流问题的基本解法 — 映像法(虚像法) * 平面映像定理
《平面映像定理》 设
f (z) 是全部奇点都位于上半面的复位势,今在
插入一无限平板作为固定边界,那么复位势
f (z) 代表的流动沿实轴 ox
( z) f ( z) f ( z)
2
压力分布是在 理想 不可压缩流体 不脱体 绕流 假设条件下得出的。因此,计算与粘 性密切相关的摩擦阻力和与分离流相关的 压差阻力时, 与实际情况会有本质的偏差, 但在圆柱绕流分离点之前,所有的理论结 果与实验结果都有较好的符合程度。 0o
-3.0 180o 150o 120o 90o 60o 30o
R
R y V Γ
§4-3 理想不可压缩流体的无旋运动(势流理论)
§4-3-5 平面势流问题的基本解法
第四章 理想流体力学专题33
* 叠加法求解要点 1.求解平面不可压缩流体无旋运动; 2.熟练掌握基本流动的复位势,流线分布和简单组合; 3.考察求解对象,构造出满足求解对象边界条件的叠 加复位势 ; 4.求得满足求解对象的复位势后,平面流动的速度分 布,等势线以及流线可由复位势直接求得; 5.根据伯努利积分可求解特定流线上的压力分布。
x y 2xy V 2 2V cos sin 4 RR R
2
V y M 2 2 C 2 x y
y
A R
B
M 2V R 2
速度为 V∞ 的无限远来流绕半径为R 的圆柱的无环量绕流的复位势:
2 1 R ( z ) V z V R ) V ( z z z
无环量绕流的速度场—— 共轭复速度
§4-3 理想不可压缩流体的无旋运动(势流理论)
第四章 理想流体力学专题11
§4-3-5 平面势流问题的基本解法 — 映像法(虚像法) * 平面映像定理
《平面映像定理》 设
f (z) 是全部奇点都位于上半面的复位势,今在
插入一无限平板作为固定边界,那么复位势
f (z) 代表的流动沿实轴 ox
( z) f ( z) f ( z)
2
压力分布是在 理想 不可压缩流体 不脱体 绕流 假设条件下得出的。因此,计算与粘 性密切相关的摩擦阻力和与分离流相关的 压差阻力时, 与实际情况会有本质的偏差, 但在圆柱绕流分离点之前,所有的理论结 果与实验结果都有较好的符合程度。 0o
-3.0 180o 150o 120o 90o 60o 30o
R
R y V Γ
§4-3 理想不可压缩流体的无旋运动(势流理论)
§4-3-5 平面势流问题的基本解法
第四章 理想流体力学专题33
* 叠加法求解要点 1.求解平面不可压缩流体无旋运动; 2.熟练掌握基本流动的复位势,流线分布和简单组合; 3.考察求解对象,构造出满足求解对象边界条件的叠 加复位势 ; 4.求得满足求解对象的复位势后,平面流动的速度分 布,等势线以及流线可由复位势直接求得; 5.根据伯努利积分可求解特定流线上的压力分布。
x y 2xy V 2 2V cos sin 4 RR R
北航水力学 第四章理想流体动力学和恒定平面势流解读

z1
p1
u12 2g
z2
p2
u22 2g
4.2.2 由动能定理推导理想流体的伯努利方程
推导过程同学们自学
z1
p1
u12 2g
z2
p2
u22 2g
本公式是由动能定理推导而得,它使伯努利方程有更加明确的 物理意义,说明伯努利方程是一能量方程。
第三节 元流伯努利方程的意义和应用
4.3.1 沿流线的伯努利方程的水力学意义
可见,在同一流线上各点的流函数为一常数,故等流函数线就是流线。
2、平面内任意两点流函数值的差等于通过这两点连线的流量。
y ABdrBnA x
d r dxi dy j
n cos i sin j dy i dx j
dr dr V ui v j
dq V
ndr
u
dy dr
v
dx dr
等 线和等Ψ线,这两族曲线互相垂直,构
成流网。
两族曲线所构成的正交网络,称为流网
流网的特征:
流网
等 线和速度矢量垂直,或者说, 等 线与等Ψ线(流线)垂直,
【例题】
已知90度角域内无粘流动,速度分布
ux kx uy ky
(k 0, x 0, y 0)
求:(1)判断该流场是否存在速度势函数, 若存在请给出并画出等势线;
流动。但粘滞性对流动 的影响很微小时,影响可以忽略。 --机械能守恒
引入势流的意义:使问题简化。
波浪运动,无分离的边界层外部的流动,多孔介质的流动(渗流) 等等可以看为势流。
4.4.1 流速势函数
以二维流动为例,根据流体运动学,它与无旋流动等价
由 ux 0 无旋流的条件→涡量 z 0
流体力学ppt课件-恒定平面势流
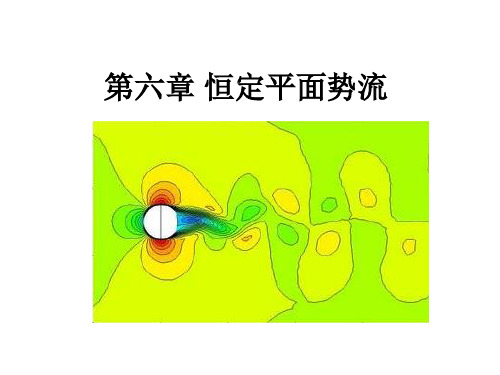
在圆柱坐标系统中,流速各项可表示为:
vr r
v
1 r
vz
z
圆柱坐标系统下拉普拉斯方程:
1 r
r
r
r
1 r2
2 2
2
z 2
0
6.2 流函数
恒定不可压缩平面二维流连续性方程表达式:
u v 0 x y
x
根据质量守恒定律,流进任意过流断面AC的流量dq应等于过 流断面AB和BC流出的流量,因此:
又因为:
dq udy vdx
dq d
对上式积分可得两条流线之间的流量q:
1 2
1 2
q
2 d
1
2
1
q0 q0
流向
左
右
流向
左
右
q
2
1
6.3几种简单的平面势流
速度势为:
m ln r 2
如果m为正,流动径向向外流,这种流动称为源流,例如泉眼向各方向的流动可作 为源流的例子,又如,离心式水泵,在某种情况下,叶轮内的流体运动可视为源流等。 如果m为负,流动流向源,这种流动称为汇流,例如地下水向井中的流动可作为汇流 的例子。流量m表示源流和汇流的强度。
u
x
v
y
w
z
不可压缩流体质量守恒定律表示如下:
V 0
不可压缩无旋流可表示为:
2 0
2 为Laplacian 算子,用笛卡尔坐标系表示为:
2 2 2
0 x2 y 2 z 2
这个微分方程在物理和工程方面经常出现,被称为拉普拉斯方 程(Laplace’s equation)。因此,无粘性不可压缩无旋流的控制 方程为拉普拉斯方程。这种类型的流动通常称为有势流。
【通用】流体力学6-势流理论.ppt

x (x,y)
vy
Q
2
y (x a)2
y2
Q
2
y (x a)2
y2
0
x a2 aQ
v0
y0
驻点
0.0
r1
y r r2
1
2
aa
Q
-Q
46
(4) 求零流线
Q
2
1
Q
2
2
v0 y
v0 y
Q
2
(1
2 )
源 汇 均匀流
tg
(1
2
)
tg1 tg2 1 tg1tg2
y
y
xa xa
A(r, )
r r2
M为偶极矩。
r2
1
2
Q B x C Q x
0.0
11
用迭加法求势函数φ
1
2
Q
2
(ln
r1
ln
r2 )
M cos 2 r
M 2
x x2 y2
0.0
y A(r, )
r1
r r2
r2
1
2
Q B x C Q x
12
流函数
1 2
Q
2
(1
2)
Q
2
( )
r2
x sin1
p
C
v2
2
C
2
(2V0
sin
)2
2 r0
单位长圆柱所受到的阻力
2
FD 0 p cos r0d 0
V0
0.0
dFL pds
d
dFD
r0
37
3 升力大小的计算:
第四章平面势流(4.1~4.4)详解

关,只是平面上点的函数。
dz
W (z) dF F F dz x (iy)
W (z) F i u iv
x x x
W (z) F 1 u iv
(iy) i y y
第四章 平面势流
§4.2 复位势和复速度
三、复速度
复 速 度 : W (z) u iv 共轭复速度: W (z) u iv 复速度与共轭复速度的乘积等于速度矢量模的平方。
B
Q = -vdx+udy
A
=
B A
Ψ x
dx +
Ψ y
dy =
B
dΨ
A
=Ψ2
-Ψ1
Ψ =Ψ2
Ψ =Ψ1 A
B
dl
u dy
v dx
第四章 平面势流
§4.1 速度势函数与流函数
二、流函数
3、流函数的性质
➢ 方 程
平面流动时,只存在z方向的涡量分量
v x
u y
x
x
y
y
2
有旋流动时: 2 或 2k
四、绕角流动
n=2 n=1
2
0
0
n= ½
2 0
n 小于 ½ 时得到大于 2π的区域,这显然没有物理意义。因此n应大于 ½ 。
第四章 平面势流
§4.3 基本流动
四、绕角流动ຫໍສະໝຸດ n=1/2n=3/2
n=2
n=3
第四章 平面势流
n=2/3
§4.3 基本流动
五、偶极子
偶极子:一对无限接近的强度相等的点源和点汇的迭加。
WW = (u - iv)(u +iv) = u2 + v2 = u u
流体力学:第八章 理想不可压缩流体平面流动

dq u ac v cb
因为:ac dy,cb dx,所以
dq udy vdx dy dx d
y x
积分, q
2 d
1
2
1
在论证流函数存在及说明其特性时,仅用了平面 流动的条件,故以上结论对任何平面流动都适用, 不论势流和涡流。
一、无旋流动(有势流动) 旋转角速度为零,通常称为势流。
x
1 ( w 2 y
v ) z
0,
或 w y
v z
y
1 ( u 2 z
w ) 0, x
或 u z
w x
z
1 2
( v x
u ) y
0,
或 v u x y
流体质点本身是否发生旋转,与流体微团 本身运动时的轨迹形状无关。
由数学分析知,上式是使udx vdy wdz为某一函数的
Cylinder with Circulation
引言
平面势流理论在流体力学中占有非常重要的地位 Why? Example
本章将简要地介绍平面势流的基本理论,分析绕流 不同形状的物体势流长的压力分布,以及流体对被绕 流物体的作用力。
§8–1 无旋流动和有旋流动
根据流体微团是否存在旋转,将流动分为两大类型: 无旋流动和有旋流动。 Two examples
涡线
涡线的表达式:
dx dy dz
x y z 通过微元断面的涡线组成涡束,涡束的表面称为涡管。 涡束断面面积和2倍旋转角速度的乘积称为涡通量,以 I表示,则微元涡通量为:
dI 2dA dA
2
速度环量:在流场中取一封闭曲线,流速沿该曲线的
积分称为沿 流线L的速度环量,用 表示:
全微分的必要充分条件。
因为:ac dy,cb dx,所以
dq udy vdx dy dx d
y x
积分, q
2 d
1
2
1
在论证流函数存在及说明其特性时,仅用了平面 流动的条件,故以上结论对任何平面流动都适用, 不论势流和涡流。
一、无旋流动(有势流动) 旋转角速度为零,通常称为势流。
x
1 ( w 2 y
v ) z
0,
或 w y
v z
y
1 ( u 2 z
w ) 0, x
或 u z
w x
z
1 2
( v x
u ) y
0,
或 v u x y
流体质点本身是否发生旋转,与流体微团 本身运动时的轨迹形状无关。
由数学分析知,上式是使udx vdy wdz为某一函数的
Cylinder with Circulation
引言
平面势流理论在流体力学中占有非常重要的地位 Why? Example
本章将简要地介绍平面势流的基本理论,分析绕流 不同形状的物体势流长的压力分布,以及流体对被绕 流物体的作用力。
§8–1 无旋流动和有旋流动
根据流体微团是否存在旋转,将流动分为两大类型: 无旋流动和有旋流动。 Two examples
涡线
涡线的表达式:
dx dy dz
x y z 通过微元断面的涡线组成涡束,涡束的表面称为涡管。 涡束断面面积和2倍旋转角速度的乘积称为涡通量,以 I表示,则微元涡通量为:
dI 2dA dA
2
速度环量:在流场中取一封闭曲线,流速沿该曲线的
积分称为沿 流线L的速度环量,用 表示:
全微分的必要充分条件。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ux , uy y x
d u x dy u y dx
d dx dy x y
流函数的极坐标表达式
d ur rd u dr
1 ur , u r r
特征1
ωz为零
平面无旋流的流函数也满足拉普拉斯方程
四、流网及其特征
流网(Flow Net):不可压缩流体平面无旋流动中, 流线簇与等势线簇构成的正交网格。 1、流网的特征
特征1 等势线与等流函数线处处正交
证明:
等势线簇:(x,y)=C
ห้องสมุดไป่ตู้
d u x dx u y dy 0
等流线簇:(x,y)=C
ux dy m2 dx uy
d ur dr u rd
1 ur , u r r
三、流函数 存在条件:不可压缩流体平面流动ψ (x,y) 。
平面流动 流线方程
dx dy ux u y
u x u y 0 x y
u x dy u y dx 0
u y u x x y
凡满足拉普拉斯方 程的函数是调和函 数,所以速度势是 调和函数
平面无旋流动或平面势流 ∵平面流动的旋转角速度只有分量ωz
∴ωz为零
u y
u x x y
d uxdx uy dy
2 2 2 0 2 x y
ux , u y x y
速度势的极坐标表达式
us s
函数(x,y,z)称为速度势(函数),即无旋流的速 度矢量是有势的。因此无旋运动(无涡流)又称 为有势流动。 上述关系式代入不可压缩流体连续性微分方程
u x u y u z 0 x y z
特征2
2 2 0 2 x y z
2 2 2
五、几种简单的平面势流 (1) 等速均匀流
流场中各点的速度矢量皆相互平行,且 大小相等的流动
ux y u y x ux x u y y
ψ = uy
若等速均匀流流速平行于x轴
= ux
若等速均匀流流速平行于y轴
ψ = -ux
= uy
(2) 源流和汇流
流体从水平的无限平面内的一点O (即源点)流出,均匀地沿径向直 线流向四周的流动称为源流 q为由源点沿z轴方向上,单位厚度 所流出的流量,称为源流强度
d u y dx u x dy 0
ux m1m2 ( )( ) 1 ux uy uy
dy u y m1 dx u x
特征2 等势线簇的势函数值沿流线方向增加,而流 线簇的流函数值则沿流线方向逆时针旋转90 ˚后所指 的方向增加。——儒科夫斯基法则。 特征3 流网中每一网格的相邻边长维持一定的比例
二、无旋流动的速度势(函数)
1 u z u y x 0 2 y z 1 u x u z y 0 2 z x 1 u y u x z 0 2 x y 或 或 或 u z u y y z u x u z z x u y u x x y
如图
环流强度 Г ,是不随圆周半径而变的 常数,具有方向性。Г>0时,为逆时 针旋转;Г <0时,为顺时针旋转。
Γ u r 0 , u 2r
Γ ln r 2 2 环流是圆周运动,但却不是有旋运动。
(4) 直角内的流动 设无旋运动的速度势为 若设 = a (x2 - y2 ) 则有 ψ = 2axy
此流动的流线是双曲线族。当ψ>0 时,x、y的符号相同,流线在I、III 象限内;ψ<0时,x、y的符号相反, 流线在II、IV象限内。当ψ = 0时, x=0或y=0,说明流线是坐标轴,称为 零流线。原点处速度为零,称为驻点。 若把零流线x、y轴的正值部分用固体壁面来代替,就得到 直角内的流动;若把x轴用固体壁面代替,则表示垂直流 向固体壁面的流动。
s n
若取δ = δψ,则δs=δn,此时流网网格为曲 边正方形
2、 流网的绘制
1)固体边界本身就是流线之一,等势线与边界正交。 2)自由液面必是流线。 3)根据流动的大致方向,按照事先选定的网格比例绘 制出流线簇和等势线簇。 3、 流网的应用 广泛用于理想不可压缩流体平面无旋流动中的速度 场、压强场求解
u y u x x y
2 2 2 0 2 x y
平面势流中,速度势函数和流函数均为调和函数 特征2 流函数的等值线是流线
d u x dy u y dx 0
( x, y ) const
特征3 任意两条流线间的流函数差值(ψ1 –ψ2 ),等 于通过两条流线间的单宽流量q。
q ur , u 0 2r
q q q u r dr u rd dr lnr ln x 2 y 2 2r 2 2
q q q y u r rd u dr rd arctan 2r 2 2 x
流体从四周沿径向均匀流入一点(汇点)的流动称为汇流 流入汇点的单位厚度流量称为 汇流强度-q。
上式是使表达式uxdx+uydy+uzdz能成为某一函数(x,y,z) 的全微分的必要和充分条件
ux dx u y dy uz dz d dx dy dz x y z
特征1
ux , u y , uz x y z
q ur , u 0 2r
q q y arctan 2 2 x q q 2 2 lnr ln x y 2 2
(3) 环流(或势涡流)
各流体质点皆绕某一固定点O做匀速圆周运动,且速 度与圆周半径成反比的流动称为环流
d u x dy u y dx
d dx dy x y
流函数的极坐标表达式
d ur rd u dr
1 ur , u r r
特征1
ωz为零
平面无旋流的流函数也满足拉普拉斯方程
四、流网及其特征
流网(Flow Net):不可压缩流体平面无旋流动中, 流线簇与等势线簇构成的正交网格。 1、流网的特征
特征1 等势线与等流函数线处处正交
证明:
等势线簇:(x,y)=C
ห้องสมุดไป่ตู้
d u x dx u y dy 0
等流线簇:(x,y)=C
ux dy m2 dx uy
d ur dr u rd
1 ur , u r r
三、流函数 存在条件:不可压缩流体平面流动ψ (x,y) 。
平面流动 流线方程
dx dy ux u y
u x u y 0 x y
u x dy u y dx 0
u y u x x y
凡满足拉普拉斯方 程的函数是调和函 数,所以速度势是 调和函数
平面无旋流动或平面势流 ∵平面流动的旋转角速度只有分量ωz
∴ωz为零
u y
u x x y
d uxdx uy dy
2 2 2 0 2 x y
ux , u y x y
速度势的极坐标表达式
us s
函数(x,y,z)称为速度势(函数),即无旋流的速 度矢量是有势的。因此无旋运动(无涡流)又称 为有势流动。 上述关系式代入不可压缩流体连续性微分方程
u x u y u z 0 x y z
特征2
2 2 0 2 x y z
2 2 2
五、几种简单的平面势流 (1) 等速均匀流
流场中各点的速度矢量皆相互平行,且 大小相等的流动
ux y u y x ux x u y y
ψ = uy
若等速均匀流流速平行于x轴
= ux
若等速均匀流流速平行于y轴
ψ = -ux
= uy
(2) 源流和汇流
流体从水平的无限平面内的一点O (即源点)流出,均匀地沿径向直 线流向四周的流动称为源流 q为由源点沿z轴方向上,单位厚度 所流出的流量,称为源流强度
d u y dx u x dy 0
ux m1m2 ( )( ) 1 ux uy uy
dy u y m1 dx u x
特征2 等势线簇的势函数值沿流线方向增加,而流 线簇的流函数值则沿流线方向逆时针旋转90 ˚后所指 的方向增加。——儒科夫斯基法则。 特征3 流网中每一网格的相邻边长维持一定的比例
二、无旋流动的速度势(函数)
1 u z u y x 0 2 y z 1 u x u z y 0 2 z x 1 u y u x z 0 2 x y 或 或 或 u z u y y z u x u z z x u y u x x y
如图
环流强度 Г ,是不随圆周半径而变的 常数,具有方向性。Г>0时,为逆时 针旋转;Г <0时,为顺时针旋转。
Γ u r 0 , u 2r
Γ ln r 2 2 环流是圆周运动,但却不是有旋运动。
(4) 直角内的流动 设无旋运动的速度势为 若设 = a (x2 - y2 ) 则有 ψ = 2axy
此流动的流线是双曲线族。当ψ>0 时,x、y的符号相同,流线在I、III 象限内;ψ<0时,x、y的符号相反, 流线在II、IV象限内。当ψ = 0时, x=0或y=0,说明流线是坐标轴,称为 零流线。原点处速度为零,称为驻点。 若把零流线x、y轴的正值部分用固体壁面来代替,就得到 直角内的流动;若把x轴用固体壁面代替,则表示垂直流 向固体壁面的流动。
s n
若取δ = δψ,则δs=δn,此时流网网格为曲 边正方形
2、 流网的绘制
1)固体边界本身就是流线之一,等势线与边界正交。 2)自由液面必是流线。 3)根据流动的大致方向,按照事先选定的网格比例绘 制出流线簇和等势线簇。 3、 流网的应用 广泛用于理想不可压缩流体平面无旋流动中的速度 场、压强场求解
u y u x x y
2 2 2 0 2 x y
平面势流中,速度势函数和流函数均为调和函数 特征2 流函数的等值线是流线
d u x dy u y dx 0
( x, y ) const
特征3 任意两条流线间的流函数差值(ψ1 –ψ2 ),等 于通过两条流线间的单宽流量q。
q ur , u 0 2r
q q q u r dr u rd dr lnr ln x 2 y 2 2r 2 2
q q q y u r rd u dr rd arctan 2r 2 2 x
流体从四周沿径向均匀流入一点(汇点)的流动称为汇流 流入汇点的单位厚度流量称为 汇流强度-q。
上式是使表达式uxdx+uydy+uzdz能成为某一函数(x,y,z) 的全微分的必要和充分条件
ux dx u y dy uz dz d dx dy dz x y z
特征1
ux , u y , uz x y z
q ur , u 0 2r
q q y arctan 2 2 x q q 2 2 lnr ln x y 2 2
(3) 环流(或势涡流)
各流体质点皆绕某一固定点O做匀速圆周运动,且速 度与圆周半径成反比的流动称为环流
