巧求面积---平移旋转
四年级秋季班第2讲 巧求面积

(2)依次连接正方形四边的中点得到的新正方形是原正方形面积的一半。
(3)平行四边形的两条对角线把平行四边形分成了四个面积相等的三角形(但是这四 个三角形不一定相同) 。
四年级秋季班第二讲——巧求面积
李拉娜
lilana927@hotmail .com
(4) 下图中两个正方形重叠部分面积是正方形 ABCD 面积的 的中心。
平移、旋转:主要通过移动的方法把分散的块集 中到一个规则的图形中。
一、 长方形的性质
( 1)交叉相乘,乘积相等。
四年级秋季班第二讲——巧求面积
李拉娜
lilana927@hotmail .com
如上图, S 1 S 4
S 2 S 3 ,也就是说,对角的两个长方形面积相乘,乘积相等。
练习 1 如图,长方形 ABCD 被分成 9 个小长方形,其中 5 个小长方形的面积如 图中所标注,求长方形 ABCD 的面积。
把阴影部分做如下的分割:
其中 C 是长为 5 厘米、宽为 2 厘米的长方形,面积为 2 5 10 平方厘米。 A 与 B 的面积之和为 66 10 56 平方厘米。 B 的面积=2×正方形边长,A 的面积=5×正方形边长。 如果把 B 的面积看成 2 份,则 A 的面积就是 5 份,A 与 B 的面积之和是 7 份,1 份就是 56 7 8 平方厘米。 那么 B 的面积就是 2 8 16 平方厘米,正方形的边长为 16 2 8 厘米。原长方形 的长为 8 5 13 厘米,宽为 8 2 10 厘米。 原长方形的面积为 13 10 130 平方厘米。 练习 3 (第 12 届“迎春杯”刊赛试题)街心花园里有一个正方形的花坛,四 周有一条宽为 1 米的甬道(如图) ,如果甬道的面积是 12 平方米,那么中间的 花坛面积是多少平方米?
巧求面积

巧求面积——方法
1、分割法:将分割出来的每一块求和 2、扩充法:将扩充的图形与多余图形求差 3、平移法:在不改变图形面积的前提下 4、旋转法:在不改变图形面积的前提下 5、交叉相乘法:适合“田字格”型
谢
谢
巧求面积——平移法
题:计算下面图形阴影部分的面积(单位:厘米)
90
10 80-10
解: (1)利用扩充法 90×80-90×10-80×10+10×10=5600(平 方厘米) (2)平移法 (90-10)×(80-10)=5600(平方厘米)
80
5
8 90-10 10
平移法:在不改变图形面积的前提下,改变 图形的位置。
巧求面积
题:如图,一块长方形的菜地,长8米,比宽多3米,周围有一条1 米宽的道路环绕着,求道路的面积是多少?
5+1+1
5 5
8 8 8+1+1
解: (1)利用扩充法 8-3=5(米) (8+1+1)×(5+1+1)-8×5=30(平方米) (2)利用分割法 8×1×2+5×1×2+1×1×4=30(平方米)
巧求面积——旋转法
题:正方形的一条边增加3厘米,另一条边增加2厘米,结果得到一 个比原正方形的面积多156平方厘米的长方形。求原正方形的边长?
解: 分割法: 156-3×2=150(平方厘米) 150÷(3+2)=30(平方厘米) 30÷1=30(厘米) 30×30=900(平方厘米)
2
3
旋转法: 156-3×2=150(平方厘米) 150÷(3+2)=30(厘米) 30×30=900(平方厘米)
巧求面积——扩充法
巧求面积

【知识梳理】本讲主要通过求一些不规则图形的面积,体会一种转化思想,重点在于把不规则图形转化为规则图形的方法,包括平移、旋转、割补、差不变原理,通过这些方法的学习,让学生体会求面积的技巧,提高学生的观察能力、动手操作能力、综合运用能力。
1、面积公式:长方形的面积=长⨯宽正方形的面积=边长⨯边长2、把不规则图形转化为规则图形的几种方法。
分割:把不规则图形分割成一些可求面积的规则图形。
添补:添上一个规则图形或者与所求图形有数量关系的图形,使原图形变为可求面积的规则图形。
平移、旋转:主要通过移动的方法把分散的块集中到一个规则的图形中。
【例题讲解】例1、你有什么好的方法计算所给图形的面积呢?(单位:厘米)4993例2、这是一个楼梯的截面图,高280厘米,每级台阶的宽和高都是20 厘米.问,此楼梯截面的面积是多少?例3、有一块菜地长16米,宽8米,菜地中间留了宽2米的路,把菜地平均分成四块,每一块地的面积是多少?例4、下图(单位:厘米)是两个相同的直角梯形重叠在一起,求阴影部分的面积.例5、一块长方形铁板,长15分米,宽12分米,如果长和宽各减少2分米,面积比原来减少多少平方分米?例6、一个边长为20厘米的正方形,依次连接四边中点得到第二个正方形,这样继续下去可得到第三个、第四个、第五个正方形.求第五个正方形的面积?【课堂巩固】1、求图中五边形的面积。
64532、如图是一个楼梯的截面图,每级台阶的宽和高都是20厘米.这楼梯的截面积是多少平方厘米?3、两个相同的直角三角形如下图所示(单位:厘米)重叠在一起,求阴影部分的面积.FBA4、 一个正方形,如果把它的相邻两边都增加6厘米,就可以得到一个新正方形,新正方形 的面积比原正方形大120平方厘米.求原正方形的面积?65、 如图是由5个大小不同的正方形叠放而成的,如果最小的正方形(阴影部分)的周长是8,那么最大的正方形的边长是 .第6题【课后练习】1、 如图是学校操场一角,请计算它的面积(单位:米)302030402、 如右图所示,图中的ABEFGD 是由一个长方形ABCD 及一个正方形CEFG 拼成的,线段的长度如图所示(单位:厘米),求ABEFGD 的周长和面积.3、四个完全相同的长方形拼成右图,大正方形的面积是l00平方分米,小正方形的面积是l6平方分米,求每个长方形的面积是多少?长方形的短边是多少分米?164、有一个边长为16厘米的正方形,连接每边的中点构成第二个正方形,再连接每边的中点构成第三个正方形,第四个正方形.求图中阴影部分的面积?。
巧用平移 妙求面积

■
■
▲乏 童
口 江 苏 高为 轩
平 移 是 一 种 重 要 的 图 形 变 换 , 也 是 解 决 某 些 问 题 很 有 效 的 手 段 .运 用 平 移 方 法 解 题 .常 能 化 难 为 易 ,化 繁 为 简 ,收 到 事 半 功 倍 的 效 果 .下 面 以 近 几 年 的 中 考 题 为 例 进 行 分 析 说 明 .
平 移 1个 单 位 :③ 得 到 一 个 新 的 矩 形 (如 图 6).在 新 得 到 的 矩 形 中 ,其 纵
向 的 长 仍 然 是 b,其 水 平 方 向 的 长 变 成 了 a卜-1.所 以 草 地 面 积 就 是 b(a卜-1):
- b.
点 拨 :在 前 面 的 三 个 图 形 中 .常 规 的 方 法 是 利 用 平 行 四 边 形 (或 分 割
大 小 相 等 的 正 方 形 ,E、F、G、日 分 别 在 AD 、
AB、BC、CD 边 上 ,且 是 某 个 dqETY形 的 顶 点 .
若 四 边 形 E粥 日 的 面 积 为 1,则 矩 形 ABCD
譬
的 面 积 为 ( ).
B
G c
A.2 B.
3
c.三
2
D 三 . 3
个 折 点 图 形 的 操 作 过 程 .进 而 展 开 联 想 .探 索
有 无 数 个 折 点 的 曲 线 的 平 移 (一 条 弯 曲 的 柏 油 小 路 ).通 过 平 移 形 成 封 闭 图 形 ,除 去 其 面 积 .
图 4
探 索 剩 余 的 面 积 是 否 相 等 .
解 :(1)画 出 图 形 如 图 5(要 求 对 应 点 在 水 平 位 置 上 ,宽 度 保 持 一 致 ).
奥数-巧求面积
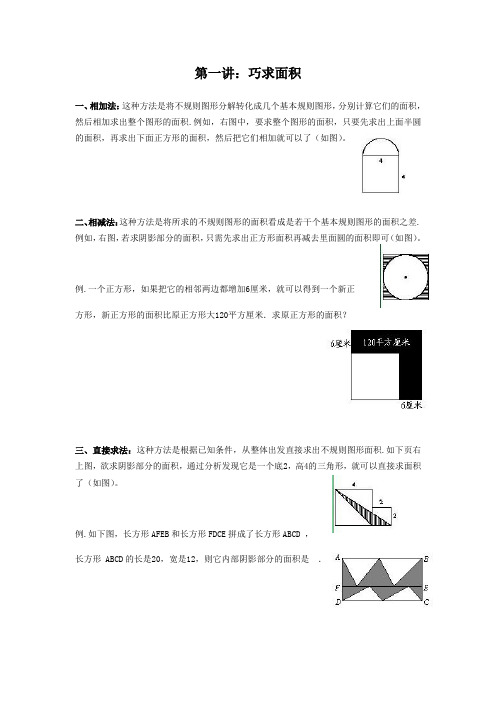
第一讲:巧求面积一、相加法:这种方法是将不规则图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加求出整个图形的面积.例如,右图中,要求整个图形的面积,只要先求出上面半圆的面积,再求出下面正方形的面积,然后把它们相加就可以了(如图)。
二、相减法:这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差.例如,右图,若求阴影部分的面积,只需先求出正方形面积再减去里面圆的面积即可(如图)。
例.一个正方形,如果把它的相邻两边都增加6厘米,就可以得到一个新正方形,新正方形的面积比原正方形大120平方厘米.求原正方形的面积?三、直接求法:这种方法是根据已知条件,从整体出发直接求出不规则图形面积.如下页右上图,欲求阴影部分的面积,通过分析发现它是一个底2,高4的三角形,就可以直接求面积了(如图)。
例.如下图,长方形AFEB和长方形FDCE拼成了长方形ABCD ,长方形 ABCD的长是20,宽是12,则它内部阴影部分的面积是.四、重新组合法:这种方法是将不规则图形拆开,根据具体情况和计算上的需要,重新组合成一个新的图形,设法求出这个新图形面积即可.例如,欲求右图中阴影部分面积,可以把它拆开使阴影部分分布在正方形的4个角处,这时采用相减法就可求出其面积了(如图)。
例.已知大正方形边长是7厘米,小正方形边长5厘米,求阴影部分的面积。
五、辅助线法:这种方法是根据具体情况在图形中添一条或若干条辅助线,使不规则图形转化成若干个基本规则图形,然后再采用相加、相减法解决即可.如右图,求两个正方形中阴影部分的面积.此题虽然可以用相减法解决,但不如添加一条辅助线后用直接法作更简便(如图)。
六、割补法:这种方法是把原图形的一部分切割下来补在图形中的另一部分使之成为基本规则图形,从而使问题得到解决.例如,如右图,欲求阴影部分的面积,只需把右边弓形切割下来补在左边,这样整个阴影部分面积恰是正方形面积的一半(如图).例.求阴影部分的面积。
四年级下册数学试题-寒假讲义 第13讲巧求面积_北师大版(2014秋)

第十三讲巧求面积知识点睛:长方形的面积=长×宽,正方形的面积=边长×边长。
但是,在平时的学习过程中,我们常常会遇到一些已知条件比较隐蔽、图形比较复杂、不能简单地用公式直接求出所求面积的题目,这就需要我们切实掌握有关概念,利用“割补”“平移”“旋转”等方法,使复杂的问题转化为普通的长方形、正方形面积的问题,从而正确解答。
例1:下图是一个养禽专业户用一段16米的篱笆围成的一个长方形养鸡场,求它的占地面积。
练习1:1、右图是某个养禽专业户用一段长13米的篱笆围成的一个长方形养鸡场,求养鸡场的占地面积。
2、用56米长的木栏围成长或宽是20米的长方形,其中一边利用围墙,怎样才能使围成的面积最大?例2:下图是一块水稻田,请计算它的面积(单位:米)练习2:1、求下图的面积。
(单位:分米)2、求下面图形的面积(单位:米)8471040302020151020155020例3:一个长方形,如果宽不变,长增加6米,那么它的面积增加54平方米;如果长不变,宽减少3米,那么它的面积减少36平方米。
这个长方形原来的面积是多少平方米?练习3:1、一个长方形,如果宽不变,长减少3米,那么它的面积减少24平方米;如果长不变,宽增加4米,那么它的面积增加60平方米。
这个长方形原来的面积是多少平方米?2、一个长方形,如果宽不变,长增加5米,那么它的面积增加30平方米;如果长不变,宽增加3米,那么它的面积增加48平方米。
这个长方形原来的面积是多少平方米?例4:如图所示,一块长方形草地。
长方形长16米,宽10米,中间有两条宽2米的道路,一条是长方形,另一条是平行四边形。
求有草部分(阴影部分)的周长。
练习4:1、求下图阴影部分的面积(单位:厘米)。
2、如图所示,公园里有一个长方形湖泊,湖上有一座景观桥(桥墩忽略不计)。
已知湖泊长30米,宽20米,桥面的宽度为2米,这座桥的面积是多少?210例5:街心花园有一个正方形花坛,四周有一条宽1米的通道(如图),如果通道的面积是12平方米,那么中间花坛的面积是多少平方米?练习5:1、有一个正方形水池,在它的周围修一条宽4米的路,这条路的面积是240平方米,这个水池的面积是多少?2、下图中阴影部分是边长为5厘米的正方形,四块完全一样的长方形的宽是8厘米,求这个图形的面积。
小学六年级奥数课件:巧求面积

例7. 如图,已知长方形ABCD的面积是54平方厘
米,BE=2AE,CF=2BF,则四边形ACFE的面
积是多少平方厘米?
A
E
B
F
D
C
解析
S△ABC=54÷ 2=27
连接CE。因为AE:EB=1:2,所以:S△ACE:S△BCE=1:2,
S△ACE=27÷ 3=9(平方厘米),S△BCE=27-9=18(平方厘米)
S△BPC的=S△BCE÷ 2=16(平方厘米) S△CDE=8× 4÷ 2=16(平方厘米) S△PDC 的面积=S△CDE÷ 2=8(平方厘米)
S阴=S正÷2-16-8=8(平方厘米)
例6.如图△ABC是一个等腰直角三角形,AB=BC=10,求图中阴 影部分的面积。(单位:分米)
解析
我们做辅助线。做AE垂直AB,EC平行AB,得到正 方形ABCE。 S半圆=5× 5× 3.14÷ 2=39.25(平方厘米) S正=10× 10=100(平方厘米) S△ADE=10× 15÷ 2=75(平方厘米) S阴=(39.25+100-75)÷2=32.125(平方厘米)
D
F
E
G
C
例4.在三角形ABC中,三角形AEO的面积是1,三角形ABO面积 是2,三角形BOD的面积是3,则四边形DCEO的面积是多少?
解析
连接OC,把DCEO分成两个三角形ECO和DCO 设ECO面积为x,DCO面积为y 由条件知,EO:OB=1:2, AO:OD=2:3
A E
则(AEO+ECO):DCO=2 :3
O
ECO:(DCO+BOD)=1:2
即: x:(y+3)=1:2
B
C
三年级奥数第11讲:巧求面积-教案

师:这确实是一种方法,老师刚刚在下面还看到有同学有不同做法,请你来说下你的思路。
生2:我是用大长方形的面积减去蓝色正方形的面积,再减去绿色正方形的面积,剩下的就是红色长方形的面积。
师:非常好,这也是一种很好的方法,你能具体说说具体的算法吗?生2: 大长方形的面积是6×10=60(平方厘米),蓝色正方形的面积是6×6=36 (平方厘米),绿色正方形的面积是4×4=16(平方厘米)师:那红色长方形的面积是多少呢?生2:60-36-16=8(平方厘米)。
师:这样求出来的答案也是8平方厘米。
这样做的同学举手示意一下。
师:看来也有很多同学是这么想的。
其实两种方法都是可以的。
同学们的思维真是活跃啊。
我们一起看下答案算对了吗。
板书:方法一:(10-6)×(6-4)=8(平方厘米)方法二:6×10-6×6-4×4=8(平方厘米)答:红色部分面积是8平方厘米。
师:刚刚我们解决了例题3,两种方法大家都会了吗?生:会了。
师:很好,很多题目我们可以从不同角度去思考。
我相信下面的练习3肯定也难不倒同学们。
大家自己动手做一做吧。
练习3:(5分)由两个完全相同的图形组成的图形(如图),计算下列图的面积。
分析:将图形进行平移、剪拼后可以发现这个图形的面积是一个边长为6厘米的大正方形减去一个边长为2厘米的小正方形的面积。
板书:6×6-2×2=32(平方厘米)答:这个图的面积是32平方厘米。
(二)例题4:(12分)一块长方形草地,长是38米,宽是28米,中间有两条宽2米的小路可以通过,这块草地的绿化面积是多少平方米?讲解重点:这个题目有2中方法,一个是用平移法,将两条小路移到一边,求空白小长方形的面积,就是绿化面积;或者可以求出两条小路的面积之和,要注意的是中间有一块2×2的地被重复计算了一次,要减掉。
再用草地面积减去小路面积,师:题目中要我们求这块草地的绿化面积是多少平方米,你们会怎么思考?生1:像上一个题目一样,我们可以用平移法把两条小路移到一边,中间就是绿化面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 解法:如上图,AC、DB两条对角线把正方形ABCD分成了4个直角三角 形,每两个直角三角形斜边重合可以拼成一个小的正方形,4个三角 形可以拼成2个相同的小正方形。这样的小正方形的边长就是大圆的 半径R,小正方形的面积正好等于正方形ABCD面积的一半。即:R2= 16÷2=8。 • 上图中EF、OG所在的直线把正方形ABCD分割成4个相同的小正方形, 这样的小正方形的边长就是小圆的半径r,小正方形的面积正好等于 正方形ABCD面积的1/4。即:r2=16÷4=4。 • 则所求阴影部分面积为: • 3.14×(R2-r2)÷2 • =3.14×(8-4)÷2 • =3.14×4÷2 • =6.28(平方厘米)
解析
如下图,将①号弓形绕P点旋转对折 后拼到②号空白处,拼成的阴影部 分正好与三角形POB重合。 所求 阴影部分总面积就等于三角形POB的
面积:4×4÷2÷2=4(平方厘米)
例2.求图中阴影部分的面积
解 析
在图中分割的两个正方形中,右边正方形的
阴影部分是半径为5的四分之一个圆,在左 边正方形中空白部分是半径为5的四分之一 个圆。 如右图所示,将右边的阴影部分平移到左边
由三段以格点为圆心,半径分别为1和2的圆弧围成.求图中阴影 部分的面积(结果保留π)
解析
将弓形CE绕点C旋转1800,则阴影部分的面积=弓形BE的面积.
巧求面积---平移旋转
知识梳理
相加法 相减法
放大法 等量代换法
割补法
巧求 面积
直接求法
重叠法 引辅助线法
平移法
旋转法
平移:沿着直线Βιβλιοθήκη 动特点:大小、形状、方向不变,位置变化
旋转:绕固定点圆周运动
特点:大小、形状不变,方向和位置变化 绕着一个点或一条线旋转
典型例题精讲
例1. 计算图中阴影部分的面积。(单位:厘米)。
所求阴影部分面积为:3.14× 42× 270/360=37.68(平方厘米)
例4. 如图,已知大圆半径是6厘米,小圆半径是3厘米,求阴影 部分面积
解析
大圆小圆是同心圆,将最左边的半径6厘米的小扇形绕圆心旋转90度,将①号阴 影部分拼到②号空白处,可以把阴影部分割补成一个1/4环形。所以图中阴影部 分面积为:3.14×(62-32)×1/4=21.195(平方厘米)
例5. 正方形ABCD面积为16平方厘米,求阴影部分面积。
解析
观察上图,以O为圆心的两个同心圆中间的环形被正方形ABCD的四条 边分成了12小块,阴影部分和空白部分各占6小块。 如下图:线段EF右边的3块阴影部分绕圆心O各旋转90度,正好填补在线
段EF左边的3小块空白处,与左边原有的3块阴影部分正好拼成半个环
正方形中。可以看出,原题图的阴影部分正
好等于一个正方形的面积,5× 5=25。
例3.图中三个圆的周长都是25.12厘米,不用测量,
计算出图中阴影部分的总面积。
解析
上图中3个圆的周长相等,即阴影部分是3个半径相等的扇形,半径 为:25.12÷ 3.14÷ 2=4(厘米) 这3个扇形半径相等,沿着梯形的边平移,再旋转后可以拼成一个大 的扇形。任意四边形的内角和都是360度,则阴影部分3个扇形拼成 的大扇形的圆心角为:360-90=270(度)
例6.图中正方形边长为8米,求阴影部分面积。
解析
如下图,画出正方形的两条对角线,把正方形分成4个相同的三角形。
再将①号②号阴影部分分别绕正方形中心点旋转90度,拼A空白处 和B空白处,阴影部分被割补成2个三角形,其面积正好等于长方形 面积的一半。所求阴影部分面积为:82÷ 2=32(平方米)
例7.已知每个网格中小正方形的边长都是1,图中的阴影图案是
