巧用平移妙求面积
人教版四年级下册数学7.3利用平移求不规则图形的面积(课件)

(1)
(2)
(画一画略) 2×4=8(cm2) 答:图形的面积是8 cm2。
4×2=8(cm2) 答:图形的面积是8 cm2。
当堂练习
1.(易错题)计算涂色部分的面积。(每个小方格的边长是1厘米)
10×3=30(cm2)
当堂练习
2. 下图是一座传统建筑中的窗格子图,涂色部分为实 木部分,实木部分的面积是多少?
7 图形的运动(二)
第3课时 利用平移求不规
则图形的面积
复习导入
求下面图形的面积。
2cm 2cm
2×2=4(cm²)
2cm 4cm
2×4=8(cm²)
探索新知
利用平移求不规则图形的面积
下面这个图形的
面积是多少? 1cm
这个图形有两条边都是 曲线,怎么计算面积?
探索新知
1cm
“数”的方法:数一数这个图
形占多少个方格,当数到不是整
格时当作半格计算。
这个图形占( 24 )个方格。 一个方格的面积是(1cm2),这个图形的面积是( 24cm2)。
探索新知
“移”的方法:我们先把左 1cm 侧的半圆剪下来,再向右
平移6格。
变成了一个长方形,它 的面积我会算啦!
6×4=24(cm²)
探索新知
回顾一下这道题,我们利用了哪种运动 方式,使图形发生了怎样的变化,从而 求出了不规则图形的面积?
平移
不规则图形
规则图形
转化面积不变Leabharlann 探索新知归纳总结:
求不规则图形的面积时,经常运用平 移等方法先把不规则图形转化为规则图形, 再求它的面积。
探索新知
1. 涂色部分占整个图形的几分之几?
1
1
利用平移计算面积ppt课件

精选ppt
13
课堂作业
求这个图形的周长和面积(每个小正方形的边长是1cm)。
精选ppt
14
感谢亲观看此幻灯片,此课件部分内容来源于网络, 如有侵权请及时联系我们删除,谢谢配合!
5
二、探索新知
回顾一下这道题,我们利用了哪种运动方式,使图形 发生了怎样的变化,从而求出了不规则图形的面积?
不规则图形
平移 转化
规则图形
面积不变
精选ppt
6
三、知识运用
1. 涂色部分占整个图形的几分之几?
(1)
Hale Waihona Puke (1)(1)(3)
(2)
(3)
这些都是不规则图 形,怎么想呢?
可以用图形运动 的知识试一试。
人教版四年级数学下册
第七单元第4课时 (图形的运动)
中社小学 林锡伟
精选ppt
1
一、复习导入
求下面图形的周长和面积。
2cm 4cm
周长:(2+4)×2=12(cm) 面积:2×4=8(cm²)
答:这个图形的周长是12cm, 面积是8cm²。
精选ppt
2
精选ppt
3
二、探索新知
精选ppt
4
精选ppt
精选ppt
7
三、知识运用
2.求这个图形的周长和面积(每个小正方形的边长是1cm)。
利用图形的 运动试一试。
..
.
.
.
.
(5+4)×2=18(cm)
答:这个图形的周长是18cm。
精选ppt
8
三、知识运用
2.求这个图形的周长和面积(每个小正方形的边长是1cm)。
《运用平移知识解决面积问题》教案

1.理论介绍:首先,我们要了解平移的基本概念。平移是指将一个图形整体沿着某一方向移动一定的距离,而不改变图形的形状和大小。平移是几何变换中的一种重要方式,它在解决面积问题时有着广泛的应用。
2.案例分析:接下来,我们来看一个具体的案例。这个案例展示了如何运用平移知识计算平移后图形的面积,以及如何求解平面图形在平移过程中的重叠部分面积。
实践活动环节,学生们分组讨论和实验操作表现得非常积极。他们通过实际动手操作,更好地理解了平移知识在解决面积问题中的应用。但在小组讨论中,我发现有些学生过于依赖同伴,缺乏独立思考。为了培养学生的独立思考能力,我计划在今后的教学中,多设计一些个人任务,鼓励学生在小组讨论前先独立思考。
学生小组讨论环节,大家对于平移在实际生活中的应用提出了很多有趣的观点。但在分享成果时,部分学生的表达不够清晰,逻辑性不强。针对这个问题,我将在今后的教学中加强学生的口头表达和逻辑思维能力训练,例如组织一些演讲活动和辩论赛。
3.重点难点解析:在讲授过程中,我会特别强调平移性质和面积计算这两个重点。对于难点部分,我会通过实际例题和图示来帮助大家理解。
(三)实践活动(用时10分钟)
1.分组讨论:学生们将分成若干小组,每组讨论一个与平移相为了加深理解,我们将进行一个简单的实验操作。这个操作将演示平移的基本原理,如使用纸片进行平移,并观察面积的变化。
四、教学流程
(一)导入新课(用时5分钟)
同学们,今天我们将要学习的是《运用平移知识解决面积问题》这一章节。在开始之前,我想先问大家一个问题:“你们在日常生活中是否遇到过需要计算图形面积或解决面积相关的问题?”比如,计算一块土地在平移后的新面积。这个问题与我们将要学习的内容密切相关。通过这个问题,我希望能够引起大家的兴趣和好奇心,让我们一同探索平移知识在解决面积问题中的奥秘。
巧用平移 妙求面积

■
■
▲乏 童
口 江 苏 高为 轩
平 移 是 一 种 重 要 的 图 形 变 换 , 也 是 解 决 某 些 问 题 很 有 效 的 手 段 .运 用 平 移 方 法 解 题 .常 能 化 难 为 易 ,化 繁 为 简 ,收 到 事 半 功 倍 的 效 果 .下 面 以 近 几 年 的 中 考 题 为 例 进 行 分 析 说 明 .
平 移 1个 单 位 :③ 得 到 一 个 新 的 矩 形 (如 图 6).在 新 得 到 的 矩 形 中 ,其 纵
向 的 长 仍 然 是 b,其 水 平 方 向 的 长 变 成 了 a卜-1.所 以 草 地 面 积 就 是 b(a卜-1):
- b.
点 拨 :在 前 面 的 三 个 图 形 中 .常 规 的 方 法 是 利 用 平 行 四 边 形 (或 分 割
大 小 相 等 的 正 方 形 ,E、F、G、日 分 别 在 AD 、
AB、BC、CD 边 上 ,且 是 某 个 dqETY形 的 顶 点 .
若 四 边 形 E粥 日 的 面 积 为 1,则 矩 形 ABCD
譬
的 面 积 为 ( ).
B
G c
A.2 B.
3
c.三
2
D 三 . 3
个 折 点 图 形 的 操 作 过 程 .进 而 展 开 联 想 .探 索
有 无 数 个 折 点 的 曲 线 的 平 移 (一 条 弯 曲 的 柏 油 小 路 ).通 过 平 移 形 成 封 闭 图 形 ,除 去 其 面 积 .
图 4
探 索 剩 余 的 面 积 是 否 相 等 .
解 :(1)画 出 图 形 如 图 5(要 求 对 应 点 在 水 平 位 置 上 ,宽 度 保 持 一 致 ).
人教版数学七年级下册平移——利用平移求不规则图形的面积课件

二、知识讲解
例题 如图(1),在一个矩形的草坪中修一条小路,若草坪的长 为40米,宽为15米,所修小路的宽度均为2米,请问:剩余草坪的 面积是多少?
40米
15米
解:剩余草坪的面积=(40-2)×15 =38×15 =570(平方米)
答:草坪的实有面积是864平方米。
有志登山顶,无志站山脚。 才自清明志自高。 丈夫志不大,何以佐乾坤。
36米
四、知识演变 街心公园里有一块草坪,长37米,宽26米,草坪中间修有1
米宽的小路,将草坪分成两块(如图)。草坪的实有面积是多少?
37米
解:草坪的实有面积=(37-1)×(26-1)
26 米
25
难点名称:利用平移将不规则图形转化为规 人这教个版 图数形学的七面级积下是册多少5c.m²?
2、某宾馆再重新装修后,准备在大厅的主楼梯上铺设某种红色地毯,已知这种地毯每平米售价30元,主楼梯道宽2米,其侧面如图所示,则购买地毯至少需要_____元.
则图形求面积 一解个:人 剩如余果草胸坪无的大面志积,=(既4使0-再2)有×壮15丽的举动也称不上是伟人。
=36×25
米
=900(平方米)
36米
答:草坪的实有面积是900平方米。
五、课堂练习
1、如图,是一块长方形草地,长方形的长是16米, 宽是10米。中间有两条道路,一条是长方形,一条是
平行四边形。草地部分的面积有 112平方米。
五、课堂练习 2、某宾馆再重新装修后,准备在大厅的主楼梯上铺设某 种红色地毯,已知这种地毯每平米售价30元,主楼梯道 宽2米,其侧面如图所示,则购买地毯至少需要_5_0_4__元.
利用平移巧求面积或长度

初中数学知识点精讲课程
利用平移巧求面积或长度
某些求图形面积的问题,若能想到用平移知识 并:利用平移的性质求长度或面积
例:如图,将三角形ABC沿BC方向平移acm得到三角形DEF,若
△ABC的周长为bcm,则四边形ABFD的周长为___________. (b+2a)cm
课堂小结
将某些求面积的图形,经过平移以后得出新的 图形,就会使计算变的很简单,所以其重点就 是找出能用平移来解决的图形。
典例精讲
典例精讲
∴S阴影部分=S平行四边形ACFD-S△ADG
典例精讲 类型二:平移中利用转化思想求面积(或长度)
如图2,在一个长方形的草坪上有两条等 宽且互相垂直的长方形小路(长度单位: m),那么草坪的面积为______ m2
典例精讲
解析:将两条小路分别作如图3所示的 平移,则草坪的面积就是图3中空白部 分(长方形)的面积,即(50-2)× (30-2)=1344 m2 .
解:∵△ABC沿BC方向平移acm得到△DEF,
∴DF=AC,AD=CF=acm, ∴四边形ABFD的周长=AB+BE+DF+AD=AB+BC+CF+AC+AD
=△ABC的周长+AD+CF=(b+2a)cm.
典例精讲
例:图1是重叠的两个直角三角形.将其中一个 直角三角形沿BC方向平移得到△DEF的位置.若 AB=8cm,BE=4cm,DG=3cm,则图中阴影部分的面 积为_____cm2 .
巧用平移妙求面积
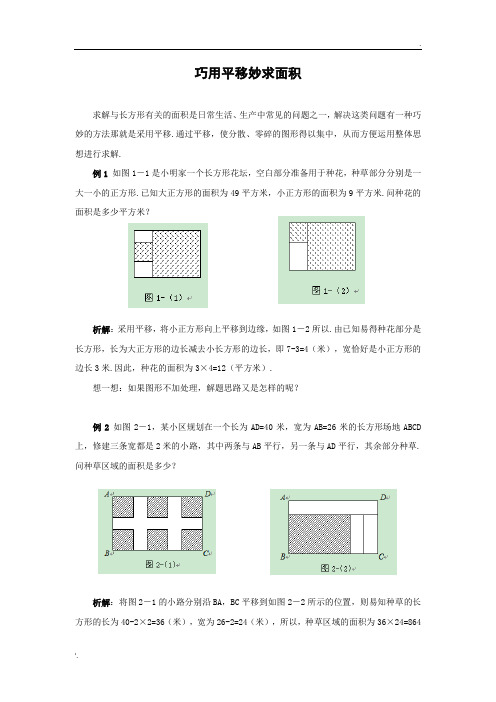
巧用平移妙求面积求解与长方形有关的面积是日常生活、生产中常见的问题之一,解决这类问题有一种巧妙的方法那就是采用平移.通过平移,使分散、零碎的图形得以集中,从而方便运用整体思想进行求解.例1如图1-1是小明家一个长方形花坛,空白部分准备用于种花,种草部分分别是一大一小的正方形.已知大正方形的面积为49平方米,小正方形的面积为9平方米.问种花的面积是多少平方米?析解:采用平移,将小正方形向上平移到边缘,如图1-2所以.由已知易得种花部分是长方形,长为大正方形的边长减去小长方形的边长,即7-3=4(米),宽恰好是小正方形的边长3米.因此,种花的面积为3×4=12(平方米).想一想:如果图形不加处理,解题思路又是怎样的呢?例2如图2-1,某小区规划在一个长为AD=40米,宽为AB=26米的长方形场地ABCD 上,修建三条宽都是2米的小路,其中两条与AB平行,另一条与AD平行,其余部分种草.问种草区域的面积是多少?析解:将图2-1的小路分别沿BA,BC平移到如图2-2所示的位置,则易知种草的长方形的长为40-2×2=36(米),宽为26-2=24(米),所以,种草区域的面积为36×24=864(平方米).想一想:如果图形不加处理,分别求出三条小路的面积,然后用场地的总面积减去三条小路的面积,求得种草区域的面积.与运用平移来解,感觉怎样?例3 如图3-1所示,在一块长为24米,宽为16米的草坪上有一条宽为2米的曲折小路,你能运用你所学的知识求出这块草坪的绿地面积吗?析解:小路的面积只与小路的宽度和长度有关,与其位置没有关系.可以将路分解成向下和向右分别平移的两部分,平移后如图3-2所示.这时,绿地转化为长22 米,宽18 米的长方形,可求得绿地的面积为:22×18=396 (平方米).想一想:直接求小路的面积是无法求解的,那么,本题中将曲折的小路进行平移,意义何在?图3-(1)图3-(2)坐标系中求图形的面积图形的面积可以利用相应的面积公式求得,但是在平面直角坐标系内的求面积问题,往往不直接给出边或高之类的条件,而是给出一些点的坐标.现对这类题目的解法举例说明如下.一、计算三角形的面积例1 如图1所示,三角形ABC 的三个顶点的坐标分别是A (-4,-3),B (0,-3),C (-2,1).求三角形ABC 的面积.分析:观察图形,在坐标系中读取三角形ABC 的一边的长度,和该边上的高的长度.因为AB ∥x 轴,所以AB 可以作为底边.解:因为AB=0-(-4)=4,AB 边上的高为h=1-(-3)=4,所以三角形ABC 的面积是:21AB ·h=21×4×4=8.评注:当两点在平行于x 轴的直线上时,两点之间的距离是两点的横坐标的差的绝对值;当两点在平行于y 轴的直线上时,两点之间的距离是两点的纵坐标的差的绝对值.如果三角形中有一边在坐标轴上或与坐标轴平行时,可以直接利用三角形的面积公式求解.例2 如图2所示,在三角形AOB 中,A ,B ,C 三点的坐标分别为(-1,2),(-3,1),(0,-1),求三角形AOB 的面积.分析:三角形的三边都不与坐标轴平行,根据平面直角系的特点,可以将三角形的面积转化为正方形EFCD 的面积减去多余的直角三角形的面积,即可求出此三角形的面积.解:如图2,作正方形EFCD ,则该正方形的面积为EF ·FC=3×3=9.因为三角形AEB 的面积是:21×AE ·EB=21×2×1=1,三角形BFC 的面积是:21BF ·FC=21×2×3=3,三角形ACD 的面积是:21×AC ·AD=21×3×1=23,所以三角形ABC 的面积是:9-1-3-23=27.点评:如果三角形的三边中没有任何一边在坐标轴上或与坐标轴平行时,则应将其进行转化为几个规则图形的面积和或差.E FD图2y BCAO 11 图1二、计算四边形的面积例3 如图3,四边形ABCD 的四个顶点的坐标分别为A (-2,2),B (-3,-3),C (3,3),D (2,1),求四边形ABCD 的面积.分析:四边形ABCD 不是规则的四边形,要求其面积,可将该四边形的面积转化为两个直角三角形和一个梯形的面积的和来计算.解:作AE ⊥BC 于E ,DF ⊥BC 于F ,则四边形ABCD 的面积=三角形ABE 的面积+梯形AEFD 的面积+三角形DFC 的面积,因为三角形ABE 的面积为:21BE ·AE=21×1×5=25,梯形AEFD 的面积为:21(DF+AE )·EF=21×(4+5)×4=18,三角形DFC 的面积为:21FC ·DF=21×1×4=2,所以四边形ABCD 的面积为:25+18+2=2221.点评:解决平面直角坐标系中的四边形的面积问题,一般思路是将不规则的图形转化为规则的图形,再利用相关的图形的面积公式求解.。
6.利用平移巧求面积或长度

解:∵△ABC沿BC方向平移acm得到△DEF, ∴DF=AC,AD=CF=acm, ∴四边形ABFD的周长=AB+BE+DF+AD=AB+BC+CF+AC+AD
=△ABC的周长+AD+CF=(b+2a)cm.
典例精讲
例:图1是重叠的两个直角三角形.将其中一个 直角三角形沿BC方向平移得到△DEF的位置.若 AB=8cm,BE=4cm,DG=3cm,则图中阴影部分的面
课堂小结
将某些求面积的图形,经过平移以后得出新的 图形,就会使计算变的很简单,所以其重点就 是找出能用平移来解决的图形。
优翼 微课
初中数学知识点精讲课程
利用平移巧求面积或长度
某些求图形面积的问题,若能想到用平移知识 并将部分图形平移后去解,那么你会品尝到方 便简捷的滋味!
典例精讲 类型一:利用平移的性质求长度或面积 例:如图,将三角形ABC沿BC方向平移acm得到三角形DEF,若
(b+2a)cm △ABC的周长为bcm,则四边形ABFD的周长为___________.
积为_____cm2 .
典例精讲
典例精讲
∴S阴影部分=S平行四边形ACFD-S△ADG
典例精讲 类型二:平移中利用转化思想求面积(或长度)
如图2,ቤተ መጻሕፍቲ ባይዱ一个长方形的草坪上有两条等 宽且互相垂直的长方形小路(长度单位: m),那么草坪的面积为______ m2
典例精讲
解析:将两条小路分别作如图3所示的 平移,则草坪的面积就是图3中空白部 分(长方形)的面积,即(50-2)× (30-2)=1344 m2 .
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
巧用平移妙求面积 Document number:NOCG-YUNOO-BUYTT-UU986-1986UT
巧用平移妙求面积
求解与长方形有关的面积是日常生活、生产中常见的问题之一,解决这类问题有一种巧妙的方法那就是采用平移.通过平移,使分散、零碎的图形得以集中,从而方便运用整体思想进行求解.
例1如图1-1是小明家一个长方形花坛,空白部分准备用于种花,种草部分分别是一大一小的正方形.已知大正方形的面积为49平方米,小正方形的面积为9平方米.问种花的面积是多少平方米
析解:采用平移,将小正方形向上平移到边缘,如图1-2所以.由已知易得种花部分是长方形,长为大正方形的边长减去小长方形的边长,即7-3=4(米),宽恰好是小正方形的边长3米.因此,种花的面积为3×4=12(平方米).
想一想:如果图形不加处理,解题思路又是怎样的呢
例2如图2-1,某小区规划在一个长为AD=40米,宽为AB=26米的长方形场地ABCD上,修建三条宽都是2米的小路,其中两条与AB平行,另一条与AD 平行,其余部分种草.问种草区域的面积是多少
析解:将图2-1的小路分别沿BA,BC平移到如图2-2所示的位置,则易知种草的长方形的长为40-2×2=36(米),宽为26-2=24(米),所以,种草区域的面积为36×24=864(平方米).
想一想:如果图形不加处理,分别求出三条小路的面积,然后用场地的总面积减去三条小路的面积,求得种草区域的面积.与运用平移来解,感觉怎样
例3 如图3-1所示,在一块长为24米,宽为16米的草坪上有一条宽为2米的曲折小路,你能运用你所学的知识求出这块草坪的绿地面积吗
析解:小路的面积只与小路的宽度和长度有关,与其位置没有
关系.可
以将路分解成
向下和向右分别平移的两部分,平移后如图3-2所示.这时,绿地转化为长22 米,宽18 米的长方形,可求得绿地的面积为:22×18=396 (平方米).
想一想:直接求小路的面积是无法求解的, 那么,本题中将曲折的小路进行平移,意义何在
坐标系中求图形的面积
图形的面积可以利用相应的面积公式求得,但是在平面直角坐标系内的求面积问题,往往不直接给出边或高之类的条件,而是给出一些点的坐标.现对这类题目的解法举例说明如下.
一、计算三角形的面积
例1 如图1所示,三角形ABC 的三个顶点的坐标分别
是A (-4,-3),B (0,-3),C (-2,1).求三角形ABC 的面积.
分析:观察图形,在坐标系中读取三角形ABC 的一边的长度,和该边上的高的长度.因为AB ∥x 轴,所以AB 可以作为底边.
图3-(1)
图3-(2)
y
B C
A O 1
1 图1
解:因为AB=0-(-4)=4,AB 边上的高为h=1-(-3)=4,所以三角形ABC 的面积是:
21AB ·h=2
1
×4×4=8. 评注:当两点在平行于x 轴的直线上时,两点之间的距离是两点的横坐标的差的绝对值;当两点在平行于y 轴的直线上时,两点之间的距离是两点的纵坐标的差的绝对值.
如果三角形中有一边在坐标轴上或与坐标轴平行时,可以直接利用三角形的面积公式求解.
例2 如图2所示,在三角形AOB 中,A ,B ,C 三点的坐标分别为(-1,2),(-3,1),(0,-1),求三角形AOB 的面积.
分析:三角形的三边都不与坐标轴平行,根据平面直角系的特点,可以将三角形的面积转化为正方形EFCD 的面积减去多余的直角三角形的面积,即可求出此三角形的面积.
解:如图2,作正方形EFCD ,则该正方形的面积为EF ·FC=3×3=9.
因为三角形AEB 的面积是:
21×AE ·EB=2
1
×2×1=1,三角形BFC 的面积是:21BF ·FC=2
1
×2×3=3,三角形ACD 的
面积是:21×AC ·AD=21×3×1=23
,所以三角形ABC 的面积
是:9-1-3-23=2
7
.
点评:如果三角形的三边中没有任何一边在坐标轴上或与坐标轴平行时,则应将其进行转化为几个规则图形的面积和或差.
二、计算四边形的面积
E F
D
图2
例3 如图3,四边形ABCD 的四个顶点的坐标分别为A
(-2,2),B (-3,-3),C (3,3),D (2,1),求四边形ABCD 的面积.
分析:四边形ABCD 不是规则的四边形,要求其面积,可将该四边形的面积转化为两个直角三角形和一个梯形的面积的和来计算.
解:作AE ⊥BC 于E ,DF ⊥BC 于F ,
则四边形ABCD 的面积=三角形ABE 的面积+梯形AEFD 的面积+三角形DFC 的面积,
因为三角形ABE 的面积为:
21BE ·AE=21×1×5=2
5
,梯形AEFD 的面积为:21(DF+AE )·EF=21
×(4+5)×4=18,三角形DFC 的面积为:
21FC ·DF=21×1×4=2,所以四边形ABCD 的面积为:25+18+2=222
1. 点评:解决平面直角坐标系中的四边形的面积问题,一般思路是将不规则的图形转化为规则的图形,再利用相关的图形的面积公式求解.。
