金融计量经济第五讲虚拟变量模型和Probit、Logit模型
logit 和probit模型的系数解释 -回复

logit 和probit模型的系数解释-回复Logit和Probit模型是常用的二元选择模型,用于分析二元变量的选择行为。
它们通常用于解释个体在做出选择时的决策,可以帮助我们理解各种影响因素对选择行为的影响。
在这篇文章中,我将逐步回答有关Logit和Probit模型的系数解释的问题,介绍这两个模型的基本原理、模型形式、系数解释和使用注意事项,以及如何解读模型中的系数。
首先,让我们从基本原理开始,了解Logit和Probit模型的背后逻辑。
Logit 和Probit模型都属于广义线性模型(Generalized Linear Models),它们基于一个相似的假设:选择行为是一个概率事件,可以由一组解释变量进行解释。
这些解释变量可以是个体特征(如年龄、性别、教育水平等),也可以是一些特定的因素(如收入水平、市场利率等)。
模型的目的是通过对这些解释变量的分析,预测和解释个体做出选择的概率。
接下来,让我们详细了解Logit和Probit模型的模型形式。
Logit模型使用的是逻辑函数(Logistic Function),而Probit模型使用的是标准正态分布的累积分布函数。
具体来说,Logit模型的形式为:p(y=1 x) = F(xβ) = 1 / (1 + e^(-xβ))其中,p(y=1 x)表示个体在给定解释变量x的情况下选择y=1的概率,F(x β)表示Logistic函数,x是解释变量的值,β是模型的系数。
相比之下,Probit模型的形式稍有不同:p(y=1 x) = Φ(xβ)其中,Φ(xβ)表示标准正态分布的累积分布函数,其他符号的含义与Logit 模型相同。
两个模型的模型形式不同,但它们都具有类似的特点:在x 趋近于正无穷时,概率趋近于1,而在x 趋近于负无穷时,概率趋近于0。
这种形式可以帮助我们理解个体选择行为的变化趋势。
现在让我们转向系数解释的问题。
模型的系数代表着解释变量对选择行为的影响程度。
金融计量经济第五讲虚拟变量模型和Probit、Logit模型

原始模型:
YX (5.8)
• 其中Y为观测值取1和0的虚拟被解释变量,X为 解释变量。
• 模型的样本形式: yi Xii
(5.9)
• 因为E(i)0
,E所(y以i)Xi
• 令: p i P ( y i 1 ) 1 p i P ( y i 0 )
• 于是有: E ( y i) 1 P ( y i 1 ) 0 P ( y i 0 ) p i
其它季度
1, 三季度
D3
0,
其它季度
• 小心“虚拟变量陷阱”!
精品课件
三、虚拟变量的应用
• 1、在常数项引入虚拟变量,改变截距。
y i0D 1 x 1 i kx k iu i (5.1)
• 对上式作OLS,得到参数估计值和回归模型:
y ˆiˆ0ˆD ˆ1 x 1 i ˆkx ki(5.2)
金融计量经济第五讲
虚拟变量模型和Probit、Logit模 型
精品课件
第一节 虚拟变量的一般应用
一、虚拟变量及其作用 1.定义:取值为0和1的人工变量,表示非量化
(定性)因素对模型的影响,一般用符号D表 示。例如:政策因素、地区因素、心理因素、 季节因素等。 2.作用: ⑴描述和测量定性因素的影响; ⑵正确反映经济变量之间的相互关系,提高模型 的精度; ⑶便于处理异常数据。
yˆt ˆ ˆxt yˆt ˆ ˆxt ˆ2 yˆt ˆ ˆxt ˆ3 yˆt ˆ ˆxt ˆ4
精品课件
一季度 二季度 三季度 四季度
例题:美国制造业的利润—销售额行为
• 模型:利 t 1 润 2 D 2 t 3 D 3 t 4 D 4 t ( 销 ) t u t售
0.503543 0.500354 1.13E+03 1.99E+09 -13241.74 1.648066
probit模型与logit模型

probit模型与lo git模型2013-03-30 16:10:17probit模型是一种广义的线性模型。
服从正态分布。
最简单的pr obit模型就是指被解释变量Y是一个0,1变量,事件发生地概率是依赖于解释变量,即P(Y=1)=f(X),也就是说,Y=1的概率是一个关于X的函数,其中f(.)服从标准正态分布。
若f(.)是累积分布函数,则其为Log istic模型Logit模型(Logitmodel,也译作“评定模型”,“分类评定模型”,又作Logi sticregres sion,“逻辑回归”)是离散选择法模型之一,属于多重变量分析范畴,是社会学、生物统计学、临床、数量心理学、市场营销等统计实证分析的常用方法。
逻辑分布(Logist ic distri butio n)公式P(Y=1│X=x)=exp(x’β)/1+exp(x’β)其中参数β常用极大似然估计。
Logit模型是最早的离散选择模型,也是目前应用最广的模型。
Logit模型是Luc e(1959)根据IIA特性首次导出的;Marsch ark(1960)证明了Log it模型与最大效用理论的一致性;Marley (1965)研究了模型的形式和效用非确定项的分布之间的关系,证明了极值分布可以推导出Logi t 形式的模型;McFadd en(1974)反过来证明了具有Log it形式的模型效用非确定项一定服从极值分布。
此后Logi t模型在心理学、社会学、经济学及交通领域得到了广泛的应用,并衍生发展出了其他离散选择模型,形成了完整的离散选择模型体系,如Probi t模型、NL模型(Nest Logitmodel)、MixedLogit模型等。
模型假设个人n对选择枝j的效用由效用确定项和随机项两部分构成:Logit模型的应用广泛性的原因主要是因为其概率表达式的显性特点,模型的求解速度快,应用方便。
Logit和Probit模型的比较结果
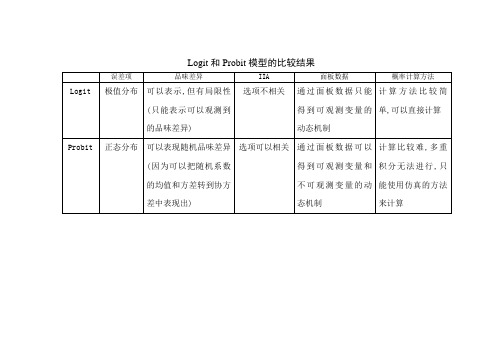
误差项
品味差异
IIA
面板数据
概率计算方法
Logit
极值分布
可以表示,但有局限性(只能表示可以观测到的品味差异)
选项不相关
通过面板数据只能得到可观测变量的动态机制
计算方法比较简单,可以直接计算
Probit
正态分布
可以表现随机品味差异(因为可以把随机系数的均值和方差转到协方差中表现出)
选项可以相关
通过面板数据可以得到可观测变量和不可观测变量的动态机制
计算比较难,多重积分无法进行,只能使用仿真的方法来计算
虚拟变量回归模型:计量经济学3

3、虚拟变量的实际应用
(1)虚拟变量可以用于研究制度变迁的影响
如:研究2001年中国加入WTO事件对中国进出 口贸易的影响,可以建立如下方程:
+d 主要贸易伙伴国 GDP+e DWTO
中国的进出口贸易总值 =a b 人民币汇率 c 中国GDP
计量经济学专题:
虚拟变量的回归与Probit模型、 Logit模型
1、虚拟变量的性质
与有明确尺度量化了的变量(GDP、产 量、价格、成本、汇率等)不同,虚拟 变量是一种定性性质的变量,如性别、 种族、国籍等只涉及“是”与“非”两 种状态的变量。 虚拟变量的取值只取0或1。1表示某种性 质出现,0表示某种性质不出现。
(3)对一个普通变量与两个两分虚拟变 量的回归
例:种族及性别差异对薪金的影响。 假定薪金除了受工作年限、性别的影响 之外,还受种族的影响。
yi 1 2 D2i 3D3i xi ui
yi 为某人的工资水平,xi 为工作年限。
yi 1 2 D2i 3D3i xi ui 虚拟变量模型:
白人女性的工资水平:
E( yi D2 0, D3 1) (1 3) xi
yi 1 2 D2i 3D3i xi ui 虚拟变量模型:
其他人种男性的平均工资:
E( yi D2 1, D3 0) (1 2) xi
其他人种女性的平均工资:
Pi P r(Y 1) P r(I i * I i ) F ( I i ) 1 2 1 2
Ii
金融计量经济第五讲虚拟变量模型和Probit、Logit模型

第二节 虚拟被解释变量模型
• 问题1:对于商业银行,企业贷款可能出现违约,也就是说一家企 业贷款后有违约和不违约两种可能,如何甄别?(李萌,2005)
• 问题2:证券投资者在特定时期内的投资选择是买或不买,如何确 定这样的选择?(王冀宁等,2003)
• 问题3:上市公司出现经营问题,可能成为ST、PT,是什么原因导 致这样的结果?
6563.76 1597.98
16.904 16.9416 157.922
0
应用例题2:股息税削减对股价的影响
• 背景资料—2005年6月14日,财政部、税务总局发文,规定对个人投资者从
上市公司取得的股息红利所得,暂减按50%计入个应纳税所得额(红利税从 20%降为10%)。
• 利用事件分析法分析该政策对股价有无显著影响,即政策出台前后股票有无 异常收益。时间窗口为发布日及前后各二天。
E( yi ) P( yi 1) X i
• 但因为
i
1 X
Xi i
当yi 1,其概率为X i 当yi 0,其概率为1 X i
• 模型具有明显的异方差性,故而用模型(5.8)直接进行参数估计 是不合适的。
• 另外,由于要求
E( yi ) P( yi 1) Xi 1
亦
难以达到。
Di 0, 其它季度的数据
, i 2,3,4
• •
原 则模 引型 入若 虚为 拟变量后的y模t 型为:
xt
ut
yt xt 2 D2t 3 D3t 4 D4t ut (5.6)
• 回归模型可视为:
yˆt ˆ ˆxt
一季度
yˆt ˆ ˆxt ˆ2 二季度
yˆt ˆ ˆxt ˆ3 三季度
二、虚拟变量的设置原则
计量经济学虚拟变量模型课件

计量经济学虚拟变量模型
21
1 正常年份 D1i 0 非正常年份
式(5.2)也可表示为
1 非正常年份 D2i 0 正常年份
Y i 0 X 1 i 1 X 2 i 2 X 3 i 3 X i u i (5.3)
其中,X 1i1 ,X 2iD 1i,X 3iD 2i,显然如下等式成立。
X1i X2i X3i
计量经济学虚拟变量模型
3
例如,性别可表现为男或女;人种可表 现为白种人和非白种人;宗教信仰可表 现为教徒和非教徒;政府的经济政策可 表现为改革开放前和改革开放后,如此 等等。
Hale Waihona Puke 计量经济学虚拟变量模型4
显然,这种不同的具体形式是无法直接引 入经济计量模型中去的。但由于这类变量 通常表现为品质、属性、种类的出现或者 未出现,所以我们可以根据质量变量的这 一特征将其数量化。
Y i1 D 1 i2 D 2 i3 X i u i (5.5)
显然模型(5.5)中,解释变量D1,D2和X之间 无完全的多重共线性。可以使用普通最小二乘 法估计式(5.5)的参数。
第五章 虚拟变量模型
在经济计量模型中除了有量的因素外 还有质的因素,质的因素包括被解释变量 为质的因素和解释变量为质的因素。如果 被解释变量为质的因素,主要是逻辑回归 要涉及的内容。
计量经济学虚拟变量模型
1
第一节 虚拟变量的概念与设定
一、虚拟变量的概念 在经济计量分析中, 经常会碰到所建模
型的被解释变量不仅受诸如收入、产量 、价格、 成本、需求、投资等数量变量
(5.4)
计量经济学虚拟变量模型
22
式(5.4)表明模型(5.3)即原模型(5.2)中有 完全的多重共线性,将导致最小二乘估计无 解。我们称该情景为掉入虚拟变量陷阱。所 以,在有截距项的情况下,如果一个质的因 素有多少个特征就引入多少个虚拟变量是行 不通的。
金融计量经济第五讲虚拟变量模型和Probit、Logit模型

• 括号内为t统计值。 • 显然,三季度和四季度与一季度差异并不明显,重 新回归,仅考虑二季度,有结果:
例子:佣金与销售额的关系:
• 模型:
Yi = α1 + β1 xi + β 2 ( xi − x* ) Di + ui 其中 : Yi是销售佣金, X i是销售额, X*是销售额基数值. 若X i > X * , 则Di = 1
• 样本回归函数: ˆ ˆ α +β x
ˆ Yi =
1
1 i
xi < x* xi ≥ x*
D1 = , 0, S < S1 , S ≥ S2 D2 = 0, S < S2
• 工资模型为: • I i = β 0 + β1[ S1 + (1 − D1i − D2i )(Si − S1 )]
+ β 2 [ D2i ( S 2 − S1 ) + D1i ( Si − S1 )] + β 3 D2i ( Si − S 2 ) + ui (5.7)
t t
一季度 ˆ β2 ˆ β3 二季度 三季度 四季度
ˆ ˆ ˆ ˆ y t = α + β xt + β 4
例题:美国制造业的利润—销售额行为 • 模型:利润t = α1 + α 2 D2t + α 3 D3t + α 4 D4t + β (销售)t + ut • 利用1965—1970年六年的季度数据,得结果:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二、虚拟变量的设置原则
• 引入虚拟变量一般取0和1。
• 对定性因素一般取级别数减1个虚拟变量。例 子1:性别因素,二个级别(男、女)取一个 虚拟变量,D=1表示男(女),D=0表示女 (男)。
• 例子2:季度因素,四个季度取3个变量。
1, 一季度 D1 0, 其它季度
1, 二季度
D2
0,
其它季度
.
例题:美国制造业的利润—销售额行为
• 模型:利 t 1 润 2 D 2 t 3 D 3 t 4 D 4 t ( 销 ) t u t售
• 利用1965—1970年六年的季度数据,得结果:
利 t 6 润 6 .3 8 1 88 3 .8D 2 2 9 t 2 2.8 1 D 3 t 7 1.8 8D 4 6 3 t 0 .03 (销 8 )t 3 售 (3.9 (2 ) .0(7 -0 ) .(4 04 .2 5 (8 3 )).33
.
例子:佣金与销售额的关系:
• 模型:
Yi 11xi 2(xi x*)Di ui
其中 :Yi是销售佣 ,Xi是 金销售 ,X额 *是销售额基 . 数值 若Xi X*,则Di 1
• 样本回归函数:
Yˆi
ˆ1 ˆ1xi ˆ1ˆ2x*(ˆ1ˆ2)xi
xi x* xi x*
.
附录:Chow检验(邹氏检验)
• 同样可以写成二个模型:
y ˆi ˆ0(ˆˆ1)x1iˆkxki D1
y ˆi ˆ0ˆ1x1iˆkxki
D0
• 可考虑同时在截距和斜率引入虚拟变量:
y i 0 0 D i (1 D i 1 ) x 1 i k x k iu i (5.
.
.
• 3、虚拟变量用于季节性因素分析。
•取
1, 当样本 i季为 度第 的数据 Di 0,其它季度的, i数 2,3据 ,4
金融计量经济第五讲
虚拟变量模型和Probit、Logit模型
.
第一节 虚拟变量的一般应用
一、虚拟变量及其作用 1.定义:取值为0和1的人工变量,表示非量化
(定性)因素对模型的影响,一般用符号D表 示。例如:政策因素、地区因素、心理因素、 季节因素等。 2.作用: ⑴描述和测量定性因素的影响; ⑵正确反映经济变量之间的相互关系,提高模型 的精度; ⑶便于处理异常数据。
量为: 1,
D 0,
t T0 tT 0
• b. 用虚拟变量表示某个特殊时期的影响;
1, D0,
tT1,T2 tT1,T2
• 模型中虚拟变量可放在截距项或斜率处。
.
• 5、分阶段计酬问题。
• 若工作报酬与业务量挂钩,且不同业务量提成比例 不一样(递增),设S1、S2为二个指标临界点
•
D 1 1 0 ,,S S 1 S S 1, S S 2S 2, D 2 1 0 ,, S S S S 2 2
• 工资模型为:
• Ii01 [S 1 (1 D 1 i D 2 i)S ( i S 1 )] 2 [D 2 i(S 2 S 1 ) D 1 i(S i S 1 ) ]3 D 2 i(S i S 2 ) u i (5.7
.
D2=1
S0
D1=1
S1
S2
.
• 作OLS得到参数估计值后,三个阶段的 报酬回归模型为: Iˆi ˆ0ˆ1Si, Si S1 Iˆi ˆ0ˆ1S1ˆ2(Si S1), S2Si S1 Iˆi ˆ0ˆ1S1ˆ2(S2S1)ˆ3(Si S2), Si S2
• 原模型若为 yt xt ut
• 则引入虚拟变量后的模型为:
y tx t2 D 2 t3 D 3 t4 D 4 t u t (5.6)
• 回归模型可视为: yˆt ˆ ˆxt
一季度
yˆt ˆ ˆxt ˆ2 二季度
yˆt ˆ ˆxt ˆ3 三季度
yˆt ˆ ˆxt ˆ4 四季度
1, 三季度
D3
ቤተ መጻሕፍቲ ባይዱ
0,
其它季度
• 小心“虚拟变量陷阱”!
.
三、虚拟变量的应用
• 1、在常数项引入虚拟变量,改变截距。
y i0D 1 x 1 i kx k iu i (5.1)
• 对上式作OLS,得到参数估计值和回归模型:
y ˆiˆ0ˆD ˆ1 x 1 i ˆkx ki(5.2)
• (5.2)相当于两个回归模型:
• 括号内为t统计值。 • 显然,三季度和四季度与一季度差异并不明显,重
新回归,仅考虑二季度,有结果:
利t 润 65.6 4 6 113.4 1D 21 t0.03(销 93)t售 (4.01()2.7)(3.717)
.
• 4、引用虚拟变量处理“时间拐点”问题。
• 常见的情况:
• a. 若T0为两个时间段之间的某个拐点,虚拟变
.
虚拟变量用于斜率
• CXYE = -1217.425 + 5.209*GMSR + 1.13*(D1*GMSR)
• 1952—1977: • CXYE = -1217.425 + 6.339*GMSR • 1978—1990: • CXYE = -1217.425 + 5.209*GMSR
.
CXYE
GMSR
.
应用例题1:Hedonic住宅价格模型
• 也称特征价格模型。其核心认为住宅价格由若干 hedonic(可享受的)特征构成,包括房屋建筑 特征、区位特征、社区特征等。
• Chow检验有二个内容,断点检验和预测检 验。和虚拟变量模型作用有相近之处的是 断点检验(Chow Breakpoint Test)。
• 步骤:在回归分析结果窗口,点 View\Stabiliti Test\Chow Breakpoint Test
• 注:邹氏应是邹至庄。
.
例1:储蓄余额与国民收入的关系
y ˆi ˆ0ˆˆ1x1iˆkxk i D1 y ˆi ˆ0ˆ1x1iˆkxk i D0
.
.
• 2、在斜率处引入虚拟变量,改变斜率。
y i0 (D 1 )x 1 i k x k iu i (5.3)
• 作OLS后得到参数估计值,回归模型为:
y ˆiˆ0 (ˆD ˆ1 )x 1 i ˆkx ki(5.4)
• CXYE = -1878.817965 + 5.965038605*GMSR + 812.1046287*D1
• 1952—1977: • CXYE = -1066.71 + 5.965*GMSR • 1978—1990: • CXYE = -1878.82 + 5.965*GMSR
.
GMSR
