青海省平安县第一高级中学2018-2019学年新高一入学分班考试数学试题-含答案
青海省平安县第一高级中学2018-2019学年高一数学必修一课后练习:1.3.1单调性与最大(小)值 Word版含答案

1.3.1单调性与最大(小)值班级:__________姓名:__________设计人__________日期__________课后练习【基础过关】1.若函数在区间上是增函数,在区间上也是增函数,则函数在区间上A.必是增函数B.必是减函数C.先增后减D.无法确定单调性2.下列函数在(0,1)上是增函数的是A. B. C. D.3.函数,在上是A.减函数B.增函数C.先减后增D.无单调性4.下面说法错误的是A.函数的单调区间一定是函数的定义域B.函数的多个单调增区间的并集不一定是其单调增区间C.具有奇偶性的函数的定义域关于原点对称D.关于原点对称的图象一定是奇函数的图象5.已知函数在区间上为减函数,则的取值范围是_____________.6.设奇函数f(x)的定义域为[-5,5],且当x∈[0,5]时,f(x)的图象如图所示,则不等式f(x)<0的解集是.7..已知函数,若.(l)求的值.(2)利用单调性定义证明函数在区间的单调性.8.首届世界低碳经济大会在南昌召开,大会以“节能减排,绿色生态”为主题.某单位在国家科研部门的支持下,进行技术攻关,采用了新工艺,把二氧化碳转化为一种可利用的化工产品.已知该单位每月的处理量最少为400吨,最多为600吨,月处理成本(元)与月处理量(吨)之间的函数关系可近似地表示为,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.(1)该单位每月处理量为多少吨时,才能使每吨的平均处理成本最低?(2)该单位每月能否获利?如果获利,求出最大利润;如果不获利,则国家至少需要补贴多少元才能使该单位不亏损?【能力提升】函数f(x)的图象如图所示.(1)说出f(x)的单调区间,以及在每一个单调区间上它是增函数还是减函数;(2)依据图象说明函数的最值情况.1.3.1单调性与最大(小)值课后作业·详细答案【基础过关】1.D【解析】因为(a,b),(c,d)不是两个连续的区间,所以无法确定其单调性.2.B【解析】选项A中y=1-2x为减函数,C中y=5为常数函数,D中的定义域为[1,+∞).3.B【解析】解答本题可先画出函数图象,由图象分析.函数f(x)的图象如图所示,由图结合单调性的定义可知,此函数在R上是增函数.4.A【解析】单调区间是定义域的子集,不一定是定义域,当多个单调区间并起来时,由单调性定义知,不再是单调区间.具有奇偶性的函数的定义域关于原点对称,是函数奇偶性判定的要求.奇函数的图象关于原点对称,反之,关于原点对称的图象一定是奇函数的图象.5.(-∞,1]6.(-2,0)∪(2,5]【解析】由图可知在区间(2,5]上f(x)<0,因为奇函数的图象关于原点对称,所以在(-2,0)上也有f(x)<0.7.(1)由2f(2)=f(3)+5,得,解得a=2.(2)由(1)知.任取x1,x2∈(1,+∞)且x1<x2,,因为1<x1<x2,所以x1-1>0,x2-1>0,x2-x1>0.所以f(x1)-f(x2)>0,即f(x1)>f(x2).所以f(x)在(1,+∞)上是减函数.8.(1)由题意可知,二氧化碳的每吨平均处理成本为令,可以证明t(x)在(0,400)为减函数,在[400,+∞)上是增函数,故每月处理量为400吨时,才能使每吨的平均处理成本最低,最低成本为200元.(2)设该单位每月获利为S,则.因为400≤x≤600,所以当x=400时,S有最大值-40 000.故该单位不获利,需要国家每月至少补贴40 000元,才能不亏损.【能力提升】(1)由题图可知:函数f(x)的单调增区间为[0,];单调减区间为(-∞,0)和(,+∞).(2)观察图象可知,函数没有最大值和最小值.。
平安县一中2018-2019学年高三上学期11月月考数学试卷含答案

平安县一中2018-2019学年高三上学期11月月考数学试卷含答案一、选择题1. 数列{a n }满足a 1=3,a n ﹣a n •a n+1=1,A n 表示{a n }前n 项之积,则A 2016的值为( )A .﹣B .C .﹣1D .12. 设0<a <b 且a+b=1,则下列四数中最大的是()A .a 2+b 2B .2abC .aD .3. 给出定义:若(其中m 为整数),则m 叫做离实数x 最近的整数,记作{x},即{x}=m在此基础上给出下列关于函数f (x )=|x ﹣{x}|的四个命题:①;②f (3.4)=﹣0.4;③;④y=f (x )的定义域为R ,值域是;则其中真命题的序号是( )A .①②B .①③C .②④D .③④4. 函数y=2|x|的定义域为[a ,b],值域为[1,16],当a 变动时,函数b=g (a )的图象可以是()A .B .C .D .5. 运行如图所示的程序框图,输出的所有实数对(x ,y )所对应的点都在某函数图象上,则该函数的解析式为()班级_______________ 座号______ 姓名_______________ 分数__________________________________________________________________________________________________________________A .y=x+2B .y=C .y=3xD .y=3x 36. 某班设计了一个八边形的班徽(如图),它由腰长为1,顶角为α的四个等腰三角形,及其底边构成的正方形所组成,该八边形的面积为()A .2sin 2cos 2αα-+B .sin 3αα+C. 3sin 1αα-+ D .2sin cos 1αα-+7. 已知椭圆(0<b <3),左右焦点分别为F 1,F 2,过F 1的直线交椭圆于A ,B 两点,若|AF 2|+|BF 2|的最大值为8,则b 的值是( )A .B .C .D .8. 已知圆C 1:x 2+y 2=4和圆C 2:x 2+y 2+4x ﹣4y+4=0关于直线l 对称,则直线l 的方程为( )A .x+y=0B .x+y=2C .x ﹣y=2D .x ﹣y=﹣29. 复数Z=(i 为虚数单位)在复平面内对应点的坐标是()A .(1,3)B .(﹣1,3)C .(3,﹣1)D .(2,4)10.十进制数25对应的二进制数是()A .11001B .10011C .10101D .1000111.正方体的内切球与外接球的半径之比为( )A .B .C .D .12.在高校自主招生中,某学校获得5个推荐名额,其中清华大学2名,北京大学2名,复旦大学1名.并且北京大学和清华大学都要求必须有男生参加.学校通过选拔定下3男2女共5个推荐对象,则不同的推荐方法共有()A .20种B .22种C .24种D .36种二、填空题13.(若集合A ⊊{2,3,7},且A 中至多有1个奇数,则这样的集合共有 个. 14.如图所示,圆中,弦的长度为,则的值为_______.C AB 4AB AC ×u u u r u u u r【命题意图】本题考查平面向量数量积、垂径定理等基础知识,意在考查对概念理解和转化化归的数学思想.15.一个算法的程序框图如图,若该程序输出的结果为,则判断框中的条件i <m 中的整数m 的值是 .16.已知=1﹣bi ,其中a ,b 是实数,i 是虚数单位,则|a ﹣bi|= .17.已知数列{a n }中,2a n ,a n+1是方程x 2﹣3x+b n =0的两根,a 1=2,则b 5= .18.已知圆的方程为,过点的直线与圆交于两点,若使C 22230x y y +--=()1,2P -C ,A B AB 最小则直线的方程是.三、解答题19.【徐州市2018届高三上学期期中】如图,有一块半圆形空地,开发商计划建一个矩形游泳池及其矩形附属设施,并将剩余空地进行绿化,园林局要求绿化面积应最大化.其中半圆的圆心为,半径为,矩形的一边在直径上,点、、、在圆周上,、在边上,且,设.(1)记游泳池及其附属设施的占地面积为,求的表达式;(2)怎样设计才能符合园林局的要求?20.(本小题满分12分)已知函数,数列满足:,().21()x f x x +={}n a 12a =11n n a f a +⎛⎫= ⎪⎝⎭N n *∈(1)求数列的通项公式;{}n a (2)设数列的前项和为,求数列的前项和.{}n a n n S 1n S ⎧⎫⎨⎬⎩⎭n n T 【命题意图】本题主要考查等差数列的概念,通项公式的求法,裂项求和公式,以及运算求解能力.21.已知△ABC 的顶点A (3,1),B (﹣1,3)C (2,﹣1)求:(1)AB 边上的中线所在的直线方程;(2)AC 边上的高BH 所在的直线方程.22.设p :关于x 的不等式a x >1的解集是{x|x <0};q :函数的定义域为R .若p ∨q 是真命题,p ∧q 是假命题,求实数a 的取值范围.23.为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行抽样检查,测得身高情况的统计图如下:(Ⅰ)估计该校男生的人数;(Ⅱ)估计该校学生身高在170~185cm之间的概率;(Ⅲ)从样本中身高在180~190cm之间的男生中任选2人,求至少有1人身高在185~190cm之间的概率. 24.已知f(x)是定义在R上的奇函数,当x<0时,f(x)=()x.(1)求当x>0时f(x)的解析式;(2)画出函数f(x)在R上的图象;(3)写出它的单调区间.平安县一中2018-2019学年高三上学期11月月考数学试卷含答案(参考答案)一、选择题题号12345678910答案D A BBCADDAA题号1112答案CC二、填空题13. 6 14.815. 6 . 16. .17. ﹣1054 .18.30x y -+=三、解答题19.(1)(2)20.21.22.23.24.。
青海省平安县第一高级中学2018-2019学年高一下学期期末训练数学试题2
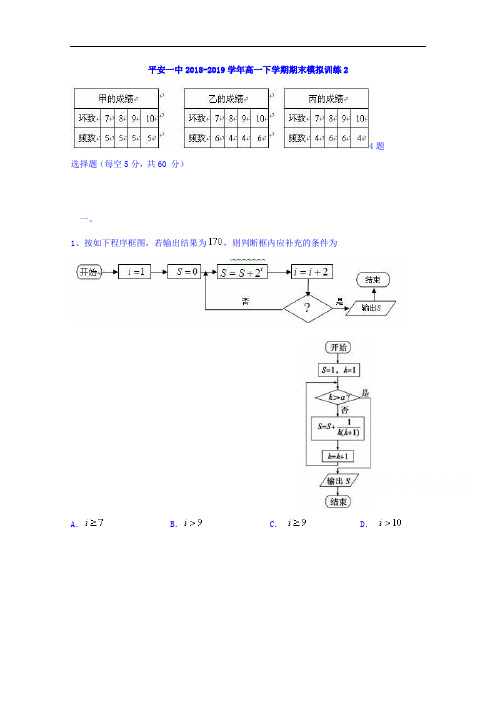
平安一中2018-2019学年高一下学期期末模拟训练24题选择题(每空5分,共60 分)一、1、按如下程序框图,若输出结果为,则判断框内应补充的条件为A. B. C. D.2、某程序框图如图所示,若该程序运行后输出的值是,则的可能值为( )3题A.B.C.D.3、200辆汽车经过某一雷达地区,时速频率分布直方图如图所示,则时速超过60km/h的汽车数量为A.65辆 B.76辆C.8辆D.95辆4、甲、乙、丙三名射箭运动员在某次测试中各射箭20次,三人的测试成绩如下表分别表示甲、乙、丙三名运动员这次测试成绩的标准差,则有A.B.C.5、从装有个红球和个黒球的口袋内任取个球,那么互斥而不对立的两个事件是( )A 至少有一个黑球与都是黑球B 至少有一个红球与都是黑球C 至少有一个黑球与至少有个红球D 恰有个黑球与恰有个黑球6、从集合中随机选取一个数记为,从集合中随机选取一个数记为,则直线不经过第三象限的概率为A. B. C. D.7、在三角形ABC中,则的值为A. B. C.D.8、在△ABC中,内角A,B,C的对边分别是a,b,c,若,,则角A= ()A. B. C.D.9、3.等差数列的前三项为,则这个数列的通项公式为()A.B. C. D.10、已知等差数列1,,等比数列3,,则该等差数列的公差为()A.3或 B.3或C.3 D.11、不等式对于一切实数恒成立,则的取值范围是A.B.C.D.12、不等式的图象为二、13、下图给出的是计算的值的一个流程图,其中判断框内应填入的条件是____________。
14、已知x,y取值如下表:从散点图中可以看出y与x线性相关,且回归方程为=0.95x+a,则a=___15、在平面直角坐标系中,横坐标与纵坐标都在集合A={0,1,2,3,4,5}内取值的点中任取一个点,此点正好在直线上的概率为.16、14.是等差数列的前n项和,(n≥5,), =336,则n的值是三、简答题17、已知,且,求的最小值并求取最小值时与的值18、某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上的40件产品作为样本称出它们的重量(单位:克),重量的分组区间为(490,495],(495,500],……,(510,515],由此得到样本的频率分布直方图,如图4所示.(Ⅰ)根据频率分布直方图,求重量超过500 克的产品数量;(Ⅱ)在上述抽取的40件产品中任取2件,设Y为重量超过505克的产品数量,求Y的分布列及数学期望.19、某班t名学生在2011年某次数学测试中,成绩全部介于80分与130分之间,将测试结果按如下方式分成五组,第一组,下表是按上述分组方法得到的频率分布表:(Ⅰ) 求t及分布表中x,y,z的值;(Ⅱ)设m,n是从第一组或第五组中任意抽取的两名学生的数学测试成绩,求事件“|m—n|≤10”的概率.20、已知的周长为,且.(1)求边长的值;(2)若,求的值.21、数列的前项和.(1)求数列的通项公式;(2)设,求数列的前项和.。
【全国百强校】青海省平安县第一高级中学2015-2016学年高一9月质量检测数学试题

青海省平安县第一高级中学2015—2016 学年高一9 月质量检测考试数学试题时间:100 分钟总分:120 分一、选择题:本大题共12 小题,每小题4 分,在每小题给同的四个选项中,只有一项是符合题目要求的.1.设全集,集合,则C U =()A. B. C. D.2、设全集U 是实数集R,M={x|x2>4},N={x|1<x<3},则图中阴影部分表示的集合是A、{x|-2≤x<1}B、{x|1<x≤2}C、{x|-2≤x≤2}D、{x|x<2}3、设A、B 是两个非空集合,定义,已知C、[0,1]D、[0, 2]4、已知函数y =f (x)的定义域为(-1,3),则在同一坐标系中,函数 f (x)的图像与直线x =2的交点个数为()A)0 个B)1 个C)2 个D)0 个或多个5、的值是()6、定义在R 上的偶函数f (x)满足f (x +2) =f (x),且在[0,1]上单调递增,设a =f (3),b =f (1.2),c =f (2),则a,b,c大小关系是( )A、b >c >aB、a >c >bC、a >b >cD、c >b >a7、已知函数f (x) =则f (3)的值等于()A、-2B、2C、1D、-18、已知函数f(x)的定义域是(0,1),那么f(2x)的定义域是()A.(0,1) B.(12,1)C.(-∞,0) D.(0,+∞)9. f (x) =的奇偶性是()A 奇函数B 偶函数C 既奇又偶函数D 非奇非偶函数10、在下列图象中,二次函数y =ax2 +bx +c与函数的图象可能是()11、已知f ( x) =,f (2) =4,则f (-2) =()A、0B、1C、2D、312.已知函数y =f (x)是定义在R上的任意不恒为零的函数,则下列判断:①为偶函数;②为非奇非偶函数;③为奇函数;④为偶函数.其中正确判断的个数有A.1 个B.2 个C.3 个D.4 个二、填空题:本大题共4 小题,每小题4 分.13、满足的集合A 的个数是_______个.14、某班共30 人,其中15 人喜爱篮球运动,10 人喜爱兵乓球运动,8 人对这两项运动都不喜爱,则喜爱篮球运动但不喜爱乒乓球运动的人数为_ __.15、已知函数f (x)为R 上的奇函数,当x≥0时,f (x) =x(x +1) .若f (a) =-2,则实数a =_____.16、已知是R 上的减函数,那么a 的取值范围是.三、解答题:解答应写出文字说明,证明过程或演算步骤。
【数学】青海省平安县第一高级中学2016-2017学年高一上学期期末测试试题(2)(解析版)

青海省平安县第一高级中学2016-2017学年高一上学期期末测试数学试题(2)一、选择题:本大题共14小题,每小题4分,共56分.在每小题的4个选项中,只有一项是符合题目要求的.1.设全集U =R ,A ={x |x >0},B ={x |x >1},则A ∩U B =(). A .{x |0≤x <1}B .{x |0<x ≤1}C .{x |x <0}D .{x |x >1}2.下列四个图形中,不是..以x 为自变量的函数的图象是( ).A . B. C. D. 3.已知函数 f (x )=x 2+1,那么f (a +1)的值为( ). A .a 2+a +2B .a 2+1C .a 2+2a +2D .a 2+2a +14.下列等式成立的是( ). A .log 2(8-4)=log 2 8-log 2 4 B .4log 8log 22=48log 2 C .log 2 23=3log 2 2D .log 2(8+4)=log 2 8+log 2 45.下列四组函数中,表示同一函数的是( ). A .f (x )=|x |,g (x )=2x B .f (x )=lg x 2,g (x )=2lg xC .f (x )=1-1-2x x ,g (x )=x +1D .f (x )=1+x ·1-x ,g (x )=1-2x 6.幂函数y =x α(α是常数)的图象( ). A .一定经过点(0,0) B .一定经过点(1,1) C .一定经过点(-1,1)D .一定经过点(1,-1)7.国内快递重量在1 000克以内的包裹邮资标准如下表:如果某人从北京快递900克的包裹到距北京1 300 km 的某地,他应付的邮资是( ). A .5.00元B .6.00元C .7.00元D .8.00元8.方程2x =2-x 的根所在区间是( ). A .(-1,0)B .(2,3)C .(1,2)D .(0,1)9.若log 2 a <0,b⎪⎭⎫⎝⎛21>1,则( ).A .a >1,b >0B .a >1,b <0C .0<a <1,b >0D .0<a <1,b <010.函数y =x 416-的值域是( ). A .[0,+∞)B .[0,4]C .[0,4)D .(0,4)11.下列函数f (x )中,满足“对任意x 1,x 2∈(0,+∞),当x 1<x 2时,都有f (x 1)>f (x 2)的是( ).A .f (x )=x1 B .f (x )=(x -1)2 C .f (x )=e xD .f (x )=ln(x +1)12.奇函数f (x )在(-∞,0)上单调递增,若f (-1)=0,则不等式f (x )<0的解集是( ). A .(-∞,-1)∪(0,1) B .(-∞,-1)∪(1,+∞) C .(-1,0)∪(0,1)D .(-1,0)∪(1,+∞)13.已知函数f (x )=⎩⎨⎧0≤ 30log 2x x f x x ),+(>,,则f (-10)的值是( ).A .-2B .-1C .0D .114.已知x 0是函数f (x )=2x +x-11的一个零点.若x 1∈(1,x 0),x 2∈(x 0,+∞),则有( ). A .f (x 1)<0,f (x 2)<0 B .f (x 1)<0,f (x 2)>0 C .f (x 1)>0,f (x 2)<0D .f (x 1)>0,f (x 2)>0二、填空题:本大题共4小题,每小题4分,共16分.15.A ={x |-2≤x ≤5},B ={x |x >a },若A ⊆B ,则a 取值范围是 . 16.若f (x )=(a -2)x 2+(a -1)x +3是偶函数,则函数f (x )的增区间是 . 17.函数y =2-log 2x 的定义域是 .18.求满足8241-x⎪⎭⎫⎝⎛>x-24的x的取值集合是.三、解答题:本大题共3小题,共28分.解答应写出文字说明、证明过程或演算步骤.19.(8分) 已知函数f(x)=lg(3+x)+lg(3-x).(1)求函数f(x)的定义域;(2)判断函数f(x)的奇偶性,并说明理由.20.(10分)已知函数f(x)=2|x+1|+ax(x∈R).(1)证明:当a>2时,f(x)在R上是增函数.(2)若函数f(x)存在两个零点,求a的取值范围.21.(10分)某租赁公司拥有汽车100辆.当每辆车的月租金为3 000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.(1)当每辆车的月租金定为3 600元时,能租出多少辆车?(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?参考答案一、选择题 1.B 【解析】U B ={x |x ≤1},因此A ∩UB ={x |0<x ≤1}.2.C3.C 4.C 5.A 6.B 7.C 8.D 9.D【解析】由log 2 a <0,得0<a <1,由b⎪⎭⎫⎝⎛21>1,得b <0,所以选D 项.10.C【解析】∵ 4x >0,∴0≤16- 4x <16,∴x416-∈[0,4).11.A【解析】依题意可得函数应在(0,+∞)上单调递减,故由选项可得A 正确. 12.A 13.D 14.B【解析】当x =x 1从1的右侧足够接近1时,x-11是一个绝对值很大的负数, 从而保证f (x 1)<0;当x =x 2足够大时,x-11可以是一个接近0的负数, 从而保证f (x 2)>0.故正确选项是B . 二、填空题 15. (-∞,-2). 16.(-∞,0). 17. [4,+∞).18. (-8,+∞). 三、解答题19.解 (1)由⎩⎨⎧0303>->+x x ,得-3<x <3,∴ 函数f (x )的定义域为(-3,3). (2)函数f (x )是偶函数,理由如下:由(1)知,函数f (x )的定义域关于原点对称, 且f (-x )=lg(3-x )+lg(3+x )=f (x ), ∴ 函数f (x )为偶函数.20.解 (1)证明:化简f (x )=⎩⎨⎧1221 ≥22<-,-)-(-,+)+(x x a x x a因为a >2,所以,y 1=(a +2)x +2 (x ≥-1)是增函数,且y 1≥f (-1)=-a ; 另外,y 2=(a -2)x -2 (x <-1)也是增函数,且y 2<f (-1)=-a . 所以,当a >2时,函数f (x )在R 上是增函数.(2)若函数f (x )存在两个零点,则函数f (x )在R 上不单调,且点(-1,-a )在x 轴下方,所以a 的取值应满足⎩⎨⎧0022<-)<-)(+(a a a 解得a 的取值范围是(0,2).21.解 (1)当每辆车的月租金定为3 600元时,未租出的车辆数为500003600 3-=12,所以这时租出了100-12=88辆车.(2)设每辆车的月租金定为x 元,则租赁公司的月收益为f (x )=⎪⎭⎫ ⎝⎛50000 3100--x (x -150)-50000 3-x ×50=-501(x -4 050)2+307 050. 所以,当x =4 050 时,f (x )最大,其最大值为f (4 050)=307 050. 当每辆车的月租金定为4 050元时,月收益最大,其值为307 050元.安徽省江南十校2017年高考数学模拟试卷(理科)(3月份)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若,则|z|=()A.B.1 C.5 D.252.设集合A={x∈Z||x|≤2},,则A∩B=()A.{1,2} B.{﹣1,﹣2}C.{﹣2,﹣1,2} D.{﹣2,﹣1,0,2}3.已知平面向量=(1,m),=(2,5),=(m,3),且(+)∥(﹣),则m=()A.B.C.D.4.已知,则sinα(sinα﹣cosα)=()A.B.C.D.5.已知MOD函数是一个求余函数,其格式为MOD(n,m),其结果为n除以m的余数,例如MOD(8,3)=2.下面是一个算法的程序框图,当输入的值为36时,则输出的结果为()A.4 B.5 C.6 D.76.质地均匀的正四面体表面分别印有0,1,2,3四个数字,某同学随机的抛掷次正四面体2次,若正四面体与地面重合的表面数字分别记为m,n,且两次结果相互独立,互不影响.记m2+n2≤4为事件A,则事件A发生的概率为()A.B.C.D.7.《九章算术》是我国古代的数字名著,书中《均属章》有如下问题:“今有五人分五钱,令上二人所得与下三人等.问各德几何.”其意思为“已知A、B、C、D、E五人分5钱,A、B两人所得与C、D、E三人所得相同,且A、B、C、D、E每人所得依次成等差数列.问五人各得多少钱?”(“钱”是古代的一种重量单位).在这个问题中,E所得为()A.钱B.钱C.钱D.钱8.如图,网格纸上小正方形的边长为1,实线画出的是某多面体的三视图,则该多面体的体积为()A.20 B.22 C.24 D.269.设△ABC的面积为S1,它的外接圆面积为S2,若△ABC的三个内角大小满足A:B:C=3:4:5,则的值为()A.B.C.D.10.若函数f(x)的图象如图所示,则f(x)的解析式可能是()A.B.C.D.11.已知球的直径SC=6,A、B是该球球面上的两点,且AB=SA=SB=3,则棱锥S﹣ABC的体积为()A.B.C.D.12.设⌈x⌉表示不小于实数x的最小整数,如⌈2.6⌉=3,⌈﹣3.5⌉=﹣3.已知函数f(x)=⌈x⌉2﹣2⌈x⌉,若函数F(x)=f(x)﹣k(x﹣2)+2在(﹣1,4]上有2个零点,则k的取值范围是()A.B.C.D.二、填空题(每题5分,满分20分,将答案填在答题纸上)13.已知实x,y数满足关系,则|x﹣2y+2|的最大值是.14.若(x+y)3(2x﹣y+a)5的展开式中各项系数的和为256,则该展开式中含字母x且x 的次数为1的项的系数为.15.已知双曲线﹣=1上一点P(x,y)到双曲线一个焦点的距离是9,则x2+y2的值是.16.将函数y=sin2x﹣cos2x的函数图象向右平移m个单位以后得到的图象与y=k sin x cos x(k >0)的图象关于对称,则k+m的最小正值是.三、解答题(本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.已知S n是数列{a n}的前n项和,且满足S n﹣2a n=n﹣4.(1)证明{S n﹣n+2}为等比数列;(2)求数列{S n}的前n项和T n.18.美团外卖和百度外卖两家公司其“骑手”的日工资方案如下:美团外卖规定底薪70元,每单抽成1元;百度外卖规定底薪100元,每日前45单无抽成,超出45单的部分每单抽成6元,假设同一公司的“骑手”一日送餐单数相同,现从两家公司个随机抽取一名“骑手”并记录其100天的送餐单数,得到如下条形图:(Ⅰ)求百度外卖公司的“骑手”一日工资y(单位:元)与送餐单数n的函数关系;(Ⅱ)若将频率视为概率,回答下列问题:②记百度外卖的“骑手”日工资为X(单位:元),求X的分布列和数学期望;②小明拟到这两家公司中的一家应聘“骑手”的工作,如果仅从日收入的角度考虑,请你利用所学的统计学知识为他作出选择,并说明理由.19.如图,四边形ABCD是边长为的正方形,CG⊥平面ABCD,DE∥BF∥CG,DE=BF= CG.P为线段EF的中点,AP与平面ABCD所成角为60°.在线段CG上取一点H,使得GH=CG.(1)求证:PH⊥平面AEF;(2)求二面角A﹣EF﹣G的余弦值.20.在平面直角坐标系中,直线不过原点,且与椭圆有两个不同的公共点A,B.(Ⅰ)求实数m取值所组成的集合M;(Ⅱ)是否存在定点P使得任意的m∈M,都有直线P A,PB的倾斜角互补.若存在,求出所有定点P的坐标;若不存在,请说明理由.21.已知函数f(x)=e x﹣1+a,函数g(x)=ax+ln x,a∈R.(Ⅰ)若曲线y=f(x)与直线y=x相切,求a的值;(Ⅱ)在(Ⅰ)的条件下,证明:f(x)≥g(x)+1;(Ⅲ)若函数f(x)与函数g(x)的图象有且仅有一个公共点P(x0,y0),证明:x0<2.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.[选修4-4:坐标系与参数方程]22.已知P为曲线上的动点,直线C2的参数方程为(t为参数)求点P到直线C2距离的最大值,并求出点P的坐标.[选修4-5:不等式选讲]23.已知关于x的方程在x∈[0,3]上有解.(Ⅰ)求正实数a取值所组成的集合A;(Ⅱ)若t2﹣at﹣3≥0对任意a∈A恒成立,求实数t的取值范围.参考答案一、选择题1.B【解析】==,则|z|==1.故选:B.2.C【解析】A={﹣2,﹣1,0,1,2},B={x|x≥或x<0},故A∩B={﹣2,﹣1,2},故选:C.3.D【解析】根据题意,向量=(1,m),=(2,5),=(m,3),则;若(+)∥(﹣),(m+1)×(m﹣5)=(m+3)×(﹣1)解可得:;故选:D.4.A【解析】,故选:A.5.D【解析】模拟执行程序框图,可得:n=36,i=2,MOD(36,2)=0,j=1,i=3满足条件i<n,MOD(36,3)=0,j=2,i=4满足条件i<n,MOD(36,4)=0,j=3,i=5满足条件i<n,MOD(36,5)=1,i=6…∵∈N*,可得i=2,3,4,6,9,12,18,∴共要循环7次,故j=7.故选:D.6.B【解析】质地均匀的正四面体表面分别印有0,1,2,3四个数字,某同学随机的抛掷次正四面体2次,正四面体与地面重合的表面数字分别记为m,n,且两次结果相互独立,互不影响.基本事件总数N=42=16,记m2+n2≤4为事件A,则事件A包含听基本事件有:(1,1),(0,1),(1,0),共3个,∴事件A发生的概率为.故选:B.7.D【解析】由题意:设A=a﹣4d,B=a﹣3d,C=a﹣2d,D=a﹣d,E=a,则,解得a=,故E所得为钱.故选:D.8.C【解析】由三视图可知:该几何体是一个棱长为3正方体去掉3个棱长为1的小正方体剩下的部分.该几何体的体积V=33﹣3×13=24.故选:C.9.D【解析】在△ABC中,∵△ABC的三个内角大小满足A:B:C=3:4:5,∴A=45°,B=60°,C=75°,那么△ABC的面积为S1=ac sin B=a2=a2外接圆面积为S2=πR2,R=,∴=.故选D.10.B【解析】由题意,x=0,y<0,排除A,0>x>﹣1,x→﹣1,y→﹣∞,排除C,D选项中,f(﹣2)=5,f(﹣3)=,不符合,排除D.故选:B.11.D【解析】∵球的直径SC=6,A、B是该球球面上的两点,且AB=SA=SB=3,∴由条件:S﹣OAB为棱长为3的正四面体,其体积为=,同理,故棱锥S﹣ABC的体积为.故选:D.12.C【解析】令F(x)=0得f(x)=k(x﹣2)﹣2,作出函数y=f(x)和y=k(x﹣2)﹣2的图象如下图所示:若函数F(x)=f(x)﹣k(x﹣2)+2在(﹣1,4]上有2个零点,则函数f(x)和g(x)=k(x﹣2)﹣2的图象在(﹣1,4]上有2个交点,经计算可得k P A=5,k PB=10,k PO=﹣1,k PC=﹣,∴k的范围是[﹣1,﹣)∪[5,10).故选:C二、填空题13.5【解答】5 由条件可知:z=x﹣2y+2过点M(﹣1,3)时z=﹣5,|z|max=5,解:作出不等式组,对应的平面区域如图:由解得M(﹣1,3),由条件可知:z=x﹣2y+2过点M(﹣1,3)时z=﹣5,|z|max=5,故答案为:5.14.﹣7【解析】(x+y)3(2x﹣y+a)5的展开式中各项系数的和为256,令x=y=1,得23×(a+1)5=256,解得a=1,所以(x+y)3(2x﹣y+1)5的展开式中含字母x且x的系数为:.故答案为:﹣7.15.133【解析】双曲线﹣=1的a=4,b=6,c==2,不妨设点P(x,y)在右支上,由条件可知P点到右焦点(2,0)的距离为9,即为=9,且﹣=1,解出x=2,y=±9,则x2+y2=52+81=133.故答案为:133.16.2+【解析】将函数y=sin2x﹣cos2x=﹣cos2x的函数图象向右平移m个单位以后得到y=﹣cos2(x ﹣m)=﹣cos(2x﹣2m)的图象,根据所得图象与y=k sin x cos x=sin2x(k>0)的图象关于对称,设点P(x0,y0)为y=﹣cos(2x﹣2m)上任意一点,则该点关于对称点为在y=sin2x(k>0)的图象上,故有,求得k=2,sin(2x0﹣)=cos(2x0﹣2m),即cos(2x0﹣)=cos(2x0﹣2m),∴﹣2m=﹣+2kπ,k∈Z,即2m=﹣2kπ,k∈Z,故m的最小正值为,则k+m的最小正值为2+.三、解答题17.(1)证明:当n=1时,a1=S1,S1﹣2a1=1﹣4,可得a1=3,S n﹣2a n=n﹣4转化为:S n﹣2(S n﹣S n﹣1)=n﹣4(n≥2),即S n=2S n﹣1﹣n+4,所以S n﹣n+2=2[S n﹣1﹣(n﹣1)+2]注意到S1﹣1+2=4,所以{S n﹣n+2}为首项为4,公比为2等比数列;(2)由(1)知:,所以,于是==.18.解:(Ⅰ)∵百度外卖规定底薪100元,每日前45单无抽成,超出45单的部分每单抽成6元,∴当送餐单数n≤45,n∈N*时,百度外卖公司的“骑手”一日工资y=100,当送餐单数n>45,n∈N*时,百度外卖公司的“骑手”一日工资y=100+(n﹣45)×6=6n﹣170,n∈N*,∴百度外卖公司的“骑手”一日工资y(单位:元)与送餐单数n的函数关系为:(Ⅱ)①记百度外卖的“骑手”日工资为X(单位:元),由条形图得X的可能取值为100,106,118,130,P(X=100)==0.2,P(X=106)==0.3,P(X=118)==0.4,P(X=130)==0.1,∴X的分布列为:E(X)=100×0.2+106×0.3+118×0.4+130×0.1=112(元).②美团外卖“骑手”日平均送餐单数为:42×0.2+44×0.4+46×0.2+48×0.1+50×0.1=45所以美团外卖“骑手”日平均工资为:70+45×1=115(元)由①知,百度外卖“骑手”日平均工资为112元.故推荐小明去美团外卖应聘.19.证明:(1)连接AC,BD交于点O,连接OP,则O为BD中点,∴OP∥DE,∴OP⊥面ABCD.∴∠P AO为AP与面ABCD所成角,∵AP与平面ABCD所成角为60°,∴∠P AO=60°.在Rt△AOP中,.Rt△AHC中,.梯形OPHC中,.∴AP2+PH2=AH2,∴AP⊥PH,又EH=FH,∴PH⊥EF,又AP∩EF=P,∴PH⊥面AEF.解:(2)∵CG面ABCD,ABCD为正方形,∴如图所示建立空间直角坐标系.G(0,0,),E(,0,),F(0,,),H(0,0,),P(,,),=(﹣,,0),=(﹣,0,),,∵PH⊥面AEF,∴面AEF的法向量为,设面EFG法向量为,则,取x=,得,设二面角A﹣EF﹣G的平面角为θ,由题意θ为钝角,则cosθ=﹣=﹣.故二面角A﹣EF﹣G的余弦值为.20.解:(1)因为直线不过原点,所以m≠0,将与联立,消去y得:,因为直线与椭圆有两个不同的公共点A,B,所以△=8m2﹣16(m2﹣4)>0,解得,所以实数m的范围组成的集合M是;(2)假设存在定点P(x0,y0)使得任意的m∈M,都有直线P A,PB的倾斜角互补,即k P A+k PB=0,令,所以,整理得:,由(1)知x1,x2是的两个根,所以,代入(*)化简得,由题意解得或所以定点P的坐标为或,经检验,满足题意,所以存在定点P使得任意的m∈M,都有直线P A,PB的倾斜角互补,坐标为或.21.解:(Ⅰ)设曲线y=f(x)在Q(x1,y1)点处切线是y=x,则由于所以x1=1,y1=1,由题意知:,于是a=0.(Ⅱ)证明:令,当x∈(0,1)时,0<e x﹣1<1,所以,即,当x∈(1,+∞)时,1<e x﹣1,所以,即,于是F(x)=f(x)﹣g(x)=e x﹣1﹣ln x在(0,1)单调递减,(1,+∞)单调递增,其最小值是F(1)=1,所以F(x)=f(x)﹣g(x)≥1,于是原不等式成立.(Ⅲ)令G(x)=e x﹣1﹣ln x﹣ax+a(x>0),则函数f(x)与函数g(x)的图象有且仅有一个公共点P(x0,y0)等价于函数G(x)有且只有一个零点x0,,注意到为(0,+∞)上的增函数且值域为R,所以在(0,+∞)上有唯一零点x1,且G'(x)在(0,x1)上为负,(x1,+∞)上为正,所以G(x1)为极小值,又函数G(x)有唯一零点x0,结合G(x)的单调性知x1=x0,所以,即,即,即.令,显然,x0是H(x)的零点,,H'(x)在(0,1)上为正,(1,+∞)上为负,于是H(x)在(1,+∞)上单调递减,注意到,所以H(x)在(1,2)内有一个零点,在[2,+∞)内无零点,所以H(x)的零点一定小于2,从而函数f(x)与函数g(x)的图象有且仅有一个公共点P(x0,y0)时一定有x0<2.22.解:由条件:.设点,点P到C2之距离。
名校推荐青海省平安县第一高级中学高一数学人教B必修1第一章 集合单元测试题

高一数学必修1:《集合》单元测试题1.已知集合}1,1{-=A ,}1|{==mx x B ,且A B A =⋃,则m 的值为 ( ) A .1B .—1C .1或—1D .1或—1或02.设{}022=+-=q px x x A ,{}05)2(62=++++=q x p x x B ,若⎭⎬⎫⎩⎨⎧=21B A ,则=B A ( ) A ⎭⎬⎫⎩⎨⎧-4,31,21 B ⎭⎬⎫⎩⎨⎧-4,21 C ⎭⎬⎫⎩⎨⎧31,21 D ⎭⎬⎫⎩⎨⎧213.函数22232xy x x -=--的定义域为 ( ) A 、(],2-∞ B 、(],1-∞ C 、11,,222⎛⎫⎛⎤-∞ ⎪ ⎥⎝⎭⎝⎦ D 、11,,222⎛⎫⎛⎫-∞ ⎪ ⎪⎝⎭⎝⎭4.设集合{}21<≤-=x x M ,{}0≤-=k x x N ,若MN M =,则k 的取值范围( ) A (1,2)- B [2,)+∞ C (2,)+∞ D ]2,1[-5 下列表示图形中的阴影部分的是( ) A ()()A C B C B ()()A B A C C ()()A B B C D ()A B C6.满足的集合的个数为( )A 6B 7C 8D 97.下列表述中错误的是( )A .若AB A B A =⊆ 则, B .若B A B B A ⊆=,则C .)(B A A)(B A D .()()()B C A C B A C U U U =8.方程组⎩⎨⎧=-=+9122y x y x 的解集是 ( ) A .()5,4 B .()4,5- C .(){}4,5- D .(){}4,5-。
CBA9 若集合{}{}22(,)0,(,)0,,M x y x y N x y x y x R y R =+==+=∈∈,则有( ) A .MN M = B . M N N = C . M N M = D .M N =∅10.设{}022=+-=q px x x A ,{}05)2(62=++++=q x p x x B ,若⎭⎬⎫⎩⎨⎧=21B A ,则=B A ( )(A )⎭⎬⎫⎩⎨⎧-4,31,21 (B )⎭⎬⎫⎩⎨⎧-4,21 (C )⎭⎬⎫⎩⎨⎧31,21 (D)⎭⎬⎫⎩⎨⎧2111. 设{}{}I a A a a =-=-+241222,,,,,若{}1I C A =-,则a=__________。
人教A版高中数学必修三试卷青海省平安县第一高级中学-高中课后练习(含答案):3.1.1随机事件的概率.docx
3.1.1随机事件的概率班级:__________姓名:__________设计人:__________日期:__________课后练习基础过关1.将一枚质地均匀的硬币连掷10次,其中正面向上恰有5次是A.必然事件B.随机事件C.不可能事件D.无法确定2.下列说法中正确的有①任何事件的概率总是在[0,1]之间;②概率是随机的,在试验前不能确定;③频率是客观存在的,与试验次数无关;④频率是概率的近似值,概率是频率的稳定值.A.①④B.②③C.①③④D.①②③④3.在100件产品中,有96件一级品,4件二级品.①在100件产品中任意抽取5件,全部是一级品;②在100件产品中任意抽取5件,全部是二级品;③在100件产品中任意抽取5件,不全是一级品;④在100件产品中任意抽取5件,至少有一件一级品.其中,是必然事件,是不可能事件,是随机事件.4.如果甲邀请乙玩一个同时抛掷两枚硬币的游戏,游戏的规则如下:同时抛出两个正面,乙得1分;抛出其他结果,甲得1分.谁先积累到10分,谁就获胜.你认为________(填“甲”或“乙”)获胜的可能性更大.5.一家保险公司想了解汽车挡风玻璃破碎的概率,公司收集了20 000辆汽车,时间从某年的5月1日到下一年的5月1日,共发现有600辆汽车的挡风玻璃破碎,则一辆汽车在一年时间里挡风玻璃破碎的概率近似为____.6.指出下列事件是必然事件、不可能事件,还是随机事件?(1)如果a,b都是实数,那么a+b=b+a.(2)从分别标有号数1,2,3,4,5,6,7,8,9,10的10张号签中任取一张,得到4号签.(3)没有水分,种子发芽.(4)某电话总机在60秒内接到至少15次呼叫.(5)在标准大气压下,水的温度达到50℃时沸腾.7.已知A,B,C三个箱子中各装有两个大小相同的球,每个箱子里的球,有一个球标有号码1,另一个标有号码2,现以A,B,C三个箱子中各模一个球.(1)若用数组(x,y,z)中x,y,z分别表示从A,B,C三个箱子中摸出的球的号码,请写出数组(x,y,z)的所有情形,并回答一共有多少种?(2)如果你猜测摸出的这三个球的号码之和,猜中有奖,那么猜什么数获奖的可能性最大?请说明理由.8.有人发现中国人的电子信箱名称里喜欢用数字,于是他做了调查,结果如下表:信箱数60 130 265 306 1 233 2 130 4 700 6 897名称里有数36 78 165 187 728 1 300 2 820 4 131字的信箱数频率(1)填写上表中的频率(结果保留到小数点后两位);(2)中国人在信箱名称里使用数字的概率约是多少?能力提升1.从含有两个正品a1,a2和一件次品b1的三件产品中,每次任取一件,每次取出后不放回,连续取两次.(1)写出这个试验的所有可能结果;(2)设A为“取出两件产品中恰有一件次品”,写出事件A对应的结果.2.某企业生产的乒乓球被指定为乒乓球比赛专用球.日前有关部门对某批产品进行了抽样检测,检测结果如下表所示:抽取球数n50 100 200 500 1 000 2 000优等品数m45 92 194 470 954 1 902优等品频率(1)计算表中乒乓球为优等品的频率.(2)从这批乒乓球产品中任取一个,检测出为优等品的概率是多少?(结果保留到小数点后三位)3.1.1随机事件的概率详细答案【基础过关】1.B【解析】“正面向上恰有5次”可能发生,也可能不发生,即该事件为随机事件.2.A【解析】频率是不能脱离试验次数的试验值,而概率是具有确定性的不依赖于试验次数的理论值,故②③不正确.①④显然正确.3.④②①③【解析】因为100件产品中只有4件二级品,因此选取5件不可能全是二级品,故易知④为必然事件,②为不可能事件,①③为随机事件.4.甲【解析】本题考查了随机事件的概率.同时抛掷两枚硬币的全部结果为:(正,正), (正,反),(反,正), (反,反)共四种,其中乙获胜的概率为P=0.25,甲获胜的概率为P=0.75,所以甲获胜的概率更大.5.0.03【解析】在一年里汽车的挡风玻璃破碎的频率为,所以估计其破碎的概率约为0.036.结合必然事件、不可能事件、随机事件的定义可知(1)是必然事件;(3),(5)是不可能事件;(2),(4)是随机事件.7.(1)数组(x,y,z)所有情形为:(1,1,1),(1,1,2),(1,2,1),(1,2,2),(2,1,1),(2,1,2),(2,2,1),(2,2,2)共8种.(2)设A i={所摸出三个球号码之和为i (i=3,4,5,6)},A3即为(1,1,1)共1种情形;A4即为(1,1,2),(1,2,1),(2,1,1)共3种情形;A5即为(1,2,2),(2,1,2),(2,2,1)共3种情形;A6即为(2,2,2)共1种情形,所以P(A3)=,P(A4)=,P(A5)=,P(A6)=.∴猜4或5获奖可能性最大.【解析】本题考查了随机事件的概率.8.(1)信箱数60 130 265 306 1 233 2 130 4 700 6 897桑水名称里有数字36 78 165 187 728 1 300 2 820 4 131的信箱数频率0.60 0.60 0.62 0.61 0.59 0.61 0.60 0.60(2)由(1)知,计算出的频率都在常数0.60左右摆动,因此,中国人在电子信箱名称里使用数字的概率约为0.60.【能力提升】1.(1)试验所有结果:,;,;,;,;,;,.共6种.(2)事件A对应的结果为:,;,;,;,.【备注】【举一反三】若把“每次取出后不放回”这一条件换成“每次取出后放回”,其余不变,请回答原题中的两个问题.2.(1)依据公式=,可以计算表中乒乓球优等品的频率依次是0.900,0.920,0.970,0.940,0.954,0.951.(2)由(1)知抽取的球数n不同,计算得到的频率值虽然不同,但随着抽球数的增多,都在常数0.950的附近摆动,所以任意抽取一个乒乓球检测时,质量检测为优等品的概率约为0.950.。
青海省平安县第一高级中学2018-2019学年高一数学下学期期末试题(无答案)
青海省平安县第一中学2018-2019年下学期期末考试高一数学试卷一、选择题:(本大题共15小题,每小题4分,共60分.在每小题给出的四个选项中只有一个选项是符合题目要求的.请将正确答案填在答题卡上)1.下列说法正确的是( )A .三点确定一个平面B 。
四边形一定是平面图形C 。
两条相交直线确定一个平面D 。
共点的三条直线确定一个平面2.已知空间中两点(123)A ,,,),24(a B ,,且||AB =10,则a 的值是()A.2 B 。
4 C. 0 D. 2或4 3.圆221:9C xy +=和圆222:8690C x y x y +-++=的位置关系是( )A. 相离 B 。
相交 C 。
内切 D 。
外切 4.直线03x 3=+-y 的倾斜角是()A .30 B .60 C .120 D .1355.若直线(1)20x m y m +++-=和直线082=++y mx 平行,则m 的值为( )D .32-A .1B .2-C .1或2-6.如图,在正方体1111D C B A ABCD -中,M 、N分别为棱BC 和棱CC 1的中点,则异面直线AC 和MN 所成的角为 ( )A .30° B.45° C.90° D . 60° 7.已知圆C :221xy +=,定点()3,4M 与圆C 上动点连线距离的最大值与最小值分别为( )A .4,3B .6,5C .6,4D .5,48。
在一个锥体中,作平行于底面的截面,若这个截面面积与底面面积之比为1∶3,则锥体被截面所分成的两部分的体积之 比为() A 。
1:B 。
1∶9 C。
D 。
1)9.设m 、n 是不同的直线,α、β、γ是 不同的平面,有以下四个命题:① 若//,//,αβαγ 则//βγ ②若αβ⊥,//m α,则m β⊥③ 若,//m m αβ⊥,则αβ⊥ ④若//,m n n α⊂,则//m α其中正确命题的序号是( )A . ①③B . ①④C 。
青海省平安县第一高级中学2017-2018学年高一入学考试数学试题 Word版含答案
平安一中 2017-2018学年高一 8 月入学考试数学试卷本试卷分为试题卷和答题卷两部分,其中试题卷由第Ⅰ卷(选择题)和第Ⅱ卷组成,共 4 页;答题卷共 4 页.满分 100 分,考试时间 90 分钟.考试结束后将答题卡和答题卷一并交回.第Ⅰ卷(选择题,共 40 分)注意事项:1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦擦 干净后,再选涂其他答案,不能答在试题卷上. 一.选择题(本大题共 10 个小题,每小题 4 分,共 40 分,在每小题给出的四个选项中,只有一项是符合题目要求的) 1. 函数 f (x ) =(x - 1) +- 1 是( )x 1A .奇函数B .偶函数C .既不是奇函数也不是偶函数D .既是奇函数,又是偶函数。
2.已知 A = {-1, 0,1, 2, 3}, B = {x | log 2 ( x - 1) ≤ 1}, 则A I B 的元素个数为( ) A .0 B .2 C .3 D .5 3.下列四个:①若 a // b ,则 a = b ;②若 a = b b ;③若 a = b b ; ④ 若 a = b )A.1 .2 C.3 D.4y = 7⎛ - 1 x + π ⎫4.函数tan ⎝ 2⎪ 的最小正周期是( ) 3 ⎭A . 4πB . 2πC . πD . π25.已知 a > 0, 且 a ≠ 1 ,函数 y = log a 能是( )x , y = a x , y = x + a 在同一坐标系中的图象可⎛ 1 ⎫6.已知幂函数 y = f ( x ) 的图像过点 2, ⎪ ,则它的单调递增区间是( )A . (- ∞,0) ⎝B . (0,+ ∞) ⎛ 1 ⎫ 4 ⎭C . (- ∞,1)⎛ 1D . (- ∞,+ ∞) π ⎫7.要得到函数y=sin - x⎪的图像,只需将函数y=sin -x + ⎪的图象()⎝ 3 ⎭ ⎝ 3 6 ⎭A .向左平移 π个单位B .向右平移 π个单位22C .向左平移 π 个单位D .向右平移 π 个单位。
青海省平安县第一高级中学2018_2019学年高二数学下学期期末试题文(无答案)
青海省平安县第一中学2018-2019年下学期期末考试高二数学(文科)试卷一、 选择题:(本大题共12小题,每小题5分,共60分。
在每个小题给出的四个选项中,只有一项符合要求。
)1.已知等差数列}{n a 满足2810+=a a ,则5=a ( )A. 5B. 10C. 20D. 402.命题p :0∀>x ,都有sinx≥-1,则( )A .p ⌝:0∃>x ,使得sin 1x <- B. p ⌝:0∀>x ,都有sinx<-1C. p ⌝:0∃>x ,使得sin 1x >-D. p ⌝:0x ∀>,都有sinx≥-13.在∆ABC 中, 15=a ,10=b ,60︒=A ,则sin =B ( )A.3B. 32D. 2 4.抛物线24x y =的焦点坐标是 ( ) A .)0,1( B .)0,41( C .1(0,)16 D . )81,0( 5.设1341:≤-≤-x P ,)0(12:22>≤-a a ax x q , 若p 是q 的充分不必要条件,则实数a 的取值范围是( )A. []3,2-B. [)∞+,3C. (),3∞+D.(),2∞+6. 已知实数y x ,满足约束条件⎪⎩⎪⎨⎧≥≤--≤-+00101x y x y x ,则y x z 2+=的最大值为( )A.2-B. 2C. 1D. 1-7.函数y =的定义域为 A . [4,1]-B .[4,0)-C . (0,1]D .[4,0)(0,1]- 8.已知曲线()y f x =在1=x 处的切线方程是1y x =-+,则(1)f 及'(1)f 的值分别为( )A . 0,1B .1,1C . 1,1-D . 0,1-9.抛物线x y 122=截直线12+=x y 所得弦长等于 ( )A .15B .152C .215D .15 10.椭圆的两个焦点分别为)0,6(1-F 、)0,6(2F ,且椭圆上一点到两个焦点的距离之和是20,则椭圆的标准方程为( )A . 13610022=+y xB . 16410022=+y x C. 11003622=+y x D. 11006422=+y x 11.已知数列1-,1a ,2a ,4-成等差数列;1-,1b ,2b ,3b ,4-成等比数列,则212a a b -的值是 ( )A. 12B. 12-C.12或12-D. 41或 41- 12.已知抛物线22y px =(0p >)与椭圆22221x ya b+=(0a b >>)有相同的焦点F ,点A 是两曲线的一个公共点,且x AF ⊥轴,则椭圆的离心率为11 C.12D.12 二. 填空题 (本大题共4小题,每小题5分,共20分)13.已知函数x x x f +=2)(, =')0(f __________________________.14. 渐近线方程为32y x =±,的双曲线方程为____________. 15.抛物线22(0)=>y px p 上一点M 到焦点的距离是(),2>p a a 点M 的横坐标是 .16.下列命题中(1)若,22bc ac <则 .a b <(2)函数2=+y x x的最小值为(3)等轴双曲线的离心率是其中正确命题的序号是__________________________.三、解答题:解答应写出文字说明,证明过程或演算步骤.17. (本小题满分10分)求函数3213()2132=-++f x x x x 的单调区间和极值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平安一中 2018年新高一 8 月入学分班考试数学试卷本试卷分为试题卷和答题卷两部分,其中试题卷由第Ⅰ卷(选择题)和第Ⅱ卷组成,共 4 页;答题卷共 4 页.满分 100 分,考试时间 90 分钟.考试结束后将答题卡和答题卷一并交回.第Ⅰ卷(选择题,共 40 分)注意事项:1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦擦 干净后,再选涂其他答案,不能答在试题卷上. 一.选择题(本大题共 10 个小题,每小题 4 分,共 40 分,在每小题给出的四个选项中,只有一项是符合题目要求的) 1. 函数 f (x ) =(x - 1) +- 1 是( )x 1A .奇函数B .偶函数C .既不是奇函数也不是偶函数D .既是奇函数,又是偶函数。
2.已知 A = {-1, 0,1, 2, 3}, B = {x | log 2 ( x - 1) ≤ 1}, 则A I B 的元素个数为( ) A .0 B .2 C .3 D .5 3.下列四个命题:①若 a // b ,则 a = b ;②若 a 则 a = b ;③若 a a // b ; ④ 若 a = b ) A.1 .2 C.3 D.4y = 7⎛ - 1 x + π ⎫4.函数tan ⎝ 2⎪ 的最小正周期是( ) 3 ⎭A . 4πB . 2πC . πD . π25.已知 a > 0, 且 a ≠ 1 ,函数 y = log a 能是( )x , y = a x , y = x + a 在同一坐标系中的图象可⎛ 1 ⎫6.已知幂函数 y =f ( x ) 的图像过点 2, ⎪ ,则它的单调递增区间是()A.(-⎝ B.+ ∞)⎛ 1 ⎫ 4 ⎭C .(-⎛ 1D .(-π ⎫7.要得到函数y=sin - x⎪的图像,只需将函数y=sin -x + ⎪的图象()⎝ 3 ⎭ ⎝ 3 6 ⎭A .向左平移 π个单位B .向右平移 π个单位22C .向左平移 π 个单位D .向右平移 π 个单位。
668.已知 2a = 3b = k (k ≠ 1) ,且 2a + b = ab ,则实数 k 的值为( ) A.6 B.9 C.12 D.189.函数 f ( x ) = 2x+ 3x 的零点所在的一个区间是 ( )A.(-2,-1)B.(-1,0)C.(0,1)D.(1,2)10.△ABC 中,已知 c osA= 5 ,sinB= 3 ,则 c osC 的值为()135A 、16 B 、56 C 、 16或56 D 、 - 16656565 6565注意事项:第Ⅱ卷(非选择题,共 60 分)1.用钢笔或圆珠笔将答案直接写在答题卷上.2.答卷前将答题卷的密封线内项目填写清楚. 二.填空题(本大题共 5 小题,每小题 4 分,共 20 分)11.如果一扇形的圆心角是 72︒ ,半径是 20c m,则扇形的面积为 cm 2 . 12.若函数 f ( x ) = log 2 (2 - ax ) 在[0,1] 上为减函数,则实数 a 的取值范围x 2 -2 x13.已知 f ( x ) 为定义在 (-1,1) 上的奇函数,当 x ∈ (0,1) 时,f ( x ) = 2 时,f ( x ) = 。
tan(2π - α ) cos( 3π- α ) cos(6π - α ).当 x ∈ (-1, 0)14.化简: 2 =tan(π - α ) sin(α + 3π ) cos(α + 3π)2 215.下列命题中,正确命题的序号是 . ① 函数 y =sin x 不是周期函数. ② 函数 y =tan x 在定义域内是增函数.1 π 5π③ 函数 y =|cos2 x + |的周期是 . ④ y =sin( x + )是偶函数,2 2 2 ⑤ 函数 y =sin(2 x + π)的图象关于点( π ,0)成中心对称图形.312三.解答题(本大题共 4 小题,共 40 分,解答应写出文字说明证明过程或推演步骤.)16.已知奇函数 f (x )是定义在(-3,3)上的减函数,且满足不等式 f (x -3 ) + f (x 2 -3)<0,的解集为 A ,B =A ∪{x | 1 ≤x ≤5} , 求函数 g (x ) = -3x 2+ 3 x -4(x ∈B )的最大值sin - π ⎫ x x 17.已知函数f (x ) = a ⎛2x ⎝⎪ + b (a > 0) 的最大值是 1,最小值是 0。
3 ⎭(1)求实数 a , b 的值.(2)求 f (x ) 的对称中心和对称轴。
18.已知函数 f ( x ) = A s in(wx + ϕ )( x ∈ R , w > 0, 0 < ϕ < π) 的部分图像如图所示。
2y(1) 求函数 f ( x ) 的解析式;(2) 求函数 g ( x ) = f ( x - π ) - f ( x + π ) 的单调递增区间。
12 1219.已知函数 f ( x ) = log 4 (4 (1)求实数 k 的值;+ 1) + kx (k ∈ R ) 是偶函数. (2)设 g ( x ) = log 4 (a g 2 围.+ a ) ,若f ( x ) =g ( x ) 有且只有一个零点,求实数 a 的取值范⎪一、选择题高一数学参考答案211、 80 12、(0,2) 13、 f ( x ) = -2 x + 2 x三、解答题14、115、 ①④16、解:不等式 f (x -3 ) + f (x 2-3)<0,可以转化为f ( x - 3) <f (3 - x 2 ) 则有⎧x - 3 > 3 - x 2 ⎪ ⎨- 3 < x - 3 < 3解得,A={ x | 2 < x ⎩- 3 < x 2- 3 < 3∴ B={ x | 1 ≤ x <},g ( x ) = -3( x - 1 ) 2 + 9 在上单调递减 2 4∴ g (x )max =g ( 1 ) = -4.⎧a + b = 1 117、解:由题可知 ⎨⎩- a + b = 0解得 a = b = 。
2 (2)由 2 x - π 3 = π + k π 得对称轴方程为 x = 5π 2 12 + k π, k ∈ Z .2 2 x - π = k π 得对称中心为 (π + k π , 1 ).3 6 2 218、解:(1) 由图可知 T = 11π - 5π ,可得T = π , w = 2, 又图像经过 ( 5π,0) 故有2 12 12 122 ⨯ 5π 12 + ϕ = k π , k ∈ Z ,得ϕ = - 5π 6 + k π , k ∈ Z . 又 0 < ϕ < π 2 ,取ϕ = π 。
过(0,1) 6 点,所以 A s in ϕ = 1 ,可得 A =2.得 f ( x ) = 2 sin(2 x + π) 。
6(2)g ( x ) =f ( x - π ) - f ( x + π ) 12 12 ∴g ( x ) = 2 s in[2( x - π ) + π ] - 2 s in[2( x + π ) + π ] = 2 s in 2x - 2 s in(2x + π12 6 12 6 3= 2 s in 2 x - 2 s in 2x cos π - 2 c os 2x s in π= sin 2 x -2x3 3= 2 s in(2x -π) 3由-π2+ 2kπ≤2x-π3≤π+2kπ,k ∈Z 得-π2 12+k π≤x ≤5π12+k π, k ∈Zt ⎩ x= - 所以 g ( x ) 的单调递增区间为[- π 12+ k π , 5π 12+ k π ], k ∈ Z .19、解: (1)由函数 f ( x ) 是偶函数可知: f ( x ) = f (- x ) , ………1 分x∴ l og (4x + 1) + kx = log (4- x + 1) - kx,化简得 l og 4 + 1 = -2kx ,4444- x + 1即 x = -2kx 对一切 x ∈ R 恒成立,∴ k = - 1.………………………3 分2(2)函数 f ( x ) 与 g ( x ) 的图象有且只有一个公共点,即方程 l og 4 (4+ 1) -1 xx = log 4 (a ⋅ 22+ a ) 有且只有一个实根…………4 分化简得:方程 2x + 1 2x= a ⋅ 2x + a 有且只有一个实根,且a ⋅ 2x + a > 0 成立, 则 a > 0 令 t = 2x > 0 ,则 (a - 1)t 2 + at - 1 = 0 有且只有一个正根…………………6 分 设 g (t ) = (a - 1)t 2 + at - 1 ,注意到 g (0) = -1 < 0 ,所以①当 a = 1 时, 有 t = 1 , 合题意; ②当 0 < a < 1 时, g (t ) 图象开口向下,且g (0) = -1 < 0 ,则需满足 ⎧⎪ 对称轴 ⎨⎪∆ = 0a 2(a - 1)> 0 ,此时有 a = -; a = -2 2 (舍去)③当a> 1 时,又g(0) =-1 ,方程恒有一个正根与一个负根.综上可知, a 的取值范围是{ - 2 }∪[1,+∞).………………………10分。
