上海市七宝中学高一入学分班数学考试卷及答案
2022新高一入学分班考数学试卷12套(含答案)

D.不能确定
α
β
B
D
C
10.如图为由一些边长为 1cm 正方体堆积在桌面形成的立方体的三视图,则该立方体露在外面部分的表面积是
________ cm2。
正视图 A. 11 B.15
左视图 C.18
俯视图 D.22
第Ⅱ卷(答卷)
二. 填空题(本大题共 5 小题, 小题 4 分,共 20 分)
11.函数 y
形 S3 ,以此类推,则 S2006 为(
A.是矩形但不是菱形; C.既是菱形又是矩形;
) B. 是菱形但不是矩形; D.既非矩形又非菱形.
9.如图 ,D 是直角△ABC 斜边 BC 上一点,AB=AD,记∠CAD= ,∠ABC= .若 10 ,则 的度数是 (
)
A
A.40
B. 50
C. 60
W=
20 30
2x 1 x
8
1 x 82
82
12
14
8
1 8
x
82
2x
40
1 x 6 6 x 11 12 x 16
化简得
W=
1 18
x2 x2
14 2x
1
26
x 6 6 x
11
………………10
分
8
1 8
x2
4x
48
12 x 16
①当 W= 1 x 2 14 时,∵ x ≥0,函数 y 随着 x 增大而增大,∵1≤ x ≤6 8
4
1
5
2
x
①
2 x 1 6 x
②
由①得:x>-1
由②得: x 4
所以原不等式组的解集为: 1 x 4
高一新生分班考试数学试卷含答案

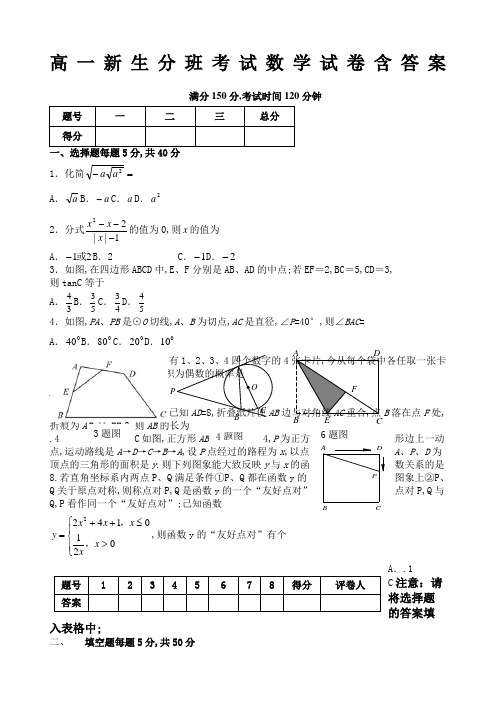
高一新生分班考试数学试卷(含答案)满分150分,考试时间120 分钟)、选择题(每题 5 分,共40 分)1.化简 a a2()A. a B.a C.a D.a22.分式x x 2的值为0,则x 的值为()| x| 1A.1或2B.2 C .1D. 23.如图,在四边形ABCD中,E、F 分别是AB、AD的中点。
若EF=2,BC=5,CD=3,则tanC 等于()A.4B.3 C.3D.435454.如图,PA、PB是⊙O切线,A、B为切点,AC是直径,∠ P=40°,则∠ BAC=()0 0 0 0A.400B.800C.200D.100入表格中。
5.在两个袋内, 卡片,则所取 分别装着写有 1、2、3、4 上数字之积为偶数的 6.如图,矩形纸片 AB 处,折痕为 AE ,且 EF=3, 动点,运动路线是 A →D →C →B →A, 设 P 点经过的路程为 x , D 为顶点的三角形的面积是 y. 则下列图象能大致反映 y 与 x 的是 () 8.若直角坐标系内两点 P 、Q 满足条件① P 、Q 都在函数 y 的 Q 关于原点对称,则称点对( P ,Q )是函数 y 的一个“友好 对( P , Q )与( Q ,P )看作同一个“友好点对”)。
已知函 2x 2 ,已知 AD=8,折 则 AB 的长为 () 如图,正方形 AB (C4D 的题边图长) 为 4, P 为正 4x 1,x 0, 则函数 y 的“友好点对”有()个D中各任取一张 ,点 B 落在点 F CAD P B C 方形边上一 以点 A 、P 、 的函数关系 图象上② P 、 点对”(点 数A ..1题号12345678得分评卷人答案C 注意:请 将选择题 的答案填A176 5 C . 16 P 使 AB 边与对) O E (6 题字的 4A 张卡片,今从每个袋x0y 1,2x二、 填空题(每题 5分,共 50 分)9.已知 a 、b 是一元二次方程 x 22x 1 0的两个 a b a b 2 ab 得分 评卷人实数根,则代数式的值等于10.有一个六个面分别标上数字 1、2、3、4、5、6 的正方体,甲、乙、丙三位同学从不同 的角度观察的结果如图所示. 如果记 2 的对面的数字为 的解 x 满足 k x k 1,k 为整数,则 k m ,3的对面的数字为 n ,则方程m x 1nE11. 1 2 ADy x f (x) y x 2f (x)C)A 3 x 3 25 1 f(1) 1 f (x) 甲 A 1 f (a) f (b) f( O 的直径,四边形 则正方形 CDM 16. 如图, CD 为 C 1 丙 题图 C 1 AB 1,BC 2 AA 1x a |x| F A cb BC 3M BB 1 A 1M 1题M 图C 1 BM 图,AB 是半圆 DEFG 都是正方形, 其中 C ,D ,E 在 AB 上,F ,N 在半圆上。
2018-2019学年上海市七宝中学高一上学期分班考试数学试题

2018-2019学年上海市七宝中学高一上学期分班考试数学试题一选择题1.已知a>b>0则下列不等式不一定成立的是()A.ab>bcB. a+c>b+cC. 1a<1bD. ac>bc2.若不等式组2113xx a-⎧⎪⎨⎪⎩ff的解为x>2,则a的取值范围是()A. a>2B. a≥2C. a<2 D a≤23.若M(-12,y1)、N(-14,y2)、P(12,y3)三点都在函数(0)ky kx=p的图像上,则y1、y2、y3大小关系为A. y2> y1> y3B. y2> y3> y1C. y3> y1> y2D. y3> y2> y14.已知y= 2x2的图像是抛物线,若抛物线不动,把x轴、y轴分别向上、向右平移2个单位,那么在新坐标系下抛物线的解析式为()A. y=2(x-2)2+2B. y=2(x+2)2-2C. y=2(x-2)2-2D. y=2(x+2)2+25.中央电视台“幸运52”栏目中的“百宝箱”互动环节,是一种竞猜游戏,游戏规则如下:在20个商标中,有5个商标牌的背面注明了一定的奖金额,其余商标的背面是一张苦脸,若翻到它就不得奖,参加这个游戏的观众有三次翻牌的机会,某观众前两次翻牌均得若干奖金,如果翻过的牌不能再翻,那么这位观众第三次翻牌获奖的概率为()A.14B.16C.15D.3206.将水匀速注入一个容器,时间(t)与容器水位(h)的关系如图,则容器形状是() 二、填空题7.2(3)0n-=,则2009(3)m n+-=8.已知a:b:c=4:5:7,a + b + c = 240,则2b-a+c =9.将一张坐标纸折叠一次,使得点(0,2)与(-2,0)重合,则点(-12,0)与点_重合10.对于整数a、b、c、d,符号a bd c表示运算ac bd-,已知1134bdp p,则b+d的值为11.定义“*”:A *B (1)(1)X Y A B A B =++++,若1*2=3,2*3= 4,则3*4= 12.分式方程133x m x x +=--有增根,则m= 13.如图是一个有规律排列的数表,请用含n 的代数式 (n 为正整数)表示数表中第n 行第n 列的数:14.已知a-b=b-c=35,a 2+b 2+c 2=1,则ab+bc+ca=15.若2610x x -+=,则2211x x +-= 16.如图,AB//CD, ∠BAP=600-α, ∠APC=45+α, ∠PCD=300-α,则α=17.关于x 的一元二次方程mx 2-x +1=0有实根,则m 的取值范围是_18.如图,点A. B 分别是棱长为2的正方体左、右两侧面的中心,一蚂蚁从点A 沿其表面爬到点B 的最短路程长度是 .19.二次函数y = x 2- 2x -3与二轴两交点之间的距离为_20.已知α、β是方程x 2- x -1=0的两个实数根,则代数式22(2)ααβ+-==_ 21.如图,在三角形纸片ABC 中,∠C=900, ∠A=300, AC=3,折叠该纸片,使点A 与点B 重合,折痕与AB 、 AC 分别相交于点E 和点D ,则折痕DE 的长为22.已知x 、y 、z 为实数,满足2623x y z x y z +-=⎧⎨-+=⎩,那么x 2+y 2+z 2的最小值是三 解答题23.一辆高铁列车与另一辆动车组列车在1320公里的京沪高速铁路上运行时,高铁列车比动车组列车平均速度每小时快99公里,用时少3小时,求这辆高铁列车全程的运行时间和平均速度.24.如图,线段AB=5,点E在线段AB上,且AE=3, GB与以AE为半径的GA相交于点C,CE 的延长线交GB于点F.(1)当直线AC是GB的切线时,求证,BF⊥AB;(2)求EF:CE的值;(3)设EF = y,BF=x,求y关于x的函数解析式,并写出它的定义域.25.如图,在平面直角坐标系中,矩形ABOC的边BO在x轴的负半轴上,边OC在y轴的正半轴上,且AB=1, OB=万,矩形ABOC绕点。
上海市名校历年高一开学分班考真题专项(等式与不等式)汇编(2023版,附答案)

上海市名校历年高一开学分班考真题专项(等式与不等式)汇编 一、单选题
A .55a b ->-
B .66a b >
二、填空题
三、解答题
、(1)现在准备养一批供游客观赏的鱼,分别在AB BC 游客要在DEF
面积越大越好.设 内喂鱼,希望DEF
(2)现在准备新建造一个走廊,方便游客通行,分别在
∠=(如图2),游客希望DEF
周长越小越好.设FEC
(1)试用解析式将y表示成(2)求三角形池塘OEF
参考答案 一、单选题
A .55a b ->-
B .66a b >
二、填空题
<=1+x
y=1+x是一个增函数
【答案】
【过程详解】试卷详细分析:
【名师点睛】本题考查分式不等式的解法,考查高次不等式
29.(2020∙上海∙高一开学考试)已知|a|<1,则
1
1a
+
与1-
【名师点睛】本题主要考查函数综合应用和均值不等式的应用,本题的关键在于由函数图像得出属于基础题.
35.(2020∙上海∙高一开学考试)关于
三、解答题
【过程详解】试卷详细分析:由已知得:的两个根是或,那么根据根与系数的关系,解得,代入所解不等式,,解得
考点:1.二次不等式的解法;
、(1)现在准备养一批供游客观赏的鱼,分别在AB BC 游客要在DEF
内喂鱼,希望DEF
面积越大越好.设(2)现在准备新建造一个走廊,方便游客通行,分别在
(1)试用解析式将y表示成(2)求三角形池塘OEF。
2018-2019学年上海市七宝中学高一下学期开学考试数学试题(解析版)

2018-2019学年上海市七宝中学高一下学期开学考试数学试题一、单选题 1.“tan a θ=”是“1cos2sin 2a θθ-=”的( )A.充分非必要条件B.必要非充分条件C.充要条件D.既非充分也非必要条件【答案】B【解析】先考查充分性,再考虑必要性得解. 【详解】当tan a θ=时,21cos22sin sin sin 22sin cos cos a θθθθθθθ-===,但是当=0θ时,1cos2sin 2θθ-分母为零,没有意义. 所以“tan a θ=”是“1cos2sin 2a θθ-=”的非充分条件;当1cos2sin 2a θθ-=时,2(),2k k k Z x πθπ≠∈∴≠. 所以21cos22sin sin =tan sin 22sin cos cos a θθθθθθθθ-===, 所以“tan a θ=”是“1cos2sin 2a θθ-=”的必要条件.所以“tan a θ=”是“1cos2sin 2a θθ-=”的必要非充分条件.故选:B 【点睛】本题主要考查三角函数的定义域和三角恒等变换,考查充分必要条件的判定,意在考查学生对这些知识的理解掌握水平和分析推理能力.2.已知f (x )=2x 4x 3,x 02x 2x 3,x 0-+≤⎧⎪--+>⎨⎪⎩,不等式f (x+a )>f (2a-x )在[a ,a+1]上恒成立,则实数a 的取值范围是( )A.(),2∞--B.(),0∞-C.()0,2D.()2,0-【答案】A【解析】试题分析:二次函数243y x x =-+的对称轴为2x =,则该函数在(,0)-∞上单调递减,则2433x x -+≥,同样函数223y x x =--+在(0,)+∞上单调递减,2-233x x ∴-+<()f x ∴在R 上单调递减;由()()2f x a f a x +>-得到2x a a x +<-,即2x a <;则2x a <在[,1]a a +上恒成立;则2(1),2a a a +<∴<-,实数a 的取值范围是(,2)-∞-,故选A ;【考点】1.分段函数的单调性;2.恒成立问题;3.有下列命题:(1)终边相同的角的同名三角比的值相等;(2)终边不同的角的同名三角比的值不同;(3)若sin 0α>,则α是第一或第二象限角;(4)△ABC 中,若A B >,则sin sin A B >;其中正确命题的个数是( )A.1个B.2个C.3个D.4个【答案】B【解析】(1),根据终边相同的角的同名三角函数值相等,判断命题正确;(2),根据终边不同的角的同名三角函数值也可能相等,判断命题错误;(3),当sin 0α>时,α是第一或第二象限角,或为终边在y 轴的正半轴上,判断命题错误;(4),根据大角对大边,利用正弦定理即可判断结论正确. 【详解】对于(1),终边相同的角的同名三角函数值相等,所以比值相等,(1)正确; 对于(2),终边不同的角的同名三角函数值也可能相等,如5sin sin66ππ=, 所以比值也可能相同,(2)错误;对于(3),若sin 0α>,则α是第一或第二象限角,或终边在y 轴的正半轴上,(3)错误;对于(4),ABC ∆中,若A B >,则a b >, 由正弦定理得2sin sin a bR A B==, 2sin 2sin R A R B ∴>,sin sin A B ∴>,(4)正确; 综上,其中正确命题的序号为(1)和(4),共2个.故选:B . 【点睛】本题主要考查了命题的真假判断,涉及三角函数的定义,角的取值和三角函数的符号,是基础题.4.设()f x 是定义域为R 的以3为周期的奇函数,且(2)0f =,则方程()0f x =在区间(6,6)-内解的个数的最小值为( ) A.15 B.13C.11D.9【答案】A【解析】根据题意,由奇函数的性质可得(0)0f =,结合函数的周期性可得f (3)0=,(3)0f -=,结合f (2)0=分析可得f (2)f =(5)(1)0f =-=,进而可得(2)(5)f f f -=-=(1)0=和f (1)f =(4)0=,(4)(1)0f f -=-=;结合奇偶性与周期性可得33()()022f f -==,进而可得99()()022f f -==,综合可得答案.【详解】根据题意,()f x 是定义在R 上的奇函数,则(0)0f =, 又由()f x 是周期为3的周期函数,则f (3)0=,(3)0f -=, 又由f (2)0=,则f (2)f =(5)(1)0f =-=, 又由函数为奇函数,则(2)(5)f f f -=-=(1)0=, 则有f (1)f =(4)0=,(4)(1)0f f -=-=,又由函数()f x 是以3为周期的奇函数,故有33()()22f f -=-且33()()22f f -=,则有33()()022f f -==,则有99()()022f f -==,综合可得:方程()0f x =在区间(6,6)-内解至少有:5-,4-,3-,2-,1-,0,1,2,3,4,5,92-,32-,32,92,共15个;故选:A . 【点睛】本题考查函数的奇偶性与周期性的综合应用,注意分析33()()022f f -==,属于基础题.二、填空题5.已知函数()f x 是幂函数,且2(4)(16)f f =,则()f x 的解析式为________ 【答案】12x【解析】设()f x x α=,根据条件建立方程求出α的值即可.【详解】设()f x x α=,2f (4)(16)f =, 2416αα∴⨯=,即1624αα=,则42α=,12α=, 即12()f x x =, 故答案为:12()f x x = 【点睛】本题主要考查幂函数解析式的求解,利用待定系数法建立方程是解决本题的关键.6.已知cos()6πα-=,则5cos()6πα+=_________ 【答案】【解析】试题分析:因为,cos()63πα-=, 所以,5cos()cos[()]cos()666πππαπαα+=--=--=。
高一新生分班考试数学试卷(含问题详解)

高一新生分班考试数学试卷(含答案)(满分150分,考试时间120分钟)题号一二 三 总分 得分[一、选择题(每题5分,共40分) 1.化简=-2a a( )A .aB .a -C .aD .2a2.分式1||22---x x x 的值为0,则x 的值为 ( )#A .21或-B .2C .1-D .2-3.如图,在四边形ABCD 中,E 、F 分别是AB 、AD 的中点。
若EF =2,BC =5,CD =3, 则tan C 等于 ( )A .43 B .35 C .34 D .454.如图,PA 、PB 是⊙O 切线,A 、B 为切点,AC 是直径,∠P = 40°,则∠BAC =( )A .040 B .080 C .020 D .010(4题图)O CB AP'BCFE (3题图)DCBAC B;5.在两个袋内,分别装着写有1、2、3、4四个数字的4张卡片,今从每个袋中各任取一张卡片,则所取两卡片上数字之积为偶数的概率是 ( ) A .21 B .165 C .167 D .436.如图,矩形纸片ABCD 中,已知AD =8,折叠纸片使AB 边与对角线AC 重合,点B 落在点F 处,折痕为AE ,且EF =3,则AB 的长为 ( ) A. 6 D. 37.如图,正方形ABCD 的边长为4,P 为正方形边上一动点,运动路线是A →D →C →B →A ,设P 点经过的路程为x ,以点A 、P 、D 为顶点的三角形的面积是y .则下列图象能大致反映y 与x 的函数关系的是 ( )/8.若直角坐标系内两点P 、Q 满足条件①P 、Q 都在函数y 的图象上②P 、Q 关于原点对称,则称点对(P ,Q )是函数y 的一个“友好点对”(点对(P ,Q )与(Q ,P )看作同一个“友好点对”)。
已知函数⎪⎩⎪⎨⎧>≤++=02101422x xx x x y ,,,则函数y 的“友好点对”有( )个A .0 C. 2注意:请将选择题的答案填入表格中。
高一新生分班考试数学试卷含答案
P DCB A 高一新生分班考试数学试卷含答案满分150分,考试时间120分钟题号 一二三总分得分一、选择题每题5分,共40分 1.化简=-2a a A .a B .a -C .a D .2a2.分式1||22---x x x 的值为0,则x 的值为A .21或-B .2C .1-D .2-3.如图,在四边形ABCD 中,E 、F 分别是AB 、AD 的中点;若EF =2,BC =5,CD =3, 则tanC 等于A .43B .35C .34D .454.如图,PA 、PB 是⊙O 切线,A 、B 为切点,AC 是直径,∠P =40°,则∠BAC = A .040B .080C .020D .0105.在两个袋内,分别装着写有1、2、3、4四个数字的4张卡片,今从每个袋中各任取一张卡片,则所取两卡片上数字之积为偶数的概率是A .21B .165C .167D .43 6.如图,矩形纸片ABCD 中,已知AD =8,折叠纸片使AB 边与对角线AC 重合,点B 落在点F 处,折痕为AE ,且EF =3,则AB 的长为.4 C 如图,正方形ABCD 的边长为4,P 为正方形边上一动点,运动路线是A →D →C →B →A ,设P 点经过的路程为x ,以点A 、P 、D 为顶点的三角形的面积是y .则下列图象能大致反映y 与x 的函数关系的是8.若直角坐标系内两点P 、Q 满足条件①P 、Q 都在函数y 的图象上②P 、Q 关于原点对称,则称点对P,Q 是函数y 的一个“友好点对”点对P,Q 与Q,P 看作同一个“友好点对”;已知函数⎪⎩⎪⎨⎧>≤++=02101422x xx x x y ,,,则函数y 的“友好点对”有个 A ..1 C 注意:请将选择题的答案填入表格中;二、 填空题每题5分,共50分题号 12345678得分评卷人答案4题图 O C B A P6题图 AB CDF E 3题图9.已知a 、b 是一元二次方程2210x x --=的两个实数根,则代数式()()2a b a b ab -+-+的值等于10.有一个六个面分别标上数字1、2、3、4、5、6的正方体,甲、乙、丙三位同学从不同的角度观察的结果如图所示.如果记2的对面的数字为m ,3的对面的数字为n ,则方程1x m n +=的解x 满足1+<<k x k ,k 为整数,则k =11.如图,直角梯形纸片ABCD中,AD y x ()f x 2y x =2()f x x =1x =(1)1f =||)(x x x f =c b a >>0=++c b a 0≠b )()()(c f b f a f ++111C B A ABC-2,1==BC AB 31=AA M 1BB 1MC AM +BM 图,AB 是半圆O 的直径,四边形CDMN 和DEFG 都是正方形,其中C,D,E 在AB 上,F,N 在半圆上;若AB=10,则正方形CDMN 的面积与正方形DEFG 的面积之和是 16.如图,CD 为直角ΔABC 斜边AB 上的高,BC 长度为1,DE ⊥AC;设ΔADE,ΔCDB,ΔABC 的周长分别是12,,p p p ;当12p p p+取最大值时,AB=17.如图放置的等腰直角∆ABC 薄片2,900==∠AC ACB 沿x 轴滚动,点A 的运动轨迹曲线与x 轴有交点,则在两个相邻交点间点A 的轨迹曲线与x 轴围成图形面积为___ 18.如图是一个数表,第1行依次写着从小到大的正整数,然后把每行相邻的两个数的和写在这两数正中间的下方,得到下一行,数表从上到下与从左到右均为无限项,则这个数表中的第11行第7个数为用具体数字作答1234567… … 4… … 486480…注意:请将填空题的答案填在下面的横线上; 三、解答题共60分19.本小题满分12分如图,抛物线1417452++-=x x y 与y 轴交于A 点,过点A 的直线与抛物线交于另一点B ,过点B 作BC ⊥x 轴,垂足为点C 3,0. 1求直线AB 的函数关系式;2动点P 在线段OC 上从原点出发以每秒一个单位的速度向C 移动,过点P 作PN ⊥x 轴,交直线AB 于点M ,交抛物线于点N ;设点P 移动的时间为t 秒,MN 的长度为s 个单位,求s 与t 的函数关系式,并写出t 的取值范围;3设在2的条件下不考虑点P 与点O ,点C 重合的情况,连接CM ,BN ,当t 为何值时,四边形BCMN 为平行四边形 问对于所求的t 值,平行四边形BCMN 能否为菱形 请说明理由.20.本小题满分12分函数)(x f ,若自变量x 00(,)x x 为坐标的点为函数()f x 得分 评卷人11题图B CE D AF 5 23 3 2 1 2 6 1 甲 乙 丙10题图 oxy C AB题图17ABC M1A 1B 1C 题图141若函数bx ax x f ++=3)(有两个关于原点对称的不动点,求a,b 应满足的条件; 2在1的条件下,若a=2,直线1)1(:-+-=b x a y l 与y 轴、x 轴分别相交于A 、B 两点,在xb y =的图象上取一点PP 点的横坐标大于2,过P 作PQ ⊥x 轴,垂足是Q ,若四边形A BQP 的面积等于2,求P 点的坐标3定义在实数集上的函数)(x f ,对任意的x 有)()(x f x f -=-恒成立;下述命题“若函数)(x f 的图像上存在有限个不动点,则不动点有奇数个”是否正确 若正确,给予证明;若不正确,举反例说明;21.本小题满分12分已知圆O轴于A 点,交y 轴正半轴于B 点 1求BAO ∠2设圆O 与x 轴的两交点是12,F F ,1F 射出经反射到2F 经过的路程3点P 是x 轴负半轴上一点,从点P 发出的光线经l 反射后与圆O 相切.若光线从射出经反射到相切经过的路程最短,求点P 的坐标 22.本小题满分12分在金融危机中,某钢材公司积压了部分圆钢,经清理知共有2009根.现将它们堆放在一起. 1若堆放成纵断面为正三角形每一层的根数比上一层根数多1根,并使剩余的圆钢尽可能地少,则剩余了多少根圆钢2若堆成纵断面为等腰梯形每一层的根数比上一层根数多1根,且不少于七层, Ⅰ共有几种不同的方案Ⅱ已知每根圆钢的直径为10cm ,为考虑安全隐患,堆放高度不得高于4m ,则选择哪个方案,最能节省堆放场地23.本小题满分12分试求出所有正整数a 使得关于x 的二次方程22(21)4(3)0ax a x a +-+-=至少有一个整数根.数学试卷答案一、选择题每题5分,共40分三、 填空题每题5分,共50分 9.1-10.011.612.1或-113.614.115.2516.217.24+π18.12288 三、解答题共60分19.解:1易知A0,1,B3,,可得直线AB 的解析式为y =121+x ……………3分2)121(1417452+-++-=-==t t t MP NP MN s)30(415452≤≤+-=t t t ………………6分3若四边形BCMN 为平行四边形,则有MN =BC ,此时,有25415452=+-t t ,解得11=t ,22=t 所以当t =1或2时,四边形BCMN 为平行四边形.………………8分①当t =1时,23=MP ,4=NP ,故25=-=MP NP MN ,又在Rt △MPC中,2522=+=PC MP MC ,故MN =MC ,此时四边形BCMN 为菱形…………10分②当t =2时,2=MP ,29=NP ,故25=-=MP NP MN ,又在Rt △MPC中,522=+=PC MP MC ,故MN ≠MC ,此时四边形BCMN 不是菱形.…………12分 20.解:1由题得x bx ax =++3有两个互为相反数的根0x ,0x -)0(0≠x 即)(0)3(2b x a x b x -≠=--+有两个互为相反数的根0x ,0x -……1分根带入得⎪⎩⎪⎨⎧=---+=--+0))(3(0)3(020020a x b x a x b x ,两式相减得0)3(20=-x b ,3=∴b ……3分方程变为)3(02-≠=-x a x 90≠>∴a a 且…………4分 2由1得3,2==b a ,所以2:+-=x y l ,即A0,2B2,0……5分设x y 3=上任意一点)2)(3,(>t tt P ,所以)2)(0,(>t t Q ……6分 又因为2-=∆AOB AOQP S S 四边形,所以22221)32(21=⨯⨯-+t t 25=∴t ……8分)56,25(P ∴……………………9分3正确①在)()(x f x f -=-令0=x 得)0()0(f f -=所以0)0(=f所以)0,0(为函数的不动点……………………10分 ②设00(,)x x 为函数()f x 图像上的不动点,则00)(x x f = 所以000)()(x x f x f -=-=-,所以),(00x x --也为函数()f x 图像上的不动点……………………12分 21.解:1由题|OA|=4,|OB|=334,所以33tan =∠BAO ,所以030=∠BAO 2分 2如图1由对称性可知,点1F 关于l 的对称点/1F 在过点()4,0A -且倾斜角为060的直线/l 上在/21AF F ∆中,0'160=∠AO F ,3811'1=-==O F AO AF AF ,3162=AF所以/21AF F ∆为直角三角形,02'190=∠F AF ;所以光线从1F 射出经反射到2F 经过的路程为3382'12'121==+=+F F MF M F MF M F …………………………6分 2如图2由对称性可知,点P 关于l 的对称点'P 在过点()4,0A -且倾斜角为060的直线/l 上Q P MQ M P MQ PM ''=+=+,所以路程最短即为/l 上点/P 到切点Q 的切线长最短; 连接',OP OQ ,在'OQP Rt ∆中,只要'OP 最短,由几何知识可知,/P 应为过原点O 且与/l 垂直的直线与/l 的交点,这一点又与点P 关于l 对称,∴260cos 0'===AO AP AP ,故点P 的坐标为()2,0-……………12分22.解:1设纵断面层数为n ,则321++即20092)1(≤+n n ,040182≤-+n n ,当62=n 时,此时剩余的圆钢为562)162(622009=+-2当纵断面为等腰梯形时,设共堆放n 层)1(.....)2()1(=-+++++++n x x x x 即4177220092)12(⨯⨯⨯=⨯=-+n x n ,……………………6分因1-n 与n 的奇偶性不同,所以12-+n x 与n 的奇偶性也不同,且12-+<n x n ,从而由上述等式得:⎩⎨⎧=-+=574127n x n 或⎩⎨⎧=-+=2871214n x n 或⎩⎨⎧=-+=981241n x n 或⎩⎨⎧=-+=821249n x n ,所以共有4种方案可供选择;-----------------------------8分3因层数越多,最下层堆放得越少,占用面积也越少,所以由2可知:若41=n ,则29=x ,说明最上层有29根圆钢,最下层有69根圆钢,两腰之长为400cm,上下底之长为280cm 和680cm,从而梯形之高为3200cm, 而400103200<+,所以符合条件;………………10分若49=n ,则17=x ,说明最上层有17根圆钢,最下层有65根圆钢,两腰之长为480cm,上下底之长为160cm 和640cm,从而梯形之高为3240cm, 显然大于4m,不合条件,舍去;综上所述,选择堆放41层这个方案,最能节省堆放场地………………12分 23.解:原方程可化为122)2(2+=+x a x ,易知2-≠x ,此时2)2(122++=x x a ……2分 因为a 是正整数,即1)2(1222≥++x x 为正整数;又0)2(2>+x ,则122)2(2+≤+x x 即0822≤-+x x ,解得24≤≤-x ;因为2-≠x 且x 是整数,故x 只能取-4,-3,-1,0,1,2,…………………………6分依次带入a 的表达式得⎩⎨⎧=-=14a x ⎩⎨⎧=-=63a x ⎩⎨⎧=-=101a x ⎩⎨⎧==3a x 从而满足题意的正整数a 的值有4个,分别为1,3,6,10…………………………12分。
新高一入学分班考数学卷(参考答案)

新高一入学分班考数学卷(名校版)参考答案一、选择题1.当m<﹣1时,方程(m3+1)x2+(m2+1)x=m+1的根的情况是()A.两负根B.两异号根,且正根的绝对值较大C.两正根D.两异号根,且负根的绝对值较大【分析】首先将方程整理为一般形式,进而利用根据根与系数的关系以及因式分解的应用,分析各式子的符号,进而得出答案.【解答】解:∵(m3+1)x2+(m2+1)x=m+1,∴(m3+1)x2+(m2+1)x﹣(m+1)=0,∴x1x2====,∵m<﹣1,∴m2﹣m+1>0,∴x1x2<0,∴方程由两异号根,∵x1+x2=﹣=,∵m<﹣1,∴m2﹣m+1>0,m+1<0,﹣(m2+1)<0,∴x1+x2>0,∴正根的绝对值较大.故选:B.2.对于数x,符号[x]表示不大于x的最大整数例如[3.14]=3,[﹣7.59]=﹣8,则关于x的方程[]=4的整数根有()A.4个B.3个C.2个D.1个【分析】根据取整函数的定义可知,4≤<5,解此方程组即可.【解答】解:∵[]=4,∴4≤<5,∴,∴,即7≤x<,故x的正数值为7,8,9.故选B.3.+的最小值为()A.B. C. D.均不是【分析】根据题意结合两点之间距离求法,利用轴对称求出最短路线进而得出答案.【解答】解:原式=+,即x轴上的点到(﹣1,1)和(2,4)的距离之和的最小值画图可知,点(4,2)关于x轴的对称点(4,﹣2)与(﹣1,1)连线与x轴的交点即为所求,此时最小值为:=.故选:B.4.在下列图形中,各有一边长为4cm的正方形与一个8cm×2cm的长方形相重叠.问哪一个重叠的面积最大()A.B.C.D.【分析】A、阴影部分是长方形,所以长方形的面积等于长和宽的乘积;B、如图,设阴影部分等腰直角的腰为x,根据勾股定理求出x的值,所以,阴影部分的面积等于正方形的面积减去俩个空白三角形的面积;C、图C,逆时针旋转90°从后面看,可与图D对比,因为图C阴影部分的倾斜度比图D阴影部分的倾斜度小,所以,图C中四边形的底比图D中四边形的底小,两图为等高不等底,所以图C阴影部分的面积小于图D阴影部分的面积;D、图D,设阴影部分平行四边形的底为x,根据正方形的面积=阴影部分的面积+两个空白三角形的面积,求出x的值,再得出阴影部分的面积;图A、图C、图D中阴影部分四边形为等高不等底,因为倾斜度不同,所以图D中阴影部分的底最大,面积也就最大;因此,只要比较图B和图D阴影的面积大小,可得到图B阴影部分的面积最大.【解答】解:A、S阴影=2×4=8(cm2);5.(2016•衡水校级模拟)设全集U=R,集合A={x|},B={x|1<2x<8},则(C U A)∩B等于()A.[﹣1,3)B.(0,2]C.(1,2]D.(2,3)【分析】分别解出集合A,B,然后根据集合的运算求解即可.【解答】解:因为集合A={x|}=(﹣∞,﹣1]∪(2,+∞),B={x|1<2x<8}=(0,3),又全集U=R,∴C U A=(﹣1,2],∴(C U A)∩B=(0,2],故选B.6.已知函数f(x)=,则f(f(2))等于()A.B.2 C.﹣1 D.1【分析】先由解析式求得f(2),再求f(f(2)).【解答】解:f(2)=,f(﹣1)=2﹣1=,所以f(f(2))=f(﹣1)=,故选A.7.设a,b是常数,不等式+>0的解集为x<,则关于x的不等式bx﹣a>0的解集是()A.x>B.x<﹣C.x>﹣D.x<8.对于任意的两个实数对(a,b)和(c,d),规定:①(a,b)=(c,d),当且仅当a=c,b=d;②运算“⊗”为:(a,b)⊗(c,d)=(ac+bd,bc﹣ad);③运算“θ”为:(a,b)θ(c,d)=(a﹣c,b﹣d).设p,q∈R,若(1,2)⊗(p,q)=(11,2),则(1,2)θ(p,q)()A.(﹣2,﹣2)B.(3,4)C.(2,1)D.(﹣1,﹣2)【分析】先根据(1,2)⊗(p,q)=(11,2),列方程组求p、q的值,再由规定运算“θ”求(1,2)θ(p,q)的结果.【解答】解:由规定②,得(1,2)⊗(p,q)=(p+2q,2p﹣q),∵(1,2)⊗(p,q)=(11,2),∴(p+2q,2p﹣q)=(11,2),由规定①,得,解得,由规定③,可知(1,2)θ(p,q)=(1,2)θ(3,4)=(1﹣3,2﹣4)=(﹣2,﹣2).故选A.二、填空题9.已知a2+4a+1=0,且,则m=.【分析】由a2+4a+1=0,得a2=﹣4a﹣1,代入所求的式子化简即可.【解答】解:∵a2+4a+1=0,∴a2=﹣4a﹣1,=====5,∴(16+m)(﹣4a﹣1)+8a+2=5(m﹣12)(﹣4a﹣1),原式可化为(16+m)(﹣4a﹣1)﹣5(m﹣12)(﹣4a﹣1)=﹣8a﹣2,即[(16+m)﹣5(m﹣12)](﹣4a﹣1)=﹣8a﹣2,∵a≠0,∴(16+m)﹣5(m﹣12)=2,解得m=.故答案为.10.已知(x﹣3)2+(y﹣4)2=4,则x2+y2的最大值为49.【分析】运用几何意义解答,x2+y2的最大值就是方程(x﹣3)2+(y﹣4)2=4所代表的圆周上的点到坐标原点的距离最大值的平方,从而可得出答案.【解答】解:x2+y2的最大值就是方程(x﹣3)2+(y﹣4)2=4所代表的圆周上的点到坐标原点的距离最大值的平方,连接坐标原点与圆心(3,4)所得的直线与圆的交点,则(x2+y2)min时,|ON|取最小,(x2+y2)max时,|OM|取最大,∵原点与圆心(3,4)的距离+半径(PM)=+2=7,∴(x2+y2)max=72=49.故答案为:49.11.如图正方形ABCD中,E是BC边的中点,AE与BD相交于F点,△DEF的面积是1,那么正方形ABCD的面积是6.【分析】先设△BEF的面积是x,由于E是BC中点,那么S△DBE=S△DCE,易求S正方形=4(1+x),又四边形ABCD是正方形,那么AD∥BC,AD=BC,根据平行线分线段成比例定理的推论可得△BEF∽△DAF,于是S△BEF:S△DAF=()2,E是BC中点可知BE:AD=1:2,于是S△DAF=4x,进而可得S正方形=S△ABF+S△BEF+S△ADF+S△DEF+S△DCE=1+x+4x+1+1+x,等量代换可得4(1+x)=1+x+4x+1+1+x,解可求x,进而可求正方形的面积.【解答】解:如右图,设△BEF的面积是x,∵E是BC中点,∴S△DBE=S△DCE,∴S△BCD=2(1+x),∴S正方形=4(1+x),∵四边形ABCD是正方形,∴AD∥BC,AD=BC,∴△BEF∽△DAF,∴S△BEF:S△DAF=()2,∵E是BC中点,∴BE=CE,∴BE:AD=1:2,∴S△DAF=4x,∵S△ABE=S△BED,∴S△ABF=S△DEF=1,∴S正方形=S△ABF+S△BEF+S△ADF+S△DEF+S△DCE=1+x+4x+1+1+x,∴4(1+x)=1+x+4x+1+1+x,解得x=0.5,∴S正方形=4(1+x)=4(1+0.5)=6.12.如图,ABCD、CEFG是正方形,E在CD上,且BE平分∠DBC,O是BD中点,直线BE、DG交于H.BD,AH交于M,连接OH,则OH=AB,BM=AB.【分析】易得△BCE≌△DCG,得到∠1=∠2,B,C,H,D四点共圆,得出OH=BD=AB,由E关于BD的对称E′,得到△BEE′是等腰三角形,BM⊥E′E于M,由角平分线到角两边的距离相等得出BM=AB.【解答】解:如图,设EE′与BD交于点M′,∵AD=CD∴AE′=CE=EF,∵∠E′AM′=∠EFM′,∠AM′E′=∠FM′F,∴△AM′E′≌△FM′E(AAS),∴EM′=E′M′,∵ME′=ME∴M与M′重合,∵BC=DC,EC=CG,∠BCE=∠DCG,在△BCE和△DCG中,,∴△BCE≌△DCG(SAS),∴∠1=∠2,∴B,C,H,D四点共圆,∴OH=BD=AB,∵E关于BD的对称E′,∵∠3=∠4,BE=BE′,∴△BEE′是等腰三角形,∴BM⊥E′E于M,∴BM=AB.故答案为:AB,AB.13.函数f(x)=λx2+(λ﹣3)x+1对于任意实数x都有f(x)≤f(λ),则函数f(x)的最大值是.【分析】根据函数有最值,首先判断出λ<0,进而利用二次函数的最值得出f(x)的最大值,使这个最大值与f(λ)相等,解方程即可得出λ的值,进而代入求出f(x)最大值.【解答】解:由题意得,f(x)有最大值,则可得λ<0,又∵f(x)=λ(x+)2+1﹣,∴f(x)的最大值为1﹣,又∵f(x)≤f(λ),∴f(λ)=λ3+(λ﹣3)λ+1=1﹣,解得:λ=1(舍去)或λ=﹣,将λ=﹣,代入可得f(x)的最大值为.故答案为:.三、解答题14.在平面直角坐标系xOy中,抛物线y=ax2+bx+2过B(﹣2,6),C(2,2)两点.(1)试求抛物线的解析式;(2)记抛物线顶点为D,求△BCD的面积;(3)若直线y=﹣x向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,求b的取值范围.【分析】(1)根据待定系数法即可解决问题.(2)求出直线BC与对称轴的交点H,根据S△BDC=S△BDH+S△DHC即可解决问题.(3)由,当方程组只有一组解时求出b的值,当直线y=﹣x+b经过点C时,求出b的值,当直线y=﹣x+b经过点B时,求出b的值,由此即可解决问题.【解答】解:(1)由题意解得,∴抛物线解析式为y=x2﹣x+2.(2)∵y=x2﹣x+2=(x﹣1)2+.∴顶点坐标(1,),∵直线BC为y=﹣x+4,∴对称轴与BC的交点H(1,3),∴S△BDC=S△BDH+S△DHC=•3+•1=3.(3)由消去y得到x2﹣x+4﹣2b=0,当△=0时,直线与抛物线相切,1﹣4(4﹣2b)=0,∴b=,当直线y=﹣x+b经过点C时,b=3,当直线y=﹣x+b经过点B时,b=5,∵直线y=﹣x向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,∴<b≤3.15.如图,A,P,B,C是圆上的四个点,∠APC=∠CPB=60°,AP,CB的延长线相交于点D.(1)求证:△ABC是等边三角形;(2)若∠PAC=90°,AB=2,求PD的长.【分析】(1)由圆周角定理可知∠ABC=∠BAC=60°,从而可证得△ABC是等边三角形;(2)由△ABC是等边三角形可得出“AC=BC=AB=2,∠ACB=60°”,在直角三角形PAC 和DAC通过特殊角的正、余切值即可求出线段AP、AD的长度,二者作差即可得出结论.【解答】(1)证明:∵∠ABC=∠APC,∠BAC=∠BPC,∠APC=∠CPB=60°,∴∠ABC=∠BAC=60°,∴△ABC是等边三角形.(2)解:∵△ABC是等边三角形,AB=2,∴AC=BC=AB=2,∠ACB=60°.在Rt△PAC中,∠PAC=90°,∠APC=60°,AC=2,∴AP==2.在Rt△DAC中,∠DAC=90°,AC=2,∠ACD=60°,∴AD=AC•tan∠ACD=6.∴PD=AD﹣AP=6﹣2=4.2.(2013•济宁)阅读材料:若a,b都是非负实数,则a+b≥.当且仅当a=b时,“=”成立.证明:∵()2≥0,∴a﹣+b≥0.∴a+b≥.当且仅当a=b时,“=”成立.举例应用:已知x>0,求函数y=2x+的最小值.解:y=2x+≥=4.当且仅当2x=,即x=1时,“=”成立.当x=1时,函数取得最小值,y最小=4.16问题解决:汽车的经济时速是指汽车最省油的行驶速度.某种汽车在每小时70~110公里之间行驶时(含70公里和110公里),每公里耗油(+)升.若该汽车以每小时x公里的速度匀速行驶,1小时的耗油量为y升.(1)求y关于x的函数关系式(写出自变量x的取值范围);(2)求该汽车的经济时速及经济时速的百公里耗油量(结果保留小数点后一位).【分析】(1)根据耗油总量=每公里的耗油量×行驶的速度列出函数关系式即可;(2)经济时速就是耗油量最小的形式速度.【解答】解:(1)∵汽车在每小时70~110公里之间行驶时(含70公里和110公里),每公里耗油(+)升.∴y=x×(+)=(70≤x≤110);(2)根据材料得:当时有最小值,解得:x=90∴该汽车的经济时速为90千米/小时;当x=90时百公里耗油量为100×(+)≈11.1升.17.正方形ABCD的边长为3,点E,F分别在射线DC,DA上运动,且DE=DF.连接BF,作EH⊥BF所在直线于点H,连接CH.(1)如图1,若点E是DC的中点,CH与AB之间的数量关系是CH=AB;(2)如图2,当点E在DC边上且不是DC的中点时,(1)中的结论是否成立?若成立给出证明;若不成立,说明理由;(3)如图3,当点E,F分别在射线DC,DA上运动时,连接DH,过点D作直线DH的垂线,交直线BF于点K,连接CK,请直接写出线段CK长的最大值.【分析】(1)首先根据全等三角形判定的方法,判断出△ABF≌△CBE,即可判断出∠1=∠2;然后根据EH⊥BF,∠BCE=90°,可得C、H两点都在以BE为直径的圆上,判断出∠4=∠HBC,即可判断出CH=BC,最后根据AB=BC,判断出CH=AB即可.(2)首先根据全等三角形判定的方法,判断出△ABF≌△CBE,即可判断出∠1=∠2;然后根据EH⊥BF,∠BCE=90°,可得C、H两点都在以BE为直径的圆上,判断出∠4=∠HBC,即可判断出CH=BC,最后根据AB=BC,判断出CH=AB即可.(3)首先根据三角形三边的关系,可得CK<AC+AK,据此判断出当C、A、K三点共线时,CK的长最大;然后根据全等三角形判定的方法,判断出△DFK≌△DEH,即可判断出DK=DH,再根据全等三角形判定的方法,判断出△DAK≌△DCH,即可判断出AK=CH=AB;最后根据CK=AC+AK=AC+AB,求出线段CK长的最大值是多少即可.【解答】解:(1)如图1,连接BE,,在正方形ABCD中,AB=BC=CD=AD,∠A=∠BCD=∠ABC=90°,∵点E是DC的中点,DE=DF,∴点F是AD的中点,∴AF=CE,在△ABF和△CBE中,∴△ABF≌△CBE,∴∠1=∠2,∵EH⊥BF,∠BCE=90°,∴C、H两点都在以BE为直径的圆上,∴∠3=∠2,∴∠1=∠3,∵∠3+∠4=90°,∠1+∠HBC=90°,∴∠4=∠HBC,∴CH=BC,又∵AB=BC,∴CH=AB.故答案为:CH=AB.(2)当点E在DC边上且不是DC的中点时,(1)中的结论CH=AB仍然成立.如图2,连接BE,,在正方形ABCD中,AB=BC=CD=AD,∠A=∠BCD=∠ABC=90°,∵AD=CD,DE=DF,∴AF=CE,在△ABF和△CBE中,∴△ABF≌△CBE,∴∠1=∠2,∵EH⊥BF,∠BCE=90°,∴C、H两点都在以BE为直径的圆上,∴∠3=∠2,∴∠1=∠3,∵∠3+∠4=90°,∠1+∠HBC=90°,∴∠4=∠HBC,∴CH=BC,又∵AB=BC,∴CH=AB.(3)如图3,,∵CK≤AC+AK,∴当C、A、K三点共线时,CK的长最大,∵∠KDF+∠ADH=90°,∠HDE+∠ADH=90°,∴∠KDF=∠HDE,∵∠DEH+∠DFH=360°﹣∠ADC﹣∠EHF=360°﹣90°﹣90°=180°,∠DFK+∠DFH=180°,∴∠DFK=∠DEH,在△DFK和△DEH中,∴△DFK≌△DEH,∴DK=DH,在△DAK和△DCH中,∴△DAK≌△DCH,∴AK=CH又∵CH=AB,∴AK=CH=AB,∵AB=3,∴AK=3,AC=3,∴CK=AC+AK=AC+AB=,即线段CK长的最大值是.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
2016学年第一学期七宝中学高一新生入学摸底考试数学试卷
一、选择题(每小题有仅一个正确答案,每题 3 分) 1. 已知0a b ,则下列不等式不一定成立的是( ).
(A )2ab b (B )a c b c (C )
11
a b
(D )ac bc
2. 若不等式组21
13
x x a
的解集为2x ,则a 的取值范围是( ). (A )2a (B )2a (C )2a (D )2a
3. 若11,2M y ,21,4N y
,31,2P y
三点都在函数k y x (0k )的图像上,则123 y y y 、、的大小关系为( ).
(A )213y y y
(B )231y y y
(C )312y y y
(D )321y y y
4. 已知22y x 的图像是抛物线,若抛物线不动,把 x 轴、 y 轴分别向上、向右平移
2 个单位, 那么在新坐标系下抛物线的解析式是( ). (A ) 2
222y x (B ) 2
222y x (C ) 2222y x
(D ) 2
222y x
5. 中央电视台“幸运 52”栏目中的“百宝箱”互动环节,是一种竞猜游戏,游戏规则如下:在 20个商标中,有 5 个商标牌的
背面注明了一定的奖金额,其余商标的背面是一张苦脸,若翻到它就不得奖、参加这个游戏的观众有三次翻牌的机会.某观众前两次翻牌均得若干奖金,如果翻过的牌不能再翻,那么这位观众第三次翻牌获奖的概率是( ). (A )14
(B )16 (C )15 (D )3
20
6. 将水匀速注入一个容器,时间(t )与容器水位(h )的关系如图所示,则容器的形状是( ).
(A )
(B )
(C )
(D )
2
二、填空题(每题 3 分) 7.
2
30n ,则
2009
3m n .
8. 已知::4:5:7a b c ,240a b c ,则2b a c .
9. 将一张坐标纸折叠一次,使得点 0,2与 2,0 重合,则点1,02
与点 重合.
10. 对于整数a 、b 、c 、d ,符号a b d c 表示运算ac bd ,已知1134
b
d ,则b d 的值为 .
11. 定义“*”:
*11X Y
A B A B A B .已知1*23 ,2*34 ,则3*4 .
12. 分式方程133
x m
x x 有增根,则m .
13. 如图是一个有规律排列的数表,请用含n 的代数式(n 为正整数)表示数表中第n 行第n 列的数: .
14. 已知3
5
a b b c ,2221a b c ,则ab bc ca 的值等于 .
15. 若2610x x ,则221
1x x
.
16. 如图所示,AB CD ,60BAP ,45APC ,30PCD ,则 .
17. 关于x 的一元二次方程210mx x 有实根,则m 的取值范围是 .。
