利用声辐射模态重构任意目标的散射声场
有限空间内基于等效源法的近场声全息测量方法研究

哈尔滨工程大学硕士学位论文摘要近场声全息技术是声场预报和声源识别的一种重要途径,通过提取声源近场附近的声场所包含的信息即可计算出声源表面声压和质点振速等声学量,进而重建出整个三维声场。
传统近场声全息技术要求所有声源均处于全息面的一边,而另一边为自由场。
实际上,声源所处的环境往往并非自由场,通常会有边界的限制,这就导致了全息测量面获得声场数据不仅仅是声源的直接辐射的声波,还包括了由于界面多次反射所产生的声波。
由此,在非自由场中,采用传统近场声全息技术通常无法实现声源的准确识别。
因此,本文提出了有限空间中基于等效源法的近场声全息技术。
本文首先针对现有的自由场中基于等效源法的近场声全息技术进行了理论研究,以点源组合和结构声源为研究对象,数值分析了该方法的可行性和有效性,并分析了全息面布放方式、全息面测点间距以及声源频率等对于重建精度的影响。
在有限空间中采用近场声全息法进行声源识别和声场重建时,由于通常会受到边界影响,无法给出格林函数的解析解。
所以本文提出采用数值计算的方式来获取有限空间中格林函数的方法,利用数值计算的格林函数来实现声源在自由场中的三维声场重建。
并将其应用于点源组合和结构声源在自由场中的声辐射预报和声场重建,分析了不同声源频率、全息面尺寸、全息测点间距以及全息面位置对于重建精度的影响。
结果表明:本文提出的方法解决了近场声全息技术只能应用于自由场和半空间声场的问题。
可以应用于非自由声场中的声场重构,具有较好的效果。
关键词:有限空间;等效源法;近场声全息技术;格林函数;声场重建ABSTRACTNear-field acoustic holography(NAH)is an important method for sound field prediction and sound source identification. Using NAH technology, the sound pressures on the surface of the sound source and the vibration velocities of the particles can be calculated by extracting sound information in the near field of the sound source, and then the entire three-dimensional sound field can be reconstructed. Traditional near-field acoustic holography technology requires all sound sources to be on the same side of the holographic surface and the other side to be a free field. Usually, the environment in which the sound source is located, however, is not a free field because of the boundary restrictions. So, the sound field data obtained by the holographic measurement surface is not only the sound waves directly radiated by the sound source, but also the multiple reflections at the interface. Therefore, the sound source cannot be identified accurately by conventional near-field acoustic holography. In this paper, proposes a near-field acoustic holography technique based on the equivalent source method in limited space has been proposed.NAH technology based on the equivalent source method in the free field is studied firstly. Then, the point source combination and structural sound source are taken as the research object, the feasibility and effectiveness of this method are analyzed numerically. And the influences of the holographic surface layout method, the distance between the measuring points of the holographic surface and the frequency of the sound source on the reconstruction accuracy have been analyzed.Aiming at the problem of sound source identification and sound field reconstruction in a limited space, the analytical solution of the Green's function cannot be given due to the limitations of the boundary properties. Therefore, this paper proposes a method to obtain the Green's function in finite space by numerical calculation,and then the three-dimensional sound field of the sound source in the free field is reconstructed by the Green’s function .It is also applied to the acoustic radiation prediction and sound field reconstruction point source combination and structured sound source. The effects of sound source frequencies, holographic surface size, holographic measurement point spacing, and holographic surface position on reconstruction accuracy are analyzed. The results show that the method proposed in this paper can be used for sound field reconstruction in non-free sound fields, and has a good effect. This method solves the limitation that traditional NAH could only be applied to free-field and half-space acoustic fields.目录第1章绪论 (1)1.1 论文背景及研究目的 (1)1.2 国内外研究现状 (2)1.2.1 近场声全息研究现状 (2)1.2.2 有限空间声场测量技术 (5)1.3 本文主要内容与章节安排 (7)1.3.1 本文主要内容 (7)1.3.2 章节安排 (7)第2章基于等效源法的近场声全息变换方法 (9)2.1 引言 (9)2.2 等效源积分方程 (9)2.3 基于等效源法的近场声全息变换方法基本原理 (11)2.4 数值仿真分析 (12)2.4.1 点源组合情况的数值仿真分析 (12)2.4.2 球壳结构近场声全息变换数值仿真分析 (14)2.5 本章小结 (18)第3章有限空间中基于等效源法的近场声全息变换方法 (21)3.1 引言 (21)3.2 有限空间中基于等效源法的近场声全息变换理论模型 (21)3.3 有限空间中声场重构 (22)3.3.1 有限元法 (22)3.3.2 有限空间中声场重构步骤 (23)3.4 有限空间中基于等效源法的近场声全息理论模型的有效性验证 (24)3.5 本章小结 (25)第4章矩形水池中近场声全息变换方法数值仿真分析 (27)4.1 引言 (27)4.2 有限空间中点源组合的数值仿真分析 (27)4.3 不同全息测量参数情况下点源组合的数值仿真分析 (31)4.3.1 全息面尺寸和测点间距对全息重建的影响 (31)哈尔滨工程大学硕士学位论文4.3.2 全息面位置对全息重建的影响 (37)4.4 本章小结 (39)第5章循环水槽中近场声全息变换方法数值仿真分析 (41)5.1 引言 (41)5.2 不同边界条件下点源组合的数值仿真分析 (41)5.2.1 阻抗边界条件 (42)5.2.2 绝对软边界 (46)5.2.3 绝对硬边界 (51)5.2.4 整体绝对硬边界 (56)5.3 球壳结构表面源强度近场声全息变换数值仿真分析 (60)5.4 本章小结 (66)结论 (68)参考文献 (70)攻读硕士学位期间发表的论文和取得的科研成果 (74)致谢 (75)第1章绪论第1章绪论1.1 论文背景及研究目的控制水下航行体的辐射噪声水平是提高其自身隐蔽性、增强自身战斗力的重要保证。
广义斯奈尔定律与声超表面

广义斯奈尔定律与声超表面朱一凡;梁彬;程建春【摘要】给出了广义斯奈尔定律的相关理论推导,并总结回顾了之前的几种设计,包括声人工结构表面和几种声超表面的案例.首先,以人工结构表面为例,以解析推导为主,结合数值模拟和实验结果,证明了人工窄井结构的异常反射现象.随后,我们回顾了声超表面的设计方法,包括折叠空间式和亥姆赫兹腔式两种典型的结构化设计.最后,我们重点回顾了一种厚度仅为1/20波长的声超表面,用于设计超薄声扩散体,称为声超表面施罗德扩散体.传统的施罗德扩散体是40年前提出的建筑声学领域的经典设计,而我们提出的声超表面施罗德扩散体在中心频率具有同样优质的漫反射效果.另外,通过混合不同目标频率的超表面单元,可以设计宽带的超薄施罗德扩散体,其带宽接近于商业化的施罗德扩散体,这个例子充分展示了声超表面在实际场合的应用潜能.%In this paper, we investigate the theoretical derivations that related to the generalized Snell's law,and also review the previousdesigns,including artificial structure surface and several examples of acoustic metasurface. Firstly,we analytically,numerically and experimentally verify the abnormal reflection in"artificial grooves"structure. Then, we summarize the design methods of acoustic metasurfaces, including coiling-up-space structure and Helmholtz-resonator structure, respectively. At last, we review one special design of acoustic metasurface with the thickness of only 1/20 wavelength, and its use in design of ultra-thin acoustic diffuser,namely"acoustic metasurface Schroeder diffuser". Conventional Schroeder diffuser is a classical design proposed 40 years ago in architectural acoustics. Our designed acoustic metasurfaceSchroeder diffuser has comparable good diffusion effect at the center frequency. In addition, by mixing the unit cells designed for four different target frequencies, we can achieve broadband metasurface-based Schroeder diffuser, with the bandwidth comparable with commercial Schroeder diffuser, adequately showing the application potentials of acoustic meatsurfaces in practical occasions.【期刊名称】《应用声学》【年(卷),期】2018(037)001【总页数】10页(P53-62)【关键词】广义斯奈尔定律;声超表面;波阵面操控;施罗德扩散体【作者】朱一凡;梁彬;程建春【作者单位】南京大学声学所微结构与创新协同中心南京210093;南京大学声学所微结构与创新协同中心南京210093;南京大学声学所微结构与创新协同中心南京210093【正文语种】中文【中图分类】O4021 引言2011年,光学上首次提出广义斯奈尔(Snell)定律[1]。
COMSOL Multiphysics 在声学领域的应用案例集

算例:1.声学器件2D轴对称喇叭单元电磁-声-固耦合分析这是一个动态电磁式圆锥形扬声器模型,通常用于中低频段声音重放,电磁场模块的小信号分析计算静电力和静态的音圈阻抗,声固耦合应用模式分析喇叭振膜的振动以及声波的辐射,最外层采用完美匹配层边界条件(PML)模拟无限大空间,输出结果包括随频率变化的灵敏度曲线和阻抗特性曲线等。
模型来源: Acoustics_Module/Industrial_Models/loudspeaker_driver。
压电声学传感器压电传感器能把电信号转换成声压辐射,反过来,也能把声场压力转换成电信号。
这种换能器采用压电材料和声场应用模式,在声场-结构交界面处考虑到了结构变形对声场的加速度影响以及声场对结构的反向压力的作用。
该模型广泛应用于阵列式麦克风,超声传感器、超声探伤、无损检测、声纳、成像等。
利用COMSOL Multiphysics的拉伸耦合变量,仅需2D 的计算即可得到3D的结果数据。
模型来源: Acoustics_Module/Tutorial_Models/piezoacoustic_transducer声表面波(SAW)气体传感器特征模态分析该案例研究了SAW气体传感器的共振频率,声表面波(SAW)是能够沿着材料表面传播的波,它的振幅随材料深度按指数规律迅速衰减。
SAW器件在很多电子元件中都有广泛的应用,例如滤波器,振荡器和传感器等。
SAW由一个相互交叉的换能器构成(IDT),换能器刻蚀在压电LiNbO3 (铌酸锂) 基底上,并覆盖一层薄的聚异丁烯 (PIB)膜,当暴露在空气中时,PIB 膜选择性的吸收CH2Cl2 (二氯甲烷, DCM) ,PIB 膜的质量随之增加,从而导致特征频率向低频扩展。
模型来源:Acoustics_Module/Industrial_Models/SAW_gas_sensor。
光声传感器特征模态光声器件广泛用于检测气体化合物的浓度,它是基于器件的光共振吸收现象,气体分子的非弹性碰撞将激发能量转换为热能,样品的调制照射会引起周期性的压力变化,该压力变化可以被光声传声器检测到,其信号检测灵敏度依赖于光声器件的几何形状,利用声学器件的共振特性可以改善其灵敏度。
【国家自然科学基金】_声场仿真_基金支持热词逐年推荐_【万方软件创新助手】_20140803
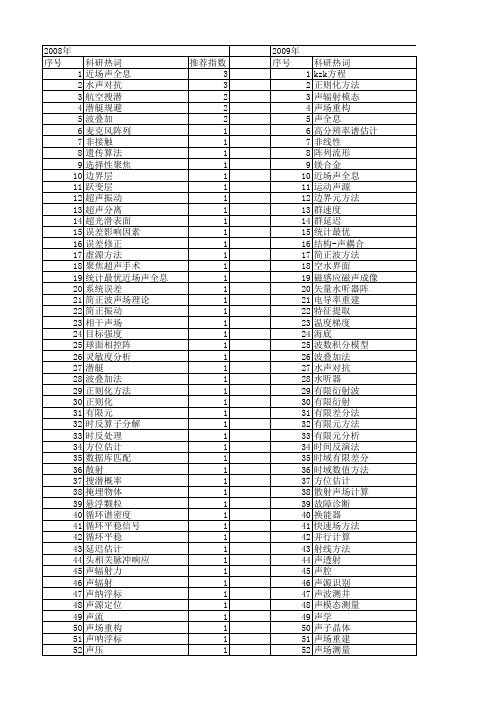
科研热词 感应式磁声成像 声场 时域有限差分法 声学 声场分布 前向散射 高强度聚焦超声 驾驶室 驻波管 障碍物 隔声量 遗传算法 透镜声呐 近场声全息 运动声源 边界元 辐射声场 超声聚焦 超声波声场 超声波 超声成像 质点振速 贝叶斯方法 衰减特性分析 虚源 自由空间 耦合 结构表面 结构振动 系数矩阵 等离子体椭球 空气耦合超声 磁声耦合效应 矢量阵 矢量水听器 矢量声场 相控阵 相关半径 盲区 目标成像 目标强度 电导率 环境不确实性 爬波 温度数据 海洋环境 测量面 测量方法 洛合兹力 洛伦兹力散度 波束形成 波叠加
科研热词 近场声全息 水声对抗 航空搜潜 潜艇规避 波叠加 麦克风阵列 非接触 遗传算法 选择性聚焦 边界层 跃变层 超声振动 超声分离 超光滑表面 误差影响因素 误差修正 虚源方法 聚焦超声手术 统计最优近场声全息 系统误差 简正波声场理论 简正振动 相干声场 目标强度 球面相控阵 灵敏度分析 潜艇 波叠加法 正则化方法 正则化 有限元 时反算子分解 时反处理 方位估计 数据库匹配 散射 搜潜概率 掩埋物体 悬浮颗粒 循环谱密度 循环平稳信号 循环平稳 延迟估计 头相关脉冲响应 声辐射力 声辐射 声纳浮标 声源定位 声流 声场重构 声呐浮标 声压
推荐指数 3 3 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
第5章 声波在目标上的反射和散射1

5.7 弹性物体散射声场及其特性
• 弹性球体的声散射
考虑点声源置于S处,它距球心的距离为r0,空 间任意点P处入射声场为:
pp坐标系原点置于球心处,则:
e D ik D 2 r0 ir 12n 02 n 1 Jn 1 2kH rn 1 1 2k0r P ncos
f x,x 1,x22 xn 0 1 n 12 n 1 sin n e in
x1 k1a x2 k2a 散射声场为:
ps 2 Pr00 a 2 fx,x1,x2ei2k0 rt
5.7 弹性物体散射声场及其特性
结论:弹性球(钢 球和铝球)形态函 数随频率有极大、 极小变化;刚性球 形态函数在低频段 起伏振荡,随着频 率的增高,逐渐趋 于1;声学软球形态 函数在很低频段大 于1,随着频率的增 加很快降至1 。
根据勒让德方程的解有:
m a m P m co s根据辐射条件 cm 0
根据贝塞尔方程的解有:
R m b m h m 1 k r c m h m 2 kr
5.6 刚性球体散射声场
散射波声压的解为:
ps amPmcoshm 1kr m0 待定常数,由边界条件确定
散射波声压表达式为:
p s m 0 im 2 m 1 P 0 d d m k k j a a d d m 1 k k h P a m a c o h m 1 k s e ir t
对于散射波的远场,利用球汉克尔函数在大宗 量条件下近似展开:
5.7 弹性物体散射声场及其特性
• 弹性物体散射声场的一般特征
具有明显频率特性 (1)宽脉冲入射信号 散射强度随频率作极大、极小急剧变化,回波波 形产生严重畸变。 (2)窄脉冲入射信号 回波为一脉冲串,每个脉冲之间的间隔基本相等, 脉冲幅度逐渐衰减,波形基本不变。
FEKO6.1_喇叭天线+目标体近场散射仿真_高级应用

天线 (主动辐射源)
目标体 (被动辐射源)
目标体(被动辐射源)的设定方法
• 在EditFEKO,对应每一个近场计算命令行(如:FE);都有一 个OF的命令函数:
– 勾选:Use only some labels for field calculation,只计算给定 Label范围内的面元电流在空间的近场分布
计算显示结果
• • • 提交计算: 后处理显示结果为:(该散射场也包含了只计算目标体的面电流贡献) 离目标越近,散射场越大
FEKO 6.2设置更方便
Scope标签中设定面元
• 联系人:jl.jiao@
模型建立
• 长度单位改为cm; • 设定以下变量:
– r0=4.8e4 – R=20 – H=40 – – – – – – – 目标体-圆柱体中心位置离开圆心的位置 目标体-圆柱体的半径 目标体-圆柱体的高度
喇叭天线部分: wa=12.96 wb=wa/2 wL=30.2 flare_a=55 flare_b=42.8 flare_h=46
计算显示结果
• • 把该工程保存为:horn_with_obj_scattering_RCS_only_obj.cfx; Cadfeko中启动EditFEKO; • 在弹出的对话框中选择:Yes
计算显示结果
• 在EditFEKO中,把光标定在OF一行,点击键盘的F1键,在弹出的对话 框中进行如下设置: • 勾选: Use only some labels for field calculation • Start Label: Cylinder1.Face139 • End Label: Cylinder1.Face141 • 点击OK
喇叭天线+目标体 散射”近场”仿真
基于远场方法的结构声辐射模态研究

的密度为 p 声速为 cr xY z为声场中任一点 , , , ( ,,) 如图 1 所示. 声场 中任意一点 Y的声压可由瑞利积分得到 引:
py ( )= 2
7 r
维普资讯
第l 4卷 1 期 20 06年 3 月
应用基础与工程科学学报
J OURN F B I C EN ND E AL O ASC S I CE A NGI E NG NE RI
中图分类号 :B 3 T 55 文献标识码 : A
,
P =[ 1 2 … p …] p p 』 v 式 中: 表示半球面上第 单元的声压. p
令平板上各单元的法向速度构成 的向量为 l则关系式( ) , , 2 可表示成矩阵形式 :
P =Z v
() 3
() 4
式中: z为 Nx 维矩阵 , M 表示平板上每个小单元的法向振速与半球面上每点声压之间的 关系
维普资讯
9 4
应用基 础与工程科学学报
12 远场方法的声辐射模态 . 当声场中的任意点 y 离开声源的距离远大于声源线度时 点 y 位于远场区 , 则式 ( ) 1 给出了声场中的远场声压 p y 和表面振速 t 之间的关系. () , ( ) 我们把平板分为 M 个面积
模态就能计算不同频率的总声功率 , 使得计算和控制声功率得以简化.
关键词 : 声辐射 ; 辐射模态 : 辐射效率 ; 声功率
自2 0世纪 9 0年代学者们提出了声辐射模态概念以来 , 国内外众多学者 , 从不同的角
度进行 了大量 的研究 ¨ 声辐射模态是振动辐射物体 的固有属性 , 引. 反映 了辐射物体的辐 射性质 , 辐射物体辐射的声功率可以表示为各阶声辐射模态能量 的叠加. 利用声辐射模态 来研究外部声辐射问题的优点在于消除结构模态中复杂的耦合项 , 使得计 算和控制声辐 射更为简单. 初步的研究H 刮已显示出声辐射模态分析方法 的应用潜力和优越性. 声辐射模态较振动模态显得更为复杂 , 内涵也更为丰富, 需要进一步研究的内容也很
(整理)《水声学》课程配套习题参考答案.

《水声学》部分习题参考答案绪论1略2略3略4略5环境噪声和海洋混响都是主动声呐的干扰,在实际工作中如何确定哪种干扰是主要的?解:根据水文条件及声呐使用场合,画出回声信号级、混响掩蔽级和噪声掩蔽级随距离变化的曲线,如下图,然后由回声信号曲线与混响掩蔽级、噪声掩蔽级曲线的交点所对应的距离来确定混响是主要干扰,还是噪声为主要干扰,如下图,r R<r n,所以混响是主要干扰。
声信号级噪声掩蔽级R6工作中的主动声呐会受到哪些干扰?若工作频率为1000Hz,且探测沉底目标,则该声呐将会受到哪些干扰源的干扰。
解:工作中的主动声呐受到的干扰是:海洋环境噪声、海洋混响和自噪声,若工作频率为1000Hz,干扰来自:风成噪声、海底混响、螺旋桨引起的自噪声及水动力噪声。
7已知混响是某主动声呐的主要干扰,现将该声呐的声源级增加10dB,问声呐作用距离能提高多少?又,在其余条件不变的情况下,将该声呐发射功率增加一倍,问作用距离如何变化。
(海水吸收不计,声呐工作于开阔水域)解:对于受混响干扰的主动声呐,提高声源级并不能增加作用距离,因为此时信混比并不改变。
在声呐发射声功率增加一倍,其余条件不变的情况下,作用距离变为原距离的42倍,即R R 412 。
第一章 声学基础1 什么条件下发生海底全反射,此时反射系数有什么特点,说明其物理意义。
解:发生全反射的条件是:掠时角小于等于全反射临界角,界面下方介质的声速大于界面上方介质的声速。
发生全反射时,反射系数是复数,其模等于1,虚部和实部的比值给出相位跳变角的正切,即全反射时,会产生相位跳变。
2 略3 略第二章 海洋声学特性1 海水中的声速与哪些因素有关?画出三种常见的海水声速分布。
解:海水中的声速与海水温度、密度和静压力(深度)有关,它们之间的关系难以用解析式表达。
CCC2 略3 略4 略5 略6 声波在海水中传播时其声强会逐渐减少。
(1)说明原因;(2)解释什么叫物理衰减?什么叫几何衰减?(3)写出海洋中声传播损失的常用TL 表达式,并指明哪项反映的主要是几何衰减,哪项反映的主要是物理衰减;(4)试给出三种不同海洋环境下的几何衰减的TL 表达式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
利用声辐射模态重构任意目标的散射声场鱼海涛;王英民;王奇【摘要】水下目标散射声场的重构可以作为水下目标散射特性的研究基础.本文主要利用声辐射模态对水下目标进行散射声场重构研究.首先,在借助声传递矩阵给出的任意结构声辐射模态的流体域求解方法基础上,通过理论证明了目标的散射声压与声辐射模态具有函数关系.其次,借助声场分布模态的概念,同时考虑到声场分布模态病态及声压测量易受噪声污染,提出基于声辐射模态的正则化散射声场重构算法.仿真结果表明,波数越低,重构所需声辐射模态阶数越少,在较高波数时仅需总模态数的大约20%即可对声场进行重构.与基于边界元的声场重构算法相比,计算量减小了至少80%,且克服了赫姆霍兹积分方程最小二乘法仅对球壳结构的重构效果较好而不适用于长条形结构重构的缺陷.%The acoustic scattering field reconstruction of underwater targets can be taken as the basis of the underwater targets scattering characteristic research.Applying acoustic radiation modes (ARM) to the acoustic scattering reconstruction of underwater targets is the main focus of the paper.Firstly,based on the ARM solving method of arbitrary structures in fluid domain,which is with the aid of acoustic transfer matrix (ATM),it was theoretically demonstrated that there was functional relationship between scattering pressure of targets and ARM.Secondly,by means of the concept of the acoustic field distribution modes and due to the ill-conditioned property of acoustic field distribution modes and the noisy contamination of acoustic pressure measurements,the regularization reconstruction algorithm of acoustic scattering field based on ARM was proposed.Simulation results show that the order number of ARM neededfor reconstruction is smaller for the lower wavenumber and that only about 20% of the total modes number can complete the reconstruction for the higher wavenumber.Hence,compared with the BEM based reconstruction algorithm,the computational amount of the ARM based one is reduced to at least four-fifths.And the drawback of Helmholtz equationleast squares (HELS) which has a better construction results for spherical structures but not for strip shaped structures has been overcome.【期刊名称】《应用声学》【年(卷),期】2017(036)003【总页数】12页(P264-275)【关键词】声辐射模态;声散射;声重构【作者】鱼海涛;王英民;王奇【作者单位】西安科技大学理学院西安 710054;西北工业大学航海学院西安710072;西北工业大学航海学院西安 710072【正文语种】中文【中图分类】TB566;O427.2随着水下目标消降噪技术的使用,在一些情况下仅使用被动声纳难以探测到水下目标,因此需要借助主动声纳获得目标的散射声场,进而确定其材质、形状、尺度等特性。
被动声纳探测基于目标的辐射噪声,对于目标的辐射可以利用声辐射模态(Acoustic radiation modes,ARM)对其进行表述。
而主动声纳探测则利用目标的散射声场,对于规则结构,如球壳、无限长圆柱壳体等可获得其解析解,但对于任意形状目标,则可通过实验或者数值解法获得。
若通过实验获得目标在不同场点处的散射声场则易受到实验条件及经费的限制,而对大型结构若通过数值解法获得,则计算耗时是阻碍其广泛应用的主要因素。
因此,对于任意形状大尺度目标需要寻求一种能够根据近场散射声压获得远场散射声场的方法,或者此方法能够根据远场声压获得近场散射声场,以进一步确定目标的尺度等特性。
近场声全息(Near- fi eld acoustic holography,NAH)自提出[1]以来,得到了长足的发展[2],被认为是一种可以方便地进行近远场外推的方法。
目前ARM仅应用于结构声辐射的研究,而NAH则主要应用在噪声振动领域,在目标声散射方面应用较少。
本文利用ARM各阶模态的正交性及目标声辐射主要由前n阶ARM确定的特性,将不同形状物体的声辐射模态作为基函数,对赫姆霍兹积分方程最小二乘法(Helmholtz equation-least squares,HELS)进行修正,拟对任意形状目标散射声场进行声场重构,以研究任意形状目标的声散射,最终实现利用任意形状目标近场的少量测点获得外部全空间的散射声场。
在NAH方面,Wu[3]对近场声全息发展的现状及所遇到的问题进行了综述,Antoni[4]指出现存的所有声场重构方法均可归结为不同空间基函数的线性组合,而对特定的声源拓扑结构和全息测量阵列几何形状,存在一个可以使重构误差最小的最佳基底。
显然将不同形状物体的声辐射模态作为基函数可以使算法适用于不同形状声源,且重构误差较小。
在声散射重构方面,Kleiner等人[5]利用平面近场声全息,从理论和实验角度对平面状散射面的散射系数进行了研究,说明近场声全息应用于散射问题的可行性。
Saijyou等人则直接将广义近场声全息方法应用于水下目标的散射场重建问题,并通过实验对有限长[6]、无限长[7]、简支[7]柱体的散射场重建结果进行了验证,表明二者之间具有良好的一致性,并进一步从能流角度[8]对近场声全息散射场进行了分析。
暴雪梅和何祚镛[9-10]在水下目标散射问题中结合使用BEM,利用NAH由散射体近场全息面上的复声压重建散射体表面的散射场声压和预报远场散射声指向性,研究结果表明,近场声全息方法应用于目标散射特性和远场声场特性的研究是可行的。
Hu等人[11]则在考虑入射波在目标上的散射效应的情况下,将平板近场声全息拓展到了噪声环境下的声源识别。
Zhao等人[12]则结合使用IBEM和HELS形成混合NAH,对HELS不擅长的任意形状物体(如发动机)和长柱状物体进行了声振耦合重构,使重构性能得以提升。
在基于ARM声场重构方面,Sarkissian[13-14]是ARM的奠基人之一,她最早将ARM应用于结构振动声源声场重构。
国内姜哲[15]基于泛函算子对赫姆霍兹表面积分方程进行简化获得了一种声辐射模态定义,并实施了不同振动声源的声场重构[16],聂永发等人[17]则以结构表面源强密度函数为参数构造了源强密度声辐射模态,并对球形声源及平板结构进行了声场重构研究。
从理论上来看,文献[15]和文献[17]的ARM计算方法均适用于任意形状目标ARM的计算,但由于文献[15]及文献[17]计算声辐射模态时均基于sinx/x,其缺点在于当x=nπ(n=1,2,3,···)弧度时,对应的矩阵元素为0,易造成所获得的声辐射模态的不准确。
文献[18]详细探讨和研究了利用声辐射模态进行辐射声功率的计算,无论在哪个封闭包络面上计算辐射声功率,在不考虑耗散的情况下,计算结果是相等的。
文献[19]在文献[18]的基础上,基于远场封闭包络与结构表面辐射声功率相等,借助声传递矩阵,将声辐射模态的求解转换到流体域,给出一种通用的任意结构声辐射模态流体域求解方法,且也适用于近场,将其称为基于声传递矩阵的声辐射模态求解方法(Acoustic radiation mode based on acoustic transfer matrix,ARM-ATM)。
本文进而借助声场分布模态的概念,同时考虑到声场分布模态病态及声压获取易受噪声污染,提出基于声辐射模态的正则化散射声场重构算法。
为了说明算法有效性,本文利用ARM-ATM获得了球、平头长柱、长椭球体的声辐射模态,并对其散射声场进行了重构,仿真结果表明本算法计算量为基于BEM的声场重构算法的1/5,且克服了HELS不适用于长柱状及长椭球体目标的缺陷。
赫姆霍兹积分方程(Helmholtz integral equation,HIE)描述了结构表面法向振速与声压的关系,离散化后,对于无限大各向同性流体中的弹性散射,目标在场点网格上的散射声压pf可以表示为[20-21]其中,p为散射问题中入射波在场点网格上的声压,vs表示结构表面节点法向振速,k为波数,z0=ρ0c0为流体的特性阻抗,c0为流体中的声速,矩阵As、Bs、Af和Bf均为BEM系数矩阵,可根据BEM理论给出。
注意到去除入射波对散射波的影响,则散射声压psc=pf-p,结构在流体中任意场点的散射声压psc可写为其中T称为声传递向量(Acoustic transfer vector,ATV,适用于单个场点)或声传递矩阵(Acoustic transfer matrix,ATM,适用于多个场点)而Z称为声辐射阻抗矩阵,定义为可见,场点散射声压psc与声传递矩阵T具有映射关系,可通过声传递矩阵T研究结构的散射声压psc。
文献[19]给出了一种在流体域求解任意结构声辐射模态的求解方法ARM-ATM,其优点在于可在场点处获得求解声辐射模态所需的耦合矩阵C,定义为其中,T为前述声传递矩阵,表示结构表面振速到场点声压的传递,F为一对角矩阵,若用SΩi表示场点球面Ω上第i个小单元的面积,则可见,耦合矩阵C与声传递矩阵T及对角矩阵F有关,声传递矩阵T本身与结构几何形状、场点位置均有关,而对角矩阵F也与场点形状及位置有关,因此,耦合矩阵C不仅与结构本身的形状有关,且与场点的形状及位置有关,但由于在推导过程中受流体域封闭包络与结构表面的辐射声功率相等条件约束,所获得的耦合矩阵C及ARM与文献[22]直接利用BEM获得的耦合矩阵C及ARM极为近似,文献[19]对此进行了较深入的讨论。
