matlab电磁场仿真作业
Matlab仿真带电粒子在匀强正交电磁场中运动.

引言在文 [1]中对匀强正交电磁场中带电粒子的运动状态进行了分析 , 得到了运动方程 , 但人们却不能对带电粒子在此电磁场中的运动有比较直观形象的想象。
Matlab 是一款通用数学工具软件 , 有许多常用数学组件 , 文 [3]作了许多相关介绍。
为了能直观形象地演示带电粒子的运动过程 , 文 [2]采用了一阶差分线性方程组进行模拟。
本文也采用了一阶差分线性方程组的方法进行数值计算 , 并得到了图形结果 , 将常见粒子的运动进行了比较 , 可以方便人们得到直观印象 , 为进一步工作提供方便。
1问题分析本文主要研究带电粒子在均匀稳定的电磁场中的运动。
带电粒子质量为 m , 电量为 q (q>0 , 此带电粒子的运动微分方程为 :m d 2! " r " E +q " v ×" B (1以电磁场中某点为原点 , 以 E 为 Oy 方向 , B 为 Oz 方向建立坐标系 O-xyz 。
由于ω=qB/m , 则 (1 式的投影方程为 :d 2x =dy d 2y qE dx d 2z #%%%%%%%$%%%%%%%%&0(2将其转换为一阶微分线性方程组 , 以便用差分替代微分作数值计算 , 令 w 1=x , w 2=dy/dx, w 3=y ,w 4=dy/dt , w 5=z , w 6=dz/dt , 则 (2 式成为 :dw 12dw 2ωw 4dw 4dw 4qE ωw 2dw 6dw 6#%%%%%%%%%%%%%%%%%’ %%%%%%%%%%%%%%%%%&0(32Matlab 数值求解与仿真演示Matlab 是一款通用性很强的优秀数学软件 , 借助于 Matlab 对 (3 式进行差分迭代 , 数值求解 , 并将结果逐点描绘 , 用图像显示其运动轨迹。
下面分三种情况考虑 :(1 电场强度和磁场强度都不为零 ; (2 电场强度为零 , 磁场强度不为零 ; (3 电场强度不为零 , 磁场强度为零。
电磁场的Matlab仿真.

Matlab 与电磁场模拟一单电荷的场分布:单电荷的外部电位计算公式:qφ=4πε0r等位线就是连接距离电荷等距离的点,在图上表示就是一圈一圈的圆,而电力线就是由点向外辐射的线。
MATLAB 程序:theta=[0:.01:2*pi]'; r=0:10;x=sin(theta*r; y=cos(theta*r; plot(x,y,'b' x=linspace(-5,5,100; for theta=[-pi/4 0 pi/4] y=x*tan(theta; hold on ; plot(x,y; end grid on单电荷的等位线和电力线分布图:二多个点电荷的电场情况:模拟一对同号点电荷的静电场设有两个同号点电荷, 其带电量分别为 +Q1和+Q2(Q1、Q2>0 距离为 2a 则两电荷在点P(x, y处产生的电势为:由电场强度可得E = -∇U, 在xOy 平面上, 电场强度的公式为:为了简单起见, 对电势U 做如下变换:。
Matlab 程序:q=1; xm=2.5; ym=2;x=linspace(-xm,xm; y=linspace(-ym,ym; [X,Y]=meshgrid(x,y;R1=sqrt((X+1.^2+Y.^2; R2=sqrt((X-1.^2+Y.^2; U=1./R1+q./R2; u=1:0.5:4; figure contour(X,Y,U,u grid onlegend(num2str(u' hold onplot([-xm;xm],[0;0] plot([0;0],[-ym;ym]plot(-1,0,'o' , 'MarkerSize' ,12 plot(1,0,'o' , 'MarkerSize' ,12 [DX,DY] = gradient(U; quiver(X,Y,-DX,-DY; surf(X,Y,U;同号电荷的静电场图像为:50403020100-22同理,将程序稍作修改,便可以得到异号电荷的静电场图像:403020100-10-20-30-4022.5三、线电荷产生的电位:设电荷均匀分布在从z=-L到z=L,通过原点的线段上,其密度为q(单位C/m,求在xy 平面上的电位分布。
带电粒子在电磁场中运动的MATLAB仿真 (1)

目录第一章概述 (1)第二章基本原理 (2)2.1 带电粒子在电磁场中运动的原理 (2)2.2质量较大的带电微粒在复合场中的运动 (2)第三章算法及仿真结果 (4)3.1具体算法 (4)3.2结果 (5)第四章结论 (7)参考文献 (8)附录 (9)第一章概述MATLAB(矩阵实验室)是MATrix LABoratory的缩写,是一款由美国The MathWorks公司出品的商业数学软件。
MATLAB是一种用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境。
除了矩阵运算、绘制函数/数据图像等常用功能外,MATLAB还可以用来创建用户界面及与调用其它语言(包括C,C++和FORTRAN)编写的程序。
MATLAB的基本数据单位是矩阵,它的指令表达式与数学、工程中常用的形式十分相似,故用MATLAB来解算问题要比用C,FORTRAN等语言完成相同的事情简捷得多,并且MATLAB具有其他高级语言难以比拟的一些优点,如编写简单、编程效率高、易学易懂等,因此MATLAB 语言也被通俗地称为演算纸式科学算法语言。
MATLAB是当今最优秀的科技应用软件之一,它以强大的科学计算与可视化功能、简单易用、开放式可扩展环境,特别是所附带的30 多种面向不同领域的工具箱支持,使得它在许多科学领域中成为计算机辅助设计和分析、算法研究和应用开发的基本工具和首选平台。
而其强大的图像绘制功能也使得它广泛用于各种数据背后现象的模拟仿真。
计算机数值模拟的研究方法已成为继实验研究和理论分析之外的第三种研究手段,在基础物理学习中适当引入计算机数值方法,有助于将一些高深的物理知识深入浅出、生动形象地学习。
随着计算机的普及,MATLAB在基础物理中的应用日益广泛。
在控制、通信、信号处理及科学计算等领域中,MATLAB 都被广泛地应用,已经被认为能够有效提高工作效率、改善设计手段的工具软件。
第二章 基本原理2.1带电粒子在电磁场中运动的原理带电粒子在磁场中运动时会受到洛伦兹力的作用,且随着初始运动方向和磁场分布的不同,其运动轨迹会发生不同的变化。
电磁场中matlab仿真实现工具箱
实验六:使用偏微分方程工具箱对电磁场的仿真一、实验目的与要求1.掌握微分方程工具箱的使用方法;2.掌握使用偏微分方程工具箱分析电磁场。
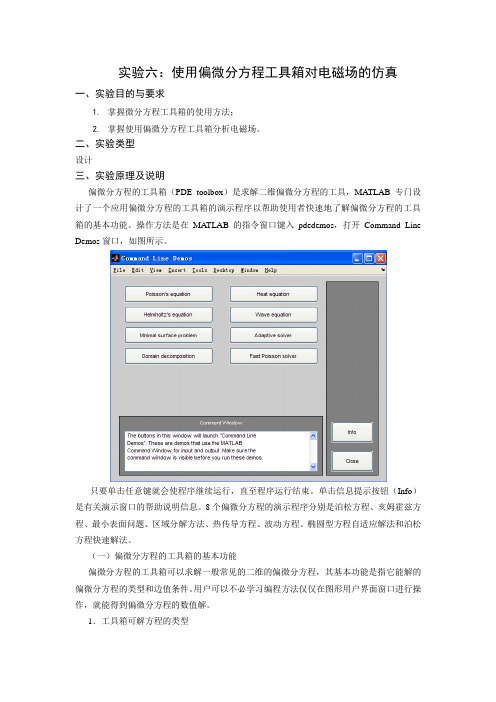
二、实验类型设计三、实验原理及说明偏微分方程的工具箱(PDE toolbox)是求解二维偏微分方程的工具,MA TLAB专门设计了一个应用偏微分方程的工具箱的演示程序以帮助使用者快速地了解偏微分方程的工具箱的基本功能。
操作方法是在MA TLAB的指令窗口键入pdedemos,打开Command Line Demos窗口,如图所示。
只要单击任意键就会使程序继续运行,直至程序运行结束。
单击信息提示按钮(Info)是有关演示窗口的帮助说明信息。
8个偏微分方程的演示程序分别是泊松方程、亥姆霍兹方程、最小表面问题、区域分解方法、热传导方程、波动方程、椭圆型方程自适应解法和泊松方程快速解法。
(一)偏微分方程的工具箱的基本功能偏微分方程的工具箱可以求解一般常见的二维的偏微分方程,其基本功能是指它能解的偏微分方程的类型和边值条件。
用户可以不必学习编程方法仅仅在图形用户界面窗口进行操作,就能得到偏微分方程的数值解。
1.工具箱可解方程的类型定义在二维有界区域Ω上的下列形式的偏微分方程,可以用偏微分方程工具箱求解:椭圆型()f au u c =+∇∙∇- 抛物型()f au u c tu d =+∇∙∇-∂∂ 双曲型()f au u c tu d =+∇∙∇-∂∂22 本征值方程()du au u c λ=+∇∙∇-式中,u 是偏微分方程的解;c 、a 、d 、f 是标量复函数形式的系数,在抛物型和双曲型方程中,它们也可以是t 的函数,λ是待求的本征值。
当c 、a 、f 是u 的函数时,称之为非线性方程,形式为()()()()u f u u a u u c =+∇∙∇-也可以用偏微分方程工具箱求解。
2.工具箱可解方程的边值条件解偏微分方程需要的边值条件一般为下面两种之一:狄里赫利(Diriclet)边值条件 hu=r广义诺曼(Generalized Neumann)边值条件 ()g qu u c n =+∇∙式中,n为边界外法向单位向量;h 、q 、r 、g 是在边界上定义的复函数。
MATLAB实验电磁实验仿真

实验四 电磁实验仿真 —点电荷电场分布的模拟一. 实验目的电磁场是一种看不见摸不着但又客观存在的物质,通过使用Matlab 仿真电磁场的空间分布可以帮助我们建立场的图景,加深对电磁理论的理解和掌握。
按照矢量分析,一个矢量场的空间分布可由其矢量线(也称力线)来形象表示。
点电荷的电场就是一个矢量场,模拟其电力线的分布可以得到电场的空间分布。
通过本次上机实验希望达到以下目的:1. 学会使用MATLAB 绘制电磁场力线图和矢量图的方法;2. 熟悉二维绘图函数contour 、quiver 的使用方法。
二. 实验原理根据库仑定律,真空中的一个点电荷q 激发的电场3r E q r=v v (高斯制) (1) 其中r 是观察点相对电荷的位置矢量。
考虑相距为d 的两个点电荷q 1和q 2,以它们的中点建立坐标(如图),根据叠加原理,q 1和q 2激发的电场为:12123312r r E q q r r =+v v v (2) 由于对称性,所有包含电荷的平面上,电场的分布一样,所以只需要考虑xy 平面上的电场分布,故121233331212(/2)(/2)ˆˆˆˆ()[]x y E E q x q x q y d q y d E j j r r r r i i -+==++++v (3)其中12 r r ==。
根据电动力学知识(参见谢处方,《电磁场与电磁波》,1.4.1节),电场矢量线(或电力线)满足微分方程: yx E dydx E = (4) 代入(3)式解得电力线满足的方程 1212(/2)(/2)q y d q y d r r C -++= (5) 其中C 是积分常数。
每一个C 值对应一根电力线。
电场的分布也可以由电势U 的梯度(gradient ,为矢量)的负值计算,根据电磁学知识,易知两点电荷q 1和q 2的电势1212q q U r r =+(6)那么电场为 E gradU U =-=-∇v (7)或者 ()(),x y x y E U E U =-∇=-∇ (8)在Matlab 中,提供了计算梯度的函数gradient()。
MATLAB仿真平面电磁波在不同媒介分界面上的入射

MATLAB仿真平面电磁波在不同媒介分界面上的入射、反射和折射一・实验目的,K进一步学习MATLAB,初步掌握GUI界面的编程.2、通过编程实现电磁波仿真效果图。
3、进一步理解平面电磁波的入射.反射和折射现象二、实验要求;1、以电场为例,动态演示平面电磁波的传播情况.2、可以任意设置媒介的介电常数和入射角。
3、考虑金属导体和空气的分界面平面电磁波的入射、反射情况。
三.实验原理;电磁波从一种媒质入射到第二种媒质时,分界直使一部分能量反射回第一种媒质,另一部分能量折射到第二种媒质中,反射液和折射波得大小和相位取决于分界面两侧的媒质特性、极化方向和入射角大小等,当电磁波入射■到理想导体表面时,会发生全反射。
这一过程中包括的主要原哩有以下三点・1、正弦平面波在媒质分界面的反射和折射规律波对分界面的入射是任意的,但为了方便,我们假设入射面与Z0 X面重合。
波在"0时发生入射和反射.在z<0时发生折射并令空间任意一点:处的入射波、反射波和折射波场强为:图表1正弦波斜入射示意图根据在z=0的界面上电场强度的切线分量相等的边界条件,有耳(工』4) =/?r(x,y70)=耳(E%0)故必有反射定律: 折射定律:2.正弦平面波对理想介质的斜入射①垂直极化液垂直极化滾对理想介质斜入射如图所示,由折射和反射定律,我们可以得到在任意媒质中的场强。
在第一煤质中民h0虑8叫*加卒8叫旳-和五久.九cos qx/冉c 呻_加2兔)《一用込绳 兀=(町sinqXef 8叫+心28毗”-两叭E (0=―力宀 %—E ®仍 cosq + 砒 cosg E 2J = g/gm團‘=(一乩ocnszy©附 隔严(為)负EW 加f 8旳图表1垂直极化波斜入射 ②平行极化波平行极化披对理想介质斜入射如图所示,由折射和反射定律,我们可以得到 在任意媒质中的场强.在第一煤质中E lx = ©0 cos q呎 + 比一海啦兔=(—為sinqXeFg* -脳兴心坏疗用^ 叭=必严曲—&AE )e*F在第二煤质中%cosq—马J72COS 爲—场COS©J72 8S02 + 场2^72COS ^/cosq +7cosq略=(召。
电磁场重难点的仿真讲解

电机学难重点的MA TLAB仿真实验报告一、实验内容及目的(1.5分)(一)实验内容1.磁性材料磁化曲线的绘制2.变压器电压变化率及效率曲线的绘制(二)实验目的1.了解磁性材料磁化曲线的非线性和饱和特性;2.掌握采用MATLAB进行曲线拟合的方法;3.了解变压器电压变化率的变化规律;4.了解负载性质对电压变化率特性特性的影响;5.了解变压器效率曲线的变化规律;6.了解负载性质对效率曲线的影响。
二、实验要求及要点描述(2.5分)(1)磁性材料磁化曲线的绘制给出的五种磁化材料的磁化数据如下:50Hz热轧硅钢片DR610-50(D21)磁化曲线50Hz热轧硅钢片DR530-50(D22)磁化曲线50Hz热轧硅钢片DR510-50(D23)磁化曲线50Hz热轧硅钢片DR490-50(D24)磁化曲线50Hz DW470-50冷轧硅钢片磁化曲线该部分实验要求如下:(1)绘制磁化曲线;(2)根据所提供的数据,合理选取全部和部分数据绘制磁化曲线,并进行比较,不少于4条曲线;(3)绘制每条磁化曲线对应的图和表;(4)在一个图中显示全部曲线,并进行区分要点分析:(1)采用屏幕图形方式直观显示;(2)利用编程方法和MATLAB的拟合函数;(3)利用多项式进行拟合(2)变压器电压变化率及效率曲线的绘制有一台单相1000KV A、66/6.6KV的变压器,实验数据如下:85.0cos 2=ϕ,滞后85.0cos 2=ϕ,0.1cos 2=ϕ情况下的电压变化率曲线和负载曲线。
要点分析:(1)采用屏幕图形方式直观显示; (2)利用MATLAB 编程实现;(3)要画出对应的阻性、感性、容性三种负载性质的特性曲线,并要通过额定点;(4)要画出对应不同的cos ϕ的效率曲线; (5)给出特征性的结论。
三、基本知识及实验方法描述(3分)(一)在非铁磁材料中,磁通密度B 和磁场强度H 之间是线性关系,其系数就是空气的磁导率μ0。
而在铁磁材料中,二者是非线性关系,称为磁化曲线。
电磁场仿真matlab

一、实验目的
一个二维静电场,电位函数为 ,边界条件如题4.29图所示,将正方形场域分成20个正方形网格。有16个内部网格点。假定16个网格点的初始值都定为零,试用超松弛法确定16个内网格点的电位值。
100V
Matlab程序如下:
M=6;
N=6; %网格节点数6*6=36个
U1=ones(N,M); %行列二维数组
U2=U1; P=1;T=0; %初始化
k=0
while(P>1e-5) %由v1迭代,算出v2,迭代精度1e-5
k=k+1; %计算迭代次数
P=0;
for i=2:N-1; %行循环
for j=2:M-1; %列循环
U2(i,j)=U1(i,j)+(U1(i,j+1)+U1(i+1,j)+U2(i-1,j)+U2(i,j-1)-4*U1(i,j))*w/4; %差分方程
hold off
三、
1、场域内等电位线、电场线分布图
所求16个内网格点电位值如下表(精度1e-5)
四、
通过这次使用matlab编写程序求解电磁场的实验,对电磁场这门课程的我有了更加直观的图形理解和计算机求解的认识。实验用超松弛法求解有界电场内的16个内网格点的过程让我亲身实践了电磁场理论计算的形象化结果,加深了我对电磁场边值问题的理解,特别是超松弛方法和简单迭代的运用。
x=1:1:M; y=1:1:N
[xx,yy]=meshgrid(x,y); %栅格
[Gx,Gy]=gradient(U2,0.6,0.6); %梯度
quiver(xx,yy,Gx,Gy,-1.0,'r'); %根据梯度画箭头
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
matlab电磁场仿真作业
一、介绍
本文将介绍matlab电磁场仿真作业的相关知识和技巧。
电磁场仿真是指利用计算机模拟电磁场的分布和变化规律,以实现对电磁场问题的
分析和解决。
matlab是一种强大的数学软件,可以用于各种科学计算、数据分析和图形处理等工作。
在电磁场仿真中,matlab具有良好的适用性和灵活性,可以方便地进行数据处理、可视化和模拟等操作。
二、基本概念
1. 电磁场
电磁场是指由带电粒子或导体所产生的物理现象,包括静电场、磁场
和电磁波等。
在空间中,任何带有电荷或运动电荷的物体都会产生相
应的电磁场。
2. 仿真
仿真是指利用计算机模拟某个系统或过程的行为方式和结果。
在电磁
场仿真中,可以通过建立数学模型来描述物理系统,并利用计算机进
行计算和可视化。
3. 离散化
离散化是指将连续变量转换为离散变量的过程。
在matlab中进行离散化操作可以将连续的电磁场分布转换为离散的数据点,以便进行计算和可视化。
三、matlab电磁场仿真的步骤
1. 建立模型
在进行电磁场仿真前,需要建立合适的模型来描述物理系统。
模型应该包括几何形状、物理特性和边界条件等信息。
可以使用matlab中的几何建模工具来创建三维模型,并定义相应的物理参数。
2. 离散化
将连续的电磁场分布离散化为数据点。
可以使用matlab中的网格生成工具来生成离散化网格,并对网格进行调整以满足精度和计算效率要求。
3. 求解方程
根据物理特性和边界条件,建立相应的方程组并求解。
常用的求解方法包括有限元法、有限差分法和边界元法等。
在matlab中,可以利用数值计算工具箱提供的函数来求解方程组。
4. 可视化
将结果可视化以便于分析和展示。
可以使用matlab中强大的图形处理工具来生成二维或三维图像,并添加必要的标注和注释。
四、实例演示
以下是一个简单的电磁场仿真实例,演示了如何在matlab中进行电磁场仿真。
1. 建立模型
假设有一个长方体导体,其底面和侧面都被接地,导体顶部施加了一个电势差为V的电源。
可以使用matlab中的几何建模工具创建一个长方体,并定义相应的边界条件和物理参数。
2. 离散化
使用matlab中的网格生成工具生成离散化网格,并对网格进行调整以满足计算要求。
3. 求解方程
根据电势差和边界条件,建立相应的方程组并求解。
在本例中,可以
利用matlab中提供的偏微分方程求解函数pdepe来求解二维泊松方程。
4. 可视化
将结果可视化以便于分析和展示。
可以使用matlab中强大的图形处理工具来生成二维或三维图像,并添加必要的标注和注释。
五、总结
本文介绍了matlab电磁场仿真作业的相关知识和技巧。
通过建立模型、离散化、求解方程和可视化等步骤,可以利用matlab进行电磁场仿真并得到相应的结果。
在实际应用中,还需要根据具体问题进行相应的
调整和优化,以满足计算精度和效率要求。
