通用2019年中考数学总复习第四章第四节全等三角形课件
中考数学总复习第四章三角形第16讲全等三角形课件

【例1】 已知:
如图,在△ABC中,D是BC的中点,ED⊥DF,求证:BE+CF>EF. 【分析】 利用中线加倍延长法结合全等三角形,把 BE,CF,EF 集中 在一个三角形中,利用三角形的两边之和大于第三边来
证明:延长 ED 到 M,使 DM=ED,连接 CM,FM,
BD=DC, ∵D 是 BC 的中点,∴BD=CD.在△EDB 与△MDC 中,∠EDB=∠CDM,
解:如图,连接CD, ∵∠C=90°,D是AB的中点, ∴CD=AB=BD, ∵AC=BC, ∴CD⊥AB,∠ACD=∠B=45°, ∴∠CDF+∠BDF=90°, ∵BD⊥DF, ∴∠EDF=90°, ∴∠EDC+∠CDF=90°, ∴∠EDC=∠BDF, ∴△ECD≌△FBD, ∴DE=DF
2.(2015·龙东地区)如图,四边形ABCD是正方形,点E在直线BC上,连 接AE.将△ABE沿AE所在直线折叠,点B的对应点是点B′,连接AB′并延 长交直线DC于点F. (1)当点F与点C重合时如图①,易证:DF+BE=AF(不需证明); (2)当点F在DC的延长线上时如图②,当点F在CD的延长线上时如图③, 线段DF,BE,AF有怎样的数量关系?请直接写出你的猜想,并选择一种 情况给予证明.(导学号 02052266)
1、字体安装与设置
如果您对PPT模板中的字体风格不满意,可进行批量替换,一次性更改各页面字体。 1. 在“开始”选项卡中,点击“替换”按钮右侧箭头,选择“替换字体”。(如下图
)
2、替换模板
模板中的图片展示页面,您可以根据需要
方法一:
2.在图“替换”下拉列表中选择要更改字体。(如下图)
1. 选中模版中的图片(有些图片与其他 本身,而
试题 如图,已知D是△ABC的边BC上的一点,E是AD上的一点,EB=EC ,∠1=∠2.求证:∠BAE=∠CAE. 错解 证明:在△AEB和△AEC中,∵AE=AE,EB=EC,∠1=∠2, ∴△AEB≌△AEC(SSA),∴∠BAE=∠CAE. 剖析 先看一个事实,如图,将等腰△ABC的底边BC延 长线上的任一点和顶点A相连,所得的△DAB和△DAC无疑是不全等的,由 此可知,有两边及其一边的对角对应相等的两个三角形(简称“边边角”) 不一定全等.因此,在判定三角形全等时,一定要留心“边边角”,别上 当哟. 正解 证明:∵EB=EC,∴∠3=∠4,又∵∠1=∠2,∴∠1+∠3=∠2 +∠4,即∠ABC=∠ACB,∴AB=AC.在△AEB和△AEC中,∵EB=EC ,∠1=∠2,AB=AC,∴△AEB≌△AEC(SAS),∴∠BAE=∠CAE
甘肃省2019年中考数学总复习-第四单元 图形初步与三角形 第15讲 全等三角形课件

∴在△ABC 与△DEF 中, ∠ = ∠,
= ,
∴△ABC≌△DEF(AAS).
,
独家教育资源为你提供,thank
2
you
考法1
考法2
考法3
角平分线的判定和性质
判定角平分线除了利用角平分线的定义以外,还有判定定理:到
角两边距离相等的点在角的平分线上.角平分线具有性质:角的平
∴BE2=18,
∴BE=CE=3 2,
∴BC=6 2.
在△ABE 与△ACD 中, ∠ = ∠,
= ,
∴△ABE≌△ACD,∴BE=CD.
方法点拨证明三角形全等有五种方法——SSS,SAS,ASA,AAS,
HL,它们各自独立,解题时应注意选择合适的方法.当然,在解决一个
问题时,有时会用到一种或多种三角形全等的判定方法.
独家教育资源为你提供,thank
= .
图2
∴△DAC≌△BAE,
∴BE=CD.
独家教育资源为你提供,thank
2
you
(3)解:由(1)(2)的解题经验可知:过点A向△ABC外作等腰直角三角
形ABD,使∠DAB=90°,AD=AB=100米,∠ABD=45°,
∴BD=100 2米,
如图3,连接CD,则由(2)可得:BE=CD,
外作等边三角形ABD和等边△ACE,连接BE,CD,请你完成图形(尺
规作图,不写作法,保留作图痕迹),并证明:BE=CD;
(2)如图2,已知△ABC,以AB,AC为边分别向外作正方形ABFD和正方
形ACGE,连接BE,CD,猜想BE与CD有什么数量关系?并说明理由;
(3)运用(1),(2)解答中所积累的经验和知识,完成下题:
中考数学 考点系统复习 第四章 三角形 第四节 全等三角形

5.(2021·兰州第20题5分)如图,点E,C在线段BF上,∠A=∠D,AB∥
DE,BC=EF.求证:AC=DF. 证明:∵AB∥DE,
∴∠ABC=∠DEF,
在△ABC与△DEF中,
∠A=∠D,
∠ABC=∠DEF, BC=EF, ∴△ABC≌△DEF(AAS),∴AC=DF.
6.(2022·兰州第19题6分)如图①是小军制作的燕子风筝,燕子风筝的 骨架图如图②所示,AB=AE,AC=AD,∠BAD=∠EAC,∠C=50°,求 ∠D的大小.
解:∵∠BAD=∠EAC, ∴∠BAD+∠CAD=∠EAC+∠CAD, 即∠BAC=∠EAD, 在△BAC与△EAD中, AB=AE,
∠BAC=∠EAD, AC=AD, ∴△BAC≌△EAD(SAS), ∴∠D=∠C=50°.
.(只需填一个即可)
∠B=∠E
4.(2020·兰州第20题6分)如图,在△ABC中,AB=AC,点D,E分别是
AC和AB的中点.求证:BD=CE. 证明:∵AB=AC,点D,E分别是AC和AB的中点,
∴AD=AE.
在△ABD和△ACE中, AB=AC,
∠A=∠A, AD=AE, ∴△ABD≌△ACE(SAS),∴BD=CE.
=EF,AD=FB,要使△ABC≌△FDE,还需添加一个条件,这个条件可以
是_∠_∠AA==∠∠FF或或ACA∥CE∥F或EBFC=或DBE_C_.(只需填一个即可) =DE
3.(2013·庆阳第19题3分)如图,已知∠1=∠2,AC=AD.请添加一个
条件,使△ABC≌△AED,则添加的条件是∠∠CC==∠∠D或DA或B=AABE=或∠ABE=或∠
命题点:全等三角形的性质与判定(省卷近5年考查5次,兰州近5年考
人教版九年级数学中考总复习《全等三角形》 (共23张PPT)

∴∠1+∠FBE=∠2+∠FBE,即∠ABE=∠CBF.
∴△ABE≌△CBF(SAS).
考题再现 1. (2014深圳)如图1-4-3-7,△ABC和△DEF中,AB=DE,∠B= ∠DEF,添加下列哪一个条件无法证明△ABC≌△DEF( C )
∴△AED≌△AEF(SAS).
考点点拨: 本考点的题型一般为解答题,难度中等. 解答本考点的有关题目,关键在于掌握全等三角形的判定方法 与思路. 注意以下要点: 判定两个三角形全等的一般方法有SSS、SAS、ASA、AAS、HL (相关要点详见“知识梳理”部分),同时要结合其他知识点 如平行线、平行四边形的性质等来证明三角形全等. 另外,注 意AAA、SSA不能判定两个三角形全等,判定两个三角形全等时, 必须有边的参与,且若有两边一角对应相等时,角必须是两边 的夹角.
3. 全等三角形的判定 (1)边边边:三边对应相等的两个三角形全等(可简写成 “SSS”). (2)边角边:两边和它们的夹角对应相等的两个三角形全等 (可简写成“SAS”). (3)角边角:两角和它们的夹边对应相等的两个三角形全等 (可简写成“ASA”). (4)角角边:两角和其中一角的对边对应相等的两个三角形 全等(可简写成“AAS”). (5)斜边直角边:斜边和一条直角边对应相等的两个直角三 角形全等(可简写成“HL”).
方法规律
中考考点精讲精练
考点1 全等三角形的概念和性质
考点精讲
【例1】(2016厦门)如图1-4-3-1,点
E,F在线段BC上,△ABF与△DCE全等,
点A与点D,点B与点C是对应顶点,AF与
DE交于点M,则∠DCE=
()
全等三角形-中考数学总复习精品课件

三角形全等的条件
如何找边相等、 角相等
1.找“角”相等的途径主要有:对顶角相等;两直线平行,同位角、 内错角相等;余角等角代换;角平分线;平行四边形对角相等等.
2.找“边”相等主要借助中点、平行四边形对边相等来证明.
三角形全等的证明
如何找边相等、 角相等
3.判定两个三角形全等的三个条件中,“边”是必不可少的.
垂足分别是点 D,E,AD=3,BE=1,则 DE 的长是( B )
3 A.2
B.2
C.2 2
D. 10
61.2如0° 图,△ABC≌△A′B′C′,其中∠A=36°,∠C′=24°,则∠B=________.
7.如图,已知∠ABC=∠DCB,添加下列条件中的一个:①∠A=∠D,②AC=DB, ③AB=DC,其中不能确定△ABC≌△DCB的是_②_____(只填序号).
A.∠A=∠D B.AC=DF C.AB=ED D.BF=EC
平移加翻折型
2.如图,在△ABC和△DEF中,AB=DE,AC=DF,BE=CF,且 BC=5,∠A=70°,∠B=75°,EC=2,则下列结论中错误的是
( C)
A.BE=3 B.∠F=35° C.DF=5 D.AB∥DE
平移型
3.如图,小强利用全等三角形的知识测量池塘两端M,N的距离,如果
对称型
解:(1)在△ABC 和△ADC 中,AABC= =AADC,,∴△ABC≌△ADC(SSS), BC=DC,
∴∠BAC=∠DAC,即 AC 平分∠BAD (2) 由 (1) 得 ∠BAE = ∠ DAE , 在 △BAE 和 △DAE 中 ,
BA=DA, ∠BAE=∠DAE,∴△BAE≌△DAE(SAS),∴BE=DE AE=AE,
2019年中考数学专题复习资料--全等三角形含答案(共11页).docx
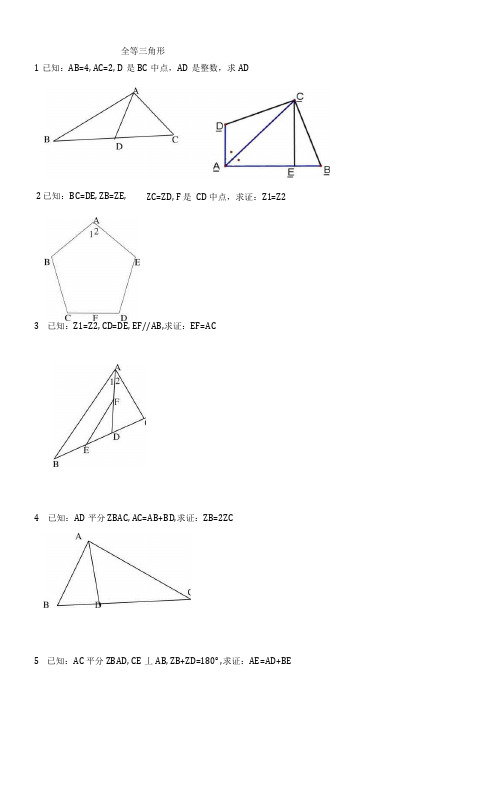
全等三角形1已知:AB=4, AC=2, D 是BC 中点,AD 是整数,求AD3 已知:Z1=Z2, CD=DE, EF//AB,求证:EF=AC4 已知:AD 平分ZBAC, AC=AB+BD,求证:ZB=2ZC5 已知:AC 平分ZBAD, CE 丄AB, ZB+ZD=180° ,求证:AE=AD+BEZC=ZD, F 是 CD 中点,求证:Z1=Z22 已知:BC=DE, ZB=ZE,6如图,四边形ABCD中,AB〃DC, BE、CE分别平分ZABC、ZBCD,且点E在AD上。
求证:BC=AB+DC。
7 已知:AB=CD, ZA=ZD,求证:ZB=ZC&P 是ZBAC 平分线AD 上一点,AC>AB,求证:PC-PB<AC-AB9 已知,E 是AB 中点,AF=BD, BD=5, AC=7,求DC13已知:如BD1AC ,分别为D、E, BD、CE相交于点F。
求证:BE=CD. 图,AB=AC, CEXAB,垂足10.如图,已知AD/7BC, ZPAB的平分线与ZCBA的平分线相交于E, CE的连线交AP于D.求证:AD+BC=AB. 11如图,AABC中,AD是ZCAB的平分线,且AB=AC+CD,求证:ZC=2ZB12 如图:AE、BC 交于点M, F 点在AM 上,BE/7CF, BE=CF。
求证:AM是△ABC的中线。
14 在AABC 中,ZACB = 90°, AC = BC ,直线MV 经过点C ,且AD 丄MZV 于D , BE L MN 于E . (1) 当直线MN绕点C旋转到图1的位置时,求证:① ^ADC竺ACEB;② DE = AD + BE ;(2)当直线MV绕点C旋转到图2的位置时,(1)中的结论还成立吗?若成立,请给出证明; 若不成立,说明理由.15如图所示,已知AE丄AB, AF丄AC, AE=AB, AF=AC。
求证:16.如图,已知AC〃BD, EA、EB分别平分ZCAB和ZE,则AB与AC+BD相等吗?请说明理由DBA, CD过点(1) EC=BF; (2) EC丄BFB C17.如图9所示,AABC是等腰直角三角形,ZACB=90° , AD是BC边上的中线,过C作AD的垂线,交AB于点E,交AD于点F,求证:ZADC=ZBDE.图9全等三角形证明经典(答案)1. 延长AD到E,使DE=AD,则三角形ADC全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE即:10-2<2AD<10+2 4<AD<6又AD是整数,则AD=52证明:连接BF和EF。
广东省2019年中考数学总复习第一部分知识梳理第四章三角形第16讲全等三角形课件
{
广东省2019年中考数学总复习:教材知 识梳理课件
6.(30分) (2018恩施)如图K1-16-5,点B,F,C,E在一 条直线上,FB=CE,AB∥ ED,AC∥FD,AD交BE于点O. 求证:AD与BE互相平分.
广东省2019年中考数学总复习:教材知 识梳理课件
{
证明:如答图1-16-1,连接BD,AE. ∵FB=CE,∴BC=EF. 又∵AB∥ED,AC∥FD, ∴∠ABC=∠DEF,∠ACB=∠DFE. 在△ABC和△DEF中, ∠ABC=∠DEF, BC=EF, ∠ACB=∠DFE, ∴△ABC≌△DEF (ASA). ∴AB=DE, 又∵AB∥DE. ∴四边形ABDE是平行四边形. ∴AD与BE互相平分.
第16讲 全等三角形
广东省2019年中考数学总复习:教材知 识梳理课件
1. (10分) 下列条件能判定两个直角三角形全等的是 ( D ) A. 一锐角对应相等 B. 两锐角对应相等 C. 一条边对应相等 D. 两条直角边对应相等 2. (10分)(2018安顺)如图K1-16-1,点D,E分别在 线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添 加下列条件仍不能判定 △ABE≌△ACD的是( D ) A.∠B=∠C B.AD=AE C.BD=CE D.BE=CD
广东省2019年中考数学总复习:教材知 识梳理课件
广东省200分)(2018衢州)如图K1-16-2,在△ABC和 △DEF中,点B,F,C,E在同一直 线上,BF=CE,AB∥DE,请添加一 个条件,使△ABC≌△DEF,这个添 加的条件可以是_________________ AB=ED(答案不唯一) (只需写一个,不添加辅助线). 4. (10分) 如图K1-16-3,在Rt△ABC中,∠C=90°, AD是∠CAB的平分线,DE⊥AB于点E. 若CD=2 cm,则DE=_________cm. 2
中考数学专题复习全等三角形省公开课一等奖百校联赛赛课微课获奖PPT课件
四、探索编拟问题型
例:如图,在△AFD和△BEC中,点A、E、F、C在同 一直线上,有以下四个论断:
①AD=CB,②AE=CF,③∠B=∠D,④ ∠A=∠C. 请用其中三个作为条件,余下一个作为结论,编一道数 学问题,并写出解答过程。
A
D
E
F
B
C
第11页
如图,已知∠1=∠2=90°,BD=CE,
③
第6页
中考系列之一:全等三角形探索型问题
一、探索条件型
这类型题给出了结论,要求探索使该结论成立所具备 条件。普通地,依据三角形全等地判定方法,补充所 缺乏条件。
例:如图,已知MB=ND,∠MBA=∠NDC,以下哪些条
件不能判定 △ABM≌△CDN( C )
A.∠M=∠N
M
N
B.AB=CD
C.AM=CN D.∠AMB=∠NCD
例:如图为人民公园中荷花池,现在测量荷花池两 旁A、B两棵大树间距离(不得直接量得)。请 你依据图形全等知识,用一根足够长绳子及标杆 为工具,设计两种不一样测量方案。
要求(1)画出设计测量示意图;
(2)写出测量方案理由。
A
B
第9页
A
B
·C
E·
·D
这类型题首先提供一个实际问题背景,按照问题要 求研究处理问题合理方案。
A D
6.9cm
A
5.5cm
B
C
B
CE
D
F
6.9cm
5.5cm
E
F
第3页
直角三角形全等条件还有
斜边和一条直角边对应相等两个直角三角形 全等.
简写成“斜边、直角边”或“HL”.
第4页
福建省福州市2019年中考数学复习第四章三角形第四节全等三角形同步-含答案
第四节全等三角形姓名:________ 班级:________ 限时:______分钟1.(2018·安徽)如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD()A.∠B=∠C B.AD=AEC.BD=CE D.BE=CD2.(2018·黔南州)下列各图中a,b,c为三角形的边长,则甲,乙,丙三个三角形和左侧△ABC全等的是( )A.甲和乙 B.乙和丙 C.甲和丙 D.只有丙3.如图,△ABC中,AB=AC,BD=CE,BE=CF,若∠A=50°,则∠DEF的度数是( )A. 75°B. 70°C. 65°D. 60°4.(2018·南京)如图,AB⊥CD,且AB=CD.E、F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为( )A.a+c B.b+c C.a-b+c D.a+b-c5.(2018·临沂)如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别是点D、E,AD=3,BE=1,则DE 的长是( )A.32B .2C .2 2D.106.(2018·济宁)在△ABC 中,点E ,F 分别是边AB ,AC 的中点,点D 在BC 边上,连接DE ,DF ,EF ,请你添加一个条件________,使△BED 与△FDE 全等.7.(2018·金华)如图,△ABC 的两条高AD ,BE 相交于点F ,请添加一个条件,使得△ADC≌△BEC(不添加其他字母及辅助线),你添加的条件是________.8.(2018·福州质检)如图,点B ,F ,C ,E 在一条直线上,AB∥DE,AC∥DF 且AC =DF ,求证:AB =DE.9.(2018·云南省卷)如图,已知AC平分∠BAD,AB=AD.求证:△ABC≌△ADC.10.(2018·泰州)如图,∠A=∠D=90°,AC=DB,AC、DB相交于点O.求证:OB=OC.11.(2018·陕西)如图,AB∥CD,E、F分别为AB、CD上的点,且EC∥BF,连接AD,分别与EC、BF相交于点G、H.若AB=CD,求证:AG=DH.12.(2017·恩施州)如图,△ABC、△CDE均为等边三角形,连接BD、AE交于点O,BC与AE交于点P. 求证:∠AOB=60°.13.(2018·恩施州)如图,点B、F、C、E在一条直线上,FB=CE,AB∥ED,AC∥FD,AD交BE于O. 求证:AD与BE互相平分.14.(2018·怀化)已知:如图,点A,F,E,C在同一直线上,AB∥DC,AB=CD,∠B=∠D.(1)求证:△ABE≌△CDF;(2)若点E,G分别为线段FC,FD的中点,连接EG,且EG=5,求AB的长.1.(2018·桂林)如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,BC=EF.(1)求证:△ABC≌△DEF;(2)若∠A=55°,∠B=88°,求∠F的度数.2.(2018·衡阳)如图,已知线段AC,BD相交于点E,AE=DE,BE=CE.(1)求证:△ABE≌△DCE;(2)当AB=5时,求CD的长.3.(2018·莆田质检)如图,在△ABC中,AB=BC,∠ABC=90°,分别以AB,AC为边在AB同侧作等边△ABD和等边△ACE,连接DE.(1)判断△ADE的形状,并加以证明;(2)过图中两点画一条直线,使其垂直平分图中的某条线段,并说明理由.4.(2018·哈尔滨)已知:在四边形ABCD中,对角线AC、BD相交于点E,且AC⊥BD,作BF⊥CD,垂足为点F,BF与AC交于点G,∠BGE=∠ADE.(1)如图①,求证:AD=CD;(2)如图②,BH是△ABE的中线,若AE=2DE,DE=EG,在不添加任何辅助线的情况下,请直接写出图②中四个三角形,使写出的每个三角形的面积都等于△ADE面积的2倍.5.(2018·滨州)已知,在△ABC中,∠A=90°,AB=AC,点D为BC的中点.(1)如图①,若点E、F分别为AB、AC上的点,且DE⊥DF,求证:BE=AF;(2)若点E、F分别为AB、CA延长线上的点,且DE⊥DF,那么BE=AF吗?请利用图②说明理由.参考答案【基础训练】1.D 2.B 3.C 4.D 5.B 6.D 是BC 的中点7.AC =BC8.证明: ∵AB∥DE,AC∥DF,∴∠B=∠E,∠ACB=∠DFE.在△ABC 和△DEF 中,⎩⎪⎨⎪⎧∠B=∠E ∠ACB=∠DFE,AC =DF∴△ABC≌△DEF(AA S ),∴AB=DE.9.证明:∵AC 平分∠BAD,∴∠BAC=∠DAC,在△ABC 和△ADC 中,⎩⎪⎨⎪⎧AB =AD ∠BAC=∠DAC,AC =AC∴△ABC≌△ADC.10.证明:在Rt △ABC 和Rt △DCB 中,⎩⎪⎨⎪⎧AC =BD ,CB =BC , ∴Rt △ABC≌Rt △DCB(HL ),∴∠OBC=∠OCB,∴BO=CO.11.证明: ∵AB∥CD.∴∠A=∠D.∵EC∥BF.∴∠BHA=∠CGD.∵AB=CD ,∴△ABH≌△DCG.∴AH=DG.∴AG=DH.12.证明:∵△ABC、△CDE 为等边三角形,∴∠ACB=∠ECD=60°,AC =BC ,CD =CE ,∴∠ACE=∠BCD,在△ACE 和△BCD 中,⎩⎪⎨⎪⎧AC =BC ,∠ACE=∠BCD,CE =CD ,∴△ACE≌△BCD(S A S ),∴∠CAE=∠CBD,∵∠AOB+∠CBD+∠BPO=180°,∠BCA +∠CAE+∠APC=180°,且∠BPO=∠APC,∴∠AOB=∠BCA=60°.13.证明:如解图,连接BD ,AE ,∵FB=CE ,∴BC=EF ,又∵AB∥ED,AC∥FD,∴∠ABC=∠DEF,∠ACB=∠DFE,在△ABC 和△DEF 中,⎩⎪⎨⎪⎧∠ABC=∠DEF,BC =EF ,∠ACB=∠DFE,∴△ABC≌△DEF(A S A),∴AB=DE ,又∵AB∥DE,∴四边形ABDE 是平行四边形,∴AD 与BE 互相平分.14.证明:(1)∵AB∥DC,∴∠A=∠C.在△ABE 和△CDF 中,⎩⎪⎨⎪⎧∠A=∠C,AB =CD ,∠B=∠D,∴△ABE≌△CDF(A S A);(2)解:∵点E ,G 分别为线段FC ,FD 的中点,∴EG=12CD ,∵EG=5,∴CD=10,∵△ABE≌△CDF,∴AB=CD =10.【拔高训练】1.(1)证明:∵AC=AD +DC ,DF =DC +CF ,且AD =CF ,∴AC=DF ,在△ABC 和△DEF 中,⎩⎪⎨⎪⎧AB =DE BC =EF ,AC =DF∴△ABC≌△DEF(SSS );(2)解:由(1)可知,∠F=∠ACB.∵∠A=55°,∠B=88°,∴∠ACB=180°-(∠A+∠B)=180°-(55°+88°)=37°,∴∠F=∠ACB=37°.2.(1)证明:在△AEB 和△DEC 中,⎩⎪⎨⎪⎧AE =DE ∠AEB=∠DEC,BE =EC∴△AEB≌△DEC(S A S ).(2)解:∵△AEB≌△DEC,∴AB=CD ,∵AB=5,∴CD=5.3.解: (1)△ADE 是等腰直角三角形.理由:在等边△ABD 和等边△ACE 中,∵BA=DA ,CA =EA ,∠BAD=∠CAE=60°,∴∠BAD-∠CAD=∠CAE-∠CAD.即∠BAC=∠EAD,∴△ABC≌△ADE.∴BC=DE ,∠ABC=∠ADE,∵AB=BC =AD ,∠ABC=90°,∴AD=DE ,∠ADE=90°,即△ADE 是等腰直角三角形.(2)连接CD ,则直线CD 垂直平分线段AE.(或连接BE ,则直线BE 垂直平分线段AC) 理由:由(1)得DA =DE.又∵CA=CE ,∴直线CD 垂直平分线段AE.4.(1)证明:∵∠BGE=∠ADE,∠BGE=∠CGF,∴∠ADE=∠CGF,∵AC⊥BD,BF⊥CD,∴∠ADE+∠DAE=∠CGF+∠GCF,∴∠DAE=∠GCF,∴AD=CD.(2)解:△ACD、△ABE、△BCE、△BHG.【解法提示】设DE =a ,则AE =2DE =2a ,EG =DE =a ,∵S △ADE =12AE·DE=12·2a·a=a 2, ∵BH 是△ABE 的中线,∴AH=HE =a ,∵AD=CD ,AC⊥BD,∴CE=AE =2a ,则S △ADC =12AC·DE=12·(2a+2a)·a=2a 2=2S △ADE ; 在△ADE 和△BGE 中,⎩⎪⎨⎪⎧∠AED=∠BEG DE =GE ,∠ADE=∠BGE∴△ADE≌△BGE(A S A),∴BE=AE =2a ,∴S △ABE =12AE·BE=12·2a·2a=2a 2, S △BCE =12CE·BE=12·2a·2a=2a 2, S △BHG =12HG·BE=12·(a +a)·2a=2a 2, 综上,面积等于△ADE 面积的2倍的三角形有△ACD、△ABE、△BCE、△BHG.5.(1)证明:连接AD ,如解图①所示.第5题解图①∵∠A=90°,AB =AC ,∴△ABC 为等腰直角三角形,∠EBD=45°.∵点D 为BC 的中点,∴AD=12BC =BD ,∠FAD=45°. ∵∠BDE+∠EDA=90°,∠EDA+∠ADF=90°,∴∠BDE=∠ADF.在△BDE 和△ADF 中,⎩⎪⎨⎪⎧∠EBD=∠FAD BD =AD ,∠BDE=∠ADF∴△BDE≌△ADF(A S A),∴BE=AF.(2)解:BE =AF ,证明如下:连接AD ,如解图②所示.第5题解图②∵∠ABD=∠BAD=45°,∴∠EBD=∠FAD=135°.∵∠EDB+∠BDF=90°,∠BDF+∠FDA=90°, ∴∠EDB=∠FDA.在△EDB 和△FDA 中,⎩⎪⎨⎪⎧∠EBD=∠FAD BD =AD∠EDB=∠FDA, ∴△EDB≌△FDA(A S A),∴BE=AF.。
中考数学总复习 第四章 三角形 第19课时 全等三角形课件
考点二:全等三角形的性质
3.全等三角形的对应边相等,全等三角形的对应角 相等; 4.全等三角形的对应边上的高相等,全等三角形的 对应边上的中线相等,全等三角形的对应角的平分 线相等.
考点三: 三角形全等的判定方法
5.三条边对应相等的两个三角形全等(简记为“边边 边”或“SSS”).
6.两条边和它们的夹角对应相等的两个三角形全 等(简记为“边角边”或“SAS”).
考点四: 利用“尺规”作三角形
10.已知三角形的三条边,求作三角形. 11.已知三角形的两条边及其夹角,求作三角形. 12.已知三角形的两个角及其夹ห้องสมุดไป่ตู้,求作三角形. 13.已知三角形的两个角及其中一个角的对边,求作 三角形. 14.已知三角形一直角边和斜边,求作三角形.
D D
DC BC(答案合理即可)
证明:(1)用“SAS”可证得 △ABC≌△DEF;(2)由△ABC≌△DEF 得∠B=∠DEF,∴AB∥DE.
考点一:全等图形及全等三角形 1.两个能够完全重合的图形称为全等图形,全 等图形的形状和大小都相同. 2.能够完全重合的两个三角形叫全等三角形.
温馨提示: 完全重合有两层含义: (1)图形的形状相同; (2)图形的大小相等.
7.两个角和它们的夹边对应相等的两个三角形全 等(简记为“角边角”或“ASA”).
8.两个角和其中一个角的对边对应相等的两个三 角形全等(简记为“角角边”或“AAS”).
温馨提示:这四个判定,无论用哪种方法,都要有三 组元素对应相等,且其中至少要有一组对应边相等.
考点三: 三角形全等的判定方法 9.斜边和一条直角边对应相等的两个直角 三角形全等(简记为“斜边直角边”或“HL”). 注意:这个判定的前提必须是直角三角形.
