第四讲 两类动力学问题 超重和失重
高考物理复习基础核心知识点典型题详解《两类动力学问题、超重与失重》精品课件

星竖直方向的速度-时间图像如图所示,设运动中不计空气阻力,燃料燃烧
时产生的推力大小恒定。下列判断正确的是 ( )
A.t2时刻卫星到达最高点,t3时刻卫星落回地面 B.卫星在0~t1时间内的加速度大于t1~t2时间内的加速度 C.t1~t2时间内卫星处于超重状态 D.t2~t3时间内卫星处于超重状态
答案
D
物体由静止开始向上运动时,物体和手掌先一起加速向上,物
体处于超重状态,之后物体和手掌分离前,应减速向上,物体处于失重状态, 故A、B均错误。当物体和手分离时,二者速度相同,又因均做减速运动,故 分离条件为a手>a物,分离瞬间物体的加速度等于重力加速度,则手的加速度 大于重力加速度,选项D正确,C错误。
列竖直方
向原理式 运动状态
F-mg=ma
F=m(g+a) 加速上升、减速下降
mg-F=ma
F=m(g-a) 加速下降、减速上升
mg-F=ma
F=0 无阻力的抛体运动情况
视重
F>mg
F<mg
F=0<mg
自测3 某研究性学习小组用实验装置模拟火箭发射卫星。火箭点燃后从 地面竖直升空,燃料燃尽后火箭的第一级和第二级相继脱落,实验中测得卫
自测2 如图所示,质量为m的小球一端用轻质细绳连在竖直墙上,另一端 用轻质弹簧连在天花板上。轻绳处于水平位置,弹簧与竖直方向夹角为 θ。已知重力加速度为g,则在剪断轻绳瞬间,小球加速度的大小为 ( )
A.0 B.g sin θ C.g tan θ D.
g cos θ
二、超重和失重 1.实重和视重 (1)实重:物体实际所受的重力,它与物体的运动状态① 无关 。
自测1 质量不可忽略的小球与轻质弹簧相连,穿在光滑的杆上,杆与水平
牛顿定律的应用-两类动力学问题与超重、失重

运动情况
超重、失重
视重
a=0
不超重也不失重
F=mg
a的方向竖直向上
超重
F=m(g+a)
a的方向竖直向下
失重
F=m(g-a)
a=g ,a的方向竖直 向下
完全失重
F=0
名师支招:
判断物体超重或失重,仅分析加速度的方向即可,只要加速度的竖直分量向
上就是超重,加速度的竖直分量向下就是失重。
*体验应用*
2.(双项选择)游乐园中,游客乘坐能做加速或减速运动的升
(2)处理连接体问题时,整体法与隔离法往往交叉使用,一般 的思路是先用整体法求加速度,再用隔离法求物体间的作用力。
(3)利用牛顿第二定律可以处理匀变速直线运动问题,也可以 定性分析非匀变速直线运动的规律,它常和力学、电磁学等有关 知识结合起来考查一些综合问题。
*体验应用*
1.[2009年高考安徽理综卷]在2008年北京残奥会开幕式上, 运动员手拉绳索向上攀登,最终点燃了主火炬,体现了残 疾运动员坚韧不拔的意志和自强不息的精神。为了探求上 升过程中运动员与绳索和吊椅间的作用,可将过程简化。 一根不可伸缩的轻绳跨过轻质的定滑轮,一端挂一吊椅, 另一端被坐在吊椅上的运动员拉住,如图3-2-1所示。设运 动员的质量为65 kg,吊椅的质量为15 kg,不计定滑轮与绳 子间的摩擦。重力加速度取g=10 m/s2。当运动员与吊椅一 起正以加速度a=1 m/s2上升时,试求: (1)运动员竖直向下拉绳的力; (2)运动员对吊椅的压力。
慢慢加速,再匀速运转。一顾客乘扶梯上楼,恰
好经历了这两个过程,如图3-2-8所示。那么下列
C 说法中正确的是(
)
A.顾客始终受到三个力的作用
超重与失重课件PPT

10、如图3-2-7所示为学校操场上一质量不计的竖直滑杆,滑杆上端固定,下端悬空为了研究学生沿杆的下滑情况,在杆的顶部装有一拉力传感器,可显示杆顶端所受拉力的大小,现有一学生(可视为质点)从上端由静止开场滑下,5 s末滑到杆底时速度恰好为零,从学生开场下滑时刻计时,传感器显示拉力随时间变化情况如图3-2-8所示,g取10 m/s2, 求(1)该学生下滑过程中的最大速率; (2)图中力F1的大小; (3)滑杆的长度.
过程分析:人随电梯一起加速下降,加速度a=0.5m/s2 ,可求出合力,然后得出压力
G
F
a
§3.7 超重和失重
2
2、一个人站在医用体重计的秤台上,不动时读数为G,此人在下蹲过程中,磅秤的读数〔 〕 A.先减小, 后复原 C.始终不变 B.先增加, 后复原 D.先减小,后增加, 最后复原
过程分析:人下蹲是由静止开场向下运动,速度增加,具有向下的加速度〔失重〕;蹲下后最终速度变为零,故还有一个向下减速的过程,加速度向上〔超重〕。
D
人在站起过程,情况又是怎样 ?
考虑
3、某人在地面上最多只能举起60kg的物体,那么 他在一以2.5m/s2的加速度匀加速下 降的电梯里最多能举起多重的物体? (g取10m/s2)
本节知识、方法归纳
1、升降机以2的加速度匀加速下降,站在升降机里的人的质量是50kg,人对升降机地板的压力是多大? (g取10 m/s )
解:对其受力分析如图:
得: F合 = G — FN=ma
由题意:FN = 475 N
故:人对地板的压力F’N= FN= 475N
FN = G — ma
7、如下图,在压力传感器的托盘上固定一个倾角为30°的光滑斜面,现将一个重4 N的物块放在斜面上,让它自由滑下,那么以下说法正确的选项是〔 〕
人教版高中物理复习课件-两类动力学问题超重和失重

應用牛頓第二定律解決兩類動力學基本問題,主要 把握兩點:兩類分析——物體的受力分析和物體的 運動過程分析;一個橋樑——物體運動的加速
度.由此可知確定物體的加速度是解決這兩類問題 的關鍵.
考點二 超重和失重現象 ►基礎梳理◄
概念 超重
定義
產生條件 視重 示例
當物體具有 向上的加速 度時,物體 對支持物的 壓力或對懸 繩的拉力比 重力大的現 象
課時9 兩類動力學問題 超重和失重
考點一 動力學的兩類基本問題
►基礎梳理◄
運用牛頓運動定律解決的動力學問題常常可以 分為兩種類型,即動力學的兩類基本問題.
(1)已知物體的受力情況,求物體的運動情況
如果已知物體的受力情況,可以由牛頓第二定 律求出物體運動的加速度,再利用運動學公式 就可以確定物體的運動情況.
(2)在完全失重狀態下,由於重力產生的一切現象 都不存在.例如,物體對水準支持面沒有壓力,對 豎直懸線沒有拉力,不能用天平測物體的品質,液 柱不產生壓強,在液體中的物體不受浮力等等.
►深化拓展◄
1.物體處於超重和失重狀態時,物體所受的重力 並沒有變化.所謂“超重”和“失重”是指視重, 其“超重”和“失重”的大小為ma.
題後反思:由物體受力情況求解運動情況的一般步 驟是:
1.確定研究對象,對研究對象進行受力分析,並 畫出物體受力圖.
2.根據力的合成或正交分解求出合外力(大小、方 向)(物體受二個以上的力作用時一般用正交分解 法).
3.根據牛頓第二定律列方程,並解出物體的加速 度.
4.結合題給物體運動的初始條件,選擇運動學公 式求出所需的運動學量.
A.箱內物體對箱子底部始終沒有壓力
B.箱子剛從飛機上投下時,箱內物體受到的支持 力最大
超重失重、等时圆和动力学两类基本问题(解析版)
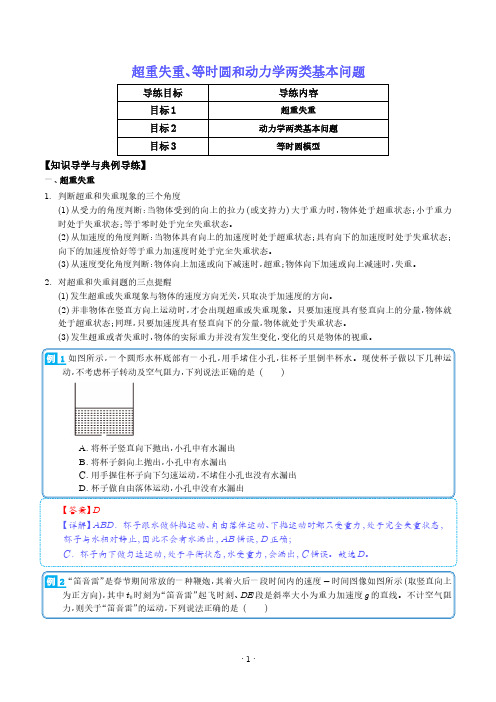
超重失重、等时圆和动力学两类基本问题导练目标导练内容目标1超重失重目标2动力学两类基本问题目标3等时圆模型【知识导学与典例导练】一、超重失重1.判断超重和失重现象的三个角度(1)从受力的角度判断:当物体受到的向上的拉力(或支持力)大于重力时,物体处于超重状态;小于重力时处于失重状态;等于零时处于完全失重状态。
(2)从加速度的角度判断:当物体具有向上的加速度时处于超重状态;具有向下的加速度时处于失重状态;向下的加速度恰好等于重力加速度时处于完全失重状态。
(3)从速度变化角度判断:物体向上加速或向下减速时,超重;物体向下加速或向上减速时,失重。
2.对超重和失重问题的三点提醒(1)发生超重或失重现象与物体的速度方向无关,只取决于加速度的方向。
(2)并非物体在竖直方向上运动时,才会出现超重或失重现象。
只要加速度具有竖直向上的分量,物体就处于超重状态;同理,只要加速度具有竖直向下的分量,物体就处于失重状态。
(3)发生超重或者失重时,物体的实际重力并没有发生变化,变化的只是物体的视重。
1如图所示,一个圆形水杯底部有一小孔,用手堵住小孔,往杯子里倒半杯水。
现使杯子做以下几种运动,不考虑杯子转动及空气阻力,下列说法正确的是()A.将杯子竖直向下抛出,小孔中有水漏出B.将杯子斜向上抛出,小孔中有水漏出C.用手握住杯子向下匀速运动,不堵住小孔也没有水漏出D.杯子做自由落体运动,小孔中没有水漏出【答案】D【详解】ABD.杯子跟水做斜抛运动、自由落体运动、下抛运动时都只受重力,处于完全失重状态,杯子与水相对静止,因此不会有水漏出,AB错误,D正确;C.杯子向下做匀速运动,处于平衡状态,水受重力,会漏出,C错误。
故选D。
2“笛音雷”是春节期间常放的一种鞭炮,其着火后一段时间内的速度-时间图像如图所示(取竖直向上为正方向),其中t0时刻为“笛音雷”起飞时刻、DE段是斜率大小为重力加速度g的直线。
不计空气阻力,则关于“笛音雷”的运动,下列说法正确的是()A.“笛音雷”在t 2时刻上升至最高点B.t 3~t 4时间内“笛音雷”做自由落体运动C.t 0~t 1时间内“笛音雷”的平均速度为v 12D.t 3~t 4时间内“笛音雷”处于失重状态【答案】D【详解】A 由图可知,t 0~t 4时间内“笛音雷”的速度一直为正值,表明其速度方向始终向上,可知,“笛音雷”在t 2时刻并没有上升至最高点,上升至最高点应该在t 4时刻之后,故A 错误;B .t 3~t 4时间内“笛音雷”速度方向向上,图像斜率为一恒定的负值,表明t 3~t 4时间内“笛音雷”实际上是在向上做竖直上抛运动,其加速度就是重力加速度g ,故B 错误;C .将A 、B 用直线连起来,该直线代表匀加速直线运动,其平均速度为v12,而AB 线段与横轴所围的面积大于AB 曲线与横轴所围的面积,该面积表示位移,根据v =ΔxΔt可知,直线代表的匀加速直线运动的平均速度大于AB 曲线代表的变加速直线运动的平均速度,即t 0~t 1时间内“笛音雷”的平均速度小于v12,故C 错误;D .根据上述,t 3~t 4时间内“笛音雷”做竖直上抛运动,加速度方向竖直向下,“笛音雷”处于失重状态,故D 正确。
动力学的两类基本问题·超重和失重

学科:物理教学内容:动力学的两类基本问题·超重和失重【教学指导】1应用牛顿运动定律求解的问题主要有两类:一类是已知受力情况求运动情况;另一类是已知运动情况求受力情况.在这两类问题中,加速度是联系力和运动的桥梁,受力分析是解决问题的关键.2在平衡状态时,物体对水平支持物的压力(或对悬绳的拉力)大小等于物体的重力.当物体在竖直方向上有加速度时,物体对支持物的压力就不等于物体的重力了.当物体的加速度向上时,物体对支持物的压力大于物体的重力,这种现象叫做超重现象;当物体的加速度向下时,物体对支持物的压力小于物体的重力,这种现象叫失重现象.特别的,当物体向下的加速度为g时,物体对支持物的压力变为零,这种状(1(2(3)在完全失重的状态下,平常一切由重力产生的物理现象都会完全消失,如单摆停摆、天平失效、3.在连接体问题中,如果不要求知道各个运动物体之间的相互作用力,并且各个物体具有大小和方向都相同的加速度,就可以把它们看成一个整体(当成一个质点).分析受到的外力和运动情况,应用牛顿第二定律求出加速度(或其他未知量);如果需要知道物体之间的相互作用力,就需要把物体从系统中隔离出来,将内力转化为外力,分析物体的受力情况和运动情况,并分别应用牛顿第二定律列出方程.隔离法和整体法是互相依存、互相补充的.两种方法互相配合交替应用,常能更有效地解决有关连接体的问【方法解析】1.对物体进行受力分析时,强调较多的是隔离法,但采用整体法求解,常能化难为易,化繁为简.如图3—2—1,物块b 沿静止的粗糙斜面a 匀速下滑,判断地面与斜面间有无摩擦力.由于系统处于平衡状态,系统的重力与地面对它们的支持力平衡,水平方向无其他外力,故在水平方向不存在相对运动的趋势,图3—2—12(1)选取研究对象.所选的研究对象可以是一个物体,也可以是多个物体组成的系统.同一题目,(2(3)根据牛顿第二定律和运动学公式列方程.由于所用的公式均为矢量,所以列方程过程中,要特别注意各量的方向.一般情况均以加速度的方向为正方向,分别用正负号表示式中各量的方向,将矢量运(4【典型例题精讲】[例1]静止在水平地面上的物体的质量为2 kg ,在水平恒力F 推动下开始运动,4 s 末它的速度达到4 m/s ,此时将F 撤去,又经6 s 物体停下来,如果物体与地面的动摩擦因数不变,求F 【解析】 物体的整个运动过程分为两段,前4 s 物体做匀加速运动,后6 s前4 sa 1=4401=-t v m/s 2=1 m/s2设摩擦力为FfF -F f =ma 1后6sa 2=6402-=-t v m/s 2=-32m/s2-F f =ma 2由①②可求得水平恒力FF =m (a 1-a 2)=2×(1+32) N =3.3 N【说明】 (1)本例属于已知运动情况求受力情况的问题.分析思路为:先由运动情况求加速度,再(2)在分析物体的运动过程中,一定弄清整个运动过程中物体的加速度是否相同,若不同,必须分段处理,加速度改变时的瞬时速度即是前后过程的联系量.分析受力时要注意前后过程中哪些力发生了变【设计意图】本题是已知运动情况求受力情况.通过本例帮助学生掌握这类问题的解题方法.同时,[例2]质量为m =2 kg 的木块原来静止在粗糙水平地面上,现在第1、3、5…奇数秒内给物体施加方向向右、大小为F 1=6 N 的水平推力,在第2、4、6…偶数秒内给物体施加方向仍向右、大小为F 2=2 N 的水平推力,已知物体与地面间的动摩擦因数μ=0.1,取g =10 m/s 2,问:(1)木块在奇数秒和偶数秒内各做什么运动? (2)经过多长时间,木块位移的大小等于40.25 m?【解析】 以木块为研究对象,它在竖直方向受力平衡,水平方向仅受推力F 1(或F 2)和摩擦力F f 的作用.由牛顿第二定律可判断出木块在奇数秒内和偶数秒内的运动,结合运动学公式,即可求出运动时(1a1=21021.0611⨯⨯-=-=-m mg F mF F fμm/s 2=2 m/s 2a2=21021.0222⨯⨯-=-=-m mg F mF F fμm/s 2=0所以,木块在奇数秒内做a =a 1=2 m/s 2的匀加速直线运动,在偶数秒内做匀速直线运动.(2)在第1 ss 1=22122121⨯⨯=at m =1 m至第1 sv1=at =2×1 m/s =2 m/s在第2 s 内,木块以第1 s 末的速度向右做匀速运动,在第2 ss2=v 1t =2×1 m =2 m 至第2 sv2=v 1=2 m/s在第3 s 内,木块向右做初速度等于2 m/s 的匀加速运动,在第3 ss3=v 2t +21at 2=2×1 m +21×2×12 m =3 m至第3 sv3=v 2+at =2 m/s +2×1 m/s =4 m/s在第4 s 内,木块以第3 s 末的速度向右做匀速运动,在第4 ss4=v 3t =4×1 m =4 m 至第4 sv4=v 3=4 m/s由此可见,从第1 s 起,连续各秒内木块的位移是从1开始的一个自然数列.因此,在n ss n =1+2+3+…+n =2)1(+n n当sn =40.25 m 时,n 的值为8<n <9.取n =8,则8 ss 8=2)18(8+m =36 m至第8 s 末,木块的速度为v 8=8 m/s设第8 s 后,木块还需向右运动的时间为t x ,对应的位移为s x =40.25 m -36 m =4.25 m ,由s x =v 8t x +21atx 2即4.25=8tx +21×2t x 2解得tx =0.5 s所以,木块位移大小等于40.25 m 时需运动的时间T =8 s +0.5 s =8.5 s【思考】 若根据v -t【思考提示】 物体的v -t由v -t 图象不难求出物体在第1 s 、第2 s 、第3 s 、第4 s …第n s 内的位移分别为1 m 、2 m 、3 m 、4 m…nm .则前n ssn =(1+2+3+…+n )m =2)1(nn +m当sn =40.25 m 时,8<n <9,前8 ss8=28)18(⨯+m =36 m8 s 后物体的位移为:sx =s -s 8=40.25 m -36 m =4.25 msx =v 8t x +21at x 2求得tx =0.5 s ,则物体发生40.25 m 的位移所需时间为8.5 s.【说明】 (1)本题属于已知受力情况求运动情况的问题,解题思路为先根据受力情况由牛顿第二定(2)根据物体的受力特点,分析物体在各段时间内的运动情况,并找出位移的一般规律,是求解本题的关键.【设计意图】 (1(2)应用数学知识解决物理问题的能力是高考考查的能力之一,当然也是高三复习重点培养的能力之一.通过本例说明了应用数列知识解决物理问题的方法.[例3]某人在地面上最多能举起60 kg 的重物,当此人站在以5 m/s 2的加速度加速上升的升降机中,最多能举起多少千克的重物?(g 取10 m/s 2)【解析】 本题属于超重的问题,分析时要抓住一点,即在不同的环境下人的最大上举力(人对物体的推力)是不变的. 这一点想明白了,之后列方程求解就简单了.某人在地面上能举起60 kg 的重物.则他的最大举力为F =600 N .设在加速上升的升降机中最多能举起质量为m 的物体.取物体m 为研究对象,它只受重力mg 和举力F 的作用,由牛顿第二定律可得:F -mg =ma所以m =510600+=+ag F kg =40 kg【思考】【思考提示】 当升降机的加速度方向向下时,此人可举起质量更大的物体,向下的加速度越接近重【说明】 (1(2)物体是处于超重状态还是处于失重状态,与物体的运动速度大小及方向无关,仅与加速度方向【设计意图】 虽然新大纲中不再把超重和失重作为知识点出现,但仍然要求做超重和失重的演示实验,这说明新大纲仍然把超重和失重作为牛顿运动定律的应用,要求学生掌握.通过本例帮助学生进一步理解超[例4]如图3—2—2所示,在倾角θ=37°的足够长的固定的斜面上,有一质量m =1 kg 的物体,物体与斜面间动摩擦因数μ=0.2,物体受到沿平行于斜面向上的轻细线的拉力F =9.6 N 的作用,从静止开始运动,经2 s 绳子突然断了,求绳断后多长时间物体速度大小达到22 m/s .(sin37°=0.6,g =10 m/s 2图3—2—2【解析】 本题为典型的已知物体受力求物体运动情况的动力学问题,物体运动过程较为复杂,应分阶段进行过程分析,并找出各过程的相关量,从而将各过程有机地串接在一起.第一阶段:在最初2 s 内,物体在F =9.6 N 拉力作用下,从静止开始沿斜面做匀加速运动,据受力分析图3—2—3图3—2—3沿斜面方向:F -mg sin θ-Ff =ma 1 沿y 方向:FN =mg cos θ 且Ff =μF Na1=m mg mg F θμθcos sin --=2 m/s 22 s 末绳断时瞬时速度v1=a 1t 1=4 m/s第二阶段:从撤去F 到物体继续沿斜面向上运动到达速度为零的过程,设加速度为a 2则a2=m mg mg )cos sin (θμθ+-=-7.6 m/s 2设从断绳到物体到达最高点所需时间为t2v2=v 1+a 2t 2所以 t 2=210a v -=0.53 s第三阶段:物体从最高点沿斜面下滑,该第三阶段物体加速度为a 3,所需时间为t 3由牛顿第二定律可知:a 3=g sin θ-μg cos θ=4.4 m/s 2,速度达到v 3=22 m/s ,所需时间t 3==-330a v 5 s综上所述:从绳断到速度为22 m/s 所经历的总时间t =t 2+t 3=0.53 s +5 s =5.53 s 【思考】 若本题的问题改为:“绳断后多长时间物体的速度大小为2 m/s ”结果如何?【思考提示】 绳断后物体的速度从4 m/s 减小到2 m/s 所用时间为:t2′=6.742212--=-'a v v s =0.26 s物体的速度减小到零后,又反向增大2 m/s 所用时间为t3′=4.42033=-'a v s =0.45 s t ′=t2+t 3′=0.53 s +0.45 s =0.98 s则从绳断后物体的速度大小达到2 m/s 所用的时间分别为0.26 s 、0.98 s【设计意图】 通过本例培养学生分析综合问题的能力.[例5]如图3—2—4所示,传输带与水平间的倾角为θ=37°,皮带以10 m/s 的速率运行,在传输带上端A 处无初速地放上质量为0.5 kg 的物体,它与传输带间的动摩擦因数为0.5 ,若传输带A 到B 的长度为16 m ,则物体从A 运动到B图3—2—4【解析】 首先判定μ与tan θ的大小关系,μ=0.5,tan θ=0.75,所以物体一定沿传输带对地下滑,不可能对地上滑或对地相对静止.其次皮带运行速度方向未知,而皮带运行速度方向影响物体所受摩擦力方向,所以应分别讨论. 当皮带的上表面以10 m/s 速度向下运行时,刚放上的物体相对皮带有向上的相对速度,物体所受滑动摩擦力方向沿斜坡向下,(如图3—2—5所示)图3—2—5a 1=m mg mg θμθcos sin +=10 m/s2物体赶上皮带对地速度需时间t 1=1a v=1s在t 1ss 1=21a 1t 12=5 ma 2=m mg mg θμθcos sin -=2 m/s2物体以2 m/s 2加速度运行剩下的11 m 位移需时间t2则s 2=v t 2+21a 2t 22即11=10t 2+21×2t 22t 2=1 s (t 2′=-11 s所需总时间t =t 1+t 2=2 s当皮带上表面以10 m/s 速度向上运行时,物体相对于皮带一直具有沿斜面向下的相对速度,物体所受滑动摩擦方向沿斜坡向上且不变,设加速度为a3则a 3=m mg mg θμθcos sin -=2 m/s2物体从传输带顶滑到底所需时间为t则s =21a 3t ′2 ; t ′=216223⨯=a s s =4 s【说明】 本题中物体在本身运动的传送带上的运动,因传输带运动方向的双向性而带来解答结果的多重性.物体所受滑动摩擦力的方向与物体相对于传输带的相对速度方向相反,而对物体进行动力学运算【设计意图】 (1)加深对摩擦力概念的理解;(2)引导学生注意问题的多解性,培养学生严谨、细致、全面的思维品质.【达标训练】【基础练习】1.一物块靠在竖直墙壁上,受到变化规律为F=kt(k>0)的水平外力作用.设物块从t=0时刻起由静止开始沿墙壁竖直下落,物块与墙壁间的摩擦力F随时间的变化图象如图3—2—6图3—2—6A.在0~t1B.在0~t1C.物块的重力大小等于aD.物块受到的最大静摩擦力恒等于b【解析】0~t1内:F增大,则F f增大,竖直方向合力向下且减小,物体做加速度减小的加速运动;t 1~t2内F f大于G,故合力向上,物体做加速度增大的减速运动;t2时刻以后,物体静止,故F f=G=a.【答案】 C2.放在光滑水平面上的物体受三个平行于水平面的共点力作用而处于静止状态,已知F2垂直于F3.若三个力中去掉F1,物体产生的加速度为2.5 m/s2;若去掉F2,物体产生的加速度为1.5 m/s2;若去掉F3,A.1.5 m/s2B.2.0 m/s2C.2.5 m/s2D.4.0 m/s2【解析】由于物体受F1、F2、F3作用而处于静止状态,故三力的合力为零.根据题意画出三个力的示意图如下图所示,去掉F时,F2、F3的合力大小等于F1F1=ma1①去掉F 2时,F1、F3的合力的大小等于F2F2=ma②去掉F 3时,F1、F2的合力的大小等于F3F 3=ma 3 ③又有F3=2221F F -a3=2222215.15.2-=-a a m/s 2=2.0 m/s 2【答案】 B3.如图3—2—7所示,一根轻弹簧的一端系着一个物体,手拉弹簧的另一端,使弹簧和物体一起在图3—2—7A B C D【解析】 当手突然停止运动则F 消失,物体仍受弹簧拉力,故仍加速向右运动;当弹簧恢复原长后,继续被压缩,则物体受弹簧弹力,故减速向右运动.【答案】 C4.如图3—2—8所示,一物体从竖直平面内圆环的最高点A 处由静止开始沿光滑弦轨道AB 下滑至B图3—2—8③只要知道倾角θA .只有① BC .①③D【解析】 设直径为d ,当物体沿与竖直方向成θ角的弦下滑时,加速度a =g cos θ,弦长s =d cos θ所以物体沿弦滑动时间t =gd a s 22=.可见,t 的大小仅由直径d 决定,而与θ无关.【答案】 D5.一间新房即将建成时要封顶,考虑到下雨时落至房项的雨滴能尽快地淌离房顶,要设计好房顶的坡度.设雨滴沿房顶下淌时做无初速度无摩擦的运动,那么,图3—2—9中所示的四种情况中符合要求的图3—2—9【解析】 如下图所示,设斜面底边长为l ,倾角为θa =g sin θs =θcos lt =θθθ2sin 4cos sin 22g l g la s ==由于l 、g 一定,所以当θ=45°时,tt min =gl 4 选项C【答案】 C6.质量为0.8 kg 的物体在一水平面上运动,图3—2—10所示的两条直线分别表示物体受到水平拉力作用和不受拉力作用的v —t 图线.则图线b 与上述的_______状态相符.该物体所受到的拉力是_______N图3—2—10【解析】 由图知,图线b 表示加速运动,图线a 表示减速运动.由图线a 知a 减=1.5 m/s 2,所以摩擦力F f =ma 减=1.2 N .由图线b 知a 加=0.75 m/s 2,因F -F f =ma 加,所以F =ma 加+F f =1.8 N【答案】 受F 拉力作用;1.87.小磁铁A 重10 N ,吸在一块水平放置的固定铁板B 的下面,如图3—2—11所示.要竖直向下将A 拉下来,至少要用15 N 的力,若A 、B 间的动摩擦因数为0.3,现用5 N 的水平力推A 时,A 的加速度大小是______m/s 2.(g =10 m/s 2图3—2—11【解析】 以小磁铁为研究对象,受力分析如下图A 、B 间弹力F N =15 N .F水-μF N =maa =1153.05⨯-=-mF F Nμ水m/s 2=0.5 m/s 2【答案】 0.58.质量为60 kg 的人站在升降机中的台秤上,升降机以2 m/s 的速度竖直下降,此人突然发现台秤的读数变为630 N ,并持续2 s ,求升降机在这2 s 内下降了多少米?(g =10 m/s 2)【解析】 人处于超重状态,升降机的加速度方向向上,它正减速下降,取运动方向为正方向,由牛mg -FN =maa =606301060-⨯=-m F mg N m/s 2=-0.5 m/s 22 svt =v 0+at =2 m/s +(-0.5)×2 m/s =1 m/s升降机在2 s 末正继续下降,它在开始减速下降的2 sh =21220+=+t v v t ×2 m =3 m【答案】 3 m【能力突破】9.在建筑工地上,有六人一起打夯,其中四个人牵绳,绳跟竖直方向成60°角,扶夯的两人用力方向竖直向上.设每人用力F 均为300 N ,每次用力时间为0.2 s ,夯重400 N .求夯上升的高度.又设夯落地时跟地面接触的时间为0.1 s ,求夯每次打击地面所受到的力.(g =10 m/s 2,【解析】 夯加速上升时的加速度为a 12F +4F cos60°-mg =ma 1a1=4040030044-⨯=-m mg F m/s 2=20 m/s 2h1=21a 1t 12=21×20×0.22 m =0.4 mv1=a 1t 1=20×0.2 m/s =4 m/sh 2=10216221⨯=gv m =0.8 mH =h1+h 2=1.2 mv2=2.11022⨯⨯=gH m/s=26m/sa2=1.062=∆∆t v m/s 2=206m/s 2F -mg =maF =m (g +a )=40×(10+206) N=2360 N【答案】 1.2 m ;2360 N10.如图3—2—12所示,在倾角为θ的光滑坡面上放一块上表面粗糙,下表面光滑的木板,木块质量为m 1,质量为m 2的人在木板上应向_____以加速度____奔跑时,可使木板不动.图3—2—12【解析】 因木板有下滑的趋势,故人对木板的摩擦力应沿斜面向上,即人应沿斜面向下奔跑.对木板进行受力分析知,人对木板的摩擦力应为m 1g sin θ.以人为研究对象,人所受的合力为:m 1g sin θ+m 2g sin θ,利用牛顿第二定律:F 合=ma 得m 1g sin θ+m 2g sin θ=m 2a ,可得a =221m m m +g sin θ【答案】 沿斜面向下;221m m m +g sin θ11.滑雪运动员依靠手中的撑杆用力往后推地,获得向前的动力.一运动员的质量是60 kg ,撑杆对地面向后的平均作用力是300 N ,力的持续作用时间是0.4 s ,两次用力之间的间隔时间是0.2 s ,不计摩擦阻力.若运动员从静止开始做直线运动,求6 s 内的位移是多少?【解析】a =60300=m F m/s 2=5 m/s 2第一个0.4 ss1=21at 2=21×5×0.42 m =0.4 m第一个0.2 ss 1′=at ·t ′=5×0.4×0.2 m =0.4 m 第二个0.4 s ,运动员的位移是:s2=at ·t +21a ·t 2=5×0.42 m +21×5×0.42 m=1.2 m =3s1第二个0.2 ss 2′=a ·2t ·t ′=0.8 m =2s 1 第三个0.4 ss3=a ·2t ·t +21a ·t 2=5s 1第三个0.2 ss 2′=a ·3t ·t ′=3s 1┇6 s 内共有10个0.6 ss =s 1+3s 1+…+19s 1+1s 1′+2s 1′+…10s 1′=62 m【答案】 62 m12.如图3—2—13所示,在倾角为θ的光滑斜面上端系一劲度系数为k 的轻弹簧,弹簧下端连有一质量为m 的小球,球被一垂直于斜面的挡板A 挡住,此时弹簧没有形变.若手持挡板A 以加速度a (a <g sin θ图3—2—13(1(2【解析】 (1mg sin θ-kx =max =k a g m )sin (-θ当x =21at 2得从挡板开始运动到球与挡板分离所经历的时间为t =kaa g m a x )sin (22-=θ(2kx ′=mg sin θx ′=k mg θsin【答案】 (1)ak )a sin g (m 2-θ(2)k mg θsin※13.据报道,1989年在美国加利福尼亚州发生的6.9级地震,中断了该地尼米兹高速公路的一段,致使公路上高速行驶的约200辆汽车发生了重大的交通事故,车里的人大部分当即死亡,只有部分系安全带的人幸免.假设汽车高速行驶的速度达到108 km/h ,乘客的质量为60 kg ,当汽车遇到紧急情况时,在2s【解析】 刹车时汽车的加速度大小为a =230=∆t v m/s 2=15 m/s 2F =ma =60×15 N =900 N【答案】 使人随汽车刹车做减速运动的力的大小为900 N ,这个力只有靠安全带提供,否则,人将由于惯性而发生事故.※14.如图3—2—14所示,质量相同的木块A 、B 用轻弹簧连接置于光滑的水平面上,开始弹簧处于自然状态.现用水平恒力F 推木块A ,则从开始到弹簧第一次被图3—2—14①两木块速度相同时,加速度aA =aB ②两木块速度相同时,加速度aA <aB ③两木块加速度相同时,速度vA <vB ④两木块加速度相同时,速度vA >v BA .只有② BC .①③D【解析】 在弹簧第一次压缩到最短的过程中,A 做加速度逐渐减小的加速运动,B 做加速度逐渐增大的加速运动,在a A =a B 之前a A >a B ,故经过相等的时间,A 增加的速度大,B 增加的速度小,所以,在a A =a B 时v A >v B ,④正确.当v A =v B 时,弹簧的压缩量最大,弹力最大,设为F m ,若F >F m ,则A 在此之前一直做加速度逐渐减小的加速运动,B 做加速度逐渐增大的加速运动,由于a A =a B 时v A >v B ,所以v A=v B 时a A <a B ;若F <F m 时,则a A =m Fa m F F B mm ,=-,虽然a A <a B .总之,在v A =v B 时,a A <a B ,②正确.所以D【答案】 D※15.某市规定卡车在市区一特殊路段的速度不得超过36 km/h ,有一辆卡车在危急情况下紧急刹车,车轮抱死滑动一段距离后停止.交警测得刹车过程中车轮在路面上擦过的笔直痕迹长9 m ,从厂家的技术手册中查得该车轮胎和地面的动摩擦因数是0.8.(1)假若你就是这位交警,请你判断卡车是否超速行驶?(2)减小刹车距离是避免交通事故的最有效的途径,刹车距离除与汽车的初速度、制动力有关外,还须考虑驾驶员的反应时间:即从发现情况到肌肉动作操纵制动器的时间.假设汽车刹车制动力是定值F ,驾驶员的反应时间为t0,汽车的质量为m ,行驶的速度为v 0.请你推导出刹车距离s【解析】 (1)急刹车时汽车做减速运动的加速度为a =mmg μ=μg =8 m/s 2v0=9822⨯⨯=as m/s =12 m/s >36 km/h(2a =mFs 1=F mv av 22220=s2=v 0t 0s =s 1+s 2=v 0t 0+Fm v 22【答案】 (1)违犯规定超速行驶;(2)s =v 0t 0+Fmv 22※16.法国人劳伦特·菲舍尔在澳大利亚伯斯的冒险世界进行了超高空特技跳水表演,他从30 m 高的塔上跳下准确地落入水池中.已知水对他的阻力(包括浮力)是他重力的3.5倍,他在空中时空气对他的阻力是他重力的0.2倍,试计算需要准备一个至少多深的水池?(g =10 m/s 2)【解析】a 1=m mgmg 2.0-=0.8 g =8 m/sv =304m/s 3082211=⨯⨯=h am/sa 2=m mg mg -5.3=2.5 g =25 m/s2h 2=252480222⨯=a v m =9.6 m即水池的深度至少为9.6 m .【答案】 9.6 m※17.如图3—2—15所示,一辆长L =2 m ,高h =0.8 m ,质量为M =12 kg 的平顶车,车顶光滑,在牵引力为零时,仍在向前运动,车与路面间的动摩擦因数μ=0.2,当车速为v 0=7 m/s 时,把一个质量为m =1 kg 的物块(视为质点)轻轻放在车顶的前端.问物块落地时,落地点距车前端多远?(重力加速g 取10 m/s 2)图3—2—15【解析】 由于m 与M 无摩擦,所以开始m 在车上静止,离开车后做自由落体运动,放上m 后地面对M 的摩擦力F 1=μ(m +M )g ,则Ma 1=)1(1M m g mF +=μ=0.3×10×)1211(+m/s 2=3.25 m/s 2 ①m 离开M 前,M 做减速运动,位移s 1=L ,设m 即将落地时车速度为v ,则由运动学公式v 02-v 2=2a 1L,v =L a v 1202-=6 m/s②物块m 下落时间t =108.022⨯=g h s =0.4 sm 离开M 后,M 的加速度a2=g M Mg M F μμ==2=3 m/s 2在0.4 ss2=v t -21a 2t 2=6×0.4 m -21×3×0.42 m =2.16 ms =s2+L =2.16 m +2 m =4.16 m【答案】 4.16 m。
第四章 6超重与失重

第四章 6 超重与失重问题站在体重计上向下蹲,你会发现,在下蹲的过程中,体重计的示数先变小,后变大,再变小。
当人静止后,保持某一数值不变。
这是为什么呢?重力的测量在地球表面附近,物体由于地球的吸引而受到重力。
测量重力常用两种方法:一种方法是,先测量物体做自由落体运动的加速度g ,再用天平测量物体的质量,利用牛顿第二定律可得G=mg另一种方法是,利用力的平衡条件对重力进行测量。
将待测物体悬挂或放置在测力计上,使它处于静止状态。
这时物体所受的重力和测力计对物体的拉力或支持力的大小相等,测力计的示数反映了物体所受的重力大小。
这是测量重力最常用的方法。
超重和失重人站在体重计上向下蹲的过程中,为什么体重计的示数会变化呢?体重计的示数称为视重,反映了人对体重计的压力。
根据牛顿第三定律,人对体重计的压力与体重计对人的支持力F N大小相等,方向相反。
如图4.6-1,选取人为研究对象。
人体受到重力mg和体重计对人的支持力F N,这两个力的共同作用使人在下蹲的过程中,先后经历加速、减速和静止三个阶段。
设竖直向下方向为坐标轴正方向。
mgF Nv 图4.6-1人加速向下运动的过程中(图4.6-2),根据牛顿第二定律,有mg -F N =maF N =m (g -a )< mg即体重计的示数所反映的视重(力)小于人所受的重力。
物体对支持物的压力(或对悬挂物的拉力)小于物体所受重力的现象,叫作失重(weightlessness )现象。
同理,人减速向下运动的过程中(图4.6-3),加速度方向与运动方向相反,有mg -F N =-maF N =m (g +a )>mg此时,体重计的示数大于人受到的重力。
物体对支持物的压力(或对悬挂物的拉力)大于物体所受重力的现象,叫作超重(overweight )现象。
当人相对于体重计静止不动时,有F N =mg 思考与讨论人站在力传感器上完成下蹲动作。
观察计算机采集的图线。
图4.6-4呈现的是某人下蹲过程中力传感器的示数随时间变化的情况。
届高考物理一轮复习 两类动力学问题 超重和失重(人教版)精品PPT课件

解析:松手前铸件做匀加速直线运动,设 加速度为a Fcos37°-f=ma① Fsin37°+FN-mg=0② f=μFN③ 解得 a=0.35 m/s2 4 s末速度 v0=at=1.4 m/s④ 松手后减速加速度的大小设为a′
2
题型二 已知物体的运动情况,确定物 体的受力情况
[例2] 升降机由静止开始上升,开始2 s 内匀加速上升8 m,以后3 s内做匀速运动 ,最后2 s内做匀减速运动,速度减小到 零.升降机内有一质量为250 kg的重物, 求整个上升过程中重物对升降机底板的压 力,并作出升降机运动的v-t图象和重物 对底板压力的F-t图象.(g取10 m/s2)
竖直向上.
根据牛顿第三定律得重物对升降机底板的 压力大小为:
FN1′=FN1=3500 N,方向竖直向下 中间3 s内物体匀速上升,由平衡条件得:
FN2=mg=250×10 N=2500 N FN2′=FN2=2500 N,方向竖直向下 物体的速度为:v2=v1=8 m/s 最后2 s内重物随升降机一起做匀减速运动
[解析] 在前 Biblioteka s 内升降机做匀加速运动,设其加速度为
a1,由匀变速运动的位移公式 x=12a1t12 解得加速度为:a1=2t12x=2× 22 8 m/s2=4 m/s2 2 s 末的速度为:v1=a1t1=4×2 m/s=8 m/s 根据牛顿第二定律得:FN1-mg=ma1 FN1=mg+ma1=250×10 N+250×4 N=3500 N,方向
两类动力学问题
超重和失重
考点一 动力学的两类基本问题
►基础梳理◄
运用牛顿运动定律解决的动力学问题常常 可以分为两种类型,即动力学的两类基本 问题.
(1)已知物体的受力情况,求物体的运动 情况
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四讲两类动力学问题超重和失重基础知识归纳1、超重与失重和完全失重(1)实重和视重①实重:物体实际所受的重力,它与物体的运动状态无关.②视重:当物体挂在弹簧测力计下或放在水平台秤上时,弹簧测力计或台秤的_示数称为视重,视重的大小等于弹簧测力计所受物体的_ 拉力_或台秤所受物体的压力。
(2)超重、失重和完全失重的比较现象实质超重物体对支持物的压力或对悬挂物的拉力大于自身重力的现象系统具有竖直向上的加速度或加速度有竖直向上的分量失重物体对支持物的压力或对悬挂物的拉力小于自身重力的现象系统具有竖直向下的加速度或加速度有竖直向下的分量完全失重物体对支持物的压力或对悬挂物的拉力等于零的现象系统具有竖直向下的加速度,且a=g①当物体处于超重和失重状态时,物体所受的重力并没有变化.②物体是否处于超重或失重状态,不在于物体向上运动还是向下运动,而是取决于加速度方向是向上还是向下.③当物体处于完全失重状态时,重力只产生使物体具有a=g的加速度效果,不再产生其他效果.④处于超重和失重状态下的液体浮力公式分别为F浮=ρV排(g+a)或F浮=ρV排(g-a),处于完全失重状态下的液体F浮=0,即液体对浸在液体中的物体不再产生浮力.2、连接体问题(1)连接体两个或两个以上存在相互作用或有一定关联的物体系统称为连接体,在我们运用牛顿运动定律解答力学问题中常会遇到.(2)解连接体问题的基本方法整体法:把两个或两个以上相互连接的物体看成一个整体,此时不必考虑物体之间的内力.隔离法:当求物体之间的作用力时,就需要将各个物体隔离出来单独分析.解决实际问题时,将隔离法和整体法交叉使用,有分有合,灵活处理.(3)整体法和隔离法的应用①解答问题时,不能把整体法和隔离法对立起来,而应该把这两种方法结合起来,从具体问题的实际情况出发,灵活选取对象,恰当地选择使用隔离法和整体法.②在使用隔离法解题时,所选取的隔离对象可以是连接体中的某一个物体,也可以是连接体中的某部分物体(包含两个或两个以上的单个物体),而这“某一部分”的选取,也应根据问题的实际情况,灵活处理.③在选用整体法和隔离法时,可依据所求的力进行选择,若为外力则应用整体法;若所求力为内力则用隔离法.但在具体应用时,绝大多数的题目要求两种方法结合应用,且应用顺序也较为固定,即求外力时,先隔离后整体;求内力时,先整体后隔离.先整体或先隔离的目的都是为了求解共同的加速度.3、整体运用牛顿第二定律应用牛顿第二定律时,若研究对象为一物体系统,可将系统的所有外力及系统内每一物体的加速度均沿互相垂直的两个方向分解,则牛顿第二定律的系统表达式为:ΣF x=m1a1x+m2a2x+…+m n a nxΣF y=m1a1y+m2a2y+…+m n a ny应用牛顿第二定律的系统表达式解题时,可不考虑系统内物体间的相互作用力(即内力),这样能达到简化求解的目的,但需把握三个关键点:(1)正确分析系统受到的外力;(2)正确分析系统内各物体加速度的大小和方向;(3)确定正方向,建立直角坐标系,并列方程进行求解.【例1】在升降电梯内的地面上放一体重计,电梯静止时,晓敏同学站在体重计上,体重计示数为50 kg,电梯运动过程中,某一段时间内晓敏同学发现体重计示数如图所示,在这段时间内下列说法中正确的是()A.晓敏同学所受的重力变小了B.晓敏对体重计的压力小于体重计对晓敏的支持力C.电梯一定在竖直向下运动D.电梯的加速度大小为g/5,方向一定竖直向下【练习1】在箱式电梯里的台秤秤盘上放着一物体,在电梯运动过程中,某人在不同时刻拍了甲、乙和丙三张照片,如图所示,乙图为电梯匀速运动的照片。
从这三张照片可判定()A.拍摄甲照片时,电梯一定处于加速下降状态B.拍摄丙照片时,电梯一定处于减速上升状态C.拍摄丙照片时,电梯可能处于加速上升状态D.拍摄甲照片时,电梯可能处于减速下降状态【练习2】如图所示,小球的密度小于杯中水的密度,弹簧两端分别固定在杯底和小球上.静止时弹簧伸长Δx.若全套装置自由下落,则在下落过程中弹簧的伸长量将( ) A.仍为ΔxB.大于ΔxC.小于Δx,大于零D.等于零【例2】如图所示,箱子的质量M=5.0kg,与水平地面的动摩擦因数μ=0.22。
在箱子顶板处系一细线,悬挂一个质量m=1.0kg的小球,箱子受到水平恒力F的作用,使小球的悬线偏离竖直方向θ=30°角,则F应为多少?(g=10m/s2)【练习3】同种材料的a、b两物体的质量分别为m1、m2,由轻质弹簧相连。
当用大小为F的恒力竖直向上拉着a,使a、b一起向上做匀加速直线运动时,弹簧伸长量为x1,如图(甲)所示;当用大小仍为F的恒力沿水平方向拉着a,使a、b一起沿水平桌面做匀加速直线运动时,弹簧伸长量为x2,如图(乙)所示,则()A.x1一定等于x2B.x1一定大于x2C.若m1>m2,则x1>x2D.若m1<m2,则x1<x2【练习4】在北京残奥会开幕式上运动员手拉绳索向上攀登,最终点燃了主火炬,体现了残疾运动员坚韧不拔的意志和自强不息的精神.为了探求上升过程中运动员与绳索和吊椅间的作用,可将过程简化.一根不可伸缩的轻绳跨过轻质的定滑轮,一端挂一吊椅,另一端被坐在吊椅上的运动员拉住,如图所示.设运动员的质量为65 kg,吊椅的质量为15 kg,不计定滑轮与绳子间的摩擦,重力加速度取g=10 m/s2.当运动员与吊椅一起正以加速度a=1m/s2上升时,试求:(1)运动员竖直向下拉绳的力;(2)运动员对吊椅的压力.【例3】如图所示,小球B放在真空容器A内,球B的直径恰好等于正方体A的边长,将它们以初速度v0竖直向上抛出,下列说法中正确的是()A.若不计空气阻力,上升过程中,A对B有向上的支持力B.若考虑空气阻力,上升过程中,A对B的压力向下C.若考虑空气阻力,下落过程中,B对A的压力向上D.若不计空气阻力,下落过程中,B对A没有压力【练习5】如图所示,带有长方体盒子的斜劈A放在固定的斜面体C的斜面上,在盒子内放有光滑球B,B恰与盒子前、后壁P、Q点相接触.若使斜劈A在斜面体C上静止不动,则P、Q对球B无压力.以下说法正确的是()A.若C的斜面光滑,斜劈A由静止释放,则P点对球B有压力B.若C的斜面光滑,斜劈A以一定的初速度沿斜面向上滑行,则P、Q对球B均无压力C.若C的斜面粗糙,斜劈A沿斜面匀速下滑,则P、Q对球B均无压力D.若C的斜面粗糙,斜劈A沿斜面加速下滑,则Q点对球B有压力【例4】如图所示,质量为M的木板可沿倾角为θ的光滑斜面下滑,木板上站着一个质量为m的人,问(1)为了保持木板与斜面相对静止,计算人运动的加速度?(2)为了保持人与斜面相对静止,木板运动的加速度是多少?【练习6】如图所示,一个质量为M 、倾角为30°的光滑斜面体放在粗糙水平桌面上,质量为m 的小木块从斜面顶端无初速度滑下的过程中,斜面体静止不动.则下列关于此斜面体对水平桌面压力F N 的大小和桌面对斜面体摩擦力F f 的说法正确的( )A .F N =Mg +mgB .F N =Mg +43mg C .F f 方向向左,大小为23mg D .F f 方向向左,大小为43mg 【练习7】如图所示,倾角α=30°、质量M =34 kg 的斜面体始终停在粗糙的水平地面上,质量m A =14 kg 、m B =2 kg 的物体A 和B ,由细线通过定滑轮连接.若A 以a =2.5 m/s 2的加速度沿斜面下滑,求此过程中地面对斜面体的摩擦力和支持力各是多少?课后作业:1.如图所示,小芳在体重计上完成下蹲动作,下列F -t 图像能反应体重计示数随时间变化的是A B C D2.汶川大地震后,为解决灾区群众的生活问题,党和国家派出大量直升机空投救灾物资.有一直升机悬停在空中向地面投放装有物资的箱子,如图3-2-10所示.设投放初速度为零,箱子所受的空气阻力与箱子下落速度的平方成正比,且运动过程中箱子始终保持图示姿态.在箱子下落过程中,下列说法正确的是( ) A .箱内物体对箱子底部始终没有压力 B .箱子刚投下时,箱内物体受到的支持力最大C .箱子接近地面时,箱内物体受到的支持力比刚投下时大D .若下落距离足够长,箱内物体有可能不受底部支持力而“飘起来”3.为了节省能量,某商场安装了智能化的电动扶梯。
无人乘行时,扶梯运转得很慢;有人站上扶梯时,它会先慢慢加速,再匀速运转。
一顾客乘扶梯上楼,恰好经历了这两个过程,如图所示。
那么下列说法中正确的是( )A. 顾客始终受到三个力的作用B. 顾客始终处于超重状态C. 顾客对扶梯作用力的方向先指向左下方,再竖直向下D. 顾客对扶梯作用的方向先指向右下方,再竖直向下4.原来做匀速运动的升降机内有一被伸长弹簧拉住的具有一定质量的物体A 静止在地板上,如图所示,现在发现A 突然被弹簧拉向右方,由此可判断,此时升降机的运动可能是( )A .加速上升B .减速上升C .加速下降D .减速下降5.如图所示是某同学站在力板传感器上做下蹲-起立的动作时记录的压力F 随时间t 变化的图线。
由图线可知该同学( )A .体重约为650 NB .做了两次下蹲-起立的动作C .做了一次下蹲-起立的动作,且下蹲后约2 s 起立D .下蹲过程中先处于超重状态后处于失重状态6.如图所示,质量分别为m 1、m 2的两个物体通过轻弹簧连接,在力F 的作用下一起沿水平方向做匀加速直线运动(m 1在光滑地面上,m 2在空中)。
已知力F 与水平方向的夹角为θ。
则m 1的加速度大小为( )A .F cos θm 1+m 2B .F sin θm 1+m 2C .F cos θm 1D .F sin θm 27.如图所示为杂技“顶竿”表演,一人站在地上,肩上扛一质量为M 的竖直竹竿,当竿上一质量为m 的人以加速度a 加速下滑时,竿对“底人”的压力大小为( )A .(M +m )gB .(M +m )g -maC .(M +m )g +maD .(M -m )g8.质量为M 的光滑圆槽放在光滑水平面上,一水平恒力F 作用在其上促使质量为m 的小球静止在圆槽上,如图所示,则( )MmA .小球对圆槽的压力为MFm +MB .小球对圆槽的压力为mFm +MC .水平恒力F 变大后,如果小球仍静止在圆槽上,小球对圆槽的压力增加D .水平恒力F 变大后,如果小球仍静止在圆槽上,小球对圆槽的压力减小9.如图所示,质量分别为M 、m 的滑块A 、B 叠放在固定的、倾角为θ的斜面上,A 与斜面间、A 与B 之间的动摩擦因数分别为μ1,μ2,当A 、B 从静止开始以相同的加速度下滑时,B 受到摩擦力( )A .等于零B .方向平行于斜面向上C .大小为μ1mgcosθD .大小为μ2mgcosθ10.如图所示,有材料相同的P 、Q 两物块通过轻绳相连,并在拉力F 作用下沿斜面向上运动,轻绳与拉力F 的方向均平行于斜面。
