均值比较与T检验实验报告
实验五 均值比较与T检验

实验五均值比较与T检验⏹均值(Means)过程对准备比较的各组计算描述指标,进行预分析,也可直接比较。
⏹单样本T检验(One-Samples T Test)过程进行样本均值与已知总体均值的比较。
⏹独立样本T检验(Independent-Samples T Test)过程进行两独立样本均值差别的比较,即通常所说的两组资料的t检验。
⏹配对样本(Paired-Samples T Test)过程进行配对资料的显著性检验,即配对t检验。
⏹单因素方差分析(One-Way ANOVA)过程进行两组及多组样本均值的比较,即成组设计的方差分析,还可进行随后的两两比较,详情请参见单因素方差分析。
预备知识:假设检验的步骤:⏹第一步,根据问题要求提出原假设(Null hypothesis)和备选假设(Alternative hypothesis);⏹第二步,确定适当的检验统计量及相应的抽样分布;⏹第三步,计算检验统计量观测值的发生概率;⏹第四步,给定显著性水平并作出统计决策。
第二步和第三步由SPSS自动完成。
假设检验中的P值⏹P值(P-value)是指在原假设为真时,所得到的样本观察结果或更极端结果的概率,即样本统计量落在观察值以外的概率。
⏹根据“小概率原理”,如果P值非常小,就有理由拒绝原假设,且P值越小,拒绝的理由就越充分。
⏹实际应用中,多数统计软件直接给出P值,其检验判断规则如下(双侧检验):⏹若P值<a,则拒绝原假设;⏹若P值≥ a ,则不能拒绝原假设。
均值比较中原假设H0:μ=μ0(即某一特定值)(适用于单样本情形)或 H0:μ1=μ2。
(适用于两独立样本情形)一、Means(均值)过程选择:分析Analyze==>均值比较Compare Means ==>均值means;1、基本功能分组计算、比较指定变量的描述统计量,还可以给出方差分析表和线性检验结果表。
优点各组的描述指标被放在一起便于相互比较,如果需要还可以直接输出比较结果,无须再次调用其他过程。
均值验证实验报告(3篇)

第1篇一、实验目的1. 理解均值验证在统计学中的意义和应用。
2. 掌握均值验证的基本方法和步骤。
3. 提高对实际数据进行统计分析的能力。
二、实验背景在统计学中,均值是衡量一组数据集中趋势的重要指标。
均值验证是对均值进行假设检验的过程,旨在判断均值是否与某一特定值相等。
本实验通过实际数据的均值验证,验证均值假设的合理性。
三、实验材料1. 实验数据:某班级50名学生的语文成绩。
2. 统计软件:SPSS、Python等。
四、实验方法1. 提取数据:将班级50名学生的语文成绩数据整理成表格形式。
2. 假设检验:假设班级学生的语文成绩均值为70分。
3. 统计分析:利用SPSS或Python进行均值验证。
五、实验步骤1. 数据输入:将班级学生的语文成绩数据输入SPSS或Python。
2. 描述性统计:计算班级学生的语文成绩均值。
3. 均值验证:a. 建立假设:H0:μ = 70,H1:μ ≠ 70(其中μ为班级学生的语文成绩均值)。
b. 确定显著性水平:α = 0.05。
c. 查找t分布表:根据自由度和显著性水平,查找t分布表得到t临界值。
d. 计算t值:根据实际数据计算t值。
e. 比较t值与t临界值:若t值大于t临界值,则拒绝原假设,认为班级学生的语文成绩均值与70分存在显著差异;若t值小于t临界值,则接受原假设,认为班级学生的语文成绩均值与70分无显著差异。
4. 结果分析:根据实验结果,判断班级学生的语文成绩均值是否与70分存在显著差异。
六、实验结果与分析1. 描述性统计结果:班级学生的语文成绩均值为65分。
2. 均值验证结果:a. 假设检验的t值为2.35。
b. 查找t分布表,得到自由度为49,显著性水平为0.05的t临界值为±1.677。
c. 由于t值(2.35)大于t临界值(±1.677),故拒绝原假设,认为班级学生的语文成绩均值与70分存在显著差异。
3. 结果分析:实验结果表明,班级学生的语文成绩均值与70分存在显著差异,说明班级学生的语文成绩整体低于70分。
均值与T检验

假设检验的SPSS操作
均值比较和T检验
4.1
Means过程 Means过程 单一样本T检验 单一样本T 两独立样本T 两独立样本T检验 两配对样本T 两配对样本T检验
• 两配对样本T检验的前提要求如下。 两配对样本T检验的前提要求如下。 • 两个样本应是配对的。在应用领域中, 两个样本应是配对的。在应用领域中, 主要的配对资料包括:具有年龄、性别、 主要的配对资料包括:具有年龄、性别、 体重、病况等非处理因素相同或相似者。 体重、病况等非处理因素相同或相似者。 首先两个样本的观察数目相同, 首先两个样本的观察数目相同,其次两样 本的观察值顺序不能随意改变。 本的观察值顺序不能随意改变。 • 样本来自的两个总体应服从正态分布。 样本来自的两个总体应服从正态分布。
• 研究问题 • 计算减肥前后是否有显著变化。数据为 计算减肥前后是否有பைடு நூலகம்著变化。 减肥茶检验_两配对样本t检验” “减肥茶检验_两配对样本t检验” • 研究一个班同学在参加了暑期数学、化学 研究一个班同学在参加了暑期数学、 培训班后,学习成绩是否有显著变化。 培训班后,学习成绩是否有显著变化。
小 结
• 两配对样本T检验的零假设H0为两总体均值 两配对样本T检验的零假设H 之间不存在显著差异。 之间不存在显著差异。 • 首先求出每对观察值的差值, 首先求出每对观察值的差值,得到差 值序列;然后对差值求均值; 值序列;然后对差值求均值;最后检验差 值序列的均值, 值序列的均值,即平均差是否与零有显著 差异。如果平均差和零有显著差异, 差异。如果平均差和零有显著差异,则认 为两总体均值间存在显著差异;否则, 为两总体均值间存在显著差异;否则,认 为两总体均值间不存在显著差异。 为两总体均值间不存在显著差异。
均值比较与T检验实验报告

实训的心得与体会
统计学中经常通过样本来分析总体,即从样本的观察或实验结果的特征来对总体的特征进行估计和推断。
本次实验使用spass软件来进行均值比较与T检验,假设检验是对给定的总体参数值,利用样本数据对其推断,并给出接受或是拒绝的过程,另外,在具体操作中,首先定义所谓的小概率,一般取或,即显著性水平。
显著性水平取得太小,容易发生为错误;取得太大,则容易发生弃真错误。
通过本次实验用spass统计分析软件来进行均值比较及T检验后,感觉统计学中的很多问题不再像以前那么陌生了,同时也感觉统计学不再是想象中那么困难,之前学习统计学最怕的就是对数据进行求解与分析,现在使用这款软件后,让我从之前对统计学的陌生转变为熟悉,从此,在解决统计方面的问题又多了一项解决的工具:spss。
5均数差别比较的t检验

样本均数间的差别原因均数差别比较的 t检验总体均数不同 总体均数相同,差别仅仅由抽样误 差引起 推断方法:计算某个统计量(如t 值),然后根据相应的概率作出推 断t检验(student’s t test)t检验优点:用于样本含量较小,并 且总体标准差σ未知时 三种t检验样本均数 X 与已知某总体均数μ0 的比较; 两组样本均数 X 1 与 X 2 的比较; 配对设计资料均数的比较。
t检验的应用条件当样本含量较小时(n<60),理论上要求样 本为来自正态分布总体的随机样本; 当做两样本均数比较时,还要求两总体 方差相等(方差齐性,即 σ12=σ22)。
在实际工作中,若上述条件略有偏离, 仍可进行t检验分析。
一、样本均数和总体均数比较的t检验 (one sample t test) 目的:推断样本所代表的未知总体 均数μ与已知总体均数μ0有无差 别。
已知的总体均数μ0一般为理论值、 标准值或经过大量观察所得的稳定 值等。
条件:当n较小时,要求样本来自于 正态分布总体假设检验的独特逻辑例 : 某病患者20人,其血沉 (mm/h)均数 为9.15,标准差为2.13,问是否该病患 者血沉与以往文献报道的均数10.50有差 别?X ± t0.05 / 2,19 s / n= 9.15 ± 2.093 × 2.13 / 20 = (8.15,10.15)11.两个假设,决策者在其中作出抉择 该病患者血沉总体均数与10.50无差别, 该病患者血沉总体均数与10.50有差别。
简写 H0:μ=10.50 H1:μ≠10.50 单凭一份样本不可能证明哪一个正确, 一般利用小概率反证法思想,从问题的 对立面出发(H0)间接判断要解决的问题 (H1)是否成立。
H0:μ=10.50H1:μ≠10.50μ = 10.50X10.50μX2. H0成立时会怎样? 所得t值因样本而 异,但其绝对值多数情况下落在0附近。
统计学两样本均数比较的t检验

处理方式
对于异常值,可以采用删除、替换或用中位数修正等方式进行处理。具体处理方式应根 据实际情况和数据分布特点进行选择,并确保处理后的数据仍然能够反映总体情况。
实验设计和伦理考虑
实验设计
在进行t检验之前,应进行充分的实验设计, 确保实验的合理性和科学性。实验设计应考 虑各种因素对实验结果的影响,并尽量减小 误差和干扰因素。
确定p值:根据t统计量和自由 度,查表或使用统计软件计算 p值。
步骤1
收集数据:分别从两个独立样 本中收集数据,并记录在表格 中。
步骤3
计算t统计量:根据两组样本的 均数和标准差,计算t统计量。
步骤5
结果解读:根据p值判断两组 样本均数之间的差异是否具有 统计学上的显著性。
结果解读
• 结果解读:根据p值的大小来判断两 组样本均数之间的差异是否具有统计 学上的显著性。通常,如果p值小于 0.05,则认为两组样本均数之间存在 显著差异;如果p值大于0.05,则认 为两组样本均数之间无显著差异。
对差值数据进行描述性统计分析, 计算差值的均值和标准差。
计算t统计量
根据差值的均值、标准差以及自 由度,计算t统计量。
收集两个配对样本的数据
确保两个样本具有相同的样本量, 且每个样本中的数值都是配对的。
判断显著性
பைடு நூலகம்根据t分布表或使用统计软件,查 找对应的p值,判断两个配对样本 均数是否存在显著差异。
结果解读
伦理考虑
在实验设计过程中,还应考虑伦理问题。应 尊重受试者的权益和尊严,确保受试者的安 全和隐私。同时,应遵循国际公认的伦理准 则和法律法规,如《赫尔辛基宣言》等。
06 案例分析
SPSS统计分析均值比较与T检验

在研究人体各部位体温是否有差别,一个人 的两个部位的温度构成一对数据。测量若干 人的同样两个部位的温度数据,可以比较这 两个部位平均温度是否有显著性差异。使用 配对t检验。
Confidence interval:95%:置信区间项,可以自定义。 Missing Values:选择对缺失值的处理方法 Exclude cases analysis by analysis:带有缺失值的观测值当它 与分析有关时才被剔除; Exclude cases listwise:剔除所有列在Test、Grouping矩形框 中的变量带缺失值的项
例题一
现有银行雇员工资为例,检验男女雇员现工 资是否有显著差异。一个是要比较salary变量 的均值,另一个是gender变量作为分水平变 量。 (data09--03) 。
分析变量的简单描述性统计量
Gender Current Salary Male
F emale
Group Statistics
以27个学生的身高为例说明操作步骤 (data11-01)
变量no编号,sex性别,age年龄,h身高,w 体重。
ANOVA table and eta:输出第一层控制变量给出的方差分析表和eta统计值η和 η2 。 η统计量表明因变量和自变量之间联系的强度。 η2 是组间平方和与总平 方和之比。
进行配对样本的T检验要求被比较的两个样 本有配对关系。要求两个样本均来自正态总 体。而且均值是对于检验有意义的描述统计 量。均值的配对比较是比较常见(见以下几 个例子)。
同一窝实验用白鼠按性别、体重相同的配对, 再随机分到实验组和对照组,分别喂加入海 藻的饲料和普通饲料,三个月后,分别将每 对白鼠置于水中,测量其到溺死前的游泳时 间。比较两组白鼠游泳时间均值,从而比较 两种饲料对抗疲劳的作用。
SPSS实验报告——均值比较
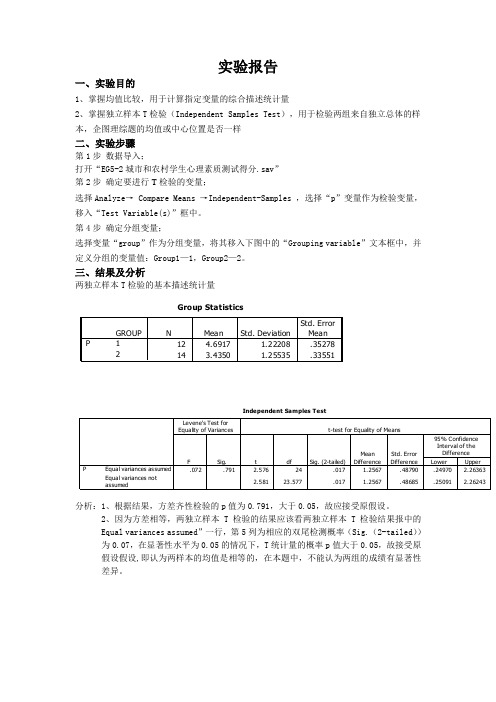
实验报告一、实验目的1、掌握均值比较,用于计算指定变量的综合描述统计量2、掌握独立样本T 检验(Independent Samples Test ),用于检验两组来自独立总体的样本,企图理综题的均值或中心位置是否一样二、实验步骤第1步 数据导入;打开“EG5-2城市和农村学生心理素质测试得分.sav ” 第2步 确定要进行T 检验的变量;选择Analyze → Compare Means →Independent-Samples ,选择“p ”变量作为检验变量,移入“Test Variable(s)”框中。
第4步 确定分组变量;选择变量“group ”作为分组变量,将其移入下图中的“Grouping variable ”文本框中,并定义分组的变量值:Group1—1,Group2—2。
三、结果及分析两独立样本T 检验的基本描述统计量Group Statistics12 4.6917 1.22208.35278143.43501.25535.33551GROUP12PNMean Std. DeviationStd. Error MeanIndependent Samples Test.072.791 2.57624.0171.2567.48790.24970 2.263632.58123.577.0171.2567.48685.250912.26243Equal variances assumedEqual variances not assumedPFSig.Levene's Test for Equality of VariancestdfSig. (2-tailed)Mean DifferenceStd. Error DifferenceLower Upper 95% Confidence Interval of the Difference t-test for Equality of Means分析:1、根据结果,方差齐性检验的p 值为0.791,大于0.05,故应接受原假设。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实训的心得与体会
统计学中经常通过样本来分析总体,即从样本的观察或实验结果的特征来对总体的特征进行估计和推断。
本次实验使用spass软件来进行均值比较与T检验,假设检验是对给定的总体参数值,利用样本数据对其推断,并给出接受或是拒绝的过程,另外,在具体操作中,首先定义所谓的小概率,一般取或,即显着性水平。
显着性水平取得太小,容易发生为错误;取得太大,则容易发生弃真错误。
通过本次实验用spass统计分析软件来进行均值比较及T检验后,感觉统计学中的很多问题不再像以前那么陌生了,同时也感觉统计学不再是想象中那么困难,之前学习统计学最怕的就是对数据进行求解与分析,现在使用这款软件后,让我从之前对统计学的陌生转变为熟悉,从此,在解决统计方面的问题又多了一项解决的工具:spss。
