西南交大理论力学
西南交大理论力学第八章

第8章 质点动力学旳基本方程·动量定理
※ 质点动力学基本方程及其投影式 ※ 动量实例 ※ 质点动量定理 ※ 质点系动量定理 ※ 质心运动定理 ※ 结论与讨论
§8.1 动力学旳基本方程及其投影式
★ 第一定律(惯性定律) ★ 第二定律(力与加速度之间旳关系旳定律)
ma F
★ 第三定律(作用与反作用定律)
P cos
P
FN
F f FN
f min
g
a
cos
tan
例题2
k
已知:弹簧-质量系统,物块旳质量为m ,弹簧旳 刚度系数为k,物块自平衡位置旳初始速度为v0。
m
v0
求:物块旳运动方程
l0
受力以及运动演示
解:这是已知力(弹簧力)求运 动规律,故为第二类动力学问 题。
k FO m m
x
l00
x
以弹簧未变形时旳平衡位置为原点建立Ox坐标系,将物块置 于任意位置 x > 0 处。物块在 x 方向只受有弹簧力F=-k x i。根 据直角坐标系中旳质点运动微分方程
p
p 0
I (e) i
q(v2v1)dt (W F1 F2 FN )dt
q(v 2v1) (W F1 F2 FN )
q(v2v1) (W F1 F2 FN )
FN FN FN
W F1 F2 FN 0
FN q(v2 v1)
q S1v1 S2v2
FNx q (v2x v1x ) FNy q (v2y v1y )
O1
(e) p=0
O
2l
mC
(b) p=mlω
O
vC
m
(c) p=mvC
C
(d) p=0
西南交通大学理论力学作业答案⑦

刚体的平面运动作业参考答案1. 图示平面机构中,曲柄OA =R ,以角速度ω 绕O 轴转动。
齿条AB 与半径为2Rr =的齿轮相啮合,并由曲柄销A 带动。
求当齿条与曲柄的交角θ =60º时,齿轮的角速度。
答案:顺时针 31ωω=提示:可先用速度投影法求出齿条上与齿轮重合点的速度。
2.图中曲柄OA 长150mm ,连杆AB 长200mm ,BD 长300mm 。
设OA ⊥OO 1时,AB ⊥OA ,θ =60º,曲柄OA 的角速度为4rad/s ;求此时机构中点B 和D 的速度以及杆AB 、O 1B 和BD 的角速度。
答案:逆时针顺时针顺时针 rad/s 34 , rad/s 4, rad/s 3 , mm/s 800 , mm/s 34001O =====BD B AB D B v v ωωω提示:在图示瞬时,杆AB 的速度瞬心为点C ,杆BD 的速度瞬心为点E 。
3.图示平面机构中,曲柄长OA =r ,以角速度ω0绕O 轴转动。
某瞬时,摇杆O 1N 在水平位置,而连杆NK 和曲柄OA 在铅垂位置。
连杆上有一点D ,其位置为DK =31NK ,求D 点的速度。
答案:←=320ωr v D 提示:在图示瞬时,杆AB 瞬时平动,杆KN 的速度瞬心为点N 。
4.杆AB 长0.4m ,其端点B 沿与水平成倾角θ =30º的斜面运动,而端点A 沿半径OA =0.6m 的圆弧运动,如图所示。
求当杆AB 水平时,端点B 的速度和加速度。
假设此时OA ⊥AB ,杆OA 的角速度为πrad/s ,角加速度为零。
答案:2m/s 42.3 , m/s 18.2==B Ba v提示:先用速度瞬心法或基点法求出杆AB 的角速度和点B 的速度;然后以A 为基点,B 为动点,用基点法计算点B 的加速度。
5.图示机构中,曲柄OA 以等角速度ω0绕O 转动,且OA =O 1B =r 。
在图示位置时∠AOO 1=90º,∠BAO =∠BO 1O =45º, 求此时B 点加速度和O 1B 杆的角加速度。
西南交大考研理论力学真题

西南交大考研理论力学真题西南交大考研理论力学真题是许多考生备战考研的重要参考资料。
理论力学作为一门基础学科,对于工程、物理等领域的研究具有重要意义。
通过分析西南交大考研理论力学真题,我们可以了解到该学科的考点和考查重点,有助于我们在备考过程中进行针对性的复习和提高。
首先,西南交大考研理论力学真题涵盖了力学的基本概念和原理,要求考生对牛顿力学、静力学、动力学等方面有深入的理解。
这些题目往往会考查考生对基本公式和定律的掌握程度,以及对力学问题的分析和解决能力。
因此,在备考过程中,我们需要牢固掌握力学的基本概念和原理,并能够熟练运用它们解决实际问题。
其次,西南交大考研理论力学真题也涉及到了一些高级的力学问题,如刚体力学、弹性力学、流体力学等。
这些问题往往需要考生具备较强的抽象思维和数学推导能力。
在备考过程中,我们需要掌握这些高级理论的基本概念和公式,能够灵活运用它们解决复杂的力学问题。
同时,我们还需要注重理论与实际问题的结合,培养自己的物理直觉和实际应用能力。
此外,西南交大考研理论力学真题还会涉及到一些工程实践中的力学问题,如结构力学、振动与控制等。
这些问题往往需要考生具备一定的工程背景和实践经验。
在备考过程中,我们需要了解这些工程实践中的力学问题的基本原理和方法,并能够将其应用到实际工程中。
同时,我们还需要关注工程实践中的新技术和新方法,不断更新自己的知识储备。
综上所述,西南交大考研理论力学真题是备战考研的重要参考资料。
通过分析这些真题,我们可以了解到该学科的考点和考查重点,有助于我们在备考过程中进行有针对性的复习和提高。
在备考过程中,我们需要牢固掌握力学的基本概念和原理,熟练运用它们解决实际问题;同时,还需要掌握高级力学理论的基本概念和公式,培养自己的抽象思维和数学推导能力;此外,还需要了解工程实践中的力学问题的基本原理和方法,并能够将其应用到实际工程中。
通过不断的学习和实践,我们相信能够在考研中取得优异的成绩。
西南交通大学理论力学复习题
题 2—22 图
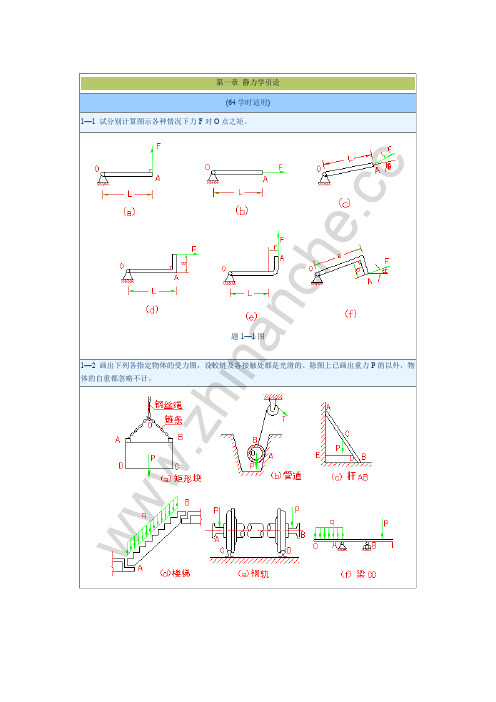
第三章 力系的平衡 (64 学时适用)
3—1 支架由 AB、AC 杆组成,A、B、C 三处都是铰接,在 A 点悬挂重量为 Q 的重物。试求在图示三种情 况下,AB、AC 杆受力的大小和拉压情况。杆的自重忽略不计。
题 3—1 图 3—2 匀速起吊预制梁如图,如果要求绳索 AB、BC 的拉力不比 W/2 大 20%,问α角应在什么范围内? 3—3 绳索 AC 与 BC 联结于 C,C 点作用有 1.2 kN 的力和另一力 P,力的方向如图。(a)若 P = 1 kN 时, 求绳索 AC 和 BC 中的拉力;(b)AC 和 BC 保持受拉,问 P 力应为多大。
题 3—9 图
题 3—10 图
3—11 已知 AB 梁上作用一力偶,力偶矩为 m,梁长为 l。试求在(a)、(b)、(c)、(d)四种情况下求 A、B 的约束反力。
题 3—11 图 3—12 已知在构件 BC 上作用有一力偶如图示,力偶矩 m = 1 kN · m,a = 0.3m,构件本身的重量略去不计。 求支座 A 和 C 的约束反力。 3—13 锻锤在工作时,如果工件作用于锤头的力有偏心。就会使锤头发生偏斜,这样在导轨上产生的压力将 加速导轨的摩擦,也影响锻件的精度。如已知打击力 P = 1000kN,偏心距 e = 20mm,锤头高度 h = 200mm, 试求锤头加给两侧导轨的压力。 3—14 两块尺寸相同的长方板由铰链 C 互相连结,两板相对位置如图示,A、B 为固定铰支座,在每一板平 面内都作用一力偶矩为 m 的力偶。如 a>b,不计板重,求 A、B 处的约束反力。若 a = b,情况将如何?
题 1—9 图
题 1—10 图
第二章 力系的合成
(64 学时适用) 2—1 螺栓上作用有 F1、F2、F3 三力,方向如图示,大小分别为 F1 = 400N,F2 = 500N,F3 = 600N。用 几何法求这三力的合力。 2—2 由一平面共点力系画出的力多边形如图示。(a)求 P1 和 P2 的合力。(b)求 P1 和 P5 的合力。(c) P1、P2 和 P3 的合力是否等于 P4 和 P5 的合力?(d)将 P1 沿 AE 和 BE 方向分解为两个分力。(e)将 P1、 P2 和 P3 的合力沿 AE 和 DE 方向分解为两个分力。(f)原力系是否平衡。
第一学期西南交大理论力学C第2次作业答案

本次作业是本门课程本学期的第2次作业,注释如下:一、单项选择题(只有一个选项正确,共15道小题)1. 平面任意力系有个独立的平衡方程。
(A)1(B) 2(C) 3(D) 4你选择的答案: C [正确]正确答案:C解答参考:2. 平面平行力系有个独立的平衡方程。
(A) 1(B) 2(C) 3(D) 4你选择的答案: B [正确]正确答案:B解答参考:3.图示结构是()。
(A) 静定(B) 一次超静定(C) 二次超静定(D)三次超静定你选择的答案: B [正确]正确答案:B解答参考:4.图示为两个相互啮合的齿轮。
作用在齿轮A上的切向力平移到齿轮B的中心。
(A) 不可以(B) 可以(C) 不能确定你选择的答案: A [正确]正确答案:A解答参考:5.图示桁架中杆件内力等于零,即所谓“零杆”为。
(A) BC, AC(B) BC, AC, AD(C) BC(D) AC你选择的答案: A [正确]正确答案:A解答参考:6.沿正立方体的前侧面作用一力,则该力。
(A) 对轴x、y、z之矩均相等(B) 对轴x、y、z之矩均不相等(C) 对轴x、y、之矩相等(D) 对轴y、z之矩相等你选择的答案: D [正确]正确答案:D解答参考:7.空间力对点之矩是。
(A) 代数量(B) 滑动矢量(C) 定位矢量(D)自由矢量你选择的答案: C [正确]正确答案:C解答参考:8. 力对轴之矩是。
(A) 代数量(B) 滑动矢量(C) 定位矢量(D) 自由矢量你选择的答案: A [正确]正确答案:A解答参考:9.空间力偶矩矢是。
(A) 代数量(B) 滑动矢量(C) 定位矢量(D) 自由矢量你选择的答案: D [正确]正确答案:D解答参考:10. 空间任意力系有个独立的平衡方程。
(A) 3(B) 4(C) 5(D)6你选择的答案: D [正确]正确答案:D解答参考:11. 空间汇交力系有个独立的平衡方程。
(A) 3(B) 4(C) 5(D) 6你选择的答案: A [正确]正确答案:A解答参考:12. 空间力偶系有个独立的平衡方程。
西南交通大学理论力学作业答案⑾

达朗伯原理作业参考答案及解答1.汽车以加速度a 作水平直线运动,如图所示。
若不计车轮质量,汽车的总质量为m ,质心距地面的高度为h 。
若汽车的前后轮轴到过质心的铅垂线的距离分别等于l 1和l 2。
试求前后轮的铅垂压力;并分析汽车行驶加速度a 为何值时其前后轮的压力相等(滚动摩擦阻力不计)?答案:hl l g a 2)(21−=2.为了用实验方法测定无轨电车的减速度,采用了液体加速度计,它是由一个盛有油并安放在铅垂平面内的折管构成。
当电车掣动时,安放在运动前进方向的一段管内的液面上升到高度h 2,而在反向的一段管内的液面则下降到高度h 1。
加速度计的安放位置如图所示,θ1=θ2=45°,且已知h 1=250mm ,h 2=750mm 。
试求此时电车的减速度大小。
2211cot cot θθh h d +=当电车掣动时,筒中两端油的高差为12h h −,取油面上一滴油为研究对象,其受力图(含虚加惯性力)如下图。
由0sin cos ,0=−⇒=∑θθmg ma Fx注意到几何关系22111212cot cot tan θθθh h h h d h h +−=−=解得 g h h h h g h h h h g g a 5.0)(cot cot )(tan 2112221112=+−=+−==θθθ3.题图所示均质杆AB 的质量为4kg ,置于光滑的水平面上。
在杆的B 端作用一水平推力F = 60N ,使杆AB 沿F 力方向作直线平移。
试求AB 杆的加速度和角θ 之值。
答案:o 33.2 ,654.0 tan ,m/s 152======θθFmg a g m F a4.在题图所示系统中,已知:均质杆AB 的长为l ,质量为m ,均质圆盘的半径为r ,质量也为m ,在水平面上作纯滚动。
在图示位置由静止开始运动。
试求该瞬时:(1)杆AB 的角加速度;(2)圆盘中心A 的加速度a A 。
解:先进行运动分析,显然杆AB 和轮A 均作平面运动,由运动学关系有AB tCAt CA A C A A l a a a a r a αα2,,=+== 取整体为研究对象,加上惯性力,其受力图见下左图各惯性力和力偶为(1)21, , 121 ,21 21y I x I I 2I 2I AB C A C A AB C A A A ml F ma F F ml M mra mr M ααα======根据达朗伯原理 由∑=−++++= 02121)( ,0)(y I x I I I I mgl lF F F r M M F MC C A CA D将式(1)代入上式得(2) 0315 22=−+gl ra l A AB α再取杆AB 为研究对象,加上惯性力,其受力图见上右图 由∑=−+= 02121 ,0)(y I I mgl lF M F MC CA将式(1)代入上式得(3) 03 22=−gl l AB α由式(2)和(3)解得0 23 ==A AB a lgα5.题图所示内侧光滑的圆环在水平面内绕过点O 的铅垂轴转动,均质细杆的A 端与圆环铰接,B 端压在环上。
西南交通大学理论力学9PPT课件

d O
dm m R 2d A m R 22 d 2 R m 2d
R
JC z
m iri20 R2 R m 2 d
21m2R 2
4. 转动惯量平行移轴定理
z
z1
r
r1 m
JzC m ir 1 2 m i(x 1 2 y 1 2)
Jz mir2 mi(x2y2) mi[x12(y1d)2]
例题5
均质圆轮半径为R、质量为m,圆轮对转轴的转动
惯量为JO。圆轮在重物P带动下绕固定轴O转动,
已知重物重量为W。
FOy
求:重物下落的加速度
JO1 3m 1l2m 2(8 3d2l2ld )
例题5
均质圆盘,质量 m,求圆盘绕 O轴的动量矩。
JC
1 mr2 2
JO JCm2e 1mr2 me2 2
1m(r2 2e2 ) 2
r C
e
O
LO
JO
1m(r2 2
2e2
)
§9.3 质点系动量矩定理
1. 质点系的动量矩定理 d dM tO (m ivi)M O (F i(e))M O (F i(i))
对于其质量为连续分布的刚体,
则上式成为定积分
Jz r2dm
M
若设想刚体的质量集中于
离z轴距离为 z 处,令
Jz=M
2 z
,则称之为对z轴的
回转半径。
z
Jz M
例题2
计算均质细长杆对通过质心
轴的转动惯量Jz
z
z
dm m dx l
JCz miri2
A
C
B
x
l x dx
l 2 mdx x2 1 ml2
西南交通大学理论力学课件5

D
在M点的运动平面内取直角坐标系 Oxy如图所示:轴 x 沿直线轨道,并指 C 向轮子滚动的前进方向,轴 y 铅直向上。 M r φ B 考虑车轮在任意瞬时位置,因车轮滚动 O A H O H 。于是,在图 MH 而不滑动,故有 示瞬时动点M 的坐标为 以 t 代入,
x OA OH AH MH MB r r sin
y
a
2
1、建立固定参考系Oxy; 2、将所考察的点置于坐 标系中的一般位置;
A
C
O
x y
x
3、根据已知的约束条件 列写点的运动方程。
运动演示
解:
考虑任意位置, M点的坐
y
标 x,y可以表示成
x (a b) cos
y b sin
运动轨迹演示
A
C
O
x y
x
消去上式中的角φ,即得M 点的轨迹方程:
速度
r x i y j z k
v r (x i y j z k) ( x i y z k ) j
(Oxyz)为定参考系
x
z
P
v
z
r
k i
O y
a
y x
j
j i k 0
v r x i y j z k vx i v y j vz k
平面运动 —— 刚体运动过程中,其上 各点到某一固定平面的距离始终保持不变。
★ 工程运动学模型及其运动形式
★
刚 体的运动形式
平面运动 —— 刚体运动过程中,其上 各点到某一固定平面的距离始终保持不变。
★ 工程运动学模型及其运动形式
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2、另一种是同力相关的量(冲量、力 矩、功等) —— 之间的关 系,从不同侧面对物体的机械运动进行深入的研究。
在一定条件下,上述特征量用这些定理来解答动力学问题非常 方便简捷 。
本章中研究质点和质点系的动量定理,建立了动量的改变 与力的冲量之间的关系,并研究质点系动量定理的另一重要形 式——质心运动定理。
1.质点的动量:质点的质量与速度的乘积 mv 称为质点的动量。
是瞬时矢量,方向与v 相同。单位是kgm/s。
2.质点系的动量:质点系中所有各质点的动量的矢量和。
n
p mivi i 1
式中n为质点数,mi为第i个质点的质量,vi为质点速度矢量。
4
动力学
第十一章 动量定理
如i质点的矢径为ri ,其速度为
时间的导数等于作用于该质点系外力的矢量和。
12
动力学
第十一章 动量定理
对上式积分,得
p
n
dp
p0
i 1
t 0
Fi ( e ) dt
或
n
p p0
I (e) i
i 1
上式为质点系动量定理的积分形式,表明在某一时间间
q
AB都是匀质杆, 质量各为m , 滑块B的质
量也为m。求当 = 45º时系统的动量。
解: 曲柄OA: 连杆AB:
m,
vC1
1 2
l
m,
vC 2
5 2
l AB
5 l
2
P为速度瞬心,
PC2
5 2
l
,AB=
滑块B: m, vC3 2l
7
动力学
第十一章 动量定理
由几何关系不难得
cosq 3 , sinq 1
q
10
10
p mvC1 mvC2 mvC3
m[(vC1 sin vC2 cosq vC3)i (vC1 cos vC2 sinq ) j]
ቤተ መጻሕፍቲ ባይዱ
m[( 1 l sin 45o 5 l cosq 2l )i ( 1 l cos 45o 5 l sinq ) j]
2
2
2
2
ml[( 1 2 5 3 2)i ( 1 2 5 1 ) j]
2 2 2 10
2 2 2 10
2ml[2i 1 j]
8
2
动力学
第十一章 动量定理
二.冲量
力与其作用时间的乘积称为力的冲量,冲量表示力在其作
用时间内对物体作用的累积效应的度量。例如,推动车子时,
较大的力作用较短的时间,与较小的力作用较长的时间,可得
到同样的总效应。
如力F是常矢量:
I Ft
如力F 是变矢量(包括大小和方向的变化):在微小时间间隔内,
i 1
i 1
i 1
因质点系动量增量为:
n
(其中
F (i) i
0)
i 1
d(mivi ) d (mivi ) dp
上式可变为
n
n
dp Fi(e)dt dIi(e) 或
i 1
i 1
d
dt
p
n i 1
F (e) i
上式是质点系动量定理的微分形式,表明质点系动量的增量等
于作用在质点系的外力元冲量的矢量和;也表明质点系动量对
力F的冲量称为元冲量。
元冲量为 dI Fdt t
而力F在时间t内的冲量为矢量积分: I Fdt 0
冲量的单位: Ns kgm/s 2 s kgm/s 与动量单位同.9
动力学
第十一章 动量定理
§11-2 动量定理
1.质点的动量定理
由质点动力学基本方程有:
d dt
(mv )
F
或 d(mv) Fdt
2
动力学
第十一章 动量定理
第十一章 动量定理
§11–1 动量与冲量 §11–2 动量定理 §11–3 质心运动定理
3
动力学
第十一章 动量定理
一、动量
§11-1 动量与冲量
在日常生活和工程实践中可看出,质点的速度和质量的乘积
表征了质点机械运动的强弱,例:枪弹:速度大,质量小; 船:
速度小,质量大。
M x (Fi(i) ) 0
设质点系有n个质点,由质点动量定理,对质点系内任一质点 i,
d(mivi ) (Fi(i) Fi(e) )dt Fi(e)dt Fi(i)dt
11
动力学
第十一章 动量定理
对整个质点系,有n 个方程,相加得
n
n
n
d(mivi ) Fi(e)dt Fi(i)dt
动力学
第十一章 动量定理
2.质点系的动量定理
质点系的内力与外力
外力:所考察的质点系以外的物体作用于该质点系中各质点的力。
内力:所考察的质点系内各质点之间相互作用的力。
对整个质点系来讲,内力系的主矢恒等于零,内力系对任一点
(或轴)的主矩恒等于零。即:
F (i) i
0;
MO (Fi(i) ) 0 或
vi
dri dt
,
代入上式,因mi不变,则有:
p
mivi
mi
dri dt
d dt
mi ri
令 m mi为质点系总质量,与重心坐
标类似,定义质点系质量中心(质心)
rC
mi ri m
有
d
d
p dt
miri dt (mrC ) mvC
上式表明,质点系的动量等于质心速度与其全部质量的乘积。
动力学
概述
动力学普遍定理概述
对质点动力学问题: 可由前一章内容建立运动微分方程求解。
对质点系动力学问题: 可以逐个质点列出其动力学微分方程 联立求解,但求解过程很复杂。
实际上的问题是: 1、联立求解微分方程(尤其是积分问题)非常困难 2、大量的问题中,不需要了解每一个质点的运 动,仅需要研
究质点系整体的运动情况。
5
动力学
第十一章 动量定理
刚体是由无限多个质点组成的不变 质点系,质心是刚体内某一确定的点。 对于质量均匀的规则刚体,质心就是几 何中心,由上式可以方便的计算刚体或 者刚体系统的动量。对刚体系有
p mivCi
6
动力学
第十一章 动量定理
〔例1〕曲柄连杆机构的曲柄OA以匀
转动,设OA=AB=l ,曲柄OA及连杆
上式是质点动量定理的微分形式,即质点的动量对时间的导数 等于作用于质点的力,或质点动量的增量等于作用在质点上的 元冲量。
对上式积分,时间由0到t,速度由v0变为v,得
t
mv mv0 Fdt I 0
上式是质点动量定理的积分形式,即在某一时间间隔内,质 点动量的变化等于作用于质点的力在此段时间内的冲量。 10
从本章起, 将要讲述解答动力学问题的其它方法, 即动力学普遍 定理(包括动量定理、动量矩定理、动能定理及由此推导出来的其它 一些定理),它们从不同的侧面揭示了质点和质点系总体的运动变 化与其受力之间的关系,可以求解质点系动力学问题。
1
动力学
概述
它们以简明的数学形式, 表明两种量 :
1、一种是同运动特征相关的量(动量、动量矩、动能等);
