《结构力学习题集》(下)-结构的极限荷载习题及答案
《结构力学》习题集及答案(下册)第十章结构弹性稳定计算
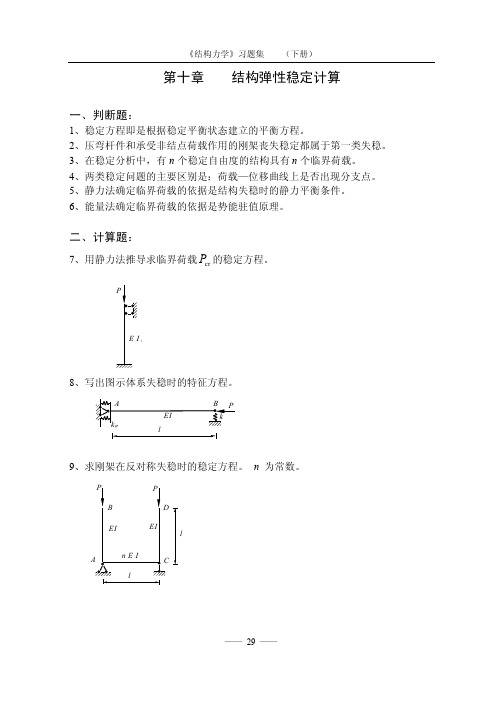
第十章 结构弹性稳定计算一、判断题:1、稳定方程即是根据稳定平衡状态建立的平衡方程。
2、压弯杆件和承受非结点荷载作用的刚架丧失稳定都属于第一类失稳。
3、在稳定分析中,有n 个稳定自由度的结构具有n 个临界荷载。
4、两类稳定问题的主要区别是:荷载—位移曲线上是否出现分支点。
5、静力法确定临界荷载的依据是结构失稳时的静力平衡条件。
6、能量法确定临界荷载的依据是势能驻值原理。
二、计算题:7、用静力法推导求临界荷载cr P 的稳定方程。
PE I ,l8、写出图示体系失稳时的特征方程。
k lEIk AB P9、求刚架在反对称失稳时的稳定方程。
n 为常数。
l Pl P n E IEIEI A C BD10、求图示完善体系的临界荷载cr P 。
转动刚度kl k r 2=,k 为弹簧刚度。
P l k r kl kEIO O EI O O11、求图示刚架的临界荷载cr P 。
已知弹簧刚度l EI k 33= 。
PEIlA BC lO O 0EI k12、求图示中心受压杆的临界荷载cr P 。
PEI l13、用静力法求图示结构的临界荷载cr P ,欲使B 铰不发生水平移动,求弹性支承的最小刚度k 值。
PlEI A Bk14、用静力法确定图示具有下端固定铰,上端滑动支承压杆的临界荷载crP。
P PEI yxδly15、用能量法求图示结构的临界荷载参数crP。
设失稳时两柱的变形曲线均为余弦曲线:yxh=-δπ(cos).12提示:cos d sin22u u u uabab⎰=+⎡⎣⎢⎤⎦⎥214。
PEIP2EI h3EA16、用能量法求中心受压杆的临界荷载crP与计算长度,BC段为刚性杆,AB段失稳时变形曲线设为:()y x a xxl=-().32EIPllEIABCyx→∞17、用能量法求图示体系的临界荷载cr P 。
l PEIEI 1=H18、用能量法求图示中心压杆的临界荷载cr P ,设变形曲线为正弦曲线。
结构力学(二)第4版龙驭球第17章结构的极限荷载

第17章 极限荷载【17-1】 验证:(a )工字形截面的极限弯矩为)41(212δδδσb hbh M s u +=。
(b )圆形截面的极限弯矩为63D M s u σ=。
(c )环形截面的极限弯矩为⎥⎦⎤⎢⎣⎡--=33)21(16D D M su δσ。
【解】(a )工字形截面的等面积轴位于中间。
静距计算公式:2021d xy y xy S y ==⎰考虑上半部分面积对等面积轴的静距(大矩形静距减两个小矩形静距):)41(21)4(21)2)((21)2(21211212222121122222212bhb b h h bh h h b bh hb h b S δδδδδδδδδδδδδδδδ+-+-=+-+-=---= 去除高阶小量后)41(21212δδδb h bh S +=因此极限弯矩为)41()(212δδδσσb h bh S S M s s u +=+= (b )静距计算公式:2021d xy y xy S y==⎰ 6322d 2))2(d(21)2(4d )2(43)2(023)2(0202222202222D uu u y D y D y y y D S D DDD =⋅=⋅=-⋅-=⋅-=⎰⎰⎰关/注;公,众。
号:倾听细雨因此极限弯矩为63D S M s s u σσ==(c )圆的静距为63D S =则圆环的静距为⎥⎦⎤⎢⎣⎡--=-=3333)21(166)2(-6D D D D S δδ 因此极限弯矩为⎥⎦⎤⎢⎣⎡--==33)21(16D D S M ss u δσσ 【17-2】 试求图示两角钢截面的极限弯矩u M 。
设材料的屈服应力为s σ。
【解】设等面积轴距上顶面距离为xmm 。
由面积轴两侧面积相等,也即面积轴以上面积等于总面积的一半,得405550))50(21(22⨯+⨯=-+x x x ,解得mm x 723.4=。
单个角钢上下截面面积矩:32323232233214879mm ])723.440(20)723.440(31)723.445(20)723.445(31[)723.445(521723.431723.4)723.445(21540mm 723.431723.4)723.450(21=+⨯++⨯-+⨯-+⨯-+⨯⨯+⨯-⨯-⨯==⨯+⨯-⨯=S S由此得截面极限弯矩s s s u S S M σσσ10838)4879540(2)(221=+⨯=+=【17-3】 试求图示各梁的极限荷载。
李廉锟《结构力学》(第5版)(下册)课后习题-第14章 结构的极限荷载【圣才出品】

第14章 结构的极限荷载复习思考题1.什么叫极限状态和极限荷载?什么叫极限弯矩、塑性铰和破坏机构?答:(1)极限状态和极限荷载的含义:①极限状态是指整个结构或结构的一部分超过某一状态就不能满足设计规定的某一功能要求时所对应的特定状态;②极限荷载是指结构在极限状态时所能承受的荷载。
(2)极限弯矩、塑性铰和破坏机构的含义:①极限弯矩是指某一截面所能承受的弯矩的最大数值;②塑性铰是指弯矩不能再增大,但弯曲变形则可任意增长的截面;③破坏机构是指出现若干塑性铰而成为几何可变或瞬变体系的结构。
2.静定结构出现一个塑性铰时是否一定成为破坏机构?n次超静定结构是否必须出现n+1个塑性铰才能成为破坏机构?答:(1)静定结构出现一个塑性铰时一定成为破坏机构。
因为根据几何组成分析,当静定结构出现一个塑性铰时,结构由几何不变变成几何可变或几何瞬变体系,此时该结构一定成为了破坏机构。
(2)n次超静定结构不必出现n+1个塑性铰才能成为破坏机构。
因为n次超静定结构出现n个塑性铰时,如果塑性铰的位置不合适,也可能使原结构变成几何瞬变的体系,此时的结构也成为了破坏机构。
3.结构处于极限状态时应满足哪些条件?答:结构处于极限状态时应满足如下三个条件:(1)机构条件机构条件是指在极限状态中,结构必须出现足够数目的塑性铰而成为机构(几何可变或瞬变体系),可沿荷载作正功的方向发生单向运动。
(2)内力局限条件内力局限条件是指在极限状态中,任一截面的弯矩绝对值都不超过其极限弯矩。
(3)平衡条件平衡条件是指在极限状态中,结构的整体或任一局部仍维持平衡。
4.什么叫可破坏荷载和可接受荷载?它们与极限荷载的关系如何?答:(1)可破坏荷载和可接受荷载的含义:可破坏荷载是指满足机构条件和平衡条件的荷载(不一定满足内力局限条件);可接受荷载是指满足内力局限条件和平衡条件的荷载(不一定满足机构条件)。
(2)与极限荷载的关系极限荷载是所有可破坏荷载中的最小者,是所有可接受荷载中的最大者。
《结构力学习题集》(下)-结构的极限荷载习题及答案

第十一章 结构的极限荷载一、判断题:1、静定结构只要产生一个塑性铰即发生塑性破坏,n 次超静定结构一定要产生n +1个塑性铰才产生塑性破坏。
2、塑性铰与普通铰不同,它是一种单向铰,只能沿弯矩增大的方向发生相对转动。
3、超静定结构的极限荷载不受温度变化、支座移动等因素影响。
4、结构极限荷载是结构形成最容易产生的破坏机构时的荷载。
5、极限荷载应满足机构、内力局限和平衡条件。
6、塑性截面系数s W 和弹性截面系数W 的关系为W W s 。
二、计算题:7、设u M 为常数。
求图示梁的极限荷载u M 及相应的破坏机构。
lM8、设极限弯矩为u M ,用静力法求图示梁的极限荷载。
B9、图示梁各截面极限弯矩均为u M ,欲使A 、B 、D 三处同时出现塑性铰。
确定铰C 的位置,并求此时的极限荷载u P 。
al b10、画出下列变截面梁极限状态的破坏机构图。
( )b( )c( )a11、图示简支梁,截面为宽b 高h 的矩形,材料屈服极限y σ。
确定梁的极限荷载u P 。
12、图示等截面梁,截面的极限弯矩为m kN 90u ⋅=M ,确定该梁的极限荷载u P 。
2m2m13、图示等截面梁,截面的极限弯矩m kN 90u ⋅=M ,求极限荷载u P 。
14、求图示梁的极限荷载u P 。
已知极限弯矩为u M 。
15、图示梁截面极限弯矩为u M 。
求梁的极限荷载u P ,并画出相应的破坏机构与M 图。
0.5l0.5l0.5l0.5l 0.5l16、求图示梁的极限荷载u q 。
17、求图示结构的极限荷载u P 。
A C 段及C E 段的u M 值如图所示。
P2m2m2m 2m18、求图示结构的极限荷载u P ,并画极限弯矩图。
各截面u M 相同。
23m1.5 1.51m19、求图示结构的极限荷载u P ,并画极限弯矩图。
=u M 常数。
l2ll2lll20、计算图示等截面连续梁的极限荷载u P 。
21、求图示等截面连续梁的屈服荷载y P 和极限荷载u P 。
龙驭球《结构力学Ⅱ》配套题库-名校考研真题(结构的极限荷载)【圣才出品】

所以由原点到 2/3l 时下降的距离为:
2l
3 d
2l 3
1
(
y)2
dx
2l 3
1
a2 (l2
3x2 )2
dx
7
a2l5
0
02
02
45
则集中荷载做的功为:
T2
ql
7 45
qa2l 6
微段上荷载所做的功为:
T1
1 2
q(l
x
dx)( y)2 dx
1 2
q(l
x)(
y)2 dx
沿杆长积分,可得:
2/7
圣才电子书 十万种考研考证电子书、题库视频学习平台
图 17-3
则由图示可得,由于杆件的倾斜会是整个系统产生向下的下降,距离为:
d dx dx cos 2 sin2 dx 1 2dx 1 ( y)2 dx
22
2
式中, y (l2 3x2 ) 。
T1
1 1 q(1 x)( y)2dx 1 q
1
(1
x)a2
(l
2
3x2
)2
dx
3
qa2l 6
02
20
20
所以外力的势能为:
V
(T1
T2 )
3 20
7 45
qa
2l
6
11 36
qa 2l 6
3/7
圣才电子书 十万种考研考证电子书、题库视频学习平台
系统的总能量为:
方程为 qu× l ×θ1x=Mu(θ1+θ1+θ2),其中 2
代入虚功方程幵整理得
qu=
由
解得 x=0.586l。将 x 值代入虚功方程,解得
《结构力学习题集》(下)-结构的动力计算习题及答案

《结构⼒学习题集》(下)-结构的动⼒计算习题及答案第九章结构的动⼒计算⼀、判断题:1、结构计算中,⼤⼩、⽅向随时间变化的荷载必须按动荷载考虑。
2、仅在恢复⼒作⽤下的振动称为⾃由振动。
3、单⾃由度体系其它参数不变,只有刚度EI 增⼤到原来的2倍,则周期⽐原来的周期减⼩1/2。
4、结构在动⼒荷载作⽤下,其动内⼒与动位移仅与动⼒荷载的变化规律有关。
5、图⽰刚架不计分布质量和直杆轴向变形,图a 刚架的振动⾃由度为2,图b 刚架的振动⾃由度也为2。
6、图⽰组合结构,不计杆件的质量,其动⼒⾃由度为5个。
7、忽略直杆的轴向变形,图⽰结构的动⼒⾃由度为4个。
8、由于阻尼的存在,任何振动都不会长期继续下去。
9、设ωω,D 分别为同⼀体系在不考虑阻尼和考虑阻尼时的⾃振频率,ω与ωD 的关系为ωω=D 。
⼆、计算题:10、图⽰梁⾃重不计,求⾃振频率ω。
l l /411、图⽰梁⾃重不计,杆件⽆弯曲变形,弹性⽀座刚度为k ,求⾃振频率ω。
12、求图⽰体系的⾃振频率ω。
l l0.5l 0.513、求图⽰体系的⾃振频率ω。
EI = 常数。
ll 0.514、求图⽰结构的⾃振频率ω。
l l15、求图⽰体系的⾃振频率ω。
EI =常数,杆长均为l 。
16、求图⽰体系的⾃振频率ω。
杆长均为l 。
17、求图⽰结构的⾃振频率和振型。
l /218、图⽰梁⾃重不计,W EI ==??2002104kN kN m 2,,求⾃振圆频率ω。
B2m2m19、图⽰排架重量W 集中于横梁上,横梁EA =∞,求⾃振周期ω。
EIEIW20、图⽰刚架横梁∞=EI 且重量W 集中于横梁上。
求⾃振周期T 。
EIEIWEI 221、求图⽰体系的⾃振频率ω。
各杆EI = 常数。
a aa22、图⽰两种⽀承情况的梁,不计梁的⾃重。
求图a 与图b 的⾃振频率之⽐。
l /2ll /2l /2(b)23、图⽰桁架在结点C 中有集中重量W ,各杆EA 相同,杆重不计。
求⽔平⾃振周期T 。
结构的极限荷载和例题讲解

简化计算: 假设材料为理想弹塑性材料,其应力~应变关系下图所示。
§12-2 极限弯矩和塑性铰 破坏机构 静定梁的计算
一、弹塑性阶段工作情况
理想弹塑性材料T形截面梁处于纯弯曲状态时
弹性状态:
图b:截面处于弹性阶段,σ<σs (屈服极限) 图c:截面最外边缘处σ=σs (达到屈服极限) 屈服弯矩(弹性极限弯矩)MS = Wσs(W:弯曲截面系数) 图d:截面处于弹塑性阶段。 靠外部分形成塑性区,其应力为常数,σ=σs , 靠内部分仍为弹性区,称弹性核,其应力直线分布 图e:截面全部达到塑性——极限情形, 这时的弯矩是该截面所能承受的最大弯矩 ——极限弯矩,以Mu 表示。
等截面超静定梁(图a) (各截面Mu相同) 弹性——弹塑性阶段——极限状态过程:
(1)弹性阶段弯矩图:P≤Ps (2首)先弹在塑A性端阶形段成M并图扩:大荷,载然超后过CP截s,面塑也性形区成
塑性性铰区。。A端首先达到Mu并出现第一个塑
(3)极限状态M图:荷载再增加,A端弯矩 增量为零,当荷载增加到使跨中截面的弯矩达 到Mu时,在该截面形成第二个塑性铰,于是梁 即变为机构,而梁的承载力即达到极限值。此 时的荷载称为极限荷载Pu——极限状态(e)。
破坏机构——极限状态: 结构出现若干塑性铰而成为几何可变或瞬变体系时 ——结构丧失承载能力
三、静定梁的计算
静定梁由于没有多余联系,因此,出现一个塑性铰时,即 成为破坏机构。
对于等截面梁,在弯矩绝对值最大截面处达到极限弯矩, 该截面形成塑性铰。
由塑性铰处的弯矩等于极限弯矩和平衡条件,就可求出静 定梁的极限荷载。
结构的极限荷载和例题 讲解
§12-1 概述
结构设计方法:
1、容许应力法(弹性分析法):
李廉锟《结构力学》(第5版)(下册)章节题库-第14章 结构的极限荷载【圣才出品】

2.用试算法求图 14-5 所示刚架的极限荷载。
图 14-5 解:(1)确定基本机构 可能出现塑性铰的截面为 A、B、C、D、E、F,h=6,静不定次数 n=3,所以,基 本机构数 m=3。 图 14-6(a)~(c)分别为机构 1,机构 2 和机构 3。 (2)试算 对组合机构进行试算如下: ①组合机构 I=机构 1+机构 3(侧移机构),如图 14-6(d)所示,虚功方程为
3.超静定梁和刚架成为破坏机构时,塑性铰的数目 m 与结构超静定次数 n 之间的关 系为( )。
A.m=n B.m>n C.m<n
1/9
圣才电子书
十万种考研考证电子书、题库视频学习平
台
D.取决于体系构造和所受荷载的情况
【答案】D
【解析】塑性铰数目与超静定次数并无必然的关系。
二、填空题 1.在同向竖向荷载作用下,连续梁的极限状态通常是______。 【答案】在各跨独立形成破坏机构
2.如图 14-1 所示梁的极限荷载
为______。
图 14-1
【答案】 【解析】图示梁为静定,先作出其弯矩图,如图 14-1(a)所示。分析可知塑性铰产
2/9
圣才电子书
生在 C 处,即
十万种考研考证电子书、题库视频学习平 台
3.如图 14-2 所示阶梯状变截面梁的极限荷载 Pu=______。
图 14-2 【答案】 【解析】注意变截面处的极限弯矩为 Mu。
三、判断题 1.一个 n 次超静定梁必须出现,n+1 个塑性铰后才可能发生破坏。( ) 【答案】× 【解析】不一定必须如此。当塑性铰的出现使某构件或某局部的构件成为破坏机构, 就发生破坏。
机构 1 则
图 14-4
5/9
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十一章结构的极限荷载一、判断题:1、 静定结构只要产生一个塑性铰即发生塑性破坏, n 次超静定结构一定要产生 n +1 个塑性铰才产生塑性破坏。
2、 塑性铰与普通铰不同,它是一种单向铰,只能沿弯矩增大的方向发生相对转动。
3、 超静定结构的极限荷载不受温度变化、支座移动等因素影响。
4、 结构极限荷载是结构形成最容易产生的破坏机构时的荷载。
5、 极限荷载应满足机构、内力局限和平衡条件。
6、塑性截面系数 W s 和弹性截面系数 W 的关系为W s W 。
、计算题:7、设M u 为常数。
求图示梁的极限荷载 M u 及相应的破坏机构。
B f M------------------------------------------D丄l&设极限弯矩为 M u ,用静力法求图示梁的极限荷载。
l/3 9、图示梁各截面极限弯矩均为 M u ,欲使A 、B 、D 三处同时出现塑性铰。
确定铰 C 的位置,并求此时的极限荷载P u 。
10、画出下列变截面梁极限状态的破坏机构图。
1 a _______ -一 b-JlAX . PB2l/311、图示简支梁,截面为宽b高h的矩形,材料屈服极限12、图示等截面梁,截面的极限弯矩为M u 90kN mM u13、图示等截面梁,截面的极限弯矩M u 90 kN m,(b)—/3M u M u I1/3 1/3 1/3------ b ------- -----------14、求图示梁的极限荷载P u。
已知极限弯矩为y。
确定梁的极限荷载P u。
,确定该梁的极限荷载P u。
2m 2m 2m求极限荷载P u。
X2115、图示梁截面极限弯矩为 M u 。
求梁的极限荷载 P u ,并画出相应的破坏机构与M 图。
0.4P16、求图示梁的极限荷载 q u 。
2qaAM u2a17、求图示结构的极限荷载 P u 。
A C 段及C E 段的M u 值如图所示。
18、求图示结构的极限荷载 P u ,并画极限弯矩图。
各截面19、求图示结构的极限荷载 P u ,并画极限弯矩图。
M uB Ccjc?-II I 2Plll+ ----------- 4 ----------- -+ ----------j ____10PBM u =80kN mTA M u =100kN m C丄D 2m u--2m― 2m2m_____PE0.510.51I0 5l 0.5l—I ----------------- V ------------0.51 ----\:B"「CFECq = 4P/32m 1m b- ----------------- 4- ------- 4M u 20kN . m3mP1.5m1.5mk ------------- --------------2a M u 相同。
常数。
20、计算图示等截面连续梁的极限荷载P u 。
A 应*BIDC__ Mu <3 Mu 丄1/2 1/2 |/222、求图示梁的极限荷载q u。
q"―二一Mu^l l l23、计算图示梁的极限荷载P uq= P/l24、计算图示结构在给定荷载作用下达到极限状态时,其所需的截面极限弯矩值M u。
A]___D T2PB E P1M u M u 121、求图示等截面连续梁的屈服荷载P y和极限荷载P u。
1/21/221/3 1/3CM u屮□ I*1.5M ul/3 2 l /3 l25、求图示梁的极限荷载P u。
M u P荷载P 作用于梁上,移动范围在 AD 内,确定极限荷载 P u 值及其作用位置。
1/226、求图示连续梁的极限荷载q u 。
qj H H n M H HM u K A.2M u I2I------------------ --------- ------------------------------------------------ 127、求图示连续梁的极限荷载P u 。
P/l1/2 1/2 l 1/2 1/2——4 ---- ----------------- +--h —28、计算图示结构的极限荷载 q u 。
已知:I = 4 m 。
30、图示等截面梁,其截面承受的极限弯矩M u 6540 kN cm ,有一位置可变的1/22P nTTnwm29、计算图示结构在给定荷载作用下达到极限状态时,其所需截面极限弯矩值 M uM uD20kN35、求图示结构的极限荷载 P u 。
31、图示等截面梁,截面的极限弯矩M u 80 kN32、图示等截面的两跨连续梁,各截面极限弯矩均为 及破坏机构。
q.................. CA1BqiiqlP= 2 —.A I B__CD8m 4m 4m 8mH ---------- 4—4—h ------------------- -34、求图示连续梁的极限荷载P u 。
| P q= P/ ( 2 a )| P | 2PA MufT^C ^M :__Da/2 a/2 2a a a a — -------------------- -4-_ ------------- J -------- 133、求图示梁的极限荷载q u 。
截面极限弯矩 M u140.25kN m 。
m ,求极限荷载q u 。
M u ,确定该梁的极限荷载 q uq4m2m---------------- 1 ---------------- 11/2 1/236、求图示结构的极限荷载P u 。
.BM u =4kN.m M u =2.4kN.m 」_2 m 1m2 m37、求图示梁的极限荷载 P u 。
I P2M uM u P 2M u11l/4l /2l /4—F------------- -38、画出图示变截面梁的破坏机构并确定极限荷载P u 。
|PAB C3 M u M u亠■ 3a …3a …3a39、求图示刚架的极限荷载参数 q u 并画M 图。
M u 为极限弯矩。
3M u 4mM u 2M u 2m 2m—r2M u------- 1 "M u■ -qP =qll40、图示刚架各截面极限弯矩均为M u ,欲使B , C , D , E 截面同时出现塑性铰而 成机构。
求P 与q 的关系并求极限荷载 P u ,Q u 。
1/241、讨论图示变截面梁的极限荷载P u 。
已知AB 段截面的极限弯矩为 M u , BC 段M u aa——-h —第十一章结构的极限荷载1、( X )2、( O )3、( O )4、( O )5、( O )6、( X )7、 M u M u (铰B 单向转动)P8、 M u2 M u10、极限状态为:2 2bhbh M u y , F u 0.75 y4 112、P u 60kN截面的极限弯矩为 M u ,且 M u >MM uP uab(a)Pu1 ( c ) -P-(b).()11、u—o13、P u 14、q u15、16、17、18、9 业135 kN l16傑l215M u2lP u2P1/15Pl /10Pl /10 2P1/15M uq u P u2a6.25kNP u = 22.1kN206.85T1.4M 图kN .m19、P u 1.3M u/lMuM u 0.2M u0.4M-1-M u20、P u21、( 1 )6PI/48A ——.—_P»D CJB J=K."Ed「”1/2 l /2 , 1/2- -4 -2/3 1/3M F-3 Pl/16 00 +6Pl/48 +3pl/48M 0 +6Pl/48 -6Pl/48 0 令M D Mu得屈服荷载石Mu,Py F28、q u 05M u29、M u402353 kN m1730、P U32.7 kN,作用在C点。
31、q u 40kN/ m22、23、24、25、26、27、P uq uP uM uP uq uP u6M u9M u6M u1.8q4M u69空M ul24M(a)梁机构 (b )联合机构33、 q u 2554 kN/ m ,塑性铰在B 处和距A 点3.31 m 处 34、 P u 2.6M u / a40、u u32、q u1166 悸 l 2 BC 跨先破坏35 P u 7M u 636、P u 5kN37、 对称性取半结构,38、 P u M u /a P u 12M机构1 - 机构2 -——39、2M U(a )(a )联合机构: (b )侧移机构:M u M u M u ( (b) 2M u),q 2 4M u 5M u /l 2 /l 2 ,q u 2 4M u / lu ,q 1 1.5MM u16M uPl q2l_4M u,(Pl2ql4)5M U内力可接受P u q u16M u41、在截面和D处岀现塑性铰时,P u 3M u aD处岀现塑性铰时,P U12aM u 3M u。
