微积分第三章第3.6节 二元函数的极值与条件极值
二元函数极值、微分方程

z 2、设函数 z z ( x , y )由 sin( x y ) e 0所确定,求 。 x
z
解 作辅助函数
F ( x, y, z ) sin( x y ) e
z
F F cos( x y ), ez x z
F z cos( x y ) x F x ez z
再求二阶偏导数,得 ( x , y ) 2 , f xy ( x , y ) 0 , f yy ( x , y ) 4 f xx
在点 ( 2, 2) 处, B 2 AC 8 0 且 A 2 0 ,所以函数 在点( 2, 2) 处取得极小值 f ( 2,2) 10 ;
1 2
y (C 1 C 2 x )e r1 x
y ex (C1 cos x C 2 sin x )
1、 求微分方程 y 2 y-3 y 3 的通解.
解、对应齐次微分方程为 y 2 y-3 y 0 2 特征方程 r 2r 3 0, 解得 r1 3, r2 1 对应齐次方程通解 Y C1e 3 x C2e x , (C1 , C2 是任意常数) ( 2、求微分方程 y 2 y y e x 的通解. 解、对应齐次微分方程为
解方程组
Fx 2 x 2 0 Fy 2 y 3 0 2 x 3 y 1 0
2 3 2 求得 x , y , 13 13 13
所以函数 f ( x , y )在条件 2 x 3 y 1 下的极值为
2 3 1 f( , ) ; 13 13 13
y 2 y y 0
2 r 2r 1 0, 特征方程 解得 r1 r2 1
多元函数的极值

对 x ,y 求偏导数, 有
l x 6x 2 ,
l y 6 y 2 ,
l x 0, 令 y 0, l
即
6 x 2 0 , 6 y 2 0 ,
1 1 解方程组得驻点 , . 3 3
则称 f (x0 , y0) 为函数 f (x , y ) 的极大值(或极小值).
极大值和极小值统称为极值.
使函数取得极大值的点(或极小值的点)(x0 , y0),
称为极大值点(或极小值点),极大值点和极小值 点统称为极值点. 定理 1 (极值存在的必要条件) 设函数 z = f (x , y ) ( x0 , y0 ), f y ( x0 , y0 ) 在点 P0( x0 , y0 ) 的偏导数 f x
A B C B 2 AC的符号
8 2 2
结 论
极大
2 2
f(2, 2) 不是极值
二、多元函数的最大值与最小值
使它到三 例 6 在 x y 坐标面上找出一点 P , 点 P1(0, 0) 、P2(1, 0) 、P3(0, 1) 距离的平方和为最 小.
1 1 1 1. a b c
又设所求平面与三个坐标面在第一卦限所围 立体的体积为 V ,所以 1 V abc . 6
z c
O
b y
a x
1 1 1 1 现在求函数 V abc 在条件 1 6 a b c
(a 0, b 0, c 0)下的最小值. 构造辅助函数 1 1 1 1 F (a , b, c ) abc ( 1) , 6 a b c
解 设水槽的长、宽、高分别为 x、y、z ,则容 积为 V = xyz ( x > 0 , y > 0 , z > 0 ),
二元函数的极值与最值

二元函数的极值与最值二元函数的极值与最值问题已成为近年考研的重点,现对二元函数的极值与最值的求法总结如下:1.二元函数的无条件极值(1) 二元函数的极值一定在驻点和不可导点取得。
对于不可导点,难以判断是否是极值点;对于驻点可用极值的充分条件判定。
(2)二元函数取得极值的必要条件: 设),(y x f z =在点),(00y x 处可微分且在点),(00y x 处有极值,则0),('00=y x f x ,0),('00=y x f y ,即),(00y x 是驻点。
(3) 二元函数取得极值的充分条件:设),(y x f z =在),(00y x 的某个领域内有连续上二阶偏导数,且=),('00y x f x 0),('00=y x f y ,令A y x f xx =),('00,B y x f xy =),('00,C y x f yy =),('00,则当02<-AC B 且 A<0时,f ),(00y x 为极大值;当02<-AC B 且A>0,f ),(00y x 为极小值;02>-AC B 时,),(00y x 不是极值点。
注意: 当B 2-AC = 0时,函数z = f (x , y )在点),(00y x 可能有极值,也可能没有极值,需另行讨论例1 求函数z = x 3 + y 2 -2xy 的极值.【分析】可能极值点是两个一阶偏导数为零的点,先求出一阶偏导,再令其为零确定极值点即可,然后用二阶偏导确定是极大值还是极小值,并求出相应的极值.【解】先求函数的一、二阶偏导数:y x x z 232-=∂∂,x y y z 22-=∂∂.x x z 622=∂∂, 22-=∂∂∂y x z , 222=∂∂yz . 再求函数的驻点.令x z ∂∂= 0,y z ∂∂= 0,得方程组⎩⎨⎧=-=-.022,0232x y y x 求得驻点(0,0)、),(3232. 利用定理2对驻点进行讨论:(1)对驻点(0, 0),由于A = 0, B =-2, C = 2,B 2-AC >0,故(0, 0)不是函数z = f (x , y ) 的极值点.(2)对驻点),(3232,由于A =4, B =-2,C = 2,B 2-AC =-4<0, 且A >0,则 2743232-=),(f 为函数的一个极小值. 例2:(2004数学一)设z=z(x,y)是由0182106222=+--+-z yz y xy x 确定的函数,求),(y x z z =的极值点和极值.【分析】 本题把极值问题与隐函数求导方法相结合,计算量是比较大的。
二元函数取极值的条件
二元函数取极值的条件
判断二元函数极值方法如下:
设:二元函数f(x,y)的稳定点为:(x0,y0),
即:∂f(x0,y0)/∂x = ∂f(x0,y0)/∂y = 0;
记::A=∂²f(x0,y0)/∂x²
B=∂²f(x0,y0)/∂x∂y
C=∂²f(x0,y0)/∂y²
∆=AC-B²
如果:∆>0
A0,f(x0,y0) 为极小值;
如果:∆0
f(0,0)=0 为最小值。
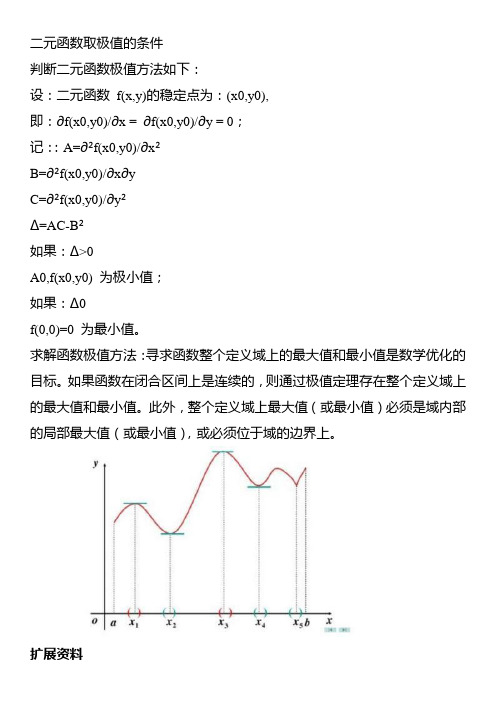
求解函数极值方法:寻求函数整个定义域上的最大值和最小值是数学优化的目标。
如果函数在闭合区间上是连续的,则通过极值定理存在整个定义域上的最大值和最小值。
此外,整个定义域上最大值(或最小值)必须是域内部的局部最大值(或最小值),或必须位于域的边界上。
扩展资料
判断函数极值定义:
若函数f(x)在x₀的一个邻域D有定义,且对D中除x₀的所有点,都有f(x)<f(x ₀),则称f(x₀)是函数f(x)的一个极大值。
同理,若对D的所有点,都有f(x)>f(x ₀),则称f(x₀)是函数f(x)的一个极小值。
极值的概念来自数学应用中的最大最小值问题。
根据极值定律,定义在一个有界闭区域上的每一个连续函数都必定达到它的最大值和最小值,问题在于要确定它在哪些点处达到最大值或最小值。
如果极值点不是边界点,就一定是内点。
因此,这里的首要任务是求得一个内点成为一个极值点的必要条件。
多元函数的极值和最值条件极值拉格朗日乘数法

当两种产品产量 为多少时? 可获得利润最大? 最大利润是多少?
解: 收益函数是 Rx, y pAx pB y 10x 9y
利润函数是
Lx, y Rx, y Cx, y
(10x 9 y) [400 2x 3y 0.013x2 xy 3y2 ]
(1)B2 AC 0 时具有极值,当 A 0或C 0时 有极大值, 当 A 0或C 0 时有极小值;
(2) B2 AC 0 时没有极值;
(3)B2 AC 0 时可能有极值,也可能没有极值.
求函数 z=f(x,y)极值的一般步骤:
第一步 解方程组 fx ( x, y) 0, f y ( x, y) 0
f x, y 3y2 6y 0 y
x 1
y1
10或
x 3 2 y2 2
得驻点 1,0, 1,2, 3,0, 3,2
(2)求二阶偏导数
f
x
x
x,
y
6
x
6;
f
yy
x,
y
6
y
6;
f
xy
x,
y
f
yx
减去总广告费, 两种方式的广告费共25千元, 怎样分配两种方式的广告费能使利润最大,最大
利润是多少?
解
约束条件下的利润函数为
Lx, y S 25,
5
具体利润函数为 L(x, y) 40x 20y 5 x 10 y
二元函数极值的定义

(2) AC B2 0时没有极值;
(3) AC B2 0时可能有极值,也可能没有极值,
还需另作讨论.
...
7
Yunnan
University
§1. 极值与最小二乘法
设f x, y在点 x0, y0 取到极值,则
则
f f x0 x, y0 y f x0 , y0
...
Yunnan University
f x, y0 f x0, y0 .
3
§1. 极值与最小二乘法
说明一元函数 f ( x, y0 )在 x x0处有极大值,
必有
f x ( x0 , y0 ) 0;
类似地可证
f y ( x0 , y0 ) 0.
推广:如果三元函数 u f ( x, y, z) 在点 P( x0 , y0 , z0 )
1=T1 ax1 b, 2=T2 ax2 b, , n=Tn axn bn ,
表示相应的偏差, 这些偏差的平方和叫做总偏差,
记为 ,即
n
= Ti axi b2 i 1
由极值的必要条件, 令
...
20
Yunnan
University
§1. 极值与最小二乘法
a
0
b
0
解之,得
n
注意: 偏导数存在的极值点
驻点
例如,点(0, 0)是函数 z xy 的驻点, zx y, zx (0,0) 0; z y x, z y (0,0) 0. 但点 (0, 0) 不是极值点.
...
5
Yunnan
University
§1. 极值与最小二乘法
函数在偏导数不存在的点仍然可能有极值。 例:
二元函数的极值

§10–7 二元函数的极值基础知识导学1. 二元函数的极值与驻点⑴ 极值与驻点①极值 设函数),(y x f z =在点),(000y x P 的某个邻域内有定义,如果对在此邻域内除点),(000y x P 外的任意点),(y x P ,均有),(),(00y x f y x f <(或),(),(00y x f y x f >),则称点),(000y x P 为函数),(y x f z =的极大值点(或极小值点).),(00y x f 称为极大值(或极小值),极大值点和极小值点统称为极值点,极大值和极小值统称为极值. ②驻点 使0),(,0),(==y x f y x f y x 同时成立的点),(y x 称为函数),(y x f z =的驻点.⑵ 极值存在的必要条件设函数),(y x f z =在点),(000y x P 的某个邻域内有定义,且存在一阶偏导数,如果),(000y x P 是极值点,则必有 0),( ,0),(0000==y x f y x f y x .注意 可导函数的极值点必定为驻点,但是函数),(y x f z =的驻点却不一定是极值点. ⑶极值存在的充分条件设函数),(y x f z =在点),(000y x P 的某个邻域内具有二阶连续偏导数,且),(000y x P 是驻点.设),(00y x f A xx =,),(00y x f B xy =,),(00y x f C yy =,则①当02<-AC B 时,点),(000y x P 是极值点,且当0<A 时,点),(000y x P 是极大值点;当0>A 时,点),(000y x P 是极小值点; ②当02>-AC B 时,点),(000y x P 不是极值点;③当02=-AC B 时,点),(000y x P 有可能是极值点也可能不是极值点.2.条件极值与拉格朗日乘数法⑴ 条件极值求多元函数的极值问题或最大值、最小值问题时,对自变量的取值往往要附加一定的约束条件,这类附有约束条件的极值问题,称为条件极值.⑵ 拉格朗日乘数法求函数),,(z y x f u =在满足约束条件0),,(=z y x ϕ下的条件极值,其常用方法是拉格朗日乘数法。
二元函数的极值与最值

2.二元函数的极值与最值二元函数的极值与最值问题已成为近年考研的重点, 现对二元函数的极值与 最值的求法总结如下: 1.二元函数的无条件极值 (1) 二元函数的极值一定在 驻点 和不可导点 取得。
对于不可导点,难以判断 是否是极值点;对于驻点可用极值的充分条件判定。
(2)二元函数取得极值的 必要条件 : 设 z f (x,y) 在点(x 0,y 0) 处可微分且在 点(x 0, y 0 )处有极值,则 f 'x (x 0,y 0) 0, f 'y (x 0, y 0) 0,即 (x 0,y 0) 是驻点。
(3) 二元函数取得极值的 充分条件 :设 z f (x,y) 在(x 0,y 0) 的某个领域内有 连续上 二阶偏导数,且 f 'x (x 0,y 0) f 'y (x 0, y 0) 0 ,令 f'xx (x 0,y 0) A , f'xy (x 0,y 0) B , f 'yy (x 0,y 0) C ,则当B 2AC 0且 A<0 时, f ( x 0 , y 0 )为极大值; 当B 2 AC 0且 A>0, f ( x 0 , y 0 )为极小值; B 2 AC 0 时,(x 0, y 0) 不是极值点。
注意: 当 B 2-AC = 0时,函数 z = f (x, y)在点( x 0 , y 0 )可能有极值,也可能没有 极值,需另行讨论 例 1 求函数 z = x 3 + y 2- 2xy 的极值. 【分析】可能极值点是两个一阶偏导数为零的点, 先求出一阶偏导, 再令其为零 确定极值点即可, 然后用二阶偏导确定是极大值还是极小值, 【解】先求函数的一、二阶偏导数:并求出相应的极值 . 2z 2 z z 3x 2y , 2y 2x . 26x ,xy x2zxy2z2y 2再求函数的驻点.令 z= 0,x得方程组23x 2y 0, 2y 2x 0.22求得驻点(0,0)、( 2,2).33利用定理 2 对驻点进行讨论:2.(1)对驻点(0, 0),由于 A = 0, B =-2, C = 2,B 2-AC 0,故(0, 0)不是函数 z = f(x, y) 的极值点.(2)对驻点( 2,2),由于 A =4, B =-2,C = 2,B 2-AC =-4 0, 且A 0,则 332 2 4 f ( 2,2) 4为函数的一个极小值.3 3 27例 2:( 2004数学一)设 z=z(x,y)是由 x 26xy 10 y 22yz z 218 0 确定的函 数,求 z z(x, y )的极值点和极值 .分析 】 本题把极值问题与隐函数求导方法相结合,计算量是比较大的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解 为求驻点,解联立方程组
f x'( x, y) 3x2 3 y 0
f
' y
(
x,
y)
3
y2
3
x
0
得到两个驻点:(0,0),(1,1)。
由于
f
'' xx
(0,0)
0,
f xy''(0,0)
3,
f
'' yy
(0,0)
0
故[ f xy''(0,0)]2
f
'' xx
有 f ( x,0) x2 ,即函数取负值,而对原点附近任何的 y,
f (0, y) y2 ,函数取正值。因此,原点(0,0)不是函数的极值点。
如果要求二元函数的极值点,应当从驻点或一阶偏导数不存在的点中 选取可能的极值点,为了判断所选的点是否是极值点,我们不加证明地给 出:
定理 3.6.2 设函数 z=f(x,y)的所有的二阶偏导数都在点 ( x0 , y0 ) 附
3
3 33
在该点处 S 3 3 R2 。 4
在闭区域 D 的边界上,即在直线 x=0,y=0 及 x y 2 上,S 恒等
于零,因此 S 在 ( 2 , 2 ) 处达到最大值,换言之,当 x y z 2 时,
33
3
即内接三角形为等边三角形时,其面积最大。
Hale Waihona Puke 以上我们讨论了二元函数的极值问题,系指自变量可任意取值,在不
受限制的情况下的极值,通常被称为无条件极值(unconditional extremum)。
有些实际问题求极值时,往往对自变量有一定的约束条件,这种带有约束
条件的极值被称为条件极值(conditional extremum)。
现在考虑函数 z=f(x,y)在约束条件φ (x,y)=0 之下的极值问题。显
x (0,0)
y (0,0)
其极大值点(0,0)就是驻点。而二元函数显然在(0,0)点有极小值
0,但在(0,0)点处,函数的两个一阶偏导数都不存在。此外,由定
理 3.12 可知,如果偏导数存在,那么,二元函数的极值点一定是驻点,
z x2 y2 ,但反之驻点却未必一定是极值点。例如,函数
z y2 x2 ,在原点处有 z 0, z 0 ,但对原点附近的任何 x 都 x y
F
'
(x,
y)
0
解以上的联立方程组,解出可能的极值点(x,y)。
3.由问题的实际意义来判定这样的点(x,y)和 是否是极值点,进而
求出要求的极值。
例 3.6.4 已知矩形周长为 2p,将它绕一边旋转而形成一个旋转体,当此旋
教学札记
转体体积为最大时,求此矩形两边之长。 解 设矩形的两边长为 x 和 y,则有 x+y-p=0,若矩形绕长为 y 的边旋
,
并
且
[
f
'' xy
(0,0)]2
f
'' xx
(0,0)
f
'' yy
(0,0)
4
0
由定理 3.6.2,(0,0)点不是 f(x,y)的极值点。
对于二元函数而言,极值也是局部性质。有些实际问题,要求二元函
教学札记 教学心得
数在某区域上的最大值和最小值。二元函数的最值点与一元函数类似,或 者出现在区域的边界上,或者是函数在区域内部的驻点和不可微点。我们 只需计算出函数在驻点和不可微点的值,再与函数在区域的边界上的值相 比较,便可从中找出函数的最大值和最小值。
值,极大值点与极小值点统称为极值点。 对于二元函数的极值,有明显的几何表示。例如,二元函数
f ( x, y) 1 x2 y2 在(0,0)处取得极大值 1,见图 3.6.1。
1
0.75
0z.5
1
0.25 0
0.5
-1
0y
-0.5 0
-0.5
定理
x 0.5
1 -1
3.6.1(极值存在的必要条件)如果函数
2
2
2
1 R2[sinx sin y sin(x y)] 2
这里 x 0, y 0, x y 2 。
y
我们的问题就是求 S 在闭区域
D {( x, y) x 0, y 0, x y 2 }
上的最大值。(见图 3.6.3)
D
x y 2
o
财经类管理类等专业财经类管理类等专业财经类管理类等专业极值极值点极值存在的条件极值极值点极值存在的条件极值极值点极值存在的条件条件极值条件极值条件极值理解极值极值点的概念学会判理解极值极值点的概念学会判理解极值极值点的概念学会判断极值的存在性会求条件极值断极值的存在性会求条件极值断极值的存在性会求条件极值利用多媒体进行启发式教学利用多媒体进行启发式教学利用多媒体进行启发式教学极值存在的条件条件极值极值存在的条件条件极值极值存在的条件条件极值条件极值条件极值条件极值在第343434节中我们讨论过一元函数的极值问题现在作为二元函数微分节中我们讨论过一元函数的极值问题现在作为二元函数微分节中我们讨论过一元函数的极值问题现在作为二元函数微分法的应用我们来考虑二元函数的极值
1.构造拉格朗日函数
F(x, y,) f (x, y) (x, y)
其中λ 为待定常数,称为拉格朗日乘数,把条件极值问题化为三元函数 F(x, y,λ )的无条件极值问题。
2.由极值存在的必要条件,令
Fx Fy
' '
f x'
' x
0
f y'
' y
0
( x0 , y0 ) 的某个邻域内有定义,且对该邻域内的任意点(x,y)都有 f ( x0 , y0 ) f ( x, y) (或f ( x0 , y0 ) f ( x, y))
则称函数 f(x,y)在 ( x0 , y0 ) 点处取得极大值(或极小值),称 ( x0 , y0 ) 为函数 f(x,y)的极大值点(或极小值点)。极大值与极小值统称为极
(0,0)
f
'' yy
(0,0)
9
0
由定理 3.6.2,(0,0)不是 f(x,y)的极值点。
又因为
f xx''(1,1)
6,
f
'' xy
(1,1)
3,
f
'' yy
(1,1)
6
故
[
f
'' xy
(1,1)]2
f
xx '' (1,1)
f
'' yy
(1,1)
27
0 ,由定理
3.16,f(x,y)在
近连续,且有
f x'( x0 ,
y0 )
0,
f
' y
(
x0
,
y0 )
0
记 那么
A
f
'' xx
(
x0
,
y0
),
B
f
'' xy
(
x0
,
y0
),C
f
(''
yy
x0 ,
y0
)
(1)当 B2 AC 0, A 0 时, f(x,y)在 ( x0 , y0 ) 处有极小值。 (2)当 B2 AC 0, A 0 时, f(x,y)在 ( x0 , y0 ) 处有极大值。 (3)当 B2 AC 0 时, f(x,y)在 ( x0 , y0 ) 处无极值。 例 3.6.1 求函数 f ( x, y) x3 y3 3xy 的极值。
然,如果我们能从φ (x,y)中解出 y=ψ (x),将其代入 z=(f x,y)中,对 z=f[x,
ψ (x)],我们便可作为一元函数来求极值了。但φ (x,y)若是一个复杂的函
数时,从中无法解出 y 或 x 来,上述方法就难于实现了。以下我们介绍求
教学札记 教学心得
条件极值常用的一种有效方法,即拉格朗日乘数法。具体步骤如下:
x
图 3.6.3
由于 S 在闭区域 D 上连续,根据连续函数的最大值最小值定理,S 在 D 上 必有最大值,最大值点或者是驻点,或者是边界点。为求驻点,我们解方 程组
S
x
'
1 2
R2[cos
x
cos( x
y)]
0
S
y
'
1 2
R2[cos
y
cos( x
y)]
0
在 D 的内部,方程组有唯一解, x 2 , y 2 , ( 2 , 2 ) 就是驻点,
第 3.6 节二元函数的极值与条件极值
微积分教学设计
教学札记
教学对象:财经类,管理类等专业
教学内容:极值、极值点、极值存在的条件、
条件极值
教学目的:理解极值、极值点的概念,学会判
断极值的存在性,会求条件极值
教学方法:利用多媒体进行启发式教学
教学重点:极值存在的条件、条件极值
