切比雪夫Ⅰ型滤波器和切比雪夫Ⅱ型滤波器的对比
IIR数字滤波器的群延时优化设计和实现论文设计
根据式（2.6）我们可以直接画出直接型结构的信号流图，如图2-1所示：
2.级联型结构
对 滤波器的系统函数进行因式分解，可以将直接型结构转变成多个一阶或二阶子网络构成的级联型网络，即：
（2.7）
数字滤波器级联型结构如图2-2所示。在该结构中，可以方便的通过控制各阶网络来控制零点位置。因此级联型结构适用于需要对系统零点进行控制的系统。由于该结构系统函数的系数较多，使得函数拆项后产生的因子较多，所以需要更多的乘法器。由于阶数较高 滤波器系统函数不易进行拆项，因此在设计高阶滤波器时，一般选择直接型结构。
表2-2IIR低通滤波器特性对比
通过表2-2可以得出，虽然巴特沃斯型滤波器的相位线性度较好，但是所需要的阶数比较高。切比雪夫Ⅰ型滤波器的线性度适中。而采用椭圆型滤波器所需滤波器的阶数最低，具有高度非线性相位，但是其频率选择性好，可以达到较好的滤波效果。
通过对 和 滤波器的比较分析，综合考虑系统频率选择性、设计难以程度等，本文将提出适用于级联型 数字滤波器的群延时优化方案。
Keywords: digital filter; group delay optimization; all-pass network equalizer; filter design;
1
1.1
现代社会早已进入数字化时代，数字信号处理技术突飞猛进，其理论算法以及实现手段均获得了较快的发展，已经成为一门必不可少的学科和技术领域。其主要内容包括对信号进行滤波、转换等一系列加工处理[2]。数字滤波技术作为数字信号处理的关键部分开始引起了人们越来越多的关注与研究。
比较直接Ⅰ型与直接Ⅱ型可知，后者比前者所需结构延时单元少，可以节省更多寄存器，更加经济。
2.级联型结构
第五章-3 切比雪夫低通滤波器
α max
切比雪夫滤波器的幅度平方函数
1 H (ω ) = 1.0357016 ω 4 − 1.0357016 ω 2 + 1.25892541
2
1 H ( s) H (− s) = 1 .0357016 s 4 + 1 .0357016 s 2 + 1 .25892541
幅度平方函数的极点
令
s 2 = −ω 2
s1 = 1.0500049e j 58.48 s 2 = 1.0500049e j121.52 s3 = 1.0500049e − j121.52 s 4 = 1.0500049e − j 58.48
系统函数H(s)的极点由幅度平方函数的左半 平面极点（s 2 , s 3 ）决定，由于n为偶数，有
1、低通滤波器转换成高通滤波器
H (ω )
低通滤波器
高通滤波器
0
ω
1、低通滤波器转换成高通滤波器
归一化低通到归一化高通的频率变换可表示为
1 sL = sH
归一化频率之间的关系为 1 ωL = ωH
将平面上的低通特 性变换为平面上的 高通特性
当ωL为0→1时，则ωH取 值为∞→1；当ωL为1→∞ 时，则ωH取值为1→0。滤 波器低通的通带变换到高 通的通带，而低通的阻带 变换到高通的阻带。
1、巴特沃思低通滤波器与切 比雪夫低通滤波器的比较
H (ω )
巴特沃思低 通滤波器
切比雪夫低 通滤波器
0
ω
三阶巴特沃思低通滤波器和切比雪夫低通滤波器幅频特性
1、巴特沃思低通滤波器与切 比雪夫低通滤波器的比较
切比雪夫滤波器是由切比雪夫多项式的正交函数 推导出来的，采用了在通带内等波动，在通带外 衰耗单调递增的准则去逼近理想滤波器特性。 在通带内是等波纹的，在阻带内则是单调下降 的，称为切比雪夫Ⅰ型。 在通带内是单调的，在阻带内是等波纹的，称为 切比雪夫Ⅱ型。
基于切比雪夫1的IIR低通滤波器
课程设计课程设计名称：DSP课程设计专业班级：电信1005班学生姓名：学号：指导教师：李相国课程设计时间：2013年6月数字信号处理专业课程设计任务书说明：本表由指导教师填写，由教研室主任审核后下达给选题学生，装订在设计（论文）首页填表说明1．“课题性质”一栏：A．工程设计；B．工程技术研究；C．软件工程（如CAI课题等）；D．文献型综述；E．其它。
2．“课题来源”一栏：A．自然科学基金与部、省、市级以上科研课题；B．企、事业单位委托课题；C．校、院（系、部）级基金课题；D．自拟课题。
1 需求分析数字滤波器是指完成信号滤波处理功能的，用有限精度算法实现的离散时间线性非时变系统，其输入是一组数字量，其输出是经过变换的另一组数字量。
因此，它本身即可以是用数字硬件装配成的一台完成给定运算的专用数字计算机，也可以是将所需运算编成程序，让通用计算机来执行。
在本次课程设计中，我做的是基于双线性变换法设计 Chebyshev-I 型 IIR 数字低通滤波器，看到这个题目，我们很快就能联系到数字信号处理中的 IIR 数字滤波器的设计，根据以前学习的东西我们知道，要想设计一个数字低通滤波器，我们可以把所给的数字指标转换为模拟参数，通过设计一个模拟低通的滤波器，对设计好的模拟低通滤波器进行数字化就可以得到一个数字低通滤波器。
在本次实验中，我们首先将所给的滤波器数字指标转换为模拟指标，利用Chebyshev-I型函数设计一个 Chebyshev-I 型低通模拟滤波器，然后对所设计好的 Chebyshev-I型低通模拟滤波器进行参数分析，接下来利用双线性变化法将此模拟低通滤波器转变为数字低通滤波器。
2 概要设计3 运行环境PC 机，windows2000及其以上，matlab 软件。
4 开发工具和编程语言MATLAB 软件，编程语言为DSP 设计语言。
5 详细设计第一步：将数字低通滤波器的性能指标转化成模拟低通滤波器指标Chebyshev-I 型IIR 数字低通滤波器的性能指标：p ω=0.25π，s ω=0.4π，p δ=0.01，s δ=0.001程序模块： %转化成模拟量 rp=-20*log10(1-lp); rs=-20*log10(ls); Omgp=tan(wp/2) Omgs=tan(ws/2) Fs=0.5;第二步：利用切比学夫逼近法设计模拟滤波器切比雪夫1低通滤波器的原理：幅度平方函数为： 其中ε为小于1的正数，表示通带内幅度波动的程度，p Ω称为通带截止频率。
巴特沃斯Ⅱ型低通滤波器和切比雪夫Ⅱ型低通滤波器IIR低通数字滤波器设计
巴特沃斯Ⅱ型低通滤波器和切比雪夫Ⅱ型低通滤波器I I R低通数字滤波器设计(总24页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--南华大学课程设计报告课程名称：数字通信课程设计设计名称： IIR低通数字滤波器设计姓名： XXXX学号: xxxx班级：xxxx指导教师：XXXX起止日期：南华大学电气工程学院制课程设计任务书学生班级： xxxx 学生姓名： phatonic 学号： XXXXXXXX 设计名称：IIR低通数字滤波器设计起止日期：指导教师： XX课程设计学生日志课程设计考勤表课程设计评语表IIR低通数字滤波器设一、设计目的和意义目的：1.深入理解数字信号处理基础知识的理解；2.加深对MATLAB基础知识的理解；3.掌握低通数字滤波器的设计方法；4.了解冲激响应不变法的基本原理和特点；5.了解双线性变换法的基本原理和特点；意义：通过课程设计设计可以加深我们对课本基础知识的理解，对已经学习的知识进行实践训练，起到了理论联系实践的作用。
在设计过程中，一定会遇到很多的困难和问题，在解决问题的过程中，不仅锻炼了我解决实际问题的能力，而且也培养了我设计的综合能力。
总之，理论联系实践，对我来说是非常的重要。
IIR低通数字滤波器设计是滤波器设计中很经典的问题，而滤波器设计则是是《数字信号处理》的核心内容。
所以，IIR低通数字滤波器设计是数字信号处理的经典内容。
二、设计原理1.数字滤波器原理与模拟滤波器类似，数字滤波器按频率特性划分为低通、高通、带通、带阻、全通等类型。
由于频率响应的周期性，频率变量以数字频率w来表示（w=ΩT=Ω/fs, Ω为模拟角频率，T为抽样时间间隔，fs为抽样频率），所以数字滤波器设计中必须给出抽样频率。
一般情况下，数字滤波器是一个线性移不变离散时间系统，利用有限精度算法来实现。
具体的实现方法有很多，不过主流的方法是：先设计出对应的模拟滤波器，再将模拟滤波器数字化为数字滤波器。
切比雪夫滤波器
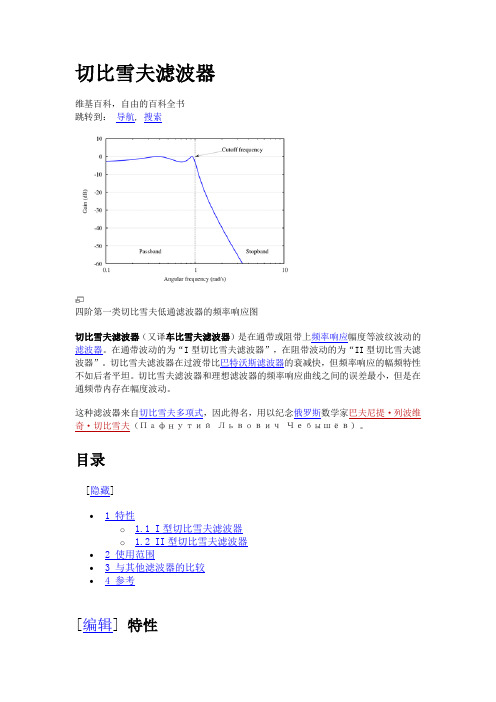
切比雪夫滤波器维基百科，自由的百科全书跳转到：导航, 搜索四阶第一类切比雪夫低通滤波器的频率响应图切比雪夫滤波器（又译车比雪夫滤波器）是在通带或阻带上频率响应幅度等波纹波动的滤波器。
在通带波动的为“I型切比雪夫滤波器”，在阻带波动的为“II型切比雪夫滤波器”。
切比雪夫滤波器在过渡带比巴特沃斯滤波器的衰减快，但频率响应的幅频特性不如后者平坦。
切比雪夫滤波器和理想滤波器的频率响应曲线之间的误差最小，但是在通频带内存在幅度波动。
这种滤波器来自切比雪夫多项式，因此得名，用以纪念俄罗斯数学家巴夫尼提·列波维奇·切比雪夫（ПафнутийЛьвовичЧебышёв）。
目录[隐藏]• 1 特性o 1.1 I型切比雪夫滤波器o 1.2 II型切比雪夫滤波器• 2 使用范围• 3 与其他滤波器的比较• 4 参考[编辑]特性[编辑] I型切比雪夫滤波器I型切比雪夫滤波器最为常见。
n阶第一类切比雪夫滤波器的幅度与频率的关系可用下列公式表示：其中：••而是滤波器在截止频率ω0的放大率 (注意: 常用的以幅度下降3分贝的频率点作为截止频率的定义不适用于切比雪夫滤波器!)•是n阶切比雪夫多项式：或:切比雪夫滤波器的阶数等于此滤波器的电子线路内的电抗元件数。
切比雪夫滤波器的幅度波动 = 分贝当,切比雪夫滤波器的幅度波动= 3分贝。
如果需要幅度在在阻频带边上衰减得更陡峭，可允许在复平面的jω轴上存在零点。
但结果会使通频带内振幅波动较大，而在阻频带内对信号抑制较弱。
这种滤波器叫椭圆函数滤波器或考尔滤波器。
[编辑] II型切比雪夫滤波器也称倒数切比雪夫滤波器，较不常用，因为频率截止速度不如I型快，也需要用更多的电子元件。
II型切比雪夫滤波器在通频带内没有幅度波动，只在阻频带内有幅度波动。
II型切比雪夫滤波器的转移函数为：参数ε与阻频带的衰减度γ有如下关系：分贝。
5分贝衰减度相当于ε = 0.6801; 10分贝衰减度相当于ε = 0.3333。
信号处理课件第6章无限冲激响应(IIR)滤波器设计
3. 滤波器的技术要求
低通：
：通带允许的最大衰减； ：阻带内应达到的最小衰减
单位 (dB)
若幅度下降到 0.707, 则幅平方下降 0.5 （半 功率点）：
若幅度下降到 0.01：
高通：
：通带允许的最大衰减； ：阻带内应达到的最小衰减
带通：
：通带允许的最大衰减； ： 阻带内应达到的最小衰减
带阻：
最直接到方法，将：
p ,s , p ,s
利用：
利用上一节的方法，可设计出模拟滤波器
G( p), G(s)
H(z)
H (z) G(s) s 1 ln z Ts
但这样做，H (z) 将不再是 z 的有理多项式，给
极－零分析带来困难。
数字滤波器的 单位抽样响应
模拟滤波器 的冲激响应
令：
冲激响应 不变法
（2）
b, a 是AF LP 的分子、分母的系数向量，B, A是转换后 的的分子、分母的系数向量；在（1）中，Wo是低通或 高通滤波器的截止频率；在（2）中，Wo是带通或带阻 滤波器的中心频率，Bw是其带宽。
4．bilinear.m ：双线性变换，由模拟滤波器 得到数字滤波器。
[Bz, Az]=bilinear(B, A, Fs) 式中B, A分别是G（s）的分子、分母多项式 的系数向量，Bz, Az分别是H(z)的分子、分 母多项式的系数向量，Fs是抽样频率。
2. 切比雪夫I型(Chebyshev-I)滤波器
3. 切比雪夫II型滤波器
4. 椭圆滤波器
Un2() ：Jacobian 函数 本课程只讨论 Butterworth 和 Chebyshev-I
滤波器的设计
二、Butterworth滤波器的设计
理想低通滤波器
切比雪夫滤波器2型滤波器：
Ha(
j)
2
1
2
1
TN (s / p ) 2
TN (s
/ )
传输函数： N
(s zl )
() : Ha (s) C0
l 1 N
, pl l jl ,l 1,2, , N.
(s pl )
l 1
, , sl l l2l2
sl
l
l2 l2
l
p
s
in[
H D (sˆ) ˆ
HLP (s) HD (sˆ) sF(sˆ)
HD (sˆ) HLP (s) sˆF1(s)
变换 : s 平面
sˆ 平面
B.1 模拟高通滤波器设计
s
pˆ p sˆ
pˆ ˆ
p
ˆ
0
p
p
ˆ p
p ˆ p
Hhp
sˆ
Hlp
s
s
pˆ
sˆ
p
,
ˆ p
p ˆ p ˆ
j)
2
1
1 2R（N2
/
）
p
其中RN（x）是雅可比(Jacobi) 椭圆函数，ε为与通带衰
减有关的参数。
特点： 1、椭圆低通滤波器是一种零、极点型滤波器，它在有限频 率范围内存在传输零点和极点。 2、椭圆低通滤波器的通带和阻带都具有等波纹特性，因此 通带、阻带逼近特性良好。 3、对于同样的性能要求，它比前两种滤波器所需用的阶数 都低，而且它的过渡带比较窄。
椭圆滤波器 [z,p,k]=ellipap(N,Rp,Rs) [num,den]=ellip(N,Rp,Rs,Wn,’s’) [num,den]=ellip(N,Rp,Rs,Wn,’type’,’s’) [N,Wn]=ellipord(Wp,Ws,Rp,Rs,’s,’) 贝塞尔滤波器滤波器 [z,p,k]=besselap(N) [num,den]=besself(N,Wn) [num,den]=besself(N,Wn,’type’)
基于切比雪夫I型的IIR数字高通滤波器设计
《数字信号处理》课程设计题目：基于切比雪夫I型的IIR数字高通滤波器设计学院名称电气工程学院指导老师班级电子信息工程学号学生姓名二0一一年六月目录（一）数字滤波器的概述-------------------------------------------3 1.1 数字滤波器的设计方法------------------------------------------------3 1.2 数字滤波器的性能要求------------------------------------------------3 1.3 数字滤波器的技术要求------------------------------------------------4 （二）基于切比雪夫I型无限脉冲响应IIR数字高通滤波器的设计依据和原理----------------------------------------------------5 2.1 课设任务------------------------------------------------------------------5 2.2 IIR数字滤波器-----------------------------------------------------------5 2.3由模拟滤波器设计IIR数字滤波器---------------------------------7 2.4 数字高通滤波器的设计（本设计采用双线性变换法）--------9 （三）基于切比雪夫I型无限脉冲响应IIR数字高通滤波器的具体设计过程-----------------------------------------------------12 3.1 计算过程-----------------------------------------------------------------12 3.2 源程序代码--------------------------------------------------------------14 3.3结果分析------------------------------------------------------------------17 （四）总结和心得体会--------------------------------------------20 （五）参考文献-----------------------------------------------------21基于切比雪夫I 型的IIR 数字高通滤波器设计（一）数字滤波器的概述 1.1 数字滤波器的设计方法数字滤波器的设计方法有多种，如双线性变换法、窗函数设计法、插值逼近法和Chebyshev 逼近法等等。
filter solutions 设计滤波器笔记总结
用Filter solutions设计滤波器笔记要求：分别设计5阶切比雪夫1型带通滤波器、切比雪夫2型带通滤波器，中心频率500MHz，带宽50MHz。
尝试选用不同的电路结构，观察所用元器件的值有何变化。
切比雪夫1型滤波器：通带中等纹波，阻带是单调的切比雪夫2型滤波器：通带中单调，阻带等纹波，即阻带中有零点（陷波点）。
（1）5阶切比雪夫1型带通滤波器：通带中等纹波，阻带是单调的图1：参数设置注释：Asymmetrical非对称的，只有带通滤波器才有此选项，用于设计非对称结构的滤波器。
Delay Equalize延迟补偿，低通和带通滤波器才有此选项，用于低通滤波器或者带通滤波器的通带群延迟补偿。
延迟补偿的概念：Tx Line:Transmission Line 传输线滤波器Sw Cap:Switched Capacitor开关电容滤波器，Active：有源滤波器，Passive:无源滤波器，Digital:数字滤波器，1st Ele Shunt:滤波器电路结构的第一个元件是并联电感。
1st Ele Series:滤波器电路的第一个元件是串联电容。
Incl Source Bias：Check to include the bias due to the source resistance to appear in the transfer function, frequency response, impedance response, and time response of your filter. For example, if the source resistance is equal to the load resistance, checking this box will cause a -6dB offset will appear in the frequency response, and a factor of .5 will appear in the transfer function and time response. This offset goes away when this box is left unchecked.This box should be left unchecked when using the transfer function for any purpose other than passive filters applications.Complex Terminations:创建滤波器复杂的驱动终端，即自定义滤波器的源终端。
切比雪夫滤波器结构
切比雪夫滤波器结构1.引言1.1 概述切比雪夫滤波器是一种常用的数字滤波器，它以俄罗斯数学家彼得·勃列兹尼卡诺夫（Peter Chebyshev）的名字命名。
切比雪夫滤波器的设计基于切比雪夫多项式，具有一些独特的特点和优势。
切比雪夫滤波器本质上是一种频率选择性滤波器，用于在数字信号处理中滤除指定频率范围的噪声或干扰。
与其他滤波器相比，切比雪夫滤波器在频率响应方面具有更强的灵活性和自由度。
它可以实现对特定频率信号的很好衰减，同时保持较为平坦的通带响应。
该滤波器的设计主要基于两个关键因素：过渡带宽和阻带衰减。
过渡带宽是指从通带到阻带的过渡区域，而阻带衰减则是指在阻带内信号的衰减量。
切比雪夫滤波器的结构特点在于其衰减特性可调节，可以根据特定需求选择不同的阻带衰减量。
这使得切比雪夫滤波器在一些应用场景中具有较大的优势，例如在语音和音频处理中，可以有效滤除噪声，提高信号质量。
此外，切比雪夫滤波器还具有一些其他优点，如具有较为紧凑的滤波器结构、较低的实现成本和较高的运算速度等。
这使得它在实际工程中得到了广泛应用。
总之，切比雪夫滤波器是一种功能强大且灵活的数字滤波器。
通过调节其阻带衰减量，可以根据具体需求实现不同的滤波效果。
在各种应用领域中，切比雪夫滤波器都具有重要的作用，并具有广阔的应用前景。
1.2文章结构1.2 文章结构本文将按照以下结构进行论述切比雪夫滤波器的结构和特点：1.2.1 引言在引言部分，将对切比雪夫滤波器进行概述，介绍其在信号处理领域的应用背景，以及本文对切比雪夫滤波器结构的研究目的。
1.2.2 切比雪夫滤波器的定义和原理在本节中，将详细介绍切比雪夫滤波器的定义和原理。
首先解释什么是切比雪夫滤波器，其基本工作原理，并讨论切比雪夫滤波器相对于其他类型滤波器的优势和适用场景。
1.2.3 切比雪夫滤波器的结构和特点该部分将重点介绍切比雪夫滤波器的结构和特点。
首先详细描述切比雪夫滤波器的不同组成部分，例如传输函数、零极点分布等。
IIR滤波器和FIR滤波器的区别与联系
IIR滤波器和FIR滤波器的区别与联系1.两种滤波器都是数字滤波器。
根据冲激响应的不同，将数字滤波器分为有限冲激响应（FIR）滤波器和无限冲激响应（IIR）滤波器。
对于FIR滤波器，冲激响应在有限时间内衰减为零，其输出仅取决于当前和过去的输入信号值。
对于IIR滤波器，冲激响应理论上应会无限持续，其输出不仅取决于当前和过去的输入信号值，也取决于过去的信号输出值。
2.FIR：有限脉冲响应滤波器。
有限说明其脉冲响应是有限的。
与IIR相比，它具有线性相位、容易设计的优点。
这也就说明，IIR滤波器具有相位不线性，不容易设计的缺点。
而另一方面，IIR却拥有FIR所不具有的缺点，那就是设计同样参数的滤波器，FIR比IIR需要更多的参数。
这也就说明，要增加DSP 的计算量。
DSP需要更多的计算时间，对DSP的实时性有影响。
以下都是低通滤波器的设计。
FIR的设计：FIR滤波器的设计比较简单，就是要设计一个数字滤波器去逼近一个理想的低通滤波器。
通常这个理想的低通滤波器在频域上是一个矩形窗。
根据傅里叶变换我们可以知道，此函数在时域上是一个采样函数。
通常此函数的表达式为：sa（n）＝sin（n∩）/n∏，但是这个采样序列是无限的，计算机是无法对它进行计算的。
故我们需要对此采样函数进行截断处理。
也就是加一个窗函数。
就是传说中的加窗。
也就是把这个时域采样序列去乘一个窗函数，就把这个无限的时域采样序列截成了有限个序列值。
但是加窗后对此采样序列的频域也产生了影响：此时的频域便不在是一个理想的矩形窗，而是成了一个有过渡带，阻带有波动的低通滤波器。
通常根据所加的窗函数的不同，对采样信号加窗后，在频域所得的低通滤波器的阻带衰减也不同。
通常我们就是根据此阻带衰减去选择一个合适的窗函数。
如矩形窗、汉宁窗、汉明窗、BLACKMAN窗、凯撒窗等。
选择一个具体的窗函数之后，根据所设计滤波器的参数来计算所需的阶数、此窗函数的表达式。
然后用这个窗函数去和采样序列相乘，就可以得到实际滤波器的脉冲响应。
切比雪夫1型滤波器讲解
目录1课题描述 (1)2设计原理 (1)2.1滤波器的分类 (1)2.2模拟滤波器的设计指标 (1)2.3切比雪夫1型滤波器 (2)2.3.1切比雪夫1型滤波器的设计原理 (3)2.3.2切比雪夫1型滤波器的设计步骤 (3)3脉冲响应不变法3.1 脉冲响应不变法原理 (6)4设计内容 (6)4.1设计步骤 64.2用MATLAB编程实现 (6)4.3设计结果分析 (10)5总结 (10)6参考文献 (10)1课题描述数字滤波器是数字信号处理的重要工具之一，它通过数值运算处理改变输入信号所含频率成分的相对比例或者滤出某些频率成分的数字器件或程序，二数字滤波器处理精度较高，体积小，稳定，重量轻，灵活，不存在阻抗匹配问题，可以实现模拟滤波器无法实现的特殊功能。
故本书课题使用MATLAB信号处理箱和运算用切比雪夫法设计数字低通滤波器。
利用脉冲响应不变法设计切比雪夫Ⅰ数字低通滤波器，通带截止频率100hz，阻带截止频率150Hz，采样频率1000hz，通带最大衰减为0.5dB，阻带最小衰减为10dB，画出幅频、相频响应曲线，并设计信号验证滤波器设计的正确性。
设计原理2.1. 滤波器的分类（1）从功能上分；低、带、高、带阻。
（2）从实现方法上分:FIR、IIR（3）从设计方法上来分：Chebyshev(切比雪夫）,Butterworth（巴特沃斯）（4）从处理信号分：经典滤波器、现代滤波器2.2 模拟滤波器的设计指标设ha（jΩ）是一个模拟滤波器的频率响应，则基于平方幅度响应J (Ω) = Ha(jΩ)的低通滤波器技术指标为： 0≤∣Ha (jΩ)∣≤1/A^2,Ωs≤∣Ω∣其中ε为通带波动系数，pΩ和sΩ是通带和阻带边缘频率。
A为阻带衰减系数从图知必须满足其中参数ε和A是数字滤波器指标2.3切比雪夫1型滤波器2.3.1 切比雪夫滤波器介绍在巴特沃兹滤波器中，幅度响应在通带和阻带内都是单调的。
因此，若滤波器的技术要求是用最大通带和阻带的逼近误差来给出的话，那么，在靠近通带低频端和阻带截止频率以上的部分都会超出技术指标。
切比雪夫1型滤波器概要
目录1 课题描述,,,,,,,,,,,,,,,,,,,,,,,,,, 12 设计原理,,,,,,,,,,,,,,,,,,,,,,,,,, 12.1 滤波器的分类,,,,,,,,,,,,,,,,,,,,,, 12.2 模拟滤波器的设计指标,,,,,,,,,,,,,,,,,, 12.3 切比雪夫1型滤波器,,,,,,,,,,,,,,,,,,, 22.3.1 切比雪夫1 型滤波器的设计原理,,,,,,,,,,, 32.3.2 切比雪夫1 型滤波器的设计步骤,,,,,,,,,,, 33 脉冲响应不变法3.1 脉冲响应不变法原理,,,,,,,,,,,,,, 64 设计内容,,,,,,,,,,,,,,,,,,,,,,,,,,, 61< I I ~4 I~I JJJJJJJJJJJJJJJJJJJJJJJJJJJ4.1 设计步骤64.2 用MATLA编程实现64.3 设计结果分析,,,,,,,,,,,,,,,,,,,,,, 105 总结,,,,,,,,,,,,,,,,,,,,,,,,,,,,, 106 参考文献101 课题描述数字滤波器是数字信号处理的重要工具之一，它通过数值运算处理改变输入信号所含频率成分的相对比例或者滤出某些频率成分的数字器件或程序，二数字滤波器处理精度较高，体积小，稳定，重量轻，灵活，不存在阻抗匹配问题，可以实现模拟滤波器无法实现的特殊功能。
故本书课题使用MATLAB信号处理箱和运算用切比雪夫法设计数字低通滤波器。
利用脉冲响应不变法设计切比雪夫I数字低通滤波器，通带截止频率100hz，阻带截止频率150Hz，采样频率1000hz，通带最大衰减为0.5dB，阻带最小衰减为10dB，画出幅频、相频响应曲线，并设计信号验证滤波器设计的正确性。
设计原理2.1. 滤波器的分类(1)从功能上分；低、带、高、带阻。
(2)从实现方法上分：FIR、IIR(3)从设计方法上来分：Chebyshev(切比雪夫)，Butterworth (巴特沃斯)(4)从处理信号分：经典滤波器、现代滤波器2.2 模拟滤波器的设计指标设ha( j ?)是一个模拟滤波器的频率响应，则基于平方幅度响应J (?) =Ha(j ?)的低通滤波器技术指标为：0 <1 Ha (j ?) I < 1/A A2, ? s<l ? I其中&为通带波动系数，P?和s?是通带和阻带边缘频率。
切比雪夫Ⅰ型滤波器和切比雪夫Ⅱ型滤波器的对比
设计流程图如下:设计思想：首先设计一个源信号和一个混合信号，通过其频谱对比得出最大和最小通带，最大和最小阻带;然后再根据得到的参数来设计切比雪夫滤波器，最后通过切比雪夫I型滤波器和切比雪夫1［型滤波器的对比来得出那种效果好。
切比雪夫滤波器设计原理：切比雪夫滤波器的振幅具有等波纹特性，它有两种形式：1)振幅特性在通带内是等波纹的、在阻带内是单调的切比雪夫I型滤波器：2)振幅特性在通带内是单调的、在阻带内是等波纹的切比雪夫II型滤波器，采用何种形式的切比雪夫滤波器取决于实际用途.切比雪夫滤波器的设计方法就是将逼近精确度均匀分布在整个通带内，或者均匀分布在整个阻带内，或者均匀分布在两者之内，这样就可以使滤波器阶数大大降低。
切比雪夫I型滤波器平方幅度响应函数表示为：|G(JC)卜[l+0c； (Q)]-,/2其中£〈1(正数)，它与通带波纹有关，0越大，波纹也越大；G(Q)是切比雪夫多项式，它被定义为：C“(G)二cos (Narccos (O)),阿W1, C A, (Q)二cosh(Narcosh(Q)), |Q| >1.而切比雪夫II型滤波器平方幅度响应函数表示为：|G(_/G)|2二{]+，{ C2 (G)/[: (Q/fX-)]2}}-1其中&〈1(正数)，表示波纹变化情况；Cc为截止频率；艸为滤波器的阶次，也是C N (Q/Q.v)的阶次。
源信号编码及其图形：t=-l::1y=(cos(2*pi*10*t)+cos (2*pi*40*t));N=length(y);f X二f f t (y);df二100/N;n二0:N/2;f=n*df;subplot (2, 1, 1);plot(f, abs(fx(n+1))*2/N); grid;titleC源波形频谱')源波形频谱图（一）混合信号编码及其图形：t二T: :1;X二(cos(2*pi*10*t)+cos(2*pi*25*t)+cos (2*pi*40*t)); N二length(X);fx=fft(X);df二100/N;n二0:N/2;f二n*df;subplot (2, 1, 2);plot(f, abs(fx(n+1))*2/N); grid;titleC混合波形频谱')图（二）从图（一）和图（二）对比可以得出：为了能达到和满足我们的要求，我们取以下的参数，最大通带wp2：,最小通带wpl:,最大阻带ws2：,最小阻带wsl：o切比雪夫I型滤波器设计如下：wsl=*p i；ws2=*p i ；%滤波器的阻带截止频率wpl=*pi;wp2=*pi ; %滤波器的通带截止频率Rp二l;As二20; %滤波器的通阻带衰减指标%转换为模拟滤波器的技术指标T=;Fs=l/T;Omgpl二(2/T)*tan(wpl/2);Omgp2二(2/T)*tan(wp2/2);Omgp二[Omgpl, Omgp2];Omgsl=(2/T)*tan(wsl/2);Omgs2=(2/T)*tan(ws2/2);Omgs=[Omgsl, Omgs2];bw=Omgp2-Omgpl ;wO=sqrt (Omgpl*Omgp2) ; %模拟通带带宽和中心频率rip P le=10' (-Rp/20) ; %滤波器的通带衰减对应的幅度值Attn二10" (-As/20) ; %滤波器的阻带衰减对应的幅度值%模拟原型滤波器计算[n, Omgn]=cheblord (Omgp, Omgs, Rp, As,' s,) %计算阶数n 和截止频率[zO, pO, kO]=cheblap (n, Rp) ; %设计归一化的模拟滤波器原型bal=kO*real (poly (z0)) ; %求原型滤波器的系数baal=real (poly(pO)) ; %求原型滤波器的系数d[ba, aa]=lp2bs (bal, aal, wO, bw);%用双线性变换法讣算数字滤波器系数[bd, ad] =bilinear (ba, aa, Fs)%求数字系统的频率特性[H, w]=freqz (bd, ad);dbH=20*logl0((abs(H)+eps)/max(abs(H)));subplot ⑵ 2, 1):plot(w/pi, abs(H));ylabel (, H ') ;xlabel 频率(\pi)') ; title ('幅度响应'):axis([0,1, 0,]); set(gca,' XTickMode',，manual1，‘ XTick', [0,,,,]);set(gca, ' YTickMode',' manual*,' YTick，, [0, Attn, ripple, 1J);grid幅度响应频率何图(三)n =3Omgn =bd 二ad 二分析：由图(三)运行结果可知，最大通带，最小通带，最大阻带，最小阻带; 切比雪夫I型滤波器的设计的个性技术指标精确度是均匀分布的。
四种低通滤波器的软件设计与性能比较
有等波纹特性，它有两种形式：1)振幅特性在通带内是等波纹的、在阻带内是单调的 切比雪夫 I 型滤波器；2)振幅特性在通带内是单调的、在阻带内是等波纹的切比雪夫 II 型滤波器，采用何种形式的切比雪夫滤波器取决于实际用途。
研究方法：Ｍatlab 设计程序。MATLAB 语言是一种简单、高效的高级语言, 是 一种内容丰富、功能强大的分析工具, 其应用范围几乎覆盖了所有的科学和工程计算 领域。MATLAB 中提供了丰富的用于模拟滤波器设计的函数, 通过编程可以很容易 实现低通、高通、带通、带阻滤波器, 并能画出滤波器的幅频特性曲线, 大大简化了 模拟滤波器的设计。本文通过传统方法与 MATLAB 编程方法的比较, 研究了用 MATLAB 实现巴特沃斯滤波器设计的。
巴特沃斯低通滤波器切比雪夫滤波器椭圆滤波器在阶数相同时有不同的幅频特性和不同的相频特性通过比较巴特沃斯低通滤波器切比雪夫型滤波器切比雪夫型滤波器椭圆滤波器等四种低通滤波器在同一阶数的幅频特性函数图形和相频特性函数图形选出性能最优的滤波器
题 目四种低通滤波器的软件设计景、目的及现实意义） 背景：美国在 1917 年发明了世界上第一台无源滤波器，50 年代无源滤波器才逐
意义：数字滤波器是现代测控系统中的重要部件, 传统设计方法的设计过程繁琐。 对传统方法与 MATLAB 编程方法进行了比较, 研究了用 MATLAB 实现巴特沃斯滤 波器的设计, 只要改变程序中相应的参数可以很容易地实现低通、高通、带通、带阻 滤波器, 简化了模拟滤波器的设计。在数字信号处理中, 数字滤波器十分重要并已获 得广泛应用, 数字滤波器与模拟滤波器比较, 具有精度高、稳定、体积小、重量轻、 灵活、不要求阻抗匹配以及实现模拟滤波器无法实现的特殊滤波功能等优点。
创新之处：对四种低通滤波器一起进行设计，在同一指数下比较性能。
切比雪夫滤波器设计
切比雪夫滤波器一 切比雪夫模拟滤波器1 切比雪夫多项式切比雪夫的振幅平方特性可以用切比雪夫多项式表示，所以这里首先简单介绍一下它的相关知识。
用)(Ωn C 表示n 阶切比雪夫多项式，当1||≤Ω时，)(Ωn C 可用下式定义：1||),cos cos()(≤ΩΩ=Ωnar C n进一步，可以将其表示为：n n n n n n c c c c C +Ω++Ω+Ω+Ω=Ω---12211)(2 切比雪夫1型模拟滤波器切比雪夫1型滤波器的振幅平方特性可以表示为：,2,1,)(11|)(|2221=Ω+=Ωn C j H n ε 或者,2,1,)/(11|)(|2221=ΩΩ+=Ωn C j H c n ε 式中，0>ε是设计参数。
直接给出其通带的波纹振幅为：2111εδ+-=如用分贝（dB ）表示波纹的大小，有)1lg(1011lg2022εε+=+-=p R3 切比雪夫滤波器的设计指标要设计切比雪夫滤波器，就必须指定若干设计参数。
从切比雪夫定义可知，由于1)1(=n C ，所以当1=Ω时，下式成立：22111|)(|ε+=Ωj H 又当s Ω=Ω时，有：222211)(11|)(|AC j H s n =Ω+=Ωε 式中，s Ω为阻带起始频率，1/A 为阻带的最大振幅（绝对）。
具体设计时，给定p s p R ,,ΩΩ及s A ，（其中p Ω为通带截止频率，21011log 10ε+-=p R ，2101log 10A A s -=）， 要确定滤波器的N c ,,Ωε（滤波器阶数），它们之间关系为：]1[log ]1[log /)1(11010210210221.020/-Ω+Ω-+=-=ΩΩ=Ω-==Ω=Ωr r psr R A p c g g N A g A ps εε二 用冲激响应不变法设计lIR 滤波器冲激响应不变法的设计原理是使得数字滤波器单位取样响应序列h(n)校仿模拟滤波器的冲响应)(t h a 。
常用的数字滤波器类型
常用的数字滤波器主要有两种，无限长单位冲激响应IIR滤波器和有限长单位冲激响应FIR 滤波器。
其中IIR数字滤波器主要有两种设计方法：①利用模拟滤波器的设计资源。
先设计一个合适的模拟滤波器，然后变换成满足预定指标的数字滤波器。
这种方法比较方便，因为模拟滤波器具有很多现成的设计公式，并且设计参数已经表格化，设计起来既方便又准确；②最优化设计方法。
先确定一种最优准则，如实际频率响应幅度与理想频率响应幅度的均方误差最小准则，或是它们的最大误差最小准则等，然后求此准则下滤波器系统函数的系数ai，bi。
这种方法需要进行大量的迭代运算，所以离不开计算机。
本文主要以设计IIR数字低通滤波器为例，介绍基于MATLAB的IIR数字滤波器设计方法，其中采用的是利用模拟滤波器设计资源的方法。
1利用模拟滤波器设计IIR数字滤波器的步骤（１）先将给定的数字滤波器的性能指标，按照某一变换（冲激响应不变法、双线性变换法等）规则转换成相应的模拟滤波器的性能指标。
（２）若设计的不是数字低通滤波器，还需将步骤（１）变换得到（高通、带通、带阻）模拟滤波器的性能指标转变成模拟低通滤波器的性能指标，因为只有模拟低通滤波器才有图表资源可以利用。
（３）根据得到的模拟低通滤波器的性能指标，利用某种模拟滤波器的逼近方法（巴特沃斯滤波器、切贝雪夫滤波器、椭圆型滤波器、贝塞尔滤波器等），设计并查表求得此模拟低通滤波器的系统函数。
（４）利用与步骤（１）和步骤（２）中的同一变换规则，将模拟低通滤波器的系统函数最终转变成所需的数字各型滤波器的系统函数。
2基于Ｍａｔｌａｂ设计ＩＩＲ数字滤波器的步骤以设计ＩＩＲ数字低通滤波器为例，给定滤波器的性能指标：设计一个数字低通滤波器，通带纹波（最大衰减）δｐ＝１ｄＢ，阻带最小衰减δｓ＝２５ｄＢ，通带截止频率ωｐ＝０．２π，阻带截止频率ωｓ＝０．４π。
根据设计要求，模拟滤波器可以采用巴特沃斯型、切贝雪夫型、椭圆型、贝塞尔型等，而本文介绍巴特沃斯型、切贝雪夫Ｉ型。
NVA中文手册
LSB
MSB
滤波器 4
数据字节 4
数据字节 5
0 1 2 3 4 5 6 7 8 9 10 11 12131415
Page 4 of 11
MEMS 振动传感器 NVA 65
CANopen 数据模式 - PDO
数据字节 0
数据字节 1
0 1 2 3 4 5 6 7 8 9 10 11 12131415
LSB
MSB
滤波器 3
数据字节2
数据字节 3
0 1 2 3 4 5 6 7 8 9 10 11 12131415
高精度的系统标定 编程设置输出信号的稳定分量 多达8个继电器 晶体管替代继电器 可提供用户更高要求的滤波器 评估步骤(记录功能，可编程触发，统计和协议功能 ) 安全冗余设计(双通道)
CANopen 技术参数
CANopen 通信剖析 Full CAN part A (11-bit) CANopen 301 V 4.1 (非隔离式总线) CANopen 输出编码: 带符号16位数
模拟量输出固定与滤波器1、滤波器2连接，由加速度传感器提供 的带符号振动信号通过滤波器滤波后输出。对应0 m/s2或0g的零 加速度值， 4-20mA模拟量接口的输出电流为12mA。利用CAN open接口，可分别对每一个模拟量通道的放大器进行设置。
CANopen接口可用于对6个滤波器的参数设置和功能启动。除了 滤波器的特性，所有参数均可由客户进行设置。
信号输出
1 个CANopen 接口，分辨率 4096 digits / g 2 个模拟量接口 4 ... 20 mA (分辨率12-bit )
4 个超出极限值状态的警告和（或）停机继电器 1 个系统故障继电器
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
设计流程图如下：
设计思想：
首先设计一个源信号和一个混合信号，通过其频谱对比得出最大和最小通带,最大和最小阻带；然后再根据得到的参数来设计切比雪夫滤波器,最后通过切比雪夫Ⅰ型滤波器和切比雪夫Ⅱ型滤波器的对比来得出那种效果好。
切比雪夫滤波器设计原理：
切比雪夫滤波器的振幅具有等波纹特性,它有两种形式：1)振幅特性在通带内是等波纹的、在阻带内是单调的切比雪夫I 型滤波器;2)振幅特性在通带内是单调的、在阻带内是等波纹的切比雪夫I Ｉ型滤波器,采用何种形式的切比雪夫滤波器取决于实际用途.
切比雪夫滤波器的设计方法就是将逼近精确度均匀分布在整个通带内，或者均匀分布在整个阻带内,或者均匀分布在两者之内,这样就可以使滤波器阶数大大降低。
切比雪夫I 型滤波器平方幅度响应函数表示为:
2
)(Ωj G =[1+2εC 2
N (Ω)]2/1- 其中 ε<1(正数)，它与通带波纹有关，ε越大,波纹也越大；C N (Ω) 是切比雪夫多项式,它被定义为:
C N （Ω)=cos （N ａr ｃｃo ｓ(Ω))，Ω≤1, C N (Ω)＝cosh （Ｎarcosh(Ω)),Ω
＞1．
而切比雪夫II 型滤波器平方幅度响应函数表示为：
)(Ωj G 2={１+2ε{ Ｃ2
N （Ω)/[2N (Ω／c Ω)］2｝}
1- 其中 ε<１(正数)，表示波纹变化情况；c Ω为截止频率;N 为滤波器的阶次,也是 C N （N ΩΩ/) 的阶次。
源信号编码及其图形：
t=-１：0．０1:1
ｙ＝(ｃos(2＊pi*10*t)+ｃos(2*pi*4０*t ））；
Ｎ＝leng ｔh(y);
fx=fft(y);
df=10０/Ｎ；
n=0:N ／2;
f=n*d ｆ;
ｓu ｂplot(2,1,１)；
p ｌot(f,ab ｓ(f ｘ(ｎ+1))＊2/Ｎ）; g ｒid;
titｌe('源波形频谱')
图（一)
混合信号编码及其图形：
ｔ=-1:0.01：１;
X＝(ｃos(2*pｉ*１０*ｔ）＋cｏs（2*ｐi＊25*t)+coｓ(2*ｐi*40*t)); N＝lｅngth(X);
ｆx=fft(X);
dｆ=100/N;
ｎ＝0:N／2；
f=n*df;
subｐlｏｔ（２,1,2);
ploｔ(f，abｓ(fx(ｎ＋1）)*２／Ｎ）; ｇrｉd；
ｔitle('混合波形频谱')
图(二)
从图（一)和图（二）对比可以得出：为了能达到和满足我们的要求,我们取以下的参数,最大通带wp２:0．5,最小通带ｗp1：0．0５,最大阻带ｗs2:０.3,最小阻带ws１:0．1。
切比雪夫Ⅰ型滤波器设计如下：
ws1＝0.１*pｉ；ws2=0.3*pi; %滤波器的阻带截止频率
wp１=0.０5*pi;wｐ２=0.5*pi；％滤波器的通带截止频率
Ｒp=1;As=２0；%滤波器的通阻带衰减指标
%转换为模拟滤波器的技术指标
T=0.01;Fs=1／T;
Ｏｍgp1=(2／Ｔ）*tａn(wｐ１/2)；Omｇp２=(2/T）＊taｎ(ｗp2/2)；
Omgｐ=[Omgp1,Omｇp2];
Oｍgｓ１＝(2／T)*tan(ws1／2）;Ｏmgs2＝(2／Ｔ）*taｎ（ws2／2)；
Oｍgs=[Omｇs１,Oｍｇs２];
bw＝Ｏｍgp2－Omgp１;w0=sqｒt(Ｏmgｐ1*Ｏmｇp2); ％模拟通带带宽和中心频率
ripｐｌｅ=10^(-Ｒp／２0); %滤波器的通带衰减对应的幅度值
Attｎ=１0^(-As／20)；%滤波器的阻带衰减对应的幅度值
%模拟原型滤波器计算
[n,Oｍgn］=cｈeb１ord（Omgp,Omｇs,Rp，Aｓ,'ｓ') %计算阶数ｎ和截止频率
[z０,p0,k０]=cheb1ap（ｎ,Rp）; %设计归一化的模拟滤波器原型
ｂａ1=ｋ0*rｅal(ｐoly(ｚ0）)；％求原型滤波器的系数ｂ
aa1=reａl(pｏｌｙ(ｐ０)); %求原型滤波器的系数ａ
[ba,aａ］=lｐ2bs（ｂa1,aa１,ｗ0，bw)；
%用双线性变换法计算数字滤波器系数
[bd,ad]=ｂiｌinｅar(bａ,aa，Fs)
%求数字系统的频率特性
[Ｈ,w]=frｅqｚ（bd,ａｄ);
dbH=２0*log10((ａbs(H)+eps)／maｘ(abs(H)））;
subplot(２,2,1);pｌot(ｗ/ｐi,aｂs(Ｈ)）；
ylabeｌ('｜H|');ｘlabel('频率(\pi)')；tiｔlｅ(＇幅度响应＇);aｘｉs(［0,1,0，1.１]); sｅt(gca,'ＸＴｉckMｏde＇,'maｎual'，'XＴｉｃｋ＇,[０,0.２,0．3，0.7,0.8］）; sｅt(gca，'ＹTickMｏde','ｍanｕal＇,'YＴick',[0，Attn,ripple，1]）;griｄ
图(三）
ｎ＝３
Oｍgn=16.１402 200.00００
bd =０.１698-０.8703 1.9961－2.５870 1.9９６1-０.87０３0．169８
ad =1.000０－2.5４50 2.533２-１．73５6 0．９60５-0.04６９-0.1６19
分析：由图（三）运行结果可知,最大通带0.5，最小通带０.０5,最大阻带0．3,最小阻带0.１;切比雪夫Ⅰ型滤波器的设计的个性技术指标精确度是均匀分布的。
而其幅度特性在通带内是等波纹的，在阻带内是单调下降的。
虽然达到了所设计滤波器的要求，滤除了我们不需要的波形,但是存在一些问题,如误差等。
切比雪夫Ⅱ型滤波器设计如下：
ｗｓ１=0.1＊pi;wｓ2=0.3*pi; %滤波器的阻带截止频率
ｗp１＝0.０5＊pi;ｗp2=０.５*pｉ; ％滤波器的通带截止频率
Rp=1;Aｓ=20;%滤波器的通阻带衰减指标
%转换为模拟滤波器的技术指标
T＝0.0１;Fs＝1/T;
Ｏｍgp1＝(2/T）＊taｎ(wｐ１/2);Omgp2=(2/T)＊ｔaｎ（wp2/2)；
Ｏmgp=[Oｍｇp1,Oｍｇp2]；
Omｇs1=(２/T)*ｔaｎ（ｗs１/2);Omgs2=(２/T)*tan(ws2/２)；
Ｏmgs=[Omgs1,Omgs2];
bw=Omgp２－Ｏｍgp１；w０=sqｒｔ(Omgp1＊Oｍgp2); %模拟通带带宽和中心频率
rｉｐｐlｅ＝10＾(-Rp／2０)；%滤波器的通带衰减对应的幅度值
Attｎ=10^(-As/２0）; ％滤波器的阻带衰减对应的幅度值
%模拟原型滤波器计算
[n,Omｇn]＝cｈeb2oｒd(Oｍｇｐ,Omgｓ,Ｒp,As，'s＇)
[z0,p0,k0］=chｅb2ap（ｎ，Ａs); ％设计归一化的ｃhｅb2型模拟滤波器原型ba1=ｋ0*real(poly（z0))；%求原型滤波器的系数b
ａa1=reａl(ｐoly(ｐ０))；％求原型滤波器的系数a
［bａ,aa]＝lp2ｂs(bａ1，aa１,w0,bw）；%变换为模拟带通滤波器
％用双线性变换法计算数字滤波器系数
［bd,ａd］=biｌｉneａr(ba,ａa,Fs）
%求数字系统的频率特性
[H,ｗ]=fｒeqz（bd,ad);
ｄbＨ=20*loｇ10（(abｓ(H)+eps)／max(abs（H））);
ｓubplot(2,2,1);plot(w/pi,ａbs(Ｈ));
ｙlabel('|H|＇）;xｌabｅl(＇频率（\pi)')；tiｔlｅ('幅度响应');axｉｓ([０,1,0，１．１]); set（gca,'XＴickＭｏde','mａnual','XＴick',［０,０.２，0.3,0．7,0.8]);
ｓet(gca，＇ＹTickMode'，'maｎｕａl',＇ＹTiｃk'，[０,Attｎ,rｉｐｐｌe，1]）；g ｒiｄ
图(四)
n =3
Omgn ＝25.７3４7 １2５．4348
bd ＝0．21７9 -0．8５32 1.５78１－1.88１9 1.5781 -0.8５3２0.2179
ad=1．０00０-2.2979 １.7４5６-0.9１83０.８465 -0.37２1 -0.0002
分析:由图（四)的运行结果可知，最大通带0.５,最小通带0.05,最大阻带0.3,最小阻带0.１;所设计的切比雪夫Ⅱ型滤波器的各项技术指标精确度是均匀分布的。
而其幅度特性在通带内是单调的,在阻带内是等波纹的。
虽然也达到了所设计滤波器的要求，滤除了我们不需要的并行,但是也还是存在误差,这是可以理解的。
由图(三)和图（四）的运行结果对比来看,切比雪夫Ⅰ型滤波器在阻带跟通带过渡时要比切比雪夫Ⅱ型滤波器过渡时平稳许多,所以切比雪夫Ⅰ型滤波器要比切比雪夫Ⅱ型滤波器所做出来的效果要好。
在实际的生活用途中,我们要根据我们的不同需求和要工作的不同场合，来选择切比雪夫Ⅰ型滤波器或者切比雪夫Ⅱ型滤波器,这样才能达到我们的要求，来满足我们的各项需要。