初中数学函数与图像汇总
初中高中数学七大函数的性质 图像

初中高中数学七大函数的性质图像1.一次函数(包括正比例函数)最简单最常见的函数,在平面直角坐标系上的图象为直线。
定义域(下面没有说明的话,都是在无特殊要求情况下的定义域):R值域:R奇偶性:无周期性:无平面直角坐标系解析式(下简称解析式):①ax+by+c=0[一般式]②y=kx+b[斜截式](k为直线斜率,b为直线纵截距,正比例函数b=0)③y-y1=k(x-x1)[点斜式](k为直线斜率,(x1,y1)为该直线所过的一个点)④(y-y1)/(y2-y1)=(x-x1)/(x2-x1)[两点式]((x1,y1)与(x2,y2)为直线上的两点)⑤x/a-y/b=0[截距式](a、b分别为直线在x、y轴上的截距)解析式表达局限性:①所需条件较多(3个);②、③不能表达没有斜率的直线(平行于x轴的直线);④参数较多,计算过于烦琐;⑤不能表达平行于坐标轴的直线和过圆点的直线。
倾斜角:x轴到直线的角(直线与x轴正方向所成的角)称为直线的倾斜角。
设一直线的倾斜角为a,则该直线的斜率k=tg(a)。
2.二次函数:题目中常见的函数,在平面直角坐标系上的图象是一条对称轴与y轴平行的抛物线。
定义域:R值域:(对应解析式,且只讨论a大于0的情况,a小于0的情况请读者自行推断)①[(4ac-b^2)/4a,正无穷);②[t,正无穷)奇偶性:偶函数周期性:无解析式:①y=ax^2+bx+c[一般式]⑴a≠0⑵a>0,则抛物线开口朝上;a<0,则抛物线开口朝下;⑶极值点:(-b/2a,(4ac-b^2)/4a);⑷Δ=b^2-4ac,Δ>0,图象与x轴交于两点:([-b+√Δ]/2a,0)和([-b+√Δ]/2a,0);Δ=0,图象与x轴交于一点:(-b/2a,0);Δ<0,图象与x轴无交点;②y=a(x-h)^2+t[配方式]此时,对应极值点为(h,t),其中h=-b/2a,t=(4ac-b^2)/4a);3.反比例函数在平面直角坐标系上的图象为双曲线。
八年级函数图像知识点总结

八年级函数图像知识点总结函数图像是中学数学中的重要部分,它贯穿了数学的各个领域。
在八年级数学中,我们学习了函数图像的一些基础知识,如函数的性质,图像的变化及其与函数性质的关系等。
在本文中,我们将对自己所学知识进行总结和归纳,帮助大家更好地理解和掌握函数图像的知识。
一、函数图像的性质函数图像有许多与函数性质相关的性质,如奇偶性、单调性、周期性等。
(1)奇偶性当函数满足f(x)=f(-x)时,函数称为偶函数,其图像关于y轴对称;当函数满足f(x)=-f(-x)时,函数称为奇函数,其图像关于原点对称。
例如,f(x)=x^2是偶函数,其图像关于y轴对称;f(x)=x^3是奇函数,其图像关于原点对称。
(2)单调性如果对于函数f(x),当x1<x2, f(x1)<f(x2)时,称函数f(x)是单调递增的;当x1<x2, f(x1)>f(x2)时,称函数f(x)是单调递减的。
例如,f(x)=x^2是单调递增的,f(x)=-x^2是单调递减的。
(3)周期性如果对于函数f(x),存在一个正数T,使得f(x+T)=f(x),称函数f(x)是周期函数,T称为函数f(x)的周期。
例如,f(x)=sinx是以2π为周期的周期函数。
二、函数图像的基本类型在八年级数学中,我们学习了三种基本的函数图像:常数函数、一次函数和二次函数。
(1)常数函数常数函数的函数表达式为f(x)=b(b为常数),函数的图像是一条平行于x轴的直线,可以表示为y=b。
例如,f(x)=3是一条平行于x轴且经过y=3的直线。
(2)一次函数一次函数的函数表达式为f(x)=kx+b(k、b为常数),函数的图像是一条斜率为k、经过y轴的截距为b的直线。
例如,f(x)=2x+1是一条斜率为2,经过y=1的直线。
(3)二次函数二次函数的函数表达式为f(x)=ax^2+bx+c(a、b、c为常数,且a不等于0),二次函数的图像是一条对称于x轴的开口向上或开口向下的抛物线。
初中数学重点梳理:函数及其图像

函数及其图像知识定位函数是初中数学的重要内容,由于它题材丰富,又易成为多种数学思想方法的载体,因此,深受各级各类竞赛命题者的亲睐,成为近几年各地竞赛的热点问题之一.另外,函数中尤其以二次函数最为重要,综合性最强,对学生思维要求更高。
本文拟对函数的竞赛题型及其解题策略作粗略概括,仅供大家参考.知识梳理知识梳理1:正反比例函数及一次函数反比例函数和一次函数在竞赛中的考查通常会把函数图像和性质跟整数解问题、图形面积问题、动点构成的等腰三角形、直角三角形相结合,往往综合性较强,难度较大。
需要我们对函数图像,常见典型问题进行总结,对它们有比较深的认识,才能游刃有余地解决各类问题。
知识梳理2:二次函数1、二次函数的系数a 、b 、c 及相关代数式的取值问题抛物线y=ax 2+bx+c 中二次项系数a 描述抛物线的开口,a>0向上,a<0向下;常数项c 描述抛物线与y 轴的交点(0,c),c>0时交点处x 轴上方,c<0时交点处x 轴的下方,c=0时时处原点;由对称轴公式x=-ab2知b 与a 一起来描述抛物线的对称轴;b 2-4ac 大于0,等于0或小于0,决定抛物线和x 轴交点的个数,等等.上面性质反之亦成立.我们还可以通过考察如x=±1时y 的值的情况,来确定a±b+c 等的符号问题.2、二次函数与整数问题二次函数与整数问题的联姻主要表现在系数a 、b 、c 为整数、整点以及某范围内的参数的整数值等.解题时往往要用到一些整数的分析方法.3、二次函数的最值问题定义域是闭区间时,二次函数存在两个最值(最大值和最小值).如果顶点横坐标在区间内,则在顶点处与距顶点较远的端点处各取一个最值;如果顶点横坐标不在区间内,则在区间两端点处各取一个最值.定义域是开区间时,二次函数只有其顶点横坐标在区间内的才在顶点处取得一个最值,否则不存在最值.4、二次函数的图象与面积问题求抛物线的顶点、两坐标轴的交点以及抛物线与其它图象的交点等点所构成的面积,关键是用含系数a、b、c的代数式表示出点的坐标或线段长,使面积问题与系数a、b、c建立联系.5、二次函数及其图像的应用.有些方程及不等式等有关问题,直接求解十分困难,若能构造二次函数关系,借助函数图像使之形象化,直观化,以形助数,会简化求解过程.例题精讲【试题来源】【题目】已知一次函数y= kx + b,kb<0,则这样的一次函数的图像必经过的公共象限有_____ 个,即第________象限。
七年级下册数学函数图像知识点

七年级下册数学函数图像知识点在数学中,函数图像是一类非常重要的图像类型,七年级下册数学的学习内容中也非常重视函数图像的学习。
本文将介绍七年级下册数学中常见的函数图像知识点。
一、一次函数图像一次函数图像是数学中最简单的一类函数图像,它的解析式通常采用 $y=kx+b$ 的形式表示。
其中,$k$ 表示斜率,$b$ 表示截距。
当 $k>0$ 时,函数图像倾斜向右上方,当 $k<0$ 时,函数图像倾斜向右下方。
二、二次函数图像二次函数图像是一种非常常见的函数图像类型,它的解析式通常采用 $y=ax^2+bx+c$ 的形式表示。
其中,$a$ 表示二次项系数,决定了图像的开口方向和大小;$b$ 表示一次项系数,决定了图像的偏移;$c$ 表示常数项,决定了图像的纵向平移。
三、反比例函数图像反比例函数图像是一类非常特殊的函数图像,可以用$y=\dfrac{k}{x}$ 的形式表示。
其中,$k$ 表示比例系数,决定了图像的形态。
反比例函数图像的特点是,它的图像经过点$(1,k)$,并且在 $x=0$ 处有一个垂直渐近线。
四、指数函数图像指数函数图像是一类比较常见的函数图像类型,它的解析式通常采用 $y=a^x$ 的形式表示。
其中,$a>0$ 且 $a\neq1$,决定了图像的变化趋势。
指数函数图像的特点是,当 $a>1$ 时,函数图像呈现出向上增长的趋势;当 $0<a<1$ 时,函数图像呈现出向下递减的趋势。
五、对数函数图像对数函数图像也是一种比较常见的函数图像类型,它的解析式通常采用 $y=\log_ax$ 的形式表示。
其中,$a>0$ 且 $a\neq1$,决定了图像的变化趋势。
对数函数图像的特点是,当 $a>1$ 时,函数图像呈现出向右上增长的趋势;当 $0<a<1$ 时,函数图像呈现出向右下递减的趋势。
以上就是七年级下册数学中常见的函数图像类型及其特点的介绍。
初中数学:掌握这15张函数图,函数真的白捡分,建议家长珍藏打印

初中数学:掌握这15张函数图,函数真的白捡分,建议家长
珍藏打印
从小学到高中,数学都是学习的大头,初中的数学在整个学习阶段中有限的尤为重要,难点自然也非常多。
但是并不是每一个难点都特别困难,今天我要跟大家分享的就是中考必考的一个知识点:“函数”。
为了帮助同学们更有效地学习,老师将“函数”做了分类讲解,每个知识点都讲得特别细,大家看看就知道了,希望大家不要忽略,吃透基础的,高分自然就来了。
●文末附有电子版资料下载方式
函数只要分清楚三个部分就行了,一次函数,反比例函数,了解清楚他们的图像与性质,弄清楚他们的平面直角坐标系与变量,函数问题就变得一目了然了。
一次函数
反比例函数
二次函数
1. 由抛物线开口方向确定a
1. 由对称轴的位置确定b、ab。
中考复习——平面直角坐标系、一次函数、反比例函数及其图象 知识点汇总及典例分析

中考复习——平面直角坐标系、一次函数、反比例函数【知识梳理】一、平面直角坐标系1. 坐标平面上的点与 有序实数对 构成一一对应;2. 各象限点的坐标的符号;3. 坐标轴上的点的坐标特征.4. 点P (a ,b )关于x 轴对称的点的坐标为 ;关于y 轴对称的点的坐标为 ;关于原点对称的点的坐标为5.两点之间的距离二、函数的概念1.概念:在一个变化过程中有两个变量x 与y ,如果对于x 的每一个值,y 都有 的值与它对应,那么就说x 是自变量,y 是x 的函数.2.自变量的取值范围: (1)使解析式 (2)实际问题具有 意义3.函数的表示方法; (1) (2) (3) 三、一次函数的概念、图象、性质1.正比例函数的一般形式是 ( ),一次函数的一般形式是 (k≠0). 2. 一次函数y kx b =+的图象是经过( , )和( , )两点的一条直线.4.若两个一次函数解析式中,k 相等,表示两直线 ;若两直线垂直,则 。
5.的大小决定直线的倾斜程度,越大,直线越 ;四、反比例函数的概念、图象、性质1.反比例函数:一般地,如果两个变量x 、y 之间的关系可以表示成y = 或 或 (k 为常数,k≠0)的形式,那么称y 是x 的反比例函数. 2. 反比例函数的图象和性质k >0,b >0k >0,b <0k <0,b >0k <0,21212211P P )0()0()2(y y y P y P -=, ,,,21212211P P )0()0()1(x x x P x P -=, , ,, 3.k 的几何含义:反比例函数y =k x(k≠0)中比例系数k 的几何意义,即过双曲线y =k x(k≠0)上任意一点P 作x 轴、y 轴垂线,设垂足分别为A 、B ,则所得矩形OAPB 的面积为 。
【例题精讲】 例1.函数22y x =-中自变量x 的取值范围是 ;函数y =x 的取值范围是 .例2.已知点(13)A m -,与点(21)B n +,关于x 轴对称,则m = ,n = . 例3.如图,在平面直角坐标系中,点A 的坐标是(10,0),点B 的 坐标为(8,0),点C 、D 在以OA 为直径的半圆M 上,且四边形OCDB 是平行四边形,点C 的坐标为例4.一次函数y=(3a+2)x -(4-b),求满足下列条件的a 、b 的取值范围。
函数图像大全

函数图像大全函数图像是数学中的重要概念之一,它可以直观地展现出函数的性质和特点。
在数学教学中,函数图像也是一个重要的教学内容,通过观察函数的图像,可以更好地理解函数的变化规律和特点。
本文将对常见的函数图像进行详细介绍,希望能够帮助读者更好地理解和掌握函数图像的相关知识。
一、线性函数图像。
线性函数是最简单的一类函数,它的图像通常是一条直线。
线性函数的一般形式为y=kx+b,其中k和b为常数,k表示直线的斜率,b表示直线与y轴的交点。
当k大于0时,直线向上倾斜;当k小于0时,直线向下倾斜;当k等于0时,直线平行于x轴。
b的取值决定了直线与y轴的交点的位置。
线性函数的图像特点明显,通过观察直线的斜率和截距,可以快速了解函数的性质。
二、二次函数图像。
二次函数的一般形式为y=ax^2+bx+c,其中a、b、c为常数且a不等于0。
二次函数的图像通常是一个抛物线,其开口方向由a的正负决定。
当a大于0时,抛物线开口向上;当a小于0时,抛物线开口向下。
二次函数的图像特点较为复杂,需要通过求导、配方法等手段来确定抛物线的顶点、焦点等重要特征点。
三、指数函数图像。
指数函数的一般形式为y=a^x,其中a为常数且a大于0且不等于1。
指数函数的图像通常是一条曲线,其特点是随着自变量x的增大,函数值呈指数增长或指数衰减。
指数函数的图像在x轴的左侧逐渐逼近y轴,而在x轴的右侧则迅速增长。
指数函数是一种常见的增长模型,在经济、生物、物理等领域有着广泛的应用。
四、对数函数图像。
对数函数的一般形式为y=loga(x),其中a为常数且a大于0且不等于1。
对数函数的图像通常是一条曲线,其特点是随着自变量x的增大,函数值呈对数增长。
对数函数的图像在x轴的右侧逐渐逼近y轴,而在x轴的左侧则迅速减小。
对数函数是一种常见的减小模型,在金融、生物、信息论等领域有着广泛的应用。
五、三角函数图像。
三角函数包括正弦函数、余弦函数、正切函数等,它们的图像都具有周期性。
经典数学函数图像大全
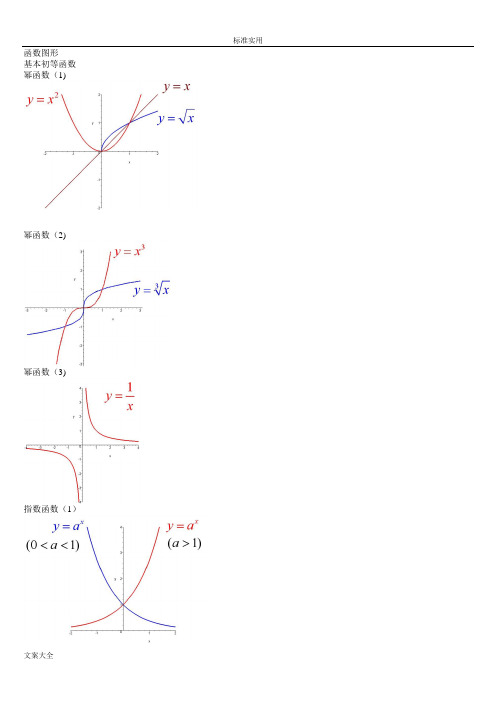
函数图形基本初等函数幂函数(1)幂函数(2)幂函数(3)指数函数(1)指数函数(2)指数函数(3)对数函数(1)对数函数(2)三角函数(1)三角函数(2)三角函数(3)三角函数(4)三角函数(5)反三角函数(1)反三角函数(2)反三角函数(3)反三角函数(4)反三角函数(5)反三角函数(6)反三角函数(7)反三角函数(8)双曲函数(1)双曲函数(2)双曲函数(3)双曲函数(4)双曲函数(5)双曲函数(6)双曲函数(7)反双曲函数(4)反双曲函数(1)反双曲函数(2)反双曲函数(3)反双曲函数(5)反双曲函数(6)y=sin(1/x) (1) y=sin(1/x) (2)y=sin(1/x) (3) y=sin(1/x) (4) y = [1/x](1) y = [1/x](2)y=21/xy=21/x (2)y=xsin(1/x)y=arctan(1/x)y=e1/xy=sinx (x->∞)绝对值函数y = |x| 符号函数y = sgnx 取整函数y= [x]极限的几何解释(1)极限的几何解释(2)极限的几何解释(3)极限的性质(1) (局部保号性)极限的性质(2) (局部保号性)极限的性质(3) (不等式性质)极限的性质(4) (局部有界性)极限的性质(5) (局部有界性)两个重要极限y=sinx/x (1)y=sinx/x (2)limsinx/x的一般形式y=(1+1/x)^x (1)y=(1+1/x)^x (2)lim(1+1/x)^x 的一般形式(1) lim(1+1/x)^x 的一般形式(2) lim(1+1/x)^x 的一般形式(3)e的值(1)e的值(2)等价无穷小(x->0)sinx等价于xarcsinx等价于xtanx等价于xarctanx等价于x1-cosx等价于x^2/2sinx等价于x数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线y=(x+1)/(x-1)y=sinx/x (x->∞) 夹逼定理(1)夹逼定理(2) 数列的夹逼性(1) 数列的夹逼性(2)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【例1】小明外出散步,从家走了20分钟后到达了一个离家900米的报亭,看了10分钟的报纸然后用了15分钟返回到家.则下列图象能表示小明离家距离y 与时间x 关系的是( )选择D 答案【例2】打开某洗衣机开关(洗衣机内无水),在洗涤衣服时,洗衣机经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量y (升)与时间x (分钟)之间满足某种函数关系,其函数图象大致为( )D 答案。
【练习一】1.(2010黑龙江绥化)六月P 市连降大雨,某部队前往救援,乘车行进一段路程之后,由于道路受阻,汽车无法通行,部队短暂休整后决定步行前往.则能反映部队离开驻地的距离s (千米)与时间t (小时)之间函数关系的大致图象是()【答案】A2.(2010广东深圳)升旗时,旗子的高度h (米)与时间t (分)的函数图像大致为( )A ./B .C .D .【答案】B3.(2010 河南模拟)如图是某蓄水池的横断面示意图,分为深水池和浅水池,如果这个蓄水池以固定的流量注水,下面能大致表示水的最大深度h与时间t之间的关系的图像是( )4.(2010四川巴中)如图3所示,以恒定的速度向此容器注水,容器内水的高度(h)与注水时间(t)之间的函数关系可用下列图像大致描述的是()5.(2010 湖北孝感)均匀地向如图所示的一个容器注水,最后把容器注满,在注水过程中,能大致反映水面高度h随时间t变化的图像是()【答案】C6.(2010内蒙呼和浩特)均匀的地向一个容器注水,最后把容器注满,在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC位一折线),则这个容器的形状为( )图3A B C D【答案】D7.(2010天津)如图,是一种古代计时器——“漏壶”的示意图,在壶内盛一定量的水,水从壶下的小孔漏出,壶壁内画出刻度,人们根据壶中水面的位置计算时间.若用x 表示时间,y 表示壶底到水面的高度,下面的图象适合表示一小段时间内y 与x 的函数关系的是(不考虑水量变化对压力的影响)(A ) (B ) (C ) (D )8.(燕山2011二模)如右图, 是一个下底小而上口大的圆台形容器,将水以恒速(即单位时间内注入水的体积相同)注入,设注水时间为t ,容器内对应的水高度为h ,则h 与t 的函数图象只可能是9.(2006·南安市)如图,一个蓄水桶,60分钟可将一满桶水放干.其中,水位h (cm )随着放水时间t (分)的变化而变化.h 与t 的函数的大致图像为( C )10. (2006·锦州市)如图是水滴入一个玻璃容器的示意图(滴水速度保持不变),下列图象能正确反映容器中水的高度(h)与时间(t)之间函数关系的是( C )11.如图,因水桶中的水由图①的位置下降到图②的位置的过程中,如果水减少的体积是y ,水位下降的高度是x ,那么能够表示y 与x 之间函数关系的图象是第(9)题12.(2010 山东省德州)某游泳池的横截面如图所示,用一水管向池内持续注水,若单位时间内注入的水量保持不变,则在注水过程中,下列图象能反映深水区水深h与注水时间t关系的是(A)(B)(C)(D)【答案】A13. (2006·江阴市)如图,圆柱形开口杯底部固定在长方体水池底,向水池匀速注入水(倒在杯外),水池中水面高度是h,注水时间为t,则h与t之间的关系大致为下图中的(B )1.点在几何图形上运动【例1】.如图(1),AB是半圆O的直径,点P从点O出发,沿OA—弧AB—BO的路径运动一周.设OP为s,运动时间为t,则下列图形能大致地刻画s与t之间关系的是()图(1)选择C答案。
【例2】.(丰台10)如图所示是张老师晚上出门散步时离家的距离y与时间x之间的函数关系的图象,若用黑点表示张老师家的位置,则张老师散步行走的路线可能是DCB①②A第5题图深水区浅水区OA.B.C.D.A .B .C .D .答案【D 】【例3】.(石景山10)如图,平面直角坐标系中,在边长为1的菱形ABCD 的边上有一动点P 从点A 出发沿A B C D A →→→→匀速运动一周,则点P 的纵坐标y 与点P 走过的路程S 之间的函数关系用图象表示大致是A B C D 选A 。
【练习二】:1.(2010四川广安)如图2,小明在扇形花台OAB 沿O A B O →→→的路径散步,能近似地刻画小明到出发点O 的距离y 与时间x 之间的函数图象是【答案】C2. 如图,一艘旅游船从A 点驶向C 点. 旅游船先从A 点沿以D 为圆心的弧AB 到B 点,然后从B 点沿直径行驶到圆D 上的C 点.假如旅游船在整个行驶过程中保持匀速,则下面各图中,能反映旅游船与D 点的距离随时间变化的图象大致是( )第8题图BAOA.B.C.D.【答案】B【例1】(09房山二模)如图, A 、B 、C 、D 为⊙O 的四等分点,动点P 从圆心O 出发,沿O C D O --- 路线作匀速运动,设运动时间为t (秒),∠APB=y (度),则下列图象中表示y 与t 之间函数关系最恰当的是选C 。
【例2】(2011年中考)如图,在Rt ABC △中,90ACB ∠=︒,30BAC ∠=︒,2AB =,D 是AB 边上的一个动点(不与点A 、B 重合),过点D 作CD 的垂线交射线CA 于点E .设AD x =,CE y =,则下列图象中,能表示y 与x 的函数关系的图象大致是( )DCBA选B 。
【练习三】:1.(2009北京)如图,C 为⊙O 直径AB 上一动点,过点C 的直线交⊙O 于D 、E 两点,∠ACD=45°,DF ⊥AB 于点F,EG ⊥AB 于点G,当点C 在AB 上运动时,设AF=x ,DE=y ,下列中图象中,能表示y 与x 的函数关系式的图象大致是( )第8题图AB C DOP B .D .A .C .CE DBA【答案】:A2.(2010房山) 如图,矩形纸片ABCD 中,BC=4,AB=3,点P 是BC 边上的动点(点P 不与点B 、C 重合).现将△PCD 沿PD 翻折,得到△PC ’D ;作∠BPC ’的角平分线,交AB 于点E .设BP= x,BE=y,则下列图象中,能表示y 与x 的函数关系的图象大致是( )A .B .C .D .【答案】:D【例1】.(09顺义一模)8. 如图1 ,在直角梯形ABCD 中,∠B=90°,DC ∥AB ,动点P 从B点出发,沿梯形的边由BC D A 运动,设点P 运动的路程为x ,△ABP 的面积为y , 如果关于x 的函数y 的图象如图2所示 ,那么△ABC 的面积为( C) A .32 B .18C .16D .10答案C 。
【例2】.(东城2010)在直角梯形ABCD 中,AB ∥CD ,BC⊥DC 于点C,AB=2,CD=3,∠D=45,动点P 从D 点出发,沿DC 以每秒1个单位长度的速度移动,到C 点停止.过P 点作PQ 垂直于直.线.AD ,垂足为Q .设P 点移动的时间为t 秒,△DPQ 与直角梯形ABCD 重叠部分的面积为S, 下列图象中,能表示S 与t 的函数关系的图象大致是( )选C. 例3.(朝阳2011二模)如图(甲),扇形OAB 的半径OA=6,圆心角∠AOB=90°,C 是上不同于A 、B 的动点,过点C 作CD ⊥OA 于点D ,作CE ⊥OB 于点E ,连结DE ,点H 在线段DE 上,且EH=32DE .设EC 的长为x ,△CEH 的面积为y ,图(乙)中表示y 与x 的函数关系式的图象可能是( )A .B .C . D.选A.【练习四】1. (门头沟2010)如图,在矩形ABCD 中,AB=2,BC=1,动点P 从点B 出发,沿路线B C D →→作匀速运动,那么△ABP 的面积S 与点P 运动的路程x 之间的函数图象大致是2.(2011顺义一摸)如图,矩形ABCD 中,1AB =,2AD =,M 是CD 的中点,点P 在矩形的边上沿A B C M →→→运动,则APM △的面积y 与点P 经过的路程x 之间的函数关系用图象表示大致是下图中的 ( )3.(2009年长春)如图,动点P 从点A 出发,沿线段AB 运动至点B 后,立即按原路返回,点P 在运动过程中速度大小不变,则以点A 为圆心,线段AP 长为半径的圆的面积S 与点P 的运动时间t 之间的函数图象大致为( ) 4. 如图,在直角梯形ABCD 中,DC ∥AB ,∠A=90°,AB=28cm ,DC=24cm ,AD=4cm ,点M 从点D 出发,以1cm/s 的速度向点C 运动,点N 从点B 同时出发,以2cm/s 的速度向点A运动,A .B .C .D .A .B . D CBA P图(乙) 图(甲)当其中一个动点到达端点停止运动时,另一个动点也随之停止运动.则四边形ANMD 的面积y (cm 2)与两动点运动的时间t (s )的函数图象大致是( )5.( 房山区2011)如图,P 是边长为1的正方形ABCD 对角线AC 上一动点(P 与A 、C 不重合),点E 在射线BC 上,且PE=PB.设AP=x,△PBE 的面积为y. 则能够正确反映y 与x 之间的函数关系的图象是6.(朝阳2010)如图,四边形ABCD 中,AD ∥BC, ∠B=60o ,AB=AD=BO=4,OC=8,点P 从B 点出发,沿四边形ABCD 的边BA→AD→DC 以每分钟一个单位长度的速度匀速运动,若运动的时间为t,△POD 的面积为S ,则S 与t 的函数图象大致为7.如图,正方形ABCD 的边长为10ABCD 的顶点上.若圆的半径为x ,且0< x ≤5面积的和为y ,则能反映y 与x 之间函数关系的大致图象是(8. (2011甘肃兰州,14,4分)如图,正方形ABCD 的边长为1,E 、F 、G 、H 分别为各边上的点,且AE=BF=CG=DH ,设小正方形EFGH 的面积为S ,AE 为x ,则S 关于x 的函数图象大A C P D致是A.B.C.D.【答案】B9.(2011安徽,10,4分)如图所示,P是菱形ABCD的对角线AC上一动点,过P垂直于AC的直线交菱形ABCD的边于M、N两点,设AC=2,BD=1,AP=x,△AMN的面积为y,则y关于x的函数图象的大致形状是()A.B.C.D.【答案】C10. (2011山东威海,12,3分)如图,在正方形ABCD中,AB=3cm,动点M自A点出发沿AB方向以每秒1cm的速度运动,同时动点N自A点出发沿折线AD—DC—CB以每秒3cm的速度运动,到达B点时运动同时停止,设△AMN的面积为y(cm2),运动时间为x(秒),则下列图象中能大致反映y与x之间的函数关系的是()11.(2010重庆綦江县)如图,在矩形ABCD中,AB=4,BC=3,点P从起点B出发,沿BC、CD逆时针方向向终点D匀速运动.设点P所走过的路程为x,则线段AP、AD与矩形的边所围成的图形的面积为y,则下列图像中能大致反映y与x函数关系的是()CDGPDC BAA .B .C .D .【答案】A12.(2010烟台)如图,AB 为半圆的直径,点P 为AB 上一动点,动点P 从点A 出发,沿AB 匀速运动到点B ,运动时间为t ,分别以AP 于PB 为直径做半圆,则图中阴影部分的面积S 与时间t 之间的函数图像大致为(D )A B C D 【答案】D【例1】.如图,点G 、D 、C 在直线a 上,点E 、F 、A 、B 在直线b 上,若a b Rt GEF ∥,△从如图所示的位置出发,沿直线b 向右匀速运动,直到EG 与BC 重合.运动过程中GEF △与矩形ABCD 重合部分....的面积(S )随时间(t )变化的图象大致是( B )答案BB图1 图2 图3GDC EF ABbaA .B .C .D .【练习五】:1.如图1,四边形ABCD 是正方形,点A 在直线MN 上,∠MAD=45°,直线MN 沿AC 方向平行移动.设移动距离为x ,直线MN经过的阴影部分面积为y ,那么表示y 与x 之间函数关系的图象大致为(常州中考)2.(2011常州中考) 已知如图,等腰三角形ABC 的直角边长为a ,正方形MNPQ的边为b (a<b),C 、M 、A 、N 在同一条直线上,开始时点A 与点M 重合,让△ABC 向右移动,最后点C 与点N 重合。
