5流体力学第五章量纲分析与相似原理5
流体力学第五章相似原理和量纲分析-35页文档资料

第五节 量纲分析法(瑞利法)
• 方程两边量纲一致
1a12a2nan 1a12a2nan 1a12a2nan
Ma v c
马赫数;是惯性力 与弹性力的比值。
c为音速
第二节 动力相似准则
(6)表面张力相似(韦伯准则)
We v2l
韦伯数;是惯性力与 张力的比值。
第三节 流动相似条件
二流动相似的必要和充分条件:
• (1)由相同的微分方程所描述;同一类流动。 • (2)单值条件(包括几何条件、边界条件、物
第二节 动力相似准则
• 牛顿相似准则
F F m maaVVdvddvdtt
F F
l2v2 l2v2
kF 1
k
k
2 l
k
2 v
Ne F
l 2v2
牛顿数,是作用力与 惯性力的比值
流场动力相似: N eNe
第二节 动力相似准则
• (1)重力相似准则(弗劳德准则)
在重力作用下相似的流动,其重力场必须相似
kFW WV Vggkkl3kg
v
v
gl12 gl12
k v kl k g
12
1
弗劳德数,是惯性力
Fr
v
gl 1
2
与重力的比值
流场重力作用相似: F rFr
第二节 动力相似准则
• (2)黏滞力相似准则(雷诺准则)
性条件、初始条件)相似。
• (3)相似准则数相等。
例题
• 当通过油池底部的管道向外输油时,如果池内油深
流体力学相似原理与

速度比尺 时间比尺 则
加速度比尺
u
up um
t
tp tm
u
up um
lp lm
tp tm
l t
a
ap am
lp lm
t
2 p
t
2 m
lp lm
( t p )2 tm
l
2 t
由于各相应点速度成比例,所以相应断面平均流速有同样的速
度比尺,即
v
vp vm
f l22v
此处 1 ,v 1 l , 则
f
l22v
l2 l2
1
故
Fp Fm 1.50kN
§5-4 量纲分析
量纲和量纲和谐原理 量纲分析法
一、量纲(dimension)和量纲和谐原理
1、量纲
表示物理量的种类,称为这个物理量的量纲(或称因次)。
a
l
2 t
则
f
3l
l
2 t
l2
l t
2
l22v
即
Fp
p
l
2 p
v
2 p
Fm mlm2 vm2
上式可写成
Fp Fm
p
l
2 p
v
2 p
m
l
2 m
vm2
—— 无量纲数
在相似原理中称为牛顿数Ne ∴ (Ne)p (Ne)m
流量:
Qp Qm
vp Ap vm Am
vl2
或
Qm
工程流体力学第五章 相似原理和量纲分析

Fe
dp A
KAdV V
K-体积模量 kK-体积模量比例尺
k k kK
K'
2
1
kF 1 2 2 k kl k
力的比例尺
也可写成:
' '2
2
2
K
柯西数 是惯性力与弹 性力的比值
2 2
推导过程
角速度比例尺:
' ' l ' k k l kl
注:确定了长度比例尺和速度比例尺,一切运动相似比例尺都可以推导出来。
注:*运动粘度比例尺的推导
d F A dy
F ma V a dy 1 则: A d dy m V A d dy A d 1
相似原理
如何去做模型?
第五章 相似原理和量纲分析
数学 分析 理论分析 数值计算 模型实验
解决流体 力学问题 的方法
实验研究
基础:相似原理 相似原理与模型试验研究方法不仅广泛应用于流体力 学,而且广泛应用于传热、燃烧过程机理等的研究中。
第一节 流动的力学相似
表 征 流 动 过 程 的 物 理 量
第五章 相似原理和量纲分析
xcli@
L/O/G/O
相似原理
相似原理 实物 模型
相似理论:
模型流场再现实物流场的准则——指导模型实验 实验结果推广到原型以及应用到相似的流动中
本章内容
1 2 3 4 1 5 流动的力学相似 动力相似准则 流动相似条件 近似模型实验 Click to add title in here 量纲分析法 连续方程
流体力学第五章b5-相似原理与量纲分析分解

特征速度 V
特征压强 p0 特征密度 ρ0
uv w
无量纲速度 u ,v ,w
无量纲压强 无量纲密度
p Vp
p0
V
V
0
有量纲的特征量T , L,G,V , P, 0, 0
无量纲量 t , x, y, z, g,u,v, w, p,
t Tt ,x Lx, y Ly,z Lz,g Gg , 0 u Vu ,v Vv ,w Vw, p p0 p, 0
对于非定常流,只有三个数是独立的
St=0,雷诺数Re ,弗汝德数Fr ,欧拉数Eu ,只有2个是独立的
流体力学与流体机械
第三节 相似准则
B5 量纲分析与相似原理 23
1雷诺数(Reynolds Number)Re 粘性力相似:Re1= Re2
Re
VL
VL
惯性力 对流惯性力=V2/L
粘性力 粘性力=μV/ρL2
流体力学与流体机械
相似的基本概念
B5 量纲分析与相似原理
4
流动相似性 几何相似
形状相似
尺度成比例
流动相似
同类现象 相似现象
遵循同一方程 物理量成比例
几何相似
尺度成比例
时间相似
时间成比例
运动相似
速度成比例
动力相似
力成比例
流体力学与流体机械
1
相似的基本概念
B5 量纲分析与相似原理
5
几何相似—模型与原型流场的几何形状相似,即相应线段
vp tp
/ vm / tm
cv ct
cl ct 2
l t2
um3
加速度比例尺:
ka
a' a
'
流体力学第5章 相似性原理和量纲分析

几何相似只有一个长度比例尺,几何相似是力学 相似的前提
二、运动相似
❖ 流场中所有对应点上对应时刻的流速方向相同大小成比例。
v3' 3
v1'
v2'
1
2
3
v3''
v1 v1
v2 v2
v3 v3
v v
kv
v1''
1
2
kv——速度比例尺
v2''
A
A
o
系统1:v
l t
o
系统2:v l t
时间比例尺 加速度比例尺
1/ p
7.5k,kpkv2'
0.001207, kv 4416(Pa)
22.5, 有
F F ' F ' 1.261104(N)
kF
k
k
2
l
k
2
v
M M ' 2030(N m)
k
k
3k
l
2
v
第五节 量纲分析法
❖一、量纲分析的概念和原理 ❖ 量纲是指物理量的性质和类别。例如长度和质量, 它们分别用 [ L ] , [ M ]表达。 ❖而单位除表示物理量的性质外,还包含着物理量的 大小,如同为长度量纲的米,厘米等单位。
如何进行模型实验: (1) 几何相似(模型和实物、攻角、位置等); (2) 确定相似准则数; (3) 确定模型尺度和速度; (4) 实验数据整理(无因次形式); (5) 试验值与实际值之间的换算。
完全相似:两个流动的全部相似准则数对应相等。不可能实现。 部分相似:满足部分相似准则数相等。
近似的模型试验:在设计模型和组织模型试验时,在 与流动过程有关的定性准则中考虑那些对流动过程起 主导作用的定性准则,而忽略那些对过程影响较小的
5 量纲分析和相似原理

5.2.2 π定理(布金汉定理,Bucking ham)
由美国物理学家Bucking ham提出。若某一物 理过程包含n个物理量,即 f (q1q2q3 qn ) 0 其中有m个基本量(量纲独立,不能互相导出), 则该物理过程可由n个物理量构成的n-m个无量纲 项所表达的关系式来描述,即 F (1 nm ) 0 由于无量纲项用π表示,因此叫作π定理。
5.1.2 无量纲量
当量纲公式中α=0、β=0、γ=0时, 物理量q 为无量纲量。 vd Re 如 雷诺准数
LT 1L dim Re dim( ) 2 1 1 LT vd
无量纲量的特点: 客观性 不受运动规模的影响 可进行超越函数运算
5.1.3 量纲和谐原理
量纲和谐原理:凡正确反映客观规律的物理 方程,其各项的量纲一定是一致的。 如粘性流体总流的柏努利方程
4)量纲分析法是沟通流体力学理论与实验之 间的桥梁。
5.3 相似理论基础
5.3.1 相似概念
几何相似:两个流动流场(原型和模型)的 几何形状相似,即相应的线段长度成比例、 夹角相等。 以p表示原型 (prototype) , m表示模型 (model) ,有
l p1 lm1 l p2 lm2 lp lm l
I m mlm2vm 2 lmvm Tm mlmvm m
即
l pvp
p
lmvm
m
(Re) p (Re)m
lv
无量纲数 Re 称为雷诺准数(Reynolds number),表示惯性力与粘滞力之比。两流动 的雷诺准数相等,粘滞力相似。
此式为管道压强损失计算公式,称为达西-魏 斯巴赫(Darcy-Weisbach)公式。
5 相似理论与量纲分析
第五章 相似理论与量纲分析实际工程中,由于流体粘性的存在和边界条件的多样性,流动现象极为复杂,往往难以通过解析的方法求解。
此时,不得不依赖实验研究。
通常,实际工程或实物(统称原型)的尺寸太大,直接进行实验会耗费大量的人力和物力,有时甚至难以实现。
因此,大多数实验都是在比原型小的模型上进行的(称为模型实验)。
通过模型实验,得出实验结果,进而预测原型中将要发生的流动现象。
那么怎样才能保证模型与原型有相同的流动规律呢?这就是相似理论要研究的问题。
量纲分析则是在观测流动现象的基础上,建立流动各影响因素的正确关系。
§5.1 相似理论5.1.1 流动相似为了保证模型流动(用下标m 表示)与原型流动(用下标p 表示)具有相同的流动规律,并能通过模型实验结果预测原型流动情况,模型与原型必须满足流动相似,即两个流动在对应时刻对应点上同名物理量具有各自的比例关系,具体地说,流动相似就是要求模型与原型之间满足几何相似、运动相似和动力相似。
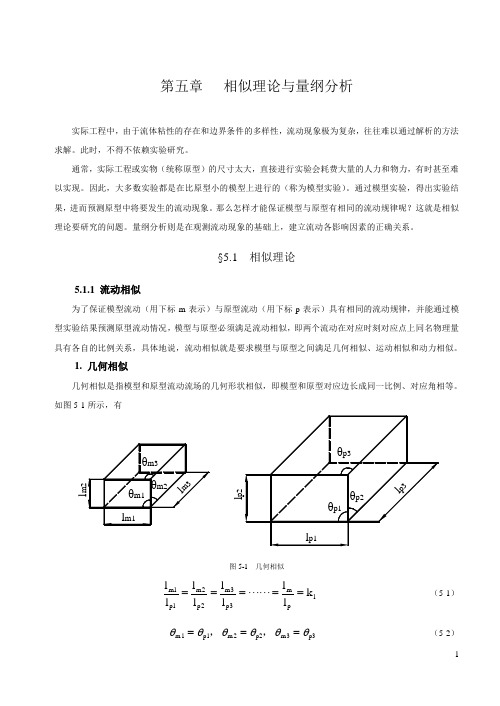
1. 几何相似几何相似是指模型和原型流动流场的几何形状相似,即模型和原型对应边长成同一比例、对应角相等。
如图5-1所示,有图5-1 几何相似l pm 3p 3m 2p 2m 1p 1m k l ll l l l l l ===== (5-1) p3m3p2m2p1m1θθθθθθ===,, (5-2)式中k l 称为长度比尺,则面积比尺2l 2p 2m p m A k l l A A k === (5-3)体积比尺3l 3p3m p m V k l l V V k === (5-4)2. 运动相似运动相似是指模型和原型流动的速度场相似,即两个流动在对应时刻对应点上的速度方向相同,大小成同一比例。
如图5-2所示,有图5-2 运动相似u pm p2m2p1m1k u uu u u u ==== (5-5) 式中k u 称为速度比尺。
由于各对应点速度成同一比例,因此相应断面的平均速度必然有同样的比尺u pmv k v v k ==(5-6) 将t l v=代入上式,得tlm p p m p p m m p m v k k t l t l t l t l v v k ==== (5-7)式中p m tt t k =称为时间比尺。
工程流体力学 第六版 第5章 相似理论与量纲分析

当F为阻力FD时,
牛顿数表示阻力系数:
CD
1
FD
2l 2
2
当F为升力FL时, 牛顿数表示升力系数:
CL
FL
1 2l 2
2
牛顿数的拓展 描述力矩M时,
可用牛顿数表示力矩系数:
CM
1
M
2l 3
2
描述功率P时, 可用牛顿数表示动力系数:
CP
P
3l 2
第5章 作业1:
工程流体力学(第6版)
第5章 习题:1、2、6、7
比值:
(
l 2 l
2
)m
l 2 2 l
(பைடு நூலகம்
l
)
m
l
(l
v
)m
l
v
定义雷诺数:
Re
l
l
v
(l为定型尺寸)
则比值为: Rem Re ——粘性力相似准则
Re的物理意义: 表征惯性力和黏性力的量级之比。
应用: 管道内有压流动; 绕流问题。
§5.2.2 压力相似准则
ma l 2 2
惯性力和压力之比:
§5.3 量纲分析法
5.3.1 量纲知识 5.3.2 瑞利法 5.3.3 π定理
5.3.1 量纲知识
单位:计量事物标准量的名称。 量纲:物理量单位的种类。
物理量
单位
量纲
质量 g、kg、t….
M
时间 长度
s、 min、 h、
T
mm、 cm、 m、km… L
温度 速度
oC、 K、oF m/s、 km/h……
Θ [υ] 或dim υ
单位因数:103 →千, k; 106 →兆, M; 109 →吉, G; 103→毫, m; 106 →微, μ; 109 →纳, n;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
选ρ、V 、d等3个
第3步、将其余的物理量作为导出量,即 FD 、μ分别与基本 量的幂次式组成П表达式(参见如下例子)。
2020/6/2
13
[例] 粗糙管中粘性流动的压降:量纲分析一般步骤
经初步分析知道,在不可压缩牛顿粘性流体在内壁粗糙的直圆管定常流 动的压降Δp与下列因素有关:管径d、管长l、管壁粗糙度ε、管内流体密 度ρ、流体的动力粘度μ,以及断面平均流速v有关。分析压强降低与相关 物理量的关系。 解:
截面宽度
外流速度
距前缘距离
低雷诺数粘性流动
Rer 2300 区分粘性流动层流与湍流态
边界层外无粘流
Re 1
粘性力相似
边界层内以 Rer 50105为界区分 层流与湍流态
2020/6/2 有压管流、射流、绕流、流体机械中的流34动
1.列举物理量。Δp,V,d,ε,ρ,μ,l,共7个
p (,V , d, ,, l)
2.选择基本量:ρ、V、d
3.列П表达式求解П数(П数为无量纲数)
① П1=ρa V bd cΔp
2020/6/2
14
即 M 0 L 0 T 0 = (M L – 3 ) a (L T – 1 )b L c (M L –1 T – 2 )
一个流动过程中各物理量在量纲上存在相互制约关系,可以 按量纲齐次性原理作分析。
类比:角色分析
2020/6/2
11
一、П定理 提议用量纲分析的是瑞利(L.Reyleigh,1877),奠定理论基础的
是布金汉(E.Buckingham,1914):
Π定理
充要条件 方法
n个物理量
r个独立
基本量
选r个独立
2020/6/2
7
六、压力场
(二)运动流场中的压强分布
压强系数
Cp
p p0
1 2
v0 2
p0 为参考压强,v0 为参考速度。
1. 惯性力对压强分布的影响
2. 粘性力对压强分布的影响
2020/6/2
8
(二)运动流场中的压强分布
压强系数的正负是与参考压强(往 往是大气压)相比,绝对值的大 小是与来流的动能相比,从图中
2020/6/2
17
[*例] 三角堰泄流量:量纲分析解与解析解比较 不可压缩流体在重力作用下,从三角堰中定常泄流,求泄流量的表达式。 解:
1.列举物理量。Q ,ρ,g ,h , 共5个
Q (, g, h, )
2.选择基本量:ρ、g、h
3.列П表达式求解П数
① 1 a g bhcQ M0 L0 T0=(ML –3)a (LT–2 )bLc( L3 T–1 )
h h'
kl
l l' l * h h'
l * 称为相似准则数或无量纲边长。
2. 流动相似
①几何相似准则数: l l * b
② 运动相似准则数: v v * U
③ 动力相似准则数: F F * (Fi为惯性力) Fi
2020/6/2
28
四、相似准则数的确定
1. 量纲分析法
对不可压缩粘性流体的流动:ρ,V,l,μ,g,Δp,ω
2020/6/2
2
一、量纲与物理方程的量纲齐次性 1. 物理量的量纲
工程单位制
大小
单位制
国际单位制
物理量
长度
英
制
基本量纲
类别
量纲
导出量纲 量纲幂次式
SI制中的基本量纲: dim m = M , dim l = L , dim t = T
质量
长度
时间
导出量纲:用基本量纲的幂次表示。
2020/6/2
3
l 2v
优点:导出的相似准则数物理意义明确;
p
Eu v2 Sr l v
适用于未知物理方程的流动。
缺点:当无法判定控制流动的物理定律时不能运用。
2020/6/2
33
五、常用的相似准则数
1. Re 数(雷诺数)
V
l
圆管流动
平均流速
管直径
Re Vl
惯性力
粘性力
钝体绕流 平板边界层
Re 1
来流速度
(Vl
)(2xu*2*x
2u*x y*2
2u*x z*2
)
Sr
l
V
不定常惯性力
迁移惯性力
Fr2 V 2
惯性力
l g 重力
Re Vl 惯性力 粘性力
Eu
p0
V 2
压力 惯性力
2020/6/2
30
2. 方程分析法
优点:导出的相似准则数物理意义明确;无量纲方程既适用于 模型也适用于原型。 缺点:不能用于未知物理方程的流动。
1 s
2020/6/2
32
迁移惯性力 FI
(
m)v v s
l3V 2 / l V 2l 2
粘性力
Fv
dv
dn
A
Vl 2
l
Vl
重力
Fg ( m)g l3g
Re V
Fr2 V 2 lg
迁移惯性力
FI V 2l 2
压差力
Fp p A pl2
不定常惯性力
FIt
(
m)
v t
2020/6/2
10
二、量纲分析与П定理
量纲分析法主要用于分析物理现象中的未知规律,通过对有关的 物理量作量纲幂次分析,将它们组合成无量纲形式的组合量,用 无量纲参数之间的关系代替有量纲的物理量之间的关系,揭示物 理量之间在量纲上的内在联系,降低变量数目,用于指导理论分 析和实验研究。
量纲分析概念 一个方程中多项量纲必须齐次;
1
Vl
Re
2
V2 lg
Fr2
3
p
V2
Eu
4
l
V
St
雷诺数 佛鲁德数
欧拉数 斯特哈尔数
优点:适用未知物理方程的流动。
缺点:选准物理量较难,物理意义不明确。
2020/6/2
29
2. 方程分析法
以N-S 方程 x 方向的投影式为例
ux t
ux
ux x
uy
ux y
uz
ux z
fx
1
p x
(
常用量 速度,加速度 体积流量,质量流量 密度,重度 力,力矩 压强,压力,弹性模量 粘度系数 其他量 角速度,角加速度 应变率
2020/6/2
dim v LT 1 dim Q L3T 1
dim a LT 2 dim m MT 1
dim ML3
dim ML2T 2
dim F MLT 2
dim s ML2T 2 1 dim i dim e L2T1
5
2. 量纲齐次性原理
同一方程中各项的量纲必须相同。用基本量纲的幂次式表示时, 每个基本量纲的幂次应相等,称为量纲齐次性。
v2 z
p
常数
(沿流线)
2g g
dim
v2 2g
LT 1
2
LT 2
1 L
因此,每一个量的量纲,既可
Cp
p p0
1 2
v0 2
可以看出,上部形成负压,而且
速度越快,实际的升力作用越大,
车容易“漂”。同时前端的正压
力与后端的负压力形成较大的压
差阻力。
• 汽车与飞机绕流: 复杂物面的压强分布
2020/6/2
9
粘性流体动力学的无量纲特征参数的意义
粘性流体运动的基本方程是一个复杂的二阶非线性偏微分方 程,除少数特殊情况外,一般很难求得这一方程的解析解。为 了实用,人们往往根据问题在几何方面、动力学方面以及传热 学方面的特征对方程进行简化,目的是略去方程中的次要项, 保留主要项,然后对简化了的方程进行求解。 为了保证判断方程中哪些项可以略去,哪些项必须保留, 有必要把原有的方程无量纲化,这时在方程中出现一系列无量 纲参数,对这些无量纲参数的数量级进行比较,就可以决定方 程中各项的取舍。
流体力学
第五章 量纲分析与相似原理
卢志民
2020/6/2
1
★本章重点掌握:
❖ 了解物理量的基本量纲和导出量纲,量纲性质. ❖ 理解相似原理的三个基本定理的内容和意义,理解力学相
似的概念; ❖ 掌握量纲分析方法(瑞利法、π定理); ❖ 掌握用力学相似定义推导相似准则; ❖ 掌握用π定理简化函数关系,用π定理导出相似律 ❖ 相似理论及其应用(相似准则、模型实验设计)
3
d
(相对粗糙度)
④ П4 =ρa V bd c l (同上)
4
l d
(几何比数)
2020/6/2
16
4.列П数方程 即
1 f ( 2 , 3, 4 )
p f (Re, , l )
1 V 2
dd
2
或
p ( l )( v2 )
= F (ε /d, 1/Re)
g d 2g
这就是达西公式, 为沿程阻力系数,表示了等直圆管中流动流体的 压降与沿程阻力系数、管长、速度水头成正比,与管径成反比。
dim L ML2T 2
dim p dim dim K ML1T 2
dim ML1T 1
dim v L2T 1
dim T 1 dim xx dim T 1
dim T 2
4
惯性矩,惯性积 动量,动量矩 能量,功,热 功率 表面张力系数 比热 导热系数 (比)熵 (比)焓,内能
2ux x2
2ux y2
2ux z 2
)
令
ux*
ux V
,u
*
y
uy V
,uz*
