相似知识点总结
相似原理知识点总结归纳

相似原理知识点总结归纳相似原理是几何学中一个重要的概念,它在数学和物理学中都有广泛的应用。
相似原理描述了两个图形的形状和大小之间的关系,它帮助我们理解并解决许多几何问题。
在这篇文章中,我们将总结和归纳相似原理的相关知识点,包括相似三角形、相似多边形、相似图形的性质以及相似原理在实际问题中的应用。
一、相似三角形相似三角形是指具有相同形状但大小不一样的三角形。
当两个三角形的对应角度相等,而对应边长之间成比例时,我们就可以说这两个三角形是相似的。
具体来说,如果三角形ABC和三角形DEF满足以下条件:1.∠A = ∠D,∠B = ∠E,∠C = ∠F2. AB/DE = BC/EF = AC/DF那么我们可以得出三角形ABC和三角形DEF是相似的。
相似三角形有一些重要的性质:1. 相似三角形的对应角度相等,对应边长成比例。
2. 相似三角形的高、中线、垂直平分线和角平分线成比例。
3. 相似三角形的面积成比例,比例为边长的比值的平方。
利用相似三角形的性质,我们可以解决很多几何问题,比如计算三角形的边长、角度,求解高、中线、垂直平分线和角平分线的长度等。
二、相似多边形相似多边形是指具有相同形状但大小不一样的多边形。
当两个多边形的对应角度相等,而对应边长之间成比例时,我们就可以说这两个多边形是相似的。
具体来说,如果多边形A1A2...An和多边形B1B2...Bn满足以下条件:1. ∠A1 = ∠B1,∠A2 = ∠B2,...,∠An = ∠Bn2. A1A2/B1B2 = A2A3/B2B3 = ... = AnA1/BnB1那么我们可以得出多边形A1A2...An和多边形B1B2...Bn是相似的。
相似多边形有一些重要的性质:1. 相似多边形的对应角度相等,对应边长成比例。
2. 相似多边形的周长之比等于它们的任意一组对应边长之比。
3. 相似多边形的面积之比等于它们的任意一对对应边的平方比。
利用相似多边形的性质,我们可以求解多边形的边长、角度,计算面积等。
(完整版)相似知识点总结
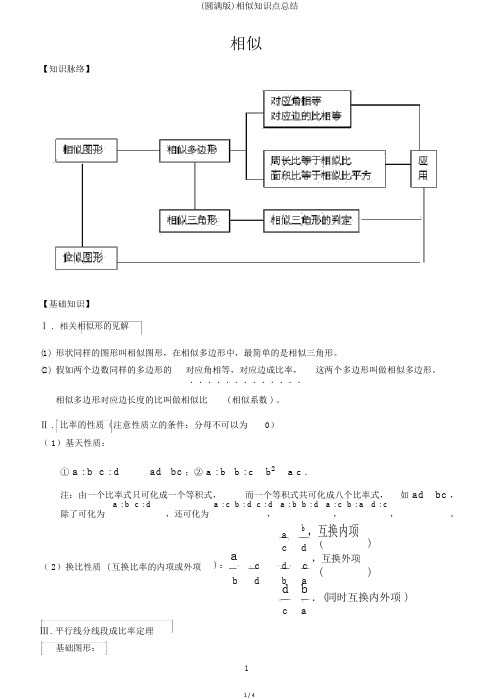
相似【知识脉络】【基础知识】Ⅰ . 相关相似形的见解(1) 形状同样的图形叫相似图形,在相似多边形中,最简单的是相似三角形。
(2) 假如两个边数同样的多边形的 对应角相等,对应边成比率, 这两个多边形叫做相似多边形。
.............相似多边形对应边长度的比叫做相似比 ( 相似系数 ) 。
Ⅱ . 比率的性质(注意性质立的条件:分母不可以为 0)( 1)基天性质:① a : b c : dad bc ;② a : b b : c b 2 a c .注:由一个比率式只可化成一个等积式, 而一个等积式共可化成八个比率式, 如 adbc ,除了可化为 a : b c : d ,还可化为 a : c b : d c : d a : b b : d a : c b : a d : c。
, , ,a b,互换内项)c d (( 2)换比性质 ( 互换比率的内项或外项 ) :ac d c ,互换外项 ( )bdbadb.(同时互换内外项 ) c aⅢ . 平行线分线段成比率定理基础图形:定理:如上图,三条平行线截两条直线, 所得的对应线段成比率.推论:平行于三角形一边的直线截其余两边(或两边的延伸线)所得的对应线段成比率.Ⅳ . 相似三角形( 1)见解:对应角相等,对应边成比率的三角形,叫做相似三角形。
相似用符号“∽” 表示,读作“相似于”。
相似三角形对应边的比叫做相似比( 或相似系数 ) 。
注:①对应性:即两个三角形相似时,必定要把表示对应极点的字母写在对应地点上,这样写比较简单找到相似三角形的对应角和对应边;② 次序性:相似三角形的相似比是有次序的;③ 两个三角形形状同样,但大小不用然同样;④全等三角形是相似比为 1 的相似三角形。
两者的差别在于全等要求对应边相等,而相似要求对应边成比率。
( 2)判断:依据相似图形的特点来判断。
(对应边成比率,对应角相等)①. 平行于三角形一边的直线 ( 或两边的延伸线 ) 和其余两边订交 , 所组成的三角形与原三角形相似;② . 假如一个三角形的两个角与另一个三角形的两个角对应相等, 那么这两个三角形相似;③. 假如两个三角形的两组对应边的比相等, 并且相应的夹角相等 , 那么这两个三角形相似;④ . 假如两个三角形的三组对应边的比相等, 那么这两个三角形相似;直角三角形相似判判断理 :直角三角形被斜边上的高分红的两个直角三角形和原三角形相似注:射影定理: 在直角三角形中,斜边上的高是两直角边在斜边上射影的比率中项。
数学相似知识点总结

数学相似知识点总结数学中的相似是指两个几何图形形状、比例和边长都相似的关系。
相似性质在几何学和代数学中有着广泛的应用。
本文将总结数学中的相似知识点,包括基本概念、相似三角形的性质和相似比的应用。
1. 基本概念在数学中,我们称两个图形相似,如果它们对应的角度相等,并且对应的边长成比例。
设有两个三角形ABC和DEF,若有以下条件满足,则两个三角形相似:1) ∠A = ∠D,∠B = ∠E,∠C = ∠F (对应角相等)2) AB/DE = BC/EF = AC/DF (对应边长成比例)2. 相似三角形的性质相似三角形有一些重要的性质,其中包括以下几点:1) 相似三角形的对应角度相等,对应边长成比例。
2) 相似三角形的对应边长比例相等,即若∆ABC ∼ ∆DEF,则AB/DE = BC/EF = AC/DF。
3) 相似三角形的高度、中线、角平分线等都成比例。
3. 相似比的应用相似比是指相似三角形中对应边长的比例关系。
它在解决实际问题中有着重要的应用,下面列举几个例子:1) 通过相似比解决测量问题:我们可以利用相似三角形的边长比例关系,通过已知边长和测量的长度,求出对应长度。
2) 通过相似比解决图像缩放问题:在计算机图形学中,我们可以利用相似比对图像进行缩放,使图像保持原来的比例和形状。
3) 通过相似比解决建模问题:在建筑和工程中,相似比可以用来对实际大小进行建模,从而进行设计和规划。
总结:相似性质是数学中重要的概念之一,它在几何学和代数学中都有广泛的应用。
相似三角形的性质和相似比的应用使我们能够更好地理解和解决实际问题。
通过相似性质,我们可以推断出一些未知信息,并应用到实际生活和学习中。
本文对数学中的相似知识点进行了总结,包括基本概念、相似三角形的性质和相似比的应用。
相似性质在解决几何和代数问题中起着重要的作用,并在实际生活中有很多实际应用。
深入理解相似性质,将有助于我们提高数学解题的能力和几何思维的发展。
生活中相似知识点总结

生活中相似知识点总结在我们的日常生活中,有很多相似的知识点。
这些知识点可能涉及到不同的领域,但它们之间可能存在着一些共同的特征或规律。
这些相似的知识点往往可以让我们更好地理解和应用到我们的生活中。
在本文中,我将总结一些生活中相似的知识点,并且探讨它们之间的联系和共同点。
一、时间和金钱的价值在生活中,时间和金钱都是非常重要的资源。
它们之间存在着很多相似的知识点。
首先,时间和金钱都是有限的资源。
无论是时间还是金钱,我们都需要在有限的资源内去做出选择,以满足我们的需求和欲望。
另外,时间和金钱都可以用来投资。
我们可以在时间和金钱上进行投资,以获取更大的回报。
而且,时间和金钱都是可以浪费的资源。
如果我们没有正确地管理和利用时间和金钱,那么我们就会浪费掉这些宝贵的资源。
另外,时间和金钱在一定程度上也是可以相互转化的。
有时候我们可以通过花费金钱来节省时间,也可以通过花费时间来赚取金钱。
这些都是时间和金钱之间的相似知识点。
二、健康和财富的管理健康和财富都是我们生活中非常重要的资源。
它们之间也存在着一些相似的知识点。
首先,健康和财富都是需要管理的资源。
我们需要通过一定的方式来管理我们的健康和财富,以保持它们的稳定和增值。
另外,健康和财富都是可以通过一定的投入来获取的。
我们可以通过花费时间和金钱来维护和增值我们的健康和财富。
而且,健康和财富在一定程度上也是可以相互转化的。
有时候我们可以通过花费一定的财富来保持健康,也可以通过保持健康来赚取更多的财富。
这些都是健康和财富之间的相似知识点。
三、社交和沟通的技巧在我们的社交和沟通中,也存在着一些相似的知识点。
首先,社交和沟通都是需要技巧的。
我们需要通过一定的方式去进行社交和沟通,以使得我们的交流更加顺畅和有效。
另外,社交和沟通也都是需要耐心和体谅的。
我们需要在社交和沟通中保持耐心,并且要善于体谅他人的立场和感受。
而且,社交和沟通在一定程度上也是可以相互促进的。
通过良好的社交,我们可以建立起良好的沟通关系,从而促进我们的交流和合作。
相似--知识点

第27章 相似-@>% )一图形的相似形状相同的图形叫作相似图形.二比例线段1.线段的比一般地,在同一单位下,量得两条线段a ,b 的长度分别是m ,n ,那么就说这两条线段的比是m ʒn ,记作a ʒb =m ʒn 或a b =m n.2.比例线段四条线段a ,b ,c ,d 中,如果a 与b 的比等于c 与d 的比,即a b =c d ,那么这四条线段a ,b ,c ,d 叫作成比例线段,简称比例线段.1.相似多边形的概念对应角相等,对应边的比相等的两个多边形叫作相似多边形.2.相似比相似多边形对应边的比称为相似比.3.相似多边形的性质相似多边形的对应角相等,对应边的比相等,周长的比等于相似比,面积的比等于相似比的平方.四相似三角形和相似多边形1.相似三角形的概念在әA B C和әA'B'C'中,如果øA=øA',øB=øB',øC=øC',A B A'B'=B C B'C'=A C A'C'=k,我们就说әA B C与әA'B'C'为相似三角形,记作әA B CʐәA'B'C',k为它们的相似比.2.相似三角形的判定定理(1)平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.平行于三角形一边的直线与其他两边的延长线相交时,此结论仍然成立.(2)如果两个三角形的三组对应边的比相等,那么这两个三角形相似.简单说成:三组边对应成比例,两三角形相似.(3)如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似.简单说成:两组边对应成比例且夹角相等,两三角形相似.(4)如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.简单说成:两组角对应相等,两三角形相似.3.相似三角形周长与面积的比(1)相似三角形周长的比等于相似比.(2)相似三角形面积的比等于相似比的平方.相似三角形对应中线的比㊁对应高线的比㊁对应角平分线的比都等于相似比.4.相似三角形的应用相似三角形在生产㊁生活中有着广泛的应用,如应用相似三角形可以间接地计算一些不易直接测量的物体的高度和宽度.解题的关键是找出相似的三角形,根据对应边成比例列出方程,建立恰当的数学模型来解决问题.五位似1.位似图形两个多边形不仅相似,而且对应顶点的连线相交于一点,对应边互相平行,像这样的两个图形叫作位似图形,对应顶点连线的交点叫作位似中心.2.位似变换的坐标在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k 或-k.3.位似图形的性质(1)位似图形上任意一对对应点到位似中心的距离之比等于相似比.(2)位似图形的对应线段的比等于相似比.(3)位似图形的周长比等于相似比.(4)位似图形的面积比等于相似比的平方.4.画位似图形的一般步骤(1)确定位似中心.(2)分别连接并延长位似中心和能代表原图的关键点.(3)根据相似比,确定能代表所作的位似图形的关键点.(4)顺次连接上述各点,得到放大或缩小的图形.。
相似图形的知识点总结(16篇)

相似图形的知识点总结(16篇)篇1:相似图形的知识点总结相似图形的知识点总结知识点1.概念把形状相同的图形叫做相似图形。
(即对应角相等、对应边的比也相等的图形)解读:(1)两个图形相似,其中一个图形可以看做由另一个图形放大或缩小得到.(2)全等形可以看成是一种特殊的相似,即不仅形状相同,大小也相同.(3)判断两个图形是否相似,就是看这两个图形是不是形状相同,与其他因素无关.知识点2.比例线段对于四条线段a,b,c,d ,如果其中两条线段的长度的比与另两条线段的长度的比相等,即(或a:b=c:d)那么这四条线段叫做成比例线段,简称比例线段.知识点3.相似多边形的性质相似多边形的性质:相似多边形的对应角相等,对应边的比相等.解读:(1)正确理解相似多边形的定义,明确“对应”关系.(2)明确相似多边形的“对应”来自于书写,且要明确相似比具有顺序性.知识点4.相似三角形的概念对应角相等,对应边之比相等的三角形叫做相似三角形.解读:(1)相似三角形是相似多边形中的一种;(2)应结合相似多边形的性质来理解相似三角形;(3)相似三角形应满足形状一样,但大小可以不同;(4)相似用“∽”表示,读作“相似于”;(5)相似三角形的对应边之比叫做相似比.知识点5.相似三角的判定方法(1)定义:对应角相等,对应边成比例的两个三角形相似;(2)平行于三角形一边的直线截其他两边(或其他两边的延长线)所构成的三角形与原三角形相似.(3)如果一个三角形的两个角分别与另一个三角形的两个角对应相等,那么这两个三角形相似.(4)如果一个三角的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似.(5)如果一个三角形的三条边分别与另一个三角形的三条边对应成比例,那么这两个三角形相似.(6)直角三角形被斜边上的高分成的两个直角三角形与原三角形都相似.知识点6.相似三角形的性质(1)对应角相等,对应边的比相等;(2)对应高的比,对应中线的比,对应角平分线的比都等于相似比;(3)相似三角形周长之比等于相似比;面积之比等于相似比的平方.(4)射影定理篇2:相似图形相似图形教学交流课教案:第四章相似图形教学目标:1、知道线段比的概念。
九年级数学相似的知识点

九年级数学相似的知识点1. 相似三角形:相似三角形是指具有相同形状但大小不同的三角形。
相似三角形的性质包括对应角相等、对应边成比例等。
通过相似三角形,可以解决一些几何问题,如计算不可测量的长度或距离。
2. 比例与相似:比例是指两个量之间的相对关系。
在相似三角形中,对应边的长度之比等于对应角的边之比。
比例与相似问题常用于解决物体的放大缩小、图形的变换等。
3. 相似多边形:相似多边形是指具有相同形状但大小不同的多边形。
相似多边形的性质包括对应角相等、对应边成比例等。
通过相似多边形,可以解决一些面积和体积比较的问题。
4. 黄金分割:黄金分割是指一条线段分割成两部分,较长部分与整体的比例等于整体与较短部分的比例。
黄金分割在艺术、建筑、设计等领域中广泛应用。
5. 图形的相似性变换:图形的相似性变换是指通过平移、旋转、镜像和缩放等变换操作使两个图形成为相似图形。
相似性变换常用于解决图形的构造、定位和证明问题。
6. 相似三角形的勾股定理:相似三角形的勾股定理是指在两个相似三角形中,两个直角边的平方的比等于两个斜边的平方的比。
7. 外接圆和内切圆:在相似三角形和相似多边形中,外接圆和内切圆分别是能够通过所有顶点(或顶点所在的边)的圆和能够被所有边(或边上的顶点)所切的圆。
外接圆和内切圆之间存在着一定的关系,如半径比例等。
8. 相似三角形的角平分线定理和中线定理:相似三角形的角平分线定理是指两个相似三角形中,两个对应角的角平分线也相似;相似三角形的中线定理是指两个相似三角形中,两个对应中位线也相似。
这些是九年级数学中与相似有关的知识点,希望对你有帮助!。
相似知识点

相似图形的相似1.定义:形状相同的图形叫做相似图形。
两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到。
2.成比例线段:对于四条线段a ,b ,c ,d ,如果其中两条线段的长度比与另两条线段的比相等,如a: b=c: d (或a/b=c/d)即ad=bc,,那么这四条线段a ,b ,c ,d 叫做成比例线段,简称比例线段。
a 、b 、c 、d叫比例的项,其中,a 、d 叫外项,b 、c 叫内项。
3.相似比:相似多边形对应边的比。
4.性质:相似多边形对应角相等,对应边的比相等。
相似三角形1.概念:对应角相等,对应边成比例的两个三角形,叫做相似三角形(相似符号为“∽”)。
2.推理:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。
注:全等一定相似,相似不一定全等(全等△是相似△中相似比为1时的特殊情况)。
3.三角形相似的判定 (1).定义判定:对应角相等、对应边成比例(2).判定1:两个角对应相等判定2:两边对应成比例且夹角相等判定3:三边对应成比例(3).Rt △相似的判定:(除上述三个外)斜边与一直角边对应成比例的两直角三角形相似。
4.三角形相似的判定定理推论推论一:顶角或底角相等的两个等腰三角形相似。
推论二:腰和底对应成比例的两个等腰三角形相似。
推论三:有一个锐角相等的两个直角三角形相似。
推论四:直角三角形被斜边上的高分成的两个直角三角形和原三角形都相似。
推论五:如果一个三角形的两边和其中一边上的中线与另一个三角形的对应部分成比例,那么这两个三角形相似。
推论六:如果一个三角形的两边和第三边上的中线与另一个三角形的对应部分成比例,那么这两个三角形相似。
ABC DE D E O B C5.(补充)射影定理:在Rt△ABC中,∠ACB=900,CD是斜边AB上的高,则AC2=AD·AB BC2=BD·AB CD2=AD·BD6.(补充)三角形的重心①概念:三角形三条中线的交点叫做三角形的重心;②三角形的重心与顶点的距离等于它与对边中点的距离的两倍。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相似
【知识脉络】
【基础知识】
Ⅰ. 有关相似形的概念
(1)形状相同的图形叫相似图形,在相似多边形中,最简单的是相似三角形。
(2)如果两个边数相同的多边形的
对应角相等,对应边成比例,.............
这两个多边形叫做相似多边形。
相似多边形对应边长度的比叫做相似比
(相似系数)。
Ⅱ. 比例的性质(注意性质立的条件:分母不能为0)
(1)基本性质:
①
bc ad d c b a ::;②2
::a b
b c b
a c .
注:由一个比例式只可化成一个等积式,而一个等积式共可化成八个比例式,
如bc ad
,除了可化为
d c b a ::,还可化为d b c a ::,b a d
c ::,c a
d b ::,c d a
b ::。
(2)换比性质(交换比例的内项或外项):
()()()a
b c d a c d c b
d
b a d b c
a
,交换内项,交换外项.同时交换内外项Ⅲ. 平行线分线段成比例定理
基础图形:
定理:如上图,三条平行线截两条直线,所得的对应线段成比例.
推论:平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例.
Ⅳ. 相似三角形
(1)概念:
对应角相等,对应边成比例的三角形,叫做相似三角形。
相似用符号“∽”表示,读作“相似于”。
相似三角形对应边的比叫做相似比(或相似系数)。
注:
①对应性:即两个三角形相似时,一定要把表示对应顶点的字母写在对应位置上,这样写比
较容易找到相似三角形的对应角和对应边;
②顺序性:相似三角形的相似比是有顺序的;
③两个三角形形状一样,但大小不一定一样;
④全等三角形是相似比为1的相似三角形。
二者的区别在于全等要求对应边相等,而相似要求
对应边成比例。
(2)判定:
根据相似图形的特征来判断。
(对应边成比例,对应角相等)
①.平行于三角形一边的直线(或两边的延长线)和其他两边相交,所构成的三角形与原三角
形相似;
②.如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似;
③.如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似;
④.如果两个三角形的三组对应边的比相等,那么这两个三角形相似;
直角三角形相似判定定理:直角三角形被斜边上的高分成的两个直角三角形和原三角形相似
注:
射影定理:
在直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项。
每
一条直角边是这条直角边在斜边上的射影和斜边的比例中项。
如图,Rt △ABC 中,∠BAC=90°,AD 是斜边BC 上的高,则AD 2
=BD ·DC ,AB 2
=BD ·BC ,AC 2
=CD ·BC 。
(3)性质:
相似三角形的性质:①相似三角形的对应角相等②相似三角形的对应边成比例
③相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比④相似三角形周长的比等于相似比⑤相似三角形面积的比等于相似比的平方(4)相似三角形的几种基本图形:
1)如图:称为“平行线型”的相似三角形(有“
A 型”与“X 型”图)
2)如图:其中∠1=∠2,则△ADE ∽△ABC 称为“斜交型”的相似三角形。
(有“反A 共角型”、
“反A 共角共边型”、
“蝶型”)
3)如图:称为“垂直型”(有“双垂直共角型”、“双垂直共角共边型(也称“射影定理型”
)”
“三垂直型”)
D
B
C
A
A
B
C
D E
1
2A
A
B
B
C
C
D
D
E E
124
1
2
E
C
A
B
D
E
A
B
C(D)
E
A
D
C
B
(1)
E
A
B
C
D
(3)
D
B
C
A
E (2)
C
D
E
A
B
4)如图:∠1=∠2,∠B=∠D ,则△ADE ∽△ABC ,称为“旋转型”的相似三角形。
Ⅴ. 位似
(1)如果两个图形不仅是相似图形,
而且每组对应顶点的连线都交于一点,
那么这样的两个图
形叫做位似图形。
这个点叫做位似中心,这时的相似比又称为位似比
注:
1)位似图形是相似图形的特例,位似图形不仅相似,而且对应顶点的连线相交于一点.
2)位似图形一定是相似图形,但相似图形不一定是位似图形.
3)位似图形的对应边互相平行或共线.
(2)位似图形的性质:
位似图形上任意一对对应点到位似中心的距离之比等于相似比。
注:位似图形具有相似图形的所有性质。
(3)画位似图形的一般步骤:
(详看例子)
B
E
A
C
D
12。
