大学物理,功和能及功能原理4.1 功 动能定理
大学物理第四章--功和能

a
l
xdx
2l
前已得出:
Af
mg(l a)2
2l
mg(l 2 a2 ) mg(l a)2 1 mv2
2l
2l
2
得v
g l
1
(l 2 a 2 ) (l a)2 2
§3 保守力的功与势能 一、 保守力
rB
B
两个质点之间的引力
B
第四章 功和能
§4.1 功 §4.2 动能定理 §4.3 保守力功与势能 §4.4 功能原理机械能守恒定律
§1 功和功率
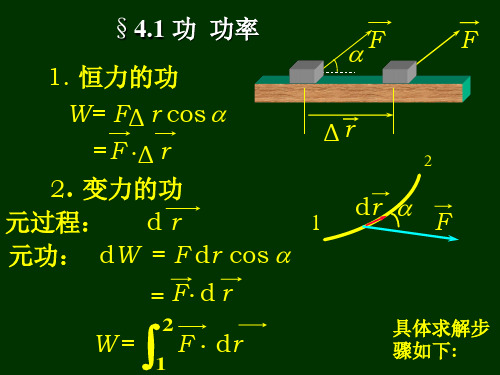
一、恒力做功 直线运动
A=Fcos S
记作A F S F r
F
F
M
M
S
位移无限小时:
dA
F
dr
dA称为元功
功等于质点受的力和它的位移的点积(标积)
例1一水平放置的弹簧,其一端固定,另一端系一小球,求小
球的位置由A到B的过程中弹力对它所做的功。(在O处弹簧无 形变)
解:根据胡克定律 F F kx
W F dr
xB Fdx
xA
xB xA
kxdx
O
1 2
A
k xB2
B
xA2
1 2
k xA2
作用在质点
上.在该质点从坐标原点运动到(0,2R)位
置过程中,力
F
对它所作的功为多少?
y
b
b
A a F.dr a (Fxdx Fydy)
R
x O
例4 如图,水平桌面上有质点 m ,桌面的摩 擦系数为μ 求:两种情况下摩擦力作的功
高校大学物理功和动能定理、势能、机械能守恒定律课件

o
x
描述矢量场基本性质的方程形式
通常:
L
f dl 0
普遍意义: 环流为零的力场是保守场, 如静电场力的环流也是零, 所以静电场也是保守场。
环流不为零的矢量场是 非保守场,如磁场。
二、势能
1.定义 令
A保 f 保 dl EPa EPb
a
b
即
o
3、万有引力做功的特点
A
Q
p
r dr r | dr | cos rdr
Gm 1m 2 A dr 2 r1 r Gm1m2 Gm1m2 ( ) ( ) r1 r2
r2
Q Gm1m2 F dr r dr 3 p r
y
P r1 r
M dr
F
N'
N
结论同前
o
r dr Q r2
x
共同特征:做功与相对路径无关,只与始末 (相对)位置有关。
一、定义保守力的两种表述
(1)一对力的功与相对移动的路径无关,而只决 定于相互作用物体的始末相对位置,这样的一对 力称为保守力 (如:万有引力、弹力、重力)
例1:质量为 m 的物体从一个半径为R的 1/4 圆弧型表面滑下,到达底部时的速度 为v,求A到B过程中摩擦力所做的功? 解1:功的定义 m o R 以m为研究对象,建 A 立自然坐标系,受力 n f 分析。 N 列切向受力方程: dv C F ma m dt dv mg B mg cos f ma m dt
AAB
B
视为恒力,直线
r3 r2 r1
A
F3
F2
A F dr
大学物理第3节 功与能 动能定理

结论:
r21
dr21
r1 r1
r21
r2
r21
r2
0 0
1)一对力的功与参考系无关。可以选择其中一个物体为 参考系。
2)若两个质点间没有相对运动或相对运动方向与作用力 方向垂直,则一对力的功为零。
§4-2 动能定理
本节内容:
4-2-1 质点的动能定理 4-2-2 质点系的动能定理
4-2-1 质点动能定理
只有一个质点时,合力的功等于各分力功的代数和。
5)在直角坐标系下功的计算:
dA (Fxi Fy j Fzk) (dxi dyj dzk)
dA Fxdx Fydy Fzdz
功率
P
dA
F dr
F v
dt dt
例:质量为0.1kg的r 质(5点/ ,3)t由3i静 2止j开始沿曲线
r
(5
/
3)t
3i
2
j
(SI)运动,在t=0到t=2s时间内,计算作用在该质 点上的合外力所做的功。
解:
方法2: 计算合外力的功可以用质点的 动能定理:
5t 2i
A
1 2
mb2
1 2
ma2
20J
4-2-2 质点系动能定理
两质 点系统m1, m2,外力 F1, F2
F1
F2
f12 , f21内力(一对力)
★功和动能与参考系的选择有关,但动能定理的形式都 相同。
S1,S2
路径
对质点1:
F1
dr1
f12
dr1
Ek1
f12 m1
s11
f21
m2
s2
对质点2: F2 dr2 f21 dr2 Ek2
大学物理课件第4章-功和能
如图,求船从离岸 x1处移到 x2 处的 过程中,力 F 对船所作的功.
F
解:判别F 是否为变力作功(大小不变,方
向变元),功属于dW变力作F功.建dx立坐F标,取dx元过co程sa
h
o x2
a
dx x x1 x
cosa x
x2 h2 x
dW F dx
x2 h2
功在数值上等于示功图
F
曲线下的面积。
3. 功率
0 x1
x2 x
dx
平均功率: P =ΔΔWt
瞬时功率:
P
= lim
Δt 0
Δ Δ
Wt =
dW dt
=
F
. dr
dt
= F .v
[ 例1 ] 有一单摆,用一水平力作用于m
使其极其缓慢上升。当θ 由 0 增大到 0 时,
求: 此力的功。
{
F T sinθ T cosθ mg
两边平方
v 2 v12
由动量守恒
2v1
v2
v 22
v
v1
v2
由机械能守 恒( 势能无变化)
v2
v12
v
2 2
v1 v2 0 两球速度总互相垂直
例8:已知半圆柱形光滑木凹槽,放在光滑桌面上,
如图,求质点下滑至最低点时给木块的压力.
解:
mv MV 0
•2.碰撞分类
正碰 斜碰
(从碰撞前后两球中心连线角度分类 )
弹性碰撞 非弹性碰撞 完全非弹性碰撞
一般非弹性碰撞
(从碰撞能量损失角度分类)
例7:在平面上两相同的球做完全弹性碰撞,其中一球开始时处于
大学物理第四章

解:利用功能原理:
A=DE
q
kF
m
Fl0tgq
=
1 2
k (l0 setq
- l0 )2
1 2
mv2
F
m
解得:
v=
2 m
Fl0tgq
-
1 m
k (l0 setq
-
l0
)2
[例13] 作业、p-55 功和能 自-20
一质量为m的球,从质量为M的圆弧
形槽中由A位置静止滑下,设圆弧形槽的半
径为R,(如图)。所有摩擦都略,试求:
+12 MV2
l
L
解得:
vr=
2(m +M) gR M
V= m
2gR M(m +M)
(2)小球到最低点B处时,槽滑行的距离。
∵ SFx = 0 ∴ DPx = 0
mvx = MVx
Am
m vxdt = M Vxdt
R
ml=ML
MB
l+L=R
L
=
mR m+M
lL
(3)小球在最低点B处时,槽对球的作用力;
1、动量: P
P = mv 2、第二定律:
F
=
dP dt
= ma
3、冲量: I
I
=
F t 2
t1
dt
4、动量原理
I = DP
5、力矩 M M = r × F
6、动量矩 L
L = r × P = r × mv
7、角动量原理:
t 2 t1
M dt
=
ω ω
2 1
J
dω
= Jω 2
功动能定理课件

汽车在启动和刹车过程中,会受到发动机或制动器产生的力和地面摩擦力的作用。通过 分析这些力对汽车运动的影响,可以得出汽车启动和刹车的动能定理表达式。通过该实 例,学生可以深入理解动能定理的基本概念和原理,并学会如何运用动能定理解析实际
问题。
04
动能定理的深入理解
动能定理与牛顿第二定律的关系
功动能定理ppt课件
contents
目录
• 功与能 • 动能定理 • 动能定理的实例分析 • 动能定理的深入理解 • 动能定理的拓展应用
01
功与能
功的定义
总结词
功是力对位移的累积效应。
详细描述
在物理学中,功被定义为力与物体在力的方向上移动的位移的乘积。公式表示 为:W = F × s。其中,W代表功,F代表力,s代表位移。
航天器轨道
动能定理可以用于分析航天器轨道的 稳定性和变化,如卫星轨道的偏心率 和近地点幅角的变化等。
THANKS
感谢观看
车辆动力学
动能定理在车辆动力学中有着广泛的 应用,如汽车、火车和飞机等交通工 具的运动分析。
机械能守恒
动能定理可以用于分析各种机械系统 中的能量守恒问题,如旋转机械、振 动系统和流体动力学等。
动能定理在科研中的应用
碰撞和冲击
动能定理在碰撞和冲击的研究中有着 重要的应用,如分析碰撞过程中的能 量损失和冲击响应等。
能守恒。
05
动能定理的拓展应用
动能定理在生活中的应用
自行车行驶
动能定理可以解释为什么自行车 行驶时会保持平衡,以及如何通 过改变速度和方向来控制自行车 的行驶。
滑板运动
动能定理可以解释滑板运动中滑 行速度和滑板质量的关系,以及 如何通过改变滑行速度和方向来 控制滑板运动。
功和能动能动能定理知识总结(最全)word资料

功和能动能动能定理知识总结(最全)word资料功和能、动能、动能定理知识总结归纳1. 能的概念:粗浅地说,如果一个物体能够对外界做功,我们就说物体具有能量。
能量有各种不同的形式。
2. 功和能关系:各种不同形式的能可通过做功来转化,能转化的多少通过功来量度,即功是能转化的量度。
3.动能定义:物体由于运动而具有的能叫做动能。
表达式:122:物体由于运动而具有的能叫做动能。
表达式:E mvk =注意:动能是状态量,只与运动物体的质量以及速率有关,而与其运动方向无关,能是标量,只有大小,没有方向,单位是焦耳(J )。
4. 动能定理的推导:设物体质量为m ,初速度为v 1,在与运动方向同向的恒定合外力F 作用下,发生一段位移s ,速度增加到v 2。
由F=ma 和联立解得:由和联立解得:F ma v v as Fs mv mv =-==-22122212212125.动能定理公式:末初W E E k k k ==-∆E注意:W 为合外力做的功或外力做功的代数和,ΔE k 是物体动能的增量;ΔE k 为正值时,说明物体动能增加,ΔE k 为负值时,说明物体动能减少。
6. 应用动能定理进行解题的一般步骤: (1)确定研究对象,明确它的运动过程;(2)分析物体在运动过程中的受力情况,明确各个力是否做功,是正功还是负功;(3)明确起始状态和终了状态的动能。
()用列方程求解总421W E E k k k ==-∆E【典型例题】例1. 用拉力F 使一个质量为m 的木箱由静止开始在水平冰道上移动了s ,拉力F 跟木箱前进的方向的夹角为α,木箱与冰道间的动磨擦因数为μ,求木箱获得的速度(如图所示)分析和解答:此题知物体受力,知运动位移s ,知初态速度,求末态速度。
可用动能定理求解。
拉力F 对物体做正功,摩擦力f 做负功,G 和N 不做功。
初动能动能,末动能E E mv k k 122012==,末动能初动能,末动能E E mv k k 122012== 由动能定理得:由动能定理得:Fs fs mv cos α-=122而:f mg F =-μα(sin )解得:v F mg F s m =--2[cos (sin )]/αμα注意:此题亦可用牛顿第二定律和运动学公式求解,但麻烦些,一般可用动能定理求解的,尽可能用此定理求解。
大学物理功和能课件讲义

解: 以雪橇、冰道和地球为一系统,由功能原理得
Af E2 E1
E2 E1 mgh
Af mg cos s' mgs mg(s's)
mg(s's) mgh
代入已知数据有 s h s' 500m
例4.5 一半径为 R的四分之一圆弧垂直固定于地面上,
止,距离为a. 在万有引力作用下,
两者距离变为b. 在此过程中,万有引
力做的功A=.
解: A Epa Epb
( Gm2 ) ( Gm2 )
a
b
Gm2 (a b)
ab
[思考]两者距离为b时的速率?
[例4-8] 质量为m的质点在指向圆心的力
F=k/r2 的作用下,作半径为r的
圆周运动,若取Ep=0,则系统的机
2. 力学中常见的势能函数
(1) 万有引力势能
由
Aab
(
Gm1m2 ra
) (
Gm1m2 rb
)
=
EPa-EPb
以r→∞时为万有引力势能零点,即令 EPy 0
由任一状态势能值的定义,可得 两物体相距r时的万有引力势能
EP引
EP引
Gm1m2 dr Gm1m2
r
r2
r
O
r
E
P引
G m1m 2 r
一、保守力的定义
1.万有引力的功 —与路径无关 rb
dr
dA以MF处G Md为rm原点rG,Mr2m
r0
dr
r2
dr r
M
r
ra m
(r0
r) r
GMm
r 2 dr
rb
A
rb
ra
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A Fdx, F ma
x1
x2
1 1 2 A mv mv 0 2 36J 2 2
d 2 x dv a 2 3t dt dt F ma 6t 2 3 2 A 6tdx 6t t dt 0 2 23
A dA F dr
a
b
F cos ds
a
b
功的计算主要在于把握对元功的分析。 不论力是在变还是位移的方向在变,我们都只 抓住在任一元位移中,它们都可视为不变的,因而 可写出元功,这叫做微元法。 12
4.1 功 动能定理
第4章 功和能
功能原理
在计算变力的功时,必须知道力随位移的函 数关系,但在有些情况下力的变化比较复杂,难 以找出这种固定的函数关系,使变力功的计算变 得复杂。 力对物体作功,其效果是使质点的运动状态 发生变化。 作功和物体状态变化有什么关系? 二、动能定理
A外 A内 Ek 即:外力的功与内力的功的代数
注意
和,等于质点系总动能的增量。 内力可以改变质点系的总动能。 16
4.1 功 动能定理
第4章 功和能
功能原理
在计算功的过程中特别要分清研究对象。
对质点有:
A Ai F合 dr
i (a )
(b)
即,合力作的功等于各力作功之和。 但对质点系: 写不出像质点那样的简单式子, 即,各力作功之和不一定等于合力的功。
dx 4t 2dt y 16t
y 16m y 32m dv y Fy m 0 dt
t 1s t 2s
A Fx dx Fy dy 320t 3dt 1200 J
1
2
28
f静
8
4.1 功 动能定理
3、功率
第4章 功和能
功能原理
A 平均功率: P t 瞬时功率:
dA F dr
例:某质点沿 x 轴作直线运动,受力为 F (4 5 x)i N , 求:质点从 x0 0 移动到 x 10m 的过程中该力所做 的功。
A dA P lim F v Fv cos t 0 t dt
dA 称为元功,
是指质点发生微小的位移过程中,力所作的功。
5
4.1 功 动能定理
2、变力曲线运动的功
第4章 功和能
功能原理
解决方法:微元积分法
dA F dr F cos | dr |
d r = ds
“化整为零,以直代曲,以恒代变,再求和”。 把路径分成许多微小的位移元; 在各段位移元上质点受的力可以看成是恒力, 在该微过程中的元功为: b dr
2
4.1 功 动能定理
重点:
第4章 功和能
功能原理
功、势能的概念及其计算; 功和能的基本规律(动能定理、功能原理、 机械能守恒定律)及应用 难点: 变力的功的计算;
势能概念的正确理解;
应用功能规律解题时,系统的划分和相应规律的 正确应用。
3
4.1 功 动能定理
第4章 功和能
功能原理
4.1
功 动能定理
729J
11
P F v 12t 3t 288W
2
4.1 功 动能定理
计算功的基本步骤:
第4章 功和能
功能原理
dA F dr
dA F cos dr F cos ds
建立坐标系; 在过程区间任选一元位移; 写出元功,分析变量关系; 积分计算功; 分析结果的物理意义。
18
4.1 功 动能定理
第4章 功和能
功能原理
1 3 例:一质量为 m = 2kg 的物体按 x t 2(m) 2
作直线运动。求:物体由 x1 = 2m 运动到 x2 = 6m 的过程中外力做的功。
方法二:功的定义
解: 方法一:动能定理
dx 3 2 t dt 2
x1= 2m, t = 0, v0= 0
1 p 2 Ek m v 2 2m
2
A Ekb Eka Ek
功和动能都与参考系有关; 动能定理仅适用于惯性系。
即:合力对质点所作的功,等于质点动能的增量。 注意
14
4.1 功 动能定理
明确几点: A Ek , 即:
第4章 功和能
功能原理
P2 P1
1 2 1 2 F dr mv2 mv1 2 2
4.1 功 动能定理
第4章 功和能
功能原理
1
4.1 功 动能定理
教学内容:
第4章 功和能
功能原理
4.1 4.2 4.3 4.4
功 动能定理 保守力及保守力的功 势能 势能曲线 势能梯度 功能原理 机械能守恒定律
教学基本要求 一、 掌握功的概念,能计算变力的功, 理解保守力作功的特点及势能的概念,会计算 万有引力、重力和弹性力的势能。 二、 掌握动能定理、功能原理和机械能 守恒定律,掌握运用守恒定律分析问题的思想 和方法。
b dr
0 90 ,
dA 0
a
P
F
90 180 , dA 0
90, F dr , dA 0
2) 功是过程量,是力对空间的积累作用。 一般来说,功的值与质点运动的路径有关。 (如摩擦力的功)
3)合力的功 各分力的功的代数和
A Fi dr Fi dr Ai
ds
P
F
由 a 移动到 b ,力的总功 等于各段上元功的代数和,
b
a
b
r
r
o
A dA F dr F cos ds
a
a
6
第4章 功和能 功能原理 4.1 功 动能定理 说明: dA F dr F cos | dr |
1)功是标量,没有方向,但有正负。
17
4.1 功 动能定理
第4章 功和能
功能原理
注意:内力能改变系统的总动能,但不能改变系统 的总动量。
因为内力总是成对出现,而一对作用力反作用 力的冲量为零,因而内力不能改变系统的动量。 但是由于质点系内各质点间可以有相对位移, 一般情况下,内力的功不一定为零,所以内力作功 可以改变质点系的总动能。 比如: 子弹射入墙中,墙对子弹的摩擦力作负功,而子 弹对墙的摩擦力不作功,所以 A内 0
4
4.1 功 动能定理 一、功
第4章 功和能
功能原理
力对质点所作的功: 力在质点位移方向的分量 与位移大小的乘积,即为力与质点位移的点积。
1、恒力直线运动的功:
A F cos | r | F Δr
位移无限小时:dA F dr
F
F
θ
Δr
dA F cos dr F cos ds = Fτ ds
13
4.1 功 动能定理
1、质点的动能定理
第4章 功和能
功能原理
dv Ft m A F dr Ft dr Ft ds, a a a dt b vb dv 1 1 2 2 A m ds m vd v m vb m va a va dt 2 2
b
b
b
动能(状态函数) 动能定理
第4章 功和能
功能原理
解: A
F dr Fdx (一维运动可以用标量)
dx F dt dt
t 0
F vdt
t
v v 0 adt 0 0
3 2 3 0 0
t 12t F dt dt 3t 2 0 2 m
3 4 3 0
A 12t 3t dt 36t dt 9t
i
7
4.1 功 动能定理
第4章 功和能
功能原理
4)在直角坐标系中功的解析式:
F Fx i Fy j Fz k
dr dxi dyj dzk
A dA F dr
a
b
A Fx dx Fy dy Fz dz
5)功的大小与参照系有关。 例如:传送带将箱子从低处 运到高处,地面上的人看摩 擦力作功了,而站在传送带 上的人看摩擦力没有作功。
4.1 功 动能定理
第4章 功和能
功能原理
例:质量为 10kg 的质点,在外力作用下做平面曲线 运动,该质点的速度为 v = 4t 2 i 16 j ,开始时 质点位于坐标原点。求:在质点从 y = 16m 到 y = 32m 的过程中,外力做的功。
d x 解: v x 4t 2 dt dy v y 16 dt dv x Fx m 80t dt
15
4.1 功 动能定理
2、质点系的动能定理 对第 i 个质点,有: 1 1 2 Ai mi v i mi v i20 2 2 1 1 2 Ai外 Ai内 m i v i m i v i20 2 2
第4章 功和能
功能原理
m1
ex Fi
in m i m2 Fi
1 1 2 2 A A m v m v 对质点系,有: i外 i内 i i i i0 2 2 质点系动能定理 Ai外 Ai内 Ek Ek 0
1)动能定理说明,做功可以引起物体动能的 变化,也可以说功是能量变化的量度。
2) 功是过程量,动能是状态量。 在计算复杂的外力作功时,只须求始末两态的 动能变化,即可求出该过程的功。
3) A 为合力做的功,而不是合力中某一个力 的功。动能定理中的速度必须相对同一个惯性系。
4) 通过作功,质点与外界进行能量交换。 动能是质点因运动而具有的做功本领。
