大学物理：3_1动能定理
大学物理-动能定理
4. 势能曲线
Ep (h)
E
Eh
Ep
o
H H h
重力势能
Ep
E
o
Ek
Ep
3-4 动能定理
Ep (x)
AE
B
Ek
Ep
o
x
弹性势能
Ek 0
x
引力势能
26
势能曲线的作用：
3-4 动能定理
（1）根据势能曲线的形状可以讨论物体的运动。
（2）利用势能曲线，可以判断物体在各个位置 所受保守力的大小和方向。
力提供园周运动的向心力而不做功，摩擦力做负
功使滑块动能减少。
W
1 mv2 2
1 2
mv0
2
(1)
34
3-4 动能定理
v2 N m
(2)
R
N m dv
(3)
dt
将式(2)代入式(3)，整理变形为
v2 dv dv d v dv R dt dt d R d
分离变量并积分，得
做功，它们所做元功之和为
dA fij dri f ji drj
因
fij f ji
mi
drji
dri
rij
rij drij
所以
fij
dA fij (dri drj ) fij drij
f ji m j drj
讨论：内力做功的特点
14
成对力的功
对它所作的功为零．
非保守力：力所作的功与路径有关． （例如摩擦力）
23
3. 势能
3-4 动能定理
哈里德大学物理第三章
注意
Fi内 0 I i内 0
i i
W
i
i内
0
二、变力的功
微元分析法：
ds dr
P
P
a
F
r
F r
o
b
取微元过程
以直代曲
以不变代变
再求和
§3-1 功 功率
ds
P
dr
P
r
a
F
r
F
o
b
元功： dW F dr F dr cosθ Fcosθds
F
M
m
r
r
o
以上这些力的共同特点？
保守力
1）做功与路径无关，只与起、末点位置有关；
2）做功等于与相互作用物体的相对位置有关的 某函数在始末位置的值之差。
势能
§3-2 保守力与非保守力 势能
二、保守力与非保守力
势能
1. 保守力与非保守力
• 做功与路径无关，只与起点、终点位置有关
b m L1 a
§3-2 保守力与非保守力 势能
保守力在 x 轴的分力，等于其相关势 能对坐标 x 的导数的负值:
F
dW F dr
x
Fx dx dEp x
m
θ
Fx
Fx
dEp x dx
§3-2 保守力与非保守力 势能
练习3：
一质量为 m 的人造地球卫星沿一圆形轨道运动，
§3-4 功能原理
1. 动能定理与功能原理的区别与联系：
功能原理是从动能定理推出的，完全包含在 动能定理之中； 由于保守力的功已反映在势能的改变中，运 用功能原理时，只需要计算非保守力的功， 而动能定理，则需要计算所有力做的功 。 2. 功与能的联系与区别： 功与能的单位与量纲相同； 功是过程量，能量是状态量； 功是能量传递和转化的一种方式和量度。
大学物理功-动能定理-保守力的功
解： 抛体在重力场中运动，
m g 是一恒量，
y
但m 的轨迹是一抛物线， 取一元位移d r
dr b
a
m g 与位移的夹角θ时时在变 在这一元段内写出元功
mg
x
dA Fdrmgdr
m gdscosmgdy
b
b
b
A
Fdr
a
Fcosds mg
a
a
dy
m g(ybya) 9
解：(1)建坐标系如图
l-a O
fμ m(lg x)/l l l μmg
A f afdra l (lx)dx μm(g lx)2l μm(g la)2
a x
2l
a 2l
注意：摩擦力作负功！ 21
(2)对链条应用动能定理：
l-x O
A＝ AP＋ Af 1 2m2v 1 2m0 2v
x
v0
0AP＋ Af
1m2v 2
x
A Pa lp d r a lm l x gd m x(l2 2 g l a 2 )
前已得出： Af
μm (gl a)2
2l
m(lg 2a2)μ m(lg a)21m2v
2l
2l
2
得 v
g l
1
(l2 a 2)μ (l a )22
13
3） A为合外力作功的代数和，不是合外力中某 一个力的功。动能定理中的速度必须相对同一 个惯性系。
4）通过作功，质点与外界进行能量交换。 如果 外力对物体做正功，质点动能增加； 如果 外力对物体做负功，质点的动能减少，
即物体克服外力作功，是以减少自身的动能为 代价。
所以，动能是物体因运动而具有的作功的本领。
动能定理原理
动能定理原理
动能定理是物理学中的一个重要定理，它描述了物体的动能与其速度的关系。
根据动能定理，一个物体的动能等于其质量与速度平方的乘积的一半。
动能定理可以表示为以下公式：
动能 = 1/2 ×质量 ×速度²
其中，动能用K表示，质量用m表示，速度用v表示。
根据动能定理，当一个物体的速度增加时，它的动能也会增加。
同样地，当一个物体的质量增加时，它的动能也会增加。
这说明物体的动能与其速度和质量直接相关。
动能定理的应用广泛。
在机械工程中，我们可以根据物体的动能来计算其所需的能量或者进行能量转化的分析。
在运动学中，我们可以利用动能定理来计算物体的速度或者质量。
在碰撞分析中，动能定理也起到了重要的作用。
需要注意的是，动能定理只适用于质点的分析，即只考虑物体的整体运动而忽略其形状和内部结构的影响。
在实际应用中，我们需要结合具体情况来确定使用动能定理的合理性与准确性。
总之，动能定理是一个重要的物理定律，在物体的运动分析和能量转化的研究中具有广泛的应用价值。
它为我们理解物体运动和能量转化的过程提供了重要的理论基础。
大学物理第二章动能定理
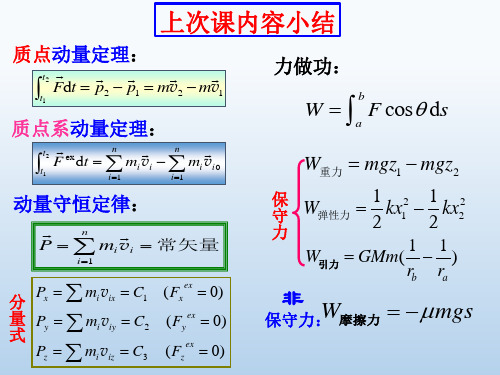
例题3. 如图，一轻绳跨过一定滑轮，两边分别拴有质量
为m及M的物体，M离地面的高度为h: (1)若滑轮质量及
摩擦力不计，m与桌面的摩擦也不计，开始时两物体均静
止，求M落到地面时的速度(m始终在桌面上); (2)若m与
桌面的静摩擦系数和滑动摩擦系数均为，结果又如何？
解：
m
(1)不计摩擦,系统(m,M,地球)机械能守恒:
v
m
0 M f c
f
s
s
Wf Wf 0
N
v c
N
WN WN 0
质点系动能定理：
质点系的动能的增量等于作用于质点系的一切外力与
内力做功之和.
W ex
W in
n i1
1 2
mi vi2
n i1
1 2
mi vi20
2.2.1 质点系动量定理
作用于质点系的合外力的冲量等于质点系动量的增量.
t2
系统内所有质点对同一参考点角动量的矢量和称为
质点系的角动量.
L Li ri pi ri mivi
i
i
i
dL dt
d dt
Li
i
Mi外
i
Mi内
i
0
M外
M 外
dL dt
积分得：
t2 t1
M外dt
L2
L1
注意：只有外力矩对质点系的角动量变化有贡献，
内力矩对质点系的角动量变化没有贡献.
W
F dr
l
F dr
acb
F dr
bda
0
a
c
F dr F dr F dr
acb
adb
bda
d
动能定理角动量定理
注意 1)守恒条件： M 0
能否为 Mdt 0 ?
2)与动量守恒定律对比：
当
F 0
时，
当
M
0
时，
p
恒矢量
L 恒矢量
彼此独立
《大学物理C》
第三章 刚体定轴转动
角动量守恒定律适用于以下情况：
(1)对于单一刚体：J、 均不变， 则匀速转动
(2) 对于系统: Ji、 均可以变化，但
角动量守恒
角动量守恒；
角动量守恒；
机械能不守恒 .
机械能不守恒 .
圆锥摆系统 动量不守恒； 角动量守恒； 机械能守恒 .
《大学物理C》
第三章 刚体定轴转动
注意：区分两类冲击摆
角动量守恒
(1)
O
l v0
m M
质点
质点 柔绳无切向力
➢水平方向： Fx = 0 ， px 守恒
mv0 = (m+M)v
➢ 对 O点：
解 碰撞前 M 落在
A点的速度
vM (2gh)1 2
碰撞后的瞬间, M、
N具有相同的线速度
N
u l
B
2
M
h
C
A
l/2 l
《大学物理C》
第三章 刚体定轴转动
角动量守恒
vM (2gh)1 2
u l
2
N
C
M h
A
B
l/2
l
解得
mvM
l 2
J
2mu
l 2
1 12
ml 2
1 2
ml 2
mvMl 2 ml 2 12 ml2
6m(2gh)1 2 2 (m 6m)l
演员 N 以 u 起 跳, 达到的高度
大学物理-第三章三大守恒定律
i
i
1 若质点系动量守恒，则动量在三个坐标轴上的分量都守恒。
2、在系统内质点间的碰撞，打击，爆炸过程中，内力很大，可 忽略重力、摩擦力等外力，可近似认为动量守恒。
上一页 下一页
3、虽然有时系统总动量不守恒，但只要系统在某个方向受 的合外力为0，则系统在该方向动量守恒。
即 F x 当 F ix 0 时 p x ， m iv ix 常量
mv1
得 F (0 .3 )22 0 32 0 2 2 0 3c0o 3 s()0 14 (N )51
0 .01
根据正弦定理
sm i 2 nvsiF n t() 18 ,即力的 v 夹 方 角 1向 6 。 为 2
上一页 下一页
例2-6质量为m=30kg的铁锤（彩电）从1m高处由静止下落，碰撞
Ixt1 t2F xd tpx2px1mx2 vmx1v Iyt1 t2F yd tpy2py1my2v my1v Izt1 t2F zd tpz2pz1mz2 vmz1v
4 . 对于碰撞、打等 击过 、程 爆， 炸物体互 之作 间用 的
称为冲力， 值其 大特 ， 点 变 t短是 化 ，峰 大 在， 某
b v2
d v
d(m v )
d p
t 2
Fm am
Fdtdp
dt dt
微分形式
dt
a
v1
I 定义 ：t1 t动2F 量 d ptp p 1 m 2d vp p 2 t 1 p 1 P 2m mv( 2v I2 t1t2v F1 d)t
（ M d)v M (d v ) d( v M d v u ) Mv
3-第3章 刚体力学基础
二、定轴转动定律
把刚体看作一个质点系
Fi
f i Δ m i a i
ri Fi ri f i Δ m i ri a i
加速度： a i a i a in
§3-2力矩 刚体定轴转动的转动定律
Mi
z M iz
Fi
Fi //
ri
mi Fi
(ri Fi ) (ri fi ) Δmi ri ai Δmi ri ai Δmi ri ain
§3-2力矩 刚体定轴转动的转动定律
M外z Miz ( mi ri 2 ) ( mi ri 2 )
i
i
i
若令
J z (mi ri 2 )
i
M 外z J z
绕定轴转动的刚体的角加速度与作用于刚体上的合外力矩成正比，与刚体的转
动惯量成反比。
注意：
——刚体定轴转动中的转动定律
（1）M和J均对于同一转轴而言；
1
2
合外力矩对定轴转动刚体所做的功等于刚体转动动能的增量。 ——刚体定轴转动时的动能定理
章目录 节目录 上一页 下一页
“十二五”普通高等教育本科国家级规划教材
大学物理学（第5版）
§3-3 刚体定轴转动的动能定理
四、机械能守恒定律
1、刚体的势能
EP mghc
m为刚体的总质量； hc为刚体质心的高度。
dm dx m dx O
r2 x2
l
dm x dx
l
x
J l x2 m dx 1 m x3 l
J 1 ml 2
J=
0
1 ml 2 3
l
1 12
3l
ml 2 m
0
l2 4
大学物理 第3章 刚体力学基础
2 1
Jd
1 2
J22
1 2
J12
2 Md (1 J2 )
1
2
力矩对刚体所做的功，等于刚体转动动能的增量。
例 如图所示，一根质量为m，长为l的均匀细棒OA，可绕固定点O在竖直平 面内转动.今使棒从水平位置开始自由下摆，求棒摆到与水平位置成30°角 时中心点C和端点A的速度.
F
·
F
式中为力F到轴的距离
F
若力的作用线不在转动在平面内，
则只需将力分解为与轴垂直、平行
r
的两个分力即可。
力对固定点的力矩为零的情况：
1、力F等于零， 2、力F的作用线与矢径r共线
（有心力对力心的力矩恒为零）。
力对固定轴的力矩为零的情况：
若力的作用线与轴平行 若力的作用线与轴相交
则力对该轴无力矩作用。
dJ R2dm
考虑到所有质元到转轴的距离均为R，所以细圆环对中心轴的转动惯量为
J dJ R2dm R2 dm mR2
m
m
(2)求质量为m，半径为R的圆盘对中心轴的转动惯量.整个圆盘可以看成许
多半径不同的同心圆环构成.为此，在离转轴的距离为r处取一小圆环，如
图2.36(b)所示，其面积为dS＝2πrdr，设圆盘的面密度(单位面积上的质量)
力矩在x,y,z轴的分量式，称力对轴的矩。例如上面所列
Ｍx , My , Mz , 即为力对Ｘ轴、Ｙ轴、Ｚ轴的矩。 设力Ｆ 的作用线就在Z轴
的转动平面内，作用点到Ｚ
轴的位矢为r，则力对Ｚ轴
的力矩为
M z rF sin
r sin F F rF sin rF
大学物理课后习题详解(第三章)中国石油大学
3-1 以速度0v 前进的炮车，向后发射一炮弹，已知炮车的仰角为θ，炮弹和炮车的质习题3-1图量分别为m 和M ，炮弹相对炮车的出口速率为v ，如图所示。
求炮车的反冲速率是多大?[解] 以大地为参照系，取炮弹与炮弹组成的系统为研究对象，系统水平方向的动量守恒。
由图可知炮弹相对于地面的速度的水平分量为v v '-θcos ，根据动量守恒定律()()v M v v m v m M '-'-=+-θcos 0所以 ()mM mv v m M v +++='θcos 0此即为炮车的反冲速率。
3-2 质量为M 的平板车，在水平地面上无摩擦地运动。
若有N 个人，质量均为m ，站在车上。
开始时车以速度0v 向右运动，后来人相对于车以速度u 向左快跑。
试证明：(1)N 个人一同跳离车以后，车速为NmM Nmuv v ++=0(2)车上N 个人均以相对于车的速度u 向左相继跳离，N 个人均跳离后，车速为()mM mum N M mu Nm M mu v v +++-++++=' 10[证明] (1) 取车和人组成的系统为研究对象，以地面为参照系，系统的水平方向的动量守恒。
人相对于地面的速度为u v -，则()()Mv u v Nm v Nm M +-=+0所以 NmM Nmuv v ++=0(2) 设第1-x 个人跳离车后，车的速度为1-x v ，第x 个人跳离车后，车的速度为x v ，根据动量守恒定律得()[]()()[]x x 1x 1v m x N M u v m v m x N M -++-=+-+-所以 ()Mm x N muv v ++-+=-11x x此即车速的递推关系式，取N x ,,2,1 =得Mm muv v ++=-1N NMm muv v ++=--22N 1N……………………()M m N muv v +-+=112 MNm muv v ++=01将上面所有的式子相加得()Mm muM m mu M m N mu M Nm mu v v ++++++-+++=210N 此即为第N 个人跳离车后的速度，即()mM mum N M mu Nm M mu v v +++-++++=' 103-3 质量为m =0.002kg 的弹丸，其出口速率为300m ，设弹丸在枪筒中前进所受到的合力800400x F -=。
动能定理教案大学
教学对象：大学物理专业学生教学目标：1. 理解动能定理的概念及其适用范围。
2. 掌握动能定理的推导过程及其应用。
3. 培养学生运用动能定理解决实际问题的能力。
教学重点：1. 动能定理的概念及其适用范围。
2. 动能定理的推导过程。
3. 动能定理的应用。
教学难点：1. 动能定理的推导过程。
2. 动能定理在复杂问题中的应用。
教学准备：1. PPT课件2. 动能定理相关习题教学过程：一、导入1. 复习动能的概念及其计算公式。
2. 引出动能定理，提出问题：如何理解动能定理？其适用范围是什么？二、讲授新课1. 动能定理的概念- 动能定理是描述物体动能变化与合外力做功之间关系的定理。
- 动能定理的数学表达式为：ΔE_k = W，其中ΔE_k表示动能的变化量，W表示合外力做的功。
2. 动能定理的适用范围- 动能定理适用于一切宏观物体，包括质点、刚体和弹性体。
- 动能定理适用于各种运动，包括匀速直线运动、匀加速直线运动、匀速圆周运动等。
3. 动能定理的推导- 以一个质点为例，推导动能定理的数学表达式。
- 分析合外力做功与质点动能变化之间的关系。
4. 动能定理的应用- 举例说明动能定理在解决实际问题中的应用。
- 分析动能定理在复杂问题中的应用，如变力作用下物体的运动。
三、课堂练习1. 学生独立完成PPT课件中的相关习题。
2. 教师解答学生提出的问题。
四、课堂小结1. 回顾本节课所学内容，总结动能定理的概念、适用范围、推导过程及应用。
2. 强调动能定理在解决实际问题中的重要性。
五、课后作业1. 完成课后习题，巩固所学知识。
2. 查阅资料，了解动能定理在实际工程中的应用。
教学反思：1. 本节课通过讲解、推导、应用等方式，使学生掌握了动能定理的概念、适用范围、推导过程及应用。
2. 在课堂练习环节，学生能够运用所学知识解决实际问题，提高了学生的实际操作能力。
3. 在教学过程中，注重培养学生的自主学习能力和创新思维，提高学生的综合素质。
大学物理 动能定理
表达式：合外力对物体所做的功等于物体动能的改变量，即W=ΔE
应用：动能定理可以用来解决许多实际问题，如机械能守恒、动能变化等问题
06
动能定理的注意事 项
动能定理适用条件
仅适用于质点，若为质点系则应将其各部分动能和势能分别求和 只有保守力做功才可用动能定理 公式中各物理量均应为同一惯性参考系中的量 动能定理既适用于直线运动，也适用于曲线运动
动能定理的应 用范围：适用 于一切宏观低 速运动的物体
动能定理的意 义：揭示了功 与能量变化之 间的关系，是 能量守恒定律
的特殊形式
动能定理中各物理量的含义
动能：物体由于运动而具有的能量，用符号E表示，单位为焦耳(J)。
势能：物体由于高度或弹性形变而具有的能量，用符号E表示，单位为焦耳(J)。
动能定理描述了物体动能的 变化与合外力做功的关系
动能定理是能量守恒定律在 力学中的具体表现
动能定理是解决力学问题的 重要工具之一
03
动能定理的表述
动能定理的数学表达式
动能定理的表 述：合力对物 体所做的功等 于物体动能的
变化量
数学表达式： 合外力对物体 所做的功等于 物体动能的变
化量，即 W=ΔE
表达式：动能定理的表达式为ΔEቤተ መጻሕፍቲ ባይዱW，其中ΔE表示物体动能的变化量，W表示物体 所受合外力做的功。
应用范围：动能定理适用于直线运动，也适用于曲线运动。
实例：以一个质量为m的物体在水平面上做匀加速直线运动为例，其受到的合外力为 F，位移为s，则根据动能定理可得Fs=ΔE，即合外力做的功等于物体动能的变化量。
动能定理在曲线运动中的应用
山东大学《理论力学》教案第13章 动能定理
第13章 动能定理一、目的要求1．对功和功率的概念有清晰的理解，能熟练地计算重力、弹性力和力矩的功。
2．能熟练地计算平动刚体、定轴转动刚体和平面运动刚体的动能，重力和弹性力的势能。
3．熟知何种约束反力的功为零，何种内力的功之和为零。
4．能熟练地应用动能定理和机械能守恒定律解动力学问题。
5．能熟练地应用动力学基本定理解动力学的综合问题。
二、基本内容1．基本概念力的功；质点和质点系的动能；动能定理；功率、功率方程、机械效率；势力场、势能、机械能守恒定律；动力学基本定理的综合应用。
2．主要公式微分形式 ∑==ni Fi W dT 1δ积分形式 ∑=-Fi W T T 12具有理想约束的质点系，其动能的改变（增量或对时间的一阶导数），等于作用于质点系的主动力的元功之和；在理想的约束条件下，质点系在某一段运动过程中起点和终点的动能改变量，等于作用于质点系的主动力在这段过程中所作的功的和。
三、重点和难点1．重点：（1）力的功和物体动能的计算。
（2）动能定理和机械能守恒定律的应用。
（3）动力学基本定理的综合问题。
2．难点：综合应用动力学基本定理求解动力学问题，运动学补充条件（方程）的提出。
四、教学建议1.教学提示（1）讲清力的功的一般形式，反复练习重力的功、弹性力的功和力矩的功的计算，搞清圆轮纯滚时摩擦力为什么不作功。
（2）在复习物理课程有关内容的基础上，熟练计算刚体系统的动能，强调动能表达式中的速度（角速度）一定用绝对速度（绝对角速度）；反复练习取整体为研究对象，用动能定理求运动的问题；强调用动能定理的积分形式可求解任何运动问题；强调用动能定理解题是以整体为研究对象。
（3）讲清动量、动量矩定理与动能定理的异同点。
通过练习，明确各定理适合求解的问题及解题特点。
（4）本章重点是动力学基本定理的综合应用，要多举各种类型的例子，把握“先求运动后求力”的解题思路，使学生熟练掌握。
强调求运动，可用动能定理，求力可用动量定理（质心运动定理）或达朗伯原理。
大学物理03-刚体力学基础
J
r
m
2
dm
• 刚体的形状（质量分布）
16
J
注 意
r
m
2
dm
只有对于几何形状规则、质量连续且均匀分布 的刚体，才能用积分计算出刚体的转动惯量
例3-2 一均匀细棒，质量为 m ，长为 l 。求该棒对下列转轴 的转动惯量：（1）通过棒中心且与棒垂直的轴；（2）通过 棒的一端且与棒垂直的轴。 解：取如图坐标，在棒上任取质元，到转轴的垂直距离为x， 长度为 d x，该质元的质量为 dm = (m/l )dx (质量为线分布)。 A L/2 C
S
O
Mz r d
P
F
M r F
O r
F
P
F
F //
大小： M rF sin Fd 方向： 由右手螺旋法则确定
转动平面
F 应该理解为外力在转动平面内的 分力F//
转动平面
在定轴转动中，M 的方向只有两种可能指向。若先选 定了转轴的正方向，则 M 与转轴方向一致时取正 值，反之为负值
11
(3) 如果有几个外力矩作用在刚体上，则合力矩等 于各个力矩的代数和
M
i i i
ri Fi
12
2
二 刚体绕定轴的转动定律
刚体可视为由许多质点组成的，而每一个质点都遵从质点力学 的规律。刚体转动定律可由牛顿第二定律直接导出。
Fi f i mi ai mi ri
一、力对转轴的力矩
力是引起质点运动状态变化的原因，而力 矩是引起转动物体运动状态变化的原因
(2) 外力F 不在转动平面内（任意力） 可将 F 分解为转动平面内的分力 F// 和垂直于转动平面的分力F F不能引起刚体转动状态的变化 力矩：
大学物理-第三章-动量守恒定律和能量守恒定律
20
★一对作用力与反作用力的功只与相对位移有关
f ji
ri
f ij
rij
rj
0
dW
jidWij
f
ji
dri
fij drj
f ji fij
fji f ji
(dd(rriidrrjj))
f ji
drij
S
S u
动量的相 对性和动量定 理的不变性
F(t)
t1 m
v1
光滑
v 2
m t2
参考系 t1 时刻 t2 时刻
动量定理
S系
S’系
mv1
mv2
m(v1 u) m(v2 u)
t2 t1
F (t )dt
mv2
mv1
5
例3-1: 作用在质量为1kg 的物体上的力 F=6t+3,如果物体在这
0＝m1(v1+v2)+m2v2
v2
m1v1 m1 m2
x
t 0
v2dt
m1 m1 m2
t 0
v1dt
L
t
0 v1dt
x m1L 0.8m m1 m2
负号表示船移动的方向与人前进的方向相反。
17
3-４ 动能定理
一、功的概念(work) 功率(power) 1、恒力的功
2、动能定理
2
1
或
F
dr
F
dr
1 2
mv22
大学物理-动能定理
xA yA zA zB
W = Wx + Wy + Wz
功的量纲和单位(焦耳 功的量纲和单位 焦耳) 焦耳
dim W = ML T ,1J = 1N × m
2 -2
第三章 动量守恒和能量守恒
5/12
物理学
第五版
3-4
动能定理
∆r
力对物体作做的功等于力在位移方向上的分量与该 位移大小的乘积作用下的功 The work on object by a force is equal to the product of the component of the force along the direction of the displacement & the magnitude of the displacement.
θi
F
*
dr θ
dr1 θ1 F 1 *
A
Fi
第三章 动量守恒和能量守恒
3/12
物理学
第五版
3-4
动能定理
讨论
1,功的正、负 功的正、 功的正
0 o < θ < 90 o ， d W > 0 o o 90 < θ < 180 ， d W < 0 θ = 90 o , F ⊥ d r , d W = 0
v1
dr
θ B
1 p 2 Ek = mv = 2 2m
第三章 动量守恒和能量守恒
2
F
v2
8/12
物理学
第五版
3-4
动能定理
质点的动能定理
(The theorem of kinetic energy of a mass point)
大学物理上公式总结(力学)(一)
大学物理上公式总结(力学)（一）引言概述：大学物理力学是物理学的基础课程之一，它涉及了许多重要的物理量和公式。
在本文档中，将对大学物理力学部分的公式进行总结和分析。
以下将以五个大点来归类和阐述这些公式，旨在帮助读者更好地理解和应用力学知识。
正文内容：一、运动学公式1. 位移公式：位移（s）等于速度（v）乘以时间（t）。
2. 速度公式：速度（v）等于位移（s）除以时间（t）。
3. 加速度公式：加速度（a）等于速度变化量（Δv）除以时间（Δt）。
4. 平均速度公式：平均速度（v）等于总位移（Δs）除以总时间（Δt）。
5. 平均加速度公式：平均加速度（a）等于速度变化量（Δv）除以总时间（Δt）。
二、力学公式1. 牛顿第一定律：物体在无外力作用下保持静止或匀速直线运动。
2. 牛顿第二定律：物体的加速度（a）等于作用在物体上的合力（F）除以物体的质量（m）。
3. 牛顿第三定律：任何两个物体之间的相互作用力大小相等、方向相反。
4. 重力公式：物体所受的重力（F）等于物体的质量（m）乘以重力加速度（g）。
5. 弹力公式：弹性力（F）等于物体的弹性系数（k）乘以物体的弹性形变量（x）。
三、动能与势能公式1. 动能公式：物体的动能（K）等于物体质量（m）乘以速度的平方（v²）再乘以0.5。
2. 势能公式（重力场）：物体在重力场中的势能（U）等于物体质量（m）乘以重力加速度（g）乘以高度（h）。
3. 动能定理：物体的净工作（功）等于物体的动能变化量（ΔK）。
4. 势能定理：物体的净工作（功）等于物体的势能变化量（ΔU）。
5. 机械能守恒定律：封闭系统中，机械能（E）等于动能与势能之和，保持不变。
四、动量与冲量公式1. 动量公式：物体的动量（p）等于物体质量（m）乘以物体的速度（v）。
2. 冲量公式：物体所受的冲量（J）等于物体的质量（m）乘以物体的加速度（a）乘以撞击时间（Δt）。
3. 动量定理：物体受到的总冲量等于物体的动量变化量。
大学物理第五讲 动量、动量守恒、功、动能和动能定理
0.3t)dt
0
36.45 (J)
24
二、质点的动能和动能定理
动能定理的推导
dA
r F
drr
F ds
ma
ds
m
dv dt
ds
mvdv
质点由a到b，力做总功为
Ek
1 mv2 2
r
r Fn
a• r
r F
•dsr
r F
• vb
b
va
Aab
b
dA
a
vb mvdv
M
LL
所以：
vr人车
vr人
m M
vr人
M M
m
vr人
12
t
M m t
0 v人车dt M 0 v人dt
vr人车
M M
m
vr人
L M mx x M L
M
M m
vr车
m M
vr人
v车
v人
m
x
M
X v车dt M v人dt
o
m x m L
M
(mvr )
1
r mv1
x
1
mvr2
7
二、质点系的动量定理
rr 设质点系中第 i 个质点受内力和外力分别为 fi 和Fi ,
应用质点动量定理
r ( Fi
r fi )dt
d
(mi
r vi
)
对整个系统求和
r r (Fi fi )dt d
大学物理动能定理思政教案
课时安排：2课时教学目标：1. 知识目标：理解并掌握动能定理的基本概念、公式及其应用。
2. 能力目标：培养学生运用动能定理解决实际问题的能力，提高学生的科学思维和创新能力。
3. 思想道德目标：通过学习动能定理，培养学生的爱国主义精神、严谨的科学态度和团队合作意识。
教学重点：1. 动能定理的基本概念和公式。
2. 动能定理在解决实际问题中的应用。
教学难点：1. 动能定理的理解和运用。
2. 思想道德教育融入教学过程。
教学过程：一、导入1. 利用多媒体展示我国航天事业取得的辉煌成就，如嫦娥五号、天问一号等，激发学生的民族自豪感和爱国情怀。
2. 引入物理学家牛顿、伽利略等人物，介绍他们在物理学领域的重要贡献，激发学生对科学研究的兴趣。
二、新课讲授1. 讲解动能定理的基本概念：动能定理是描述物体在运动过程中动能变化与所受合外力做功之间关系的定律。
2. 推导动能定理的公式：F合·s=ΔEk，其中F合表示合外力，s表示物体位移，ΔEk表示动能的变化。
3. 通过实例讲解动能定理的应用，如汽车刹车、弹簧振子等。
三、思想道德教育融入教学过程1. 结合我国航天事业的发展，引导学生思考：是什么力量推动了我国航天事业的快速发展？答案：是科技创新、团结协作、坚持不懈的精神。
2. 通过分析牛顿、伽利略等物理学家的事迹，教育学生要树立严谨的科学态度，勇于探索未知领域。
3. 强调团队合作的重要性，鼓励学生在学习过程中相互帮助、共同进步。
四、课堂练习1. 给出几个实际问题，让学生运用动能定理进行求解，巩固所学知识。
2. 学生分组讨论，针对实际问题提出解决方案，培养学生的创新意识和团队协作能力。
五、总结1. 总结动能定理的基本概念、公式及其应用。
2. 强调思想道德教育的重要性，引导学生树立正确的价值观。
教学反思：1. 本节课通过引入我国航天事业的发展，激发了学生的民族自豪感和爱国情怀，将思政教育融入教学过程。
2. 通过实例讲解动能定理的应用，提高了学生的科学思维和创新能力。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
力的空间累积效应:
F
对
r
积累
2.3 能量守恒定律
W，动能定理.
一功
力对质点所作的功为力在质点位移方向的分量与
位移大小的乘积 . （功是标量，过程量）
dW
F
cos
dr
F cosds
dW F dr
dri
i
B
*
dr Fi
dr1*A1
F1
F
2.3.1 功 动 能 定 理
注意
内力可以改变质点系的动能
2.3.1 功 动 能 定 理
2.3 能量守恒定律
例：一质量为M的小车与地面光滑接触，初始 静止，一质量为m物体以初速度v0滑到小车上， 物体与小车间摩擦系数为，小车长为d，当 物体碰到小车前挡板时速度为v，此时小车移 动了距离为l。试问系统动量守恒吗？动能守 恒吗?
2.3.1
dr
2.3 能量守恒定律
F cos
W
B F dr
B
F cosdr
A
A
r
合力的功 = 分力的功的代数和
W
Fi
dr
Fi
o
dr
rA dr
Wi i
rB
F
Fxi
Fy
j
Fz k
dr dxi dyj dzk
W Fxdx Fydy Fzdz
W Wx Wy Wz
2.3.1 功 动 能 定 理
2.3 能量守恒定律
平均功率 瞬时功率
P A t
P lim
A
dA
F
v
t0 t dt
P Fvcos
P
dA
M
d
M
dt
dt
2.3.1 功 动 能 定 理
2.3 能量守恒定律
例：质量为m的物体放在水平桌面上，
物体和桌面的摩擦系数为 ，物体在
外力作用下沿半径为R圆由a运动到b，
F
2.3.1 功 动 能 定 理
动能（状态函数）
2.3 能量守恒定律
Ek
1 mv2 2
p2 2m
动能定理
合外力对质点所作的功, 等于质点动能的增量 .
A Ek2 E k1
注意
功和动能都与 参考系有关；动能定理
仅适用于惯性系 .
2.3.1 功 动 能 定 理
2.3 能量守恒定律
质点系统动能定理
2.3 能量守恒定律
例：质量为m的物体以一初速度v0切入一个 固定在光滑桌面上半径为R的半圆屏障，并
沿屏障运动，已知m与屏障之间的摩擦系数
为 ，试求质点沿屏障由a点运动到b点的
过程中摩擦力所作的功。
a
f a
m
m
v0
Nn
b
b
这是物体在变力作用下求功的例子
2.3.1 功 动 能 定 理
2.3 能量守恒定律
二 动能定理
B B
A A F dr A F dr cos Ftds
Ft
m
dv dt
A
B
m
dvds
v2 mvdv
A dt
v1
1 2
mv22
1 2
mv12
dri
B
i *
dr Fi
dr1*A1
F1
2.3.1 功 动 能 定 理
2.3 能量守恒定律
几点说明:
1、功是标量。 功没 有方向，但有正负 dW F dr
0 90, dW 0
90 180 , dW 0
90
F
dr
dW 0
２、功是个过程量
３、功是个相对量
2.3.1 功 动 能 定 理
2.3 能量守恒定律
３、一对作用力和反作用力的元功：
移动了半个圆周，求在这一过程中摩擦 力的功。
这是力的大小不变，物体沿曲线运 动的例子
2.3.1 功 动 能 定 理
2.3 能量守恒定律
例：设作用于质量m=2kg的物体上的力 F=6t(F的单位为N，t的单位为s），如 果物体由静止出发沿力的作用方向作直 线运动，求在头2s的时间内，这个力做 了多少功？
每一个质点都满足动能定理，则都有
A1
1 2
m1v12
1 2
m1v120
Ai
1 2
mi vi2
1 2
mi vi20
以上各式左
右分别相加
Ai
1 2
mi vi2
1 2
mi
vi20
2.3.1 功 动 能 定 理 质点系动能定理：
2.3 能量守恒定律
A A内 A外 Ek Ek0 E
质点系动能的增量等于作用在系统内各质点 的力（包括内力和外力）所做的功的代数和
dA f b d r ab
mB
mA fA
rAB rA
fB
rB o
2.3.1 功 动 能 定 理
2.3 能量守恒定律
力矩的功
dA F dr F (d r ) d (r F)
d M M d
A dA 0 M d
力矩所做的功就是产生力矩的力所做的功，只不 过是用角量表示而已。